Abstract
The potential involvement of polysulfide radical anions Sn•− is a recurring theme in discussions of the basic and applied chemistry of elemental sulfur. However, while the spectroscopic features for n = 2 and 3 are well-established, information on the structures and optical characteristics of the larger congeners (n = 4–8) is sparse. To aid identification of these ephemeral species we have performed PCM-corrected DFT calculations to establish the preferred geometries for Sn•− (n = 4–8) in the polar media in which they are typically generated. TD-DFT calculations were then used to determine the number, nature and energies of the electronic excitations possible for these species. Numerical reliability of the approach was tested by comparison of the predicted and experimental excitation energies found for S2•− and S3•−. The low-energy (near-IR) transitions found for the two acyclic isomers of S4•− (C2h and C2v symmetry) and for S5•− (Cs symmetry) can be understood by extension of the simple HMO π-only chain model that serves for S2•− and S3•−. By contrast, the excitations predicted for the quasi-cyclic structures Sn•− (n = 6–8) are better described in terms of σ → σ* processes within a localized 2c-3e manifold.
1. Introduction
Polysulfide radical anions Sn•− (n = 2–8) play a pivotal role as intermediates in the sulfur ↔ sulfide redox cycle [1,2,3,4]. The influence of these short-lived species is frequently invoked in contemporary investigations of sulfur chemistry, including alkali-metal-sulfur batteries [5,6,7], organic syntheses [8], biological chemistry [9,10], geochemical processes involving metal transport [11,12,13] and quantum-dot sensitized solar cells [14,15]. In solution, polysulfide radical anions are readily oxidized by atmospheric oxygen, but the smaller members can be trapped in an aluminosilicate matrix and are known to be the chromophores in yellow (S2•−), blue (S3•−) and green (simultaneous presence of S2•− and S3•−) ultramarines [16] and related sodalite-group minerals [17]. The diatomic S2•− and the triatomic S3•− (C2v) radical anions are readily detected in solution or in the solid state by their characteristic UV-visible, Raman or EPR spectra [18]. Indeed, one or more of these techniques is commonly invoked to provide evidence for the role of S3•− as an in-situ generated reagent in organic synthesis [8].
In contrast to the well-established spectroscopic signatures of S2•− and S3•−, evidence for the larger members of the family (n = 4–8) is fragmentary and often conflicting. Of these species, S4•− has a long but somewhat checkered history. In 1970, as part of his pioneering study on solutions of alkali-metal polysulfides in electron-pair donor solvents, e.g., DMF, HMPA, Seel attributed a visible absorption at ca. 515 nm to S4•− [19], but later the band was reassigned to a dimer [20], an example of which has recently been structurally characterized in a dinuclear Bi(III)Bi(III) complex [21]. In 1983 Clark et al. investigated the nature of the sulfur chromophore in ultramarine pink by Raman spectroscopy [22], but they were unable to distinguish between S4 and S4•− (or even S3Cl). The association of a 490 nm band with S4•− has nonetheless persisted [9,23], and Chiba and co-workers have recently invoked formation of the radical anion during the photolysis of the closed-shell dianion S42− [24,25,26,27]. The use of other techniques to identify S4•− in solution, notably Raman and IR spectroscopy [28,29,30], has been pursued, but band assignments based on calculated vibrational frequencies have been questioned [3]. Likewise, an EPR signal observed in solutions of lithium polysulfide solutions in DMF was proposed to belong to S4•− [31], but the isotropic g-value (2.031) lies close to that of the dominant radical anion S3•− (2.029) [32]. In principle, high field EPR spectroscopy could be used to distinguish between these (and other) polysulfide radical anions, and on this basis Chukanov et al. recently suggested the presence of S4•− in various sodalite minerals [33].
The larger anions Sn•− (n = 5–8) are also acknowledged as potentially important intermediates in the S8 ↔ S2− redox processes, as in the electrochemical reduction of cyclo-S8, redox transformations in alkali metal-sulfur batteries [27] and the formation of polysulfides from photoexcited quantum dots [14,15]. Exploration of the stepwise electrochemical reduction of cyclo-S8 in non-aqueous solvents has been extensively pursued, with formation of S82− generally accepted by the battery community to occur first (Scheme 1) [3]. Initially, in 1970, Merritt and Sawyer claimed the preliminary formation of the one-electron reduction product S8•− [34], then revised this interpretation to a two-electron transfer [35], in agreement with the work of Bonnaterre and Cauquis [36] and also supported by results obtained by Hardacre and coworkers using ionic liquids as the solvent medium [37]. However, in 2008, the results of a detailed cyclic voltammetric study of the reduction of S8 in various solvents were consistent with the formation of S82− via two consecutive one-electron steps [38]. The potential for the involvement of S4•− in the S8 reduction process has been argued [39,40,41,42], but in the absence of a clear spectroscopic signature for the anion, the issue has not been resolved. Although symmetrical dissociation of S82− to give two S4•− radical anions is calculated to be exergonic [43], and an absorption band at ca. 700 nm was assigned to S4•− [44,45] in spectrochemical studies of the reduction of sulfur in DMSO and DMF, others insist that it has never been detected [46].
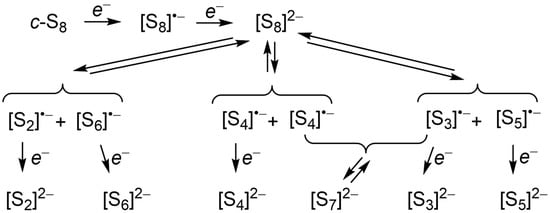
Scheme 1.
Possible radical anion intermediates in the stepwise electrochemical reduction of c-S8.
Surprisingly, although the preparation and structural characterization of several salts of the S82− were reported more than 30 years ago [47,48], there is limited information on the behavior of ion-separated salts of S82− in non-aqueous solvents. Formation of S82− from S8 has traditionally been interpreted to be followed by disproportionation to S62− and ¼S8 [39,43,49], the former dissociating to afford S3•− [48]. However, a disproportionation process simply represents a mass balance, and belies the reality that the formation of an eight-membered S8 ring must involve the intermediacy of long chain polysulfide dianions Sn2− with n > 8 and, possibly, polysulfide radical anions such as Sn•− (n = 4, 6) [3]. Alternative fates for S82− in dilute solution can be envisaged (Scheme 1) in terms of equilibria involving its symmetric and asymmetric dissociation to afford, in principle, the entire series of polysulfide radical anions Sn•− (n = 2–6). Longer chain closed-shell dianions such as S102− and S122−, salts of which have recently been characterized [50,51], can then be viewed as arising from the reverse process, that is, symmetric coupling of the radical anions S5•− and S6•−, respectively, while association of S3•− and S4•− yields S72−. Unfortunately, information on the electrochemical reduction of the cyclic allotropes S6 and S7 is lacking. That being said, in 2002 Dehnicke and coworkers isolated and structurally characterized crystals of the (orange/red) radical ion salt [Ph4P][S6], the only such characterization of an ion-separated salt of a polysulfide radical anion [52]. The importance of this result is discussed below.
As demonstrated in this brief survey, there are many unsettled questions regarding the basic chemistry of elemental sulfur, in particular relating to the stability, structure and properties of radical ion products that may be generated during the sequential reduction of cyclo-S8 or the oxidation of the sulfide ion S2− [1]. These questions have given rise to ongoing controversies, many relating to the colors of these ephemeral species—what do they look like, and do they exist if they cannot be seen?
While the colors of S2•− and S3•− are well characterized, the optical properties of the larger putative polysulfide radical anions have been explored only to a very limited extent. Fabian et al. used density functional theory (DFT) methods to probe the excited states of S4•−, and predicted a strong absorption in the near-IR region, with a weaker band near 350 nm for cis S4•−(C2v) isomer, which is slightly more stable than the trans (C2h) isomer [53]. More recently, and using DFT and CASSCF methods, Rejmak confirmed that the cis S4•− radical anion could be identified by a strong absorption in the near-IR region [54] and proposed that the red chromophore in ultramarine red is neutral S4 rather than the corresponding radical anion. Surprisingly, the excited state properties of the remaining radical ions in the series, that is Sn•− (n = 5–8), have never been explored theoretically, perhaps because even their ground state geometries have remained somewhat of a puzzle.
The principal objective of the present article is to redress this issue, to fill in the blanks not only in regard to the spectroscopic signatures of these radical anions, that is, their excited state properties, but also to establish their ground state structures, particularly in solution in polar solvents, the media in which they are most likely to be generated.
2. Results
2.1. Structural Trends
In the following sections we describe the structural features and relative energies provided by spin unrestricted PBE0/D3/def2-QZVP calculations for the family of radical anions Sn•− (n = 4–8). The results build upon the earlier systematic studies of Hunsicker et al. [55], Steudel [40] and Wong [56], but include several alternative shapes not previously considered. The possible effects of solvation are heavily stressed, as our overall aim has been to identify structures most likely to be present in solution in the polar solvents typically used for the spectroscopic observation of these species. To this end we performed not only standard “gas phase” geometry optimizations but also optimizations employing the polarized continuum model (PCM) to simulate solvation effects, with DMF (ε = 37.2) serving as a representative example. As observed by Steudel, the inclusion of solvation using the PCM approach leads to only minor geometrical adjustments, and for this reason only the “gas phase” structural parameters are presented in the main text (see Figure S1 for PCM-adjusted numbers). Solvation effects, however, have important energetic consequences, favoring structures with large molecular dipoles, and can play a pivotal role in adjusting the balance between structural alternatives which are otherwise closely matched energetically.
2.1.1. S2•− and S3•−
Like molecular oxygen, the diatomic molecule S2 possesses a triplet ground state [57]. Addition of an electron to one of the two half-filled πg* orbitals, to afford the 2Πg radical anion S2•−, leads to an elongation of the S–S bond, calculated here = 1.996 Å. Attachment of a third sulfur introduces the possibility of structural options for S3•−, namely linear (D∞h), equilateral and isosceles triangular (D3h and C2v, respectively); the last is established as the energetically preferred. Structural parameters calculated here for the 2B1 state, an S–S bond distance of 1.984 Å and inter-bond angle of 115.7°, are consistent with previous estimates [58,59].
2.1.2. S4•−
Based on both experimental and theoretical evidence [48,49,60] the geometry of a discrete neutral S4 molecule displays C2v symmetry, consisting of a planar broken-ring structure with one “long” S–S bond, calculated here = 3.222 Å. The most appealing option for the corresponding S4•−anion is also a planar C2v structure (Figure 1a), akin to the neutral form but with the “long” S–S bond further stretched (calculated here = 3.505 Å). However, a C2h isomer (Figure 1b), generated from the C2v by a 180° rotation about the central S–S linkage, is also possible.
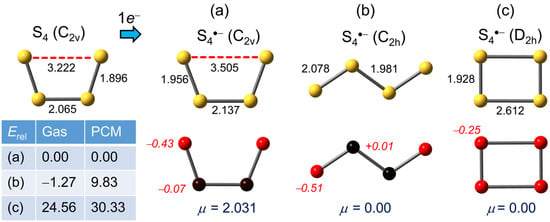
Figure 1.
(U)PBE0/D3/def2-QZVP optimized geometries (distances in Å) for S4•−, with Mulliken charges (in italics) and dipole moments μ (in Debye). Relative gas phase and PCM (=DMF) corrected total energies Erel are in kJ mol−1.
Frequency calculations confirm that both the C2v (cis) and C2h (trans) forms are true energetic minima, the latter being slightly more stable in the gas phase. But the energetic competition between the two ceases upon inclusion of PCM (=DMF) solvation, with the centrosymmetric (μ = 0) C2h isomer rising relative to the C2v form by nearly 10 kJ mol−1. The presence of both isomers in solvents with a low dielectric constant may nonetheless be possible. Other structures, based on closed rings, have been explored by previous workers and found to be energetically much more high-lying. Re-examination here of these variants, none of which represents a true energetic minimum, indicates the centrosymmetric (μ = 0) D2h modification (Figure 1c), formed by a Jahn–Teller distortion of a putative D4h geometry [61], is the most stable of the closed-ring group, although it still lies well above the C2v form and, with the inclusion of PCM, its relative energy rises even higher.
2.1.3. S5•−
While the structure of neutral S5 is unknown, an open envelope-like or chair shape with Cs symmetry has been predicted in previous studies [62,63], with the S–S bond bisected by the mirror plane slightly elongated. We concur with this result, and calculate the unique S–S distance = 2.157 Å. The apparent weakening may be attributed, in valence bond parlance, to lone-pair repulsion arising from the eclipsed alignment of the two neighboring S–S bonds. One-electron reduction to the radical anion S5•− leads to a variety of structural alternatives, the most obvious involving complete separation (to 4.095 Å) of the already weakened mirror-bisected linkage, to afford the distorted Cs chair illustrated in Figure 2a. Vibrational analysis confirms that the optimized structure represents a true energetic minimum and, as indicated by the associated Mulliken charge densities, negative charge is heavily localized on the two sulfurs associated with the “broken” bond. As expected, charge polarization, and its impact on the molecular dipole, increases with the inclusion of PCM (Table S1).
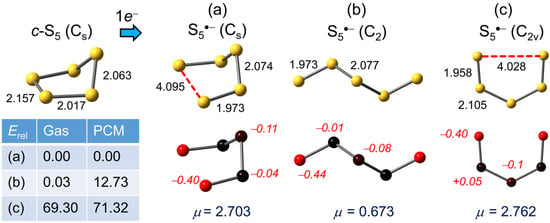
Figure 2.
(U)PBE0/D3/def2-QZVP optimized geometries (distances in Å) for S5•−, with Mulliken charges (in italics) and dipole moments μ (in Debye). Relative gas phase and PCM (=DMF) corrected total energies Erel are in kJ mol−1.
Open-chain structures for S5•− are also possible; several variants have been explored by previous workers, but in our hands these all gravitate on optimization towards the twisted chain (C2 symmetry) minimum shown in Figure 2b. It is almost co-energetic with the Cs chair, perhaps not surprisingly as the two structures are interconvertible by a 180° rotation of one of the terminal bonds. However, by virtue of the lower dipole moment of the open-chain form, a substantial gap opens with the inclusion of PCM. In addition, we have considered two “forced” planar modifications, one being the cis-cis C2v geometry shown in Figure 2c. While it does not represent a stable minimum, and its relative energy is substantially higher than the related Cs chair, its electronic structure provides a useful conceptual link (vide infra) to the shorter chain anions (n = 2–4). For the corresponding cis-trans isomer, which is isostructural with the closed shell SSNSS− anion [63,64], the energy gap is considerably less, both in the gas phase (26.1 kJ mol−1) and in DMF (32.6 kJ mol−1), but is still not a true minimum.
2.1.4. S6•−
Here we have the unique advantage of experimental structural information on both the neutral molecule and its radical anion. The cyclic, chair-shaped structure of S6, with D3d symmetry and all neighboring bonds staggered, has been characterized crystallographically [65]; the observed S–S distance = 2.057(18) Å compares well with the value calculated here = 2.054 Å (Figure 3). In the corresponding radical anion S6•−, identified in the crystal structure of the tetraphenylphosphonium salt [Ph4P][S6], the cyclic chair shape is retained (Figure 3a), despite some disorder, but with two elongated S–S bonds = 2.634(4) Å [47]. In their report, however, the authors cautioned that the apparently high molecular symmetry (C2h) observed for the anion might be dictated by the high lattice symmetry (space group C2/c), and provided BP86/TZ2P results indicating that a distorted chair structure (Figure 3b) with C2 symmetry was actually more stable.
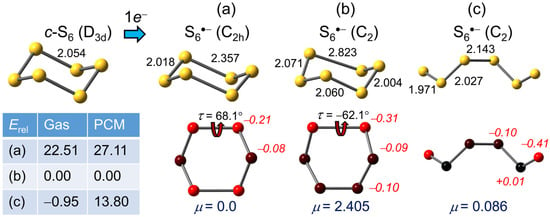
Figure 3.
(U)PBE0/D3/def2-QZVP optimized geometries (distances in Å) for S6•−, with Mulliken charges (in italics) and dipole moments (μ) in Debye. Relative gas phase and PCM (=DMF) corrected total energies Erel are in kJ mol−1.
From a theoretical perspective, one-electron reduction of the high-symmetry geometry of neutral S6 gives rise to an orbitally degenerate ground state for the resulting radical anion S6•−. Thus, when using D3h symmetry constraints as a starting point for a geometry optimization, the symmetric chair immediately breaks symmetry and undergoes a first-order Jahn–Teller distortion [61] to C2h symmetry, affording two elongated S–S bonds, calculated here = 2.357 Å (Figure 3a), somewhat shorter than that observed experimentally. However, as observed earlier, while this centrosymmetric C2h structure represents a stationary point it is not an energy minimum. Upon release of symmetry constraints, it undergoes a second-order distortion to the C2 modification (Figure 3b), in which one of the two elongated S–S bonds in the C2h geometry stretches further to 2.823 Å, a result in accord with the earlier DFT work [47]. By our calculations the energy difference between the C2h and C2 structures is large (22.5 kJ mol−1), even in the gas phase, and increases to 27.5 kJ mol−1 with the inclusion of PCM (μ = 0 in the C2h form).
In addition to the nominally closed-ring variants for S6•− several open chain options have been considered. Of these, we find the lowest energy C2 structure (Figure 3c), which can be converted into the quasi-cyclic form by a ca. 180° rotation about the central S–S bond, constitutes a true minimum. Predictably, in the gas phase the total energies of the two rotamers are almost identical, but in accord with the low dipole moment of the open chain form the balance changes sharply in favor of the ring structure when the PCM is included.
2.1.5. S7•−
Neutral S7 possesses a chair-like structure with Cs symmetry [66,67], with the unique mirror-bisected bond lengthened to 2.18 Å (calculated here = 2.171 Å) by the effects of lone-pair repulsion occasioned by the eclipsed alignment of the neighboring bonds, as seen in c-S5. In the structure of the global energetic minimum for S7•− the cyclic chair motif found in the neutral molecule is retained, but the already weakened mirror-bisected linkage is lengthened to 2.946 Å in the radical anion (Figure 4a), with the associated Mulliken charge densities heavily localized on the two sulfurs linked by the weakened bond.
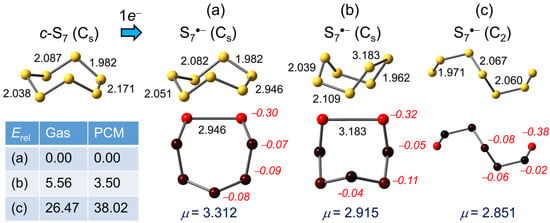
Figure 4.
(U)PBE0/D3/def2-QZVP optimized geometries (distances in Å) for S7•−, with Mulliken charges (in italics) and dipole moments (μ) in Debye. Relative gas phase and PCM (=DMF) corrected total energies Erel are in kJ mol−1.
Not surprisingly, a boat-shaped conformation (Figure 4b), in which the unique S–S bond is a little longer (3.183 Å) than in the chair, is also possible. This feature may be of relevance to optical properties, as its relative energy lies only slightly above that of the chair in both the gas phase and solution, so that the two conformers may coexist in equilibrium in solution. Outside of this pair of quasi-cyclic structures there is an open chain variant with C2 symmetry (Figure 4c). It represents a local energy minimum, but is significantly less stable than the chair/boat structures in the gas phase, the gap increasing when PCM is invoked.
2.1.6. S8•−
The eight-membered ring found in orthorhombic α-sulfur displays a classic crown conformation with D4d symmetry, with all neighboring bonds (measured at 2.055(2) Å, calculated here = 2.044 Å) mutually staggered [68]. The structural changes accompanying formation of S8•− follow a similar pattern to that seen for S6•−. Addition of an electron to the cyclo-S8 in D4d symmetry affords a degenerate ground state for the resulting radical anion, thereby setting up a first order Jahn–Teller distortion [61], which in this case affords the “squeezed” C2v crown geometry shown in Figure 5a.
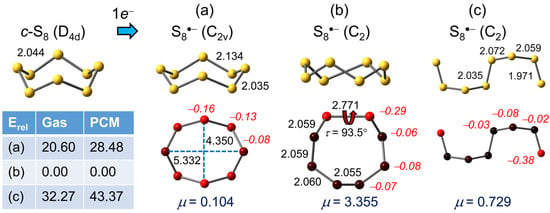
Figure 5.
(U)PBE0/D3/def2-QZVP optimized geometries (distances in Å) for S8•−, with Mulliken charges (in italics) and dipole moments (μ) in Debye. Relative gas phase and PCM (=DMF) corrected total energies Erel are in kJ mol−1.
While this high-symmetry structure is not an energy minimum, the possibility of trapping it in a crystal lattice, as in the case of the C2h form of S6•−, is worthy of consideration. That being said, upon release of all symmetry constraints the C2v structure evolves into a C2 variant (Figure 5b) which, like the C2 structure of S6•−, displays one elongated S–S bond, calculated here = 2.771 Å. Outside of distorted crown geometries, there are few energetically viable alternatives. Of these, the open-chain C2-symmetry motif (Figure 5c) represents the only true minimum, but its energy lies well above that of the C2 crown. Given its relatively low polarity, inclusion of PCM further widens the energy gap.
In summary, the smaller members (n = 3, 4) of the polysulfide radical anion family adopt open chain structures, in part because they have no choice, as there is too much ring strain in the cyclic alternatives. That being said, when alternatives exist, as in the C2v (cis) and C2h (trans) options for S4•−, solvent effects may well dictate the outcome, with the non-centric cis isomer being preferred in polar solvents and the centric trans isomer possibly being viable in non-polar solvents. For medium-sized rings, i.e., n = 5, 6, closed or broken-ring structures compete with open-chain variants, and again the choice may depend upon the polarity of the solvent employed, with polar environments or lattice constraints (for n = 6)) favoring the cyclic or quasi-cyclic modifications. In the following sections we focus on the structures most likely preferred in the latter environments. Finally, when n = 7 and 8, the stability of the cyclic structures clearly outranks the open-chain alternatives, regardless of solvent effects. Dynamic equilibria between cyclic and acyclic forms are unlikely, a conclusion which may have consequences for the mechanism of formation of S82− [39].
2.2. Electronic Spectra
Using the polar-medium preferred geometries afforded by the unrestricted DFT calculations described above, single point TD-DFT calculations were performed on the radical anions Sn•− (n = 2–8), to explore the number, nature and energies of the possible electronic excitations. A compilation of the relevant states, dominant orbital transitions, frequencies ν, wavelengths λ and oscillator strengths f is provided in Table 1.

Table 1.
TD-DFT electronic excitations for Sn•− (n = 2–8).
As when dealing with geometrical trends, presentation and discussion of the results is developed according to the value of n, beginning with the three short-chain anions (n = 2–4), where the electronic excitations are all clearly π → π*. From there on (n = 5–8) the non-planar, distorted or broken-ring geometries militate against the use of conventional σ/π symmetry descriptors which usually aid with band assignments, but for n = 5 the calculated spectrum can still be rationalized by extension of the simple π-only model. Finally, the single elongated S–S linkages found in the quasi-cyclic structures (n = 6–8), which are broadly consistent with localized two-center three-electron (2c-3e) bonds, reminiscent of those found in transient organic disulfide radical anions (RS-SR)•− [69,70], give rise to low energy excitations that are best described as σ → σ* processes within the 2c-3e manifold.
2.2.1. Sn•− (n = 2–4)
The origin of the electronic excitations in the short-chain radical anions Sn•− (n = 2–4) can be readily understood with reference to the manifold of π-orbitals predicted by the classical Hückel molecular orbital (HMO) linear chain model [71,72], using linear arrays of overlapping sulfur 3p-orbitals as a basis set. For such systems the eigenvalues ej are given by the analytical expression ej = α + 2β cos (jπ/N + 1), where α and β are the respective Coulomb and resonance parameters, and N is the number of orbitals (atomic centers) in the chain. Schematic plots of the resulting π-energy levels and MOs are illustrated in Figure 6. Within this framework, a single π → π* excitation ν1 is expected for the diatomic anion S2•−, with a slightly lower energy nπ → π* transition ν1 anticipated for the triatomic chain S3•−. Extrapolation to planar open chain S4•− systems suggests two excitations ν1 and ν2 are possible. Of these, ν1 is predicted to occur at still lower energy, and its magnitude can be estimated by calibration against the known value of ν1 for S3•− (λmax = 615–620 nm in DMF or HMPA) [73]. Based on this simple model the first transition ν1 in both isomers of S4•−is predicted to shift well beyond the visible region. For the cis (C2v) isomer a second excitation ν2 is anticipated towards the UV region, while for the trans (C2h) form ν2 should not be observed at all, as it is symmetry-forbidden (g → g).
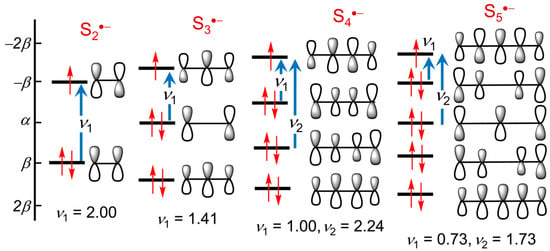
Figure 6.
HMO energy levels for arrays of 3p-orbitals in model open chain Sn•− (n = 2–5) radical anions; excitation energies ν1, ν2 are in units of β.
The TD-DFT calculations refine the qualitative predictions of the HMO model, confirming the nature of the expected transitions (Figure 7) and affording numerical estimates for the π → π* excitation energies involved for both the cis (C2v) and trans (C2h) isomers. Calculated spectra for Sn•− (n = 2–4) are shown in Figure 8.
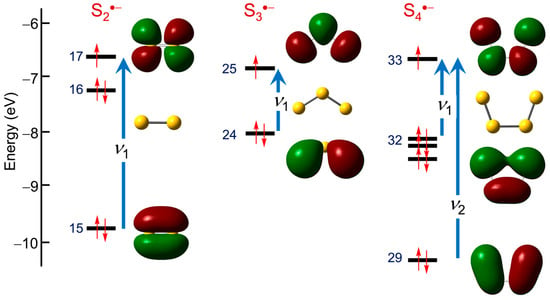
Figure 7.
Spin-restricted TD-DFT frontier orbitals and excitations for S2•−, S3•− and cis-S4•−.
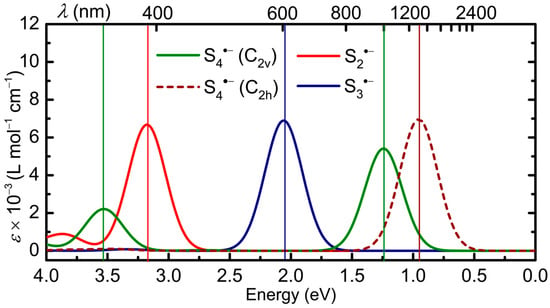
Figure 8.
TD-DFT calculated electronic spectra in DMF of Sn•− (n = 2, 3, 4), with HWHM = 0.18 eV; band assignments in Table 1.
The close correspondence between experimental λmax values for n = 2 (~400 nm) [18] and n = 3 (615–620 nm in DMF or HMPA) [73] and those predicted by TD-DFT (Table 1) provide strong support for the choice of functional, and hence confidence in the calculated values for n = 4. The results for n = 4 are also in good qualitative agreement with those reported earlier [48,49], and thus help clarify some of the controversies surrounding the spectrophotometric identification of putative S4•− species. For both the cis and trans isomers, the first transition (ν1, 32β → 33β) lies at or beyond the edge of the visible region (998 nm and 1300 nm, respectively), and for the cis isomer the second (ν2, 29β → 33β) is predicted to have λmax = 351 nm, placing it relatively close to S2•− and also many closed-shell dianionic species, e.g., S32− [42], as well as other radical anions, e.g., S5•− (vide infra), from which it would be hard to distinguish. For the trans isomer, the second transition (ν2, 29β → 33β) is symmetry-forbidden and has zero oscillator strength (f = 0). It will therefore display no signature at all in the visible region, regardless of its concentration in solution. In this light, assertions that S4•− has “never been observed” [39,43] by time-resolved spectroelectrochemistry perhaps deserve a second thought; absence of evidence is not evidence of absence.
2.2.2. S5•−
TD-DFT analysis of the optical properties of S5•−, using the coordinates of the chair-shaped Cs structure identified above as the most stable in polar media, affords an electronic spectrum (Figure 9) consisting of a series of bands spread across the entire visible and near-IR regions. However, in contrast to the three short-chain anions already discussed, the chair geometry of S5•− is not planar (although the molecule is bisected by a mirror plane), as a result of which rigorous characterization of individual orbitals and excitations between them according to their reflection symmetry in that plane, the classical σ/π classification, is no longer possible.
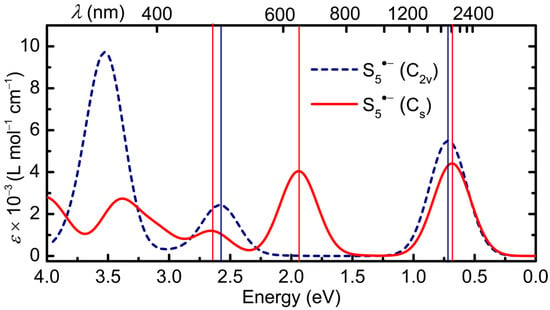
Figure 9.
Calculated electronic spectrum of S5•− in DMF, in C2v and Cs symmetry, with HWHM = 0.18 eV; band assignments in Table 1.
To resolve this difficulty, we examined the orbital make-up and electronic excitations found for the hypothetical planar variation with C2v symmetry. While it is considerably less stable than the Cs form, by virtue of increased lone-pair repulsions, its higher symmetry allows for a clearer evaluation of its spectral signature, particularly in relation to the HMO open-chain model developed above. Indeed, it is immediately apparent by inspection of the frontier orbitals illustrated in Figure 10 that excitations 40β → 41β and 38β → 41β listed in Table 1 correspond to the two lowest energy π → π excitations ν1 and ν2 predicted by the HMO linear chain model with N = 5 (Figure 6). As expected, ν1 lies deep into the near-IR (λmax = 1732 nm), extending the shift to lower energy seen in cis and trans S4•− (λmax = 998 and 1299 nm, respectively), with ν2 likewise red-shifted to λmax = 478 nm (from 351 nm in cis S4•−). The third, very intense excitation, from 39β → 42β, with λmax = 352 nm, is not related to the chain model, nor even to a π → π transition, but is rather a lone-pair σ → σ process arising from the artificially enforced planarity of the structure.
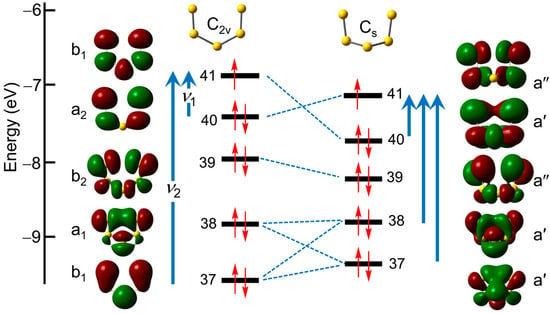
Figure 10.
Correlation of spin-restricted TD-DFT frontier orbitals and electronic excitations for S5•− in C2v and Cs symmetry.
With this information in hand, the origin of the optical signature of the Cs form emerges. The three lowest-lying states can each be described in terms a single dominant excitation from one of the doubly occupied molecular orbitals to the singly occupied molecular orbital (SOMO), that is, the lowest unoccupied molecular orbital (LUMO) for the unrestricted β-spins listed in Table 1. Moreover, correlation of the orbitals for the C2v and Cs geometries confirms that the HMO chain model still applies, albeit more loosely because of the loss of planarity and consequent σ/π mixing. Thus, while the ordering of orbitals 40 and 41 is reversed, the first excitation, 40β → 41β (λmax = 1810 nm) can be considered a quasi- π → π transition related to ν1 in the HMO model. The next two, 38β → 41β (λmax = 638 nm) and 37β → 41β (λmax = 467 nm), also involve heavily hybridized orbitals, but both are quasi- π → π processes that can be traced back to ν2. The higher energy (>3 eV) absorptions comprise a series of less well-defined states arising from multiple excitations (see Table S2).
2.2.3. S6•−
Addressing the optical properties of the S6•− anion presents a quandary. The crystallographic evidence indicates a symmetric chair structure with C2h symmetry, while DFT optimizations point towards a distorted C2 version. There are merits to both positions. In solution, and in the absence of environmental constraints, the lower-symmetry C2 geometry is probably preferred, but the high space group symmetry of the [Ph4P][S6] salt appears to hold the chair in the higher-symmetry C2h form. In that light we have performed TD-DFT calculations on both options, using geometries taken from the respective structural optimizations.
As a first step, however, we focus on a qualitative model for describing the two elongated bonds in the symmetric structure. Building on the ideas developed earlier by Dehnicke and coworkers [47], Figure 11a illustrates the two strongly coupled σ and σ* orbitals arising from combinations of two S3 fragments. A second-order Jahn–Teller distortion from C2h to C2 will give rise to mixing of the bg SOMO and bu LUMO, and a widening of the energy gap between them. Figure 11b refines this model, by showing the relevant spin-restricted Kohn–Sham orbitals and eigenvalues for the C2 structure, that is, two heavily hybridized, but basically S–S σ-bonding, occupied orbitals (46 and 48), and a more localized σ*-orbital (49).
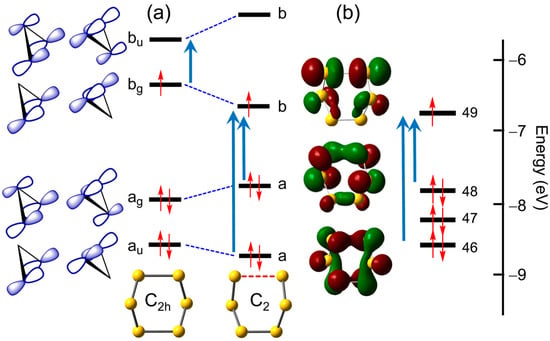
Figure 11.
(a) Sketch of frontier orbital energies following distortion of S6•− from C2h to C2 symmetry. (b) Spin-restricted TD-DFT frontier orbitals and electronic excitations for S6•− in C2 symmetry.
Given this conceptual framework, the optical signatures predicted for the two geometries are readily explained. As shown in Figure 12, the C2h structure displays a single well-resolved band with λmax = 1007 nm, which corresponds not to electron promotion from the HOMO to the SOMO, which is symmetry-forbidden (g → g) in C2h, but rather to the SOMO-to-LUMO excitation shown in Figure 11a (49α → 50α, Table 1). In addition, there are a series of less well-defined states that give rise to a broad absorption that extends into the UV region.
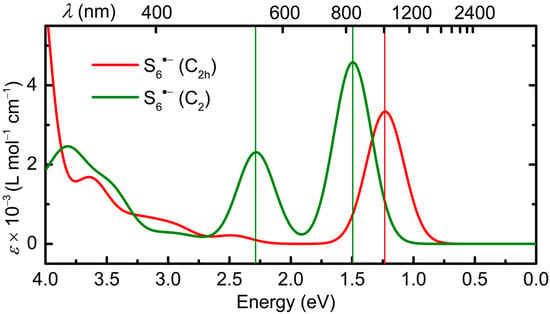
Figure 12.
Calculated electronic spectrum of S6•− in DMF, in C2h and C2 symmetry, with HWHM = 0.18 eV; band assignments in Table 1.
For the distorted C2 symmetry structure, the excited state manifold is quite different. Two bands are predicted in the visible and near-IR region (λmax = 543 nm and 830), which arise primarily from the (now allowed) excitations, 46β → 49β and 48β → 49β (Table 1), from occupied orbitals to the SOMO, both of which are essentially σ → σ* processes. As in the case of the C2h geometry, there is a broad band extending into the UV region associated with a series of higher energy but less well-defined states.
In summary, the optical properties of both variations of the S6•− radical anion are associated with transitions associated with the lengthened S–S σ-bonds. In both its excited and ground states, the S6•− radical anion behaves like a cyclic molecule.
2.2.4. S7•− and S8•−
The two largest radical anions (n = 7 and 8) are the easiest to analyze, as the structural perturbations occasioned by addition of an electron to the parent homocycles are small. Based on the structural parameters provided by the DFT optimizations of the chair and boat conformers of S7•−, both of Cs symmetry, and of the C2 distorted crown geometry of S8•−, all three rings experience a lengthening of one of the S–S bonds, an effect which can best be described in terms of the formation of a largely localized 2c-3e σ-bond.
The TD-DFT calculations reinforce this picture, providing a description for the first excited state which involves promotion of an electron between the associated σ- and σ*-orbitals of the 2c-3e manifold, that is, the β-spin HOMO and LUMO of the two conformers of S7•− (56β → 57β) and those of S8•− (64β → 65β) shown in Figure 13. These transitions give rise to single bands with large oscillator strength in the low-energy visible or near-IR region (Figure 14). As expected, there is a notable difference between the band maxima of the chair (λmax = 709 nm) and boat (λmax = 864 nm) conformations of S7•− which can be traced back to the longer S···S separation found in the latter (Figure 4).
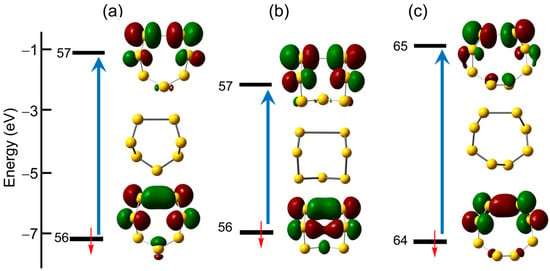
Figure 13.
Unrestricted TD-DFT frontier orbitals and calculated σ → σ* electronic excitations found for the (a) chair and (b) boat conformations of S7•− and (c) the C2-distorted crown structure of S8•−.
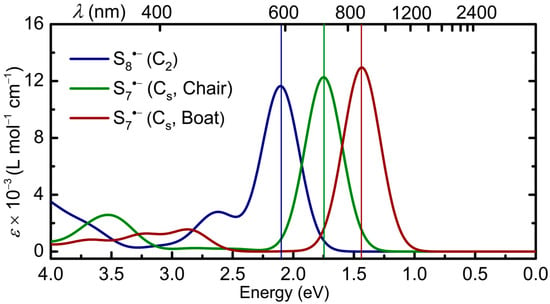
The higher transition energy predicted for S8•− (λmax = 589 nm) can be attributed to a similar effect, the shorter S···S separation stemming from the mutual staggering of the neighboring bonds and consequent relief from the effects of lone-pair repulsion. Secondary, less intense absorptions, with λmax = 474 nm (S8•−), 358 nm (S7•−, chair) and 435 nm (S7•−, boat), are also predicted. These are associated with poorly defined, higher-lying states (Table S2), but their presence may aid in identification. That being said, the strong low energy σ → σ* excitation, which dominates the spectrum of all three species, represents the most distinguishing optical feature.
3. Discussion
As indicated in the introduction, there are considerable differences of opinion as to when and where the radical anions Sn•− (n = 4–8) might be found. While their participation in the multistep redox equilibria associated with the operation of sulfide/polysulfide photoconductor cells, alkali-metal/sulfur batteries, as well as in many biological and organic transformations, is frequently implied, their identification in these complex systems has, not surprisingly, proved elusive. Equally, extensive and detailed spectroscopic and spectroelectrochemical studies, utilizing a wide range of techniques (optical, IR, Raman, EPR spectra), have been unable to provide decisive answers.
The purpose of the present work has been two-fold. Firstly, the most stable structures of the putative radical anions Sn•− (n = 4–8) in polar solvents have been identified using high-level DFT methods. Secondly, TD-DFT calculations, performed on the most stable structural candidates, have been used to map out the number, nature and energies of the photochemically accessible excited states for these species. Critical to the validity of this latter step was the ability to assess the numerical reliability of the methods used (choice of LC-functional for TD-DFT work) by comparison of the predicted excitation energies with experimental values for the well-known radical anions S2•− and S3•−. Even so, we neither expect nor claim that the present TD-DFT calculated transition energies will provide a perfect match with experiment for the larger members of the series, especially for the low-energy (near-IR and beyond) excitations. Taken together, however, the results on the entire series of anions Sn•− (n = 2–8) provide a frame of reference for distinguishing between different members of the family. Equally important, from an interpretational viewpoint, has been the use of the classical one-electron HMO chain model [74,75] to anticipate both the number and approximate energies of π → π transitions, again using S2•− and S3•− as reference points. The TD-DFT results suggest that the calculated spectra for S4•−, and even S5•−, can be effectively rationalized by this approach. By contrast, the low energy excitations predicted for the essentially cyclic structures of Sn•− (n = 6–8) are best described in terms of σ → σ* processes within a relatively localized 2c-3e manifold.
The availability of this information opens the door to the design of experimental strategies for the generation, observation and perhaps even isolation of the radical anions Sn•− (n = 4–8). We begin by considering the seminal 1991 report by Rauchfuss and coworkers on the structure and spectroscopic properties of the open-chain octasulfide dianion S82− in the absence of counterion pairing effects [48]. As noted earlier, these authors attributed the strong band with λmax = 618 nm that emerged upon dilution of a solution of [Mn(N-MeIm)6][S8] (N-MeIm = N-methylimidazole) in N-MeIm to the presence of the radical anion S3•−. At the time they rationalized the generation of S3•− in terms of a disproportionation of S82− to ¼S8 and S62−, and subsequent dissociation of the latter, following the conventional interpretation of the electrochemistry community [35,49]. Other radical anions, notably Sn•− (n = 4, 5), were not included in the analysis, in part because their optical signatures were unknown. Given the present TD-DFT results, however, the potential involvement of these seemingly missing radical anions can be examined. In particular, we consider the possibility that both might be formed, along with S3•−, by either symmetric or asymmetric dissociation of the S82− dianion, as indicated in Scheme 1. In addition to the overall thermodynamics of such processes [43], mechanistic considerations may also be important—how easy is it to rupture the distinct S–S bonds along the chain? In response to this question, we suggest that dissociation may proceed via four-center intermediates, as illustrated in Scheme 2. Indeed, in the case of symmetric dissociation, an example of a four-center π-dimer has been characterized crystallographically [21].
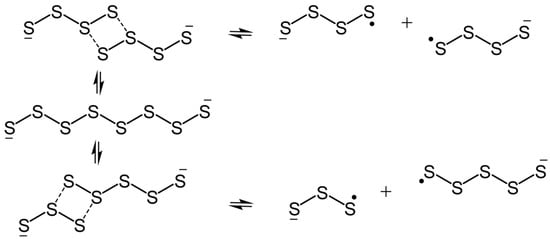
Scheme 2.
Symmetric and asymmetric dissociation of S82− to the radical anions Sn•− (n = 3, 4, 5).
As an example of the spectroscopic ramifications of this interpretation, we compare in Figure 15 the experimental spectrum for the highly diluted solution of S82−, as reported by Rauchfuss, with an equally weighted composite of the TD-DFT calculated spectra for S3•− and S5•−, the two products of an asymmetric dissociation. In the mid-range visible region, the correspondence is remarkable, not only in terms of the overlap and coalescence of the two bands calculated for n = 3, 5, but also the presence of the weaker band near 480 nm which, on the present basis, may be assigned to n = 5 (calculated λmax = 467 nm). Below 400 nm the match is less than ideal, but could be improved by inclusion into the composite of cis S4•− (calculated λmax = 351 nm), the unique symmetric dissociation product. Alternatively, these higher energy absorptions may arise from undissociated S62−. That being said, the absence of bands attributable to S2•− or S6•− suggests dissociation of S82− into these species does not occur to any great extent.
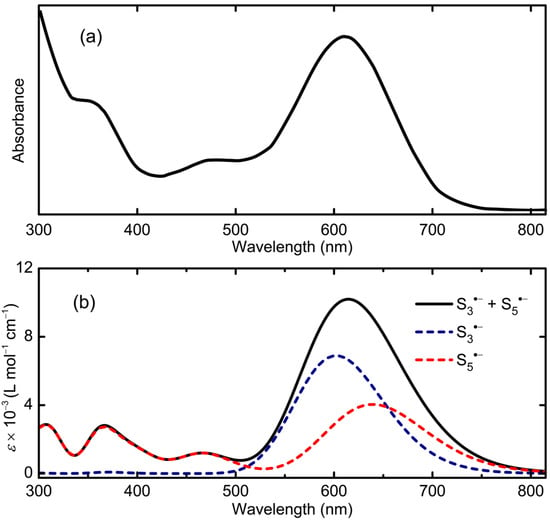
Figure 15.
(a) Optical spectrum of 0.001 M solution of [Mn(N-MeIm)6][S8] in N-MeIm, reproduced from [48]; copyright American Chemical Society. (b) Calculated composite spectrum, with HWHM = 0.18 eV, for equally weighted mixture of S3•− and S5•− in DMF.
By itself, this single spectral deconvolution exercise does not constitute proof for multiple dissociation pathways, but critical support for the concept could be readily achieved by inspection of the near-IR region of dilute solutions of S82−, where one or both of the low-energy (ν1) bands of S4•− and S5•− should be present. Moreover, similar spectroscopic analysis at high dilution of solutions of salts of the known hepta- and hexasulfide dianions S72− and S62− should reveal predicable patterns of radical anions, the former affording S3•− and S4•− (but possibly not S5•−) and the latter specifically S3•−; indeed, for S62− this result has already been confirmed [48]. In the same way, observation of the cyclic radical anions Sn•− (n = 6–8) may be possible, by examination of highly diluted solutions of long chain dianions such S102− [49] and S122− [50].
In addition to routes to the radical anions which rely solely on dissociative equilibria between radical anions and closed-shell dianions, direct chemical synthesis may be possible, as in the case of the radical anion salt [Ph4P][S6], which was prepared by the rather unusual reaction of H2S and Me3SiN3 in the presence of [Ph4P][N3] [52]. If this procedure could be adapted to incorporate the use of other bulky cations, e.g., PPN+, different crystal morphologies might be generated. That being the case, would the structure of the resulting anion be constrained to C2h symmetry, as in [Ph4P][S6], or display the more stable distorted C2 shape? Even in the solid state, the expected optical signatures (Figure 12) are predicted to be quite different. Alternatively, not only S6•− but also S7•− and S8•− could be accessible by electrochemical reduction of the appropriate neutral allotrope [76,77,78]. The latter two anions have very distinct optical profiles, although we add the caveat that the footprint of S8•− may easily be confused with that of S3•−.
Chemical reduction methods, for example using organometallic reducing agents such as cobaltocene, which is known to afford salts of closed [79] and open shell anions [80] with sulfur-based electron acceptors, may also provide access to salts of S8•−. In this connection Woollins et al. obtained the salt [Cp2Co][S3N3] from the reaction of S4N4 with cobaltocene in THF [81]. This transformation probably involves the initial generation of the radical anion S4N4•−, known from electrochemical studies to be formed by one-electron reduction of S4N4, which then undergoes ring contraction to produce S3N3− [77].
Just as chemical oxidation of cyclo-S8 has afforded the radical cation S8•+ [78], treatment of salts of the dianions S72− [82] and S82− [47,48] with mild oxidants, e.g., iodine or N-bromosuccinimide, might well yield the corresponding radical anions S7•− and S8•−. An alternative to chemical oxidation is the use of photolysis to generate polysulfide radical anions from the corresponding dianions. This approach is based on the recent work of Chiba and co-workers on the production of polysulfide radical anions Sn•− (n = 3, 4) [25,26,27] via photolysis of the polysulfide dianion S42−, as well as on insights provided by investigations into the photoelectrochemical oxidation of S2− by metal-sulfide quantum dots [14,15].
Last, but not least, we acknowledge the role that serendipity has played in the advancement of the chemistry of polysulfide radical anions. For example, the procedures used to achieve the isolation and characterization of S6•− [52] and of the π-dimer of S4•− [21] would have been difficult to predict a priori, but their somewhat fortuitous discovery strengthens the conviction that continued exploration will yield new insights. Towards that end the present results may prove useful.
4. Computational Methods
Unrestricted density functional theory (DFT) calculations were performed with the Gaussian 16 suite of programs [74], using the default ultrafine integration grids. Geometry optimizations employed the hybrid-adapted Perdew–Burke–Ernzerhof functional (PBE0) [75,83] and Ahlrichs’ quadruple-ξ valence def2-QZVP basis set [84], without additional diffuse functions [85] but with Grimme’s empirical correction (D3) [81,86] included to account for possible dispersion effects [87]. For most anions several geometries, both cyclic and acyclic, were considered, and wherever a stationary point was located a full vibrational analysis was performed to determine whether or not it corresponded to a true energy minimum. Preferred geometries were further optimized with the inclusion of the polarized continuum model (PCM) [88] to account for the effects of solvation, dimethylformamide (DMF) being set as a representative polar solvent. Listings of total energies, vibrational frequencies and cartesian coordinates, with and without PCM, are provided in the SI.
The optical properties of the polysulfide radical anions were explored using single point unrestricted time-dependent (TD) DFT calculations, with the same def2-QZVP basis set and PCM included. The use of several long range corrected (LC) functionals, which are known to provide reasonable estimates of low energy (charge transfer, Rydberg-like) excitations in molecular species [89,90], including radicals [91] and sulfur-containing radical anions [92], was explored. The best results, reported here, employed the empirical dispersion-corrected density functional ωB97XD [93], which is well recognized for its overall performance [94]. All tabulated excitation energies refer to spin-unrestricted calculations, but for ease of visualization some of the orbital energy diagrams are based on spin-restricted wavefunctions. All spectral plots, prepared using Gaussview 6 [95], employed Gaussian band shapes with the half-width at half maximum (HWHM) value set at 0.18 eV. The associated extinction coefficients were derived using routines available within Gaussview. Kohn–Sham wavefunctions were also plotted using Gaussview.
5. Conclusions
The DFT and TD-DFT calculations reported here represent the first comprehensive attempt both to predict and to rationalize the optical properties of the entire family of polysulfide radical anions Sn•− (n = 2–8). Our results confirm earlier predictions [52,53] that the first π → π transition for both the cis (C2v) and slightly less stable trans (C2h) isomers of S4•− should occur in the near-IR region. However, a second π → π transition at around 350 nm is expected for the cis isomer of S4•−. Based on Seel’s early results [19,20], a band near 490 nm has often been attributed to this species, but these conclusions are questionable [3]. At least in dilute solution this band may originate from S5•−, the most stable form of which possesses an acyclic structure with Cs symmetry, and is predicted to display three optical absorption bands, two in the visible and one in the near-IR region.
The S6•− radical anion is an interesting and unique example of a polysulfide radical anion that has been structurally characterized in the solid state. In the ion-separated salt [Ph4P][S6] the anion displays a cyclic structure (C2h symmetry) with two long S–S bonds [51], while DFT geometry optimization points to a distorted cyclic structure (C2 symmetry) with one long S–S bond as a more stable arrangement. The predicted electronic spectra for these two forms are very different, with λmax = 1007 nm vs. 830 and 543 nm, respectively.
To date the heptasulfide radical anion S7•− has received scant attention, but the present DFT results point to a cyclic structure with two energetically similar conformers, chair and boat (Cs symmetry), both displaying one long S−S bond best described in terms of a localized 2c-3e σ-interaction. Electronic excitation within this manifold gives rise to a strong visible/near-IR absorption with calculated values of λmax = 709 nm and 864 nm for chair and boat, respectively. The octasulfide radical anion S8•−, which carries particular significance as the initial product of the electrochemical reduction of cyclo-S8 [3], is also predicted to possess a distorted cyclic structure (C2 symmetry) exhibiting, like S7•−, a single elongated 2c-3e S−S bond. The associated σ → σ* excitation generates a strong visible absorption band with a calculated λmax = 589 nm.
Supplementary Materials
The following supporting information (21 pages total) can be downloaded at: https://www.mdpi.com/article/10.3390/molecules28155654/s1, Figure S1: Optimized geometrical parameters; Table S1: Total electronic energies; Table S2: Excitation energies, oscillator strengths and orbital contributions; Tables S3–S11: Gaussian archive entries; Tables S12–S17: Frequency calculations.
Author Contributions
The two authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support from NSERC (Canada).
Data Availability Statement
Details of the computational data are in the Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chivers, T. Ubiquitous trisulphur radical ion S3•−. Nature 1974, 252, 32–33. [Google Scholar] [CrossRef]
- Steudel, R. Inorganic polysulfides Sn2− and radical anions Sn•−. In Elemental Sulfur and Sulfur-Rich compounds II. Topics in Current Chemistry; Steudel, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 231, pp. 127–152. [Google Scholar]
- Steudel, R.; Chivers, T. The role of polysulfide dianions and radical anions in the chemical, physical and biological sciences, including sulfur-based batteries. Chem. Soc. Rev. 2019, 48, 3279–3319. [Google Scholar] [CrossRef] [PubMed]
- Laitinen, R.S.; Oilunkaniemi, R.; Chivers, T.; McGeachie, L.; Kelly, P.F.; King, R.S.P. Polychalcogen molecules, ligands, and ions Part 2: Catenated acyclic molecules, ions, and p-block element derivatives. In Reference Module in Chemistry, Molecular Sciences and Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2023; pp. 970–1020. [Google Scholar]
- Zheng, D.; Wang, G.; Liu, D.; Si, J.; Ding, T.; Qu, D.; Yang, X.; Qu, D. The progress of Li−S batteries—Understanding of the sulfur redox mechanism: Dissolved polysulfide ions in the electrolytes. Adv. Mater. Technol. 2018, 3, 1700233. [Google Scholar] [CrossRef]
- Zhao, E.; Nie, K.; Yu, X.; Hu, Y.-S.; Wang, F.; Xiao, J.; Li, H.; Huang, X. Advanced characterization techniques in promoting mechanism understanding for lithium-sulfur batteries. Adv. Func. Mater. 2018, 28, 1707543. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Z.-W.; Peng, H.-J.; Huang, J.-Q.; Zhang, Q. A toolbox for lithium-sulfur research: Methods and protocols. Small Methods 2017, 1, 1700134. [Google Scholar] [CrossRef]
- Song, P.; Rao, W.; Chivers, T.; Wang, S.-Y. Applications of trisulfide radical anion S3•− in organic chemistry. Org. Chem. Front. 2023, 10, 3378–3401. [Google Scholar] [CrossRef]
- Bogdándi, V.; Ida, T.; Sutton, T.R.; Bianco, C.; Ditrói, T.; Koster, G.; Henthorn, H.A.; Minnion, M.; Toscano, J.P.; van der Vliet, A.; et al. Speciation of reactive sulfur species and their reactions with alkylating agents: Do we have any clue about what is present in the cell? Br. J. Pharmacol. 2019, 176, 646–670. [Google Scholar] [CrossRef] [PubMed]
- Cortese-Krott, M.M.; Kuhnle, G.G.C.; Dyson, A.; Fernandez, B.O.; Grman, M.; DuMond, J.F.; Barrow, M.P.; McLeod, G.; Nakagawa, H.; Ondrias, K.; et al. Key bioactive reaction products of the NO/H2S interaction are S/N hybrid species, polysulfides, and nitroxyl. Proc. Natl. Acad. Sci. USA 2015, 112, E4651–E4660. [Google Scholar] [CrossRef] [PubMed]
- Pokrovski, G.S.; Dubrovinsky, L.S. The S3•− ion is stable in geological fluids at elevated temperatures and pressures. Science 2011, 331, 1052–1054. [Google Scholar] [CrossRef] [PubMed]
- Pokrovski, G.S.; Kokh, M.A.; Guillaume, D.; Borisova, A.Y.; Gisquet, P.; Hazemann, J.-L.; Lahera, E.; Del Net, W.; Proux, O.; Testemale, D.; et al. Sulfur radical species form gold deposits on earth. Proc. Nat. Acad. Sci. USA 2015, 112, 13484–13489. [Google Scholar] [CrossRef]
- Pokrovski, G.S.; Kokh, M.A.; Desmaele, E.; Laskar, C.; Bazarkina, E.F.; Borisova, A.Y.; Testemale, D.; Hazemann, J.-L.; Vuilleumier, R.; Ferlat, G.; et al. The trisulfur radical ion S3•− controls platinum transport by hydrothermal fluids. Proc. Nat. Acad. Sci. USA 2021, 118, e2109768118. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; McNaughter, P.D.; O’Brien, P.; Minamimoto, H.; Murakoshi, K. Photoelectrochemical formation of polysulfide at PbS QD-sensitized plasmonic electrodes. J. Phys. Chem. Lett. 2019, 10, 5357–5363. [Google Scholar] [CrossRef] [PubMed]
- Chakrapani, V.; Baker, D.; Kamat, P.V. Understanding the role of the sulfide redox couple (S2−/Sn2−) in quantum dot-sensitized solar cells. J. Am. Chem. Soc. 2011, 133, 9607–9615. [Google Scholar] [CrossRef]
- Reinen, D.; Lindner, G.-G. The nature of the chalcogen colour centres in ultramarine type solids. Chem. Soc. Rev. 1999, 28, 75–84. [Google Scholar] [CrossRef]
- Chukanov, N.V.; Sapozhnikov, A.N.; Shendrik, R.Y.; Vigasina, M.F.; Steudel, R. Spectroscopic and crystal-chemical features of sodalite-group minerals from gem lazurite deposits. Minerals 2020, 10, 1042. [Google Scholar] [CrossRef]
- Chivers, T.; Elder, P.J.W. Ubiquitous trisulfur radical anion: Fundamentals and applications in materials science, electrochemistry, analytical chemistry, and geochemistry. Chem. Soc. Rev. 2013, 42, 5996–6005. [Google Scholar] [CrossRef]
- Seel, F. Polysulfide radical anions. Angew. Chem. Int. Ed. 1973, 12, 420–421. [Google Scholar] [CrossRef]
- Seel, F.; Guttler, H.-J.; Simon, G.; Wieckowski, A. Colored sulfur species. Pure Appl. Chem. 1977, 49, 45–54. [Google Scholar] [CrossRef]
- Schwamm, R.J.; Lein, M.; Coles, M.P.; Fitchett, C.M. Bismuth (III) complex of the S4•− radical anion: Dimer formation via pancake bonds. J. Am. Chem. Soc. 2017, 139, 16490–16493. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.J.H.; Dines, T.J.; Kurmoo, M. The nature of the sulfur chromophore in ultramarine blue, green, violent, and pink and of the selenium chromophore in ultramarine selenium. Characterization of radical anions by electronic and resonance Raman spectroscopy and the determination of their excited-state geometries. Inorg. Chem. 1983, 22, 2766–2772. [Google Scholar]
- Rauh, R.D.; Shuker, F.S.; Marston, J.M.; Brummer, S.B. Formation of lithium polysulfides in aprotic media. J. Inorg. Nucl. Chem. 1977, 39, 1761–1766. [Google Scholar] [CrossRef]
- Li, H.; Tang, X.; Pang, J.H.; Wu, X.; Yeow, E.K.L.; Wu, J.; Chiba, S. Polysulfide anions as visible light photoredox catalysts for aryl cross-couplings. J. Am. Chem. Soc. 2021, 143, 481–487. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, Y.; Chiba, S. Leveraging of sulfur anions in photoinduced molecular transformations. JACS Au 2021, 1, 2121–2129. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, Y.; Chiba, S. Anti-Markovnikov hydroarylation of alkenes via polysulfide anion photocatalysis. Chem. Commun 2021, 57, 6264–6267. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Chiba, S. Synthesis of α-tertiary amines by polysulfide anions photocatalysis via single-electron transfer and hydrogen atom transfer in relays. Chem. Catal. 2022, 2, 1128–1142. [Google Scholar] [CrossRef]
- Hagen, M.; Schiffels, P.; Hammer, M.; Dörfler, S.; Tübke, J.; Hoffmann, M.; Althues, H.; Kaskel, S. In-situ Raman investigation of polysulfide formation in Li-S cells. J. Electrochem. Soc. 2013, 160, A1205–A1215. [Google Scholar] [CrossRef]
- Clark, R.J.H.; Cobbold, D.G. Characterization of sulfur radical anions in solutions of alkali polysulfides in DMF and HMPA and in the solid state in ultramarine blue, green, and red. Inorg. Chem. 1978, 17, 3169–3174. [Google Scholar] [CrossRef]
- Wu, H.-L.; Huff, L.A.; Gewirth, A.A. In-situ Raman spectroscopy of sulfur speciation in Li-S batteries. Appl. Mater. Interfaces 2015, 7, 1709–1719. [Google Scholar] [CrossRef]
- Levillain, E.; Leghié, P.; Gobeltz, N.; Lelieur, J.-P. Identification of the S4•− radical anion in solution. New J. Chem. 1997, 21, 335–341. [Google Scholar]
- Wujcik, K.H.; Wang, D.R.; Raghunathan, A.; Drake, M.; Pascal, T.A.; Prendergast, D.; Balsara, N.P. Lithium polysulfide radical anions in ether-based solvents. J. Phys. Chem. C 2016, 120, 18403–18410, and references cited therein. [Google Scholar] [CrossRef]
- Chukanov, N.V.; Shendrik, R.Y.; Vigasina, M.F.; Pekov, I.V.; Sapozhnikov, A.N.; Shcherbakov, V.D.; Varlamov, D.A. Crystal chemistry, isomorphism, and thermal conversions of extra-framework components in sodalite-group minerals. Minerals 2022, 12, 887. [Google Scholar] [CrossRef]
- Merritt, M.V.; Sawyer, D.T. Electrochemical reduction of elemental sulfur in aprotic solvents. Formation of a stable S8•− species. Inorg. Chem. 1970, 9, 211–215. [Google Scholar] [CrossRef]
- Martin, R.P.; Doub, W.H.; Roberts, J.L.; Sawyer, D.T. Further studies of the electrochemical reduction of sulfur in aprotic solvents. Inorg. Chem. 1973, 12, 1921–1924. [Google Scholar] [CrossRef]
- Bonnaterre, R.; Cauquis, G. Spectrophotometric study of the electrochemical reduction of sulphur in organic media. J. Chem. Soc. Chem. Commun. 1972, 293–294. [Google Scholar] [CrossRef]
- Manan, N.S.A.; Aldous, L.; Alias, Y.; Murray, P.; Yellowlees, L.J.; Lagunas, M.C.; Hardacre, C. Electrochemistry of sulfur and polysulfides in ionic liquids. J. Phys. Chem. B 2011, 115, 13873–13879. [Google Scholar] [CrossRef]
- Jung, Y.; Kim, S.; Kim, B.S.; Han, D.H.; Park, S.M.; Kwak, J. Effect of organic solvents and electrode materials on electrochemical reduction of sulfur. J. Electrochem. Soc. 2008, 3, 566–577. [Google Scholar] [CrossRef]
- Gaillard, F.; Levillain, E.; Lelieur, J.-P. Polysulfides in DMF: Only the radical anions S3•− and S4•− are reducible. J. Electroanal. Chem. 1997, 432, 129–138. [Google Scholar] [CrossRef]
- Evans, A.; Montenegro, M.I.; Pletcher, D. The mechanism for the cathodic reduction of sulphur in DMF: Low temperature voltammetry. Electrochem. Commun. 2001, 3, 514–518. [Google Scholar] [CrossRef]
- Levillain, E.; Gaillard, F.; Leghié, P.; Demortier, A.; Lelieur, J.-P. On the understanding of the reduction of sulfur (S8) in dimethylformamide (DMF). J. Electroanal. Chem. 1997, 420, 167–177. [Google Scholar] [CrossRef]
- Leghié, P.; Lelieur, J.-P.; Levillain, E. Final comment on Reply to “Comments on the mechanism of the electrochemical reduction of sulphur in DMF”. Electrochem. Commun. 2002, 4, 406–411. [Google Scholar] [CrossRef]
- Steudel, R.; Steudel, Y. Polysulfide chemistry in sodium-sulfur batteries and related systems: A computational study by G3X(MP2) and PCM calculations. Chem. Eur. J. 2013, 19, 3162–3176. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.-S.; Park, S.-M. In situ spectroelectrochemical studies on the reduction of sulfur in dimethyl sulfoxide solutions. J. Electrochem. Soc. 1993, 140, 115–122. [Google Scholar] [CrossRef]
- Han, D.-H.; Kim, B.-S.; Choi, S.-J.; Jung, Y.; Kwak, J.; Park, S.-M. Time-resolved in situ spectroelectrochemical study on reduction of sulfur in DMF. J. Electrochem. Soc. 2004, 151, E283–E290. [Google Scholar] [CrossRef]
- Cuisinier, M.; Hart, C.; Balusubramanian, M.; Garsuch, A.; Nazar, L.F. Radical or not radical: Revisiting lithium-sulfur electrochemistry in non-aqueous solvents. Adv. Energy Mater. 2015, 5, 1401801. [Google Scholar] [CrossRef]
- Schliephke, A.; Falius, H.; Buchkremer-Hermanns, H.; Bottcher, P. Preparation and crystal structure of the bis(triethylammonium) octasulfide, [HN(C2H5)3]2S8. Z. Naturforsch. 1988, 43b, 21–24. [Google Scholar]
- Dev, S.; Ramli, E.; Rauchfuss, T.B.; Wilson, S.R. Synthesis and structure of [M(N-methylimidazole)6]S8 (M = Mn, Fe, Ni, Mg). Polysulfide salts prepared by the reaction of N-methylimidazole + metal powder + sulfur. Inorg. Chem. 1991, 30, 2514–2519. [Google Scholar] [CrossRef]
- Fujinaga, T.; Kuwamoto, T.; Okazaki, S.; Hojo, M. Electrochemical Reduction of Elemental Sulfur in Acetonitrile. Bull. Chem. Soc. Jpn. 1980, 53, 2851–2855. [Google Scholar] [CrossRef]
- Mondal, M.K.; Zhang, L.; Feng, Z.; Tang, S.; Feng, R.; Zhao, Y.; Tan, G.; Ruan, H.; Wang, X. Tricoordinate pnictogen-centered radical anions: Isolation, characterization, and reactivity. Angew. Chem. Int. Ed. 2019, 58, 15829–15833. [Google Scholar] [CrossRef]
- Liebing, P.; Kühling, M.; Swanson, C.; Feneberg, M.; Hilfert, L.; Goldhahn, R.; Chivers, T.; Edelmann, F.T. Catenated and spirocyclic polychalcogenides from potassium carbonate and elemental chalcogens. Chem. Commun. 2019, 55, 14965–14967. [Google Scholar] [CrossRef] [PubMed]
- Neumüller, B.; Schmock, F.; Kirmse, R.; Voigt, A.; Diefenbach, A.; Bickelhaupt, F.M.; Dehnicke, K. (Ph4P)S6−A compound containing the cyclic radical anion S6•−. Angew. Chem. Int. Ed. 2002, 39, 4580–4582. [Google Scholar] [CrossRef]
- Fabian, J.; Komiha, N.; Linguerri, R.; Rosmus, P. The absorption wavelengths of sulfur chromophores of ultramarines calculated by TD-DFT. J. Mol. Struct. THEOCHEM 2006, 801, 63. [Google Scholar] [CrossRef]
- Rejmak, P. Computational refinement of the puzzling red tetrasulfur chromophore in ultramarine pigments. PhysChemChemPhys 2020, 22, 22684–22698. [Google Scholar] [CrossRef]
- Hunsicker, S.; Jones, R.O.; Ganteför, G. Rings and chains in sulfur cluster anions S− to S9−: Theory (simulated annealing) and experiment (photoelectron detachment). J. Chem. Phys. 1995, 102, 5917–5936. [Google Scholar] [CrossRef][Green Version]
- Wong, M.W. Quantum-chemical calculations of sulfur-rich compounds. Elemental Sulfur and Sulfur-Rich compounds II. Topics in Current Chemistry; Steudel, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 231, pp. 1–29. [Google Scholar]
- Swope, W.C.; Lee, Y.-P.; Schaefer, H.F. Diatomic sulfur: Low lying bound molecular electronic states of S2. J. Chem. Phys. 1979, 70, 947–953. [Google Scholar] [CrossRef]
- Zakrzewski, V.G.; von Niessen, W. Structures, stabilities and adiabatic ionization and electron affinity energies of small sulfur clusters. Theor. Chim. Acta 1994, 88, 75–96. [Google Scholar] [CrossRef]
- Koch, W.; Natterer, J.; Heinemann, C. Quantum chemical study on the equilibrium geometries of S3 and S3−, The electron affinity of S3 and the low lying electronic states of S3−. J. Chem. Phys. 1995, 102, 6159–6167. [Google Scholar] [CrossRef]
- Wong, M.W.; Steudel, R. Structure and spectra of tetrasulfur S4 − an ab initio MO study. Chem. Phys. Lett. 2003, 379, 162–169. [Google Scholar] [CrossRef]
- Pearson, R.G. Symmetry Rules for Chemical Reactions: Orbital Topology and Elementary Processes; John Wiley and Sons: New York, NY, USA, 1976; pp. 78–79. [Google Scholar]
- Jones, R.O.; Ballone, P. Density functional and Monte Carlo studies of sulfur. I. Structure and bonding in Sn rings and chains (n = 2–18). J. Chem. Phys. 2003, 118, 9257–9265. [Google Scholar] [CrossRef]
- Chivers, T.; Laidlaw, W.G.; Oakley, R.T.; Trsic, M. Synthesis, crystal and molecular structure of [(Ph3P)2N+][S4N−], and the electronic structure of the acyclic anion, S4N−. J. Am. Chem. Soc. 1980, 102, 5773–5781. [Google Scholar] [CrossRef]
- Burford, N.; Chivers, T.; Cordes, A.W.; Oakley, R.T.; Pennington, W.T.; Swepston, P.N. Variable geometry of the S4N− anion: Crystal and molecular structure of Ph4As+S4N− and a refinement of the structure of PPN+ S4N− (PPN = [Ph3P]2N+). Inorg. Chem. 1981, 20, 4430–4432. [Google Scholar] [CrossRef]
- Donohue, J.; Caron, A.; Goldish, E. The crystal and molecular structure of S6 (sulfur-6). J. Am. Chem. Soc. 1961, 83, 3748–3751. [Google Scholar] [CrossRef]
- Steudel, R.; Steidel, J.; Pickardt, J.; Schuster, F.; Reinhardt, R. X-ray structural analyses of two allotropes of cycloheptasulfur (γ and δ-S7). Z. Naturforsch. 1980, 35b, 1378–1383. [Google Scholar] [CrossRef][Green Version]
- Schmidt, M.; Block, B.; Block, H.H.; Köpf, H.; Wilhelm, E. Cycloheptasulfur, S7, and cyclododecasulfur, S12: Two new sulfur rings. Angew. Chem. Int. Ed. 1968, 7, 632–633. [Google Scholar] [CrossRef]
- Rettig, S.R.; Trotter, J. Refinement of the structure of orthorhombic sulfur, α-S8. Acta Crystallogr. 1987, C43, 2260–2262. [Google Scholar] [CrossRef]
- Bonini, M.G.; Augusto, O. Carbon dioxide stimulates the production of thiyl, sulfinyl, and disulfide radical anion from thiol oxidation by peroxynitrite. J. Biol. Chem. 2001, 276, 9749–9754. [Google Scholar] [CrossRef]
- Yamaji, M.; Tojo, S.; Takehira, K.; Tobita, S.; Fujitsuka, M.; Majima, T. S-S bond mesolysis in α,α′-dinaphthyl disulfide radical anion generated during γ-radiolysis and pulse radiolysis in organic solution. J. Phys. Chem. A 2006, 110, 13487–13491. [Google Scholar] [CrossRef]
- Albright, T.A.; Burdett, J.K.; Whangbo, M.-H. Orbital Interactions in Chemistry; John Wiley and Sons: New York, NY, USA, 1985; pp. 212–213. [Google Scholar]
- Heilbronner, E.; Bock, H. The HMO Model and its Application. 1. Basis and Manipulation; John Wiley and Sons: New York, NY, USA, 1976; pp. 131–132. [Google Scholar]
- Chivers, T.; Drummond, I. Characterization of the trisulfur radical anion S3•− in blue solutions of alkali polysulfides in hexamethylphosphoramide. Inorg. Chem. 1972, 11, 2525–2527. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. (Eds.) Gaussian 16; Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Berry, D.E.; Fawkes, K.L.; Chivers, T. Student-designed experiment: Preparation and mass spectrum of cyclohexasulfur. Chem. Educ. 2001, 6, 109–111. [Google Scholar] [CrossRef]
- Boeré, R.T.; Chivers, T.; Roemmele, T.L.; Tuononen, H.M. An electrochemical and electronic structure investigation of the [S3N3]∙ radical and kinetic modeling of the [S4N4]n/[S3N3]n (n = 0, −1) interconversion. Inorg. Chem. 2009, 48, 7294–7306. [Google Scholar] [CrossRef]
- Derendorf, J.; Jenne, C.; Keßler, M. The first step of the oxidation of elemental sulfur: Crystal structure of the homopolyatomic sulfur radical cation [S8]∙+. Angew. Chem. Int. Ed. 2017, 56, 8281–8284. [Google Scholar] [CrossRef]
- Jagg, P.N.; Kelly, P.F.; Rzepa, H.S.; Williams, D.J.; Woollins, J.D.; Wylie, W. The preparation, x-ray crystal structure and theoretical study of [CoCp2][S3N3], (Cp = cyclopentadienyl), a novel stacking compound incorporating multiple C-H—N(pπ) interactions. J. Chem. Soc. Chem. Commun. 1991, 942–944. [Google Scholar] [CrossRef]
- Konchenko, S.N.; Gritsan, N.P.; Lonchakov, A.V.; Irtegova, I.G.; Mews, R.; Ovcharenko, V.I.; Radius, U.; Zibarev, A.V. Cobaltocenium [1,2,5]thiadiazolo[3,4-c][1,2,5]thiadiazolidyl: Synthesis, structure, and magnetic properties. Eur. J. Inorg. Chem. 2008, 2008, 3833–3838. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Chivers, T.; Edelmann, F.; Richardson, J.F.; Schmidt, K.J. A convenient synthesis, X-ray crystal structure and Raman spectrum of the heptasulfide ion, S72−, in [PPN]2S7.2EtOH. Can. J. Chem. 1986, 64, 145–151. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V.J. Toward reliable density functional methods without adjustable parameters: The PBE0 model. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Treitel, N.; Shenhar, R.; Aprahamian, I.; Sheradsky, T.; Rabinovitz, M. Calculations of PAH anions: When are diffuse functions necessary? Phys. Chem. Chem. Phys. 2004, 6, 1113–1121. [Google Scholar] [CrossRef]
- Grimme, S. Supramolecular binding thermodynamics by dispersion-corrected density functional theory. Chem. Eur. J. 2012, 18, 9955–9965. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-corrected mean-field electronic structure methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
- Wang, C.-W.; Hui, K.; Chai, J.-D. Short- and long-range corrected hybrid density functionals with the D3 dispersion corrections. J. Chem. Phys. 2016, 145, 204101. [Google Scholar] [CrossRef]
- Li, S.L.; Truhlar, D.G. Improving Rydberg excitations within time-dependent density functional theory with generalized gradient approximations: The exchange-enhancement-for-large-gradient scheme. J. Chem. Theory Comput. 2015, 11, 3123–3130. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Liu, W. Critical assessment of TD-DFT for excited states of open-shell systems: I. doublet–doublet transitions. J. Chem. Theory Comput. 2016, 12, 238–260. [Google Scholar] [CrossRef]
- Fedunov, R.G.; Pozdnyakov, I.P.; Isaeva, E.A.; Zherin, I.I.; Egorov, N.B.; Glebov, E.M. Sulfur-containing radical anions formed by photolysis of thiosulfate: Quantum-chemical analysis. J. Phys. Chem. A 2023, 127, 4704–4714. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Liang, J.; Feng, X.; Hait, D.; Head-Gordon, M. Revisiting the performance of time-dependent density functional theory for electronic excitations: Assessment of 43 popular and recently developed functionals from rungs one to four. J. Chem. Theory Comput. 2022, 18, 3460–3473. [Google Scholar] [CrossRef] [PubMed]
- GaussView, Version 6.0.16; Dennington, R., Keith, T.A., Millam, J.M., Eds.; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).