Abstract
The current race for space exploration has hastened the development of electrochemical technologies for the in-situ utilisation of planetary resources for the synthesis of vital chemicals such as O2 and fuels. Understanding the physicochemical properties, such as the density and kinematic viscosity, of aqueous solutions is essential for the design of electrochemical devices for the electrolysis of water and CO2, particularly at low temperatures. The density and kinematic viscosity of highly concentrated Mg(ClO4)2 and KOH solutions have been determined, both at low temperatures and in the presence of CO2 gas. It was found that, for all of the solutions, independent of the concentration or nature of the electrolyte, as the temperature was decreased to 255 K, the density and the viscosity of the solutions increased. Upon saturation with CO2, no significant change to the density and viscosity of Mg(ClO4)2, at all of the temperatures measured, was observed. Conversely, the CO2 saturated solutions of KOH showed significant changes in density and viscosity at all temperatures, likely due to the formation of carbonates. The effects of these changes on the diffusion coefficient for dissolved CO2 is also discussed.
1. Introduction
The current exploration of extra-terrestrial surfaces relies on unmanned probes, such as Curiosity on the surface of Mars, Rosetta and its associated lander, Philae, which landed on the comet Churyumov–Gerasimenko, and the Voyager probes. However, human exploration and colonisation to the farthest reaches of our solar system face many challenges, which need to be overcome. To explore and colonise other planets for extended periods of time, human astronauts will need essential supplies, such as oxygen and chemicals that can be used as fuels. However, there are prohibitive weight limits to space travel; therefore, the practice of in-situ resource utilisation to generate products with local materials is essential in this endeavour. For example, future plans for the exploration of the Martian surface by humans involve refueling the ascent vehicles on the surface using in-situ resources. Transporting the necessary fuel from Earth would require almost 40 Mt of oxygen and methane, which clearly poses a significant challenge in weight transport [1,2] However, the first experiments to generate oxygen on the surface have already taken place. By December 2021, the Mars Oxygen In Situ Resource Utilisation experiment (MOXIE) had generated around 50 g of O2 via a solid oxide fuel cell at 800 °C from the compressed Martian atmosphere [1].
Other electrocatalytic processes could be carried out to produce the necessary chemicals, such as hydrogen or methane, through the electrolysis of CO2 dissolved in water [3,4]. The Phoenix lander observed gulley formations on the surface of Mars, likely caused by the flow of liquid over the surface, which, coupled with soil analysis, led to the conclusion that perchlorate brines exist under certain conditions on the surface of Mars [5,6,7,8,9,10,11]. Previous research has shown that lowering the temperature below 0 °C increases the production of CH4 and CO and decreases the production of H2 when CO2 is electrocatalytically reduced in brines of Mg(ClO4)2 [3]. The non-standard temperature and pressure conditions of extra-terrestrial regions need to be considered when designing catalytic processes, and they can sometimes be advantageous.
Parameters such as the pressure, temperature and electrolyte salinity are a rich area of research for the electrocatalytic conversion of CO2 on Earth [12,13,14] The ever-increasing concentration of CO2 in our atmosphere is causing climate change at an alarming rate. One avenue to mitigate the excessive accumulation of CO2 in the atmosphere is to capture CO2 at major production sites and either store it underground as CO2 clathrates or convert it to value-added products [15,16,17,18,19,20]. The electrocatalytic reduction of CO2 is one of many potential methods of CO2 conversion. Using concentrated electrolytes and low temperatures for a CO2 reduction reaction (CO2RR) is another avenue to increase CO2 solubility. Up to a point, the addition of salts to water lowers the freezing point, which means that electrocatalytic reactions can be carried out in the liquid phase at sub-zero temperatures [21,22,23,24,25].
It has been demonstrated that electrochemical processes can be carried out in solid aqueous electrolytes [26,27]; however, by increasing the electrolyte concentration, the freezing point of the solution can be depressed to maintain a liquid phase, which is more technologically advantageous. Blagden’s Law, Equation (1), can be used to estimate the depression in the freezing point of the electrolyte, ΔT, where K is the cryoscopic constant of the solvent, m is the molality (moles solute per kg solvent) and i is the Van’t Hoff factor, which describes the number of ions a species forms when fully dissociated.
Care should be taken when using Equation (1) as it does not account for the chemical activity of the ions and is only applicable for ideal solutions. Equation (1) can be used for general approximations, such as for the freezing point of sea water; however, at high concentrations, non-linear behaviour occurs and the freezing point begins to rise again [28,29]. Using brines as electrolytes enables the depression of the freezing point whilst, in theory, also favouring the increase in the solubility of certain gases, such as CO2, methane and O2 [30]. As such, the increase in the reactants might also increase the rate of the electrochemical reaction involving these gases. For example, in Mg(ClO4)2 brines, as the temperature is lowered to −35 °C, the solubility of O2 increases to around 1.1 mM and the current, due to O2 reduction, increases [31]. In previous works, we have also reported an increase in the reaction rate of the electrochemical conversion of CO2 and methane at sub-zero temperatures in aqueous brines of Mg(ClO4)2 and KOH [3].
At high pressures or low temperatures, gas clathrates are formed, where cages of water molecules encapsulate gas molecules [32]. These phases are well-known as, in the mining industry, they can form in gas pipelines, causing costly blockages, and because CH4 versions are found in permafrost or in the deep ocean. The CH4 hydrates found in the ocean and permafrost are a double-edged sword; they could be a huge reservoir of energy if electrocatalytic technology can be developed to exploit them, but there is a small possibility that if oceanic temperatures continue to rise, the hydrates may become unstable, releasing CH4 into the atmosphere and leading to runaway warming [33,34]. Several groups have explored the opportunity recovery of energy from CH4 clathrates and simultaneously sequestrated CO2 as clathrates through the direct swapping of CH4 by CO2 in one clathrate cavity.
Changes in temperature not only have an effect on the solubility of CO2 in aqueous electrolytes, but they also have a marked effect on the dynamic viscosity, η, and the density, ρ. These factors are not only important in the engineering of future technology, but also for fundamental processes such as the mass transport of ions. The Nernst-Plank Equation (2) is used to describe the mass transfer to an electrode, encompassing the processes of diffusion, convection and migration.
where at a distance x from an electrode for a species i, J is the flux (mol s−1 cm−2), D is the diffusion coefficient (cm2 s−1), C is the concentration (mol cm−3), z is the charge, F is the Faraday constant, R is the gas constant, T is the temperature (K), φ is the electrostatic potential (V) and v is the velocity (cm s−1). The diffusion coefficient, D, can be derived from the Einstein-Stokes Equation (3),
where kB is the Boltzmann constant, reff is the effective radius of the species (m) and η is the dynamic viscosity of the solution (Pa s). The dynamic viscosity is derived from the kinematic viscosity, ν (m2 s−1), and the density via Equation (4).
when designing electrolysers for any catalytic process involving a liquid reaction media, the viscosity of the media is important for the physical design aspects as the viscosity will affect the flow-through components. However, as Equation (2) shows, the flux of any reactants or products of the reaction is heavily influenced by the diffusion coefficient, which is, in-turn, heavily affected by the viscosity. Given the importance of the viscosity for mass transport during electrochemical reactions, such as CO2 conversion [35,36,37,38] and water splitting [39], herein we report the values of the density and dynamic viscosity at sub-zero temperatures down to 255 K for Mg(ClO4)2 and KOH brines in the absence of, and upon saturation with, CO2 gas.
These results can then be used to better understand the anti-Arrhenius behaviour seen during the electrochemical conversion of CO2 and the oxidation of methane at temperatures below −5 °C reported in our previous work [3]. A more complete understanding of the electrochemical conversion of CO2 at low temperatures will further promote the design of electrochemical devices for space exploration and colonisation.
2. Results and Discussion
2.1. Determination of the Density of Mg(ClO4)2 and KOH Solutions as a Function of Temperature
Figure 1 shows the densities of the Mg(ClO4)2 and KOH solutions as a function of the temperature. As expected, the density of all the solutions increases linearly with the decreasing temperature. At 255 K, 3.8 mol kg−1 is close to the saturation of the Mg(ClO4)2 solution, and below this temperature, precipitation of 6H2O·Mg(ClO4)2 occurs [28], which is the most stable form under Martian conditions [40]. Upon CO2 saturation, the solution of 3.8 m Mg(ClO4)2 showed no significant change in the density at any T measured, suggesting little absorption of CO2 in the solution. These results are in agreement with the poor solubility of CO2 at the pH of the Mg(ClO4)2 solutions (pH = 8). The previous work by our group using mass spectroscopy found that, in the same electrolyte, the concentration of CO2 increased from 1.12 mM at 293.15 K to 5.08 mM at 253 K [3]. However, such small changes in the concentration of CO2 in the solution are below the detection limit and within the standard deviation of the measurements using the methodology used in this work.
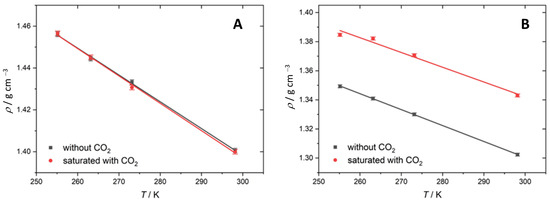
Figure 1.
Density as a function of temperature between 255 K and 298 K with CO2 (red) and without CO2 (black). (A) Results for 3.8 m Mg(ClO4)2. (B) Results for 8.5 m KOH.
Upon saturation with CO2, the density of 8.5 m KOH increases by 0.04 g cm−3 across all the measured temperatures (Table 1). This indicates that the amount of CO2 absorbed is constant over all temperatures in this range. Alternatively, as in the case of the Mg(ClO4)2, the variation in the concentration of CO2 is, again, too small to be seen via this methodology. In this regard, previous works have shown that, at room temperature, the concentration of absorbed CO2 increases with the concentration of KOH [41] due to the formation of (bi)carbonates, but at very high concentrations of the electrolyte, the CO2 solubility is limited due to the so-called “salting out” effect [42,43]. The balance between these factors—that is, (bi) carbonate formation and the salting out effect—and the expected increase in the CO2 solubility due to the lower temperature may account for the observed constant CO2 concentration across the temperatures measured.

Table 1.
Measured density of 3.8 m Mg(ClO4)2 and 8.5 m KOH solutions, with and without CO2 saturation.
2.2. Determination of the Viscosity of the Mg(ClO4)2 and KOH Solutions as a Function sof Temperature
The measured kinematic viscosity, ν, was converted to the dynamic viscosity, η, via Equation (4), and the results are shown in Table 2. For ν, the expanded uncertainty was 6 × 10−4 mm s−1. Over the temperature range investigated, the values of the viscosity for both the Mg(ClO4)2 and KOH solutions fit an Arrhenius relationship, Equation (5),
where R is the gas constant, A is the preexponential factor (Pa s) and Ea is the activation energy (kJ mol−1). The Arrhenius plots are shown in Figure 2A,B. Figure 2A shows little difference between η for the CO2 saturated and unsaturated Mg(ClO4)2 solution. This agrees with the interpretation of the ρ results, where there is little absorption of CO2. Previous work has attributed the increase in viscosity for concentrated Mg(ClO4)2 solutions to the formation of solvation spheres on a picosecond timescale around the ions, which act as suspended spheres in the solution, which in turn increases the viscosity [44].

Table 2.
Calculated η values for Mg(ClO4)2 and KOH solutions with and without saturation with CO2.
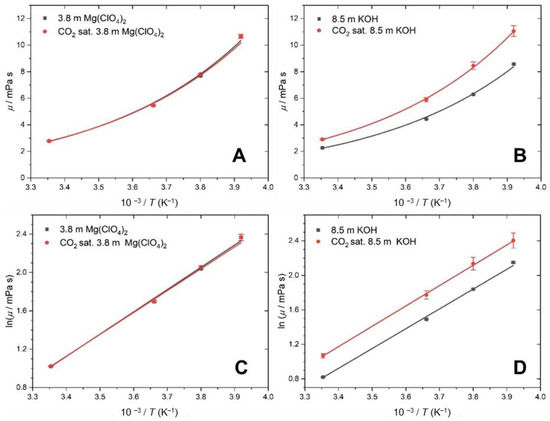
Figure 2.
Viscosity as a function of temperature (black) without CO2 and (red) upon saturation with CO2. (A,C) Results for 3.8 m Mg(ClO4)2. (B,D) Results for 8.5 m KOH.
On the other hand, Figure 2B shows an increase in the difference in η for the unsaturated and CO2 saturated KOH solutions as the temperature decreases. As ρ indicates that the concentration of CO2 is constant across the temperature range, the change in η must be due to changes in the strength of the intermolecular forces of attraction. When the CO2 dissolves, it reacts with the available water and sets up an equilibrium between CO32−, HCO3− and H2CO3. In concentrated KOH, the most abundant ion is HCO3−, which causes an associated lowering of the pH [41]. The carbonate ions can form hydrogen bonds and interact with the wider water network, which increases the intermolecular forces of attraction, and therefore the viscosity.
In order to obtain the activation energy of the system, Figure 2C,D show the Arrhenius linear representation of the measured values of the viscosity as a function of the temperature using Equation (6).
η∞ can be interpreted as the viscosity of the solution at infinite temperature (Pa s) and Ea is the energy input needed for molecules in the solution to flow past each other. These parameters are derived for each of the solutions, as shown in Table 3. There is a small increase in Ea when KOH is saturated with CO2, which supports the idea that there is an increase in the strength of the interactions between the ions.

Table 3.
Viscosity at infinite temperature and the activation energy for each solution derived from the linear fit in Figure 2C,D.
2.3. Determination of the Diffusion Coefficient of CO2 in Mg(ClO4)2 and KOH
Using the values for η determined in the previous section and Equation (3), the values for D were calculated, and the results are shown in Table 4. The hydrodynamic radius of the CO2 was assumed to be the same as in pure water [45], but loosely dependent on the temperature [46] As T decreases, the diffusion coefficient also decreases in both solutions. The larger η values for 8.5 m KOH correspond with lower D values compared to 3.8 m Mg(ClO4)2. According to Equation (2), the lower values of the diffusion coefficient indicate a lower flux and a decrease in the mass transport of CO2 through the solutions. The results obtained using pulsed-field gradient 13C NMR showed a trend of a decrease in D with increasing salinity of the brines; for example, 2.06 10−9 m2 s−1 in 1.0 m NaCl decreasing to 1.29 10−9 m2 s−1 in 5.0 m NaCl [45]. The results obtained using a Taylor dispersion method show that D also decreases with the temperature in pure water [46]; therefore, the results presented in Table 4 fit with the trends presented in the literature.

Table 4.
Calculated diffusion coefficient for CO2 in 3.8 m Mg(ClO4)2 and 8.5 m KOH at various temperatures.
Interestingly, our previous work showed an increase in the electrochemical conversion of CO2 in brines at sub-zero temperatures, with and without mass transport control. Therefore, even though the physicochemical properties of the solution, such as the density and viscosity, influence the diffusion of the gaseous reactant species, other intrinsic parameters promote Anti-Arrhenius behaviour so that, at low temperatures, the catalytic activity increases.
3. Materials and Methods
3.1. Preparation of Materials
Solutions of KOH (Sigma Aldrich, Gillingham, UK > 85%) and Mg(ClO4)2 (Alfa Aesar, Heysham, UK > 95%) were prepared by weighing out the required mass of solid using an analytical balance (measuring to 0.01 mg) and dissolving in a weighed mass of ultrapure water (Millipore Milli-Q® Integral 3, 18.2 MΩ cm−1, <5 ppb total organic carbon) to make the correct concentration in mol kg−1. All solutions were left in a temperature controlled 1:1 glycerol:water bath and cooled using a HUBER TC45E cooler with a temperature control ±0.5 K until they reached the desired temperature. Solutions were saturated with CO2 (BOC, N4 grade) by bubbling for 20 min at room temperature and pressures of 0.5 bar, and then for another 10 min at each temperature before each measurement was taken. Given the units involved in Equation (1), all the concentrations in the manuscript are reported in molality (moles solute per kg solvent). The supplier and purity of the reactants are included in Table 5.

Table 5.
CAS registry number, supplier and purity of materials used in this work.
3.2. Density Measurements
Pycnometers (±0.0100 cm3) were acquired from Fisher Scientific and calibrated using acetonitrile (Fisher Scientific, Morecambe, UK, 99.9%, Extra Dry over Molecular Sieves) at 298 K, 273 K, 263 K and 255 K. For density measurements, the pycnometers were filled with solutions that had been pre-cooled in the temperature-controlled bath and then left again to reach the desired temperature before measurements were taken (usually > 10 min). The reported densities for 8.5 m KOH and 3.8 m Mg(ClO4)2 are an average of at least 12 measurements from three different samples. The reported error is calculated via the root sum of the squares of the error in the pycnometer and the error in the calibration curve fit (error in volume of pycnometer ± 3 × 10−4 cm−3).
3.3. Viscosity Measurements
To measure the kinematic viscosity, an Ubbelohde viscometer (Paragon Scientific, Birkenhead, UK, ±0.17%) suspended in the same temperature-controlled bath was used. When solutions were introduced to the viscometer, the sample was again left to cool to temperature before any measurement took place. The flow time was measured with a digital stopwatch capable of measuring ±0.1 s. Kinematic viscosity (ν) was calculated using the equation,
where t is the flow time and A is the calibration constant of the viscometer. Kinematic viscosities are an average of at least 15 measurements from three different samples and the standard deviation of the measurements taken as the error.
The measured kinematic viscosity, ν, was converted to the dynamic viscosity, η, via Equation (4) and the errors propagated via root sum of the squares.
3.4. Methodology Validation
To validate the methodology, density and viscosity measurements were determined for pure water and KOH solutions and are compared to previous works. As can be seen in Table 6, in the case of water, both the density and the dynamic viscosity are within 1% of the literature results [47]. For 8.5 m KOH, the density value reported in this work is within 1% of the literature value; however, the dynamic viscosity has a 4% deviation [48]. Such an error can be associated with the hygroscopic nature of KOH solutions causing a decrease in the concentration of the solutions during measurement of the viscosity.

Table 6.
Comparison between density and viscosity measurements obtained in this work and in previous reports. a Reference [47]. b Calculated from reference [48].
For 3.8 m Mg(ClO4)2, there are few values in the literature with which to compare. However, for 4.23 m Mg(ClO4)2 at 298 K, Sohnel et al. recorded a value of ρ = 1.4373 g cm−3 [49]. Herein, we record ρ = 1.4006 g cm−3 at the same temperature for the lower concentration of 3.8 m. Similarly, for 8.21 m KOH at 273 K, Kelly et al. recorded ρ = 1.4373 g cm−3 and η = 4.409 mPa s [50]. In comparison, the values recorded herein for 8.5 m KOH at 273 K are 1.3300 g cm−3 and 4.44 mPa s. Again, we ascribe deviations to the hygroscopic nature of concentrated KOH solutions.
4. Conclusions
The density and dynamic viscosity of the highly concentrated KOH and Mg(ClO4)2 solutions were measured and reported at temperatures below 273 K. The high electrolyte concentration results in the depression of the freezing point of the aqueous solution down to 255 K. It was found that as the temperature decreased, the η and ρ for all the solutions increased. The ρ increased linearly and the η followed an Arrhenius relationship. Given the importance of these solutions for the development of electrolysers on other planetary objects, the density and dynamic viscosity of the same KOH and Mg(ClO4)2 solutions saturated with CO2 are also reported.
The 3.8 m Mg(ClO4)2 showed no significant differences in η or ρ at any measured temperature after saturation with CO2. The results are associated with the poor solubility of CO2 at the pH of the Mg(ClO4)2. Conversely, the 8.5 m KOH solutions showed marked changes in their physicochemical behaviour upon saturation with CO2. A constant increase in the ρ was observed; at the same time, a much greater increase was observed in the η at lower temperatures. We conclude that the formation of (bi) carbonate species due to the reaction between the CO2 and KOH increased the strength of the interactions between the ions, resulting in a larger change in the viscosity at lower temperatures.
At low temperatures, the diffusion coefficient of CO2 is significantly reduced in these solutions, which will result in less mass transport through the electrolyte. This indicates that the increase in the CO2 reduction current at low temperatures seen in our previous work is due to an increase in the kinetics of the reaction, not an increase in the transport of CO2 to the electrode surface [3]. However, the benefit of the increased activity at low temperatures is finely balanced with the disadvantageous increase in the viscosity of the solutions and the decrease in the diffusion of CO2.
On the basis of these results, we believe that the increase in the electrochemical activity in the electrochemical reduction of CO2, and possibly the oxidation of CH4 at low temperatures [3], could be related to the large DC electric field near the surface due to changes in the double layer (DL) associated with the high concentration of the electrolyte and the low temperature. The electric field from the solvated cations in the DL can substantially favour the formation of key intermediates of the reactions, thus increasing the kinetics of the reaction [51]. These insights are crucial for the further investigation of catalytic reactions at low temperatures in brines.
Author Contributions
Conceptualization, E.S. and P.R.; Validation, E.S.; Formal analysis, E.S.; Investigation, E.S.; Data curation, P.R.; Writing—original draft, E.S.; Writing—review & editing, E.S. and P.R.; Supervision, P.R.; Project administration, P.R.; Funding acquisition, P.R. All authors have read and agreed to the published version of the manuscript.
Funding
E.S. acknowledges the University of Birmingham and the EPSRC Centre for Doctoral Training in Carbon Capture and Storage and Cleaner Fossil Energy for financial support through Ph.D. scholarships at the School of Chemistry. P.R. acknowledges the University of Birmingham for financial support through the Ikerbasque foundation. P.R. also acknowledges funding from Leverhulme grant RPG-2021-013.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Not applicable.
Abbreviations
| MOXIE | Mars Oxygen In Situ Resource Utilisation experiment |
| CO2RR | CO2 reduction reaction |
| ΔT | depression in freezing point of the electrolyte |
| K | cryoscopic constant of the solvent |
| m | molality (moles solute per kg solvent) |
| i | Van’t Hoff factor |
| η | dynamic viscosity (mPa s) |
| ρ | density (g cm−3) |
| J | flux (mol s−1 cm−2) |
| D | diffusion coefficient (cm2 s−1) |
| C | is the concentration (mol cm−3) |
| z | charge |
| F | Faraday constant |
| R | gas constant |
| T | temperature (K), |
| φ | electrostatic potential (V), |
| v | velocity (cm s−1) |
| ν | kinematic viscosity (mm2 s−1) |
| A | preexponential factor (Pa s), |
| Ea | activation energy (kJ mol−1) |
References
- Hoffman, J.A.; Hecht, M.H.; Rapp, D.; Hartvigsen, J.J.; SooHoo, J.G.; Aboobaker, A.M.; McClean, J.B.; Liu, A.M.; Hinterman, E.D.; Nasr, M.; et al. Mars Oxygen ISRU Experiment (MOXIE)-Preparing for human Mars exploration. Sci. Adv. 2022, 8, eabp8636. [Google Scholar] [CrossRef]
- Hecht, M.; Hoffman, J.; Rapp, D.; McClean, J.; SooHoo, J.; Schaefer, R.; Aboobaker, A.; Mellstrom, J.; Hartvigsen, J.; Meyen, F.; et al. Mars Oxygen ISRU Experiment (MOXIE). Space Sci. Rev. 2021, 217, 9. [Google Scholar] [CrossRef]
- Sargeant, E.; Kolodziej, A.; Le Duff, C.S.; Rodriguez, P. Electrochemical Conversion of CO2 and CH4 at Subzero Temperatures. ACS Catal. 2020, 10, 7464–7474. [Google Scholar] [CrossRef]
- Gayen, P.; Sankarasubramanian, S.; Ramani, V.K. Fuel and oxygen harvesting from Martian regolithic brine. Proc. Natl. Acad. Sci. USA 2020, 117, 31685–31689. [Google Scholar] [CrossRef]
- Hecht, M.H.; Kounaves, S.P.; Quinn, R.C.; West, S.J.; Young, S.M.M.; Ming, D.W.; Catling, D.C.; Clark, B.C.; Boynton, W.V.; Hoffman, J.; et al. Detection of Perchlorate and the Soluble Chemistry of Martian Soil at the Phoenix Lander Site. Science 2009, 325, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Smith, P.H.; Tamppari, L.K.; Arvidson, R.E.; Bass, D.; Blaney, D.; Boynton, W.V.; Carswell, A.; Catling, D.C.; Clark, B.C.; Duck, T.; et al. H2O at the Phoenix Landing Site. Science 2009, 325, 58–61. [Google Scholar] [CrossRef] [PubMed]
- Toner, J.; Catling, D. Chlorate brines on Mars: Implications for the occurrence of liquid water and deliquescence. Earth Planet. Sci. Lett. 2018, 497, 161–168. [Google Scholar] [CrossRef]
- Primm, K.; Gough, R.; Chevrier, V.; Tolbert, M. Freezing of perchlorate and chloride brines under Mars-relevant conditions. Geochim. Cosmochim. Acta 2017, 212, 211–220. [Google Scholar] [CrossRef]
- Chevrier, V.F.; Fitting, A.B.; Rivera-Valentín, E.G. Limited Stability of Multicomponent Brines on the Surface of Mars. Planet. Sci. J. 2022, 3, 125. [Google Scholar] [CrossRef]
- Jo, S.W.; Kim, J.Y.; Lee, M.W.; Kim, Y.; Ahn, H.S. Highly Selective Reduction of CO2 to Methane Induced by Subzero Depression of the Electrode Surface Temperature. ACS Catal. 2023, 13, 5122–5126. [Google Scholar] [CrossRef]
- Shahid, M.; Chambers, B.; Sankarasubramanian, S. Methane and oxygen from energy-efficient, low temperature in situ resource utilization enables missions to Mars. AIChE J. 2023, 69, e18010. [Google Scholar] [CrossRef]
- König, M.; Vaes, J.; Klemm, E.; Pant, D. Solvents and Supporting Electrolytes in the Electrocatalytic Reduction of CO2. iScience 2019, 19, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Papasizza, M.; Yang, X.; Cheng, J.; Cuesta, A. Electrocatalytic reduction of CO2 in neat and water-containing imidazolium-based ionic liquids. Curr. Opin. Electrochem. 2020, 23, 80–88. [Google Scholar] [CrossRef]
- Birdja, Y.Y.; Pérez-Gallent, E.; Figueiredo, M.C.; Göttle, A.J.; Calle-Vallejo, F.; Koper, M.T. Advances and challenges in understanding the electrocatalytic conversion of carbon dioxide to fuels. Nat. Energy 2019, 4, 732–745. [Google Scholar] [CrossRef]
- Zheng, J.; Chong, Z.R.; Qureshi, M.F.; Linga, P. Carbon Dioxide Sequestration via Gas Hydrates: A Potential Pathway toward Decarbonization. Energy Fuels 2020, 34, 10529–10546. [Google Scholar] [CrossRef]
- Fan, L.; Xia, C.; Yang, F.; Wang, J.; Wang, H.; Lu, Y. Strategies in catalysts and electrolyzer design for electrochemical CO2 reduction toward C2+ products. Sci. Adv. 2020, 6, eaay3111. [Google Scholar] [CrossRef]
- Monzó, J.; Malewski, Y.; Kortlever, R.; Vidal-Iglesias, F.J.; Solla-Gullón, J.; Koper, M.T.M.; Rodriguez, P. Enhanced electrocatalytic activity of Au@Cu core@shell nanoparticles towards CO2 reduction. J. Mater. Chem. A 2015, 3, 23690–23698. [Google Scholar] [CrossRef]
- Le Duff, C.S.; Lawrence, M.J.; Rodriguez, P. Role of the adsorbed oxygen species in the selective electrochemical reduction of CO2 to alcohols and carbonyls on copper electrodes. Angew. Chemie Int. Ed. 2017, 12919–12924. [Google Scholar] [CrossRef]
- Nitopi, S.; Bertheussen, E.; Scott, S.B.; Liu, X.; Engstfeld, A.K.; Horch, S.; Seger, B.; Stephens, I.E.; Chan, K.; Hahn, C.; et al. Progress and Perspectives of Electrochemical CO2 Reduction on Copper in Aqueous Electrolyte. Chem. Rev. 2019, 119, 7610–7672. [Google Scholar] [CrossRef]
- Lawrence, M.J.; Celorrio, V.; Sargeant, E.; Huang, H.; Rodríguez-López, J.; Zhu, Y.; Gu, M.; Russell, A.E.; Rodriguez, P. Insight into the Activity and Selectivity of Nanostructured Copper Titanates during Electrochemical Conversion of CO2 at Neutral pH via In Situ X-ray Absorption Spectroscopy. ACS Appl. Mater. Interfaces 2022, 14, 2742–2753. [Google Scholar] [CrossRef]
- Ndlovu, P.; Babaee, S.; Naidoo, P. Review on CH4-CO2 replacement for CO2 sequestration and CH4/CO2 hydrate formation in porous media. Fuel 2022, 320, 123795. [Google Scholar] [CrossRef]
- Liu, T.; Wu, P.; Chen, Z.; Li, Y. Review on Carbon Dioxide Replacement of Natural Gas Hydrate: Research Progress and Perspectives. Energy Fuels 2022, 36, 7321–7336. [Google Scholar] [CrossRef]
- Tung, Y.-T.; Chen, L.-J.; Chen, Y.-P.; Lin, S.-T. In situ methane recovery and carbon dioxide sequestration in methane hydrates: A molecular dynamics simulation study. J. Phys. Chem. B 2011, 115, 15295–15302. [Google Scholar] [CrossRef] [PubMed]
- Wilson, I.; Saini, S.; Sreenivasan, H.; Sahu, C.; Krishna, S.; Gupta, P. Review and Perspectives of Energy-Efficient Methane Production from Natural Gas Hydrate Reservoirs Using Carbon Dioxide Exchange Technology. Energy Fuels 2023, 37, 9841–9872. [Google Scholar] [CrossRef]
- Ding, Y.-L.; Wang, H.-Q.; Lv, T. Effect of Gas Exchange Interval on CH4 Recovery Efficiency and Study of Mechanism of CH4 Hydrate Replacement by CO2 Mixture. Front. Energy Res. 2021, 9, 4–11. [Google Scholar] [CrossRef]
- Frese, U.; Iwasita, T.; Schmickler, W.; Stimming, U. Hydrogen evolution in liquid and frozen aqueous electrolyte. J. Phys. Chem. 1985, 89, 1059–1062. [Google Scholar] [CrossRef]
- Borkowska, Z.; Cappadonia, M.; Stimming, U. Interfacial and bulk electrolyte properties in frozen electrolyte studies. Electrochim. Acta 1992, 37, 565–568. [Google Scholar] [CrossRef]
- Pestova, O.N.; Myund, L.A.; Khripun, M.K.; Prigaro, A.V. Polythermal Study of the Systems M(ClO4)2-H2O (M2+ = Mg2+, Ca2+, Sr2+, Ba2+). Russ. J. Appl. Chem. 2005, 78, 409–413. [Google Scholar] [CrossRef]
- Haynes, W. Concentrative properties of aqueous solutions: Density, refractive index, freezing point depression, and viscosity. In CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2012; pp. 5–128. ISBN 9781439880494. [Google Scholar]
- Diamond, L.W.; Akinfiev, N.N. Solubility of CO2 in water from −1.5 to 100 °C and from 0.1 to 100 MPa: Evaluation of literature data and thermodynamic modelling. Fluid Phase Equilib 2003, 208, 265–290. [Google Scholar] [CrossRef]
- Elliott, J.; Ngamchuea, K.; Batchelor-McAuley, C.; Compton, R.G. Martian Redox Chemistry: Oxygen Reduction in Low-Temperature Magnesium Perchlorate Brines. J. Phys. Chem. Lett. 2017, 8, 6171–6175. [Google Scholar] [CrossRef]
- Sloan, E.D.; Koh, C.A. Clathrate Hydrates of Natural Gases, 3rd ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
- Dean, J.F. Old methane and modern climate change. Science 2020, 367, 846–848. [Google Scholar] [CrossRef] [PubMed]
- Ruppel, C.D.; Kessler, J.D. The interaction of climate change and methane hydrates. Rev. Geophys. 2017, 55, 126–168. [Google Scholar] [CrossRef]
- Gupta, N.; Gattrell, M.; MacDougall, B. Calculation for the cathode surface concentrations in the electrochemical reduction of CO2 in KHCO3 solutions. J. Appl. Electrochem. 2006, 36, 161–172. [Google Scholar] [CrossRef]
- Varela, A.S.; Kroschel, M.; Reier, T.; Strasser, P. Controlling the selectivity of CO2 electroreduction on copper: The effect of the electrolyte concentration and the importance of the local pH. Catal. Today 2016, 260, 8–13. [Google Scholar] [CrossRef]
- Raciti, D.; Mao, M.; Wang, C. Mass transport modelling for the electroreduction of CO2 on Cu nanowires. Nanotechnology 2018, 29, 044001. [Google Scholar] [CrossRef]
- Zhang, B.A.; Ozel, T.; Elias, J.S.; Costentin, C.; Nocera, D.G. Interplay of Homogeneous Reactions, Mass Transport, and Kinetics in Determining Selectivity of the Reduction of CO2 on Gold Electrodes. ACS Cent. Sci. 2019, 5, 1097–1105. [Google Scholar] [CrossRef]
- Goyal, A.; Koper, M.T.M. Understanding the role of mass transport in tuning the hydrogen evolution kinetics on gold in alkaline media. J. Chem. Phys. 2021, 155, 134705. [Google Scholar] [CrossRef]
- Robertson, K.; Bish, D. Stability of phases in the Mg(ClO4)2·nH2O system and implications for perchlorate occurrences on Mars. J. Geophys. Res. Planets 2011, 116, 1–7. [Google Scholar] [CrossRef]
- Zhong, H.; Fujii, K.; Nakano, Y.; Jin, F. Effect of CO2 Bubbling into Aqueous Solutions Used for Electrochemical Reduction of CO2 for Energy Conversion and Storage. J. Phys. Chem. C 2015, 119, 55–61. [Google Scholar] [CrossRef]
- Dinh, C.-T.; Burdyny, T.; Kibria, M.G.; Seifitokaldani, A.; Gabardo, C.M.; de Arquer, F.P.G.; Kiani, A.; Edwards, J.P.; De Luna, P.; Bushuyev, O.S.; et al. CO2 electroreduction to ethylene via hydroxide-mediated copper catalysis at an abrupt interface. Science 2018, 360, 783–787. [Google Scholar] [CrossRef]
- Gilbert, K.; Bennett, P.C.; Wolfe, W.; Zhang, T.; Romanak, K.D. CO2 solubility in aqueous solutions containing Na+, Ca2+, Cl−, SO42− and HCO3−: The effects of electrostricted water and ion hydration thermodynamics. Appl. Geochem. 2016, 67, 59–67. [Google Scholar] [CrossRef]
- Omta, A.W.; Kropman, M.F.; Woutersen, S.; Bakker, H.J. Negligible Effect of Ions on the Hydrogen-Bond Structure in Liquid Water. Science 2003, 301, 347–349. [Google Scholar] [CrossRef] [PubMed]
- Cadogan, S.P.; Hallett, J.P.; Maitland, G.C.; Trusler, J.P.M. Diffusion Coefficients of Carbon Dioxide in Brines Measured Using 13 C Pulsed-Field Gradient Nuclear Magnetic Resonance. J. Chem. Eng. Data 2015, 60, 181–184. [Google Scholar] [CrossRef]
- Cadogan, S.P.; Maitland, G.C.; Trusler, J.M. Diffusion Coefficients of CO2 and N2 in Water at Temperatures between 298.15 K and 423.15 K at Pressures up to 45 MPa. J. Chem. Eng. Data 2014, 59, 519–525. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2004; Volume 85. [Google Scholar]
- Sipos, P.M.; Hefter, G.; May, P.M. Viscosities and Densities of Highly Concentrated Aqueous MOH Solutions (M+ = Na+, K+, Li+, Cs+, (CH3)4 N+) at 25.0 °C. J. Chem. Eng. Data 2000, 45, 613–617. [Google Scholar] [CrossRef]
- Sohnel, O.; Novotny, P.; Solc, Z. Densities of aqueous solutions of 18 inorganic substances. J. Chem. Eng. Data 1984, 29, 379–382. [Google Scholar] [CrossRef]
- Kelly, W.R.; Borza, P.F.; Harriger, R.D. Densities and Viscosities of Potassium Hydroxide Solutions at Low Temperatures. J. Chem. Eng. Data 1965, 10, 233–234. [Google Scholar] [CrossRef]
- Chen, L.D.; Urushihara, M.; Chan, K.; Nørskov, J.K. Electric Field Effects in Electrochemical CO2 Reduction. ACS Catal. 2016, 6, 7133–7139. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).