Structure, Stability, and Superconductivity of Two-Dimensional Janus NbSH Monolayers: A First-Principle Investigation
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
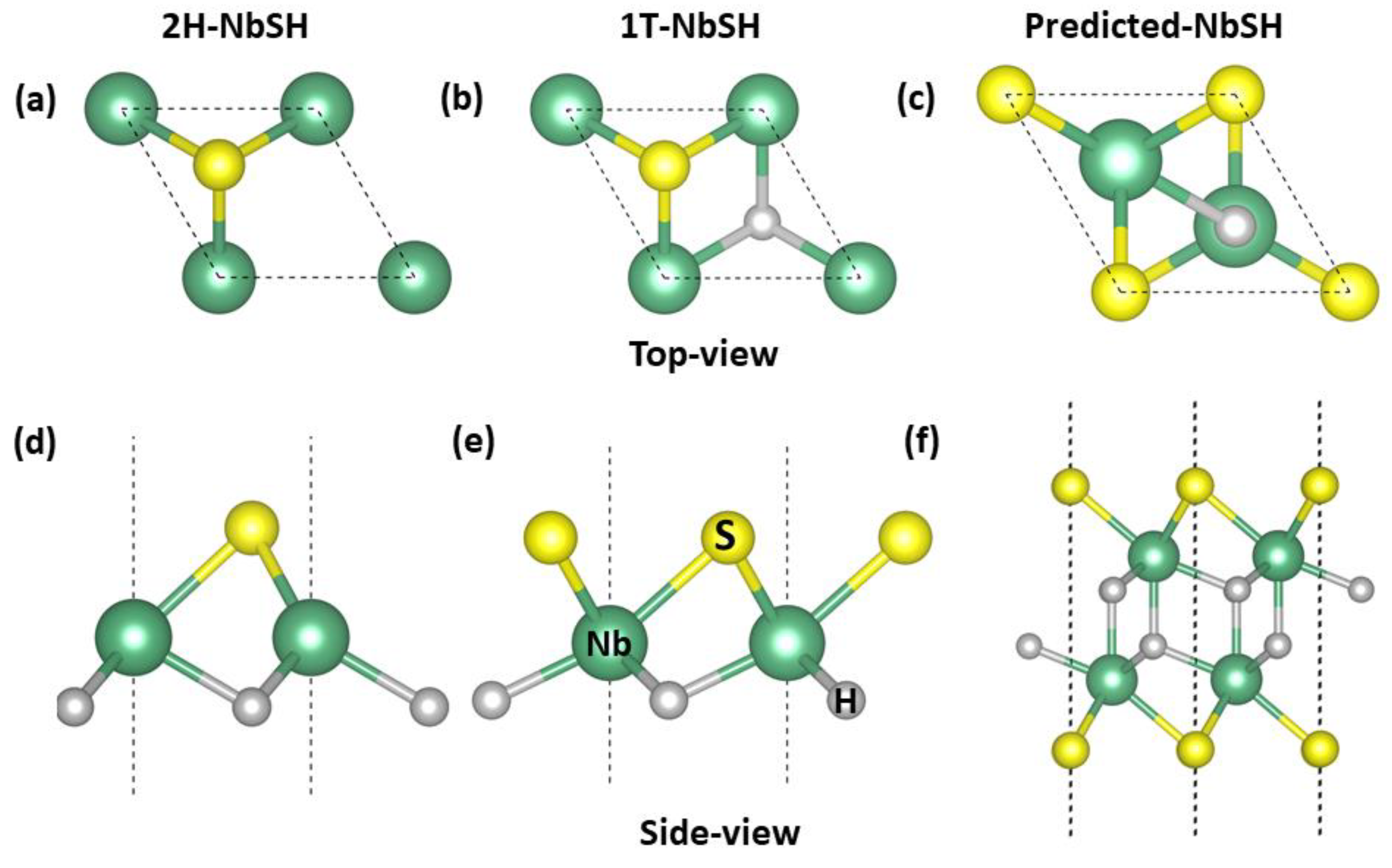
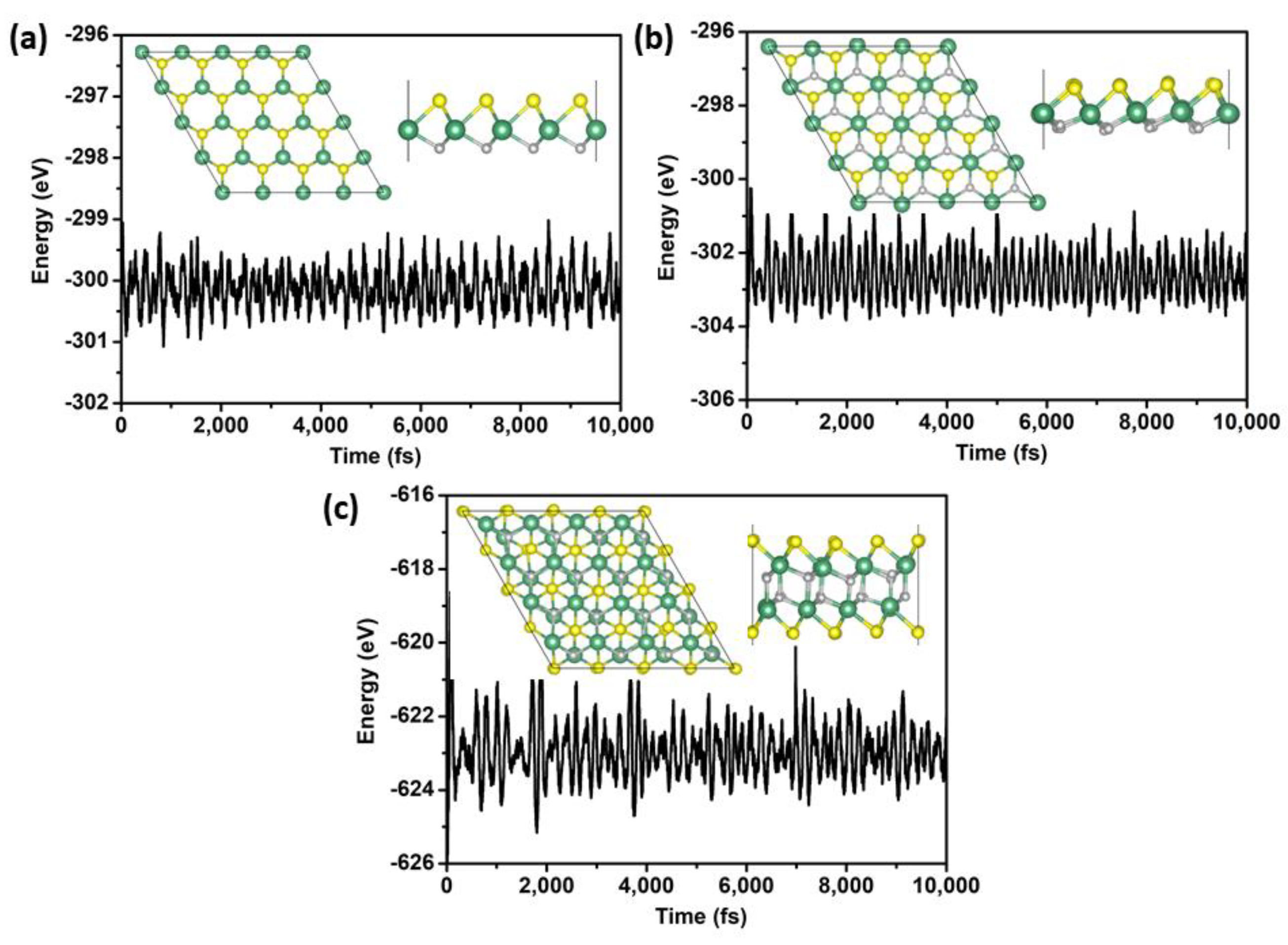
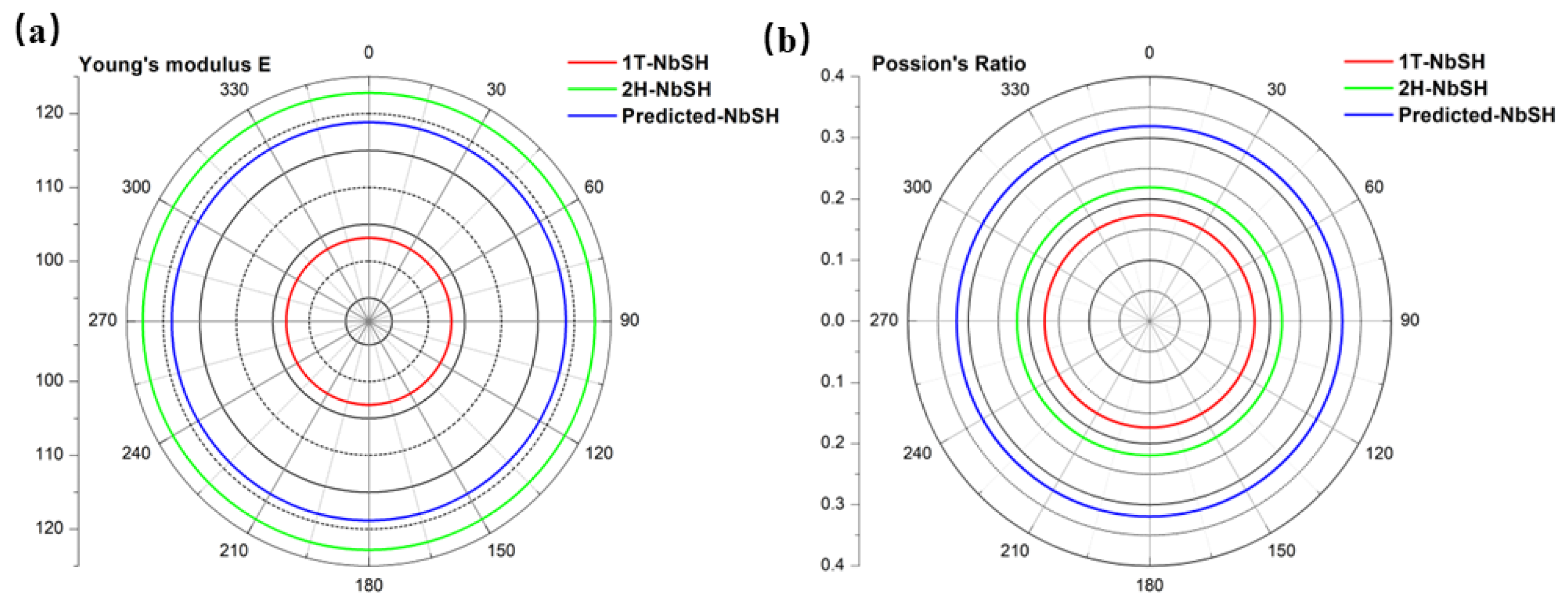
3.1. Structure and Stability
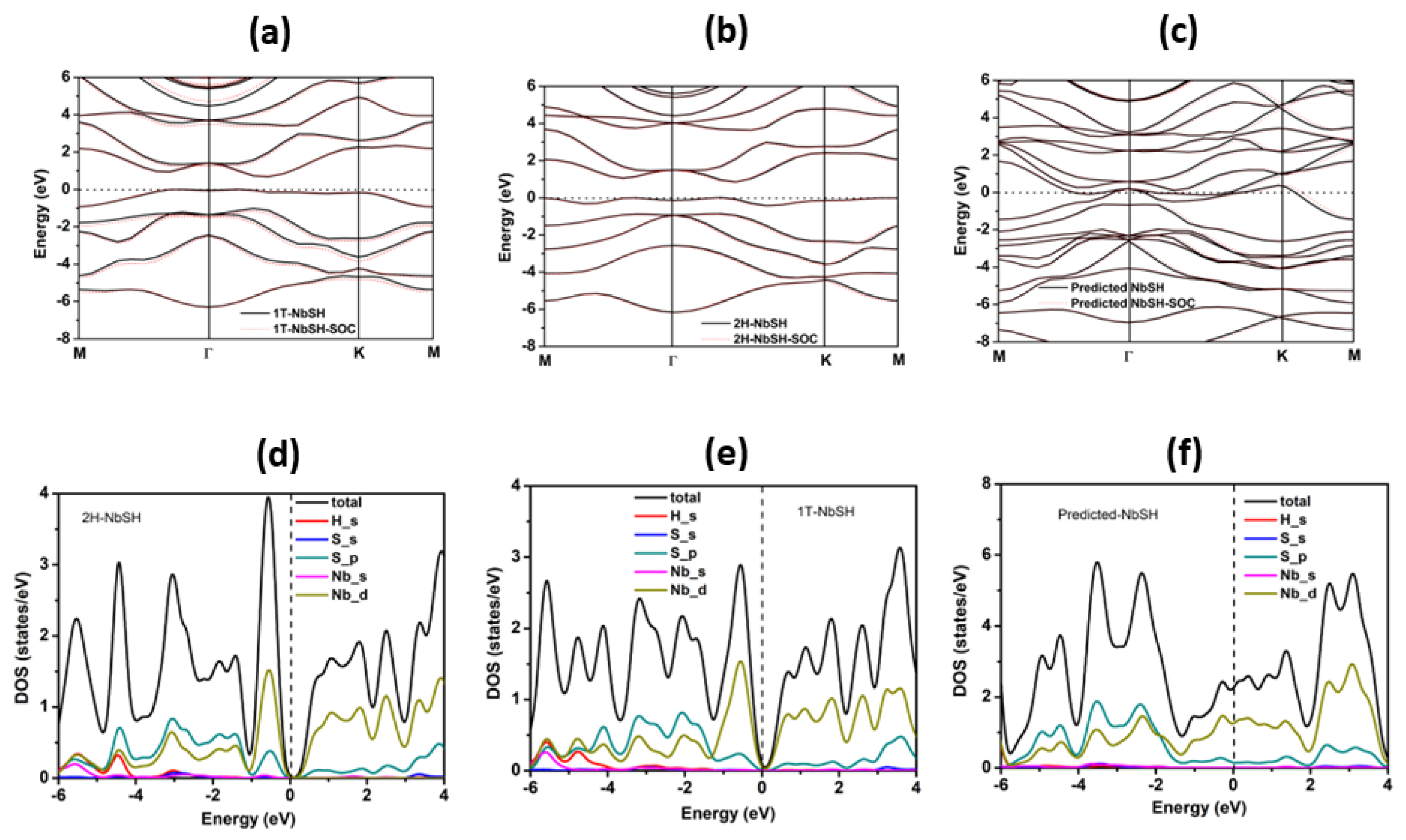
3.2. Electronic Properties
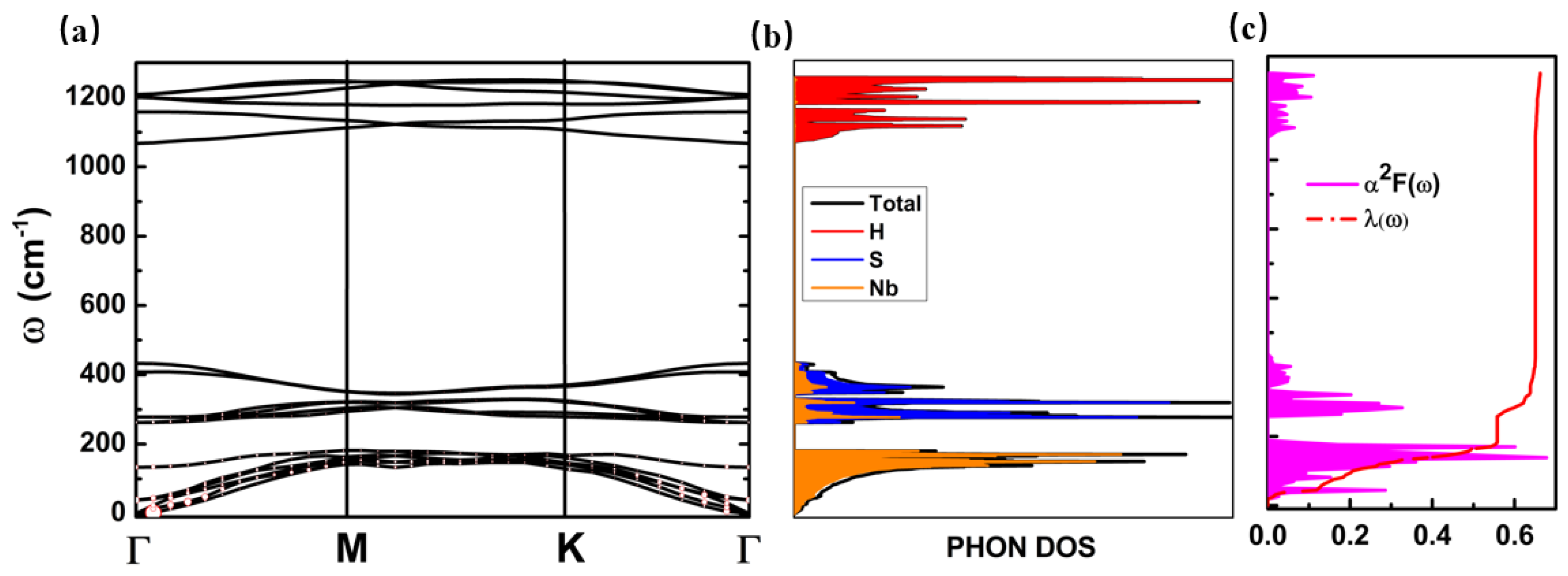
3.3. Superconductivity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.; Khotkevich, V.; Morozov, S.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.-Y.; Sun, S.-H.; Sun, X.-J.; Zhao, Y.-R.; Chen, L.; Yang, Y.; Lü, W.; Li, D.-B. Plasma-induced, nitrogen-doped graphene-based aerogels for high-performance supercapacitors. Light Sci. Appl. 2016, 5, 16130. [Google Scholar] [CrossRef] [PubMed]
- Wei, W.; Sun, K.; Hu, Y.H. An efficient counter electrode material for dye-sensitized solar cells-flower-structured 1T metallic phase MoS2. J. Mater. Chem. A 2016, 4, 12398–12401. [Google Scholar] [CrossRef]
- Zhuang, H.L.; Hennig, R.G. Single-layer group-III monochalcogenide photocatalysts for water splitting. Chem. Mater. 2013, 25, 3232–3238. [Google Scholar] [CrossRef]
- Ding, Y.C.; Xiao, B.; Li, J.L.; Deng, Q.J.; Xu, Y.H.; Wang, H.F.; Rao, D.W. Improved Transport Properties and Novel Li Diffusion Dynamics in van der Waals C2N/Graphene Heterostructure as Anode Materials for Lithium-Ion Batteries: A First-Principles Investigation. J. Phys. Chem. C 2019, 123, 3353–3367. [Google Scholar] [CrossRef]
- Liu, W.; Guo, X.; Schwartz, J.; Xie, H.; Dhale, N.U.; Sung, S.H.; Kondusamy, A.L.N.; Wang, X.; Zhao, H.; Berman, D. A three-stage magnetic phase transition revealed in ultrahigh-quality van der Waals bulk magnet CrSBr. ACS Nano 2022, 16, 15917–15926. [Google Scholar] [CrossRef]
- Liu, W.; Osanloo, M.R.; Wang, X.; Li, S.; Dhale, N.; Wu, H.; Van de Put, M.L.; Tiwari, S.; Vandenberghe, W.G.; Lv, B. New Verbeekite-type polymorphic phase and rich phase diagram in the PdSe 2−xTex system. Phys. Rev. B 2021, 104, 024507. [Google Scholar] [CrossRef]
- Singh, R.; Bester, G. Hydrofluorinated graphene: Two-dimensional analog of polyvinylidene fluoride. Phys. Rev. B 2011, 84, 155427. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, J.; Yang, M.; Xie, Q.; Peng, H.; Liu, Z. Janus graphene from asymmetric two-dimensional chemistry. Nat. Commun. 2013, 4, 1443. [Google Scholar] [CrossRef]
- Trivedi, D.B.; Turgut, G.; Qin, Y.; Sayyad, M.Y.; Hajra, D.; Howell, M.; Liu, L.; Yang, S.; Patoary, N.H.; Li, H. Room-temperature synthesis of 2D Janus crystals and their heterostructures. Adv. Mater. 2020, 32, 2006320. [Google Scholar] [CrossRef] [PubMed]
- Lu, A.-Y.; Zhu, H.; Xiao, J.; Chuu, C.-P.; Han, Y.; Chiu, M.-H.; Cheng, C.-C.; Yang, C.-W.; Wei, K.-H.; Yang, Y. Janus monolayers of transition metal dichalcogenides. Nat. Nanotechnol. 2017, 12, 744–749. [Google Scholar] [CrossRef] [PubMed]
- Sant, R.; Gay, M.; Marty, A.; Lisi, S.; Harrabi, R.; Vergnaud, C.; Dau, M.T.; Weng, X.; Coraux, J.; Gauthier, N. Synthesis of epitaxial monolayer Janus SPtSe. npj 2D Mater. Appl. 2020, 4, 41. [Google Scholar] [CrossRef]
- Tang, X.; Kou, L. 2D Janus transition metal dichalcogenides: Properties and applications. Phys. Status Solidi (B) 2022, 259, 2100562. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, S.; Kholmanov, I.; Dong, L.; Er, D.; Chen, W.; Guo, H.; Jin, Z.; Shenoy, V.B.; Shi, L. Janus monolayer transition-metal dichalcogenides. ACS Nano 2017, 11, 8192–8198. [Google Scholar] [CrossRef]
- Shi, W.; Fan, K.; Wang, Z. Catalytic activity for the hydrogen evolution reaction of edges in Janus monolayer MoXY (X/Y = S, Se, and Te). Phys. Chem. Chem. Phys. 2018, 20, 29423–29429. [Google Scholar] [CrossRef]
- Guan, Z.; Ni, S.; Hu, S. Tunable electronic and optical properties of monolayer and multilayer Janus MoSSe as a photocatalyst for solar water splitting: A first-principles study. J. Phys. Chem. C 2018, 122, 6209–6216. [Google Scholar] [CrossRef]
- Ge, L.; Fu, Z.; Lu, Y. Activating basal plane of Janus VSSe for efficient hydrogen evolution reaction by non-noble metal element doping: A first-principal study. Int. J. Hydrogen Energy 2022, 47, 34924–34931. [Google Scholar] [CrossRef]
- You, L.; Wang, Y.; Zhou, K. 2D Pentagonal Pd-Based Janus Transition Metal Dichalcogenides for Photocatalytic Water Splitting. Phys. Status Solidi RRL 2022, 16, 2100344. [Google Scholar] [CrossRef]
- Mohanta, M.K.; De Sarkar, A. Interfacial hybridization of Janus MoSSe and BX (X = P, As) monolayers for ultrathin excitonic solar cells, nanopiezotronics and low-power memory devices. Nanoscale 2020, 12, 22645–22657. [Google Scholar] [CrossRef]
- Jin, C.; Tang, X.; Tan, X.; Smith, S.C.; Dai, Y.; Kou, L. A Janus MoSSe monolayer: A superior and strain-sensitive gas sensing material. J. Mater. Chem. A 2019, 7, 1099–1106. [Google Scholar] [CrossRef]
- Cui, Y.; Peng, L.; Sun, L.; Li, M.; Zhang, X.; Huang, Y. Structures, stabilities and piezoelectric properties of Janus gallium oxides and chalcogenides monolayers. J. Phys. Condens. Matter 2019, 32, 08LT01. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Zhou, S.; Bai, Y.; Zhao, J. Enhanced piezoelectric effect in Janus group-III chalcogenide monolayers. Appl. Phys. Lett. 2017, 110, 163102. [Google Scholar] [CrossRef]
- Dong, L.; Lou, J.; Shenoy, V.B. Large in-plane and vertical piezoelectricity in Janus transition metal dichalchogenides. ACS Nano 2017, 11, 8242–8248. [Google Scholar] [CrossRef] [PubMed]
- Yagmurcukardes, M.; Sevik, C.; Peeters, F. Electronic, vibrational, elastic, and piezoelectric properties of monolayer Janus MoSTe phases: A first-principles study. Phys. Rev. B 2019, 100, 045415. [Google Scholar] [CrossRef]
- Ghobadi, N.; Rudi, S.G.; Soleimani-Amiri, S. Electronic, spintronic, and piezoelectric properties of new Janus Zn A X Y (A = Si, Ge, Sn, and X, Y = S, Se, Te) monolayers. Phys. Rev. B 2023, 107, 075443. [Google Scholar] [CrossRef]
- Bezzerga, D.; Haidar, E.-A.; Stampfl, C.; Mir, A.; Sahnoun, M. Ferro-piezoelectricity in emerging Janus monolayer BMX2 (M = Ga, In and X = S, Se): Ab initio investigations. Nanoscale Adv. 2023, 5, 1425–1432. [Google Scholar] [CrossRef]
- Frey, N.C.; Bandyopadhyay, A.; Kumar, H.; Anasori, B.; Gogotsi, Y.; Shenoy, V.B. Surface-engineered MXenes: Electric field control of magnetism and enhanced magnetic anisotropy. ACS Nano 2019, 13, 2831–2839. [Google Scholar] [CrossRef]
- Abdollahi, M.; Tagani, M.B. Janus 2H-VSSe monolayer: Two-dimensional valleytronic semiconductor with nonvolatile valley polarization. J. Phys. Condens. Matter 2022, 34, 185702. [Google Scholar] [CrossRef]
- Zhang, C.; Nie, Y.; Sanvito, S.; Du, A. First-principles prediction of a room-temperature ferromagnetic Janus VSSe monolayer with piezoelectricity, ferroelasticity, and large valley polarization. Nano Lett. 2019, 19, 1366–1370. [Google Scholar] [CrossRef]
- Koo, H.C.; Kim, S.B.; Kim, H.; Park, T.E.; Choi, J.W.; Kim, K.W.; Go, G.; Oh, J.H.; Lee, D.K.; Park, E.S. Rashba effect in functional spintronic devices. Adv. Mater. 2020, 32, 2002117. [Google Scholar] [CrossRef] [PubMed]
- Bihlmayer, G.; Rader, O.; Winkler, R. Focus on the Rashba effect. New J. Phys. 2015, 17, 050202. [Google Scholar] [CrossRef]
- Liu, Q.; Guo, Y.; Freeman, A.J. Tunable Rashba effect in two-dimensional LaOBiS2 films: Ultrathin candidates for spin field effect transistors. Nano Lett. 2013, 13, 5264–5270. [Google Scholar] [CrossRef] [PubMed]
- Chuang, P.; Ho, S.-C.; Smith, L.W.; Sfigakis, F.; Pepper, M.; Chen, C.-H.; Fan, J.-C.; Griffiths, J.; Farrer, I.; Beere, H.E. All-electric all-semiconductor spin field-effect transistors. Nat. Nanotechnol. 2015, 10, 35–39. [Google Scholar] [CrossRef]
- Liu, H.-Y.; Wang, Y.-Y.; Chen, Z.-Y.; Hou, T.-P.; Wu, K.-M.; Lin, H.-F. Spin–orbit splitting and piezoelectric properties of Janus Ge2XY (X ≠ Y = P, As, Sb and Bi). Phys. Chem. Chem. Phys. 2023, 25, 16559–16569. [Google Scholar] [CrossRef]
- Tripathy, N.; De Sarkar, A. Anisotropy in colossal piezoelectricity, giant Rashba effect and ultrahigh carrier mobility in Janus structures of quintuple Bi2X3 (X = S, Se) monolayers. J. Phys. Condens. Matter 2023, 35, 335301. [Google Scholar] [CrossRef]
- Vu, T.V.; Phuc, H.V.; Kartamyshev, A.; Hieu, N.N. Enhanced out-of-plane piezoelectricity and carrier mobility in Janus γ-Sn2XY (X/Y = S, Se, Te) monolayers: A first-principles prediction. Appl. Phys. Lett. 2023, 122, 061601. [Google Scholar] [CrossRef]
- Liu, P.-F.; Zheng, F.; Li, J.; Si, J.-G.; Wei, L.; Zhang, J.; Wang, B.-T. Two-gap superconductivity in a Janus MoSH monolayer. Phys. Rev. B 2022, 105, 245420. [Google Scholar] [CrossRef]
- Ku, R.; Yan, L.; Si, J.-G.; Zhu, S.; Wang, B.-T.; Wei, Y.; Pang, K.; Li, W.; Zhou, L. Ab initio investigation of charge density wave and superconductivity in two-dimensional Janus 2 H/1 T-MoSH monolayers. Phys. Rev. B 2023, 107, 064508. [Google Scholar] [CrossRef]
- Zhuang, H.L.; Johannes, M.D.; Singh, A.K.; Hennig, R.G. Doping-controlled phase transitions in single-layer MoS2. Phys. Rev. B 2017, 96, 165305. [Google Scholar] [CrossRef]
- Guillamón, I.; Suderow, H.; Vieira, S.; Cario, L.; Diener, P.; Rodiere, P. Superconducting density of states and vortex cores of 2H-NbS2. Phys. Rev. Lett. 2008, 101, 166407. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- McMillan, W. Transition temperature of strong-coupled superconductors. Phys. Rev. 1968, 167, 331. [Google Scholar] [CrossRef]
- Giustino, F. Electron-phonon interactions from first principles. Rev. Mod. Phys. 2017, 89, 015003. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892. [Google Scholar] [CrossRef] [PubMed]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, R. AELAS: Automatic ELAStic property derivations via high-throughput first-principles computation. Comput. Phys. Commun. 2017, 220, 403–416. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Hung, N.T.; Nugraha, A.R.; Saito, R. Two-dimensional MoS2 electromechanical actuators. J. Phys. D Appl. Phys. 2018, 51, 075306. [Google Scholar] [CrossRef]
- Xiang, P.; Sharma, S.; Wang, Z.M.; Wu, J.; Schwingenschlögl, U. Flexible C6BN monolayers as promising anode materials for high-performance K-ion batteries. ACS Appl. Mater. Interfaces 2020, 12, 30731–30739. [Google Scholar] [CrossRef]
- Ahmad, S.; Mukherjee, S. A comparative study of electronic properties of bulk MoS2 and its monolayer using DFT technique: Application of mechanical strain on MoS2 monolayer. Graphene 2014, 3, 50633. [Google Scholar] [CrossRef]
- Yang, L.-M.; Bacic, V.; Popov, I.A.; Boldyrev, A.I.; Heine, T.; Frauenheim, T.; Ganz, E. Two-dimensional Cu2Si monolayer with planar hexacoordinate copper and silicon bonding. J. Am. Chem. Soc. 2015, 137, 2757–2762. [Google Scholar] [CrossRef]
- Guan, J.; Zhu, Z.; Tománek, D. Phase coexistence and metal-insulator transition in few-layer phosphorene: A computational study. Phys. Rev. Lett. 2014, 113, 046804. [Google Scholar] [CrossRef]
- Mouhat, F.; Coudert, F.-X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
- Wei, Q.; Peng, X. Superior mechanical flexibility of phosphorene and few-layer black phosphorus. Appl. Phys. Lett. 2014, 104, 251915. [Google Scholar] [CrossRef]
- Cooper, R.C.; Lee, C.; Marianetti, C.A.; Wei, X.; Hone, J.; Kysar, J.W. Nonlinear elastic behavior of two-dimensional molybdenum disulfide. Phys. Rev. B 2013, 87, 035423. [Google Scholar] [CrossRef]
- Motizuki, K.; Nishio, Y.; Shirai, M.; Suzuki, N. Effect of intercalation on structural instability and superconductivity of layered 2H-type NbSe2 and NbS2. J. Phys. Chem. Solids 1996, 57, 1091–1096. [Google Scholar] [CrossRef]
- Navarro-Moratalla, E.; Island, J.O.; Manas-Valero, S.; Pinilla-Cienfuegos, E.; Castellanos-Gomez, A.; Quereda, J.; Rubio-Bollinger, G.; Chirolli, L.; Silva-Guillén, J.A.; Agraït, N. Enhanced superconductivity in atomically thin TaS2. Nat. Commun. 2016, 7, 11043. [Google Scholar] [CrossRef]
- Yan, R.; Khalsa, G.; Schaefer, B.T.; Jarjour, A.; Rouvimov, S.; Nowack, K.C.; Xing, H.G.; Jena, D. Thickness dependence of superconductivity in ultrathin NbS2. Appl. Phys. Express 2019, 12, 023008. [Google Scholar] [CrossRef]
- Fang, Y.; Pan, J.; Zhang, D.; Wang, D.; Hirose, H.T.; Terashima, T.; Uji, S.; Yuan, Y.; Li, W.; Tian, Z. Discovery of superconductivity in 2M WS2 with possible topological surface states. Adv. Mater. 2019, 31, 1901942. [Google Scholar] [CrossRef]
| Strain Index | Strain Vector | Elastic Energy |
|---|---|---|
| 1 | (δ, 0, 0) | |
| 2 | (δ, δ, 0) |
| Structure | C11 | C22 | C12 | C66 |
|---|---|---|---|---|
| 2H-NbSH | 129.0 | 129 | 28.3 | 50.4 |
| 1T-NbSH | 106.3 | 106.3 | 18.5 | 43.9 |
| Predicted NbSH | 132.3 | 122.5 | 42.2 | 45.0 |
| Biaxial Strain | λ | ωlog (cm−1) | TC (K) |
|---|---|---|---|
| +0.01% | 0.70 | 163.6 | 5.40 |
| 0.00% | 0.71 | 171.1 | 6.10 |
| −0.06% | 0.80 | 162.3 | 7.62 |
| −1.08% | 0.81 | 194.7 | 9.38 |
| −1.38% | 0.73 | 196.1 | 7.43 |
| −0.02% | 0.64 | 221.8 | 6.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Pu, C.; Zhou, D. Structure, Stability, and Superconductivity of Two-Dimensional Janus NbSH Monolayers: A First-Principle Investigation. Molecules 2023, 28, 5522. https://doi.org/10.3390/molecules28145522
Li Y, Pu C, Zhou D. Structure, Stability, and Superconductivity of Two-Dimensional Janus NbSH Monolayers: A First-Principle Investigation. Molecules. 2023; 28(14):5522. https://doi.org/10.3390/molecules28145522
Chicago/Turabian StyleLi, Yan, Chunying Pu, and Dawei Zhou. 2023. "Structure, Stability, and Superconductivity of Two-Dimensional Janus NbSH Monolayers: A First-Principle Investigation" Molecules 28, no. 14: 5522. https://doi.org/10.3390/molecules28145522
APA StyleLi, Y., Pu, C., & Zhou, D. (2023). Structure, Stability, and Superconductivity of Two-Dimensional Janus NbSH Monolayers: A First-Principle Investigation. Molecules, 28(14), 5522. https://doi.org/10.3390/molecules28145522







