Thermodynamic Consideration of the Solid Saponin Extract Drop–Air System
Abstract
1. Introduction
2. Results and Discussion
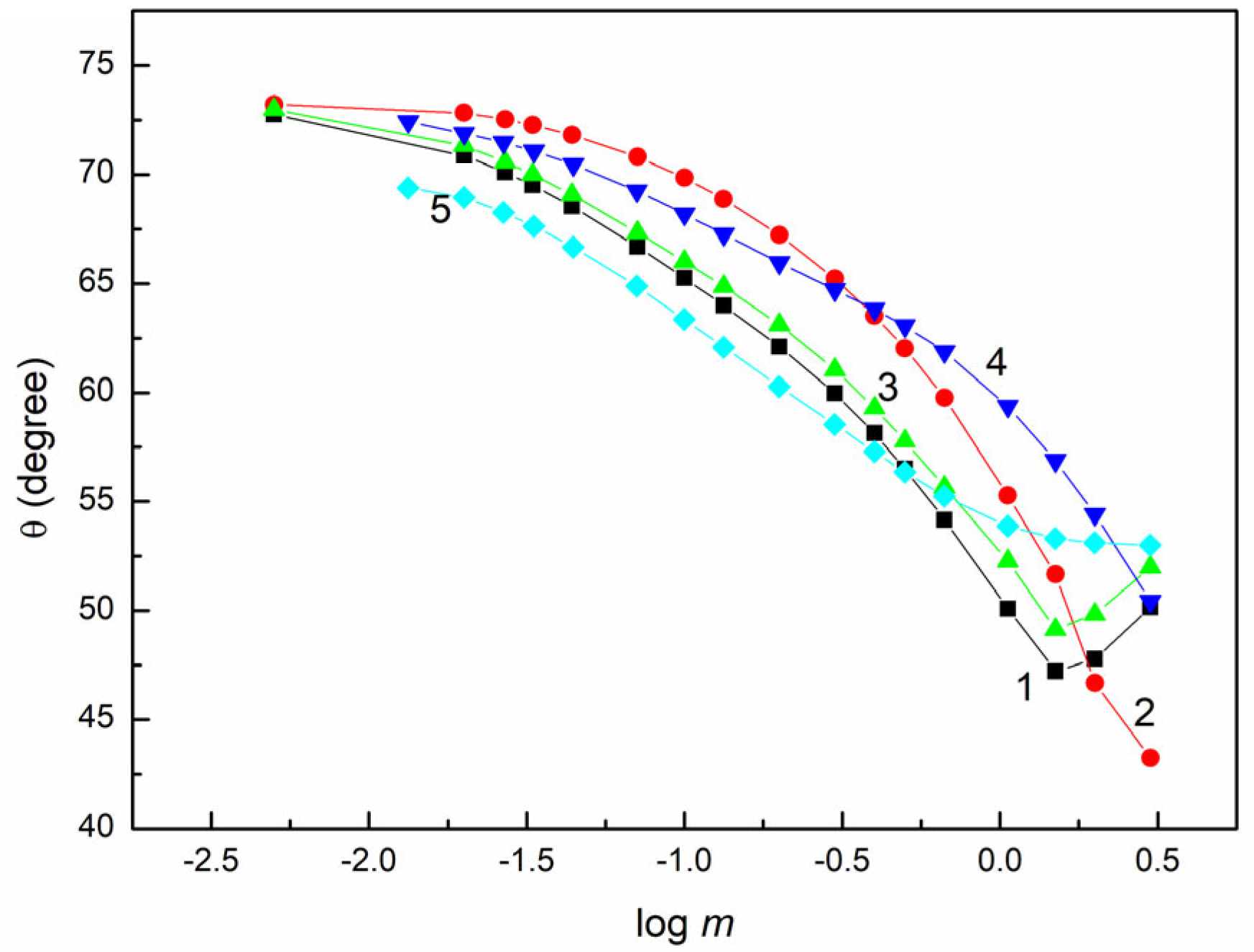
2.1. Contact Angle
2.2. Wettability of PTFE
2.3. Wettability of PMMA
2.4. Wettability of Glass
2.5. Concentration of the Extract Fractions at the Interfaces
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Nizioł-Łukaszewska, Z.; Bujak, T. Saponins as natural raw materials for increasing the safety of bodywash cosmetic use. J. Surfact. Deterg. 2018, 21, 767–776. [Google Scholar] [CrossRef]
- Tamura, Y.; Miyakoshi, M.; Yamamoto, M. Application of saponin-containing plants in foods and cosmetics. In Aleternative Medicine; Sakagami, H., Ed.; InTech: Rijeka, Croatia, 2012; pp. 83–101. [Google Scholar]
- Hussain, M.; Debnath, B.; Qasim, M.; Bamisile, B.S.; Islam, W.; Hameed, M.S.; Wang, L.; Qiu, D. Role of saponins in plant defense against specialist herbivores. Molecules 2019, 24, 2067. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kaminaga, H.; Navarro, R.R.; Iimura, Y. Application of aqueous saponin on the remediation of polycyclic aromatic hydrocarbons-contaminated soil. J. Environ. Sci. Health A Tox. Hazard Subst. Environ. Eng. 2012, 47, 1138–1145. [Google Scholar] [CrossRef] [PubMed]
- Jung, M.-H.; Jung, S.-J.; Kim, T. Saponin and chitosan-based oral vaccine against viral haemorrhagic septicaemia virus (VHSV) provides protective immunity in olive flounder (Paralichthys olivaceus). Fish Shellfish Immunol. 2022, 126, 336–346. [Google Scholar] [CrossRef] [PubMed]
- Man, S.; Gao, W.; Zhang, Y.; Huang, L.; Liu, C. Chemical study and medical application of saponins as anti-cancer agents. Fitoterapia 2010, 7, 703–714. [Google Scholar] [CrossRef]
- Lucchesei, A.; Gherlone, E.; Prtellpand, M.; Bertoss, D. Tooth orthodontic movement after maxillofacial surgery. European J. Inflamm. 2012, 10, 227–232. [Google Scholar] [CrossRef]
- D’Orto, B.; Chiavenna, C.; Leone, R.; Longoni, M.; Nagni, M.; Capparè, P. Marginal bone loss compared in internal and external implant connections: Retrospective clinical study at 6-years follow-up. Biomedicines 2023, 11, 1128. [Google Scholar] [CrossRef]
- Budala, D.G.; Martu, M.-A.; Maftei, G.-A.; Diaconu-Popa, D.A.; Danila, V.; Luchian, I. The role of natural compounds in optimizing contemporary dental treatment—Current status and future trends. J. Funct. Biomater. 2023, 14, 273. [Google Scholar] [CrossRef]
- Mitra, S.; Dungan, S.R. Micellar Properties of Quillaja Saponin. 1. Effects of temperature, salt, and pH on solution properties. J. Agric. Food Chem. 1997, 45, 1587–1595. [Google Scholar] [CrossRef]
- Balakrishnan, S.; Varughese, S.; Deshpande, A.P. Micellar characterisation of Saponin from Sapindus mukorossi. Tenside Surfact. Det. 2013, 43, 262–268. [Google Scholar] [CrossRef]
- Rosen, M.J. Surfactants and Interfacial Phenomena, 3rd ed.; Wiley Intersccience: New York, NY, USA, 2004. [Google Scholar]
- Zisman, W.A. Contact angle wettability and adhesion. In Advances in Chemistry Series; Fowkes, F.M., Ed.; American Chemical Society: Washington, DC, USA, 1964; Volume 43, pp. 1–51. [Google Scholar]
- Bernett, M.K.; Zisman, W.A. Relation of wettability by aqueous solutions to the surface constitution of low-energy solids. J. Phys. Chem. 1959, 63, 1241–1246. [Google Scholar] [CrossRef]
- Bargeman, D.; van Voorst Vader, F. Effect of surfactants on contact angles at nonpolar solids. J. Colloid Interface Sci. 1973, 42, 467–472. [Google Scholar] [CrossRef]
- Kitazaki, Y.; Hata, T. Surface-chemical criteria for optimum adhesion. 3. Variability of critical surface tension (gamma-c) and its choice. J. Adhes. 1972, 4, 123–132. [Google Scholar] [CrossRef]
- Fowkes, F.M. Attractive forces at interfaces. Ind. Eng. Chem. 1964, 56, 40–52. [Google Scholar] [CrossRef]
- van Oss, C.J. Interfacial Forces in: Aqueous Media, 1st ed.; Marcel Dekker: New York, NY, USA, 1994. [Google Scholar]
- van Oss, C.J.; Good, R.J. Surface tension and the solubility of polymers and biopolymers: The role of polar and apolar interfacial free energies. J. Macromol. Sci.-Chem. A 1989, 26, 1183–1203. [Google Scholar] [CrossRef]
- van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Monopolar surfaces. Adv. Colloid Interface Sci. 1987, 28, 35–64. [Google Scholar] [CrossRef]
- Rekiel, E.; Zdziennicka, A.; Jańczuk, B. Effect of ethanol on wetting and adhesion properties of rhamnolipid. Int. J. Adhes. Adhes. 2021, 110, 102955. [Google Scholar] [CrossRef]
- Adamson, W.; Gast, A.P. Physical Chemistry of Surfaces, 6th ed.; Wiley Interscience: New York, NY, USA, 1997. [Google Scholar]
- Zdziennicka, A.; Szymczyk, K.; Krawczyk, J.; Jańczuk, B. Some remarks on the solid surface tension determination from contact angle measurements. App. Surf. Sci. 2017, 405, 88–101. [Google Scholar] [CrossRef]
- Zdziennicka, A.; Krawczyk, J.; Szymczyk, K.; Jańczuk, B. Components and parameters of liquids and some polymers surface tension at different temperature. Colloids Surf. A Physicochem. Eng. Asp. 2017, 529, 864–875. [Google Scholar] [CrossRef]
- Good, R.J. Contact angle, wetting, and adhesion: A critical review. J. Adhes. Sci. Technol. 1992, 6, 1269–1302. [Google Scholar] [CrossRef]
- Neumann, A.W. Contact angles and their temperature dependence. Thermodynamic status, measurements, interpretation and application. Adv. Colloid Interface Sci. 1974, 4, 105–191. [Google Scholar] [CrossRef]
- Zdziennicka, A.; Jańczuk, B. Modification of adsorption, aggregation and wetting properties of surfactants by short chain alcohols. Adv. Colloid Interface Sci. 2020, 284, 102249. [Google Scholar] [CrossRef] [PubMed]
- Hu, P.; Adamson, A.W. Adsorption and contact angle studies. II. Water and organic substances on polished polytetrafluoroethylene. J. Colloid Interface Sci. 1977, 59, 605–614. [Google Scholar] [CrossRef]
- Owens, N.F.; Richmond, P.; Gregory, D.; Mingins, J.; Chan, D. Contact angles of pure liquids and surfactants on low-energy surfaces. In Wetting, Spreading and Adhesion; Padday, J.F., Ed.; Academic Press: London, UK, 1978. [Google Scholar]
- van Oss, C.J.; Constanzo, P.M. Adhesion of anionic surfactants to polymer surfaces and low-energy materials. J. Adhes. Sci. Technol. 1992, 4, 477–487. [Google Scholar] [CrossRef]
- Zdziennicka, A.; Krawczyk, J.; Szymczyk, K.; Jańczuk, B. Macroscopic and microscopic properties of some surfactants and biosurfactants. Int. J. Mol. Sci. 2018, 19, 1934. [Google Scholar] [CrossRef]
- Rekiel, E.; Zdziennicka, A.; Jańczuk, B. Mutual influence of ethanol and surfactin on their wetting and adhesion properties. Colloids Surf. A Physicochem. Eng. Asp. 2021, 627, 127161. [Google Scholar] [CrossRef]
- Lucassen-Reynders, E.H. Contact angles and adsorption on solids. J. Phys. Chem. 1963, 67, 969–972. [Google Scholar] [CrossRef]
- Rekiel, E.; Sumłek, W.; Zdziennicka, A.; Kaczorek, E.; Jańczuk, B. Wetting properties of Saponaria officinalis saponins. Colloids Surf. A Physicochem. Eng. Asp. 2020, 584, 123980. [Google Scholar] [CrossRef]
- Grzywaczyk, A.; Smułek, W.; Zgoła-Grześkowiak, A.; Kaczorek, E.; Zdziennicka, A.; Jańczuk, B. Nanofiltered saponin-rich extract of Saponaria officinalis—Adsorption and aggregation properties of particular fractions. Colloids Surf. A Physicochem. Eng. Asp. 2023, 661, 130937. [Google Scholar] [CrossRef]
- Rekiel, E.; Zdziennicka, A.; Szymczyk, K.; Jańczuk, B. Thermodynamic Analysis of the Adsorption and Micellization Activity of the Mixtures of Rhamnolipid and Surfactin with Triton X-165. Molecules 2022, 27, 3600. [Google Scholar] [CrossRef]
- De Boer, J.H. The Dynamic Character of Adsorption; Oxford University: Oxford, UK, 1953. [Google Scholar]


| Fraction | |||||
|---|---|---|---|---|---|
| PTFE | |||||
| E0 | 89.84536 | 5.34745 | 0.05219 | 15.26601 | 0.77681 |
| E1 | 87.70078 | 3.12596 | 0.1369 | 19.76883 | 1.49907 |
| E2 | 89.34443 | 5.57735 | 0.05371 | 15.71605 | 0.82901 |
| E3 | 84.94747 | 19.48124 | 2.7536 | 5.87263 | 0.08604 |
| E4 | 92.02671 | 6.71405 | 0.06221 | 9.44685 | 0.39655 |
| PMMA | |||||
| E0 | 42.63048 | 24.11468 | 0.90393 | 6.75639 | 0.05314 |
| Glass | |||||
| E0 | 21.62536404 | 28.02520023 | 0.83668873 | 6.0955882 | 0.05097999 |
| Fraction | Slope | Constant | [mN/m] |
|---|---|---|---|
| PTFE | |||
| E0 | −0.99927 | 46.54963 | 23.28331 |
| E1 | −0.99741 | 46.47121 | 23.26573 |
| E2 | −0.99696 | 46.43604 | 23.25337 |
| E3 | −1.00392 | 46.86771 | 23.38801 |
| E4 | −1.00165 | 46.71216 | 23.33683 |
| PMMA | |||
| E0 | −0.53197 | 58.50527 | 38.18957 |
| E1 | −0.55895 | 60.50714 | 38.81275 |
| E2 | −0.47278 | 54.28383 | 36.85807 |
| E3 | −0.43314 | 51.2961 | 35.7928 |
| E4 | −0.37529 | 47.19545 | 34.31673 |
| Glass | |||
| E0 | −0.15585353 | 51.39862153 | 60.88827 |
| E1 | - | - | - |
| E2 | 0.06059295 | 35.62625951 | 33.59089 |
| E3 | 0.13605857 | 30.06522735 | 26.4645 |
| E4 | 0.14747917 | 29.23123737 | 25.47431 |
| E0 | −0.15585353 | 51.39862153 | 60.88827 |
| Fraction | (⨯10−6 mol/m2) | (kJ/mol) from Modified Langmuir Equation [32,34] | (kJ/mol) Equation (8) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| from Gibbs Equation [31] | Equation (7) | 500 | 3000 | 500 | 3000 | ||||||
| PTFE | |||||||||||
| E0 | 1.93 | 1.8 | −32.67 | −37.06 | −34.07 | −38.43 | |||||
| E1 | 2.30 | 2.4 | −29.42 | −33.74 | −30.56 | −34.93 | |||||
| E2 | 1.93 | 1.9 | −32.83 | 37.20 | −33.45 | −37.82 | |||||
| E3 | 1.70 | 1.7 | −30.83 | −35.24 | −33.06 | −37.42 | |||||
| E4 | 1.81 | 1.8 | −32.23 | −36.59 | −36.17 | −40.54 | |||||
| PMMA | |||||||||||
(⨯10−6 mol/m2) | Equation (7) | (kJ/mol) from modified Langmuir equation [32,34] | (kJ/mol) Equation (8) | ||||||||
| SV | SL | ||||||||||
| from Gibbs equation [31] | |||||||||||
| 500 | 3000 | 500 | 3000 | ||||||||
| SV | SL | SV | SL | ||||||||
| E0 | 0.24 | 1.25 | −0.52 | 1.0 | −26.82 | −31.28 | −31.18 | −35.54 | −35.46 | −39.83 | |
| E1 | 0.25 | 1.61 | −0.51 | - | −24.22 | −28.33 | −28.51 | −32.65 | - | - | |
| E2 | 0.36 | 1.27 | −0.45 | - | −27.72 | −31.33 | −32.53 | −35.60 | - | - | |
| E3 | 0.39 | 1.09 | −0.42 | - | −27.36 | −30.04 | −31.62 | −34.38 | - | - | |
| E4 | 0.49 | 1.19 | −0.39 | - | −28.76 | −31.13 | −33.13 | −35.42 | - | - | |
| Glass | |||||||||||
(⨯10−6 mol/m2) | Equation (7) | (kJ/mol) from modified Langmuir equation [32,34] | (kJ/mol) Equation (8) | ||||||||
| SV Equation | SL Equation | 500 | 3000 | 500 | 3000 | ||||||
| from Gibbs equation [31] | SV | SL | SV | SL | |||||||
| E0 | 0.38 | 0.68 | −0.15 | 1.4 | −28.61 | −29.65 | −32.97 | −33.81 | −36.78 | −41.15 | |
| E1 | 1.13 | 0.87 | - | - | −22.75 | −27.04 | −27.11 | −31.35 | - | - | |
| E2 | 0.78 | 0.69 | 0.066 | - | −30.33 | −29.68 | −34.57 | −33.85 | - | - | |
| E3 | 0.83 | 0.60 | 0.13 | - | −29.33 | −28.48 | −33.69 | −32.85 | - | - | |
| E4 | 0.82 | 0.58 | 0.14 | - | −30.06 | −29.37 | −34.43 | −33.60 | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grzywaczyk, A.; Smułek, W.; Kaczorek, E.; Zdziennicka, A.; Jańczuk, B. Thermodynamic Consideration of the Solid Saponin Extract Drop–Air System. Molecules 2023, 28, 4943. https://doi.org/10.3390/molecules28134943
Grzywaczyk A, Smułek W, Kaczorek E, Zdziennicka A, Jańczuk B. Thermodynamic Consideration of the Solid Saponin Extract Drop–Air System. Molecules. 2023; 28(13):4943. https://doi.org/10.3390/molecules28134943
Chicago/Turabian StyleGrzywaczyk, Adam, Wojciech Smułek, Ewa Kaczorek, Anna Zdziennicka, and Bronisław Jańczuk. 2023. "Thermodynamic Consideration of the Solid Saponin Extract Drop–Air System" Molecules 28, no. 13: 4943. https://doi.org/10.3390/molecules28134943
APA StyleGrzywaczyk, A., Smułek, W., Kaczorek, E., Zdziennicka, A., & Jańczuk, B. (2023). Thermodynamic Consideration of the Solid Saponin Extract Drop–Air System. Molecules, 28(13), 4943. https://doi.org/10.3390/molecules28134943









