Entropy Related to K-Banhatti Indices via Valency Based on the Presence of C6H6 in Various Molecules
Abstract
1. Introduction
2. Definitions of Entropies via K-Banhatti Indices
- The first K-Banhatti entropy
- The Second K-Banhatti entropy
- Entropy related to the first K-hyper Banhatti index
- Entropy related to the second K-hyper Banhatti index
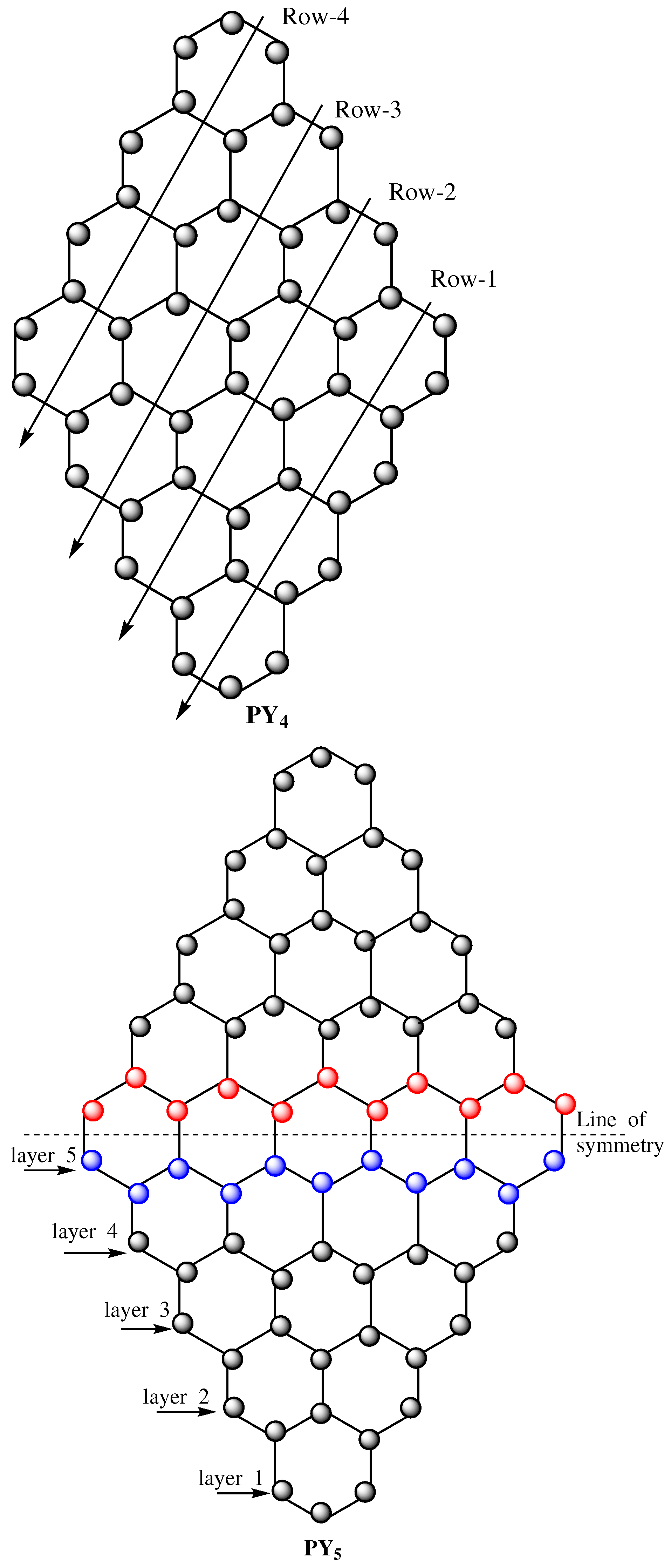
3. The Pyrene Network
- Entropy related to the first K-Banhatti index of
- The second K-Banhatti entropy of
- Entropy related to the first K-hyper Banhatti index of
- Entropy related to the second K-hyper Banhatti index
Characteristics of K-Banhatti Indices of
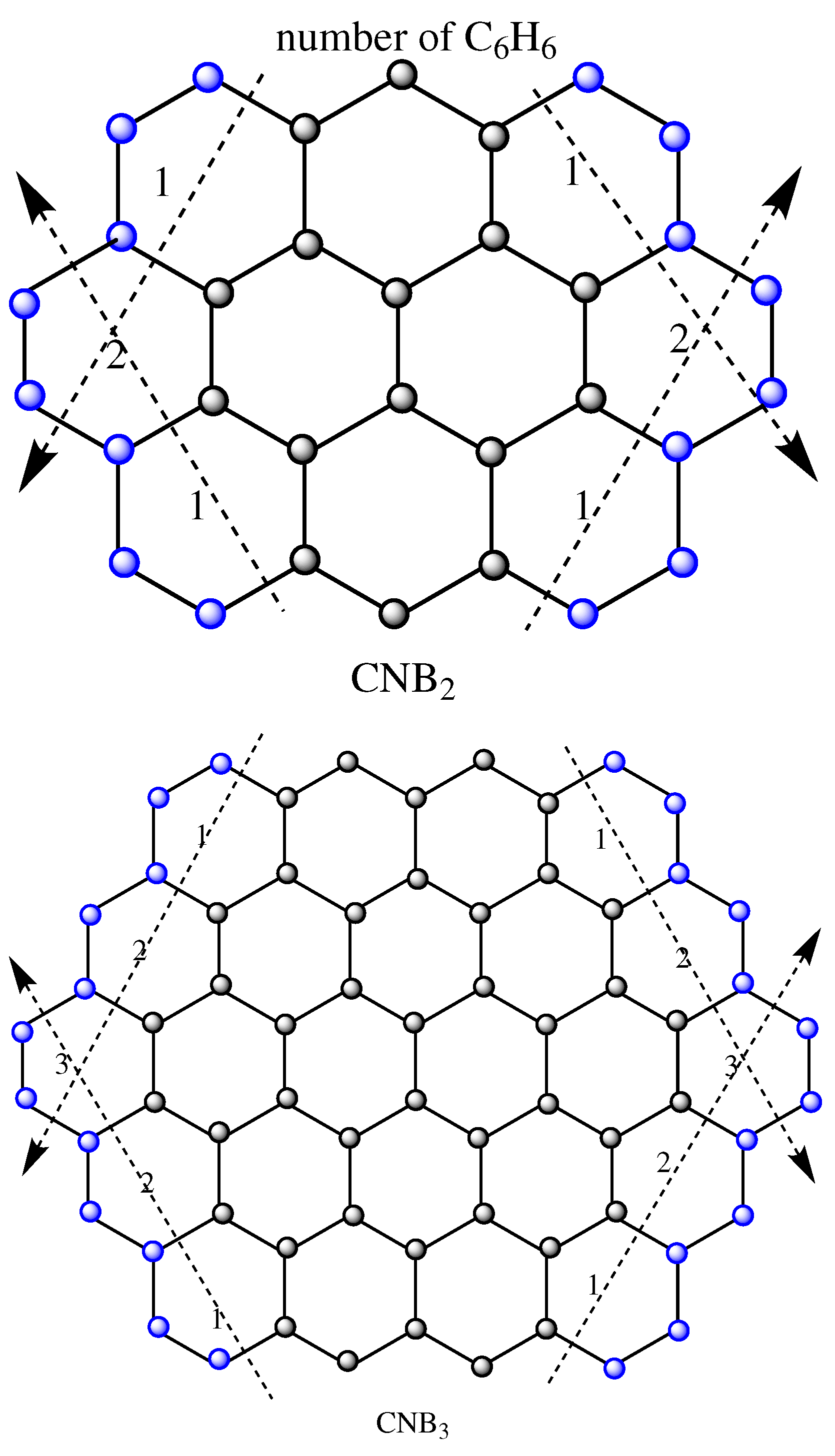
4. Circumnaphthalene Series of Benzenoid
- Entropy related to the 1st K-Banhatti index of
- The second K-Banhatti entropy of
- Entropy related to the first -hyper Banhatti index of
- Entropy related to the second K-hyper Banhatti index CNBn
Characteristics of K-Banhatti Indices of
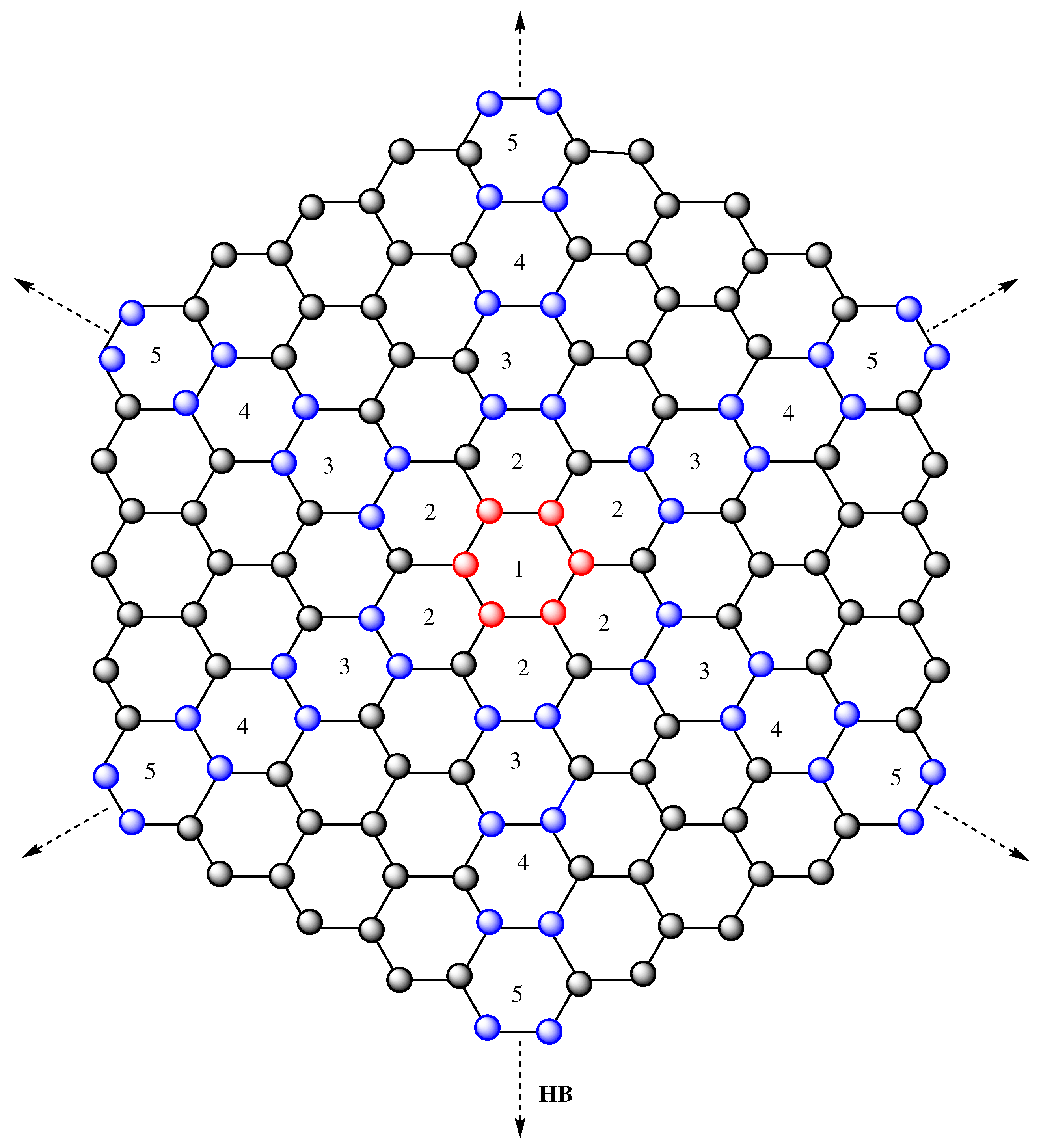
5. The Honeycomb Benzenoid Network
- Entropy related to the first K-Banhatti index of
- The second K-Banhatti entropy of
- Entropy related to the first K-hyper Banhatti index of
- Entropy related to the second K-hyper Banhatti index
Characteristics of K-Banhatti Indices of
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Tag El Din, E.S.M.; Sultan, F.; Ghani, M.U.; Liu, J.B.; Dehraj, S.; Cancan, M.; Alharbi, F.M.; Alhushaybari, A. Some Novel Results Involving Prototypical Computation of Zagreb Polynomials and Indices for SiO 4 Embedded in a Chain of Silicates. Molecules 2022, 28, 201. [Google Scholar] [CrossRef]
- Shannon, C.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Ali, A.; Furtula, B.; Redžepović, I.; Gutman, I. Atom-bond sum-connectivity index. J. Math. Chem. 2022, 60, 2081–2093. [Google Scholar] [CrossRef]
- Ghani, M.U.; Kashif Maqbool, M.; George, R.; Ofem, A.E.; Cancan, M. Entropies Via Various Molecular Descriptors of Layer Structure of H3BO3. Mathematics 2022, 10, 4831. [Google Scholar] [CrossRef]
- Liu, J.B.; Arockiaraj, M.; Arulperumjothi, M.; Prabhu, S. Distance based and bond additive topological indices of certain repurposed antiviral drug compounds tested for treating COVID-19. Int. J. Quantum Chem. 2021, 121, e26617. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.B.; Wang, S.; Wang, C.; Hayat, S. Further results on computation of topological indices of certain networks. IET Control Theory Appl. 2017, 11, 2065–2071. [Google Scholar] [CrossRef]
- Liu, J.B.; Gao, W.; Siddiqui, M.K.; Farahani, M.R. Computing three topological indices for Titania nanotubes TiO2 [m, n]. AKCE Int. J. Graphs Comb. 2016, 13, 255–260. [Google Scholar] [CrossRef]
- Liu, J.B.; Shafiq, M.K.; Ali, H.; Naseem, A.; Maryam, N.; Asghar, S.S. Topological Indices of m th Chain Silicate Graphs. Mathematics 2019, 7, 42. [Google Scholar] [CrossRef]
- Alam, A.; Ghani, M.U.; Kamran, M.; Shazib Hameed, M.; Hussain Khan, R.; Baig, A.Q. Degree-Based Entropy for a Non-Kekulean Benzenoid Graph. J. Math. 2022, 2022, 2288207. [Google Scholar]
- Rashevsky, N. Life, information theory, and topology. Bull. Math. Biophys. 1955, 17, 229–235. [Google Scholar] [CrossRef]
- Trucco, E. A note on the information content of graphs. Bull. Math. Biophys. 1956, 18, 129–135. [Google Scholar] [CrossRef]
- Chu, Y.M.; Khan, A.R.; Ghani, M.U.; Ghaffar, A.; Inc, M. Computation of Zagreb Polynomials and Zagreb Indices for Benzenoid Triangular & Hourglass System. Polycycl. Aromat. Compd. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Liu, J.B.; Younas, M.; Habib, M.; Yousaf, M.; Nazeer, W. M-Polynomials and Degree-Based Topological Indices of VC 5 C 7 [p, q] and HC 5 C 7 [p, q] Nanotubes. IEEE Access 2019, 7, 41125–41132. [Google Scholar] [CrossRef]
- Ghani, M.U.; Sultan, F.; El Sayed, M.; Cancan, M.; Ali, S. SiO4 characterization in a chain and C6 H6 embedded in a Non-kekulean structure for Kulli Temperature indices. Res. Square 2022. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Ghani, M.U.; Sultan, F.; Inc, M.; Cancan, M. Connecting SiO 4 in Silicate and Silicate Chain Networks to Compute Kulli Temperature Indices. Molecules 2022, 27, 7533. [Google Scholar] [CrossRef] [PubMed]
- Hamid, K.; Muhammad, H.A.B.; Iqbal, M.W.; Hamza, M.A.; Bhatti, S.U.; Aqeel, M. Topological analysis empowered bridge network variants by dharwad indices. Online Open Access 2022, 41. [Google Scholar] [CrossRef]
- Wang, W.; Naeem, M.; Rauf, A.; Riasat, A.; Aslam, A.; Anoh Yannick, K. On Analysis of Banhatti Indices for Hyaluronic Acid Curcumin and Hydroxychloroquine. J. Chem. 2021, 2021, 7468857. [Google Scholar] [CrossRef]
- Mowshowitz, A. Entropy and the complexity of graphs: I. An index of the relative complexity of a graph. Bull. Math. Biophys. 1968, 30, 175–204. [Google Scholar] [CrossRef]
- Dehmer, M.; Varmuza, K.; Borgert, S.; Emmert-Streib, F. On entropy-based molecular descriptors: Statistical analysis of real and synthetic chemical structures. J. Chem. Inf. Model. 2009, 49, 1655–1663. [Google Scholar] [CrossRef]
- Hamid, K.; Iqbal, M.W.; Arif, E.; Mahmood, Y.; Khan, A.S.; Kama, N.; Azmi, A.; Ikram, A. K-Banhatti Invariants Empowered Topological Investigation of Bridge Networks. CMC-Comput. Mater. Contin. 2022, 73, 5423–5440. [Google Scholar] [CrossRef]
- Kulli, V. On K Banhatti indices of graphs. J. Comput. Math. Sci. 2016, 7, 213–218. [Google Scholar]
- Anjum, M.S.; Safdar, M.U. K Banhatti and K hyper-Banhatti indices of nanotubes. Eng. Appl. Sci. Lett. 2019, 2, 19–37. [Google Scholar] [CrossRef]
- Amigó, J.M.; Balogh, S.G.; Hernández, S. A brief review of generalized entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef] [PubMed]
- Tsai, M.H. Physical properties of high entropy alloys. Entropy 2013, 15, 5338–5345. [Google Scholar] [CrossRef]
- Gao, W.; Muzaffar, B.; Nazeer, W. K-Banhatti and K-hyper Banhatti indices of dominating David derived network. Open J. Math. Anal. 2017, 1, 13–24. [Google Scholar] [CrossRef]
- Manzoor, S.; Chu, Y.M.; Siddiqui, M.K.; Ahmad, S. On topological aspects of degree based entropy for two carbon nanosheets. Main Group Met. Chem. 2020, 43, 205–218. [Google Scholar] [CrossRef]
- Ghani, M.U.; Sultan, F.; Tag El Din, E.S.M.; Khan, A.R.; Liu, J.B.; Cancan, M. A Paradigmatic Approach to Find the Valency-Based K-Banhatti and Redefined Zagreb Entropy for Niobium Oxide and a Metal–Organic Framework. Molecules 2022, 27, 6975. [Google Scholar] [CrossRef]
- Yang, W.; Xu, K.; Lian, J.; Ma, C.; Bin, L. Integrated flood vulnerability assessment approach based on TOPSIS and Shannon entropy methods. Ecol. Indic. 2018, 89, 269–280. [Google Scholar] [CrossRef]



| Atomic Bond Type | |||
|---|---|---|---|
| Number of atom bonds | 6 |
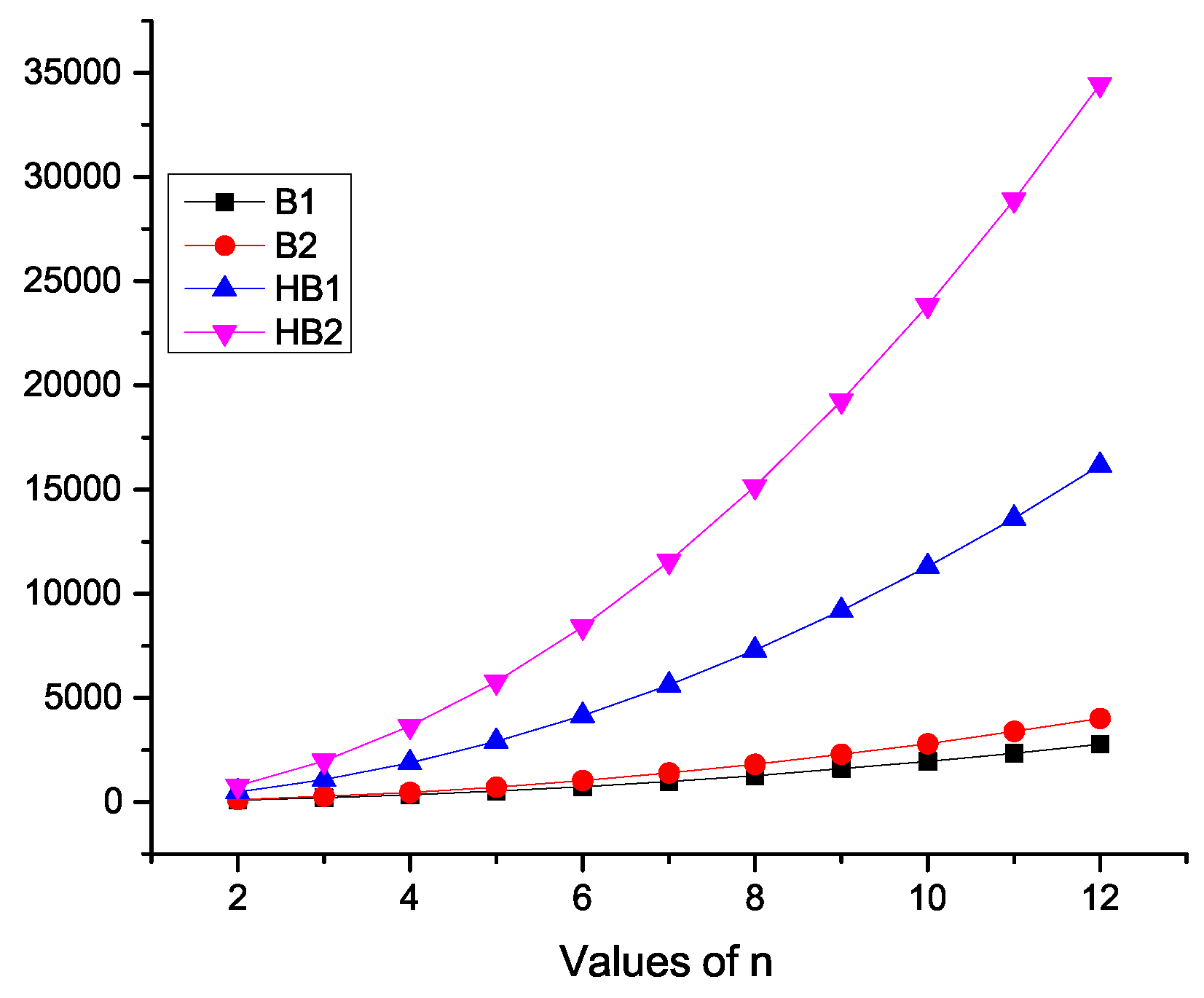
| Values of n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 94 | 200 | 342 | 520 | 734 | 984 | 1270 | 1592 | 1950 | 2344 | 2774 | |
| 117 | 264 | 465 | 720 | 1029 | 1392 | 1809 | 2280 | 2805 | 3384 | 4017 | |
| 476 | 1072 | 1884 | 2912 | 4156 | 5616 | 7292 | 9184 | 11,292 | 13,616 | 16,156 | |
| 789 | 1968 | 3633 | 5784 | 8421 | 11,544 | 15,153 | 19,248 | 23,829 | 28,896 | 34,449 |
| Types of Atomic Bond | |||
|---|---|---|---|
| 6 |
| Values of n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 218 | 494 | 8787 | 1370 | 1970 | 2678 | 3494 | 4418 | 5450 | 6590 | |
| 75 | 57 | 291 | 678 | 1245 | 1965 | 2847 | 3891 | 5097 | 6465 | 7995 | |
| 280 | 232 | 1180 | 2776 | 5020 | 7812 | 11,452 | 15,640 | 20,476 | 25,960 | 32,092 | |
| 915 | 321 | 2211 | 5559 | 10,365 | 16,629 | 24,351 | 33,531 | 44,169 | 56,265 | 69,819 |
| Types of Atomic Bonds | |||
|---|---|---|---|
| Cardinality of atomic bonds | 6 |
| Values of n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 104 | 344 | 692 | 1148 | 1712 | 2384 | 3164 | 4052 | 5048 | 6152 | 7364 | |
| 180 | 498 | 978 | 1620 | 2424 | 3390 | 4518 | 5808 | 7260 | 8874 | 10650 | |
| 828 | 2208 | 4236 | 6912 | 10,236 | 14,208 | 18,828 | 24,096 | 30,012 | 36,576 | 43,788 | |
| 1428 | 4290 | 8610 | 14,388 | 21,624 | 30,318 | 40,470 | 52,080 | 65,148 | 79,674 | 95,658 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghani, M.U.; Campena, F.J.H.; Maqbool, M.K.; Liu, J.-B.; Dehraj, S.; Cancan, M.; Alharbi, F.M. Entropy Related to K-Banhatti Indices via Valency Based on the Presence of C6H6 in Various Molecules. Molecules 2023, 28, 452. https://doi.org/10.3390/molecules28010452
Ghani MU, Campena FJH, Maqbool MK, Liu J-B, Dehraj S, Cancan M, Alharbi FM. Entropy Related to K-Banhatti Indices via Valency Based on the Presence of C6H6 in Various Molecules. Molecules. 2023; 28(1):452. https://doi.org/10.3390/molecules28010452
Chicago/Turabian StyleGhani, Muhammad Usman, Francis Joseph H. Campena, Muhammad Kashif Maqbool, Jia-Bao Liu, Sanaullah Dehraj, Murat Cancan, and Fahad M. Alharbi. 2023. "Entropy Related to K-Banhatti Indices via Valency Based on the Presence of C6H6 in Various Molecules" Molecules 28, no. 1: 452. https://doi.org/10.3390/molecules28010452
APA StyleGhani, M. U., Campena, F. J. H., Maqbool, M. K., Liu, J.-B., Dehraj, S., Cancan, M., & Alharbi, F. M. (2023). Entropy Related to K-Banhatti Indices via Valency Based on the Presence of C6H6 in Various Molecules. Molecules, 28(1), 452. https://doi.org/10.3390/molecules28010452










