Bridges and Vertices in Heteroboranes

Abstract

A number of (hetero)boranes are known in which a main group atom X ‘bridges’ a B—B connectivity in the open face, and in such species X has previously been described as simply a bridge or, alternatively, as a vertex in a larger cluster. In this study we describe an approach to distinguish between these options based on identifying the best fit of the experimental {B_x} cluster fragment with alternate exemplar {B_x} fragments derived from DFT-optimized [B_nH_n]²⁻ models. In most of the examples studied atom X is found to be better regarded as a vertex, having ‘a ‘verticity’ of ca. 60–65%. Consideration of our results leads to the suggestion that the radial electron contribution from X to the overall skeletal electron count is more significant than the tangential contribution.

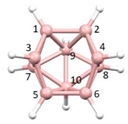
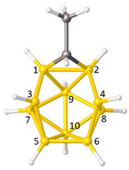
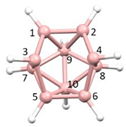
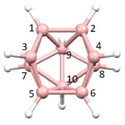
1. Introduction

Boron cluster chemistry, which traces its roots to the seminal works of Stock [1], Lipscomb [2], Hawthorne [3] and many others, is now a mature but still developing field which sits at the intersection of organic, inorganic and organometallic chemistry. From the earliest times it was appreciated that the polyhedral nature of these species meant that the bonding within them could not be explained by simple 2-centre-2-electon interactions and that a delocalized model was required. The critical breakthroughs in rationalization of their structures occurred in the early 1970s. First, Williams recognized that the structures of the boranes fell into well-defined groups, being either closed polyhedra (given the prefix closo) or open fragments thereof (nido, arachno, hypho, etc.) [4]. This was important because previously there had been the general belief that structurally the majority of the open boranes were simply fragments of an icosahedron. Williams identified that, e.g., the structure of B₁₀H₁₄ was in fact a nido fragment of the 11-vertex octadecahedron, whilst that of B₅H₁₁ was an arachno fragment of the 7-vertex pentagonal bipyramid. These structural relationships between the closed polyhedra and their nido and arachno fragments were later to be popularized in a classic figure by Rudolph [5], Figure 1. Second, and most importantly, Wade subsequently provided an explanation for these structural patterns in terms of the number of skeletal electron pairs (SEPs) available [6]. In brief, for an n vertex polyhedron a closo species has (n + 1) SEPs, a nido species (n + 2), an arachno species (n + 3), etc.

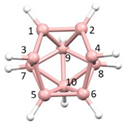
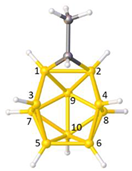
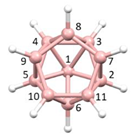
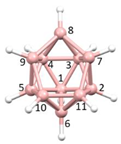
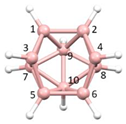
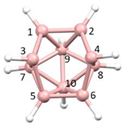
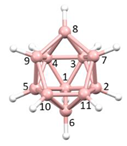
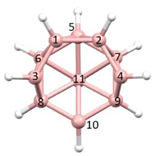
A particularly important feature of boron cluster chemistry is the number and diversity of heteroatom fragments, from across a broad spectrum of the periodic table, that can occupy vertices of the polyhedron. Thus, for example, in [3-(C₅H₅)-closo-3,1,2-CoC₂B₉H₁₁] [7,8] the Co and C atoms occupy vertices of the resulting icosahedron (Figure 2a), whilst in [nido-6-SB₉H₁₁] [9] the S atom occupies a vertex of the resulting nido fragment of an octadecahedron (Figure 2b). Importantly, the same electron-counting rules which describe the boranes apply to these heteroboranes, with the {CoCp} fragment providing 1 vertex and 2 skeletal electrons, the {CH} fragments 1 vertex and 3 skeletal electrons and the {S} fragment 1 vertex and 4 skeletal electrons.

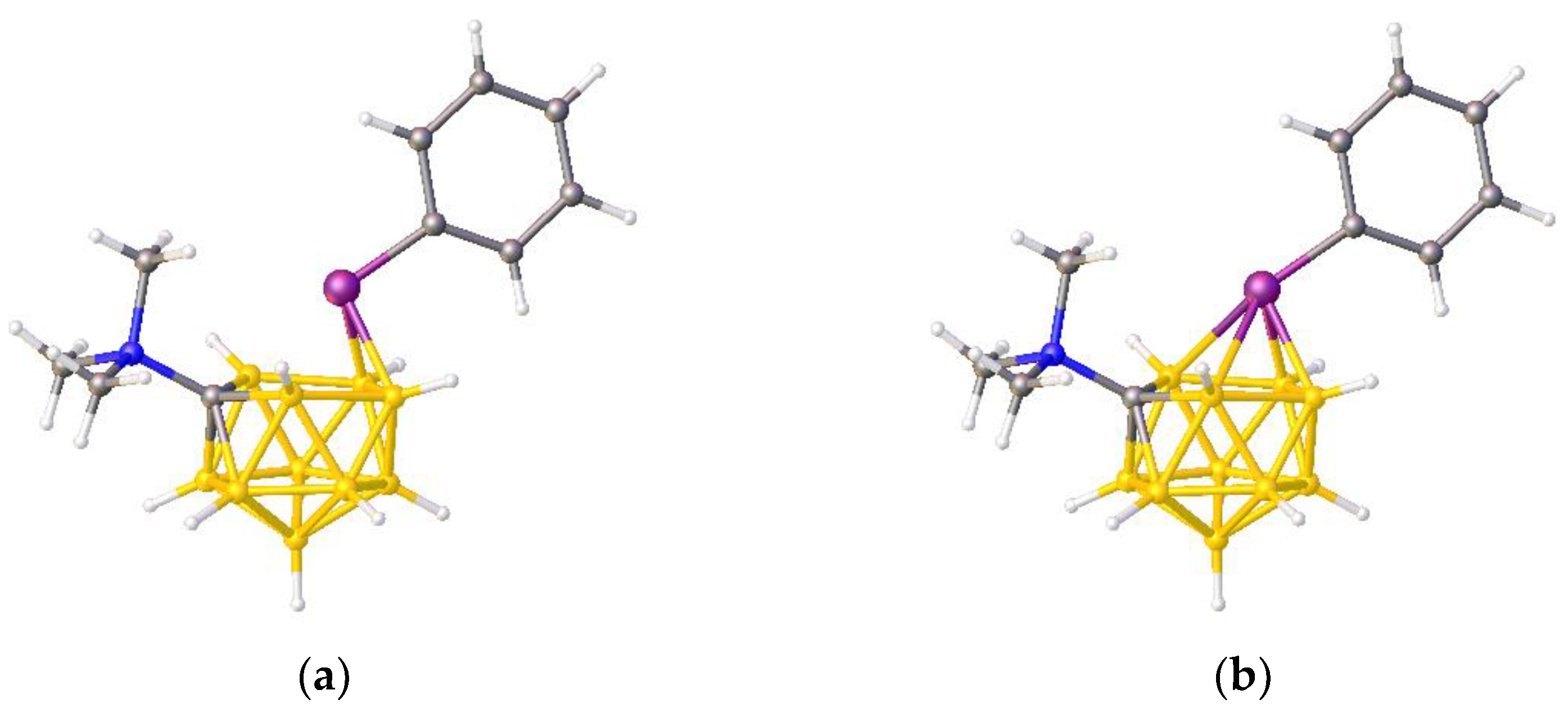
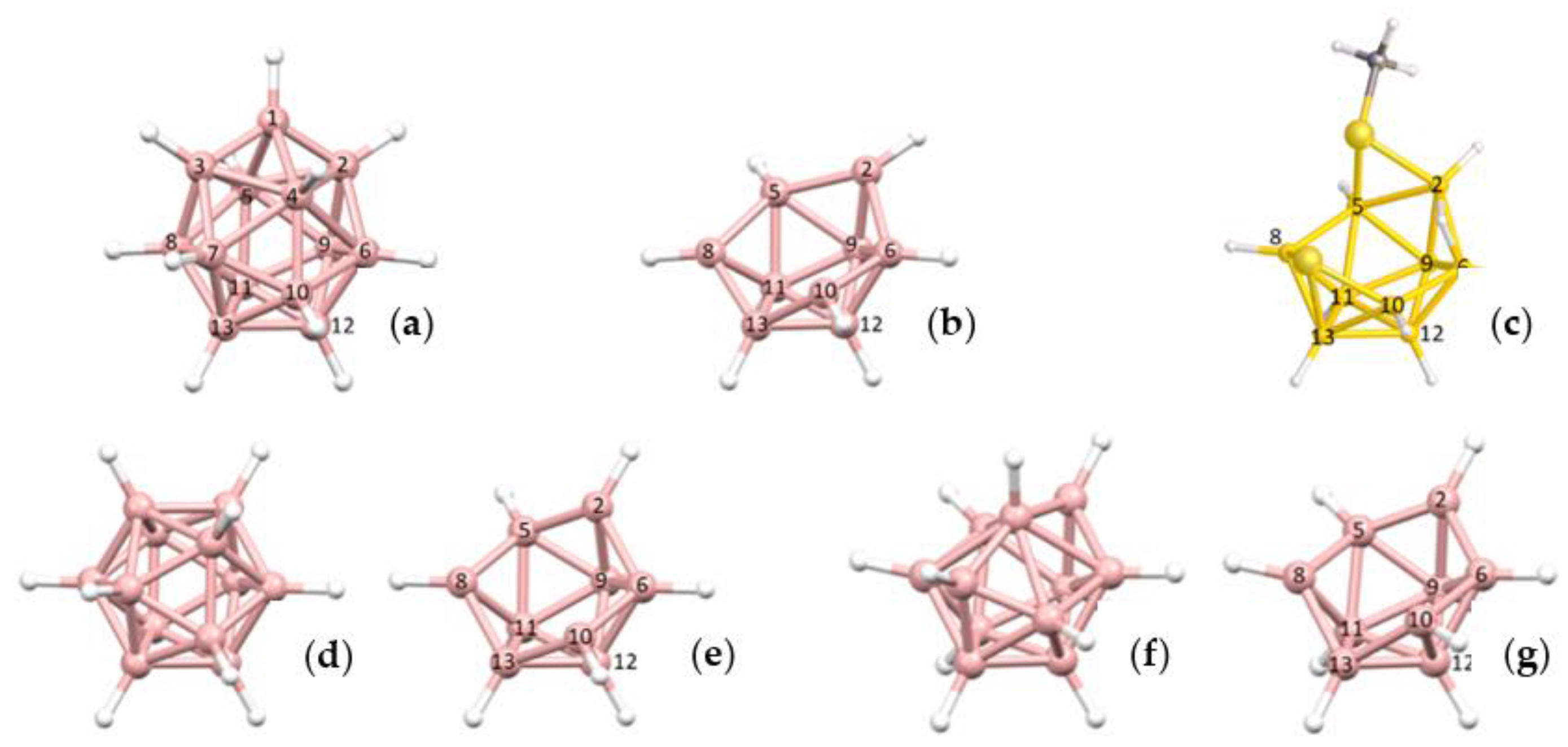
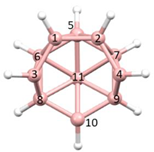
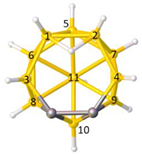
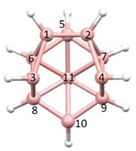
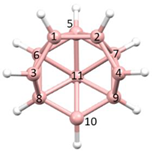
In this contribution we are concerned with heteroboranes in which a main group heteroatom could either be considered as a vertex or as a bridge to the cluster, and we describe a method to distinguish between these alternatives based on the differing effects that a heteroatom bridge or vertex has on the structure of the {B_x} fragment of the molecule. To illustrate the problem, consider the species [Me₃NCB₁₀H₁₀PPh] [10], assigned the refcode PACBOR in the Cambridge Structural Database (CSD) [11]. As described in the publication, and as implied by Figure 3a, PACBOR is considered to be an 11-vertex nido CB₁₀ species with a {PPh} fragment bridging a B—B edge in the open face. In this description the P atom is not formally a vertex, the {PPh} unit contributes just 2e to the cluster bonding, and consequently the {B₁₀} residue would be an arachno fragment of an icosahedron, characterized by 13 SEP. Alternatively, simply redrawing the molecule with two additional P—B connectivities (Figure 3b) implies that the P atom is a cluster vertex. In this description PACBOR would be a 12-vertex nido PCB₁₀ species in which the {PPh} fragment contributes 1 vertex and 4 skeletal electrons. Now the {B₁₀} residue would be described as a hypho fragment of a 13-vertex parent (docosahedron), characterized by 14 SEP.

To distinguish between these alternatives, and hence to afford the more appropriate description of PACBOR, we need to see if the experimental {B₁₀} residue fits better with exemplar arachno or hypho {B₁₀} fragments, but first we need to establish if such exemplar fragments are themselves distinguishable. This is because, as shown in Figure 4, these fragments are topologically identical and, moreover, they are further topologically identical with a 12-SEP nido {B₁₀} fragment. So, faced with an experimental {B₁₀} fragment of this topology (from a crystallographic study) how do we know if it is best described as nido, arachno or hypho? More generally, how do we distinguish between topologically equivalent {B_x} fragments of different parent polyhedra? One approach for the {B₁₀} fragments could be to use the dimensions of the fragment, since as we go from nido {B₁₀} to arachno {B₁₀} to hypho {B₁₀} the cluster gets progressively shorter, deeper and broader (see Figure S1 in Supplementary Materials for detail) but this is not the best method and certainly not general for other fragments. Rather we make use of Structure Overlay (SO) calculations implemented in Mercury [12], as described in the Method section. The present study complements our earlier one using the same principle of structure overlay to distinguish between transition- or post-transition-metal bridges and vertices in species of the type [MB₁₀H₁₂] [13].

2. Results

2.1. PACBOR, [Me₃NCB₁₀H₁₀PPh]

As noted above, for PACBOR the possible alternatives are as follows; if the P atom is merely a bridge the {B₁₀} residue is an arachno fragment of an icosahedron but if the P atom is a vertex the {B₁₀} residue is a hypho fragment of a docosahedron. These exemplar fragments with the same topology were taken from DFT-optimized [B₁₂H₁₂]²⁻ and [B₁₃H₁₃]²⁻, respectively and a structure overlay calculation performed between them. See

Table 1. Structure Overlay calculation between the exemplar arachno {B₁₀} fragment (left) and exemplar hypho {B₁₀} fragment (right).

	Atom	Misfit (Å)
	1	0.111
	2	0.111
	3	0.163
	4	0.163
	5	0.111
	6	0.111
	7	0.086
	8	0.086
	9	0.028
	10	0.028
	rms	0.109

for atom numbering and SO results. A rms misfit value of 0.109 Å confirms that the exemplar fragments can be distinguished. The {B₁₀} residue of PACBOR, taken from the crystallographic study, was then overlaid against each of the exemplar fragments affording the results shown in

Table 2. Structure Overlay calculations (Å) between the experimental {B₁₀} fragment of PACBOR and exemplar arachno {B₁₀} fragment (left) and exemplar hypho {B₁₀} fragment (right).

	PACBOR/a-{B10}			PACBOR/h-{B10}
	1	0.088		1	0.047
	2	0.083		2	0.045
	3	0.127		3	0.089
	4	0.131		4	0.086
	5	0.075		5	0.044
	6	0.070		6	0.042
	7	0.062		7	0.025
	8	0.076		8	0.014
	9	0.013		9	0.030
	10	0.035		10	0.050
	rms	0.083		rms	0.053

. A rms misfit of 0.053 Å for the hypho fragment against a rms misfit of 0.083 Å for the arachno fragment shows that the {B₁₀} residue of PACBOR is better described as hypho. Consequently, the P atom is better regarded as a vertex than as a bridge meaning that the molecule overall is better described as a nido 12-vertex phosphacarborane than a nido 11-vertex carborane with a μ-PPh. Note that this conclusion is at variance with the description of PACBOR in both the original publication [10] and the name of this compound assigned in the CSD.

In an attempt to describe concisely the nature of the P atom in PACBOR (i.e., bridge or vertex) we re-introduce [13] the term verticity. For an atom X bonded to an experimental {B_x} fragment A overlaid against two exemplar {B_x} fragments B and C (with C being the more open fragment):

Verticity of X = {(rms misfit B/C + rms misfit A/B − rms misfit A/C)/2 × (rms misfit B/C)} × 100%

This affords verticity on a scale from 0% (misfit of A with B is 0) to 100% (misfit of A with C is 0). For PACBOR the verticity of the P atom is thus calculated as:

Verticity of P = {(0.109 + 0.083 − 0.053)/2 × 0.109} × 100%

i.e., a verticity of 63.8%. Clearly, a verticity > 50% means that the atom should be regarded more as a vertex than as a bridge whereas a verticity < 50% implies the opposite.

2.2. The Thermodynamic Isomer of [C₂B₁₀H₁₃]⁻

Two-electron reduction of either [closo-1,2-C₂B₁₀H₁₂] or [closo-1,7-C₂B₁₀H₁₂] affords [nido-7,9-C₂B₁₀H₁₂]²⁻, whose structure is that of a fragment of a docosahedron. Protonation of the dianion yields [C₂B₁₀H₁₃]⁻ [14], known in two isomeric forms, a kinetic isomer which retains the structure of the dianion and a thermodynamic isomer, usually described as comprising a nido 11-vertex CB₁₀ cage (fragment of an icosahedron) whose open face has a {CH₂} group bridging a B—B edge. Although neither the kinetic nor thermodynamic isomers per se have been studied crystallographically they are both so characterized in derivative form, the kinetic isomer as the [PMePh₃]⁺ salt of the C,C’-dimethyl analogue [15]. There are four crystallographic determinations of derivatives of the thermodynamic isomer [16,17,18], of which two, MMUHDB [17] and YACRIE [18], are of high precision. We have studied MMUHDB and YACRIE to establish if the ‘bridging’ C atom is better regarded as a bridge or a vertex.

The anion MMUHDB and molecule YACRIE are shown in Figure 5. The ‘bridging’ unit is {C(H)Me} with the Me group exo and the C—H bond endo to the polyhedron. The alternative descriptions of the {B₁₀} fragment here are the same as for PACBOR; if the {C(H)Me} unit is a bridge the polyhedron is a nido 11-vertex CB₁₀ cage of which the {B₁₀} fragment would be described as arachno, but if the ‘bridging’ C is really a vertex we have a nido 12-vertex C₂B₁₀ system of which the {B₁₀} fragment would be hypho. In

Table 3. Structure Overlay calculations (Å) between the experimental {B₁₀} fragment of MMUHDB and exemplar arachno {B₁₀} fragment (left) and exemplar hypho {B₁₀} fragment (right).

	MMUHDB/a-{B10}			MMUHDB/h-{B10}
	1	0.102		1	0.060
	2	0.091		2	0.059
	3	0.151		3	0.128
	4	0.150		4	0.132
	5	0.061		5	0.061
	6	0.062		6	0.059
	7	0.083		7	0.014
	8	0.084		8	0.014
	9	0.018		9	0.032
	10	0.020		10	0.026
	rms	0.093		rms	0.071

and

Table 4. Structure Overlay calculations (Å) between the experimental {B₁₀} fragment of YACRIE and exemplar arachno {B₁₀} fragment (left) and exemplar hypho {B₁₀} fragment (right).

	YACRIE/a-{B10}			YACRIE/h-{B10}
	1	0.111		1	0.076
	2	0.105		2	0.075
	3	0.151		3	0.122
	4	0.157		4	0.126
	5	0.067		5	0.057
	6	0.064		6	0.055
	7	0.074		7	0.021
	8	0.077		8	0.017
	9	0.030		9	0.046
	10	0.024		10	0.011
	rms	0.096		rms	0.072

are the results of SO calculations between the experimental MMUHDB and YACRIE {B₁₀} fragments and the exemplar fragments. In both cases the better fit is with the hypho exemplar, implying that the ‘bridging’ C atom is better described as a cluster vertex rather than a bridge. Calculated verticities for the C atom are 60.1% and 61.0%, respectively.

Interestingly, although MMUHDB is described as having a bridging {C(H)Me} unit [17] the species is named in the CSD as though both C atoms are vertices. Conversely, the publication describing YACRIE perceptively suggests that the ‘bridging’ C be regarded ‘as an integral part of the cluster’ [18] whilst in the CSD the compound is named as having a μ-(9,10-ethylidene) fragment.

2.3. ZONCOU and FAFYAN, a Case of Mistaken Identity

In 1995 Paetzold et al. published the synthesis and structure of ZONCOU, [PhNB₁₁H₁₁NEt₃], Figure 6a [19], and in 2002 the same group reported FAFYAN, [MeNB₁₁H₁₁NHEt₂], Figure 6b [20]. Although the Paetzold group described both species as azaboranes, thus clearly identifying the N(Ph) and N(Me) atoms as vertices, in the CSD FAFYAN is named as a 12-vertex azaborane whilst ZONCOU is described as an 11-vertex borane with a triply bridging phenylimino group.

This has prompted us to examine these two structures by SO calculations to establish the true nature of the N(Ph) and N(Me) atoms. The first obvious comment is that the two cages ‘look’ almost superimposable, implying that one is incorrectly described in the CSD. The second important point is that the N atoms in question make three short connectivities to B atoms, 1.5–1.6 Å. This is quite different to the situation in the previous species, PACBOR, MMUHDB and YACRIE, where the P or C atoms made only two short connections, ca. 2.0 Å in PACBOR and ca. 1.6 Å in MMUHDB and YACRIE, and implies that the N(Ph) and N(Me) atoms in ZONCOU and FAFYAN have considerable vertex character.

This is confirmed by our analysis. Initially we overlaid the {B₁₁} fragments of ZONCOU and FAFYAN with each other, with the results shown in

Table 5. Structure Overlay calculation between the {B₁₁} fragments of ZONCOU (left) and FAFYAN (right).

	Atom	Misfit (Å)
	1	0.008
	2	0.018
	3	0.009
	4	0.010
	5	0.009
	6	0.017
	7	0.021
	8	0.017
	9	0.027
	10	0.026
	11	0.026
	rms	0.019

. The extremely small rms misfit value, 0.019 Å, confirms that the two cages are isostructural. We next compared each of the experimental {B₁₁} fragments with exemplars, but now we need different exemplars to those used previously. If the N atom is a bridge the {B₁₁} unit is a nido fragment of an icosahedron, but if it is a vertex the cage is a nido NB₁₁ cluster the {B₁₁} component of which is an arachno fragment of a docosahedron. Note that in this description the nido 12-vertex NB₁₁ parent has a different topology (a degree-5 vertex missing) to the nido 12-vertex PCB₁₀ parent of PACBOR and nido C₂B₁₀ parent of MMUHDB and YACRIE (the degree-4 vertex missing). These differing topologies are possible because of the relatively low symmetry (C_2v) of the docosahedron.

The result of overlaying the exemplars is shown in

Table 6. Structure Overlay calculation between the exemplar nido {B₁₁} fragment (left) and exemplar arachno {B₁₁} fragment (right).

	Atom	Misfit (Å)
	1	0.001
	2	0.084
	3	0.045
	4	0.045
	5	0.083
	6	0.067
	7	0.181
	8	0.400
	9	0.181
	10	0.188
	11	0.188
	rms	0.170

. The rms misfit value is 0.170 Å, in large measure due to a substantial misfit of B8, meaning that the two exemplars can be distinguished structurally. Next, we overlaid the {B₁₁} fragments of ZONCOU and FAFYAN with each of the exemplar {B₁₁} fragments. Because ZONCOU and FAFYAN are isostructural we present only the results for ZONCOU (

Table 7. Structure Overlay calculations (Å) between the experimental {B₁₁} fragment of ZONCOU and exemplar nido {B₁₁} fragment (left) and exemplar arachno {B₁₁} fragment (right).

	ZONCOU/n-{B11}			ZONCOU/a-{B11}
	1	0.052		1	0.051
	2	0.174		2	0.093
	3	0.030		3	0.026
	4	0.031		4	0.030
	5	0.167		5	0.087
	6	0.105		6	0.043
	7	0.203		7	0.095
	8	0.497		8	0.095
	9	0.210		9	0.121
	10	0.338		10	0.152
	11	0.323		11	0.140
	rms	0.238		rms	0.094

) with those for FAFYAN deposited as Supplementary Materials (Table S1).

Clearly there is a much better fit of the experimental {B₁₁} fragment with the arachno exemplar (again note the very large misfit of B8 with the nido exemplar) meaning that the N(Ph) atom in ZONCOU should be regarded as a vertex rather than as a bridge. The verticity of N(Ph) is calculated as 92.3%. For FAFYAN the results are very similar; rms misfits of 0.227 Å against the nido exemplar and 0.081 Å against the arachno exemplar, resulting in a verticity of N(Me) of 92.9%.

In summary, both ZONCOU and FAFYAN are clearly azaboranes, with the former erroneously described in the CSD. The extremely high verticities are fully consistent with the N vertices making three short connections to B atoms in the cluster.

2.4. YELXES, S Bridge or Vertex?

The molecule [MeS₂B₉H₁₀], YELXES [21], is shown in perspective view in Figure 7. It features two heteroatoms one, S2, making three short connections to B atoms and the other a S(Me) unit bound to only two B atoms. As noted in the previous section the S2 heteroatom connected to three B atoms can be reasonably assumed to be a cluster vertex, and the question that then arises is whether the S(Me) atom is better regarded as a bridge or as a vertex.

If the S(Me) atom is a true vertex the cluster in YELXES is an arachno {S₂B₉} polyhedron, a fragment of a docosahedron although with a different topology to the arachno {B₁₁} fragments of ZONCOU and FAFYAN, again a consequence of the low symmetry of the docosahedron. Although this description is favored in the publication describing YELXES [21], two alternatives for a S(Me) bridge are also discussed, that in which it is a 3-e 2-orbital donor and that in which it is a 1-e 1-orbital source. If the former the cluster would be arachno {SB₉}, a fragment of an icosahedron with the same topology as the arachno {B₁₀} fragments of PACBOR, MMUHDB and YACRIE. If the latter the cluster would be nido {SB₉}, derived from an octadecahedron by removal of the degree-6 vertex.

This leads to three possible descriptions of the {B₉} fragment of YELXES; the {B₉} fragment of an arachno {S₂B₉} cluster would be a klado fragment of a docosahedron [22], the {B₉} fragment of an arachno {SB₉} cluster would be a hypho fragment of an icosahedron; and the {B₉} fragment of a nido {SB₉} cluster would be an arachno fragment of an octadecahedron. To illustrate these options Figure 8 shows (a) a numbered docosahedron, (b) a klado fragment thereof, (c) the molecule YELXES reoriented to present the same view of the {B₉} fragment, (d) an icosahedron, (e) a hypho fragment thereof, (f) an octadecahedron, and (g) an arachno fragment thereof. The three {B₉} fragments all share the same topology and numbering.

Thus, there are now three exemplar {B₉} fragments to consider, arachno, hypho and klado and in

Table 8. Structure Overlay calculations (Å) between exemplar klado, hypho and arachno {B₉} fragments.

Vertex	k-{B9}/h-{B9}	k-{B9}/a-{B9}	h-{B9}/a-{B9}
2	0.338	0.205	0.185
5	0.165	0.168	0.143
6	0.043	0.127	0.142
8	0.240	0.247	0.137
9	0.035	0.080	0.070
10	0.114	0.096	0.137
11	0.057	0.017	0.045
12	0.020	0.027	0.045
13	0.098	0.076	0.169
rms	0.159	0.137	0.129

are presented the results of SO calculations in which the three exemplar fragments are compared. The rms misfit values confirm that all three possibilities may be structurally distinguished, and we note that the two largest misfits are between klado/hypho and klado/arachno, i.e., between situations where the S(Me) is a vertex and both the bridge options.

Table 9. Structure Overlay calculations (Å) between the experimental {B₉} fragment of YELXES and exemplar klado, hypho and arachno {B₉} fragments.

Vertex	YELXES/k-{B9}	YELXES/h-{B9}	YELXES/a-{B9}
2	0.105	0.280	0.142
5	0.156	0.070	0.173
6	0.072	0.042	0.169
8	0.117	0.134	0.142
9	0.064	0.059	0.128
10	0.110	0.064	0.090
11	0.075	0.099	0.069
12	0.060	0.077	0.049
13	0.096	0.193	0.028
rms	0.096	0.135	0.122

shows the result of SO calculations of the {B₉} fragment of YELXES with each of these exemplars. The fit is best with the klado exemplar suggesting that YELXES is best regarded as an arachno S₂B₉ cluster in which the S(Me) atom is a vertex, rather than an arachno SB₉ cluster with a 3-e 2-orbital bridging S(Me) or a nido SB₉ cluster with a 1-e 1-orbital bridging S(Me). Note that a similar bonding mode for the two S(Me) units of [(MeS)₂B₆H₈] has previously been suggested [23]. In YELXES the verticity of the S(Me) atom is 62.3% using the klado and hypho {B₉} misfit values, and 59.5% using the klado and arachno values.

2.5. BUPPEI, an Example Too Far?

In the preceding sections we have shown that the ‘bridging’ atoms (which come from groups 14, 15 and 16) in PACBOR, MMUHDB, YACRIE and YELXES are better described as vertices rather than bridges, and to extend our study we were therefore interested in an example involving a group 13 element. The anion BUPPEI (Figure 9a) consists of a {B(H)NMe₂} unit bonded to an open 13-vertex C₂B₁₁ cage via two short B—B connectivities [24]. The same publication also describes the anion BUPPIM (Figure 9b) which has an analogous structure but with only a bridging H atom. The bridging H in BUPPIM can only be a bridge, but in principle the {B(H)NMe₂} unit in BUPPEI could be either a bridge or vertex, so we have analyzed these two structures by SO calculations.

If the ‘bridging’ B in BUPPEI is merely a bridge the cluster is a nido-C₂B₁₁ one of which the {B₁₁} unit would be a hypho fragment of the 14-vertex parent [B₁₄H₁₄]²⁻, but if it is a vertex the cage is nido-C₂B₁₂ and the {B₁₁} fragment would be a klado fragment of the 15-vertex [B₁₅H₁₅]²⁻. For BUPPIM the only option is that the {B₁₁} fragment is hypho. In

Table 10. Structure Overlay calculation between the exemplar hypho {B₁₁} fragment (left) and exemplar klado {B₁₁} fragment (right).

	Atom	Misfit (Å)
	1	0.222
	2	0.222
	3	0.355
	4	0.355
	5	0.066
	6	0.099
	7	0.098
	8	0.055
	9	0.055
	10	0.251
	11	0.025
	rms	0.201

we show the result of a SO calculation between these two exemplar {B₁₁} fragments. The individual atom misfits are greatest at the B atoms in the open face (B1, B2, B3, B4) and at B10, the atom below the cage C atoms. The large rms misfit of 0.201 Å establishes that the exemplars can be distinguished.

In

Table 11. Structure Overlay calculations (Å) between the experimental {B₁₁} fragment of BUPPEI (unprimed cage) and exemplar hypho {B₁₁} fragment (left) and exemplar klado {B₁₁} fragment (right).

	BUPPEI/h-{B11}			BUPPEI/k-{B11}
	1	0.075		1	0.150
	2	0.062		2	0.165
	3	0.094		3	0.267
	4	0.103		4	0.258
	5	0.034		5	0.095
	6	0.059		6	0.047
	7	0.060		7	0.046
	8	0.043		8	0.023
	9	0.031		9	0.037
	10	0.052		10	0.222
	11	0.012		11	0.015
	rms	0.062		rms	0.151

we overlay the experimental {B₁₁} fragment of BUPPEI (unprimed cage, one of two crystallographically-independent anions) with the exemplar hypho and klado fragments sharing the same topology. Clearly the fit is better with the less open, hypho fragment (rms misfit 0.062 Å) than with the more open klado fragment (rms misfit 0.151 Å). This affords a verticity for the ‘bridging’ B of only 27.9%, implying it really is better described as a bridge and not a vertex. Table S2 in Supplementary Materials contains the almost identical results of the equivalent calculations using the primed cage; rms misfit vs. hypho exemplar 0.063 Å, vs. klado exemplar 0.147 Å, verticity of B 29.1%.

For comparison we have also overlaid the {B₁₁} fragment of BUPPIM with the hypho and klado exemplars, and the results are shown in

Table 12. Structure Overlay calculations (Å) between the experimental {B₁₁} fragment of BUPPIM and exemplar hypho {B₁₁} fragment (left) and exemplar klado {B₁₁} fragment (right).

	BUPPIM/h-{B11}			BUPPIM/k-{B11}
	1	0.062		1	0.180
	2	0.064		2	0.175
	3	0.062		3	0.317
	4	0.054		4	0.324
	5	0.021		5	0.086
	6	0.050		6	0.050
	7	0.051		7	0.052
	8	0.028		8	0.042
	9	0.026		9	0.043
	10	0.050		10	0.273
	11	0.016		11	0.023
	rms	0.047		rms	0.181

. The rms misfit vs. the hypho exemplar is 0.047 Å (smaller than that for BUPPEI) and that vs. the klado exemplar is 0.181 Å (larger than that for BUPPEI). This affords a ‘verticity’ for the bridging H atom (which, of course, can only be a bridge) of 16.7%. Although these structural differences between the {B₁₁} fragments of BUPPEI and BUPPIM are only small we believe they are important, as detailed in the ‘Discussion’ section below.

3. Discussion

We have used Structure Overlay calculations to analyze boron clusters which contain an open face onto which a main group heteroatom X is bound by two short B—X connectivities for a variety of atoms X; B (BUPPEI [24]), C (MMUHDB [17] and YACRIE [18]), P (PACBOR [10]) and S (YELXES [21]). Our approach is based on the fact that considering the atom X as a bridge or a cluster vertex will result in different formal descriptions of the {B_x} residue of the cluster. We have overlaid the structure of the experimental {B_x} residue with those of exemplar {B_x} fragments having the same topology derived from closo species [B_nH_n]²⁻ optimized by DFT calculation, and used the better or best fit to identify the better or best description for the experimental {B_x} residue and hence better or best description of X as a bridge or vertex.

In describing their experimental results, some authors have simply assumed that X is a bridge and not a formal part of the cluster (PACBOR, MMUHDB and YACRIE, although in the last case the authors also cast some doubt about this assumption). Others have argued (as it turns out correctly) that X is a vertex whilst also discussing the possibility of it as a bridge (YELXES). Yet, others have assumed (as it turns out incorrectly) that X is a vertex without any explanation (BUPPEI). However, as far as we are aware no previous method to distinguish between bridge or vertex options has been proposed.

We find that, with the exception of BUPPEI, in all the cases we have considered X is better described as a vertex and we have attempted to quantify this with the term verticity. For MMUHDB, YACRIE, PACBOR and YELXES the calculated verticities are remarkably consistent, 60–65%. We recognize that these values are not particularly high, and certainly not as high as those (>90%) we have found when similarly analyzing heteroatoms bound by three short B connectivities (ZONCOU [19] and FAFYAN [20]) [25]. Nevertheless, verticities of ca. 60% do suggest that the better description of the atom X in MMUHDB, YACRIE, PACBOR and YELXES is as a cluster vertex. The exception is BUPPEI, in which the verticity of the bridging B atom is only ca. 28%, implying that this atom is better described as a bridge than a vertex, and that the correct formal description of the anion is as a nido C₂B₁₁ species with a bridging B and not as a nido C₂B₁₂ species [24]. How can we rationalize these results?

Formally, electron donation to the cluster from all these ‘bridging’ units is from two sources; those electrons involved in the (radial) interaction between X and the cluster (i.e., in simple terms those electrons donated via the B—X connectivities) and those electrons in either a (tangential) lone pair or 2-centre-2-electron bond on X which is endo with respect to the cluster. The {C(H)Me} fragments of MMUHDB and YACRIE provide 2 radial electrons as does the {PPh} fragment of PACBOR, whilst the {SMe} group of YELXES provides 3 such electrons. In BUPPEI, however, only 1 radial electron is formally donated to the cluster. In all cases these contributions to the overall skeletal electron count are then formally enhanced by the endo electron pair. Note that in ZONCOU and FAFYAN the orientation of the Ph or Me substituent implies no endo lone pair on the N atoms, with all the (4) donated electrons being radial.

Our structure overlay results, and the conclusions regarding the formal descriptions of X as either a bridge or vertex which derive from them, may be understood at a simple level if we assume that the radial electron donation from X is more important than donation of the endo electron pair. In this way the 2- or 3-electron radial donations of {C(H)Me}, {PPh} and {SMe}, supplemented by relatively weak endo donation, achieve verticities > 50% (making the atom X formally a vertex) but they do not approach the very high verticities seen in ZONCOU and FAFYAN where the N heteroatoms are fully integrated into the cluster framework and the total skeletal electron count does not depend on endo electrons. In contrast weak endo donation is insufficient to raise the verticity in BUPPEI (which has only 1-electron radial donation) above the 50% threshold and consequently the {B(H)NMe₂} group is formally described as a bridge. Note, however, that the {B(H)NMe₂} in BUPPEI has a higher verticity than the simple bridging H atom in BUPPIM since in the latter case there are no endo electrons to be donated.

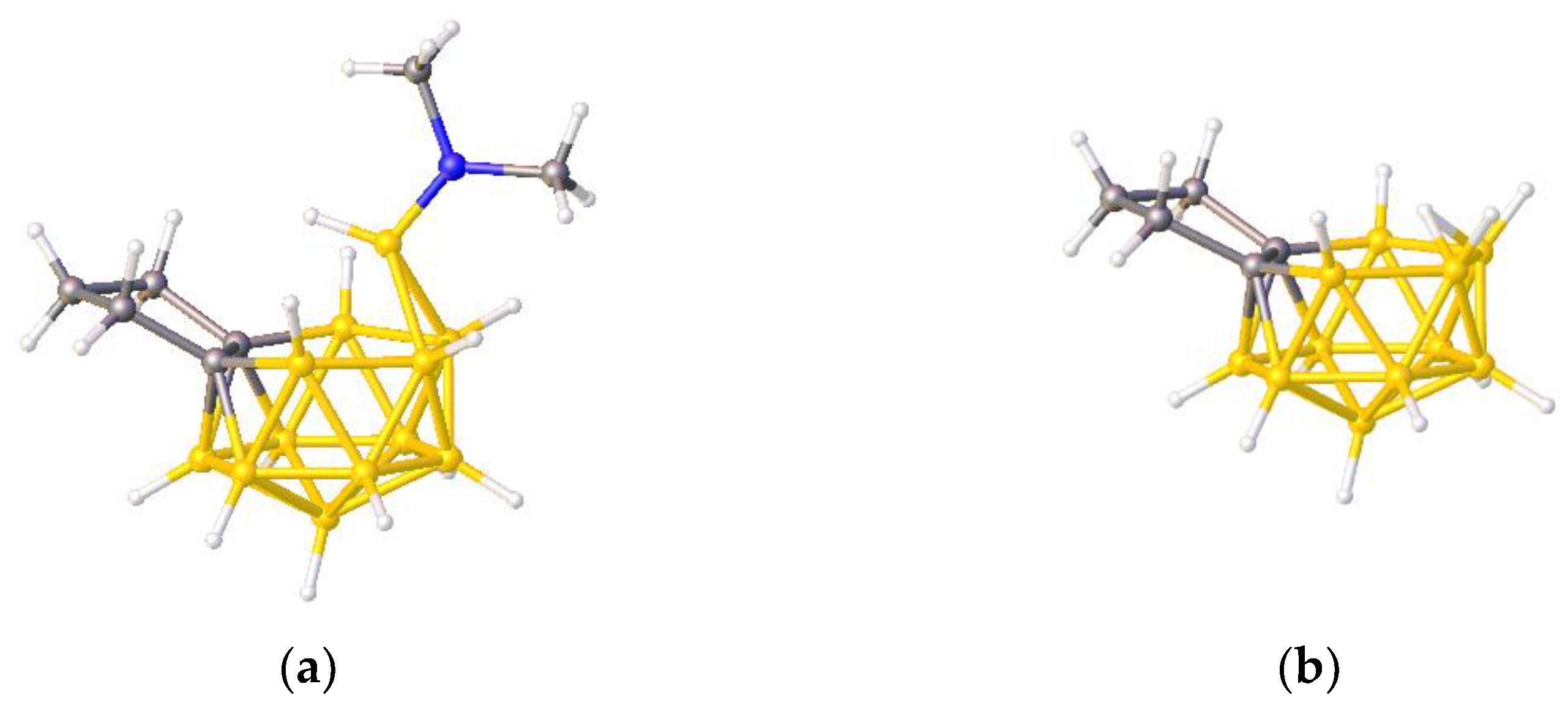
A useful test of our explanation would be consider the effect of a ‘bridging’ {B(H)NMe₃} unit as opposed to a bridging {B(H)NMe₂} unit, since the former would provide 2 radial electrons as opposed to just 1 and should, therefore, assume more vertex character. Since we have been unable to locate a (hetero)borane with a ‘bridging’ {B(H)NMe₃} fragment in the CSD we have constructed one from BUPPEI. Initially (to check the validity of the process) we have simply optimized the anion BUPPEI by DFT calculation and in Table S3 of Supplementary Materials are presented the results of structure overlay calculations of the {B₁₁} fragment of the optimized model and the unprimed and primed experimental {B₁₁} fragments. In both cases the very small rms misfit values of 0.019 Å confirm the validity of the optimization. Consequently, we have constructed the neutral species [(CH₂)₃C₂B₁₁H₁₁{B(H)NMe₃}] (compound 1) from the coordinates of BUPPEI and optimized its structure. 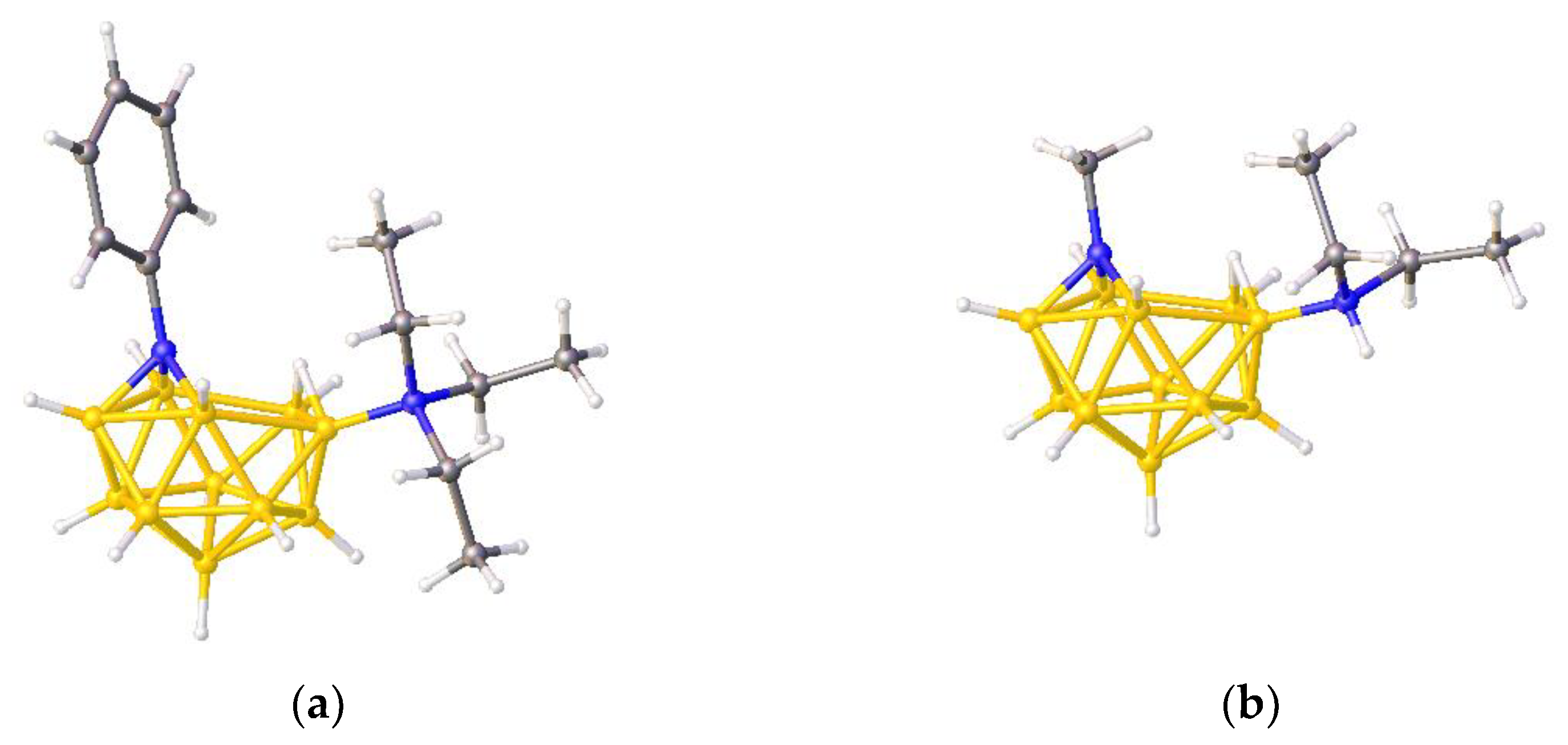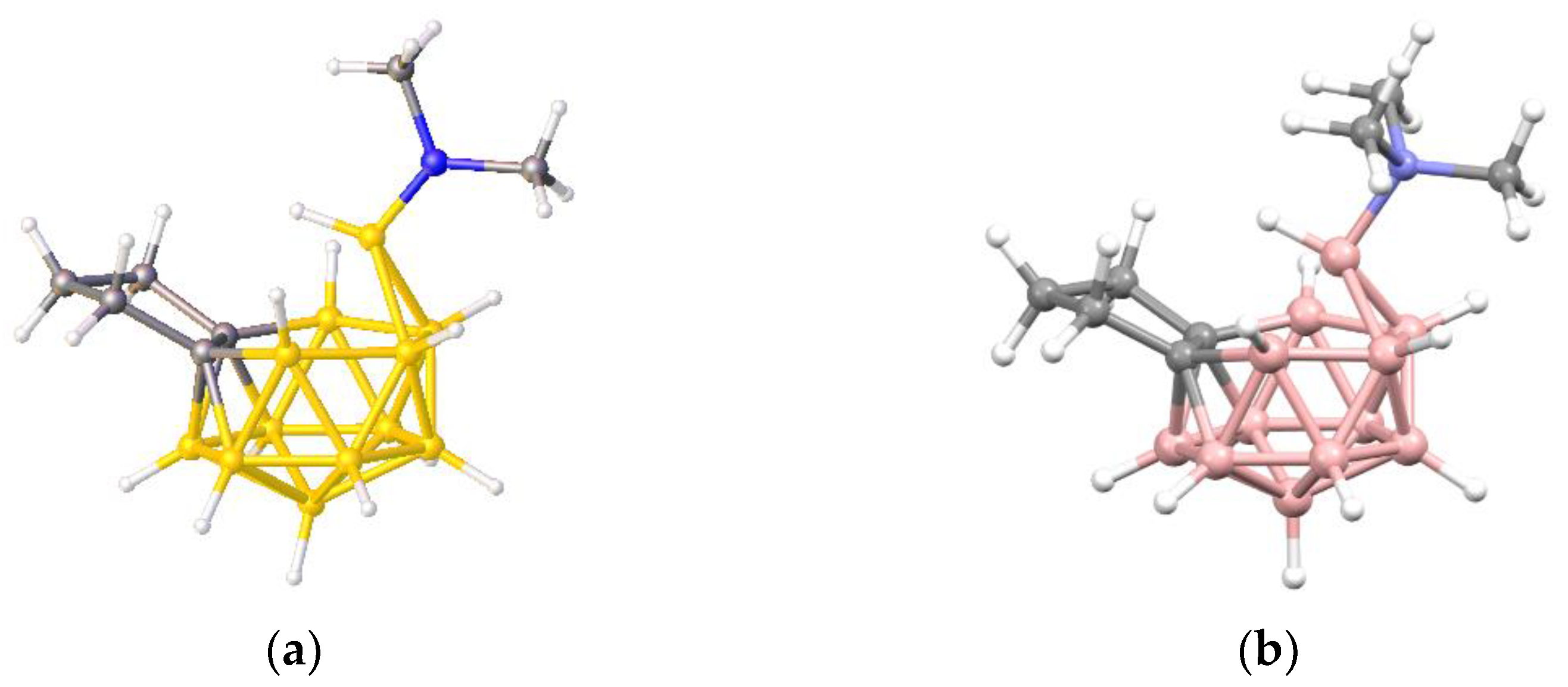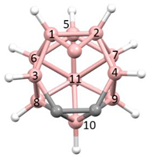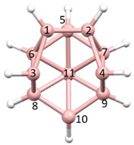Figure 10b shows a perspective view of 1 (since this is an optimized model and not a real molecule B atoms are shown in pink) adjacent to BUPPEI (Figure 10a). Note that, in terms of their overall skeletal electron count, the anion BUPPEI and neutral species 1 are isoelectronic, the anionic charge of BUPPEI being compensated by an additional radial electron from the bridge in 1. Initial comparison of the two structures does suggest a somewhat greater degree of vertex character for the bridging B of 1 since, in addition to the two short B—B distances of 1.788 and 1.790 Å (c.f. 1.868–1.890 Å in BUPPEI) the bridging B is only 2.155 and 2.168 Å from the other two B atoms in the open face (c.f. 2.388–2.442 Å in BUPPEI).

Table 13. Structure Overlay calculations (Å) between the {B₁₁} fragment of DFT-optimized compound 1 (center) and exemplar hypho {B₁₁} fragment (left) and exemplar klado {B₁₁} fragment (right).

	1/h-{B11}			1/k-{B11}
	1	0.093		1	0.137
	2	0.090		2	0.138
	3	0.169		3	0.188
	4	0.168		4	0.189
	5	0.017		5	0.059
	6	0.055		6	0.051
	7	0.056		7	0.051
	8	0.025		8	0.031
	9	0.026		9	0.031
	10	0.098		10	0.163
	11	0.024		11	0.005
	rms	0.091		rms	0.115

reports the results of structure overlay calculations of the {B₁₁} fragment of 1 with both the hypho and klado {B₁₁} exemplars. Although the rms misfit with the hypho exemplar is still the smaller (meaning that the bridging B is still better described as a bridge) it is greater than that for BUPPEI and, correspondingly, the rms misfit with the klado exemplar is smaller than that for BUPPEI. For the bridging B atom the verticity is 44.0% in compound 1 compared to only ca. 28% in BUPPEI, supporting the idea that formally increasing the radial electron donation of the bridging unit from 1 to 2 electrons significantly increases the vertex character.

4. Conclusions

A number of borane and heteroborane compounds are known in which main group atoms ‘bridge’ a B—B connectivity on the open face and a valid question is whether that ‘bridge’ really is just a bridge or if it is better regarded as a vertex in a larger cluster. We have used Structure Overlay calculations comparing the {B_x} fragments of crystallographically studied species with those of exemplar fragments taken from optimized alternates in an attempt to address this question. We find that in most cases the main group ‘bridge’ is, in fact, better regarded as a vertex. We have rationalized our results by considering that the radial electron donation of a ‘bridging’ unit makes a more significant contribution to the overall skeletal electron count than does donation of an endo electron pair.

In an earlier study [13] we have used structure overlay calculations to analyze the bridge or vertex nature of transition-metal and post-transition-metal fragments in the family of metallaboranes [MB₁₀H₁₂]. The essential finding of this work was that a strong correlation existed between verticity and the number of available frontier orbitals of the metal fragment. Overall, there are two important conclusions common to both studies: First, the principle of structure overlay is highly appropriate in comparing the structures of two polyhedra since there is generally an unmanageable number of possible parameters (e.g., bond lengths, interbond angle, torsion angles etc) for such conventional comparison. Second, the verticity of a fragment, be it main group or transition-metal, in a heteroborane can span a wide range of values. It is not always the case that the fragment is very obviously a bridge or very obviously a vertex and a pragmatic approach to the question of bridge or vertex has to be adopted; nevertheless, via structure overlay calculations, we can now at least conclude that, for example, ‘the atom is better regarded as a vertex than a bridge.’

5. Method

As noted in the Introduction, whether a heteroatom is a bridge on or a vertex in a boron-based cluster results in a difference of 1 atom in the vertex count and 1 SEP in the skeletal electron count of the whole cluster and hence the {B_x} residue. The two alternative {B_x} fragments are topologically equivalent. The experimental {B_x} fragment is taken from a crystallographic study of the heteroborane. Wherever possible we restrict ourselves to studies of high precision which are free from crystallographic disorder, at least in the cluster fragment. We then construct appropriate exemplar {B_x} fragments by optimizing by DFT calculation (BP86/6-31G**; see Supplementary Materials for details) the closo species [B_nH_n]²⁻ and then excluding vertices to afford the {B_x} fragment with correct topology. Next, we perform a structure overlay calculation on the two alternative exemplar fragments. Output from this is a list of individual atom misfit values and an overall rms misfit (Å), a high rms misfit showing that the two exemplar fragments can be distinguished. We then overlay the experimental {B_x} fragment with each of the exemplar {B_x} fragments to establish which is the better fit (lower rms misfit). This, then, provides evidence for describing the heteroatom as either a bridge or vertex.