DPD Simulation on the Transformation and Stability of O/W and W/O Microemulsions
Abstract
:1. Introduction
2. Simulation Methodology
2.1. Dissipative Particle Dynamics Theory
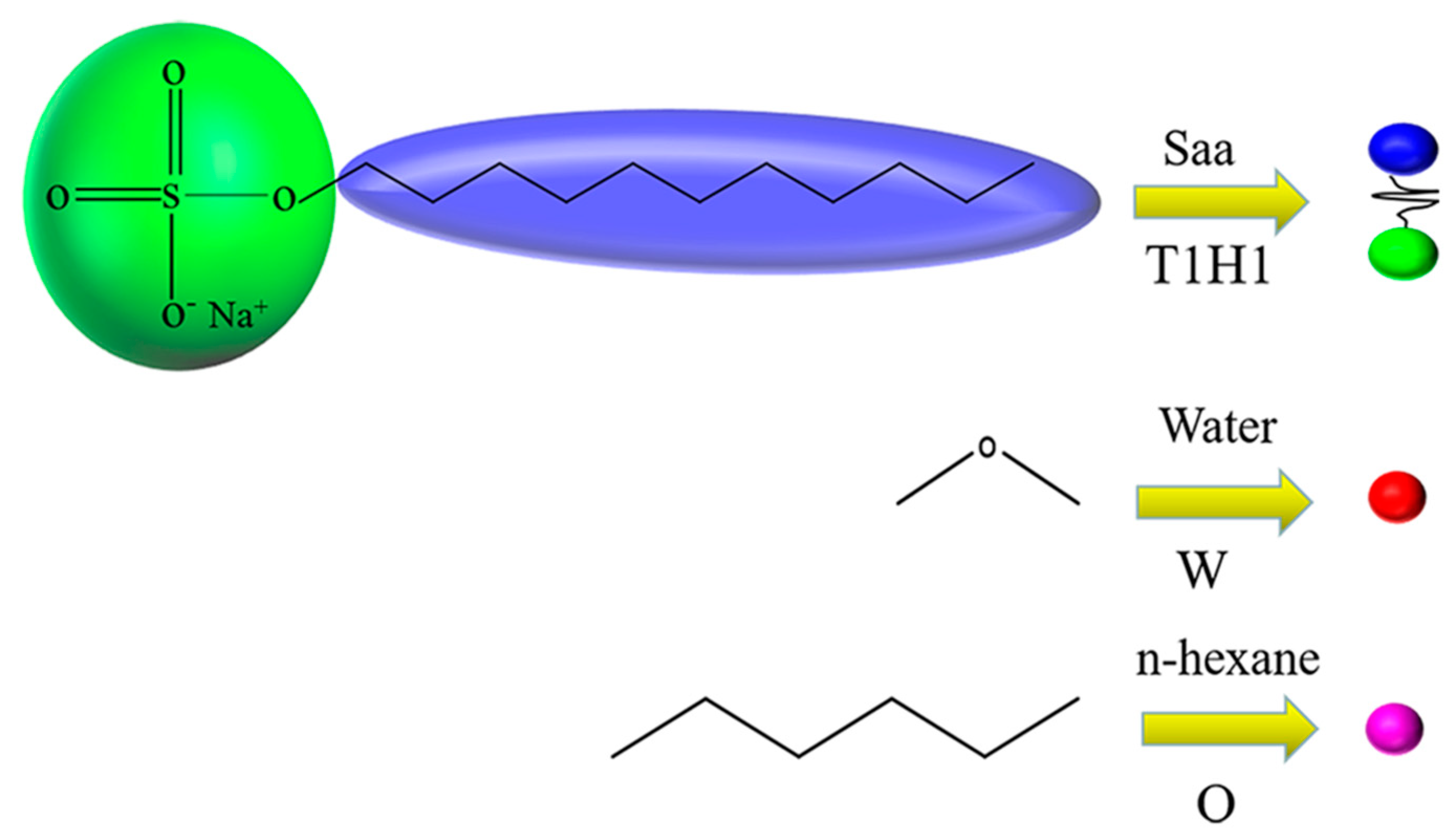
2.2. Models and Interaction Parameters
3. Results and Discussion
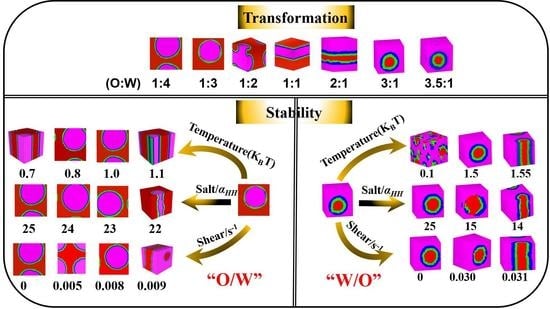
3.1. Transformation of W/O and O/W Microemulsion Systems
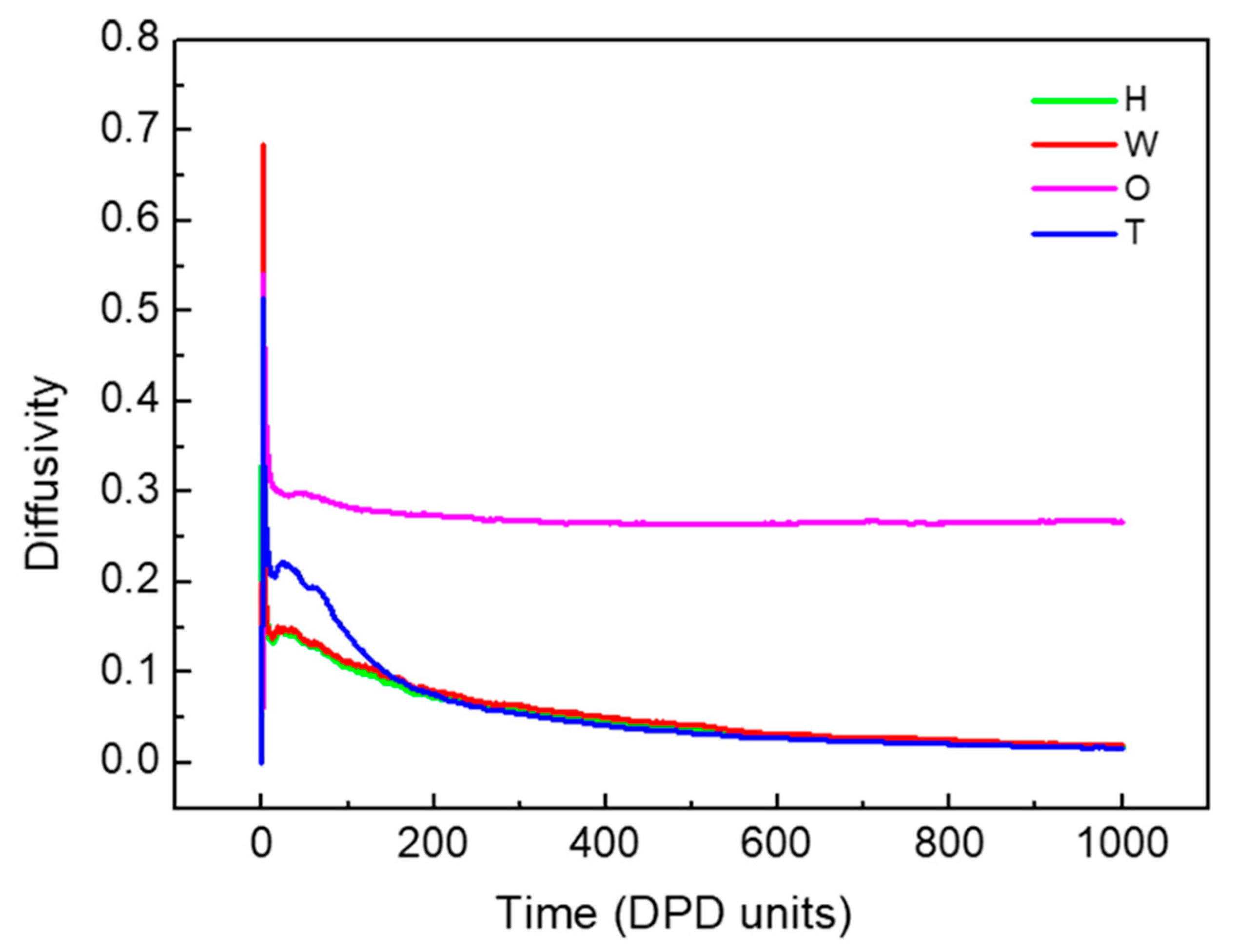
3.1.1. Dynamics of the W/O and O/W Microemulsion Systems Formation
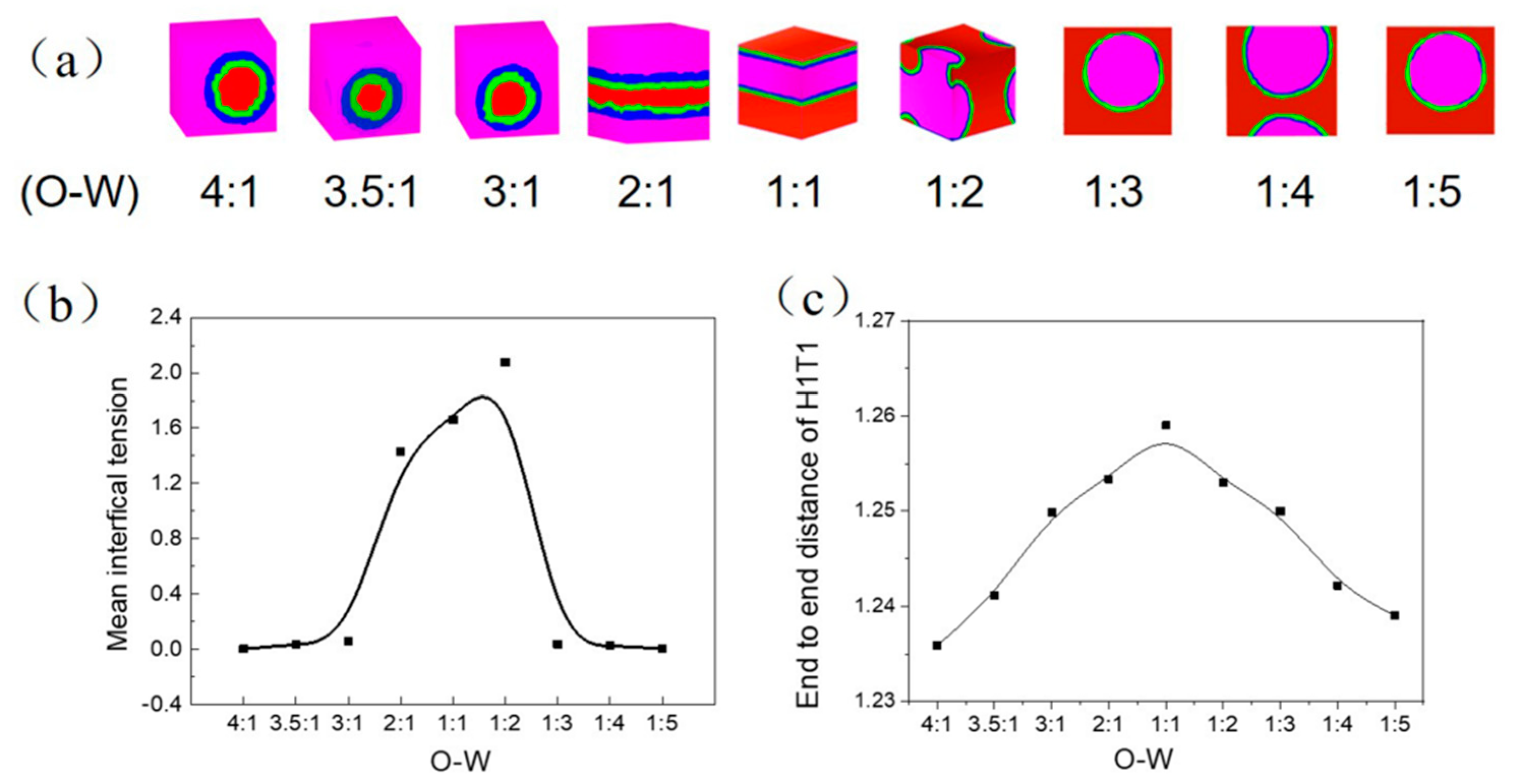
3.1.2. Influence of Oil-Water Ratio on the Transformation of W/O and O/W Microemulsion Systems
3.2. Stability of the W/O and O/W Microemulsion Systems
3.2.1. Influence of Temperature on the W/O and O/W Microemulsion Systems
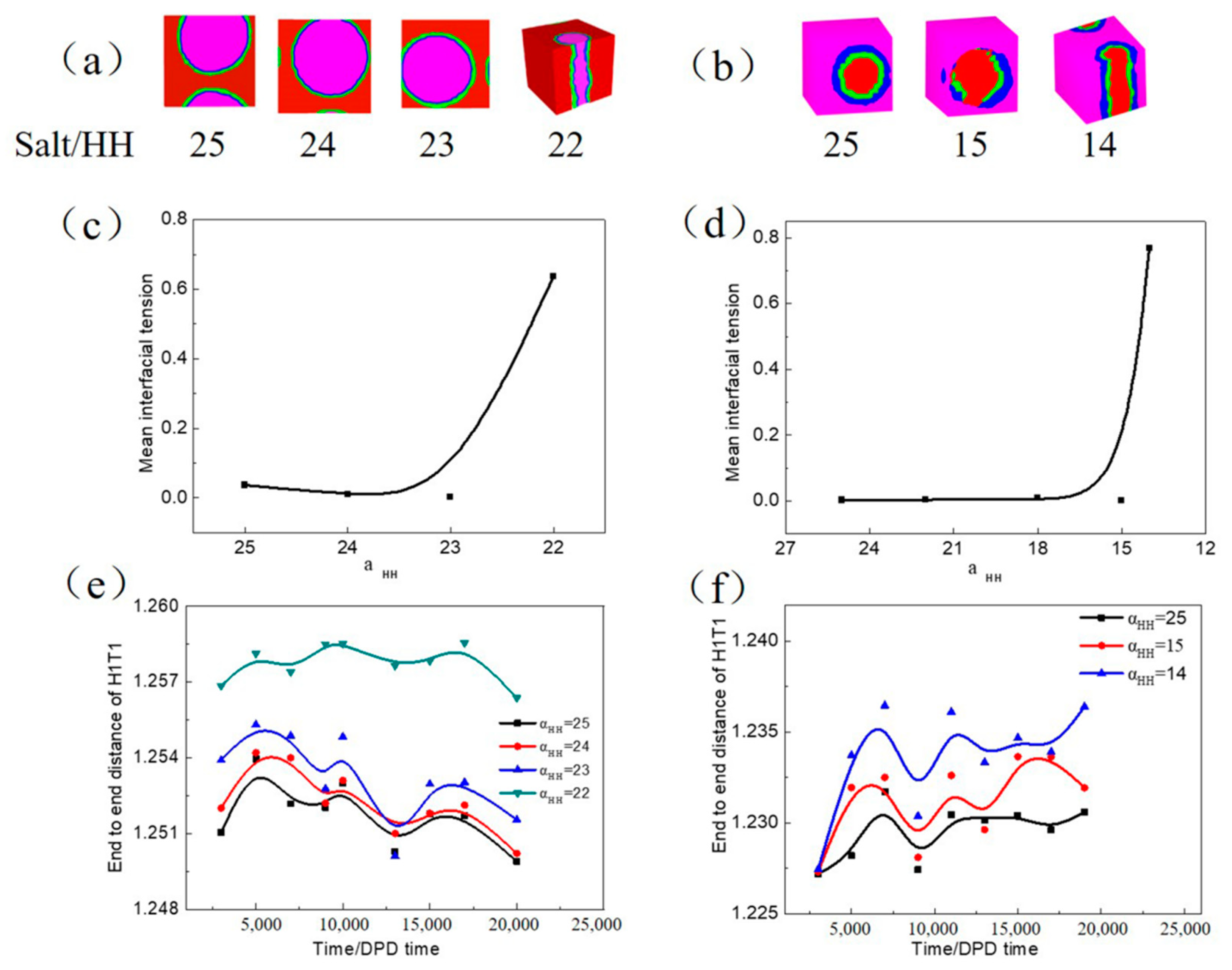
3.2.2. Influence of Inorganic Salt on the W/O and O/W Microemulsion Systems
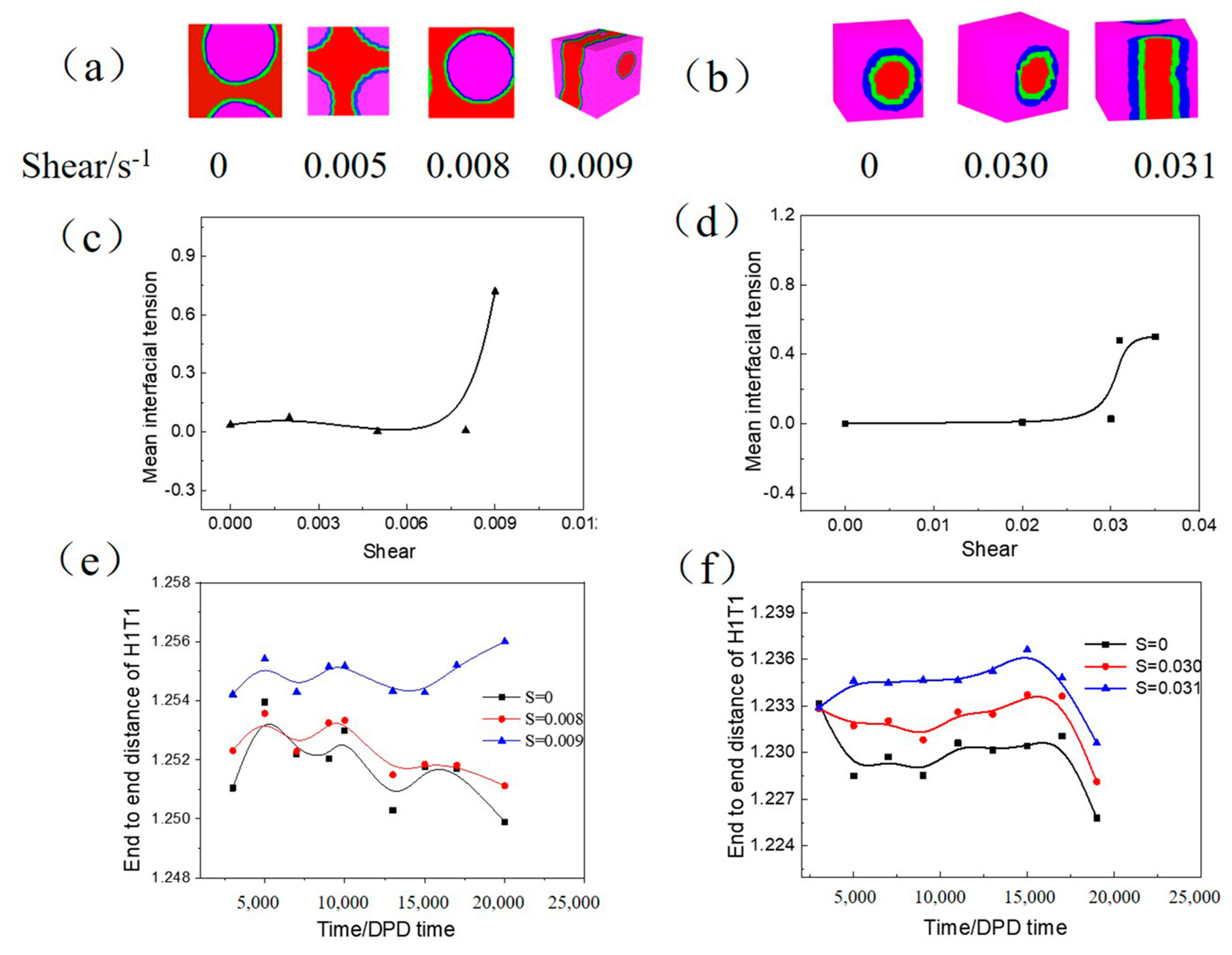
3.2.3. Influence of Shear on the W/O and O/W Microemulsion Systems
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Sample Availability
References
- Huang, Y.; Ni, N.; Zhao, L.; Zhang, J.; Shen, L. The preparation, evaluation and phase behavior of linker-based coix seed oil microemulsion. J. Mol. Liq. 2020, 319, 114314. [Google Scholar] [CrossRef]
- Posocco, P.; Perazzo, A.; Preziosi, V.; Laurini, E.; Pricl, S.; Guido, S. Interfacial tension of oil/water emulsions with mixed non-ionic surfactants: Comparison between experiments and molecular simulations. RSC Adv. 2016, 6, 4723–4729. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Sun, J.; Wang, D.; Wang, Z. Investigation of the phase behavior of food-grade microemulsions by mesoscopic simulation. Colloid Surf. A 2015, 487, 75–83. [Google Scholar] [CrossRef]
- Yew, H.C.; Misran, M.B. Nonionic Mixed Surfactant Stabilized Water-in-Oil Microemulsions for Active Ingredient In Vitro Sustained Release. J. Surfactants Deterg. 2015, 19, 49–56. [Google Scholar] [CrossRef]
- Subongkot, T.; Ngawhirunpat, T. Development of a novel microemulsion for oral absorption enhancement of all-trans retinoic acid. Int. J. Nanomed. 2017, 12, 5585–5599. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Subongkot, T.; Sirirak, T. Development and skin penetration pathway evaluation of microemulsions for enhancing the dermal delivery of celecoxib. Colloids Surf. B Biointerfaces 2020, 193, 111103. [Google Scholar] [CrossRef]
- Gundogdu, E.; Alvarez, I.G.; Karasulu, E. Improvement of effect of water-in-oil microemulsion as an oral delivery system for fexofenadine: In vitro and in vivo studies. Int. J. Nanomed. 2011, 6, 1631–1640. [Google Scholar] [CrossRef] [Green Version]
- You, J.; Meng, S.; Ning, Y.K.; Yang, L.Q.; Zhang, X.W.; Wang, H.N.; Li, J.J.; Yin, F.M.; Liu, J.; Zhai, Z.Y.; et al. Development and application of an osthole microemulsion hydrogel for external drug evaluation. J. Drug Deliv. Sci. Technol. 2019, 54, 101331. [Google Scholar] [CrossRef]
- Jaimes-Lizcano, Y.A.; Wang, Q.; Rojas, E.C.; Papadopoulos, K.D. Evaporative destabilization of double emulsions for effective triggering of release. Colloid Surf. A 2013, 423, 81–88. [Google Scholar] [CrossRef]
- Zhu, T.; Kang, W.; Yang, H.; Li, Z.; Zhou, B.; He, Y.; Wang, J.; Aidarova, S.; Sarsenbekuly, B. Advances of microemulsion and its applications for improved oil recovery. Adv. Colloid Interface Sci. 2021, 299, 102527. [Google Scholar] [CrossRef]
- Zhou, Y.; Yin, D.; Wang, D.; Zhang, C.; Yang, Z. Experiment investigation of microemulsion enhanced oil recovery in low permeability reservoir. J. Mater. Res. Technol. 2020, 9, 8306–8313. [Google Scholar] [CrossRef]
- Mangaiyarkarasi, R.; Priyanga, M.; Santhiya, N.; Umadevi, S. In situ preparation of palladium nanoparticles in ionic liquid crystal microemulsion and their application in Heck reaction. J. Mol. Liq. 2020, 310, 113241. [Google Scholar] [CrossRef]
- Congiu, A.; Gila, L.; Caccianotti, L.; Fusco, R.; Busto, C.; Zanardi, S.; Salvalaggio, M. Microemulsions for luminescent solar concentrator application. Sol. Energy 2021, 216, 338–350. [Google Scholar] [CrossRef]
- Fatma, N.; Ansari, W.H.; Panda, M.; Kabir-ud-Din. A Systematic Study of Mixed Surfactant Solutions of a Cationic Ester-Bonded Dimeric Surfactant with Cationic, Anionic and Nonionic Monomeric Surfactants in Aqueous Media. J. Surfactants Deterg. 2013, 16, 609–620. [Google Scholar] [CrossRef]
- Wu, J.; Mei, P.; Chen, W.; Li, Z.B.; Tian, Q.; Mei, Q.X. Surface Properties and Solubility Enhancement of Anionic/Nonionic Surfactant Mixtures Based on Sulfonate Gemini Surfactants. J. Surfactants Deterg. 2019, 22, 1331–1342. [Google Scholar] [CrossRef]
- Khimani, M.; Vora, S. Effect of Inorganic Additives on a Conventional Anionic-Nonionic Mixed Surfactants System in Aqueous Solution. J. Surfactants Deterg. 2011, 14, 545–554. [Google Scholar] [CrossRef]
- Pan, Y.; Xu, Y.; Zhu, L.; Liu, X.; Zhao, G.; Wang, S.; Yang, L.; Ma, T.; Liu, H. Stability and rheological properties of water-in-oil (W/O) emulsions prepared with a soyasaponin-PGPR system. Future Foods 2021, 4, 100096. [Google Scholar] [CrossRef]
- Li, J.Q.; Li, Y.F.; Zhong, J.F.; Teng, J.; Zang, H.; Song, H. Effect of cellulose nanocrystals on the formation and stability of oil in water emulsion formed by octenyl succinic anhydride starch. LWT 2021, 151, 112214. [Google Scholar] [CrossRef]
- Seddari, S.; Moulai-Mostefa, N.; Sabbache, H. Effect of pH on the stability of W/O/W double emulsions prepared by the mixture of biopolymers using direct method. Mater. Today Proc. 2021, 49, 1030–1034. [Google Scholar] [CrossRef]
- Zhong, M.; Sun, Y.; Sun, Y.; Huang, Y.; Qi, B.; Li, Y. The effect of salt ion on the freeze-thaw stability and digestibility of the lipophilic protein-hydroxypropyl methylcellulose emulsion. LWT 2021, 151, 112202. [Google Scholar] [CrossRef]
- Ravera, F.; Dziza, K.; Santini, E.; Cristofolini, L.; Liggieri, L. Emulsification and emulsion stability: The role of the interfacial properties. Adv. Colloid Interface Sci. 2021, 288, 102344. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; He, M.; Yang, H.; Wang, N.; Kong, Y.; Li, Y.; Teng, F. Effect of soybean lipophilic protein–methyl cellulose complex on the stability and digestive properties of water-in-oil-in-water emulsion containing vitamin B12. Colloid Surf. A 2021, 629, 127364. [Google Scholar] [CrossRef]
- Okuro, P.K.; Gomes, A.; Costa, A.L.R.; Adame, M.A.; Cunha, R.A. Formation and stability of W/O-high internal phase emulsions (HIPEs) and derived O/W emulsions stabilized by PGPR and lecithin. Food Res. Int. 2019, 122, 252–262. [Google Scholar] [CrossRef]
- Huang, W.; Zhu, D.; Fan, Y.; Xuea, X.; Yanga, H.; Jiang, L.; Jiang, Q.; Chen, J.; Jiang, B.; Komarneni, S. Preparation of stable inverse emulsions of hydroxyethyl methacrylate and their stability evaluation by centrifugal coefficient. Colloid Surf. A 2020, 604, 125309. [Google Scholar] [CrossRef]
- Kayali, I.; Karaein, M.; Qamhieh, K.; Wadaah, S.; Ahmad, W.; Olsson, U. Phase Behavior of Bicontinuous and Water/Diesel Fuel Microemulsions Using Nonionic Surfactants Combined with Hydrophilic Alcohol Ethoxylates. J. Dispers. Sci. Technol. 2015, 36, 10–17. [Google Scholar] [CrossRef]
- Kayali, I.; Karaein, M.; Ahmed, W.; Qamhieh, K.; Olsson, U. Alternative Diesel Fuel: Microemulsion Phase Behavior and Combustion Properties. J. Dispers. Sci. Technol. 2016, 37, 894–899. [Google Scholar] [CrossRef]
- Acharya, B.; Guru, P.S.; Dash, S. Tween-80-n-Butanol-Diesel-Water Microemulsion System-A Class of Alternative Diesel Fuel. J. Dispers. Sci. Technol. 2014, 35, 1492–1501. [Google Scholar] [CrossRef]
- Acharya, B.; Dash, S. Tuning commercial diesel to microemulsified and blended form: Phase behavior and implications. J. Dispers. Sci. Technol. 2019, 40, 1159–1168. [Google Scholar] [CrossRef]
- Ashikhmin, A.; Piskunov, M.; Yanovsky, V.; Yan, W.M. Properties and Phase Behavior of Water-in-Diesel Microemulsion Fuels Stabilized by Nonionic Surfactants in Combination with Aliphatic Alcohol. Energy Fuels 2020, 34, 2135–2142. [Google Scholar] [CrossRef]
- Ashihmin, A.; Piskunov, M.; Roisman, I.; Yanovsky, V. Thermal stability control of the water-in-diesel microemulsion fuel produced by using a nonionic surfactant combined with aliphatic alcohols. J. Dispers. Sci. Technol. 2020, 41, 771–778. [Google Scholar] [CrossRef]
- Lbadaoui-Darvas, M.; Garberoglio, G.; Karadima, K.S.; Cordeiro, M.N.D.S.; Nenes, A.; Takahama, S. Molecular simulations of interfacial systems: Challenges, applications and future perspectives. Mol. Simul. 2021, 1–38. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Y.L.; Li, X.G.; Sun, H.; He, L. Mechanisms on the stability and instability of water in oil emulsion stabilized by interfacially active asphaltenes: Role of hydrogen bonding reconstructing. Fuel 2021, 297, 120763. [Google Scholar] [CrossRef]
- Ma, J.; Song, X.Y.; Peng, B.L.; Zhao, T.; Luo, J.H.; Shi, R.F.; Zhao, S.L.; Liu, H.L. Multiscale molecular dynamics simulation study of polyoxyethylated alcohols self assembly in emulsion systems. Chem. Eng. Sci. 2020, 231, 116252. [Google Scholar] [CrossRef]
- Wang, F.X.; Cao, J.H.; Ling, Z.Y.; Zhang, Z.G.; Fang, X.M. Experimental and simulative investigations on a phase change material nano emulsion based liquid cooling thermal management system for a lithium ion battery pack. Energy 2020, 207, 118215. [Google Scholar] [CrossRef]
- Maiti, A.; McGrother, S. Bead-bead interaction parameters in dissipative particle dynamics: Relation to bead-size, solubility parameter, and surface tension. J. Chem. Phys. 2004, 120, 1594–1601. [Google Scholar] [CrossRef] [PubMed]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Groot, R.D.; Madden, T.J. Dynamic simulation of diblock copolymer microphase separation. J. Chem. Phys. 1998, 108, 8713–8724. [Google Scholar] [CrossRef]
- Lavagnini, E.; Cook, J.L.; Warren, P.B.; Williamson, M.J.; Hunter, C.A. A Surface Site Interaction Point Method for Dissipative Particle Dynamics Parametrization: Application to Alkyl Ethoxylate Surfactant Self-Assembly. J. Phys. Chem. B 2020, 124, 5047–5055. [Google Scholar] [CrossRef]
- Wang, X.; Santo, K.P.; Neimark, A.V. Modeling Gas-Liquid Interfaces by Dissipative Particle Dynamics: Adsorption and Surface Tension of Cetyl Trimethyl Ammonium Bromide at the Air-Water Interface. Langmuir 2020, 36, 14686–14698. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.B.; Li, C.L.; Sun, S.Q.; Hu, S.Q. CO2 responsive Pickering emulsion stablized by modified silica nanoparticles A dissipative particle dynamics simulation study. J. Ind. Eng. Chem. 2021, 97, 492–499. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, B.; Zhang, H. Mesoscopic simulation on the microemulsion system stabilized by bola surfactant. J. Dispers. Sci. Technol. 2021. [Google Scholar] [CrossRef]
- Zhang, H.; Li, D.; Pei, L.; Zhang, L.J.; Wang, F. The Stability of the Micelle Formed by Chain Branch Surfactants and Polymer Under Salt and Shear Force: Insight from Dissipative Particle Dynamics Simulation. J. Dispers. Sci. Technol. 2015, 37, 270–279. [Google Scholar] [CrossRef]
- Rekvig, L.; Kranenburg, M.; Hafskiold, B.; Smit, B. Effect of surfactant structure on interfacial properties. Europhys. Lett. 2003, 63, 902–907. [Google Scholar] [CrossRef]
- Wang, S.; Yang, S.; Wang, R.; Yan, Z. Dissipative particle dynamics study on the temperature dependent interfacial tension in surfactant-oil-water mixtures. J. Pet. Sci. Eng. 2018, 169, 81–95. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, Z.; Wu, Z.; Wang, F.; Xu, B.; Wang, S.; Zhang, L. Investigation on the formation and stability of microemulsions with Gemini surfactants: DPD simulation. J. Dispers. Sci. Technol. 2021. [Google Scholar] [CrossRef]
- Chen, Z.; Cheng, X.; Cui, H.; Cheng, P.; Wang, H. Dissipative particle dynamics simulation of the phase behavior and microstructure of CTAB/octane/1-butanol/water microemulsion. Colloid Surf. A 2007, 301, 437–443. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, N.; Xu, Y.; Wang, Q.; Huang, P.; Nishinari, K.; Fang, Y. Improving the Stability of Oil Body Emulsions from Diverse Plant Seeds Using Sodium Alginate. Molecules 2019, 24, 3856. [Google Scholar] [CrossRef] [Green Version]



| W | H | T | O | |
|---|---|---|---|---|
| W | 25 | |||
| H | 25.34 | 25 | ||
| T | 151.52 | 177.82 | 25 | |
| O | 103.24 | 143.61 | 25.94 | 25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zhang, H.; Wu, Z.; Zhu, Z.; Jia, X. DPD Simulation on the Transformation and Stability of O/W and W/O Microemulsions. Molecules 2022, 27, 1361. https://doi.org/10.3390/molecules27041361
Li M, Zhang H, Wu Z, Zhu Z, Jia X. DPD Simulation on the Transformation and Stability of O/W and W/O Microemulsions. Molecules. 2022; 27(4):1361. https://doi.org/10.3390/molecules27041361
Chicago/Turabian StyleLi, Menghua, Haixia Zhang, Zongxu Wu, Zhenxing Zhu, and Xinlei Jia. 2022. "DPD Simulation on the Transformation and Stability of O/W and W/O Microemulsions" Molecules 27, no. 4: 1361. https://doi.org/10.3390/molecules27041361
APA StyleLi, M., Zhang, H., Wu, Z., Zhu, Z., & Jia, X. (2022). DPD Simulation on the Transformation and Stability of O/W and W/O Microemulsions. Molecules, 27(4), 1361. https://doi.org/10.3390/molecules27041361