Tetrel Bonding in Anion Recognition: A First Principles Investigation
Abstract
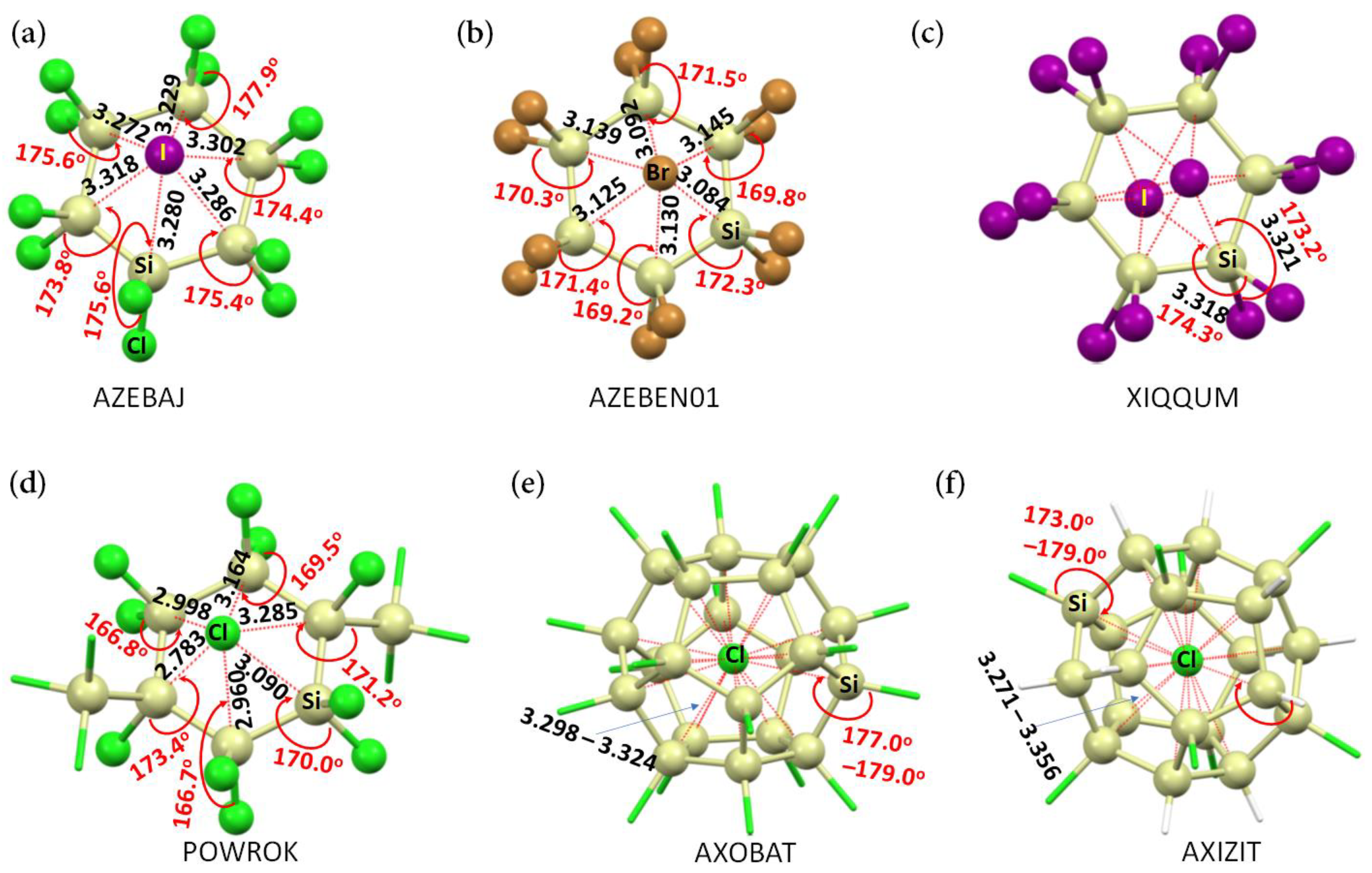
1. Introduction
2. Computational Methods
3. Results
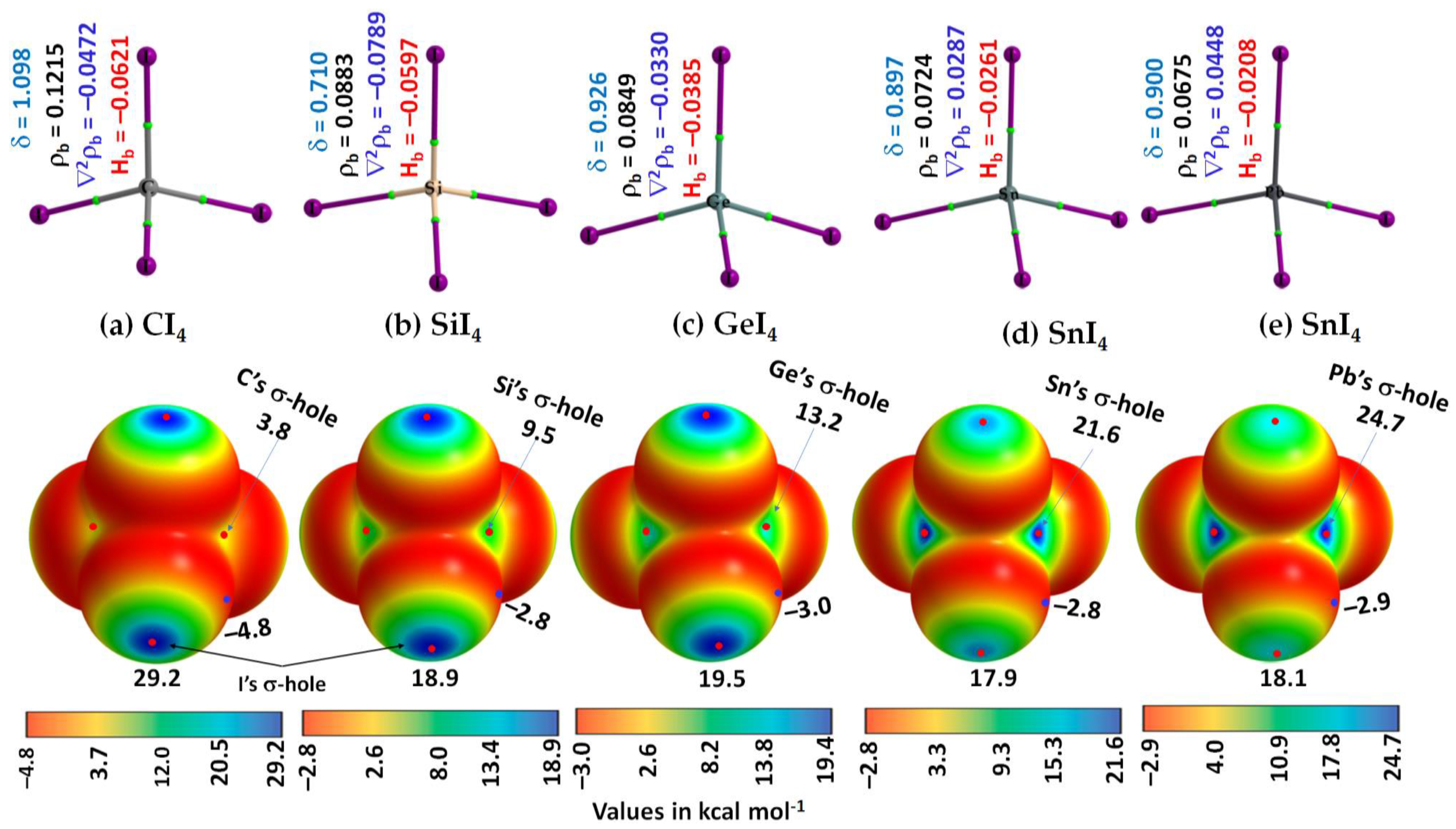
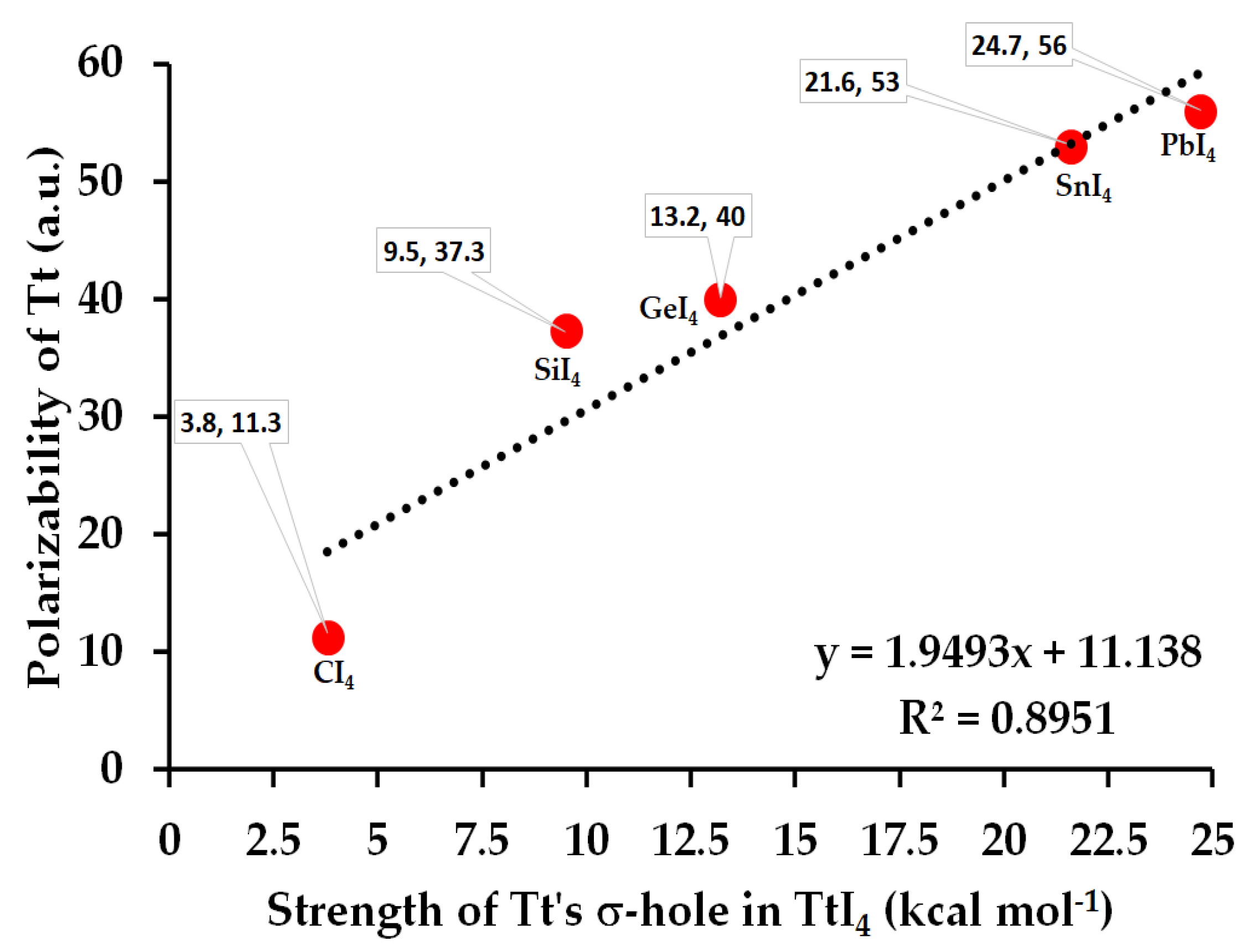
3.1. The Monomer Properties
3.2. The Complex Properties
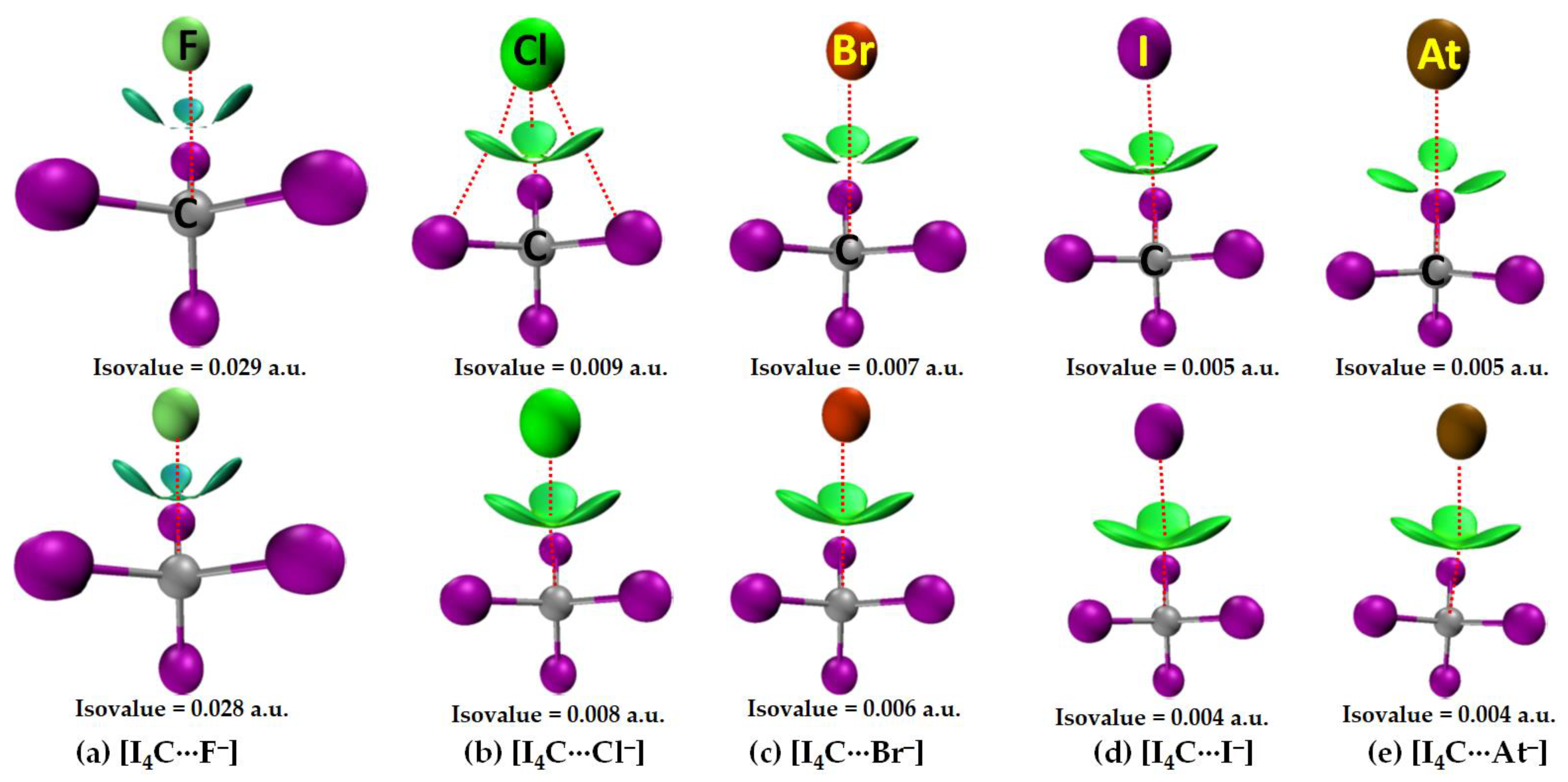
3.2.1. The [I4C···X−] Series
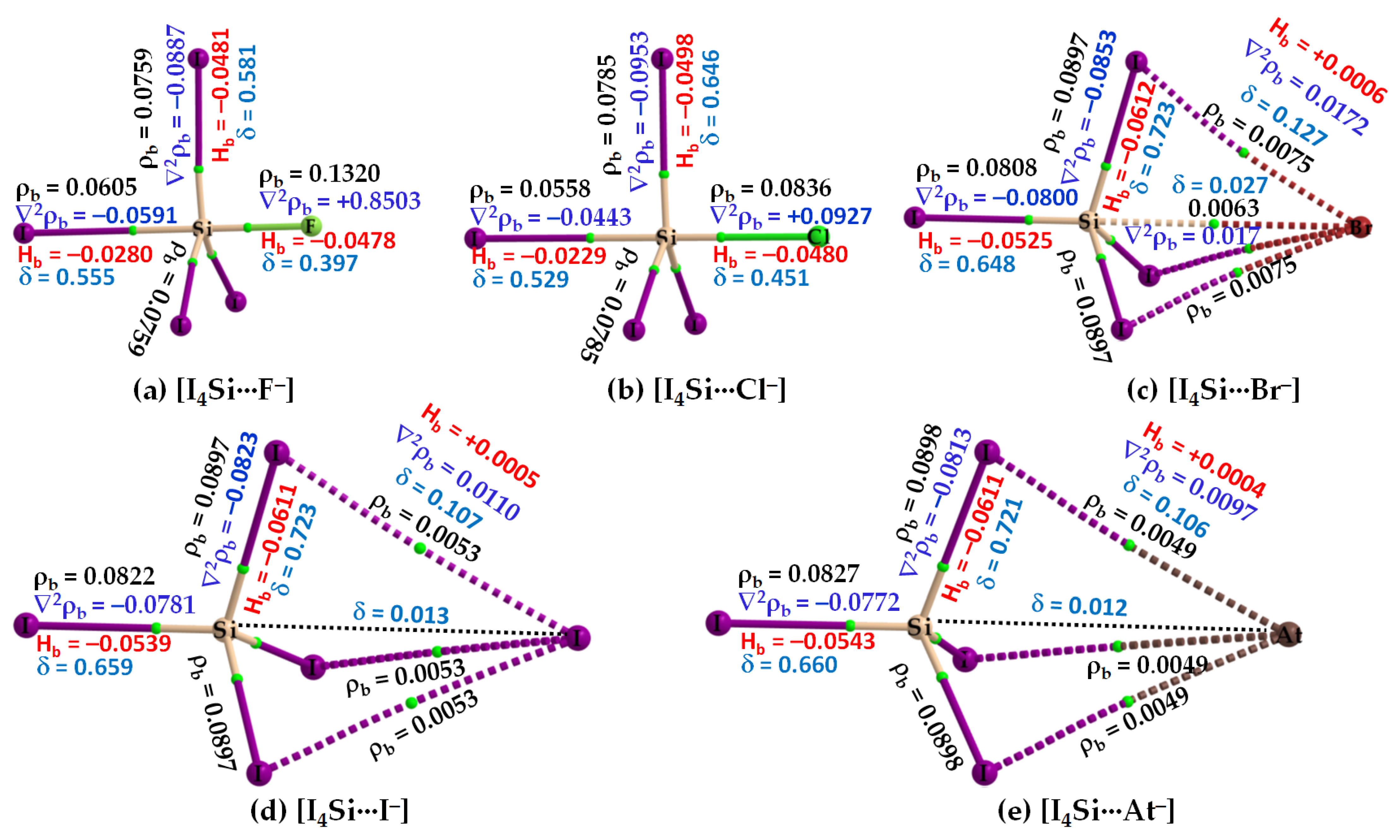
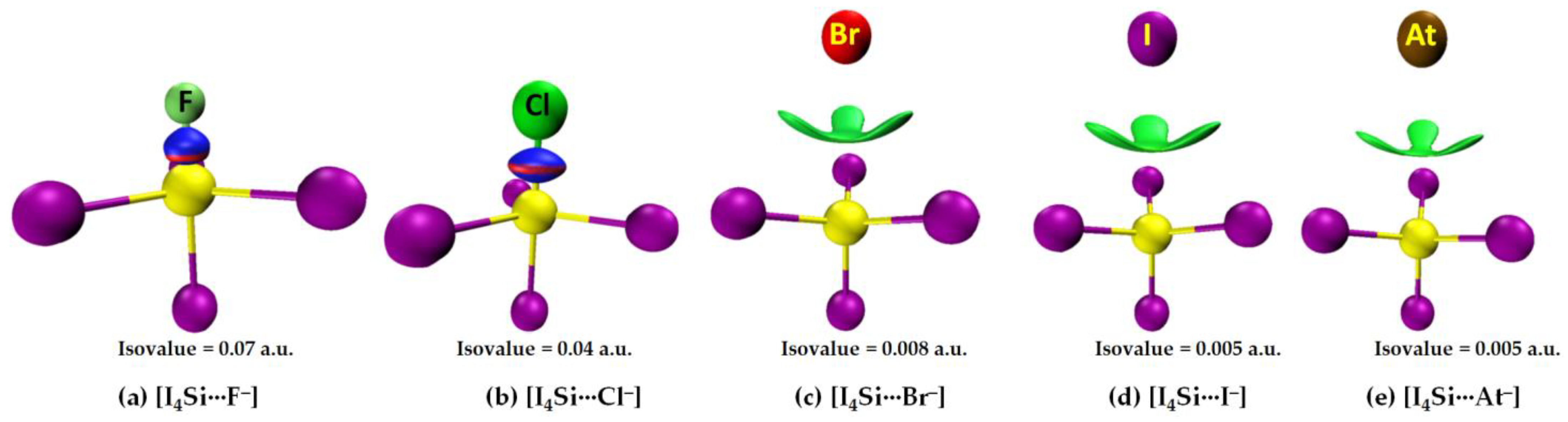
3.2.2. The [I4Tt···X−] (Tt = Si, Ge) Series
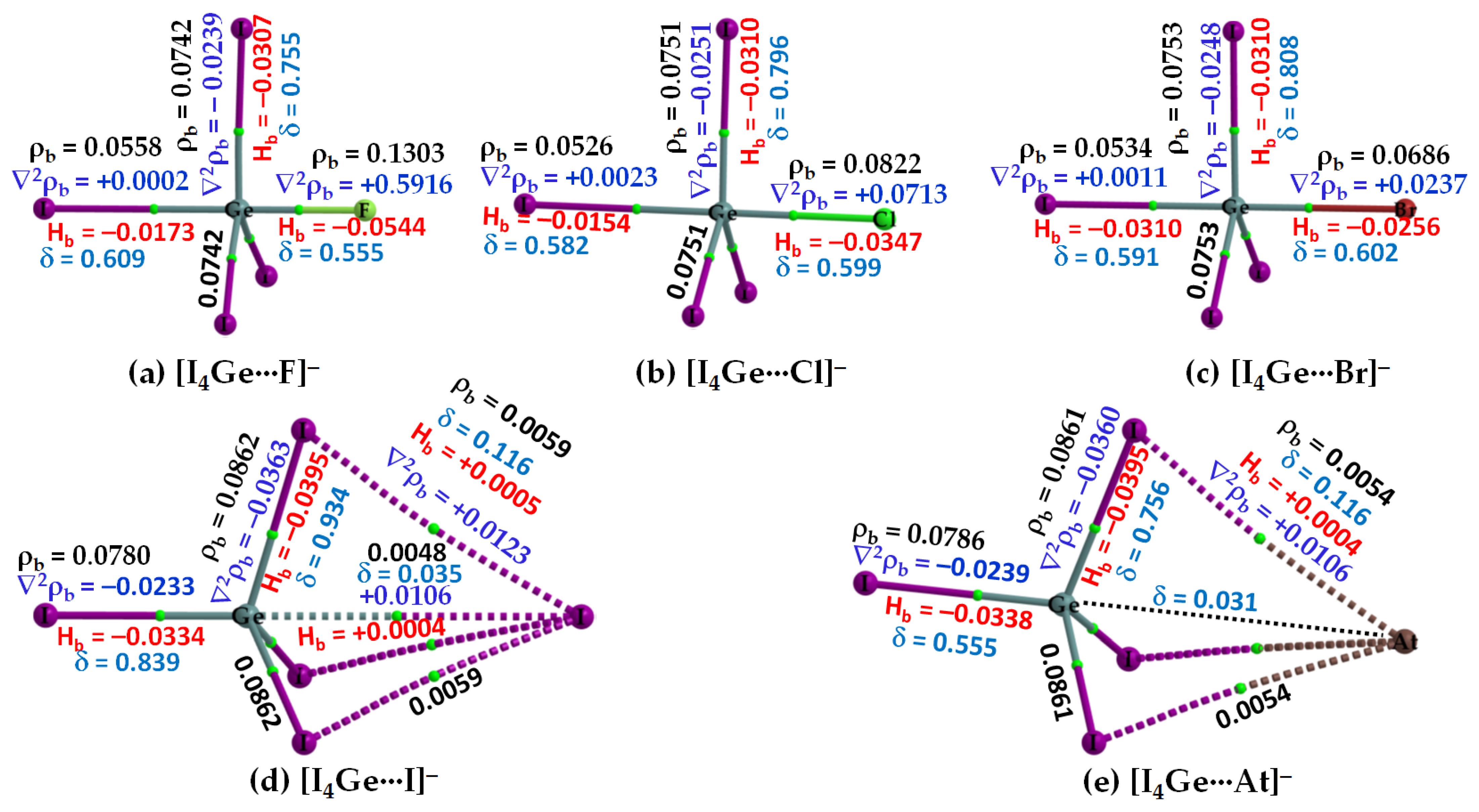
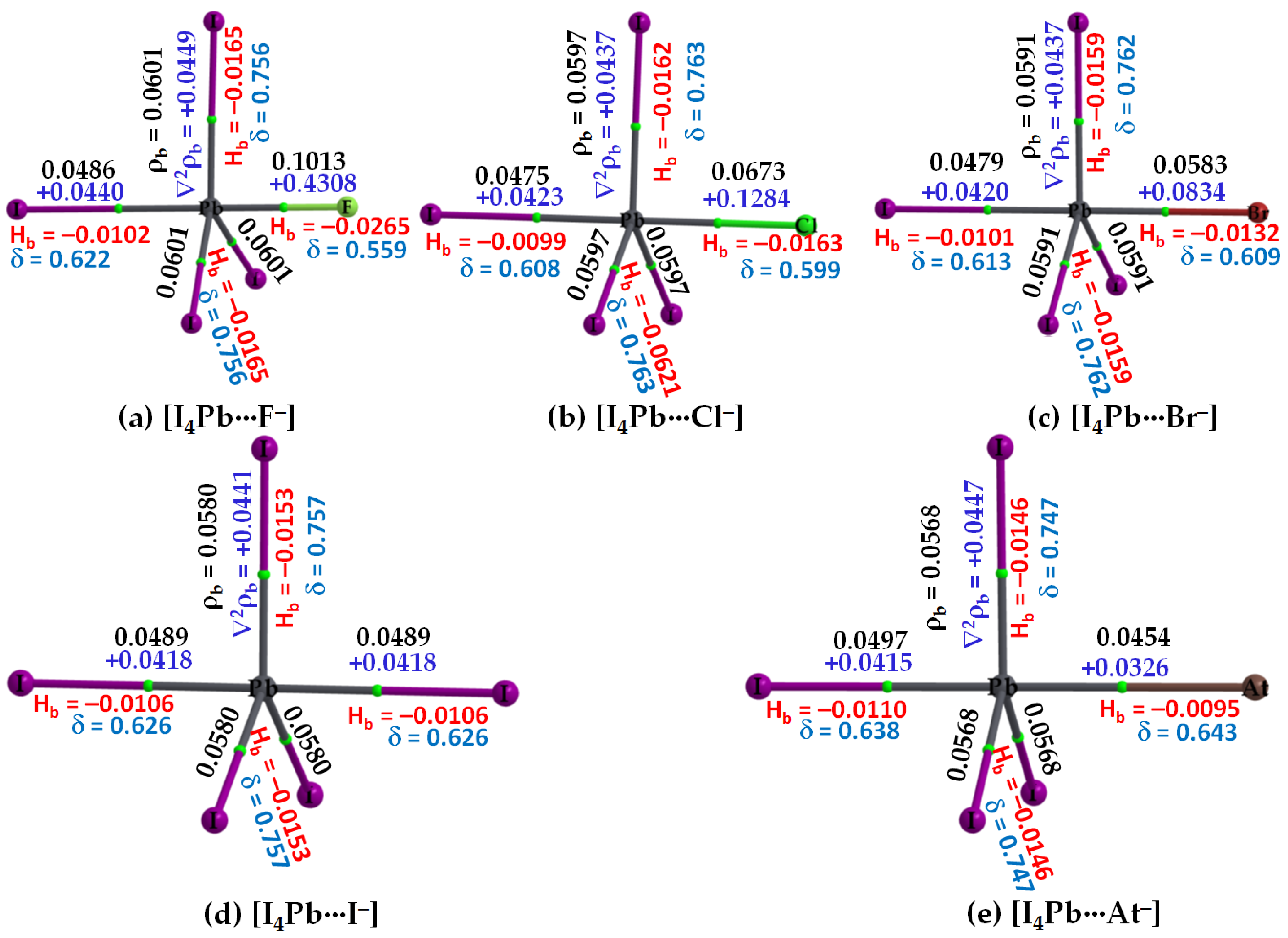
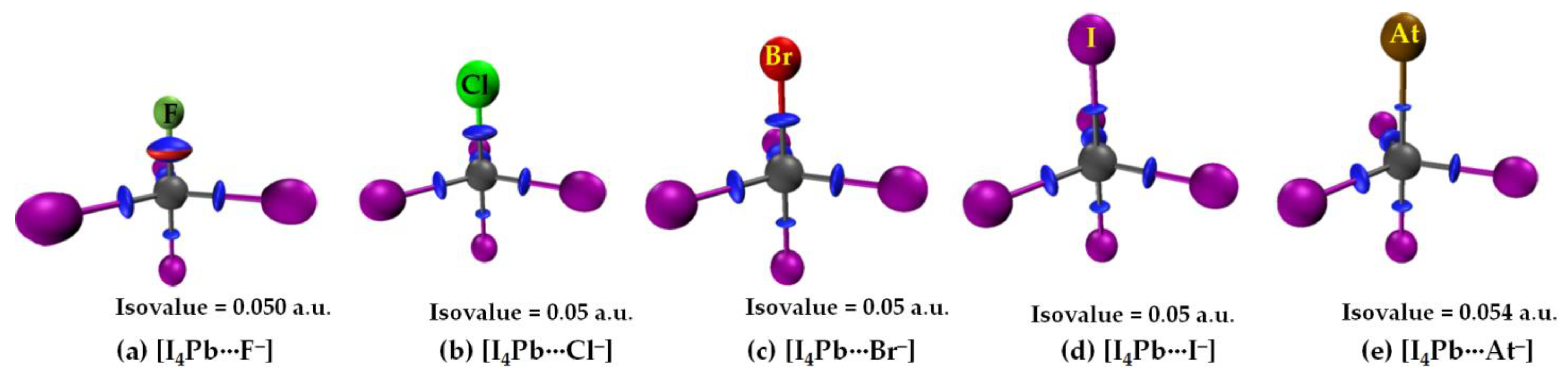
3.2.3. The [I4Tt···X−] (Tt = Sn, Pb) Series
3.2.4. IGM-δginter Analysis
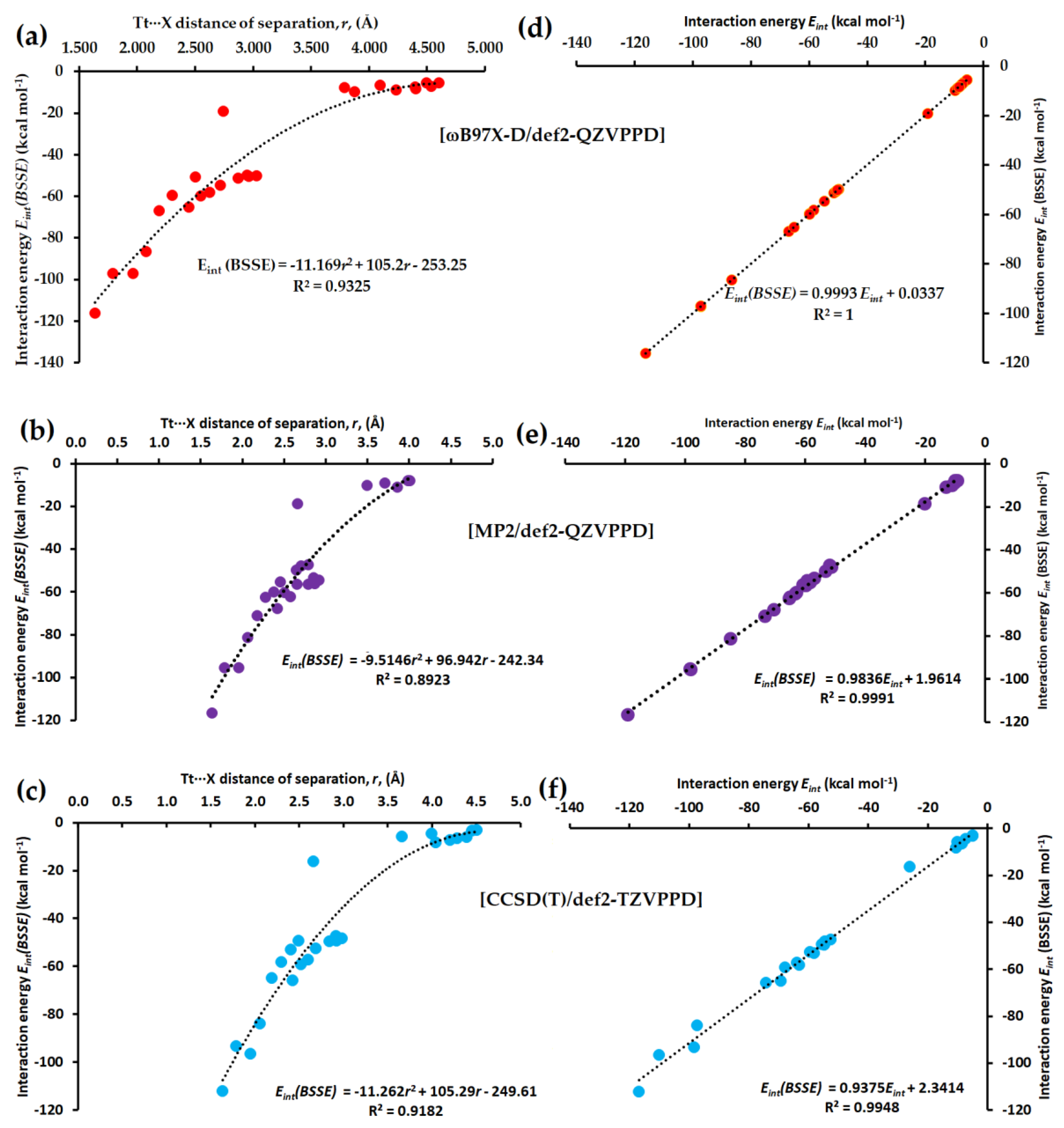
3.2.5. Interaction Energies
4. Discussion and Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sethio, D.; Raggi, G.; Lindh, R.; Erdélyi, M. Halogen Bond of Halonium Ions: Benchmarking DFT Methods for the Description of NMR Chemical Shifts. J. Chem. Theory Comput. 2020, 16, 7690–7701. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, D.-X.; Huang, Z.-T.; Wang, M.-X. Ion Pair Receptors Based on Anion–π Interaction. Chem. Commun. 2011, 47, 8112–8114. [Google Scholar] [CrossRef]
- Beer, P.D.; Gale, P.A. Anion Recognition and Sensing: The State of the Art and Future Perspectives. Angew. Chem. Int. Ed. 2001, 40, 486–516. [Google Scholar] [CrossRef]
- Lim, J.Y.C.; Beer, P.D. Sigma-Hole Interactions in Anion Recognition. Chem 2018, 4, 731–783. [Google Scholar] [CrossRef]
- Yu, B.; Pletka, C.C.; Iwahara, J. Quantifying and Visualizing Weak Interactions between Anions and Proteins. Proc. Natl. Acad. Sci. USA 2021, 118, e2015879118. [Google Scholar] [CrossRef]
- Applications of Supramolecular Anion Recognition|Chemical Reviews. Available online: https://pubs.acs.org/doi/10.1021/acs.chemrev.5b00099 (accessed on 18 October 2022).
- Wu, X.; Gilchrist, A.M.; Gale, P.A. Prospects and Challenges in Anion Recognition and Transport. Chem 2020, 6, 1296–1309. [Google Scholar] [CrossRef]
- Langton, M.J.; Serpell, C.J.; Beer, P.D. Anion Recognition in Water: Recent Advances from a Supramolecular and Macromolecular Perspective. Angew. Chem. Int. Ed. 2016, 55, 1974–1987. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. B 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Berger, R.; Duff, K.; Leighton, J.L. Enantioselective Allylation of Ketone-Derived Benzoylhydrazones: Practical Synthesis of Tertiary Carbinamines. J. Am. Chem. Soc. 2004, 126, 5686–5687. [Google Scholar] [CrossRef]
- Wieghardt, K.; Kleine-Boymann, M.; Nuber, B.; Weiss, J.; Zsolnai, L.; Huttner, G. Macrocyclic Complexes of Lead(II): Crystal Structures of LPb(ClO4)2 and LPb(NO3)2 (L = 1,4,7-Triazacyclononane). Inorg. Chem. 1986, 25, 1647–1650. [Google Scholar] [CrossRef]
- Dai, X.; Choi, S.-B.; Braun, C.W.; Vaidya, P.; Kilina, S.; Ugrinov, A.; Schulz, D.L.; Boudjouk, P. Halide Coordination of Perhalocyclohexasilane Si6X12 (X = Cl or Br). Inorg. Chem. 2011, 50, 4047–4053. [Google Scholar] [CrossRef]
- Teichmann, J.; Köstler, B.; Tillmann, J.; Moxter, M.; Kupec, R.; Bolte, M.; Lerner, H.-W.; Wagner, M. Halide-Ion Diadducts of Perhalogenated Cyclopenta- and Cyclohexasilanes. Z. Für Anorg. Und Allg. Chem. 2018, 644, 956–962. [Google Scholar] [CrossRef]
- Tillmann, J.; Meyer, L.; Schweizer, J.I.; Bolte, M.; Lerner, H.-W.; Wagner, M.; Holthausen, M.C. Chloride-Induced Aufbau of Perchlorinated Cyclohexasilanes from Si2Cl6: A Mechanistic Scenario. Chem. A Eur. J. 2014, 20, 9234–9239. [Google Scholar] [CrossRef]
- Bamberg, M.; Bursch, M.; Hansen, A.; Brandl, M.; Sentis, G.; Kunze, L.; Bolte, M.; Lerner, H.-W.; Grimme, S.; Wagner, M. [Cl@Si20H20]−: Parent Siladodecahedrane with Endohedral Chloride Ion. J. Am. Chem. Soc. 2021, 143, 10865–10871. [Google Scholar] [CrossRef]
- Taylor, M.S. Anion Recognition Based on Halogen, Chalcogen, Pnictogen and Tetrel Bonding. Coord. Chem. Rev. 2020, 413, 213270. [Google Scholar] [CrossRef]
- Scheiner, S. Tetrel Bonding as a Vehicle for Strong and Selective Anion Binding. Molecules 2018, 23, 1147. [Google Scholar] [CrossRef]
- Scheiner, S.; Michalczyk, M.; Zierkiewicz, W. Coordination of Anions by Noncovalently Bonded σ-Hole Ligands. Coord. Chem. Rev. 2020, 405, 213136. [Google Scholar] [CrossRef]
- Molina, P.; Zapata, F.; Caballero, A. Anion Recognition Strategies Based on Combined Noncovalent Interactions. Chem. Rev. 2017, 117, 9907–9972. [Google Scholar] [CrossRef]
- Liu, Y.-Z.; Yuan, K.; Lv, L.-L.; Zhu, Y.-C.; Yuan, Z. Designation and Exploration of Halide–Anion Recognition Based on Cooperative Noncovalent Interactions Including Hydrogen Bonds and Anion−π. J. Phys. Chem. A 2015, 119, 5842–5852. [Google Scholar] [CrossRef]
- Esrafili, M.D.; Mousavian, P. Strong Tetrel Bonds: Theoretical Aspects and Experimental Evidence. Molecules 2018, 23, 2642. [Google Scholar] [CrossRef]
- Bartashevich, E.; Matveychuk, Y.; Tsirelson, V. Identification of the Tetrel Bonds between Halide Anions and Carbon Atom of Methyl Groups Using Electronic Criterion. Molecules 2019, 24, 1083. [Google Scholar] [CrossRef]
- Grabowski, S.J. Tetrel Bond–σ-Hole Bond as a Preliminary Stage of the SN2 Reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef]
- Bartashevich, E.V.; Mukhitdinova, S.E.; Klyuev, I.V.; Tsirelson, V.G. Can We Merge the Weak and Strong Tetrel Bonds? Electronic Features of Tetrahedral Molecules Interacted with Halide Anions. Molecules 2022, 27, 5411. [Google Scholar] [CrossRef]
- Scheiner, S. Origins and Properties of the Tetrel Bond. Phys. Chem. Chem. Phys. 2021, 23, 5702–5717. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Significant Evidence of C⋯O and C⋯C Long-Range Contacts in Several Heterodimeric Complexes of CO with CH3–X, Should One Refer to Them as Carbon and Dicarbon Bonds! Phys. Chem. Chem. Phys. 2014, 16, 17238–17252. [Google Scholar] [CrossRef]
- Mani, D.; Arunan, E. The X–C⋯Y (X = O/F, Y = O/S/F/Cl/Br/N/P) ‘Carbon Bond’ and Hydrophobic Interactions. Phys. Chem. Chem. Phys. 2013, 15, 14377–14383. [Google Scholar] [CrossRef]
- Matczak, P. Theoretical Investigation of the N→Sn Coordination in (Me3SnCN)2. Struct. Chem. 2015, 26, 301–318. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. Definition of the Tetrel Bond. Available online: https://Arxiv.Org/Abs/2210.10649 (accessed on 17 November 2022).
- Breneman, C.M.; Martinov, M. 3—The Use of Electrostatic Potential Fields in QSAR and QSPR. In Theoretical and Computational Chemistry; Murray, J.S., Sen, K., Eds.; Molecular Electrostatic Potentials; Elsevier: Amsterdam, The Netherlands, 1996; Volume 3, pp. 143–179. [Google Scholar]
- Murray, J.S.; Politzer, P. The Molecular Electrostatic Potential: A Tool for Understanding and Predicting Molecular Interactions. In Molecular Orbital Calculations for Biological Systems; Sapse, A.-M., Ed.; Oxford University Press: Oxford, UK, 1998; ISBN 978-0-19-509873-0. [Google Scholar]
- Politzer, P.; Murray, J.S. Molecular Electrostatic Potentials: Significance and Applications. In Chemical Reactivity in Confined Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; pp. 113–134. ISBN 978-1-119-68335-3. [Google Scholar]
- Politzer, P.; Murray, J.S. Quantitative Analyses of Molecular Surface Electrostatic Potentials in Relation to Hydrogen Bonding and Co-Crystallization. Cryst. Growth Des. 2015, 15, 3767–3774. [Google Scholar] [CrossRef]
- Varadwaj, A.; Marques, H.M.; Varadwaj, P.R. Nature of Halogen-Centered Intermolecular Interactions in Crystal Growth and Design: Fluorine-Centered Interactions in Dimers in Crystalline Hexafluoropropylene as a Prototype. J. Comput. Chem. 2019, 40, 1836–1860. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. The Pnictogen Bond, Together with Other Non-Covalent Interactions, in the Rational Design of One-, Two- and Three-Dimensional Organic-Inorganic Hybrid Metal Halide Perovskite Semiconducting Materials, and Beyond. Int. J. Mol. Sci. 2022, 23, 8816. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. The Phosphorus Bond, or the Phosphorus-Centered Pnictogen Bond: The Covalently Bound Phosphorus Atom in Molecular Entities and Crystals as a Pnictogen Bond Donor. Molecules 2022, 27, 1487. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood. Inorganics 2019, 7, 40. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Does Chlorine in CH3Cl Behave as a Genuine Halogen Bond Donor? Crystals 2020, 10, 146. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. The Pnictogen Bond Formation Ability of Bonded Bismuth Atoms in Molecular Entities in the Crystalline Phase: A Perspective. Available online: https://Arxiv.Org/Abs/2209.07319 (accessed on 17 November 2022).
- Bader, R.F.W. Atoms in Molecules. Available online: https://pubs.acs.org/doi/pdf/10.1021/ar00109a003 (accessed on 19 October 2022).
- Bader, R.F.W. Atoms in Molecules. In Encyclopedia of Computational Chemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; ISBN 978-0-470-84501-1. [Google Scholar]
- Bader, R.F.W.; Bayles, D. Properties of Atoms in Molecules: Group Additivity. J. Phys. Chem. A 2000, 104, 5579–5589. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Nguyen-Dang, T.T. Quantum Theory of Atoms in Molecules–Dalton Revisited. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Academic Press: Cambridge, MA, USA, 1981; Volume 14, pp. 63–124. [Google Scholar]
- Lefebvre, C.; Rubez, G.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Hénon, E. Accurately Extracting the Signature of Intermolecular Interactions Present in the NCI Plot of the Reduced Density Gradient versus Electron Density. Phys. Chem. Chem. Phys 2017, 19, 17928–17936. [Google Scholar] [CrossRef]
- Lefebvre, C.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. The Independent Gradient Model: A New Approach for Probing Strong and Weak Interactions in Molecules from Wave Function Calculations. Chemphyschem 2018, 19, 724–735. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. The Nitrogen Bond, or the Nitrogen-Centered Pnictogen Bond: The Covalently Bound Nitrogen Atom in Molecular Entities and Crystals as a Pnictogen Bond Donor. Compounds 2022, 2, 80–110. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Frisch, M.J.; Head-Gordon, M.; Pople, J.A. A Direct MP2 Gradient Method. Chem. Phys. Lett. 1990, 166, 275–280. [Google Scholar] [CrossRef]
- Frisch, M.J.; Head-Gordon, M.; Pople, J.A. Semi-Direct Algorithms for the MP2 Energy and Gradient. Chem. Phys. Lett. 1990, 166, 281–289. [Google Scholar] [CrossRef]
- Head-Gordon, M.; Head-Gordon, T. Analytic MP2 Frequencies without Fifth-Order Storage. Theory and Application to Bifurcated Hydrogen Bonds in the Water Hexamer. Chem. Phys. Lett. 1994, 220, 122–128. [Google Scholar] [CrossRef]
- Purvis, G.D.; Bartlett, R.J. A Full Coupled-cluster Singles and Doubles Model: The Inclusion of Disconnected Triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Janssen, C.L.; Schaefer, H.F., III. An Efficient Reformulation of the Closed-Shell Coupled Cluster Single and Double Excitation (CCSD) Equations. J. Chem. Phys. 1988, 89, 7382–7387. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT. 2016. Available online: https://gaussian.com/citation/ (accessed on 19 October 2022).
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Wu, Q.; Xie, X.; Li, Q.; Scheiner, S. Enhancement of Tetrel Bond Involving Tetrazole-TtR3 (Tt = C, Si; R = H, F). Promotion of SiR3 Transfer by a Triel Bond. Phys. Chem. Chem. Phys. 2022, 24, 25895–25903. [Google Scholar] [CrossRef]
- An, X.; Yang, X.; Li, Q. Tetrel Bonds between Phenyltrifluorosilane and Dimethyl Sulfoxide: Influence of Basis Sets, Substitution and Competition. Molecules 2021, 26, 7231. [Google Scholar] [CrossRef]
- Varadwaj, A.; Marques, H.M.; Varadwaj, P.R. Is the Fluorine in Molecules Dispersive? Is Molecular Electrostatic Potential a Valid Property to Explore Fluorine-Centered Non-Covalent Interactions? Molecules 2019, 24, 379. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of Atoms in Molecules: Atomic Volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. Can Combined Electrostatic and Polarization Effects Alone Explain the F···F Negative-Negative Bonding in Simple Fluoro-Substituted Benzene Derivatives? A First-Principles Perspective. Computation 2018, 6, 51. [Google Scholar] [CrossRef]
- Varadwaj, P.R. Does Oxygen Feature Chalcogen Bonding? Molecules 2019, 24, 3166. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. The Stibium Bond or the Antimony-Centered Pnictogen Bond: The Covalently Bound Antimony Atom in Molecular Entities in Crystal Lattices as a Pnictogen Bond Donor. Int. J. Mol. Sci. 2022, 23, 4674. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. σ-Hole Interactions: Perspectives and Misconceptions. Crystals 2017, 7, 212. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T.; Resnati, G. The σ-Hole Revisited. Phys. Chem. Chem. Phys. 2017, 19, 32166–32178. [Google Scholar] [CrossRef]
- σ-Hole Bonding: Molecules Containing Group VI Atoms|SpringerLink. Available online: https://link.springer.com/article/10.1007/s00894-007-0225-4 (accessed on 9 November 2022).
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen Bonding: The Sigma-Hole. Proceedings of “Modeling Interactions in Biomolecules II”, Prague, September 5th–9th, 2005. J. Mol. Model 2007, 13, 291–296. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- AIMAll (Version 19.10.12), Todd, A. Keith, TK Gristmill Software, Overland Park KS, USA, 2019. (Aim.Tkgristmill.Com). Available online: http://aim.tkgristmill.com/references.html (accessed on 24 October 2022).
- Multiwfn. Available online: http://sobereva.com/multiwfn/ (accessed on 24 October 2022).
- Fradera, X.; Austen, M.A.; Bader, R.F.W. The Lewis Model and Beyond. J. Phys. Chem. A 1999, 103, 304–314. [Google Scholar] [CrossRef]
- Outeiral, C.; Vincent, M.A.; Martín Pendás, Á.; Popelier, P.L.A. Revitalizing the Concept of Bond Order through Delocalization Measures in Real Space. Chem. Sci. 2018, 9, 5517–5529. [Google Scholar] [CrossRef]
- Matito, E.; Poater, J.; Solà, M.; Duran, M.; Salvador, P. Comparison of the AIM Delocalization Index and the Mayer and Fuzzy Atom Bond Orders. J. Phys. Chem. A 2005, 109, 9904–9910. [Google Scholar] [CrossRef]
- Firme, C.L.; Antunes, O.A.C.; Esteves, P.M. Relation between Bond Order and Delocalization Index of QTAIM. Chem. Phys. Lett. 2009, 468, 129–133. [Google Scholar] [CrossRef]
- Kaduk, J.A. Use of the Inorganic Crystal Structure Database as a Problem Solving Tool. Acta Crystallogr. B 2002, 58, 370–379. [Google Scholar] [CrossRef]
- Hellenbrandt, M. The Inorganic Crystal Structure Database (ICSD)—Present and Future. Crystallogr. Rev. 2004, 10, 17–22. [Google Scholar] [CrossRef]
- Belsky, A.; Hellenbrandt, M.; Karen, V.L.; Luksch, P. New Developments in the Inorganic Crystal Structure Database (ICSD): Accessibility in Support of Materials Research and Design. Acta Crystallogr. B 2002, 58, 364–369. [Google Scholar] [CrossRef]
- Allmann, R.; Hinek, R. The Introduction of Structure Types into the Inorganic Crystal Structure Database ICSD. Acta Crystallogr. A 2007, 63, 412–417. [Google Scholar] [CrossRef]
- Inorganic Crystal Structure Database. Available online: https://icsd.products.fiz-karlsruhe.de/en (accessed on 21 October 2022).
- Cremer, D.; Kraka, E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
- Grabowski, S.J. The Nature of Triel Bonds, a Case of B and Al Centres Bonded with Electron Rich Sites. Molecules 2020, 25, 2703. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Marques, H.M.; Varadwaj, A.; Yamashita, K. Chalcogen···Chalcogen Bonding in Molybdenum Disulfide, Molybdenum Diselenide and Molybdenum Ditelluride Dimers as Prototypes for a Basic Understanding of the Local Interfacial Chemical Bonding Environment in 2D Layered Transition Metal Dichalcogenides. Inorganics 2022, 10, 11. [Google Scholar]
- Varadwaj, P.; Varadwaj, A.; Marques, H. Very Strong Chalcogen Bonding: Is Oxygen in Molecules Capable of Forming It? A First-Principles Perspective. arXiv 2020, arXiv:2210.11919. [Google Scholar]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. DFT-B3LYP, NPA-, and QTAIM-Based Study of the Physical Properties of [M(II)(H2O)2(15-Crown-5)] (M = Mn, Fe, Co, Ni, Cu, Zn) Complexes. J. Phys. Chem. A 2011, 115, 5592–5601. [Google Scholar] [CrossRef]
- Zhurova, E.A.; Tsirelson, V.G. Electron Density and Energy Density View on the Atomic Interactions in SrTiO3. Acta Crystallogr. B 2002, 58, 567–575. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Nagle, J.K. 2018 Table of Static Dipole Polarizabilities of the Neutral Elements in the Periodic Table. Mol. Phys. 2019, 117, 1200–1225. [Google Scholar] [CrossRef]
- Grabowski, S.J. Lewis Acid Properties of Tetrel Tetrafluorides—The Coincidence of the σ-Hole Concept with the QTAIM Approach. Crystals 2017, 7, 43. [Google Scholar] [CrossRef]
- Jabłoński, M. Does the Presence of a Bond Path Really Mean Interatomic Stabilization? The Case of the Ng@Superphane (Ng = He, Ne, Ar, and Kr) Endohedral Complexes. Symmetry 2021, 13, 2241. [Google Scholar] [CrossRef]
- Lane, J.R.; Contreras-García, J.; Piquemal, J.-P.; Miller, B.J.; Kjaergaard, H.G. Are Bond Critical Points Really Critical for Hydrogen Bonding? J. Chem. Theory Comput. 2013, 9, 3263–3266. [Google Scholar] [CrossRef]
- Thomsen, D.L.; Axson, J.L.; Schrøder, S.D.; Lane, J.R.; Vaida, V.; Kjaergaard, H.G. Intramolecular Interactions in 2-Aminoethanol and 3-Aminopropanol. J. Phys. Chem. A 2013, 117, 10260–10273. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the Hydrogen Bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the Halogen Bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Aakeroy, C.B.; Bryce, D.L.; Desiraju, G.R.; Frontera, A.; Legon, A.C.; Nicotra, F.; Rissanen, K.; Scheiner, S.; Terraneo, G.; Metrangolo, P.; et al. Definition of the Chalcogen Bond (IUPAC Recommendations 2019). Pure Appl. Chem. 2019, 91, 1889–1892. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. Definition of the Pnictogen Bond: A Perspective. Inorganics 2022, 10, 149. [Google Scholar] [CrossRef]
- Liu, N.; Li, Q.; Scheiner, S.; Xie, X. Resonance-Assisted Intramolecular Triel Bonds. Phys. Chem. Chem. Phys. 2022, 24, 15015–15024. [Google Scholar] [CrossRef]
- Alvarez, S. A Cartography of the van Der Waals Territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef]
- Astatine|At (Element)–PubChem. Available online: https://pubchem.ncbi.nlm.nih.gov/element/Astatine#section=Atomic-Weight (accessed on 25 October 2022).
- Politzer, P.; Murray, J.S. The Use and Misuse of van Der Waals Radii. Struct. Chem. 2021, 32, 623–629. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Hexahalogenated and Their Mixed Benzene Derivatives as Prototypes for the Understanding of Halogen···halogen Intramolecular Interactions: New Insights from Combined DFT, QTAIM-, and RDG-Based NCI Analyses. J. Comput. Chem. 2015, 36, 2328–2343. [Google Scholar] [CrossRef]
- Johansson, M.P.; Swart, M. Intramolecular Halogen–Halogen Bonds? Phys. Chem. Chem. Phys. 2013, 15, 11543–11553. [Google Scholar] [CrossRef]
- Xu, H.; Cheng, J.; Yang, X.; Liu, Z.; Li, W.; Li, Q. Comparison of σ-Hole and π-Hole Tetrel Bonds Formed by Pyrazine and 1,4-Dicyanobenzene: The Interplay between Anion–π and Tetrel Bonds. ChemPhysChem 2017, 18, 2442–2450. [Google Scholar] [CrossRef]
- Van der Maelen, J.F.; Cabeza, J.A. A Topological Analysis of the Bonding in [M2(CO)10] and [M3(μ-H)3(CO)12] Complexes (M = Mn, Tc, Re). Theor. Chem. Acc. 2016, 135, 64. [Google Scholar] [CrossRef]
- Grabowski, S.J. Chapter 1 Hydrogen Bond—Definitions, Criteria of Existence and Various Types. In Understanding Hydrogen Bonds: Theoretical and Experimental Views; Royal Society of Chemistry: London, UK, 2020; pp. 1–40. [Google Scholar] [CrossRef]
- Desiraju, G.R. Hydrogen Bridges in Crystal Engineering: Interactions without Borders. Acc. Chem. Res. 2002, 35, 565–573. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Hybrid Organic–Inorganic CH3NH3PbI3 Perovskite Building Blocks: Revealing Ultra-Strong Hydrogen Bonding and Mulliken Inner Complexes and Their Implications in Materials Design. J. Comput. Chem. 2017, 38, 2802–2818. [Google Scholar] [CrossRef]


| Monomer | Property | Expt. a | [MP2/def2-QZVPPD] | [ωB97X-D/def2-QZVPPD] |
|---|---|---|---|---|
| CI4 | r(C–I) | 2.154 | 2.131 | 2.254 |
| ∠I–C–I | 109.47 | 109.47 | 109.47 | |
| SiI4 | r(Si–I) | 2.434 | 2.403 | 2.434 |
| ∠I–Si–I | 109.47 | 109.47 | 109.47 | |
| GeI4 | r(Ge–I) | 2.574 | 2.463 | 2.518 |
| ∠I–Ge–I | 109.47 | 109.47 | 109.47 | |
| SnI4 | r(Sn–I) | 2.650 | 2.463 | 2.518 |
| ∠I–Sn–I | 109.47 | 109.47 | 109.47 | |
| PbI4 | r(Pb–I) | --- | 2.705 | 2.749 |
| ∠I–Pb–I | --- | 109.47 | 109.47 |
| System | [ωB97X-D/def2-TZVPPD] | [ωB97X-D/def2-QZVPPD] | [MP2/def2-QZVPPD] | [CCSD(T)/def2-TZVPPD] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eint | Eint(BSSE) | r(Tt···X) | Eint | Eint(BSSE) | r(Tt···X) | Eint | Eint(BSSE) | r(Tt···X) | Eint | Eint(BSSE) | r(Tt···X) b | |
| [I4C···F−] | −27.36 | −19.72 | 2.690 | −19.23 | −19.2 | 2.744 | −20.11 | −18.7 | 2.663 | −26.00 | −16.35 | 2.665 |
| [I4C···Cl−] | −10.97 | −8.10 | 3.671 | −7.87 | −7.84 | 3.787 | −11.08 | −10.07 | 3.496 | −9.99 | −5.93 | 3.665 |
| [I4C···Br−] | −8.12 | −6.61 | 4.001 | −6.65 | −6.61 | 4.097 | −10.13 | −8.93 | 3.710 | −7.25 | −4.64 | 3.996 |
| [I4C···I−] | −6.02 | −5.43 | 4.422 | −5.60 | −5.57 | 4.494 | −9.25 | −7.87 | 3.990 | −4.80 | −3.38 | 4.454 |
| [I4C···At−] | −5.98 | −5.48 | 4.558 | −5.59 | −5.57 | 4.603 | −10.08 | −7.95 | 4.009 | −4.99 | −3.20 | 4.506 |
| [I4Si···F−] | −115.85 | −115.48 | 1.643 | −116.22 | −116.16 | 1.638 | −119.11 | −116.45 | 1.639 | −116.81 | −112.15 | 1.637 |
| [I4Si···Cl−] | −67.28 | −66.93 | 2.191 | −66.95 | −66.88 | 2.190 | −73.40 | −71.00 | 2.177 | −69.23 | −64.99 | 2.192 |
| [I4Si···Br−] | −9.75 | −9.61 | 3.875 | −9.85 | −9.80 | 3.875 | −62.88 | −60.00 | 2.380 | −58.1 | −53.16 | 2.408 |
| [I4Si···I−] | −7.42 | −7.36 | 4.398 | −7.52 | −7.49 | 4.398 | −53.22 | −49.92 | 2.646 | −8.51 | −6.60 | 4.287 |
| [I4Si···At−] | −7.13 | −7.08 | 4.542 | −7.23 | −7.21 | 4.539 | −13.09 | −10.87 | 3.862 | −8.44 | −6.13 | 4.397 |
| [I4Ge···F−] | −96.99 | −96.53 | 1.797 | −97.3 | −97.17 | 1.792 | −98.42 | −95.4 | 1.787 | −98.24 | −93.43 | 1.789 |
| [I4Ge···Cl−] | −60.16 | −59.75 | 2.305 | −59.77 | −59.66 | 2.305 | −65.32 | −62.64 | 2.279 | −62.93 | −58.36 | 2.300 |
| [I4Ge···Br−] | −51.15 | −50.74 | 2.505 | −50.93 | −50.8 | 2.505 | −58.29 | −55.28 | 2.456 | −54.44 | −49.32 | 2.497 |
| [I4Ge···I−] | −8.86 | −8.79 | 4.233 | −8.98 | −8.94 | 4.233 | −51.17 | −47.91 | 2.703 | −10.46 | −8.28 | 4.049 |
| [I4Ge···At−] | −8.34 | −8.28 | 4.401 | −8.44 | −8.41 | 4.401 | −51.73 | −47.2 | 2.787 | −9.95 | −7.42 | 4.203 |
| [I4Sn···F−] | −108.88 | −99.20 | 1.965 | −97.22 | −97.14 | 1.966 | −98.18 | −95.5 | 1.955 | −109.92 | −96.48 | 1.950 |
| [I4Sn···Cl−] | −72.20 | −67.68 | 2.442 | −65.22 | −65.14 | 2.447 | −70.39 | −67.92 | 2.417 | −74.18 | −65.88 | 2.427 |
| [I4Sn···Br−] | −61.88 | −59.33 | 2.751 | −58.32 | −58.21 | 2.625 | −65.06 | −62.14 | 2.576 | −63.91 | −57.29 | 2.605 |
| [I4Sn···I−] | −52.78 | −51.71 | 2.873 | −51.46 | −51.38 | 2.869 | −59.74 | −56.43 | 2.792 | −54.65 | −49.58 | 2.847 |
| [I4Sn···At−] | −51.94 | −51.05 | 2.967 | −50.56 | −50.50 | 2.966 | −60.82 | −56.21 | 2.866 | −55.43 | −49.34 | 2.928 |
| [I4Pb···F−] | −98.33 | −88.98 | 2.075 | −86.54 | −86.48 | 2.078 | −84.82 | −81.43 | 2.063 | −97.33 | −84.05 | 2.057 |
| [I4Pb···Cl−] | −67.00 | −62.66 | 2.541 | −59.88 | −59.81 | 2.548 | −63.4 | −60.33 | 2.506 | −67.71 | −59.33 | 2.521 |
| [I4Pb···Br−] | −58.51 | −56.07 | 2.715 | −54.77 | −54.67 | 2.716 | −59.91 | −56.49 | 2.655 | −59.42 | −52.72 | 2.690 |
| [I4Pb···I−] | −51.42 | −50.43 | 2.950 | −49.89 | −49.83 | 2.948 | −57.06 | −53.30 | 2.854 | −52.54 | −47.36 | 2.916 |
| [I4Pb···At−] | −51.74 | −50.91 | 3.034 | −50.20 | −50.15 | 3.032 | −59.42 | −54.41 | 2.919 | −54.51 | −48.30 | 2.984 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varadwaj, P.R. Tetrel Bonding in Anion Recognition: A First Principles Investigation. Molecules 2022, 27, 8449. https://doi.org/10.3390/molecules27238449
Varadwaj PR. Tetrel Bonding in Anion Recognition: A First Principles Investigation. Molecules. 2022; 27(23):8449. https://doi.org/10.3390/molecules27238449
Chicago/Turabian StyleVaradwaj, Pradeep R. 2022. "Tetrel Bonding in Anion Recognition: A First Principles Investigation" Molecules 27, no. 23: 8449. https://doi.org/10.3390/molecules27238449
APA StyleVaradwaj, P. R. (2022). Tetrel Bonding in Anion Recognition: A First Principles Investigation. Molecules, 27(23), 8449. https://doi.org/10.3390/molecules27238449








