Thermal Conductivity of Solid Triphenyl Phosphite
Abstract
1. Introduction
2. Results
2.1. The Thermal Conductivity of the Glass State
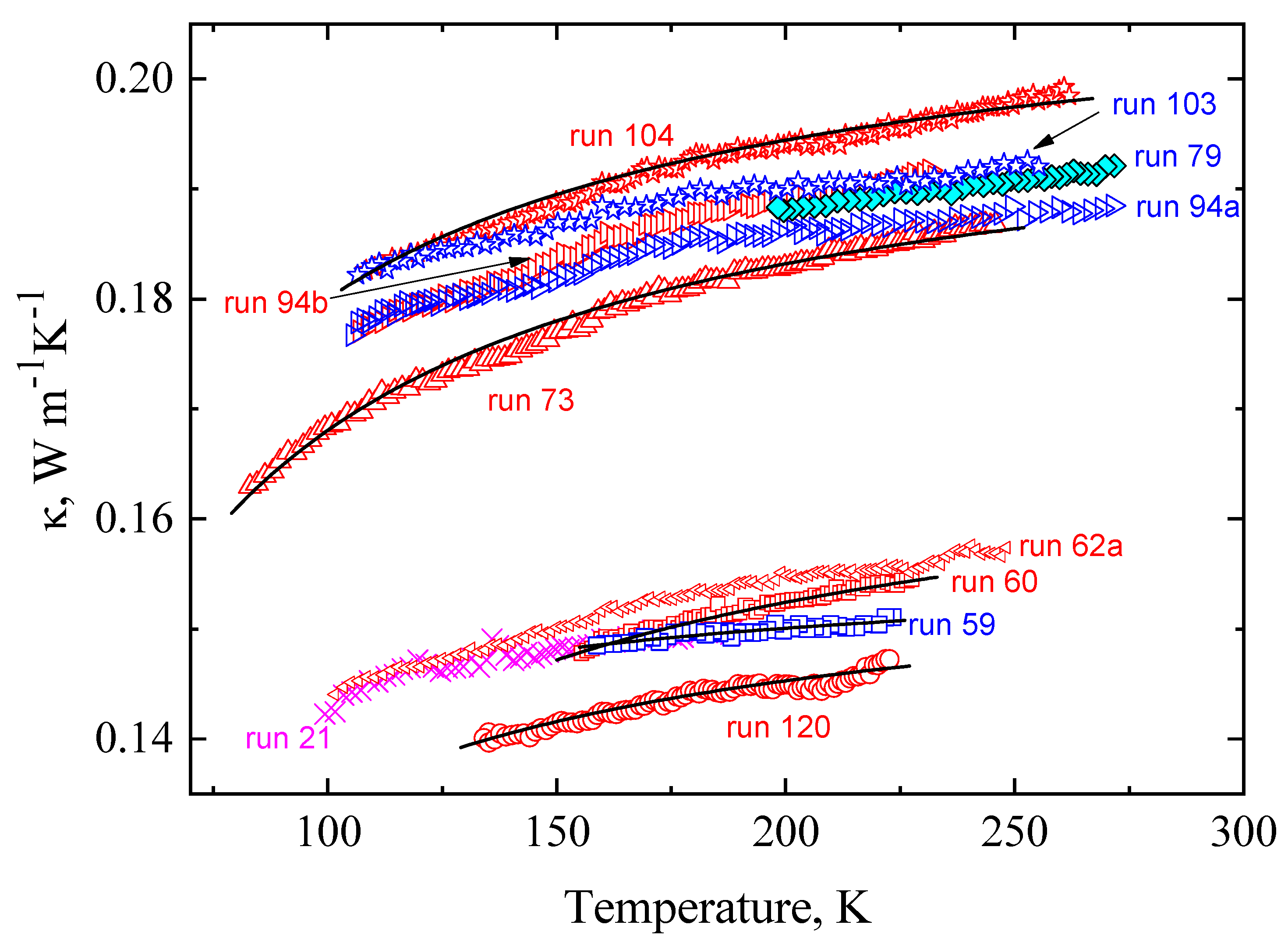
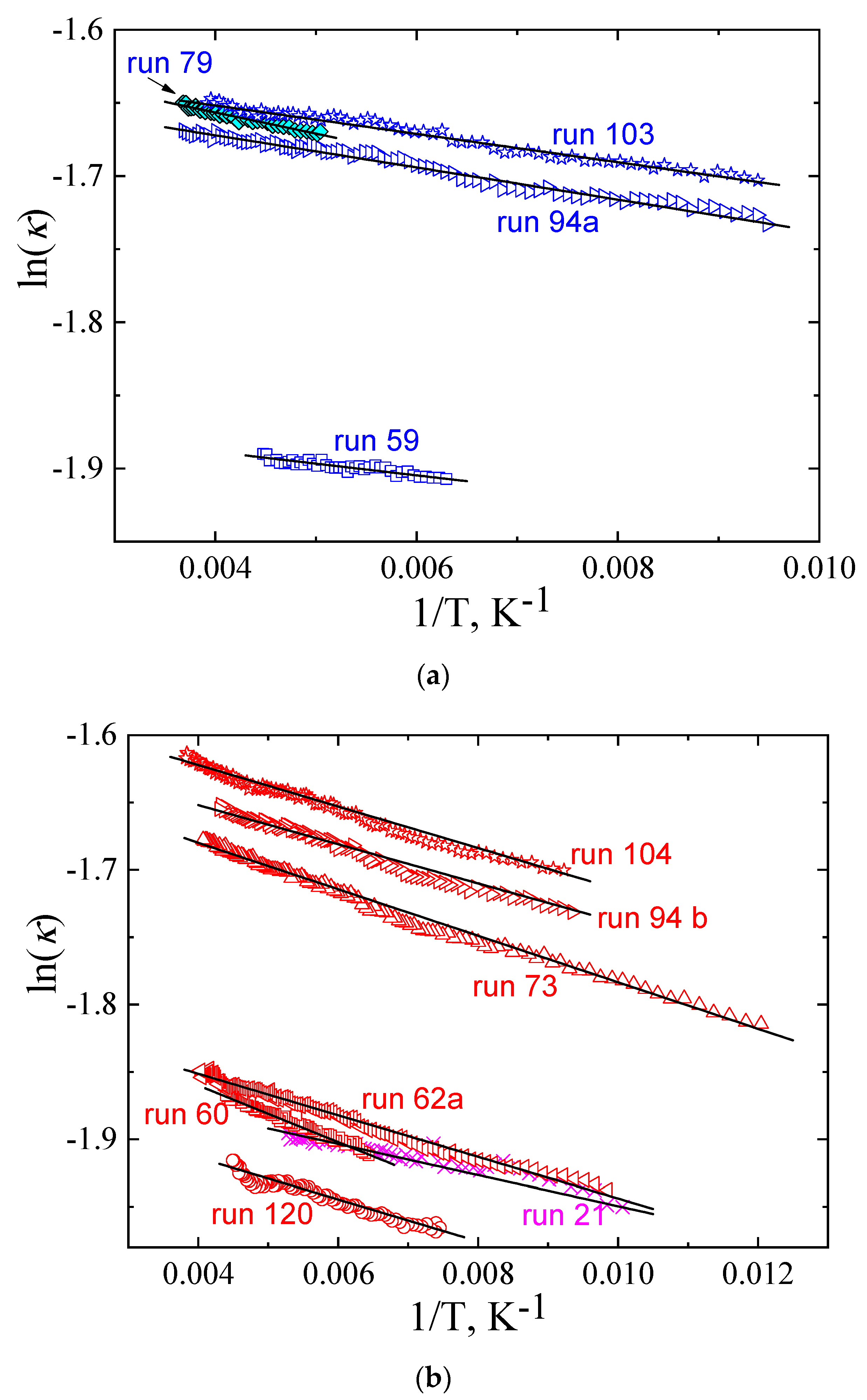
2.2. The Thermal Conductivity of the Glacial State
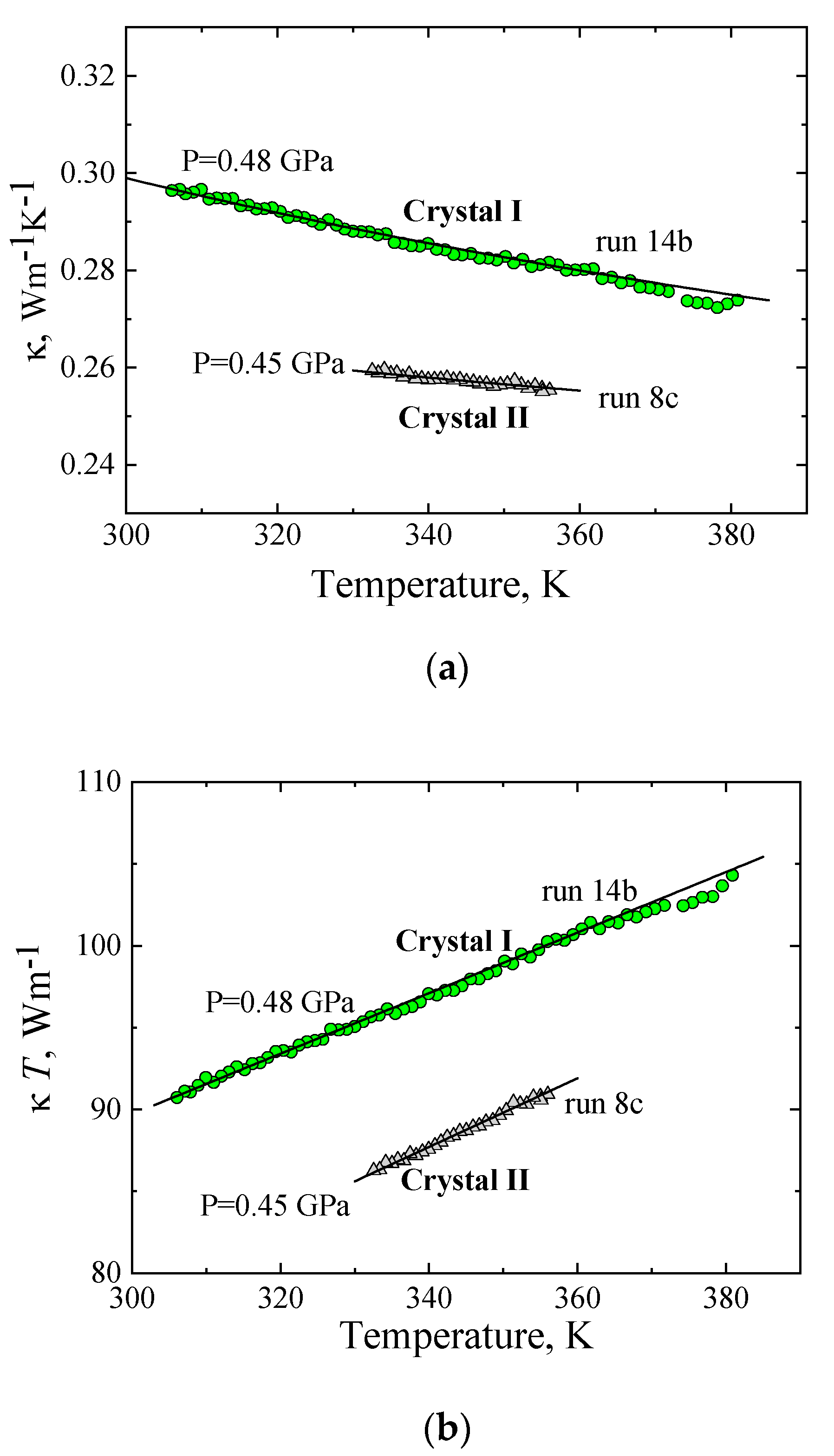
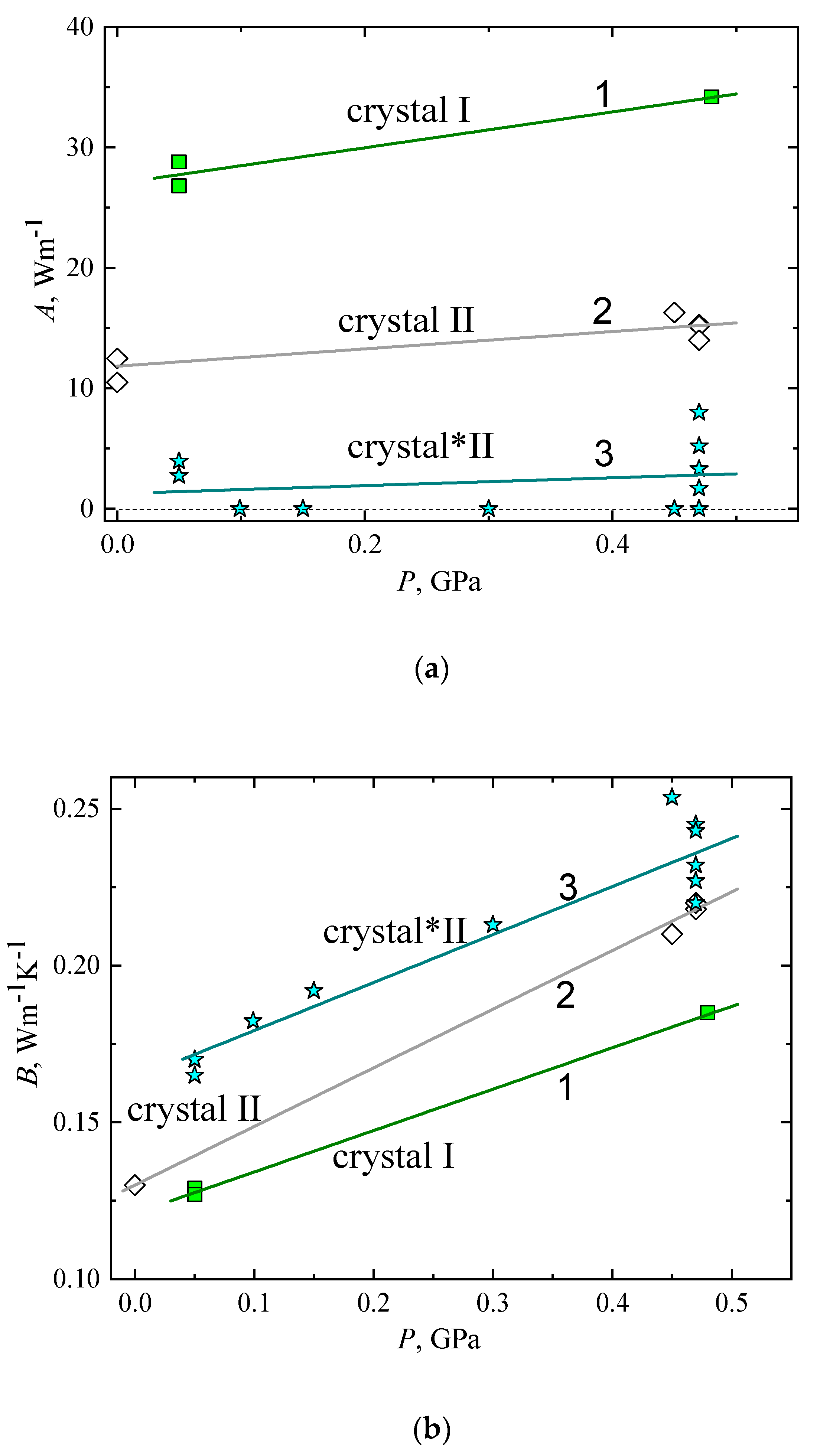
2.3. The Thermal Conductivity of Crystal I, Crystal II, and Crystal*II
2.4. Phase Transformations
2.5. Transitional Pressure–Temperature Diagram
3. Discussion
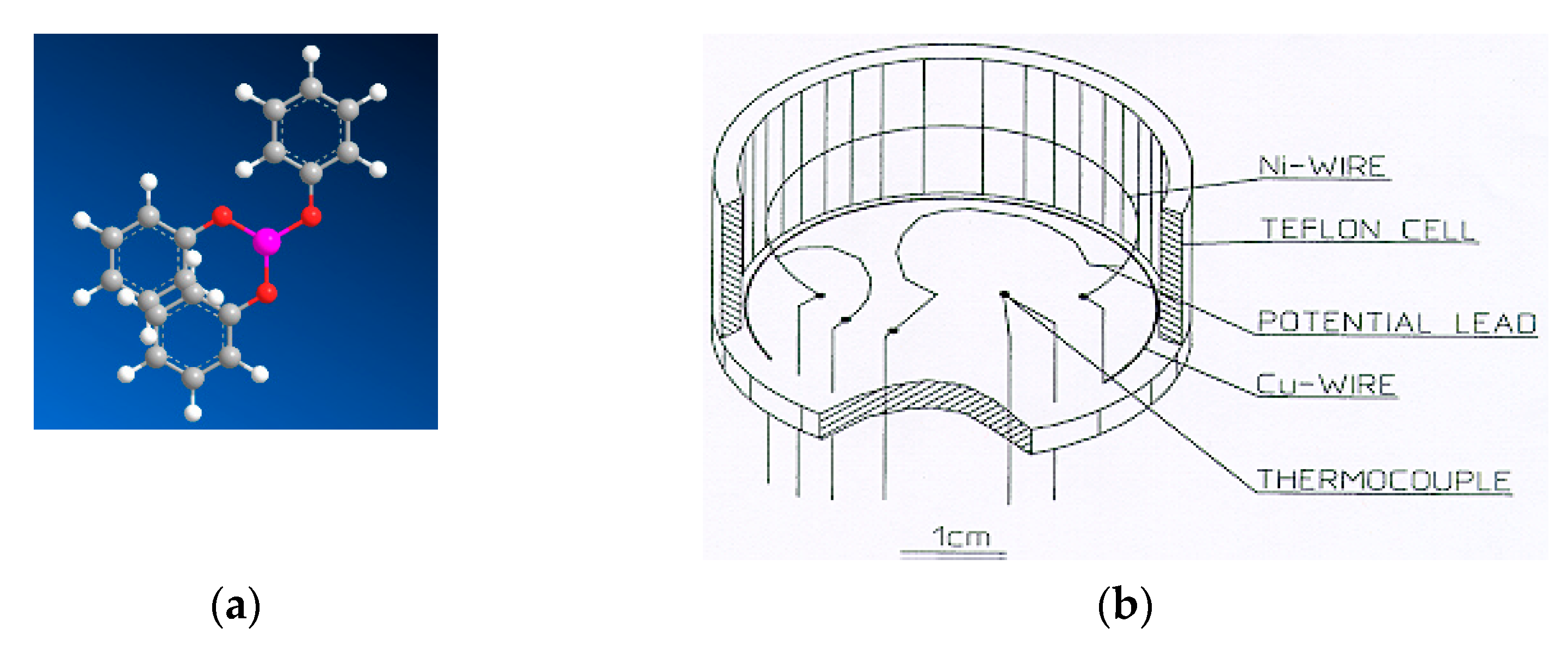
4. Materials and Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berman, R. Thermal Conduction in Solids; Clarendon Press: Oxford, UK, 1976; p. 193. [Google Scholar]
- Konstantinov, V.A.; Manzhelii, V.G.; Strzhemechny, M.A.; Smirnov, S.A. The Λ∝ 1/T law and isochoric thermal conductivity of rare gas crystals. Sov. J. Low Temp. Phys. 1988, 14, 48–54. [Google Scholar]
- Allen, P.B.; Feldman, J.L. Thermal conductivity of disordered harmonic solids. Phys. Rev. B 1993, 48, 12581–12588. [Google Scholar] [CrossRef] [PubMed]
- Feldman, J.L.; Kluge, M.D.; Allen, P.B.; Wooten, F. Thermal conductivity and localization in glasses: Numerical study of a model of amorphous silicon. Phys. Rev. B 1993, 48, 12589–12602. [Google Scholar] [CrossRef] [PubMed]
- Allen, P.B.; Feldman, J.L.; Fabian, J.; Wooten, F. Diffusons, locons and propagons: Character of atomie yibrations in amorphous Si. Philos. Mag. B 1999, 79, 1715–1731. [Google Scholar] [CrossRef]
- McGaughey, A.J.H.; Kaviany, M. Thermal conductivity decomposition and analysis using molecular dynamics simulations. Part I. Lennard-Jones argon. Int. J. Heat Mass Transf. 2004, 47, 1783–1798. [Google Scholar] [CrossRef]
- Krivchikov, A.I.; Sharapova, I.V.; Korolyuk, O.A.; Romantsova, O.O.; Bermejo, F.J. Experimental evidence of the role of quasilocalized phonons in the thermal conductivity of simple alcohols in orientationally ordered crystalline phases. Low Temp. Phys. 2009, 35, 891–897. [Google Scholar] [CrossRef]
- Korolyuk, O.A. Thermal conductivity of molecular crystals of monatomic alcohols: From methanol to butanol. Low Temp. Phys. 2011, 37, 416–419. [Google Scholar] [CrossRef]
- Krivchikov, A.I.; Romantsova, O.O.; Korolyuk, O.A.; Vdovichenko, G.A.; Horbatenko, Y.V. Specific features of heat transfer in the orientationally ordered phases of molecular crystals in the region with predominant phonon-phonon scattering. Low Temp. Phys. 2015, 41, 551–556. [Google Scholar] [CrossRef]
- Krivchikov, A.I.; Korolyuk, O.; Sharapova, I.V.; Tamarit, J.L.; Bermejo, F.J.; Pardo, L.C.; Rovira-Esteva, M.; Ruiz-Martin, M.D.; Jezowski, A.; Baran, J.; et al. Effects of internal molecular degrees of freedom on the thermal conductivity of some glasses and disordered crystals. Phys. Rev. B 2012, 85, 014206. [Google Scholar] [CrossRef]
- Romantsova, O.O.; Horbatenko, Y.V.; Krivchikov, A.I.; Korolyuk, O.A.; Vdovichenko, G.A.; Zloba, D.I.; Pyshkin, O.S. Anomalous heat transfer in two polymorphs of para-bromobenzophenone. Low Temp. Phys. 2017, 43, 395–399. [Google Scholar] [CrossRef]
- Krivchikov, A.I.; Jeżowski, A. Thermal conductivity of glasses and disordered crystals. In Low-Temperature Thermal and Vibrational Properties of Disordered Solids: A Half-Century of Universal “Anomalies” of Glasses; Ramos, M.A., Ed.; World Scientific Publishing Europe Ltd.: London, UK, 2022; Chapter 3; pp. 69–112. [Google Scholar] [CrossRef]
- Babkov, L.M.; Baran, J.; Davydova, N.A.; Ivlieva, I.V.; Ponezha, E.A.; Reznichenko, V.Y. Infrared Spectra of Triphenyl Phosphite and Their Interpretation on the Basis of Quantum Chemistry Calculation. Ukr. J. Phys. 2016, 61, 471–477. [Google Scholar] [CrossRef]
- Ha, A.; Cohen, I.; Zhao, X.; Lee, M.; Kivelson, D. Supercooled Liquids and Polyamorphism. J. Phys. Chem. 1996, 100, 1–4. [Google Scholar] [CrossRef]
- van Miltenburg, K.; Blok, K. Calorimetric Investigation of a New Solid Phase in Triphenylphosphite. J. Phys. Chem. 1996, 100, 16457–16459. [Google Scholar] [CrossRef]
- Mizukami, M.; Kobashi, K.; Hanaya, M.; Oguni, M. Presence of Two Freezing-In Processes Concerning α-Glass Transition in the New Liquid Phase of Triphenyl Phosphite and Its Consistency with “Cluster Structure” and “Intracluster Rearrangement for α Process” Models. J. Phys. Chem. B 1999, 103, 4078–4088. [Google Scholar] [CrossRef]
- Krivchikov, A.I.; Andersson, O. Thermal Conductivity of Triphenyl Phosphite’s Liquid, Glassy, and Glacial States. J. Phys. Chem. B 2016, 120, 2845–2853. [Google Scholar] [CrossRef] [PubMed]
- Wiedersich, J.; Kudlik, A.; Gottwald, J.; Benini, G.; Roggatz, I.; Rössler, E. On Polyamorphism of Triphenyl Phosphite. J. Phys. Chem. B 1997, 101, 5800–5803. [Google Scholar] [CrossRef]
- Johari, G.P.; Ferrari, C. Calorimetric and Dielectric Investigations of the Phase Transformations and Glass Transition of Triphenyl Phosphite. J. Phys. Chem. B 1997, 101, 10191–10197. [Google Scholar] [CrossRef]
- Tarnacka, M.; Madejczyk, O.; Dulski, M.; Maksym, P.; Kaminski, K.; Paluch, M. Is There a Liquid–Liquid Phase Transition in Confined Triphenyl Phosphite? J. Phys. Chem. C 2017, 121, 19442–19450. [Google Scholar] [CrossRef]
- Kobayashi, M.; Tanaka, H. The reversibility and first-order nature of liquid–liquid transition in a molecular liquid. Nat. Commun. 2016, 7, 13438. [Google Scholar] [CrossRef]
- Demirjian, B.G.; Dosseh, G.; Chauty, A.; Ferrer, M.L.; Morineau, D.; Lawrence, C.; Takeda, A.K.; Kivelson, D.; Brown, S. Metastable Solid Phase at the Crystalline-Amorphous Border: The Glacial Phase of Triphenyl Phosphite. J. Phys. Chem. B 2001, 105, 2107–2116. [Google Scholar] [CrossRef]
- Lefort, R.; Hédoux, A.; Guinet, Y.; Cochin, E.; Descamps, M. Fast intramolecular dynamics of triphenyl phosphite investigated by 2H NM. Eur. Phys. J. B 2002, 30, 519–525. [Google Scholar] [CrossRef]
- Senker, J.; Sehnert, J.; Correll, S. Microscopic Description of the Polyamorphic Phases of Triphenyl Phosphite by Means of Multidimensional Solid-State NMR Spectroscopy. J. Am. Chem. Soc. 2004, 127, 337–349. [Google Scholar] [CrossRef] [PubMed]
- Mierzwa, M.; Paluch, M.; Rzoska, S.J.; Zioło, J. The Liquid−Glass and Liquid−Liquid Transitions of TPP at Elevated Pressure. J. Phys. Chem. B 2008, 112, 10383–10385. [Google Scholar] [CrossRef]
- Hédoux, A.; Guinet, Y.; Derollez, P.; Hernandez, O.; Paccou, L.; Descamps, M. Micro-structural investigations in the glacial state of triphenyl phosphite. J. Non-Cryst. Solids 2006, 352, 4994–5000. [Google Scholar] [CrossRef]
- Mei, Q.; Siewenie, J.E.; Benmore, C.J.; Ghalsasi, P.; Yarger, J.L. Orientational Correlations in the Glacial State of Triphenyl Phosphite. J. Phys. Chem. B 2006, 110, 9747–9750. [Google Scholar] [CrossRef]
- Hédoux, A.; Guinet, Y.; Descamps, M. Size dependence of the Raman spectra in an amorphous-nanocrystalline mixed phase: The glacial state of triphenyl phosphite. J. Raman Spectrosc. 2001, 32, 677–688. [Google Scholar] [CrossRef]
- Hedoux, A.; Dore, J.; Guinet, Y.; Bellissent-Funel, M.C.; Prevost, D.; Descamps, M.; Grandjean, D. Analysis of the local order in the glacial state of triphenyl phosphite by neutron diffraction. Phys. Chem. Chem. Phys. 2002, 4, 5644–5648. [Google Scholar] [CrossRef]
- Tanaka, H. Liquid–liquid transition and polyamorphism. J. Chem. Phys. 2020, 153, 130901. [Google Scholar] [CrossRef]
- Hédoux, A.; Guinet, Y.; Derollez, P.; Hernandez, O.; Lefort, R.; Descamps, M. A contribution to the understanding of the polyamorphism situation in triphenyl phosphite. Phys. Chem. Chem. Phys. 2004, 6, 3192–3199. [Google Scholar] [CrossRef]
- Baran, J.; Davydova, N.A.; Drozd, M. Polymorphism of triphenyl phosphite. J. Chem. Phys. 2014, 140, 104512. [Google Scholar] [CrossRef] [PubMed]
- Baran, J.; Davydova, N.A.; Drozd, M.; Krivchikov, A. Effect of the clay nanomaterial laponite on the crystallization characteristics of nanocomposites TPP/laponite. Mol. Cryst. Liq. Cryst. 2020, 696, 65–74. [Google Scholar] [CrossRef]
- Andersson, S.P.; Ross, R.G. Thermal conductivity and heat capacity per unit volume of poly(methyl methacrylate) under high pressure. Int. J. Thermophys. 1994, 15, 949–962. [Google Scholar] [CrossRef]
- Cahill, D.G.; Watson, S.K.; Pohl, R.O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 1992, 46, 6131–6140. [Google Scholar] [CrossRef] [PubMed]
- Andersson, O. Simulation of a glass transition in a hot-wire experiment using time-dependent heat capacity. Int. J. Thermophys. 1997, 18, 195–208. [Google Scholar] [CrossRef]
- Cohen, I.; Ha, A.; Zhao, X.; Lee, M.; Fischer, T.; Strouse, M.J.; Kivelson, D. A Low-Temperature Amorphous Phase in a Fragile Glass-Forming Substance. J. Phys. Chem. 1996, 100, 8518–8526. [Google Scholar] [CrossRef]
- Simoncelli, M.; Marzari, N.; Mauri, F. Unified theory of thermal transport in crystals and glasses. Nat. Phys. 2019, 15, 809–813. [Google Scholar] [CrossRef]
- Isaeva, L.; Barbalinardo, G.; Donadio, D.; Baroni, S. Modeling heat transport in crystals and glasses from a unified lattice-dynamical approach. Nat. Commun. 2019, 10, 1–6. [Google Scholar] [CrossRef]
- Huang, M.; Liu, X.; Zhang, P.; Qian, X.; Feng, Y.; Li, Z.; Pan, W.; Wan, C. Thermal conductivity modeling on highly disordered crystalline Y1−xNbxO1.5+x: Beyond the phonon scenario. Appl. Phys. Lett. 2021, 118, 073901. [Google Scholar] [CrossRef]
- Kumar, G.; Van Gessel, F.G.; Elton, D.C.; Chung, P.W. Phonon Lifetimes and Thermal Conductivity of the Molecular Crystal α-RDX. MRS Adv. 2019, 4, 2191–2199. [Google Scholar] [CrossRef]
- Larkin, J.M.; McGaughey, A.J.H. Thermal conductivity accumulation in amorphous silica and amorphous silicon. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Cheng, Z.; Weidenbach, A.; Feng, T.; Tellekamp, M.B.; Howard, S.; Wahila, M.J.; Zivasatienraj, B.; Foley, B.; Pantelides, S.T.; Piper, L.F.J.; et al. Diffuson-driven ultralow thermal conductivity in amorphous Nb2O5 thin films. Phys. Rev. Mater. 2019, 3, 025002. [Google Scholar] [CrossRef]
- Chen, X.; Weathers, A.; Carrete, J.; Mukhopadhyay, S.; Delaire, O.; Stewart, D.; Mingo, N.; Girard, S.N.; Ma, J.; Abernathy, D.; et al. Twisting phonons in complex crystals with quasi-one-dimensional substructures. Nat. Commun. 2015, 6, 6723. [Google Scholar] [CrossRef] [PubMed]
- Hanus, R.; George, J.; Wood, M.; Bonkowski, A.; Cheng, Y.; Abernathy, D.L.; Manley, M.E.; Hautier, G.; Snyder, G.J.; Hermann, R.P. Uncovering design principles for amorphous-like heat conduction using two-channel lattice dynamics. Mater. Today Phys. 2021, 18, 100344. [Google Scholar] [CrossRef]
- Hanus, R.; Gurunathan, R.; Lindsay, L.; Agne, M.T.; Shi, J.; Graham, S.; Snyder, G.J. Thermal transport in defective and disordered materials. Appl. Phys. Rev. 2021, 8, 031311. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, X.; Feng, T.; Wang, J.; Ruan, X. Vibrational hierarchy leads to dual-phonon transport in low thermal conductivity crystals. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef]
- Zhou, Y. Assessing the quantum effect in classical thermal conductivity of amorphous silicon. J. Appl. Phys. 2021, 129, 235104. [Google Scholar] [CrossRef]
- Lundgren, N.W.; Barbalinardo, G.; Donadio, D. Mode localization and suppressed heat transport in amorphous alloys. Phys. Rev. B 2021, 103, 024204. [Google Scholar] [CrossRef]
- Ohnishi, M.; Tadano, T.; Tsuneyuki, S.; Shiomi, J. Strong Phonon Anharmonicity of Clathrate Compound at High Temperature. arXiv 2021, arXiv:2103.00413. [Google Scholar]
- Aryana, K.; Stewart, D.A.; Gaskins, J.T.; Nag, J.; Read, J.C.; Olson, D.H.; Grobis, M.K.; Hopkins, P.E. Tuning network topology and vibrational mode localization to achieve ultralow thermal conductivity in amorphous chalcogenides. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Braun, J.L.; King, S.W.; Hoglund, E.R.; Gharacheh, M.A.; Scott, E.A.; Giri, A.; Tomko, J.A.; Gaskins, J.T.; Al-Kukhun, A.; Bhattarai, G.; et al. Hydrogen effects on the thermal conductivity of delocalized vibrational modes in amorphous silicon nitride (a−SiNx:H). Phys. Rev. Mater. 2021, 5, 035604. [Google Scholar] [CrossRef]
- Qian, X.; Zhou, J.; Chen, G. Phonon-engineered extreme thermal conductivity materials. Nat. Mater. 2021, 20, 1188–1202. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Guo, Y.; Bescond, M.; Chen, J.; Nomura, M.; Volz, S. Heat Conduction Theory Including Phonon Coherence. Phys. Rev. Lett. 2022, 128, 015901. [Google Scholar] [CrossRef] [PubMed]
- Caldarelli, G.; Simoncelli, M.; Marzari, N.; Mauri, F.; Benfatto, L. A many-body Green’s function approach to lattice thermal transport. arXiv 2022, arXiv:2202.02246. [Google Scholar] [CrossRef]
- Bernges, T.; Hanus, R.; Wankmiller, B.; Imasato, K.; Lin, S.; Ghidiu, M.; Gerlitz, M.; Peterlechner, M.; Graham, S.; Hautier, G.; et al. Considering the Role of Ion Transport in Diffuson-Dominated Thermal Conductivity. Adv. Energy Mater. 2022, 12, 2200717. [Google Scholar] [CrossRef]
- Hernandez, O.; Hédoux, A.; Lefebvre, J.; Guinet, Y.; Descamps, M.; Papoular, R.; Masson, O. Ab initio structure determination of triphenyl phosphite by powder synchrotron X-ray diffraction. J. Appl. Crystallogr. 2002, 35, 212–219. [Google Scholar] [CrossRef]
- Senker, J.; Lüdecke, J. Structure Determination for the Crystalline Phase of Triphenyl Phosphite by Means of Multi-Dimensional Solid-State NMR and X-ray Diffraction. Z. Für Nat. B 2001, 56, 1089–1099. [Google Scholar] [CrossRef]
- Golovanov, D.G.; Lyssenko, K.A.; Antipin, M.Y.; Vygodskii, Y.S.; Lozinskaya, E.I.; Shaplov, A.S. Long-awaited polymorphic modification of triphenyl phosphite. CrystEngComm 2005, 7, 465–468. [Google Scholar] [CrossRef]
- Håkansson, B.; Andersson, P.; Bäckström, G. Improved hot-wire procedure for thermophysical measurements under pressure. Rev. Sci. Instrum. 1988, 59, 2269–2275. [Google Scholar] [CrossRef]
- Andersson, O.; Inaba, A. Thermal conductivity of crystalline and amorphous ices and its implications on amorphization and glassy water. Phys. Chem. Chem. Phys. 2005, 7, 1441–1449. [Google Scholar] [CrossRef]

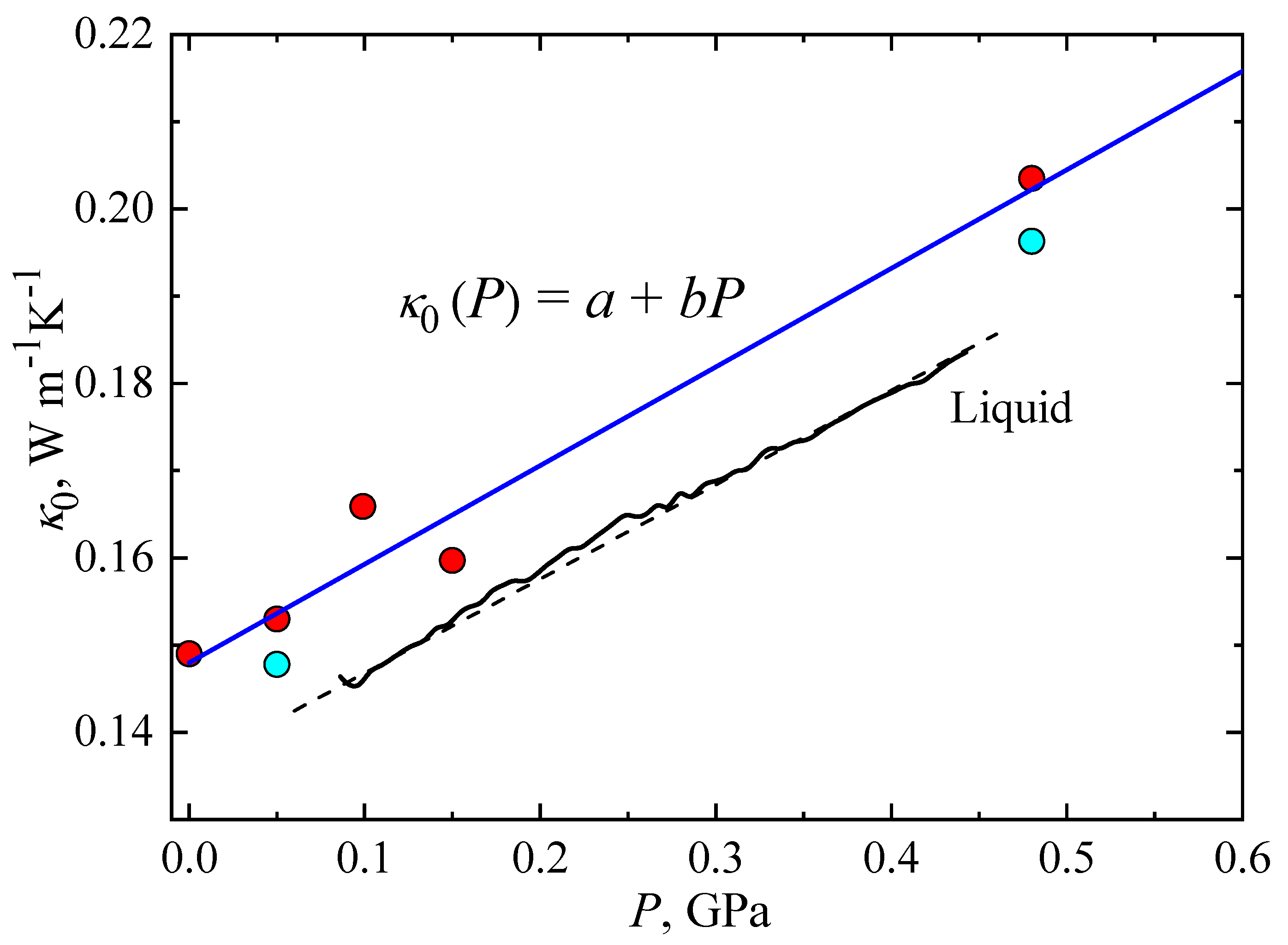
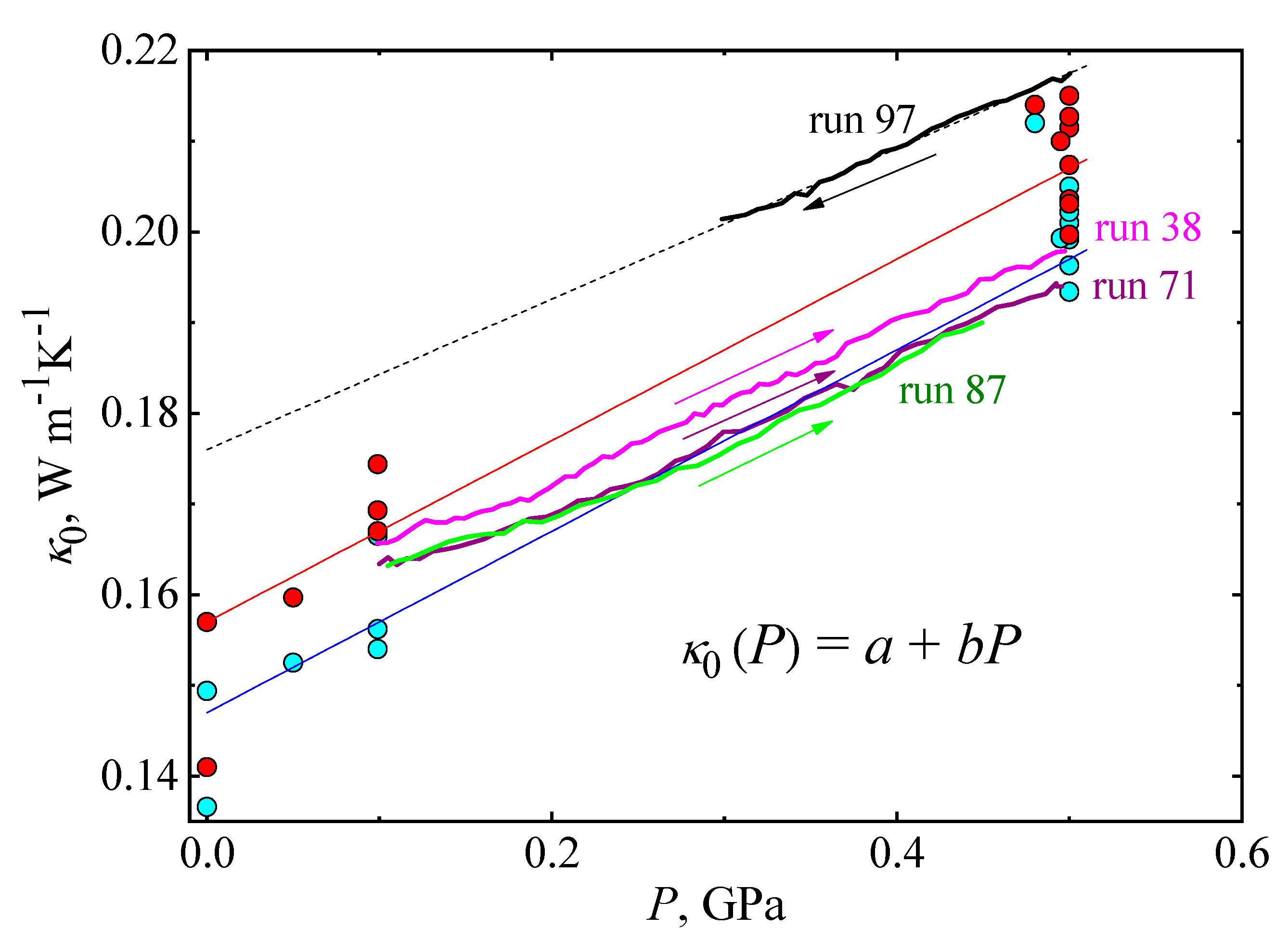



| P, GPa | run | κ0, Wm−1K−1 | E, K | ΔT, K | Experimental Conditions |
|---|---|---|---|---|---|
| 0 | 43 | 0.149 | 14 | 166–206 | Cooling from liquid (to glass) at −1.7 K/min. Measurements of κ on heating at 0.46 K/min. |
| 0.05 | 03 | 0.148 | 11.1 | 175–96 | Cooling from liquid at −2 K/min, and (simultaneous) measurements of κ on cooling. |
| 0.05 | 04 | 0.153 | 13.6 | 98–210 | Continued run 03, measurements of κ on heating at 0.3 K/min. |
| 0.05 | 18 | 0.153 | 13.8 | 183–203 | Cooling from liquid at −1.6 K/min, measurements of κ on heating at 0.4 K/min |
| 0.10 | 36 | 0.166 | 25 | 190–214 | Cooling from liquid −1.3 K/min, measurements of κ on heating at 0.58 K/min. |
| 0.15 | 27a | 0.16 | 11.5 | 204–225 | Cooling from liquid at −1.6 K/min, measurements of κ on heating at 0.4 K/min. |
| 0.48 | 10 | 0.196 | 10 | 237–89 | Cooling from liquid at −2.0 K/min, measurements of κ on cooling. |
| 0.48 | 11 | 0.204 | 14.6 | 89–267 | Continued run 10, measurements on heating at 0.08 K/min. |
| P, GPa | run | κ0, Wm−1K−1 | E, K | ΔT, K | Experimental Conditions |
|---|---|---|---|---|---|
| 0 | 110 | 0.137 | 12.0 | 169–126 | Cooling |
| 0 | 110 | 0.141 | 16.6 | 128–204 | Heating |
| 0 | 120 | 0.149 | 8.8 | 187–133 | Cooling |
| 0 | 120 | 0.157 | 15.5 | 133–197 | Heating |
| 0.05 | 20 | 0.152 | 7.0 | 191–100 | Cooling |
| 0.05 | 21 | 0.16 | 11.5 | 98–182 | Heating |
| 0.10 | 107 | 0.167 | 7.0 | 217–98 | Cooling |
| 0.10 | 108 | 0.174 | 12.0 | 97–213 | Heating |
| 0.10 | 59 | 0.156 | 8.0 | 223–159 | Cooling |
| 0.10 | 60 | 0.169 | 21.0 | 156–227 | Continued run 59, heating |
| 0.10 | 61 | 0.154 | 6.0 | 160–100 | Cooling |
| 0.10 | 62a | 0.167 | 15.4 | 100–250 | Continued run 60, heating |
| 0.48 | 13 | 0.212 | 13.3 | 297–89 | Cooling |
| 0.48 | 14a | 0.214 | 14.1 | 87–260 | Continued run 13, heating |
| 0.49 | 103 | 0.199 | 9.7 | 255–105 | Cooling |
| 0.49 | 104 | 0.21 | 15.4 | 106–260 | Continued run 103, heating |
| 0.5 | 39a | 0.199 | 18.1 | 235–171 | Cooling |
| 0.5 | 39b | 0.204 | 21.0 | 171–230 | Continued run 39a, heating |
| 0.5 | 72 | 0.193 | 14.0 | 236–82 | Cooling |
| 0.5 | 73 | 0.2 | 17.3 | 82–236 | Continued run 72, heating |
| 0.5 | 75 | 0.201 | 17.0 | 220–260 | Cooling |
| 0.5 | 76 | 0.211 | 28.0 | 220–272 | Continued run 75, heating |
| 0.5 | 79 | 0.202 | 14.5 | 270–198 | Cooling |
| 0.5 | 80 | 0.207 | 19.0 | 200–256 | Continued run 79, heating |
| 0.5 | 81 | 0.205 | 17.0 | 277–222 | Continued run 80, cooling |
| 0.5 | 82 | 0.213 | 25.0 | 222–270 | Continued run 81, heating |
| 0.5 | 94a | 0.196 | 11.0 | 270–105 | Cooling |
| 0.5 | 94b | 0.203 | 14.5 | 105–230 | Heating after cooling |
| 0.5 | 96 | 0.215 | 14.0 | 160–274 | Heating |
| P, GPa | run | A, Wm−1 | B, Wm−1K−1 | Temperature Interval, K | Experimental Conditions |
|---|---|---|---|---|---|
| Crystal I | |||||
| 0.05 | 23a | 26.8 | 0.129 | 296–106 | Cooling, −1.4 K/min |
| 0.05 | 23b | 28.8 | 0.127 | 106–290 | Heating, 0.5 K/min |
| 0.48 | 14b | 34.2 | 0.185 | 380–306 | Cooling, −0.15 K/min |
| Crystal II | |||||
| 0 | 42a | 12.5 | 0.13 | 273–197 | Cooling, −1.4 K/min, |
| 0 | 42b | 12.5 | 0.13 | 197–270 | Continued run 42a; heating, 0.4 K/min |
| 0 | 43 | 10.5 | 0.13 | 231–255 | Heating, 0.46 K/min |
| 0.45 | 08c | 16.3 | 0.21 | 357–330 | Cooling, −0.2 K/min |
| 0.47 | 50e | 15.3 | 0.218 | 300–200 | Cooling |
| 0.47 | 51a | 15.2 | 0.22 | 183–348 | Heating |
| 0.47 | 51b | 14 | 0.22 | 351–298 | Cooling |
| Crystal*II | |||||
| 0.05 | 05 | 2.76 | 0.17 | 260–102 | Cooling, −1.4 K/min |
| 0.05 | 06a | 3.94 | 0.165 | 100–270 | continued run 05; heating, 0.2 K/min |
| 0.10 | 62b | 0 | 0.182 | 264–286 | Heating, 0.4 K/min |
| 0.15 | 27b | 0 | 0.192 | 265–299 | Heating, 0.4 K/min |
| 0.3 | 32 | 0 | 0.213 | 296–317 | Heating, 0.37 K/min |
| 0.45 | 08b | 0 | 0.254 | 297–356 | Heating, 0.46 K/min |
| 0.47 | 48 | 3.3 | 0. 22 | 267–116 | Cooling, −1.6 K/min |
| 0.47 | 49a | 1.7 | 0.232 | 113–322 | Continued run 48; heating |
| 0.47 | 49b | 5.2 | 0.227 | 322–296 | Continued run 49a; cooling |
| 0.47 | 50a | 0 | 0.245 | 297–323 | Continued run 49b; heating |
| 0.47 | 50b | 8 | 0.227 | 341–297 | Cooling |
| 0.47 | 50c | 3.3 | 0.243 | 297–356 | Heating |
| Aav, Wm−1 | dAav/dP, Wm−1GPa−1 | Bav, Wm−1K−1 | dBav/dP, Wm−1K−1GPa−1 | a, Wm−1K−1 | b, Wm−1K−1GPa−1 | |
|---|---|---|---|---|---|---|
| crystal I | 27 | 14.9 | 0.121 | 0.132 | ||
| crystal II | 11.9 | 7.17 | 0.13 | 0.187 | ||
| crystal*II | 1.27 | 3.28 | 0.164 | 0.153 | ||
| glacial | - | - | 0.147 (cooling) 0.157 (heating) | 0.1 0.1 | ||
| glass | - | - | 0.148 | 0.113 |
| Contributions | Glass-like Behavior | Crystal-like Behavior |
|---|---|---|
| Dp (ω, T) | ω−4 | T−1ω−1 |
| Ddiff (ω) | ω−1 | ω−1 |
| κp (T), high-temperature limit | T0 | T−1 |
| κdiff (T), high-temperature limit | exp(−E/T) | exp(−E/T) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krivchikov, A.; Andersson, O.; Korolyuk, O.; Kryvchikov, O. Thermal Conductivity of Solid Triphenyl Phosphite. Molecules 2022, 27, 8399. https://doi.org/10.3390/molecules27238399
Krivchikov A, Andersson O, Korolyuk O, Kryvchikov O. Thermal Conductivity of Solid Triphenyl Phosphite. Molecules. 2022; 27(23):8399. https://doi.org/10.3390/molecules27238399
Chicago/Turabian StyleKrivchikov, Alexander, Ove Andersson, Oksana Korolyuk, and Oleksii Kryvchikov. 2022. "Thermal Conductivity of Solid Triphenyl Phosphite" Molecules 27, no. 23: 8399. https://doi.org/10.3390/molecules27238399
APA StyleKrivchikov, A., Andersson, O., Korolyuk, O., & Kryvchikov, O. (2022). Thermal Conductivity of Solid Triphenyl Phosphite. Molecules, 27(23), 8399. https://doi.org/10.3390/molecules27238399






