A Mathematical Model for Sublimation of a Thin Film in Trace Explosive Detection Problem
Abstract
1. Introduction
2. Problem Setting
2.1. Assumptions
2.2. Basic Equations
3. Results and Discussion
3.1. Input Data for Estimations
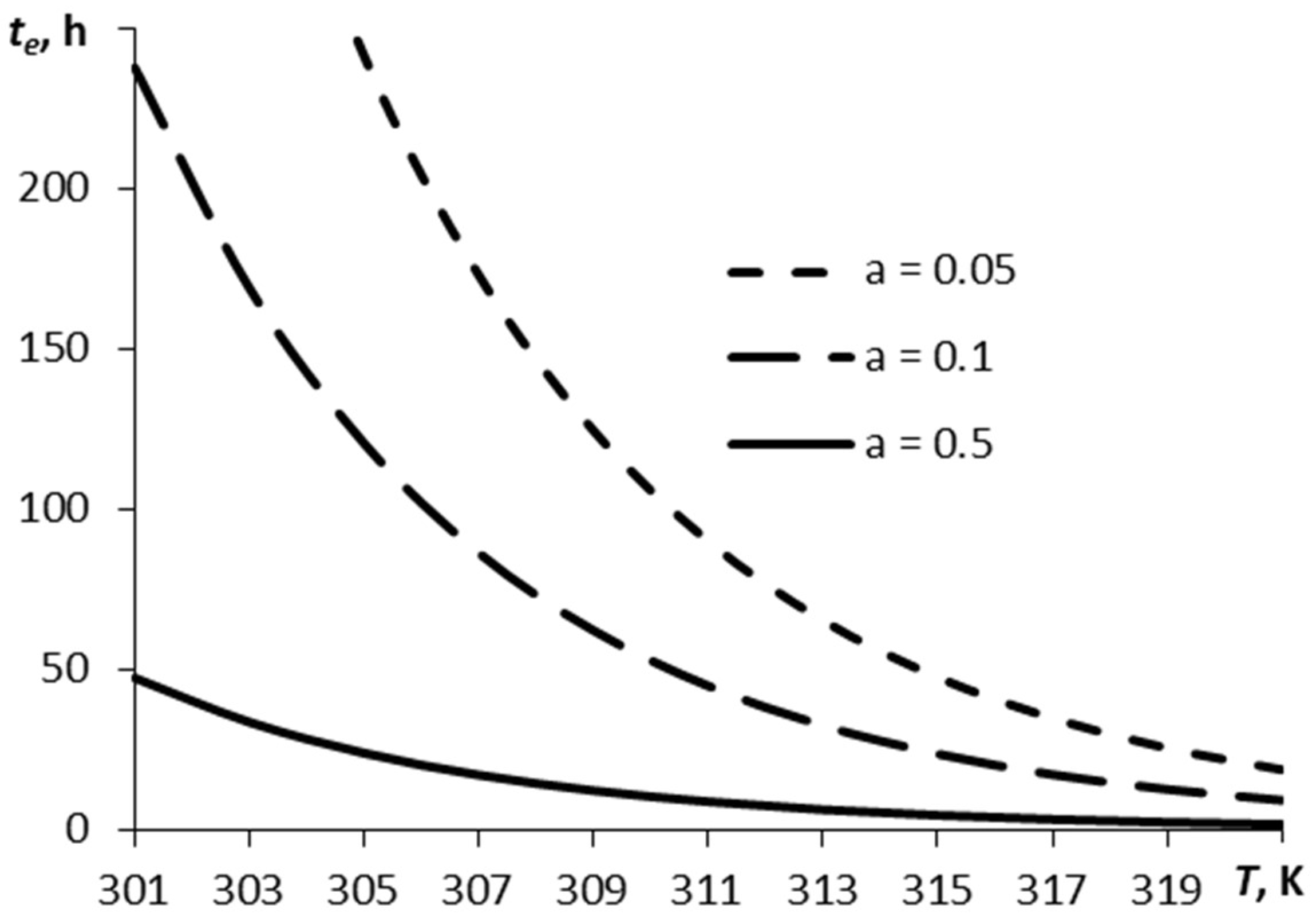
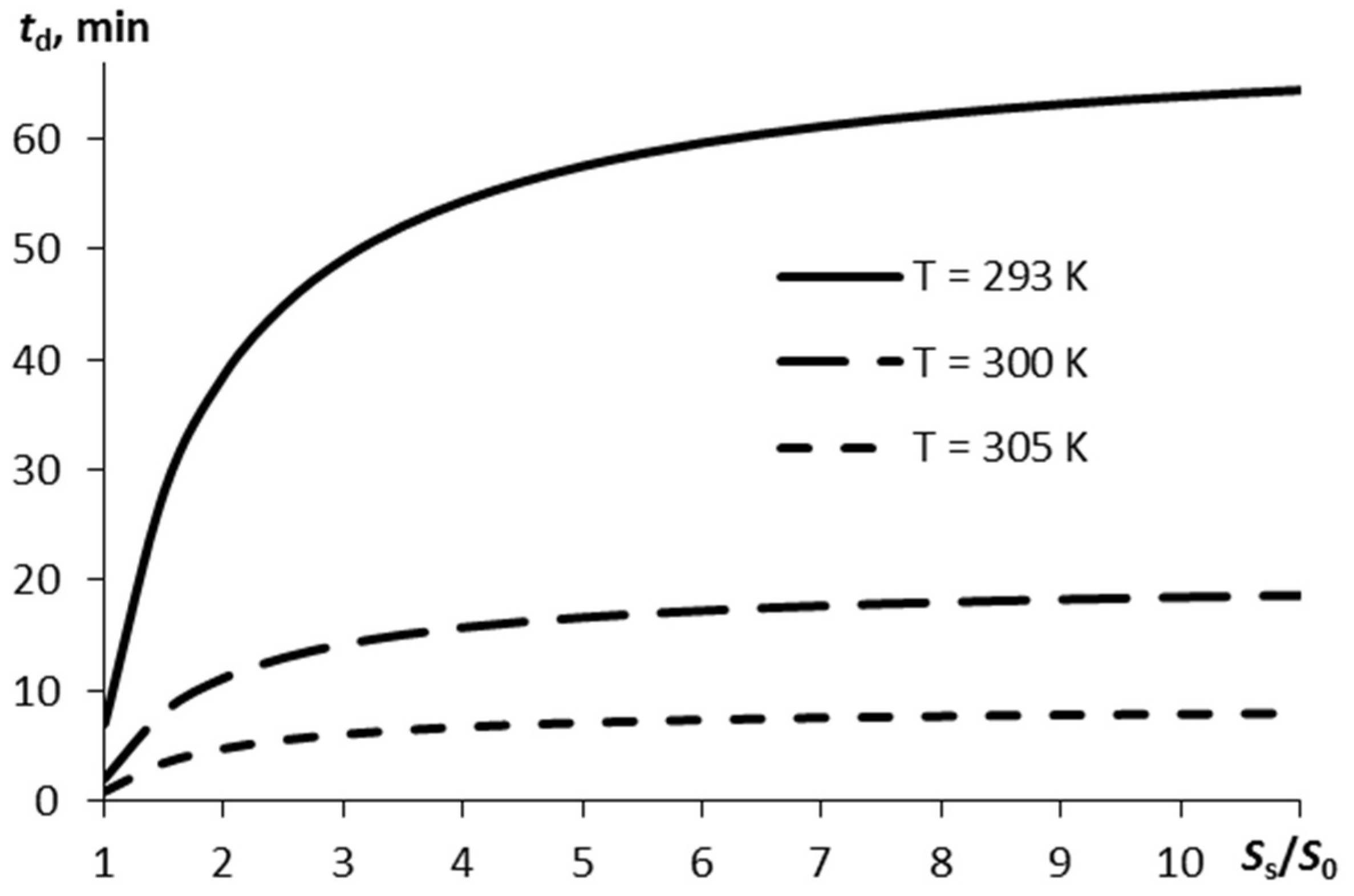
3.2. Parametric Estimations
3.3. Comparison of Sublimation Behaviors of Different Explosives
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature and Abbreviations
| T | K | Temperature |
| m | kg | Weight of explosive |
| ρ | kg/m3 | Density of explosive |
| v | kg/s | Mass rate of vaporization |
| H | J/kg | Heat of phase transformation |
| A | Pa | Pre-exponential factor |
| α | Portion of molecular flow condensing on the surface | |
| ps | Pa | Partial pressure of saturated vapor |
| R | m2·kg/(d2· K mol) | Universal gas constant |
| M | kg/mol | Molecular weight of explosive |
| Δmd | kg | Minimum vapor mass corresponding to detection threshold |
| m0 | kg | Initial mass of film |
| S | m2 | Surface area of film |
| h | m | Film height |
| Ss | m2 | Surface area of substrate |
| Sssa | m2/kg | Specific surface area of substrate |
| β | 1/s | A set of variables from Equation (5) |
| te | s | Typical time of sublimation |
| RDX | Hexogen | |
| HMX | Octogen | |
| TNT | Trinitrotoluene | |
| TNA | Picramide |
References
- Existing and Potential Standoff Explosives Detection Techniques. Committee of the Review Existing and Potential Standoff Explosives Detection Techniques; The National Academies Press: Washington, DC, USA, 2004; 148p.
- Yinon, J. (Ed.) Counterterrorist Detection Techniques of Explosives; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Skvortsov, L.A. Laser methods for detecting explosive residues on surfaces of distant objects. Quantum Electron. 2012, 42, 1. [Google Scholar] [CrossRef]
- Gruznov, V.M.; Baldin, M.N.; Pryamov, M.V.; Maksimov, E.M. Determination of explosive vapor concentrations with remote sampling in the control of objects. J. Anal. Chem. 2017, 72, 1155–1160. [Google Scholar] [CrossRef]
- Moore, D.S. Instrumentation for trace detection of high explosives. Rev. Sci. Instrum. 2004, 75, 2499–2512. [Google Scholar] [CrossRef]
- Östmark, H.; Wallin, S.; Ang, H.G. Vapor pressure of explosives: A critical review. Propellants Explos. Pyrotech. 2012, 37, 12–23. [Google Scholar] [CrossRef]
- Baldin, M.N.; Bobrovnikov, S.M.; Vorozhtsov, A.B.; Gorlov, E.V.; Gruznov, V.M.; Zharkov, V.I.; Panchenko, Y.N.; Pryamov, M.V.; Sakovich, G.V. On the effectiveness of joint laser and gas chromatographic remote detection of explosive traces. Atmos. Ocean. Opt. 2018, 32, 988. [Google Scholar]
- Bobrovnikov, S.M.; Vorozhtsov, A.B.; Gorlov, E.V.; Zharkov, V.I.; Sakovich, G.V. Two-pulse laser-induced fragmentation/ laser-induced fluorescence method for the detection of vapors of high-energy materials. In Proceedings of the XVth International Workshop High Energetic Materials (HEMs-2019): Demilitarization, Antiterrorism and Civil Applications 2019, Monte Carlo, Monaco, 28–31 October 2019; pp. 20–21. [Google Scholar]
- Gruznov, V.M.; Bobrovnikov, S.M.; Baldin, M.N.; Gorlov, E.V.; Vorozhtsov, A.B.; Tivileva, M.I. The effect of the high efficiency of laser detection of objects containing explosives by solid traces detection compared to vapors detection. Int. J. Energ. Mater. Chem. Propuls. 2020, 19, 319–327. [Google Scholar] [CrossRef]
- Gresham, G.L.; Davies, J.P.; Goodrich, L.D.; Blackwood, L.G.; Liu, B.Y.; Thimsen, D.; Yoo, S.H.; Hallowell, S.F. Development of particle standards for testing detection systems: Mass of RDX and particle size distribution of composition 4 residues. In Cargo Inspection Technologies; International Society for Optics and Photonics: Bellingham, WA, USA, 1994; Volume 2276, pp. 34–44. [Google Scholar]
- Gromov, D.G.; Gavrilov, S.A. Manifestation of the heterogeneous mechanism upon melting of low-dimensional systems. Phys. Solid State 2009, 51, 2135. [Google Scholar] [CrossRef]
- Mu, R.; Ueda, A.; Wu, M.H.; Tung, Y.S.; Henderson, D.O.; Chamberlain, R.T.; Mercado, A. Experimental and theoretical demonstration of the interfacial interaction potential between an adsorbed film and a smooth substrate. J. Phys. Chem. B 2000, 104, 105–109. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, T.; Liu, Y.; Yang, L.; Zhou, Z. Vaporation characteristics of low-melting nitrocompounds by isothermal thermogravimetry. J. Therm. Anal. Calorim. 2013, 112, 1523–1532. [Google Scholar] [CrossRef]
- Gershanik, A.P.; Zeiri, Y. Sublimation rate of TNT microcrystals in air. J. Phys. Chem. A 2010, 114, 12403–12410. [Google Scholar] [CrossRef] [PubMed]
- Hikal, W.M.; Weeks, B.L. Sublimation kinetics and diffusion coefficients of TNT, PETN, and RDX in air by thermogravimetry. Talanta 2014, 125, 24–28. [Google Scholar] [CrossRef] [PubMed]
- Pacheco-Londoño, L.C.; Ruiz-Caballero, J.L.; Ramírez-Cedeño, M.L.; Infante-Castillo, R.; Gálan-Freyle, N.J.; Hernández-Rivera, S.P. Surface persistence of trace level deposits of highly energetic materials. Molecules 2019, 24, 3494. [Google Scholar] [CrossRef] [PubMed]
- Kudryashova, O.B.; Pavlenko, A.A.; Titov, S.S.; Vorozhtsov, A.B. A mathematical model for evaporation of explosive thin film. J. Energetic Mater. 2021, 39, 246–254. [Google Scholar] [CrossRef]
- Hikal, W.M.; Bhattacharia, S.K.; Vaughn, M.W.; Weeks, B.L. Sublimation and Diffusion Kinetics of 2, 4, 6-Trinitrotoluene (TNT) Single Crystals by Atomic Force Microscopy (AFM). Molecules 2022, 27, 5482. [Google Scholar] [CrossRef] [PubMed]
- Ermolin, N.E.; Zarko, V.E. Mechanism and kinetics of thermal decomposition of cyclic nitramines. Combust. Explos. Shock Waves 1997, 33, 10–31. [Google Scholar] [CrossRef]
- Rosen, J.M.; Dickinson, C. Vapor pressures and heats of sublimation of some high-melting organic explosives. J. Chem. Eng. Data 1969, 14, 120–124. [Google Scholar] [CrossRef]

| Explosive | Vaporization Heat, kJ/kg | Pre- Exponential Factor A, Pa | Density ρ, kg/m3 | Molecular Weight M, kg/mol | References |
|---|---|---|---|---|---|
| RDX | 588 | 1.65·1016 | 1858 | 0.220 | [19,20] |
| HMX | 586 | 132·1016 | 1910 | 0.296 | [19,20] |
| TNA | 511 | 2.15·1016 | 1800 | 0.228 | [20] |
| TNT | 409 | 2.01·1010 | 1600 | 0.227 | [14] |
| Explosive | Vapor Mass in the Air after 30 min, ng | Typical Time of Layer Sublimation, S0 = 1 cm2 and h = 0.1 μm |
|---|---|---|
| RDX | 0.05 | 195 h |
| HMX | 6·10−8 | 108 h |
| TNA | 8.9 | 44 min |
| TNT | 0.19 | 41 h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudryashova, O.B.; Titov, S.S. A Mathematical Model for Sublimation of a Thin Film in Trace Explosive Detection Problem. Molecules 2022, 27, 7939. https://doi.org/10.3390/molecules27227939
Kudryashova OB, Titov SS. A Mathematical Model for Sublimation of a Thin Film in Trace Explosive Detection Problem. Molecules. 2022; 27(22):7939. https://doi.org/10.3390/molecules27227939
Chicago/Turabian StyleKudryashova, Olga B., and Sergey S. Titov. 2022. "A Mathematical Model for Sublimation of a Thin Film in Trace Explosive Detection Problem" Molecules 27, no. 22: 7939. https://doi.org/10.3390/molecules27227939
APA StyleKudryashova, O. B., & Titov, S. S. (2022). A Mathematical Model for Sublimation of a Thin Film in Trace Explosive Detection Problem. Molecules, 27(22), 7939. https://doi.org/10.3390/molecules27227939







