Mn2 Dimers Encapsulated in Silicon Cages: A Complex Challenge to MC-SCF Theory
Abstract
1. Introduction
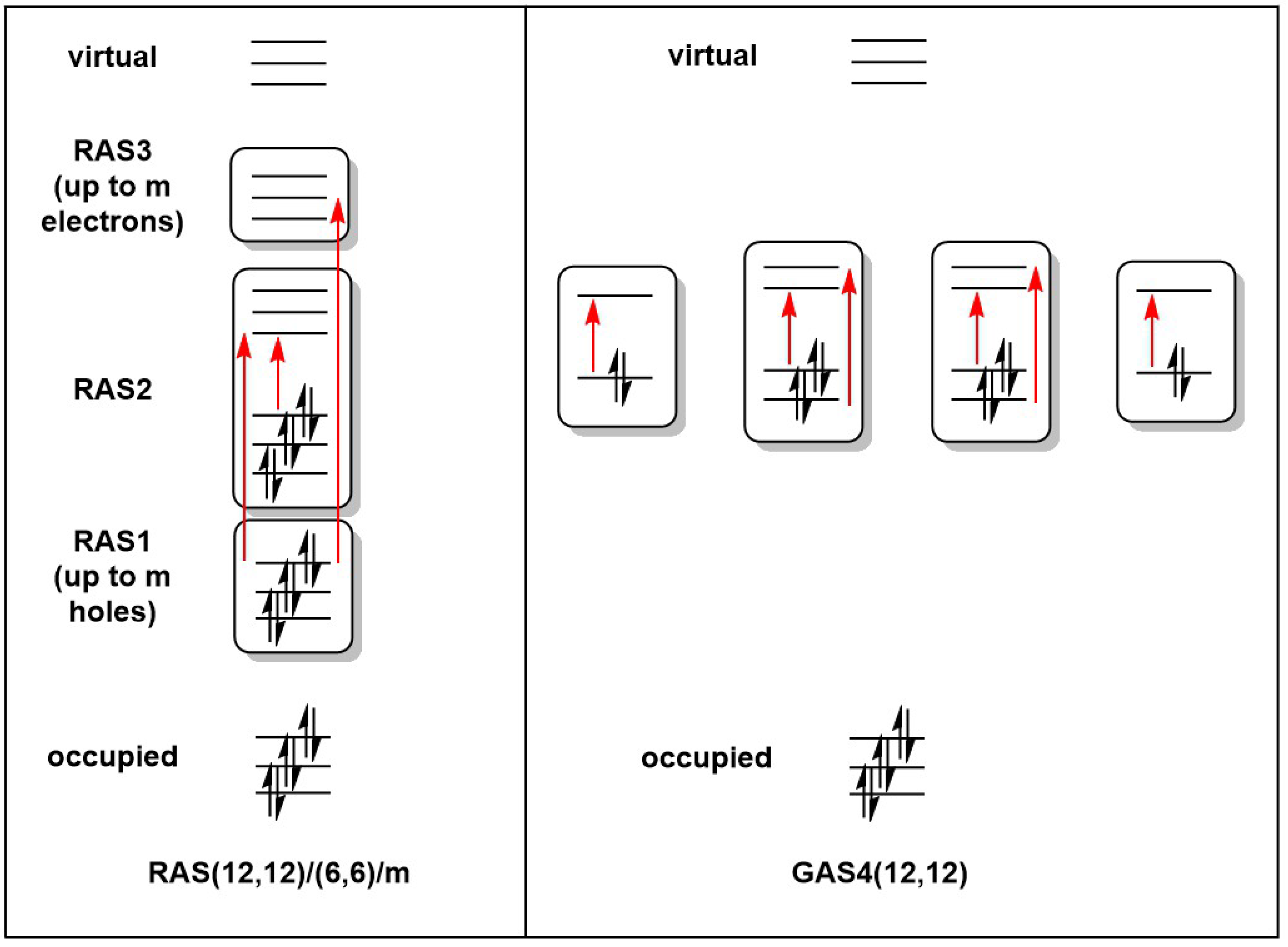
2. Materials and Methods
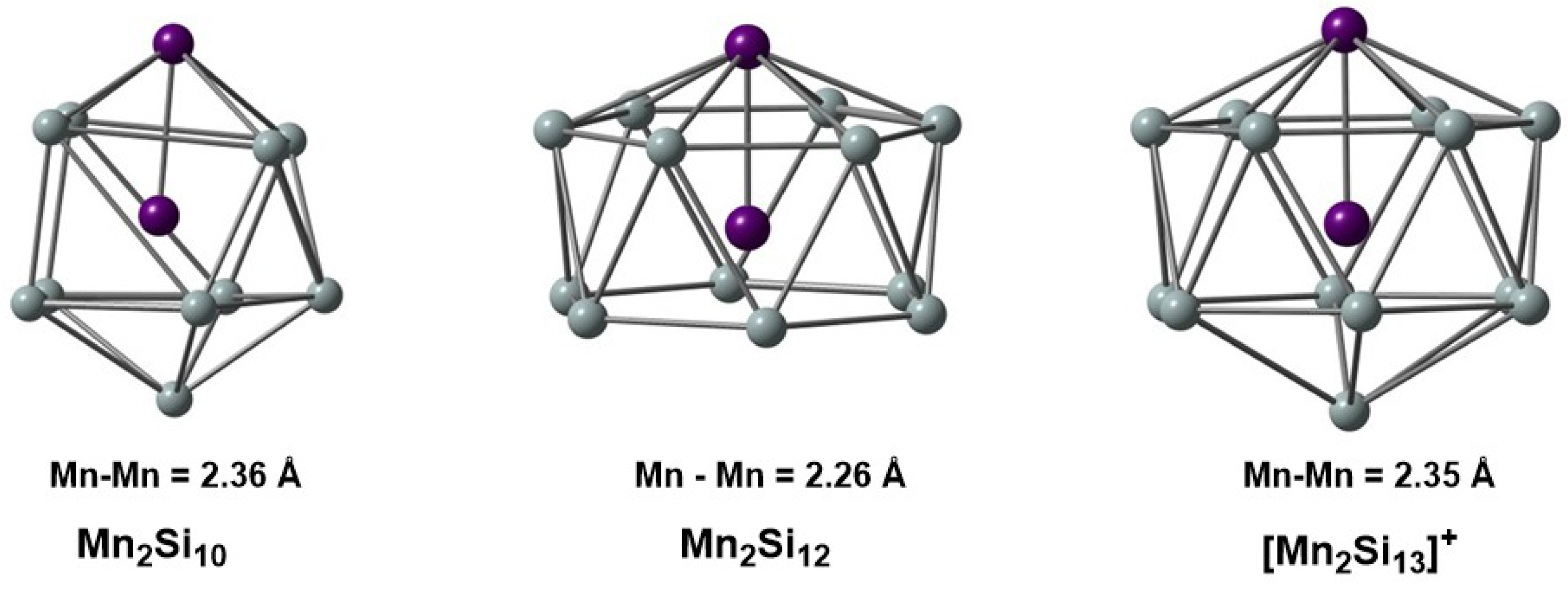
3. Results
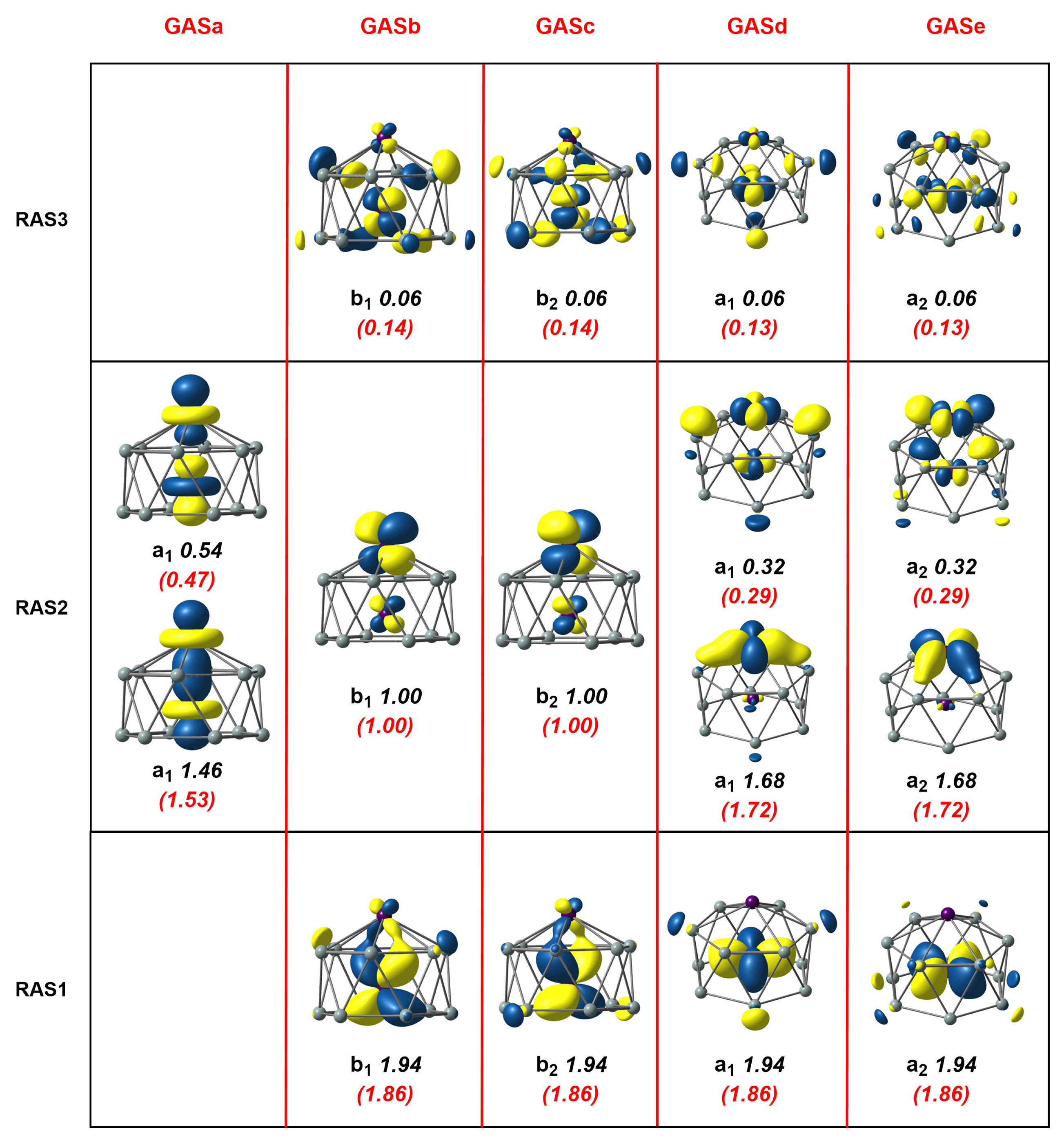
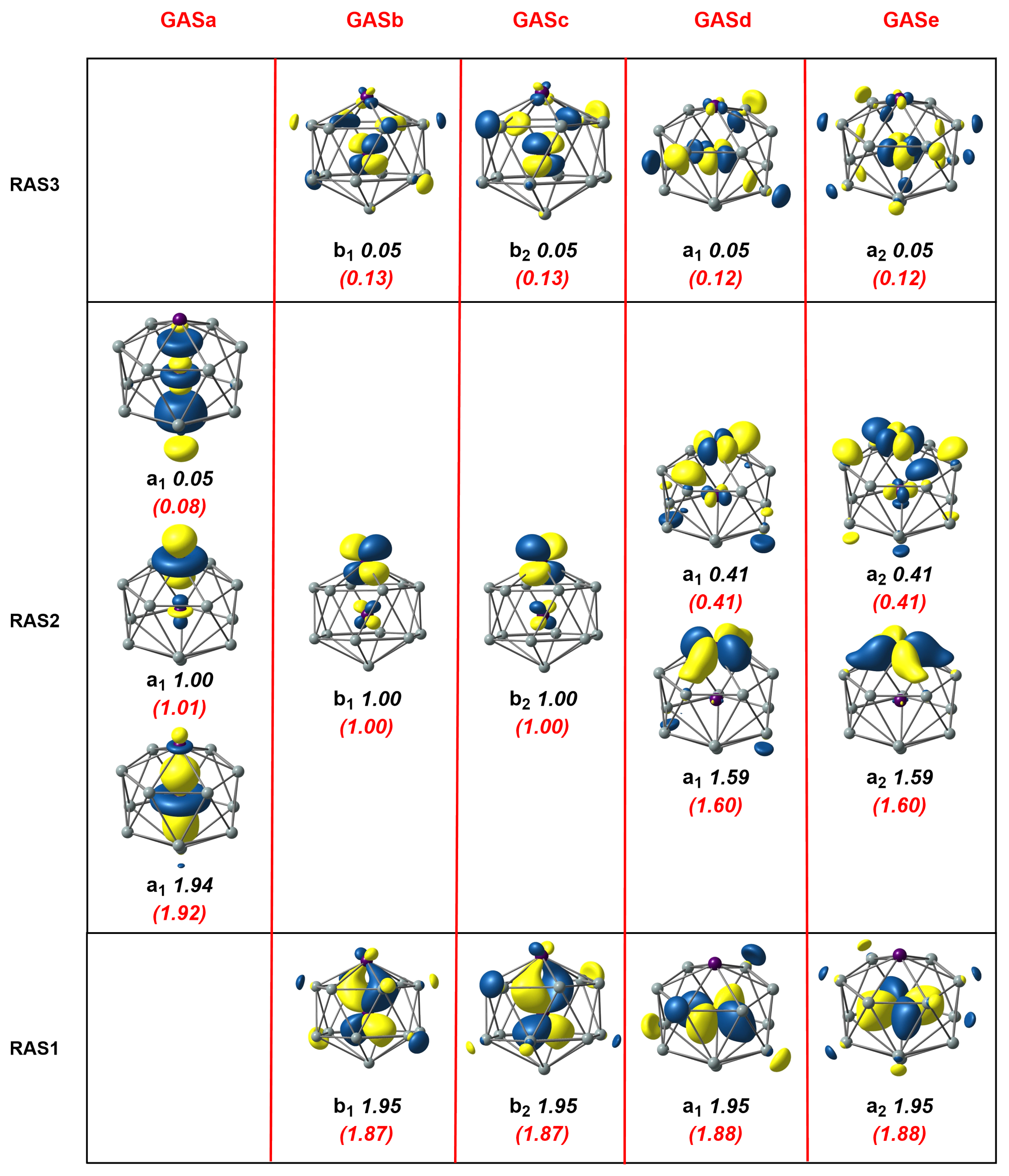
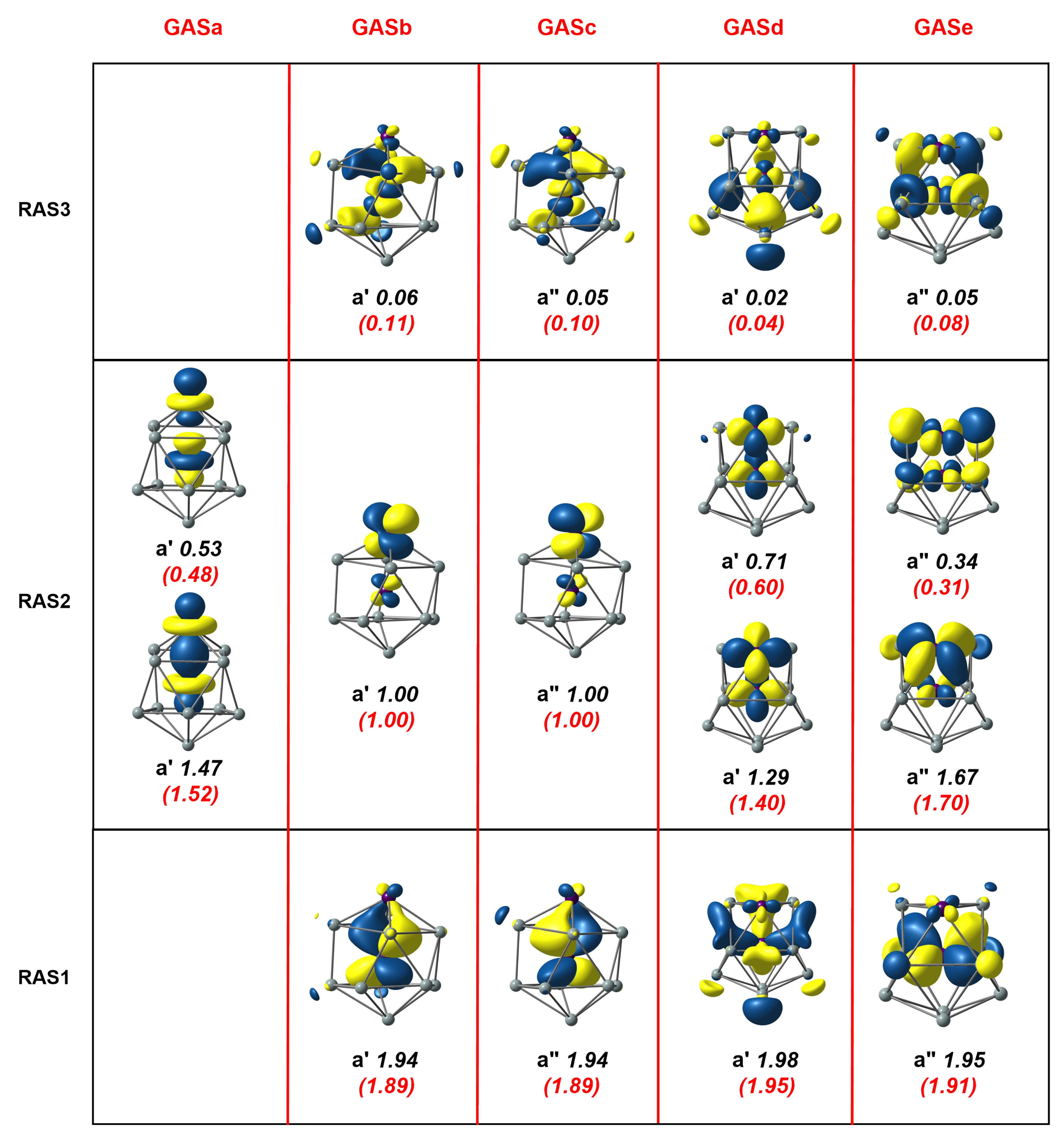
3.1. Mn2Si12
3.2. [Mn2Si13]+
3.3. Mn2Si10
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| MC-SCF | Multiconfigurational Self-Consistent Field |
References
- Kumar, V.; Kawazoe, Y. Metal-encapsulated fullerene-like and cubic caged clusters of silicon. Phys. Rev. Lett. 2001, 87, 045503. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Kawazoe, Y. Metal-encapsulated caged clusters of germanium with large gaps and different growth behavior than silicon. Phys. Rev. Lett. 2002, 88, 235504. [Google Scholar] [CrossRef]
- Beck, S.M. Studies of silicon cluster-metal atom compound formation in a supersonic molecular beam. J. Chem. Phys. 1987, 87, 4233–4234. [Google Scholar] [CrossRef]
- Khanna, V.; Singh, R.; Claes, P.; Nguyen, M.T.; Fielicke, A.; Janssens, E.; Lievens, P.; McGrady, J.E. Evolution of vibrational spectra in the manganese–silicon clusters Mn2Sin, n = 10, 12, and 13, and cationic [Mn2Si13]+. J. Phys. Chem. A 2022, 126, 1617–1626. [Google Scholar] [CrossRef]
- Lu, S.J.; Wu, Y.F. The aromatic fullerene-like silicon cage with 12 Si5 pentagons stabilized by a V3 unit. Theor. Chem. Acc. 2020, 139, 116. [Google Scholar] [CrossRef]
- Huang, X.; Lu, S.J.; Liang, X.; Su, Y.; Sai, L.; Zhang, Z.G.; Zhao, J.; Xu, H.G.; Zheng, W. Structures and electronic properties of [V3Sin]− (n = 3–14) clusters: A combined ab initio and experimental study. J. Phys. Chem. C 2015, 119, 10987–10994. [Google Scholar] [CrossRef]
- Pham, H.T.; Phan-Dang, C.T.; Trung, N.T.; Ngan, V.T. Transformation between hexagonal prism and antiprism of the singly and doubly Cr-doped Ge12 clusters. J. Phys. Chem. A 2019, 123, 10721–10729. [Google Scholar] [CrossRef]
- Brynda, M.; Gagliardi, L.; Roos, B.O. Analysing the chromium–chromium multiple bonds using multiconfigurational quantum chemistry. Chem. Phys. Lett. 2009, 471, 1–10. [Google Scholar] [CrossRef]
- Roos, B.O. The ground state potential for the chromium dimer revisited. Coll. Czech. Chem. Comm. 2003, 68, 265–274. [Google Scholar] [CrossRef]
- Andersson, K.; Roos, B.; Malmqvist, P.Å.; Widmark, P.O. The Cr2 potential energy curve studied with multiconfigurational second-order perturbation theory. Chem. Phys. Lett. 1994, 230, 391–397. [Google Scholar] [CrossRef]
- Roos, B.O.; Malmqvist, P.Å.; Gagliardi, L. Exploring the actinide– actinide bond: Theoretical studies of the chemical bond in Ac2, Th2, Pa2, and U2. J. Am. Chem. Soc 2006, 128, 17000–17006. [Google Scholar] [CrossRef]
- Zhang, L.J.; Yang, B.; Li, D.Z.; Farooq, U.; Xu, X.L.; Zheng, W.J.; Xu, H.G. Appearance of V-encapsulated tetragonal prism motifs in [VSi10]− and [VSi11]− clusters. Phys. Chem. Chem. Phys. 2020, 22, 22989–22996. [Google Scholar] [CrossRef]
- Yang, B.; Xu, H.; Xu, X.; Zheng, W. Photoelectron spectroscopy and theoretical study of CrnSi15-n (n = 1–3): Effects of doping Cr atoms on the structural and magnetic properties. J. Phys. Chem. A 2018, 122, 9886–9893. [Google Scholar] [CrossRef]
- Zamudio-Bayer, V.; Leppert, L.; Hirsch, K.; Langenberg, A.; Rittmann, J.; Kossick, M.; Vogel, M.; Richter, R.; Terasaki, A.; Möller, T.; et al. Coordination-driven magnetic-to-nonmagnetic transition in manganese-doped silicon clusters. Phys. Rev. B 2013, 88, 115425. [Google Scholar] [CrossRef]
- Fielicke, A.; von Helden, G.; Meijer, G. Far-infrared of isolated transition metal clusters. Eur. Phys. J. D 2005, 34, 83–88. [Google Scholar] [CrossRef]
- Arcisauskaite, V.; Fijan, D.; Spivak, M.; Graaf, C.D.; McGrady, J.E. Biradical character in the ground state of [Mn@Si12]+: A DFT and CASPT2 study. Phys. Chem. Chem. Phys. 2016, 18, 24006–24014. [Google Scholar] [CrossRef]
- Ngan, V.T.; Gruene, P.; Claes, P.; Janssens, E.; Fielicke, A.; Nguyen, M.T.; Lievens, P. Disparate effects of Cu and V on structures of exohedral transition metal-doped silicon clusters: A combined far-infrared spectroscopic and computational study. J. Am. Chem. Soc. 2010, 132, 15589–15602. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Tran, Q.T.; Tran, V.T. The ground and excited low-lying states of VSi20/-/+ clusters from CASSCF/CASPT2 calculations. Chem. Phys. Lett. 2019, 721, 111–116. [Google Scholar] [CrossRef]
- Tran, V.T.; Tran, X.M.T.; Nguyen, M.T.; Nguyen, H.T.; Tran, Q.T. A new interpretation of the photoelectron spectrum of VSi4− cluster by density functional theory and multiconfigurational CASSCF/CASPT2 calculations. Chem. Phys. Lett. 2017, 690, 140–146. [Google Scholar] [CrossRef]
- Tran, V.T.; Tran, Q.T. The electronic structures of CoGen−/0 (n = 1–3) clusters from multiconfigurational CASSCF/CASPT2 and RASSCF/RASPT2 calculations. J. Phys. Chem. A 2018, 122, 6407–6415. [Google Scholar] [CrossRef]
- Tran, V.T.; Nguyen, M.T.; Tran, Q.T. Computational investigation of the geometrical and electronic structures of VGen−/0 (n = 1–4) clusters by density functional theory and multiconfigurational CASSCF/CASPT2 method. J. Phys. Chem. A 2017, 121, 7787–7796. [Google Scholar] [CrossRef] [PubMed]
- Ngan, V.T.; Pierloot, K.; Nguyen, M.T. Mn@Si14+: A singlet fullerene-like endohedrally doped silicon cluster. Phys. Chem. Chem. Phys. 2013, 15, 5493–5498. [Google Scholar] [CrossRef]
- Malmqvist, P.A.; Rendell, A.; Roos, B.O. The restricted active space self-consistent-field method, implemented with a split graph unitary group approach. J. Phys. Chem. 1990, 94, 5477–5482. [Google Scholar] [CrossRef]
- Ghosh, S.; Cramer, C.J.; Truhlar, D.G.; Gagliardi, L. Generalized-active-space pair-density functional theory: An efficient method to study large, strongly correlated, conjugated systems. Chem. Sci. 2017, 8, 2741–2750. [Google Scholar] [CrossRef]
- Vogiatzis, K.D.; Li Manni, G.; Stoneburner, S.J.; Ma, D.; Gagliardi, L. Systematic expansion of active spaces beyond the CASSCF limit: A GASSCF/SplitGAS benchmark study. J. Chem. Theory Comput. 2015, 11, 3010–3021. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Li Manni, G.; Gagliardi, L. The generalized active space concept in multiconfigurational self-consistent field methods. J. Chem. Phys. 2011, 135, 044128. [Google Scholar] [CrossRef]
- Odoh, S.O.; Manni, G.L.; Carlson, R.K.; Truhlar, D.G.; Gagliardi, L. Separated-pair approximation and separated-pair pair-density functional theory. Chem. Sci. 2016, 7, 2399–2413. [Google Scholar] [CrossRef]
- Morgan, H.W.T.; Csizi, K.S.; Huang, Y.S.; Sun, Z.M.; McGrady, J.E. Open shells in endohedral clusters: Structure and bonding in the [Fe2Ge16]4− anion and comparison to isostructural [Co2Ge16]4−. J. Phys. Chem. A 2021, 125, 4578–4588. [Google Scholar] [CrossRef]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1-118. J. Comp. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
- Fdez Galván, I.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From source code to insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef] [PubMed]
- Aquilante, F.; Autschbach, J.; Baiardi, A.; Battaglia, S.; Borin, V.A.; Chibotaru, L.F.; Conti, I.; De Vico, L.; Delcey, M.; Fernández Galván, I.; et al. Modern quantum chemistry with [Open]Molcas. J. Chem. Phys. 2020, 152, 214117. [Google Scholar] [CrossRef] [PubMed]
- Pierloot, K.; Dumez, B.; Widmark, P.; Roos, B. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theor. Chim. Acta 1995, 90, 87–114. [Google Scholar] [CrossRef]
- Malmqvist, P.Å.; Pierloot, K.; Shahi, A.R.M.; Cramer, C.J.; Gagliardi, L. The restricted active space followed by second-order perturbation theory method: Theory and application to the study of CuO2 and Cu2O2 systems. J. Chem. Phys. 2008, 128, 204109. [Google Scholar] [CrossRef] [PubMed]
| Cluster | ||||||||
|---|---|---|---|---|---|---|---|---|
| PBE | PBE0 | PBE | PBE0 | PBE | PBE0 | PBE | PBE0 | |
| Mn2Si10 | 3.00 | 4.56 | −0.58 | −2.56 | −0.41 | 0.00 | 2.95 | 5.01 |
| Mn2Si12 | 2.83 | 4.24 | −0.22 | −2.73 | −0.61 | 0.49 | 2.53 | 5.05 |
| [Mn2Si13]+ | 3.41 | 4.14 | 0.67 | 2.18 | −1.08 | −3.33 | 4.31 | 6.01 |
| Cluster | HF | RAS | GAS | ||||
|---|---|---|---|---|---|---|---|
| E | CSFs | E | E | CSFs | E | E | |
| Mn2Si10 | −5188.2275 | 1,031,552 | −5188.4276 | 0.2001 | 1,142,494 | −5188.4724 | 0.2449 |
| Mn2Si12 | −5766.0617 | 515,828 | −5766.1772 | 0.1155 | 1,142,494 | −5766.2152 | 0.1535 |
| [Mn2Si13]+ | −6054.6867 | 1,632,392 | −6054.7848 | 0.0981 | 3,469,636 | −6054.8647 | 0.1780 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khanna, V.; McGrady, J.E. Mn2 Dimers Encapsulated in Silicon Cages: A Complex Challenge to MC-SCF Theory. Molecules 2022, 27, 7544. https://doi.org/10.3390/molecules27217544
Khanna V, McGrady JE. Mn2 Dimers Encapsulated in Silicon Cages: A Complex Challenge to MC-SCF Theory. Molecules. 2022; 27(21):7544. https://doi.org/10.3390/molecules27217544
Chicago/Turabian StyleKhanna, Vaibhav, and John Ewart McGrady. 2022. "Mn2 Dimers Encapsulated in Silicon Cages: A Complex Challenge to MC-SCF Theory" Molecules 27, no. 21: 7544. https://doi.org/10.3390/molecules27217544
APA StyleKhanna, V., & McGrady, J. E. (2022). Mn2 Dimers Encapsulated in Silicon Cages: A Complex Challenge to MC-SCF Theory. Molecules, 27(21), 7544. https://doi.org/10.3390/molecules27217544






