Near-Threshold and Resonance Effects in Rotationally Inelastic Scattering of D2O with Normal-H2
Abstract
1. Introduction
2. Results
2.1. Experimental Results
2.1.1. D2O Beam
2.1.2. Normal-H2 Beam
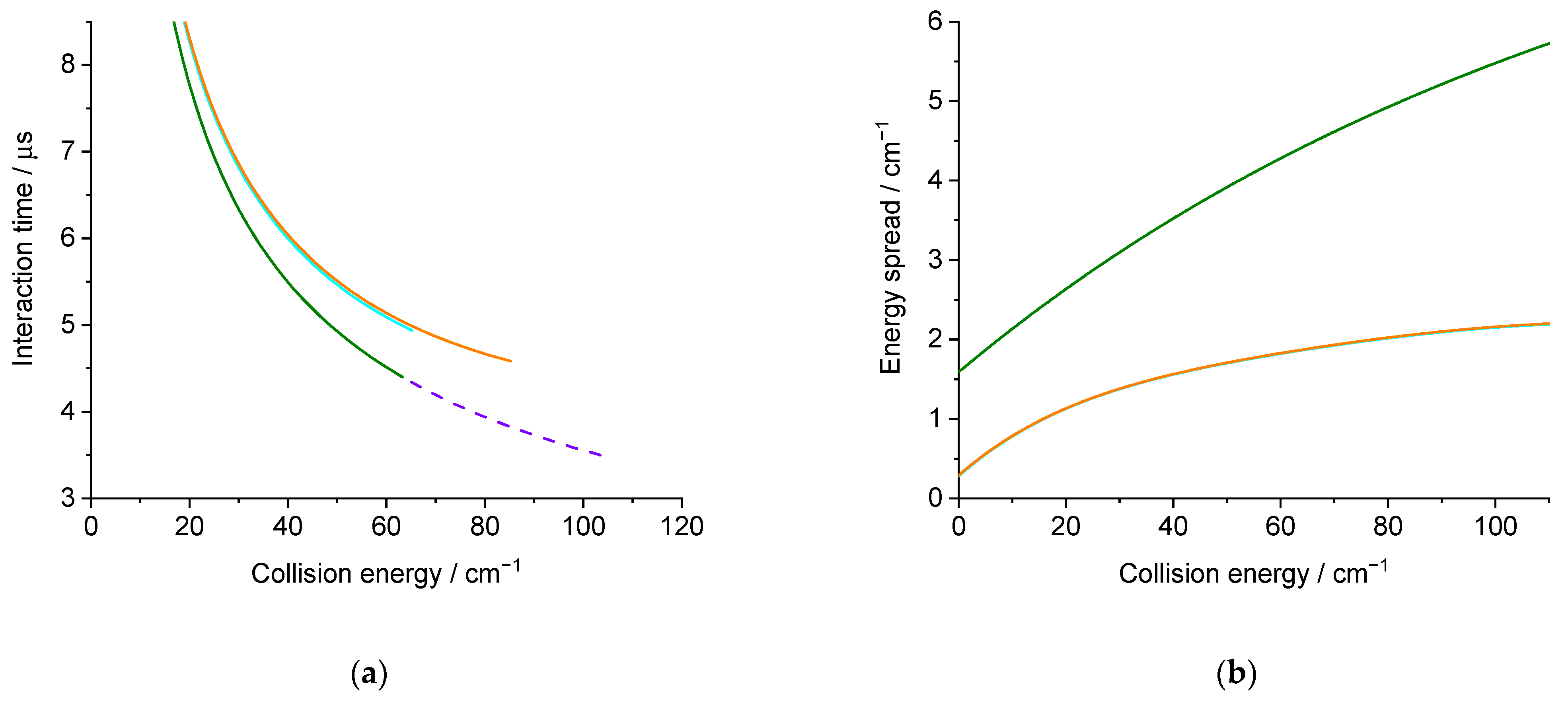
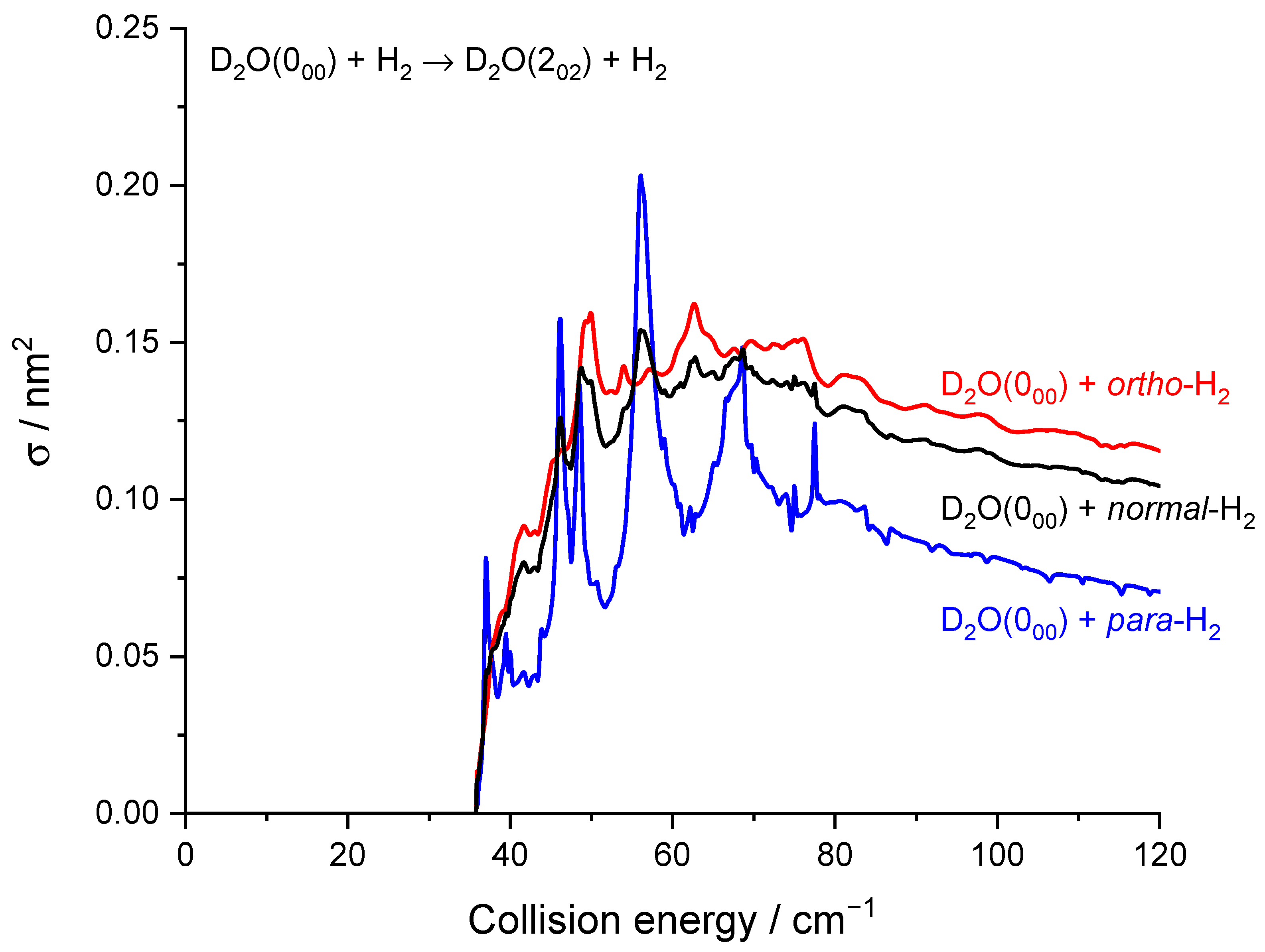
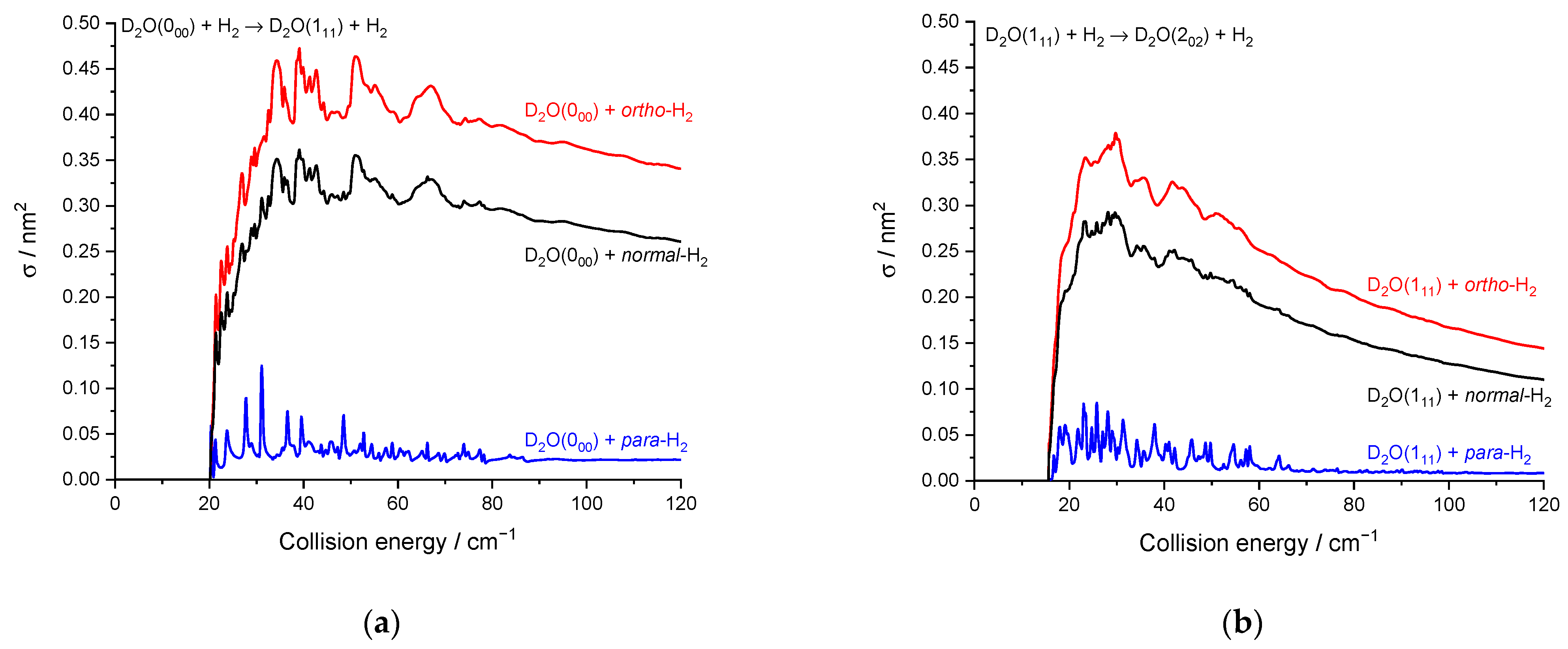
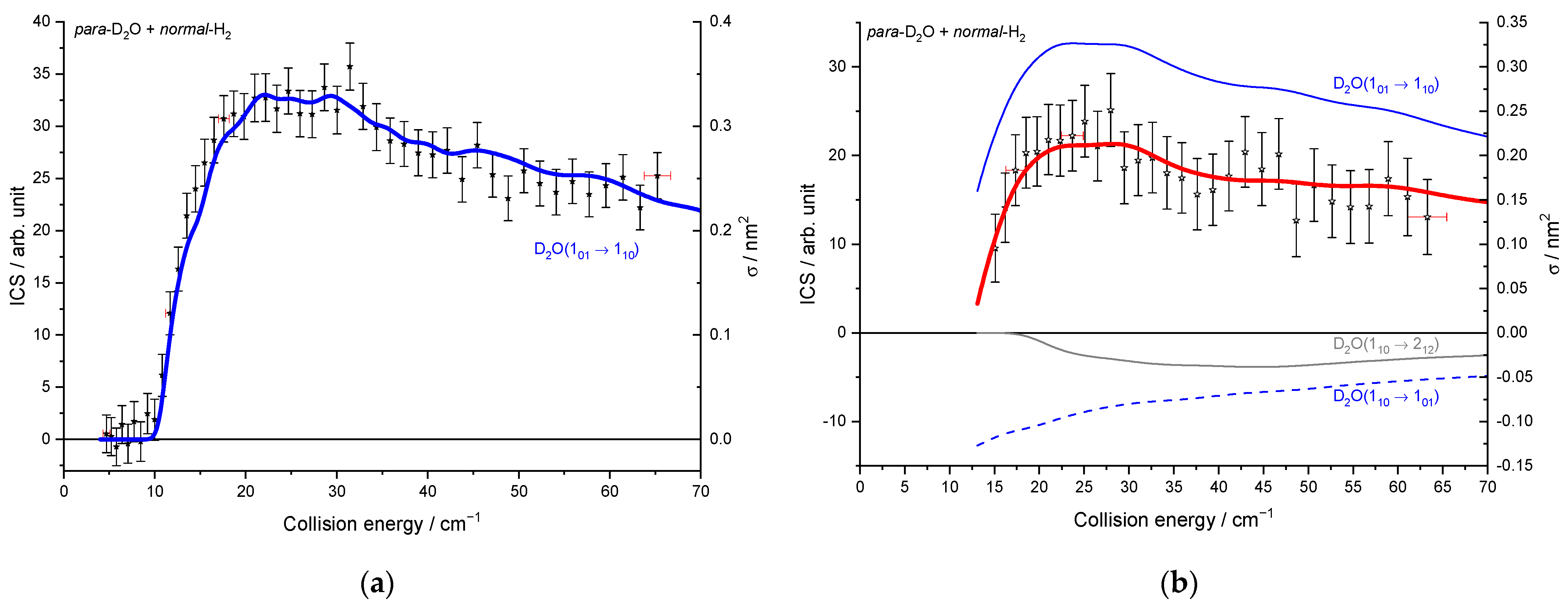
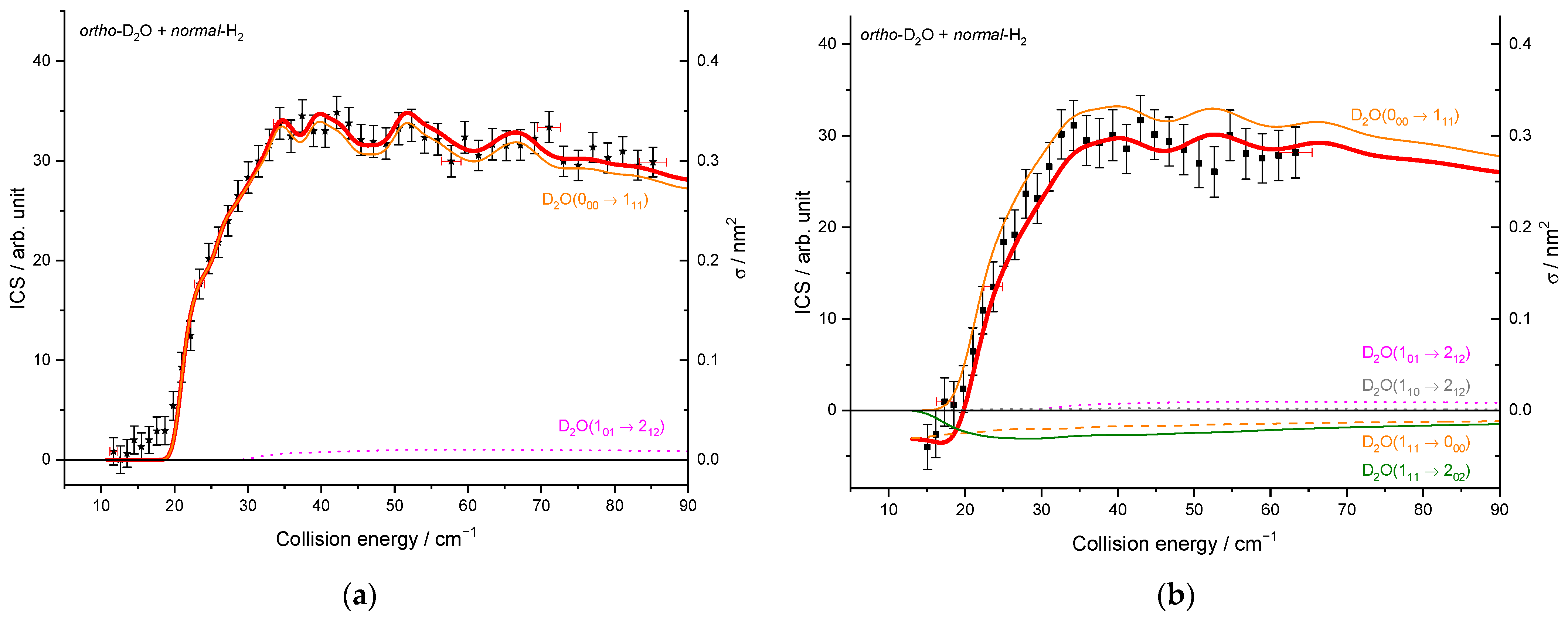
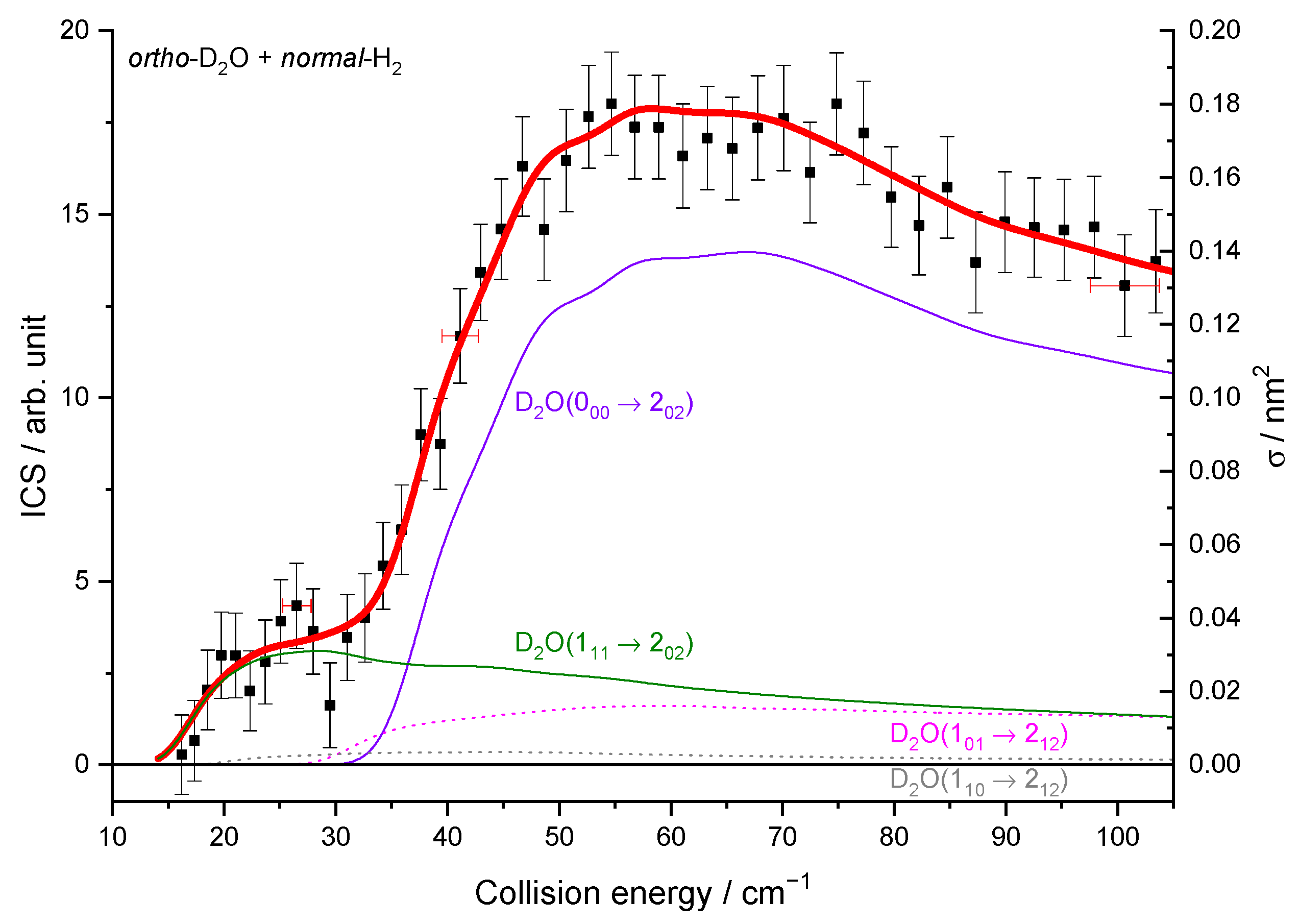
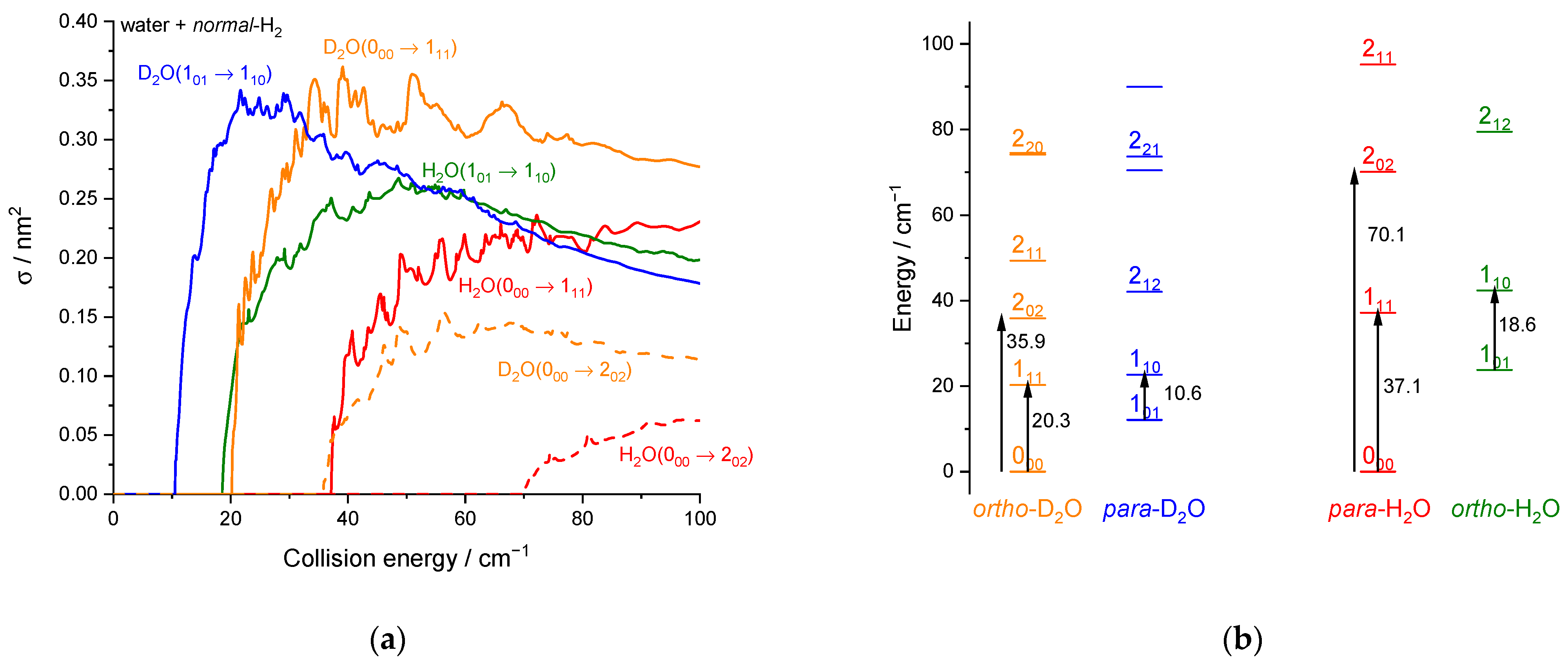
2.1.3. Integral Cross-Sections
2.2. Theoretical Results
3. Discussion
4. Methods
4.1. Theoretical Calculations
4.2. Crossed Molecular Beams
4.2.1. Experimental Procedure
4.2.2. Data Treatment for Comparisons
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Cheung, A.C.; Thornton, D.D.; Rank, D.M.; Welch, W.J.; Townes, C.H. Detection of Water in Interstellar Regions by its Microwave Radiation. Nature 1969, 221, 626–628. [Google Scholar] [CrossRef]
- Van Dishoeck, E.F.; Kristensen, L.E.; Mottram, J.C.; Benz, A.O.; Bergin, E.A.; Caselli, P.; Herpin, F.; Hogerheijde, M.R.; Johnstone, D.; Liseau, R.; et al. Water in star-forming regions: Physics and chemistry from clouds to disks as probed by Herschel spectroscopy. A&A 2021, 648, A24–A57. [Google Scholar] [CrossRef]
- Jensen, S.S.; Jorgensen, J.K.; Furuya, K.; Haugbolle, T.; Aikawa, Y. Modeling chemistry during star formation: Water deuteration in dynamic star-forming regions. A&A 2021, 649, A21–A66. [Google Scholar] [CrossRef]
- Butner, H.M.; Charnley, S.B.; Ceccarelli, C.; Rodgers, S.D.; Pardo, J.R.; Parise, B.; Cernicharo, J.; Davis, G.R. Discovery of interstellar heavy water. Astrophys. J. 2007, 659, L137–L140. [Google Scholar] [CrossRef]
- Vastel, C.; Ceccarelli, C.; Caux, E.; Coutens, A.; Cernicharo, J.; Bottinelli, S.; Demyk, K.; Faure, A.; Wiesenfeld, L.; Scribano, Y.; et al. Ortho-to-para ratio of interstellar heavy water. A&A 2010, 521, L31–L35. [Google Scholar] [CrossRef]
- Levine, R.D.; Bernstein, R.B. Molecular Reaction Dynamics and Chemical Reactivity; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Gordon, I.E.; Rothman, L.S.; Hargreaves, R.J.; Hashemi, R.; Karlovets, E.V.; Skinner, F.M.; Conway, E.K.; Hill, C.; Kochanov, R.V.; Tan, Y.; et al. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- Bergeat, A.; Morales, S.B.; Naulin, C.; Wiesenfeld, L.; Faure, A. Probing Low-Energy Resonances in Water-Hydrogen Inelastic Collisions. Phys. Rev. Lett. 2020, 125, 143402. [Google Scholar] [CrossRef]
- Zoltowski, M.; Lique, F.; Karska, A.; Zuchowski, P.S. Rotational excitation of highly excited H2O by H2. MNRAS 2021, 502, 5356–5361. [Google Scholar] [CrossRef]
- Bickes, R.W., Jr.; Duquette, G.; van den Meijdenberg, C.J.N.; Rulis, A.M.; Scoles, G.; Smith, K.M. Molecular beam scattering experiments with polar molecules: Measurement of differential collision cross sections for H2O+H2, He, Ne, Ar, H2O and NH3+H2, He, NH3. J. Phys. B Atom. Mol. Phys. 1975, 8, 3034–3043. [Google Scholar] [CrossRef]
- Weida, M.J.; Nesbitt, D.J. High-resolution diode laser study of H2–H2O van der Waals complexes: H2O as proton acceptor and the role of large amplitude motion. J. Chem. Phys. 1999, 110, 156–167. [Google Scholar] [CrossRef]
- Ziemkiewicz, M.P.; Pluetzer, C.; Nesbitt, D.J.; Scribano, Y.; Faure, A.; van der Avoird, A. Overtone vibrational spectroscopy in H2-H2O complexes: A combined high level theoretical ab initio, dynamical and experimental study. J. Chem. Phys. 2012, 137, 084301. [Google Scholar] [CrossRef] [PubMed]
- Forney, D.; Jacox, M.E.; Thompson, W.E. Infrared absorptions of the H2O-H2 complex trapped in solid neon. J. Chem. Phys. 2004, 121, 5977–5984. [Google Scholar] [CrossRef] [PubMed]
- Dutta, J.M.; Jones, C.R.; Goyette, T.M.; de Lucia, F.C. The Hydrogen and Helium Pressure Broadening at Planetary Temperatures of the 183 and 380 GHz Transitions of Water Vapor. Icarus 1993, 102, 232–239. [Google Scholar] [CrossRef]
- Drouin, B.; Wiesenfeld, L. Low-temperature water–hydrogen-molecule collisions probed by pressure broadening and line shift. Phys. Rev. A 2012, 86, 022705. [Google Scholar] [CrossRef]
- Yang, C.-H.; Sarma, G.; Parker, D.H.; ter Meulen, J.J.; Wiesenfeld, L. State-to-state differential and relative integral cross sections for rotationally inelastic scattering of H2O by hydrogen. J. Chem. Phys. 2011, 134, 204308. [Google Scholar] [CrossRef]
- Bergeat, A.; Faure, A.; Morales, S.B.; Moudens, A.; Naulin, C. Low-Energy Water−Hydrogen Inelastic Collisions. J. Phys. Chem. A 2020, 124, 259–264. [Google Scholar] [CrossRef]
- Belpassi, L.; Reca, M.L.; Tarantelli, F.; Roncaratti, L.F.; Pirani, F.; Cappelletti, D.; Faure, A.; Scribano, Y. Charge-Transfer Energy in the Water-Hydrogen Molecular Aggregate Revealed by Molecular-Beam Scattering Experiments, Charge Displacement Analysis, and ab Initio Calculations. J. Am. Chem. Soc. 2010, 132, 13046–13058. [Google Scholar] [CrossRef]
- van der Avoird, A.; Scribano, Y.; Faure, A.; Weida, M.J.; Fair, J.R.; Nesbitt, D.J. Intermolecular potential and rovibrational states of the H2O–D2 complex. Chem. Phys. 2012, 399, 28–38. [Google Scholar] [CrossRef]
- Scribano, Y.; Faure, A.; Wiesenfeld, L. Communication: Rotational excitation of interstellar heavy water by hydrogen molecules. J. Chem. Phys. 2010, 133, 231105. [Google Scholar] [CrossRef]
- Faure, A.; Wiesenfeld, L.; Scribano, Y.; Ceccarelli, C. Rotational excitation of mono- and doubly-deuterated water by hydrogen molecules. MNRAS 2012, 420, 699–704. [Google Scholar] [CrossRef][Green Version]
- Valiron, P.; Wernli, M.; Faure, A.; Wiesenfeld, L.; Rist, C.; Kedzuch, S.; Noga, J. R12-calibrated H2O-H2 interaction: Full dimensional and vibrationally averaged potential energy surfaces. J. Chem. Phys. 2008, 129, 134306-14. [Google Scholar] [CrossRef] [PubMed]
- Sarma, G.; Yang, C.-H.; Saha, A.K.; Parker, D.H.; Wiesenfeld, L. Rotational excitation of HDO and D2O by H2: Experimental and theoretical differential cross-sections. J. Chem. Phys. 2013, 138, 024314. [Google Scholar] [CrossRef] [PubMed]
- Bergeat, A.; Morales, S.B.; Naulin, C.; Klos, J.; Lique, F. Quantum Behavior of Spin-Orbit Inelastic Scattering of C-Atoms by D2 at Low Energy. Front. Chem. 2019, 7, 164. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.-H.; Sarma, G.; ter Meulen, J.J.; Parker, D.H.; Western, C.M. REMPI spectroscopy and predissociation of the C1B1(v = 0) rotational levels of H2O, HOD and D2O. Phys. Chem. Chem. Phys. 2010, 12, 13983–13991. [Google Scholar] [CrossRef]
- Western, C.M. PGOPHER, A Program for Simulating Rotational, Vibrational and Electronic Spectra. J. Quant. Spectrosc. Radiat. Trans. 2017, 186, 221–242. [Google Scholar] [CrossRef]
- Ziemkiewicz, M.P.; Pluetzer, C.; Wojcik, M.; Loreau, J.; van der Avoird, A.; Nesbitt, D.J. Near infrared overtone (νOH = 2 ← 0) spectroscopy of Ne-H2O clusters. J. Chem. Phys. 2017, 146, 104204. [Google Scholar] [CrossRef]
- Hou, D.; Ma, Y.-T.; Zhang, X.-L.; Li, H. A full-dimension intra- and inter-molecular ab initio potential energy surface and predicted infrared spectra for H2O-He. J. Mol. Spectrosc. 2016, 330, 217–227. [Google Scholar] [CrossRef]
- Pratt, S.T.; Dehmer, P.M.; Dehmer, J.L. Photoionization of excited molecular states. H2 C1Πu. Chem. Phys. Lett. 1984, 105, 28. [Google Scholar] [CrossRef]
- Ma, Q.; van der Avoird, A.; Loreau, J.; Alexander, M.H.; van de Meerakker, S.Y.T.; Dagdigian, P.J. Resonances in rotationally inelastic scattering of NH3 and ND3 with H2. J. Chem. Phys. 2015, 143, 044312. [Google Scholar] [CrossRef]
- van der Avoird, A.; Nesbitt, D.J. Rovibrational states of the H2O–H2 complex: An ab initio calculation. J. Chem. Phys. 2011, 134, 044314. [Google Scholar] [CrossRef]
- Hutson, J.M.; Green, S. MOLSCAT: MOLecular SCATtering; Version 14; Astrophysics Source Code Library: Houghton, MI, USA, 2012; Available online: https://ui.adsabs.harvard.edu/abs/2012ascl.soft06004H/abstract (accessed on 20 September 2022).
- Harvey, A.H.; Lemmon, E.W. Correlation for the Vapor Pressure of Heavy Water from the Triple Point to the Critical Point. J. Phys. Chem. Ref. Data 2002, 31, 173–181. [Google Scholar] [CrossRef]
- Naulin, C.; Bergeat, A. Low-energy Scattering in Crossed Molecular Beams. In Book Cold Chemistry: Molecular Scattering and Reactivity Near Absolute Zero; Osterwalder, A., Dulieu, O., Eds.; The Royal Society of Chemistry: London, UK, 2018; pp. 92–149. [Google Scholar]
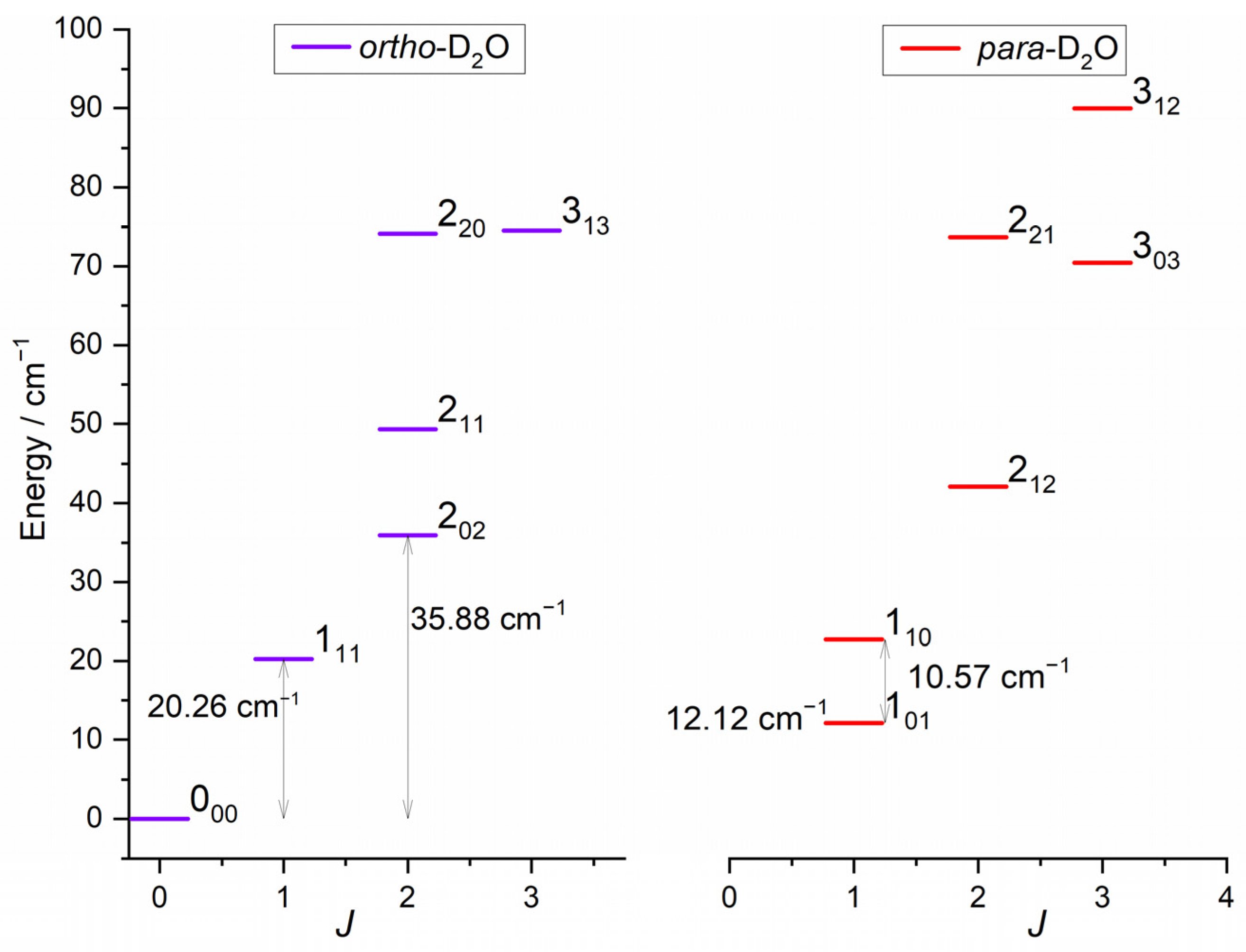
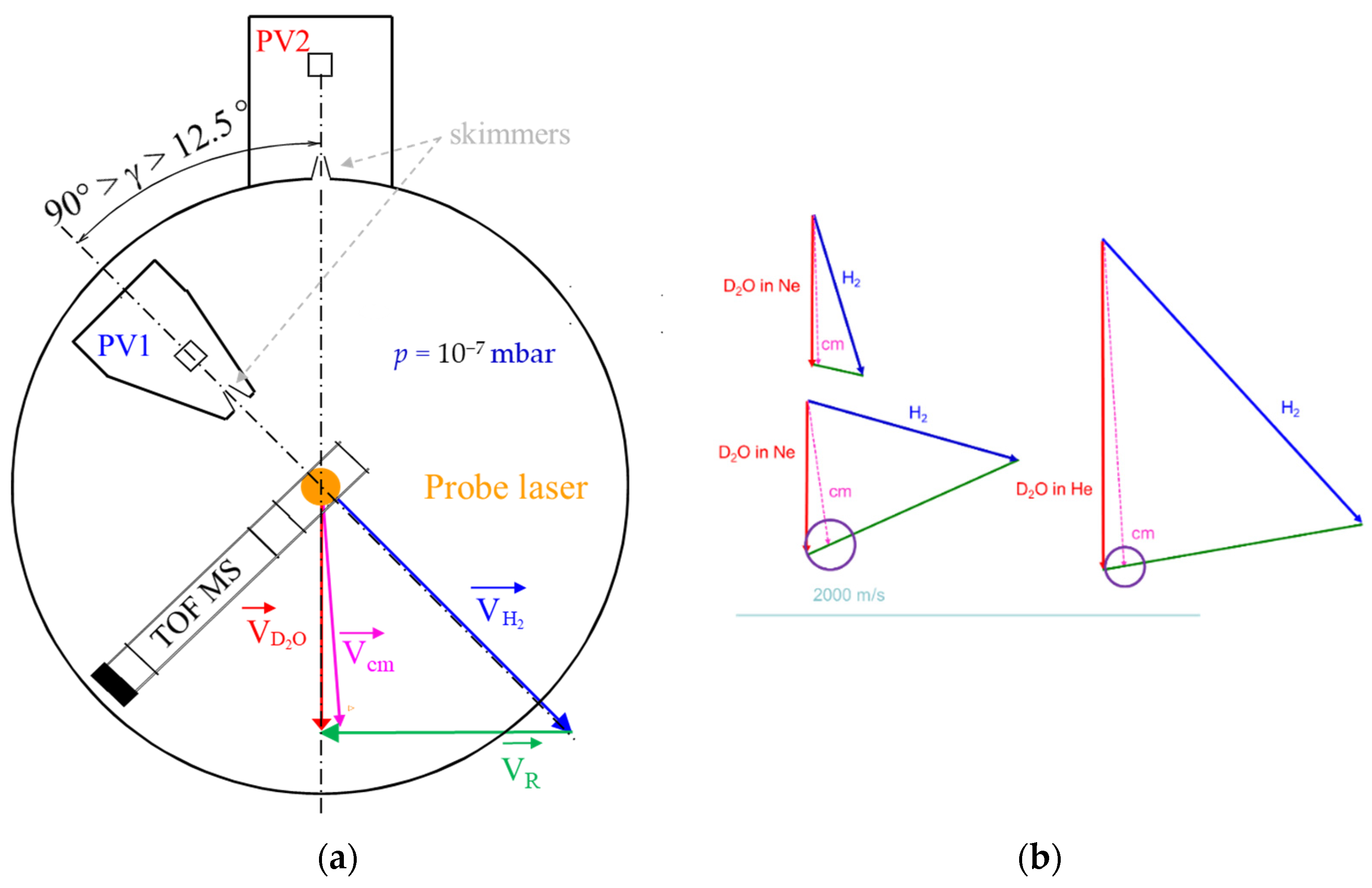
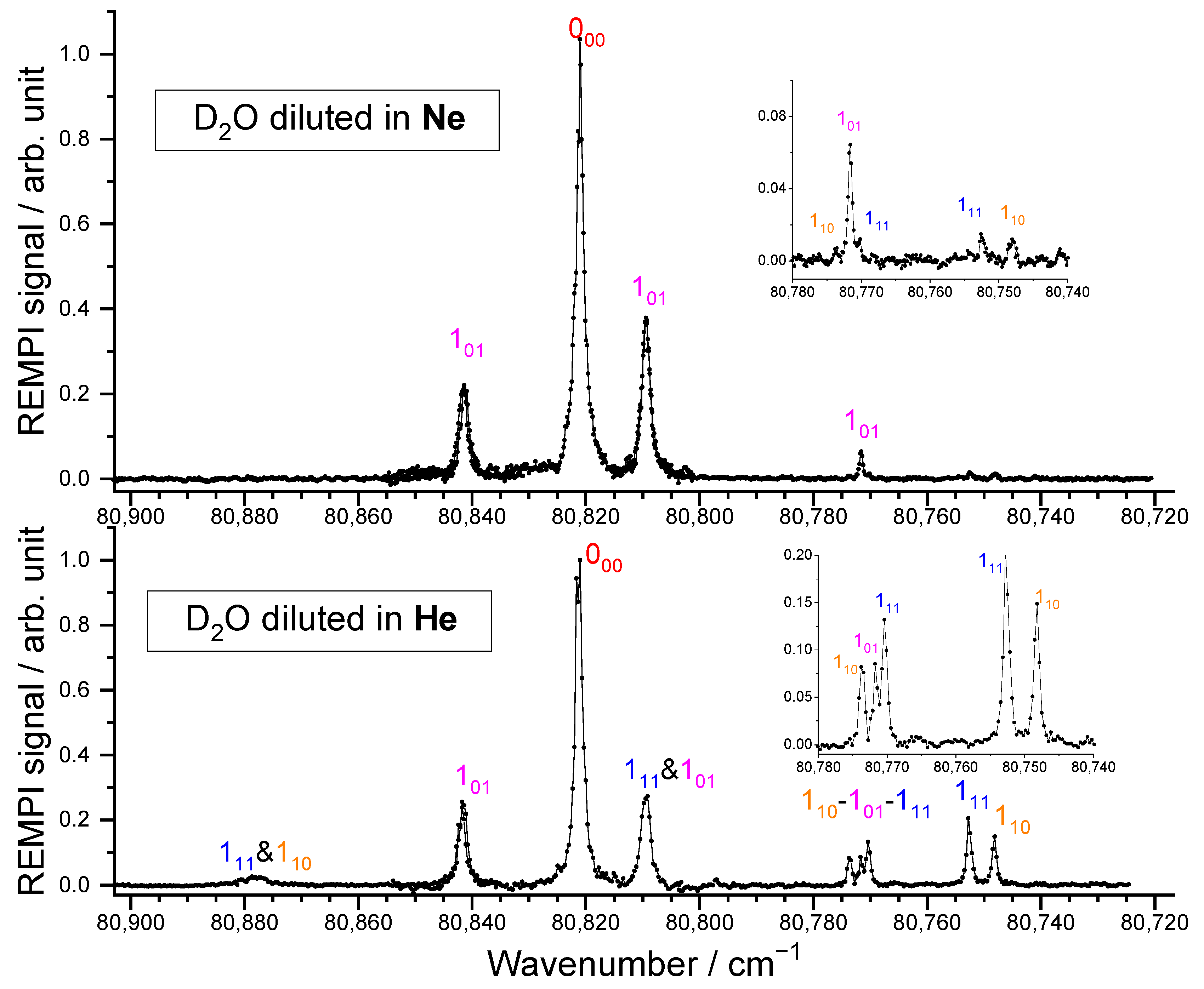
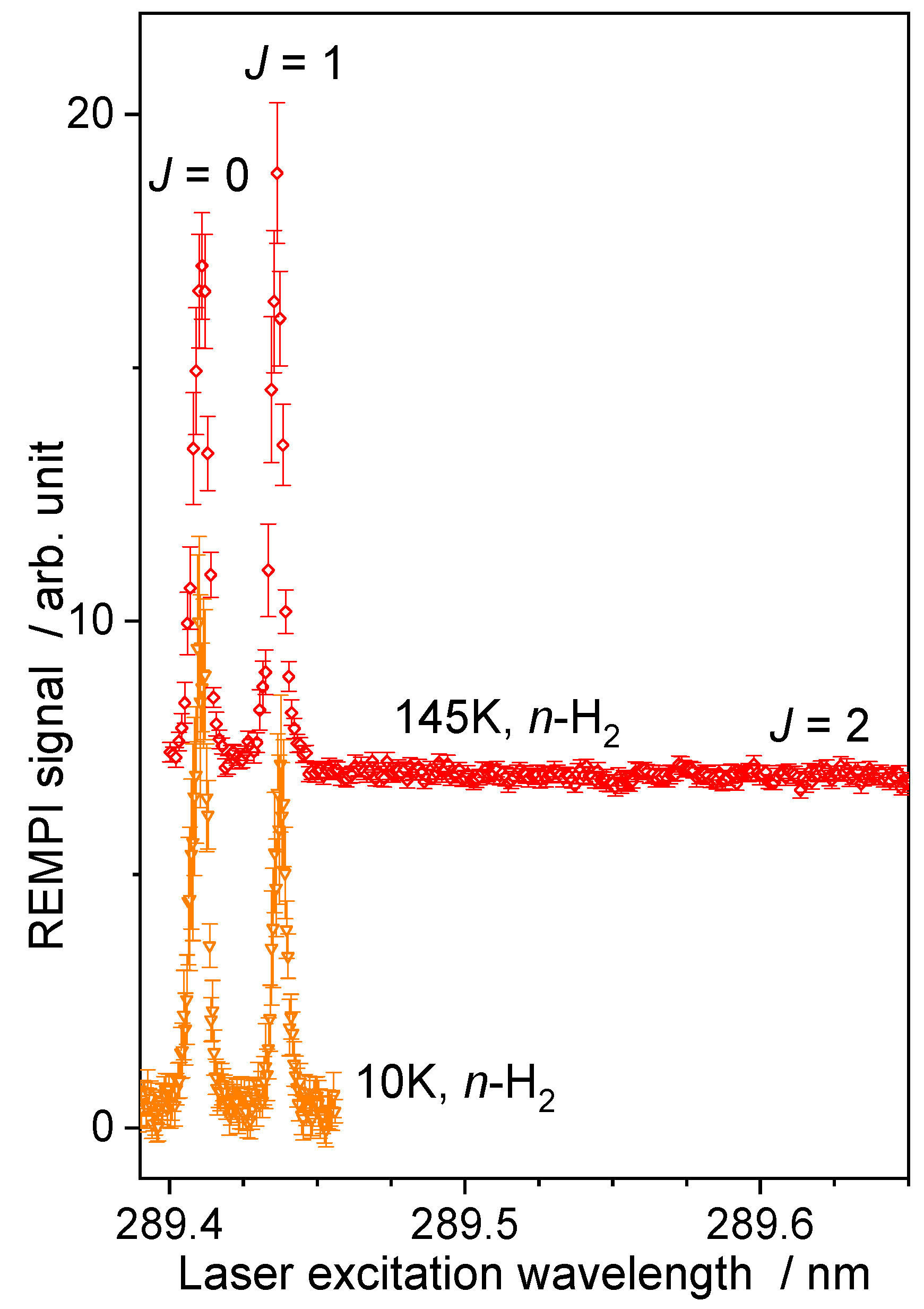


| Beam | Velocity 1 /m s−1 | Velocity Spread 1 HWHM/m s−1 | Pulse Duration 2 HWHM/µs | Angle Spread 3 HWHM/° |
|---|---|---|---|---|
| D2O in He | 1858 ± 30 | 44 | 15.0 | 0.79 |
| normal-H2 at 145 K | 1959 ± 30 | 44 | 7.9 | 1.17 |
| D2O in Ne | 853 ± 24 | 14 | 19.3 | 0.71 |
| normal-H2 at 10 K | 947 ± 28 | 49 | 11.5 | 1.17 |
| Contributions | D2O in He | D2O in Ne |
|---|---|---|
| ortho-D2O:para-D2O 1 | 2/3:1/3 | 2/3:1/3 |
| 000:111 2 | 90:10 | 100:0 |
| 101:110 2 | 83:17 | 100:0 |
| 212 in 202 3 | 0.20 | |
| 212 in 111 3 | 0.12 | 0.12 |
| D2O(jkakc) | Wavelength | n Laser Shots/Angle | Intersection Angles |
|---|---|---|---|
| 202 | 247.340 nm | 2275 | 35°–13° (−0.5°) |
| 111 with D2O in Ne | 247.670 nm | 3585 | 70°–23°(−1°) |
| 111 with D2O in He | 247.670 nm | 3691 | 27°–12.5°(−0.5°) |
| 110 with D2O in Ne | 247.684 nm | 2482 | 60°–13°(−1°) |
| 110 with D2O in He | 247.684 nm | 2684 | 27°–12.5°(−0.5°) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergeat, A.; Faure, A.; Wiesenfeld, L.; Miossec, C.; Morales, S.B.; Naulin, C. Near-Threshold and Resonance Effects in Rotationally Inelastic Scattering of D2O with Normal-H2. Molecules 2022, 27, 7535. https://doi.org/10.3390/molecules27217535
Bergeat A, Faure A, Wiesenfeld L, Miossec C, Morales SB, Naulin C. Near-Threshold and Resonance Effects in Rotationally Inelastic Scattering of D2O with Normal-H2. Molecules. 2022; 27(21):7535. https://doi.org/10.3390/molecules27217535
Chicago/Turabian StyleBergeat, Astrid, Alexandre Faure, Laurent Wiesenfeld, Chloé Miossec, Sébastien B. Morales, and Christian Naulin. 2022. "Near-Threshold and Resonance Effects in Rotationally Inelastic Scattering of D2O with Normal-H2" Molecules 27, no. 21: 7535. https://doi.org/10.3390/molecules27217535
APA StyleBergeat, A., Faure, A., Wiesenfeld, L., Miossec, C., Morales, S. B., & Naulin, C. (2022). Near-Threshold and Resonance Effects in Rotationally Inelastic Scattering of D2O with Normal-H2. Molecules, 27(21), 7535. https://doi.org/10.3390/molecules27217535






