Transformation Kinetics of LiBH4–MgH2 for Hydrogen Storage
Abstract
1. Introduction
2. Results and Discussion
2.1. Material Characterization by XRD and Kinetic Performance
2.2. Observation of MgB2 Using TEM
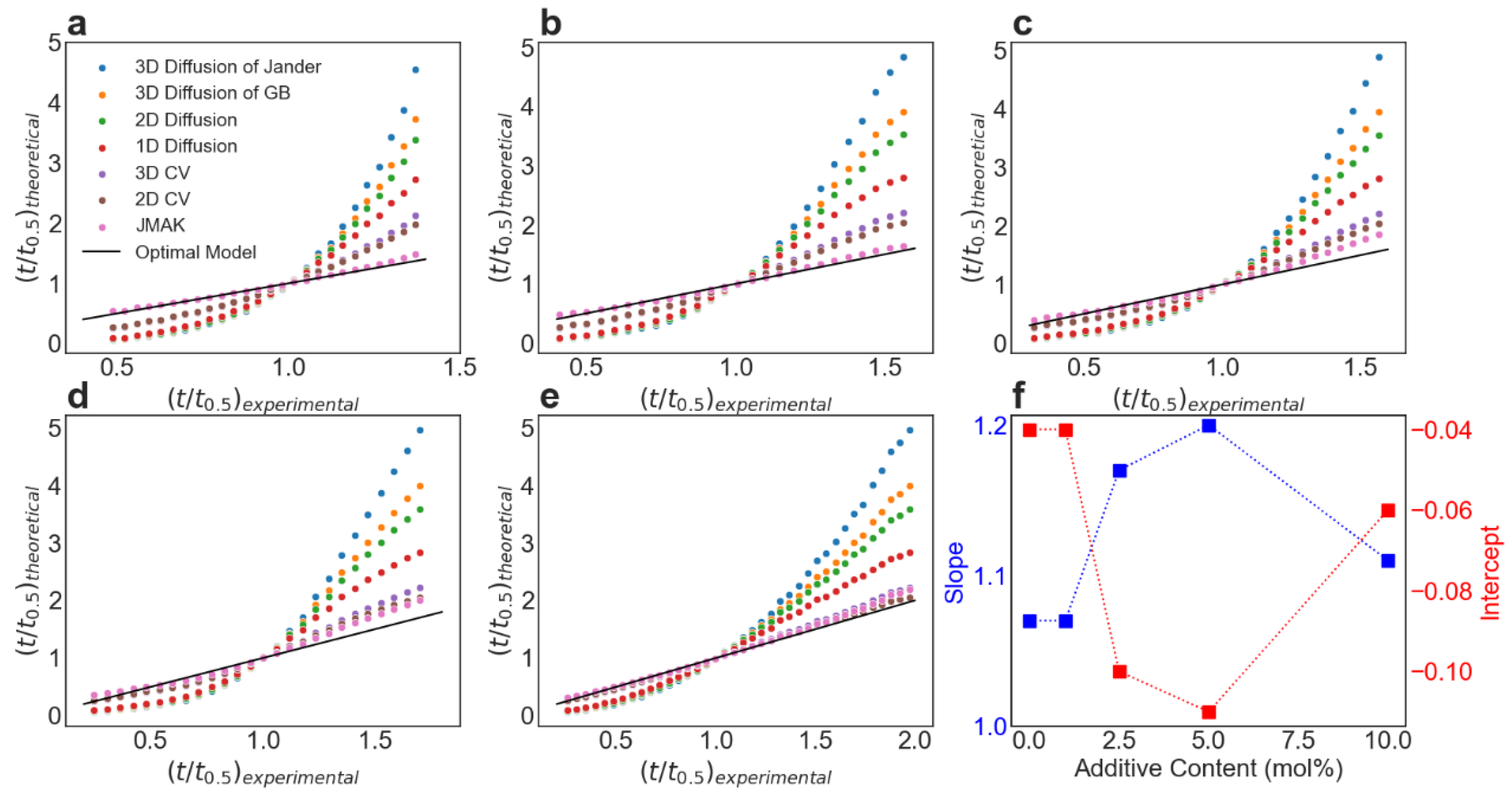
2.3. Kinetic Modeling
3. Materials and Methods
3.1. Material Preparations
3.2. Kinetics Measurements
3.3. XRD Experiments
3.4. TEM Experiments
4. Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Twidell, J. Renewable Energy Resource; Routledge: London, UK, 2021. [Google Scholar]
- von Colbe, J.B.; Ares, J.R.; Barale, J.; Baricco, M.; Buckley, C.; Capurso, G.; Gallandat, N.; Grant, D.M.; Guzik, M.N.; Jacob, I.; et al. Application of hydrides in hydrogen storage and compression: Achievements, outlook and perspectives. Int. J. Hydrogen Energy 2019, 44, 7780–7808. [Google Scholar] [CrossRef]
- Yu, X.; Tang, Z.; Sun, D.; Ouyang, L.; Zhu, M. Recent advances and remaining challenges of nanostructured materials for hydrogen storage applications. Prog. Mater. Sci. 2017, 88, 1–48. [Google Scholar] [CrossRef]
- Pistidda, C. Solid-State Hydrogen Storage for a Decarbonized Society. Hydrogen 2021, 2, 428–443. [Google Scholar] [CrossRef]
- Züttel, A. Hydrogen storage methods. Naturwissenschaften 2004, 91, 157–172. [Google Scholar] [CrossRef] [PubMed]
- Rivard, E.; Trudeau, M.; Zaghib, K. Hydrogen Storage for Mobility: A Review. Materials 2019, 12, 1973. [Google Scholar] [CrossRef] [PubMed]
- Rusman, N.; Dahari, M. A review on the current progress of metal hydrides material for solid-state hydrogen storage applications. Int. J. Hydrogen Energy 2016, 41, 12108–12126. [Google Scholar] [CrossRef]
- Milanese, C.; Jensen, T.R.; Hauback, B.C.; Pistidda, C.; Dornheim, M.; Yange, H.; Lombardoe, L.; Zuettele, A.; Filinchuk, Y.; Ngene, P.; et al. Complex hydrides for energy storage. Int. J. Hydrogen Energy 2019, 44, 7860–7874. [Google Scholar] [CrossRef]
- Jepsen, J.; Milanese, C.; Puszkiel, J.; Girella, A.; Schiavo, B.; Lozano, G.A.; Capurso, G.; von Colbe, J.M.B.; Marini, A.; Kabelac, S.; et al. Fundamental Material Properties of the 2LiBH4-MgH2 Reactive Hydride Composite for Hydrogen Storage: (I) Thermodynamic and Heat Transfer Properties. Energies 2018, 11, 1081. [Google Scholar] [CrossRef]
- Jepsen, J.; Milanese, C.; Puszkiel, J.; Girella, A.; Schiavo, B.; Lozano, G.A.; Capurso, G.; von Colbe, J.M.B.; Marini, A.; Kabelac, S.; et al. Fundamental Material Properties of the 2LiBH4-MgH2 Reactive Hydride Composite for Hydrogen Storage: (II) Kinetic Properties. Energies 2018, 11, 1170. [Google Scholar] [CrossRef]
- Vajo, J.J.; Skeith, S.L.; Mertens, F. Reversible Storage of Hydrogen in Destabilized LiBH4. J. Phys. Chem. B 2005, 109, 3719–3722. [Google Scholar] [CrossRef]
- Vajo, J.J.; Olson, G.L. Hydrogen storage in destabilized chemical systems. Scr. Mater. 2007, 56, 829–834. [Google Scholar] [CrossRef]
- Mauron, P.; Buchter, F.; Friedrichs, O.; Remhof, A.; Bielmann, M.; Zwicky, C.N.; Züttel, A. Stability and reversibility of LiBH4. J. Phys. Chem. B 2008, 112, 906–910. [Google Scholar] [CrossRef] [PubMed]
- Bösenberg, U.; Doppiu, S.; Mosegaard, L.; Barkhordarian, G.; Eigen, N.; Borgschulte, A.; Jensen, T.R.; Cerenius, Y.; Gutfleisch, O.; Klassen, T.; et al. Hydrogen sorption properties of MgH2–LiBH4 composites. Acta Mater. 2007, 55, 3951–3958. [Google Scholar] [CrossRef]
- Vajo, J.J.; Salguero, T.T.; Gross, A.F.; Skeith, S.L.; Olson, G.L. Thermodynamic destabilization and reaction kinetics in light metal hydride systems. J. Alloys Compd. 2007, 446-447, 409–414. [Google Scholar] [CrossRef]
- Bösenberg, U.; Ravnsbæk, D.B.; Hagemann, H.; D’Anna, V.; Minella, C.B.; Pistidda, C.; van Beek, W.; Jensen, T.R.; Bormann, R.; Dornheim, M. Pressure and temperature influence on the desorption pathway of the LiBH4−MgH2 composite system. J. Phys. Chem. C 2010, 114, 15212–15217. [Google Scholar] [CrossRef]
- Shao, H.; Felderhoff, M.; Weidenthaler, C. Kinetics enhancement, reaction pathway change, and mechanism clarification in LiBH4 with Ti-catalyzed nanocrystalline MgH2 composite. J. Phys. Chem. C 2015, 119, 2341–2348. [Google Scholar] [CrossRef]
- Bösenberg, U.; Kim, J.; Gosslar, D.; Eigen, N.; Jensen, T.R.; Von Colbe, J.B.; Zhou, Y.; Dahms, M.; Kim, D.; Gunther, R.; et al. Role of additives in LiBH4–MgH2 reactive hydride composites for sorption kinetics. Acta Mater. 2010, 58, 3381–3389. [Google Scholar] [CrossRef]
- Jin, O.; Shang, Y.; Huang, X.; Mu, X.; Szabó, D.V.; Le, T.T.; Wagner, S.; Kübel, C.; Pistidda, C.; Pundt, A. Microstructural Study of MgB2 in the LiBH4-MgH2 Composite by Using TEM. Nanomaterials 2022, 12, 1893. [Google Scholar] [CrossRef]
- Le, T.-T.; Pistidda, C.; Puszkiel, J.; Riglos, M.V.C.; Karimi, F.; Skibsted, J.; GharibDoust, S.P.; Richter, B.; Emmler, T.; Milanese, C.; et al. Design of a Nanometric AlTi Additive for MgB2-Based Reactive Hydride Composites with Superior Kinetic Properties. J. Phys. Chem. C 2018, 122, 7642–7655. [Google Scholar] [CrossRef]
- Deprez, E.; Justo, A.; Rojas, T.; López-Cartés, C.; Minella, C.B.; Bösenberg, U.; Dornheim, M.; Bormann, R.; Fernández, A. Microstructural study of the LiBH4–MgH2 reactive hydride composite with and without Ti-isopropoxide additive. Acta Mater. 2010, 58, 5683–5694. [Google Scholar] [CrossRef]
- Deprez, E.; Muñoz-Márquez, M.A.; Roldán, M.A.; Prestipino, C.; Palomares, F.J.; Minella, C.B.; Bösenberg, U.; Dornheim, M.; Bormann, R.; Fernández, A. Oxidation State and Local Structure of Ti-Based Additives in the Reactive Hydride Composite 2LiBH4 + MgH2. J. Phys. Chem. C 2010, 114, 3309–3317. [Google Scholar] [CrossRef]
- Herley, P.J.; Jones, W. Transmission Electron Microscopy of Beam-sensitive Metal Hydrides*. Z. Für Phys. Chem. 1986, 147, 147–159. [Google Scholar] [CrossRef]
- Lee, S. Crystal growth of MgB2. Phys. C: Supercond. 2003, 385, 31–41. [Google Scholar] [CrossRef]
- Zhang, M.X.; Kelly, P.M. Edge-to-edge matching model for predicting orientation relationships and habit planes—The improvements. Scr. Mater. 2005, 52, 963–968. [Google Scholar] [CrossRef]
- Zhang, M.-X.; Kelly, P. Edge-to-edge matching and its applications: Part II. Application to Mg–Al, Mg–Y and Mg–Mn alloys. Acta Mater. 2005, 53, 1085–1096. [Google Scholar] [CrossRef]
- Kelly, P.; Zhang, M.-X. Edge-to-edge matching—The fundamentals. Metall. Mater. Trans. A 2006, 37, 833–839. [Google Scholar] [CrossRef]
- Parker, G. Encyclopedia of Materials: Science and Technology; Elsevie: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Zhang, J.-M.; Zhang, Y.; Xu, K.-W.; Ji, V. Anisotropic elasticity in hexagonal crystals. Thin Solid Films 2007, 515, 7020–7024. [Google Scholar] [CrossRef]
- Milman, V.; Warren, M. Elastic properties of TiB2 and MgB2. J. Phys. Condens. Matter 2001, 13, 5585. [Google Scholar] [CrossRef]
- Cline, C.F.; Dunegan, H.L.; Henderson, G.W. Elastic Constants of Hexagonal BeO, ZnS, and CdSe. J. Appl. Phys. 1967, 38, 1944–1948. [Google Scholar] [CrossRef]
- Christian, J.W. The Theory of Transformations in Metals and Alloys; Newnes: London, UK, 2002. [Google Scholar]
- Avrami, M. Kinetics of phase change. I General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Q. A review on kinetic models and corresponding analysis methods for hydrogen storage materials. Int. J. Hydrogen Energy 2016, 41, 18072–18087. [Google Scholar] [CrossRef]
- Jones, L.; Dollimore, D.; Nicklin, T. Comparison of experimental kinetic decomposition data with master data using a linear plot method. Thermochim. Acta 1975, 13, 240–245. [Google Scholar] [CrossRef]
- Sharp, J.H.; Brindley, G.W.; Achar, B.N.N. Numerical Data for Some Commonly Used Solid State Reaction Equations. J. Am. Ceram. Soc. 1966, 49, 379–382. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-State Kinetic Models: Basics and Mathematical Fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef] [PubMed]
- Puszkiel, J.A. Tailoring the Kinetic Behavior of Hydride Forming Materials for Hydrogen Storage, in Gold Nanoparticles-Reaching New Heights; IntechOpen: London, UK, 2018. [Google Scholar]
- Gilbert, P. Iterative methods for the three-dimensional reconstruction of an object from projections. J. Theor. Biol. 1972, 36, 105–117. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]






| MgB2 on Mg | , −9.3% | , 4.2% |
| MgB2 on TiB2 | , −8.9% | , −1.7% |
| , −1.7% |
| Lattice Plane | |||
|---|---|---|---|
| (GPa) | 184.7 | 326.9 | 326.9 |
| (J/m3) | 7.4 × 108 (on Mg) 7.3 × 108 (on TiB2) | 2.9 × 108 (on Mg) 4.7 × 107 (on TiB2) | 4.7 × 107 (on TiB2) |
| Model | |
|---|---|
| Two-dimensional growth of contracting volume (2D CV) | |
| Three-dimensional growth of contracting volume (3D CV) | |
| One-dimensional diffusion (1D Diffusion) | |
| Two-dimensional diffusion (2D Diffusion) | |
| Three-dimensional diffusion of Ginstling-Braunshtein equation (3D Diffusion of GB) | |
| Three-dimensional diffusion of Jander equation (3D Diffusion of Jander) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, O.; Shang, Y.; Huang, X.; Szabó, D.V.; Le, T.T.; Wagner, S.; Klassen, T.; Kübel, C.; Pistidda, C.; Pundt, A. Transformation Kinetics of LiBH4–MgH2 for Hydrogen Storage. Molecules 2022, 27, 7005. https://doi.org/10.3390/molecules27207005
Jin O, Shang Y, Huang X, Szabó DV, Le TT, Wagner S, Klassen T, Kübel C, Pistidda C, Pundt A. Transformation Kinetics of LiBH4–MgH2 for Hydrogen Storage. Molecules. 2022; 27(20):7005. https://doi.org/10.3390/molecules27207005
Chicago/Turabian StyleJin, Ou, Yuanyuan Shang, Xiaohui Huang, Dorothée Vinga Szabó, Thi Thu Le, Stefan Wagner, Thomas Klassen, Christian Kübel, Claudio Pistidda, and Astrid Pundt. 2022. "Transformation Kinetics of LiBH4–MgH2 for Hydrogen Storage" Molecules 27, no. 20: 7005. https://doi.org/10.3390/molecules27207005
APA StyleJin, O., Shang, Y., Huang, X., Szabó, D. V., Le, T. T., Wagner, S., Klassen, T., Kübel, C., Pistidda, C., & Pundt, A. (2022). Transformation Kinetics of LiBH4–MgH2 for Hydrogen Storage. Molecules, 27(20), 7005. https://doi.org/10.3390/molecules27207005











