Numerical Interchain Mean-Field Theory for the Specific Heat of the Bimetallic Ferromagnetically Coupled Chain Compound MnNi(NO2)4(en)2 (en = Ethylenediamine)
Abstract
1. Introduction
2. Experiment
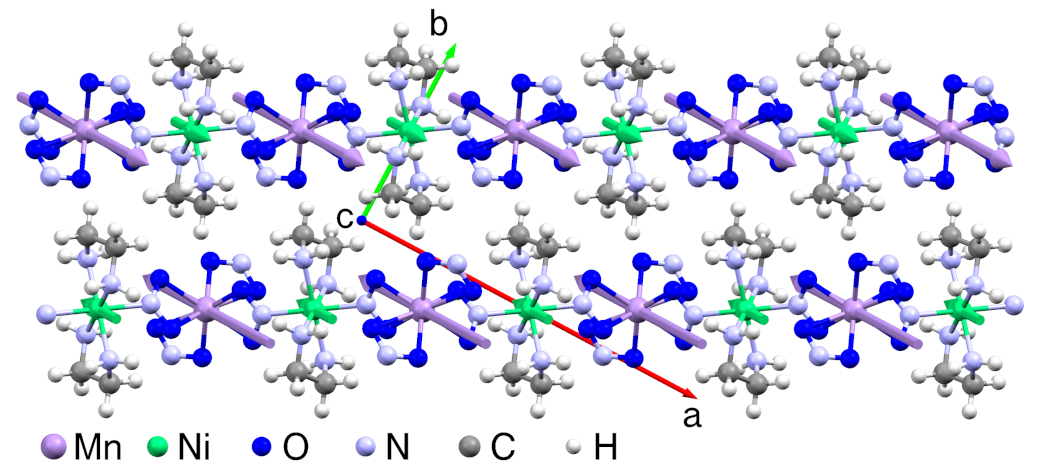
2.1. MnNi(NO)(en) (en = Ethylenediamine)
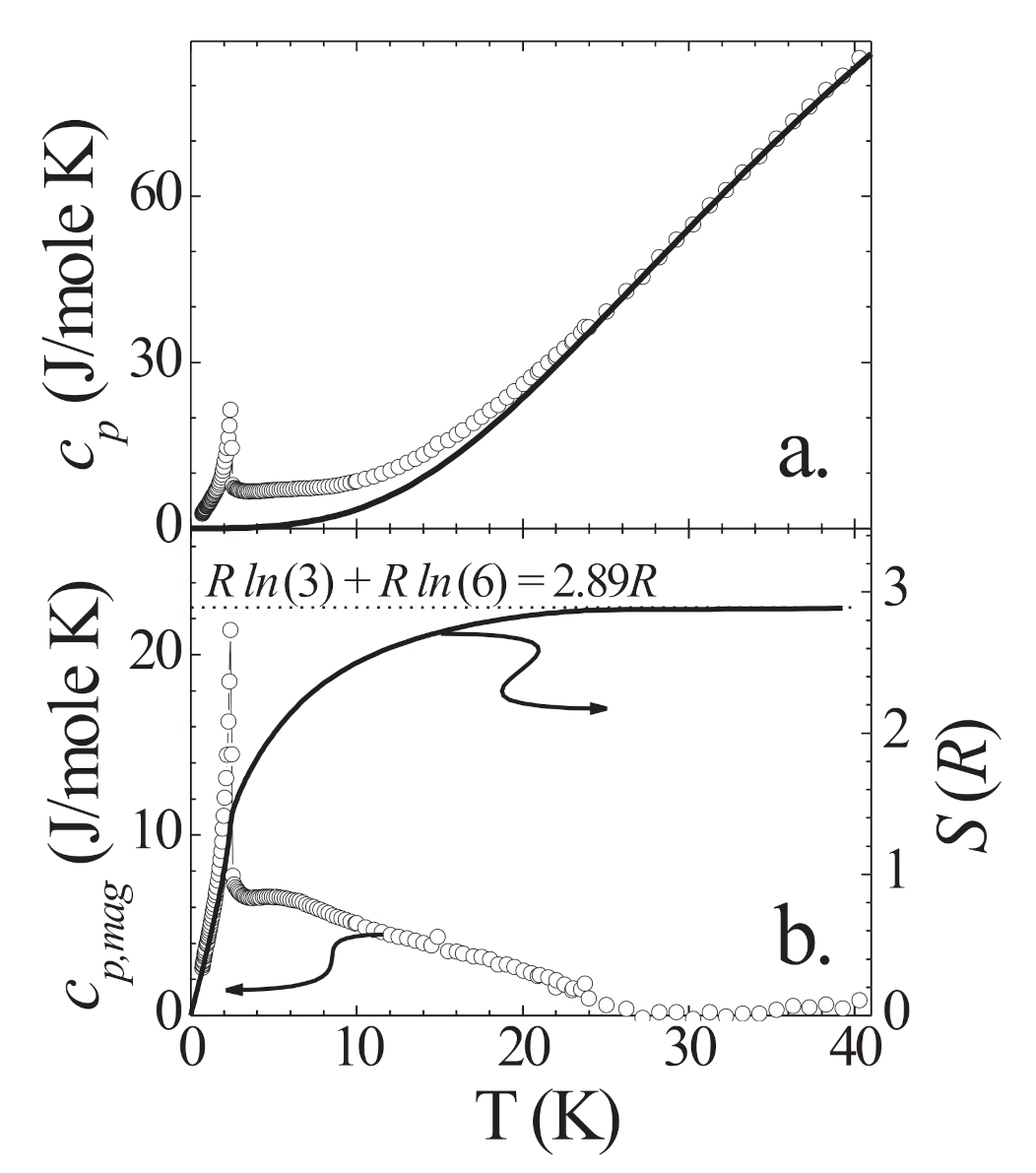
2.2. Specific Heat
3. Theory
3.1. Model
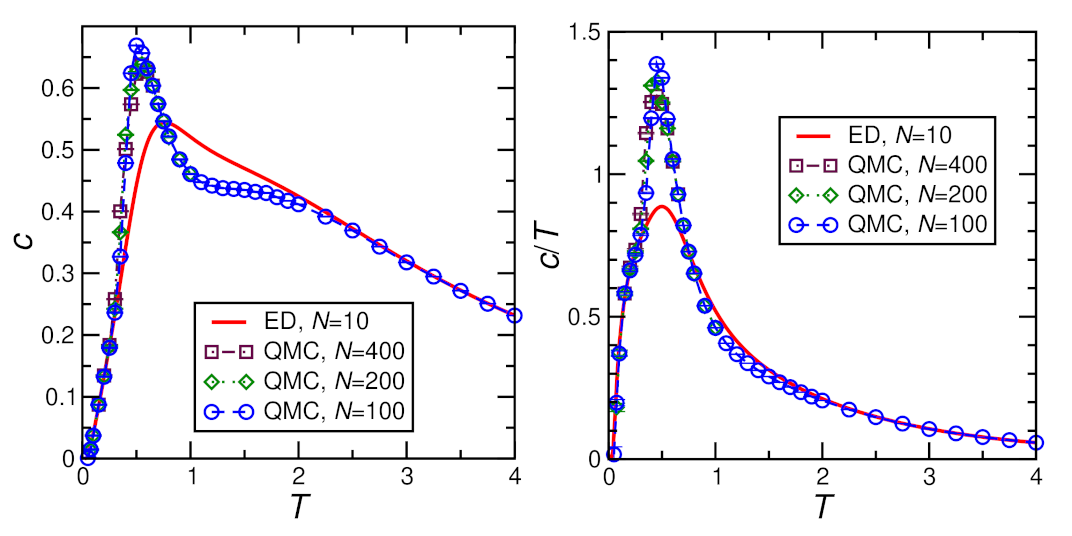
3.2. Numerical Treatment of Decoupled Chains
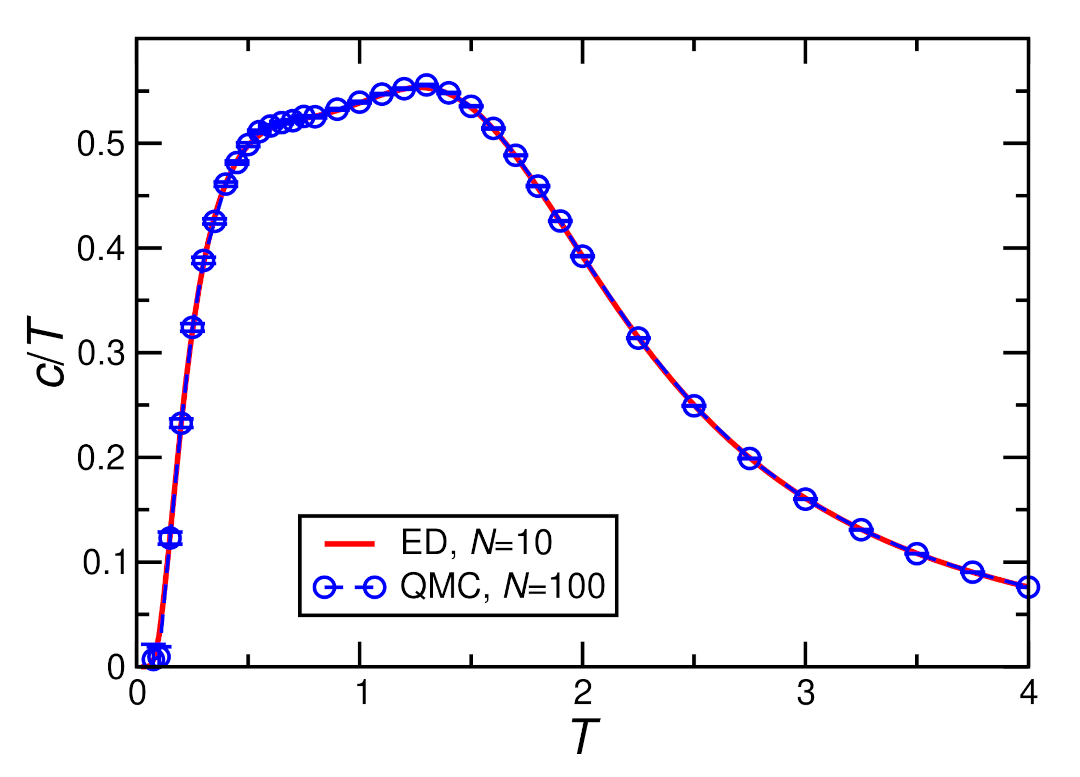
3.3. Mean-Field Treatment of the Interchain Coupling
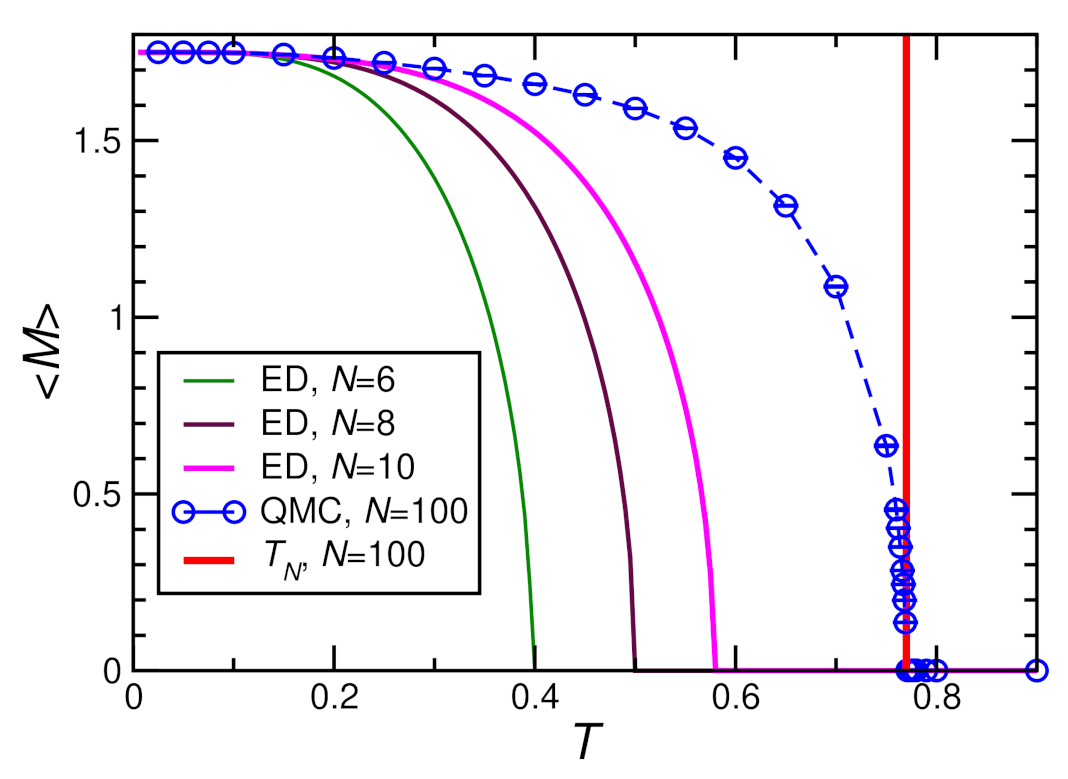
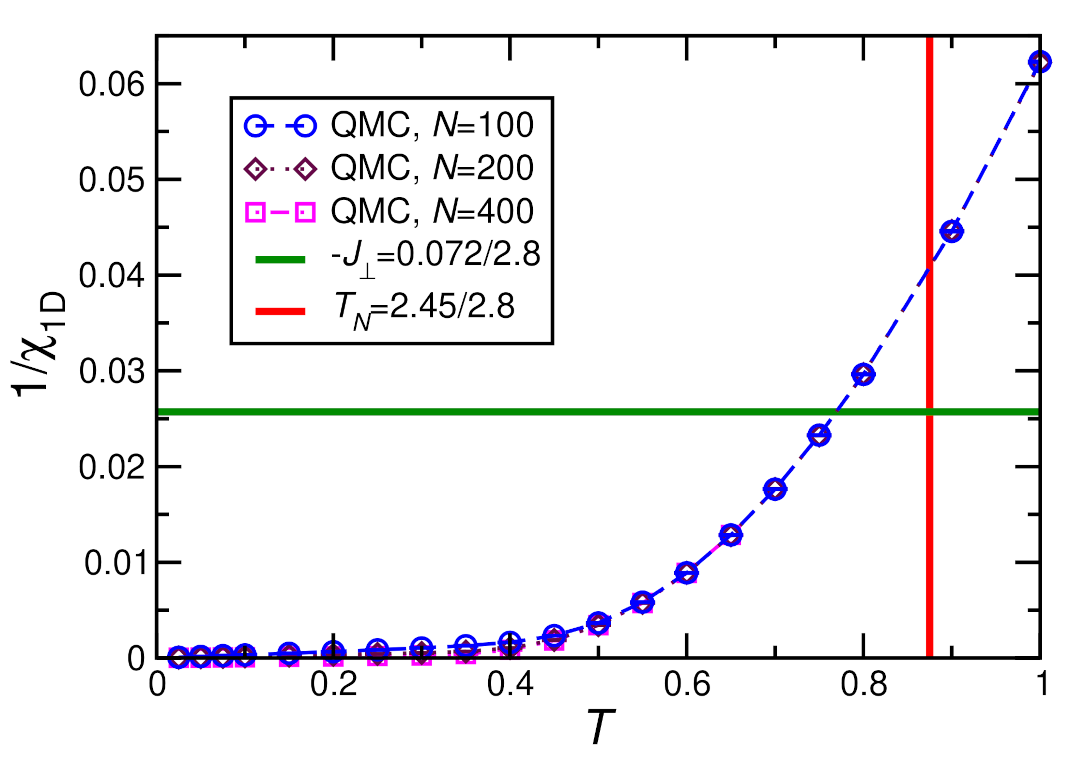
3.3.1. Magnetic Susceptibility and Ordering Temperature
3.3.2. Specific Heat
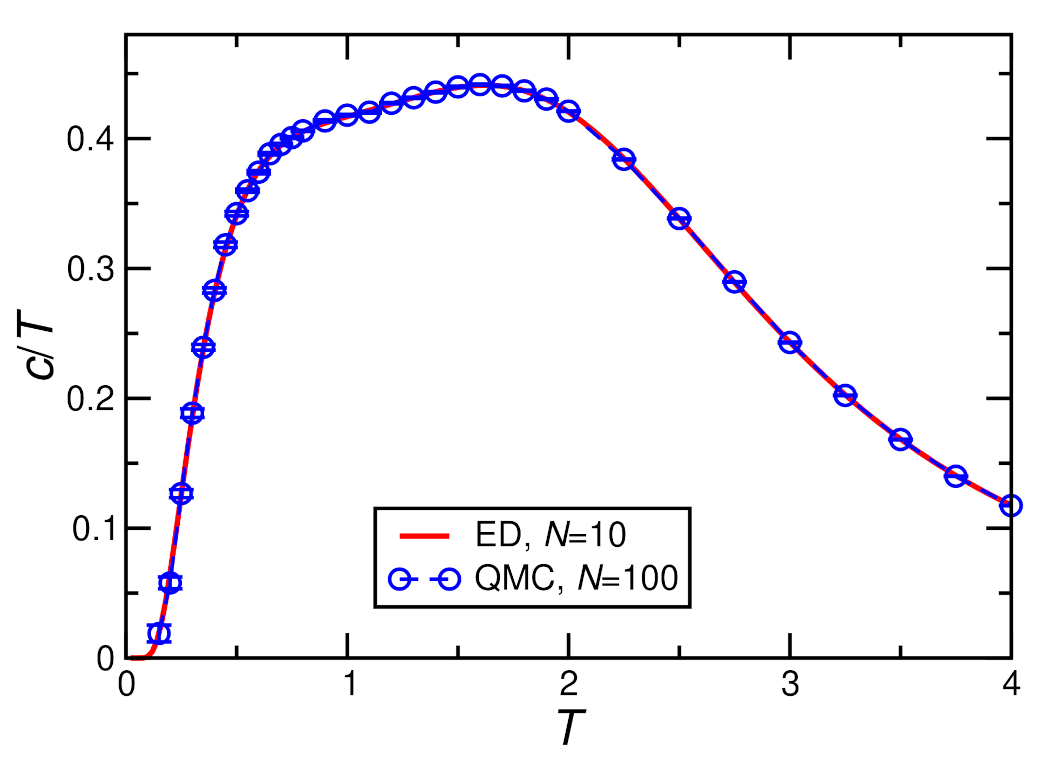
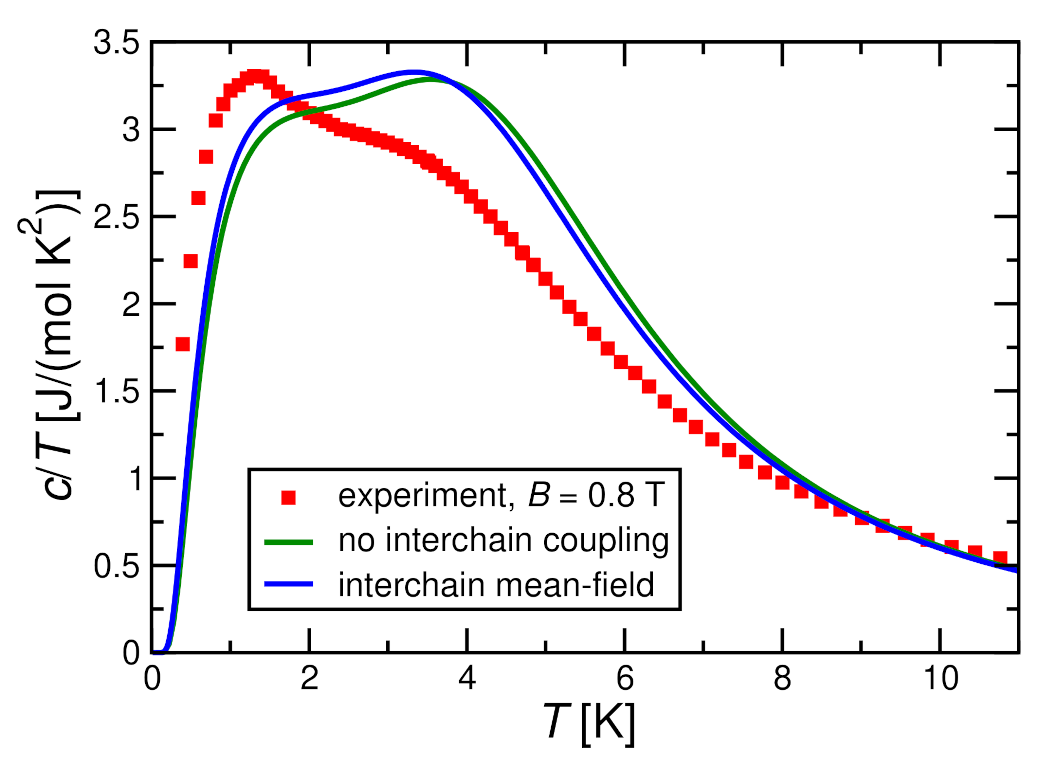
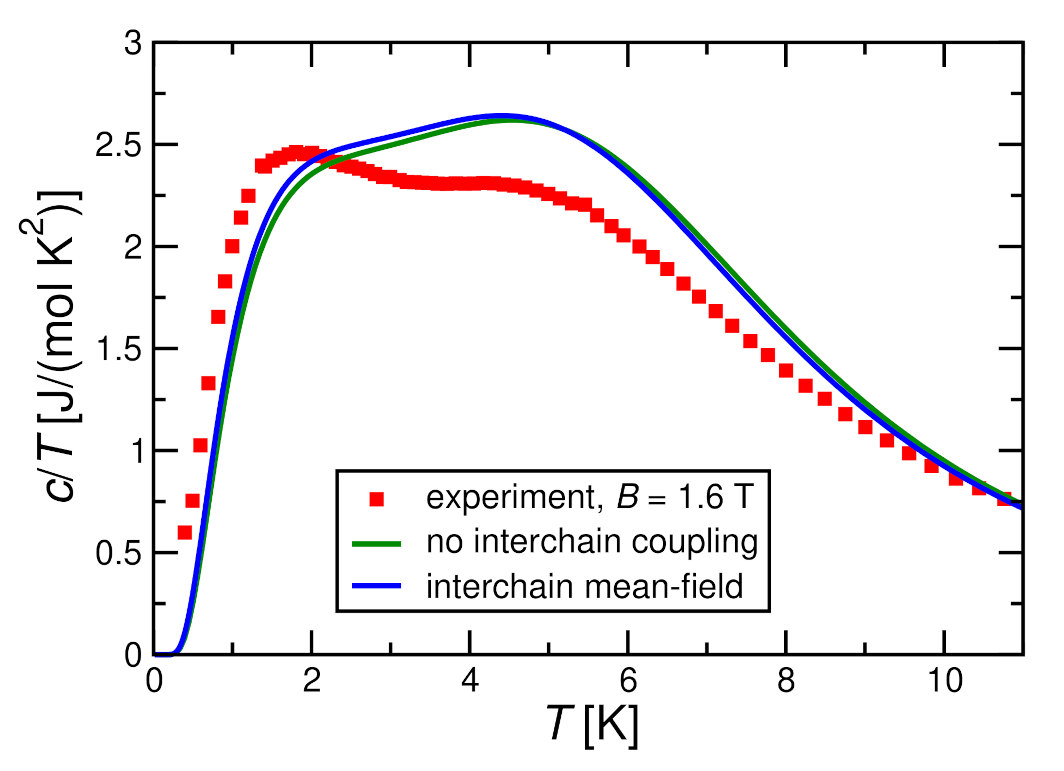
3.3.3. Comparison with Experimental Specific Heat
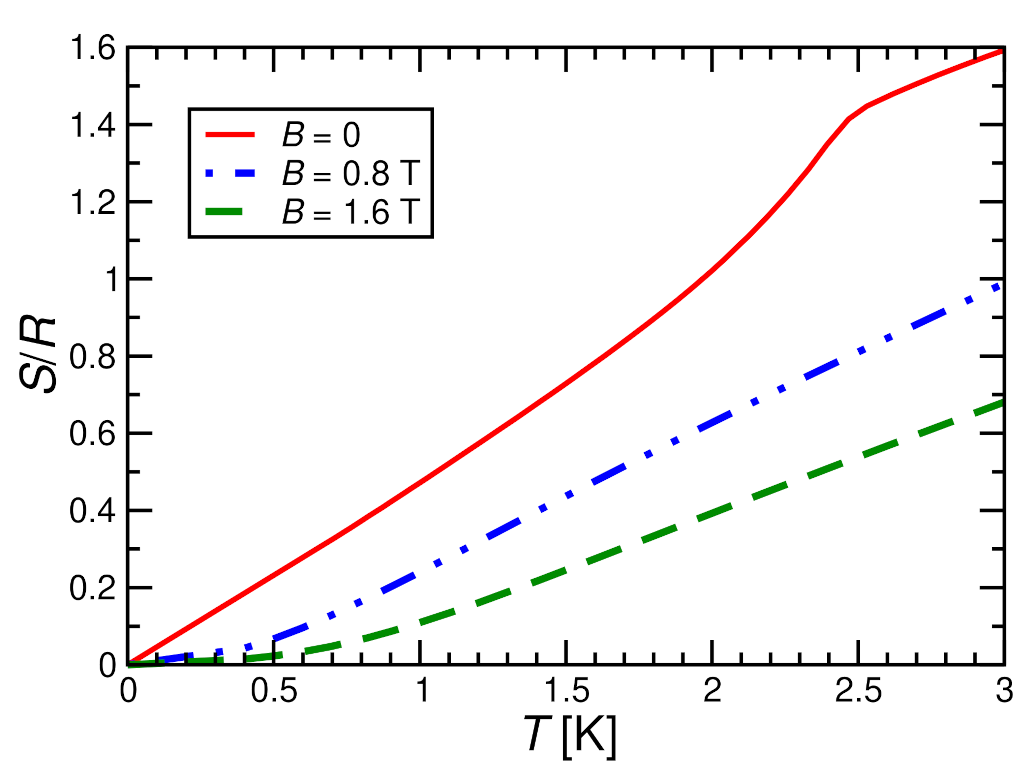
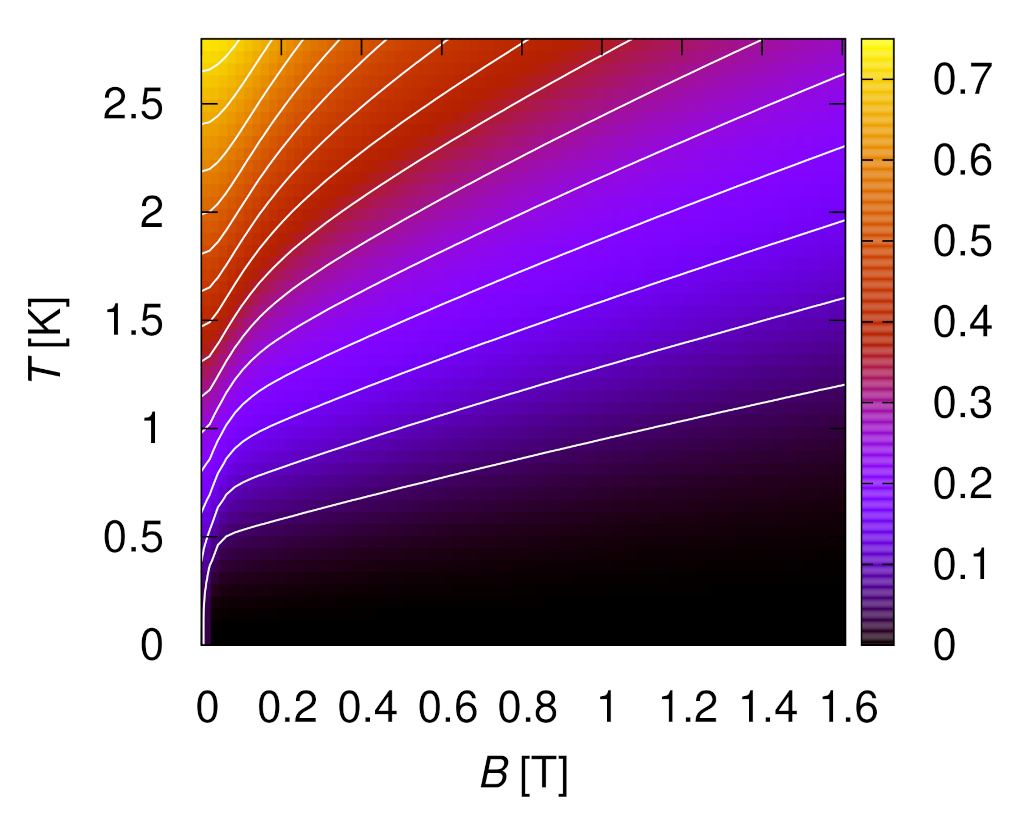
4. Magnetocaloric Properties
5. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
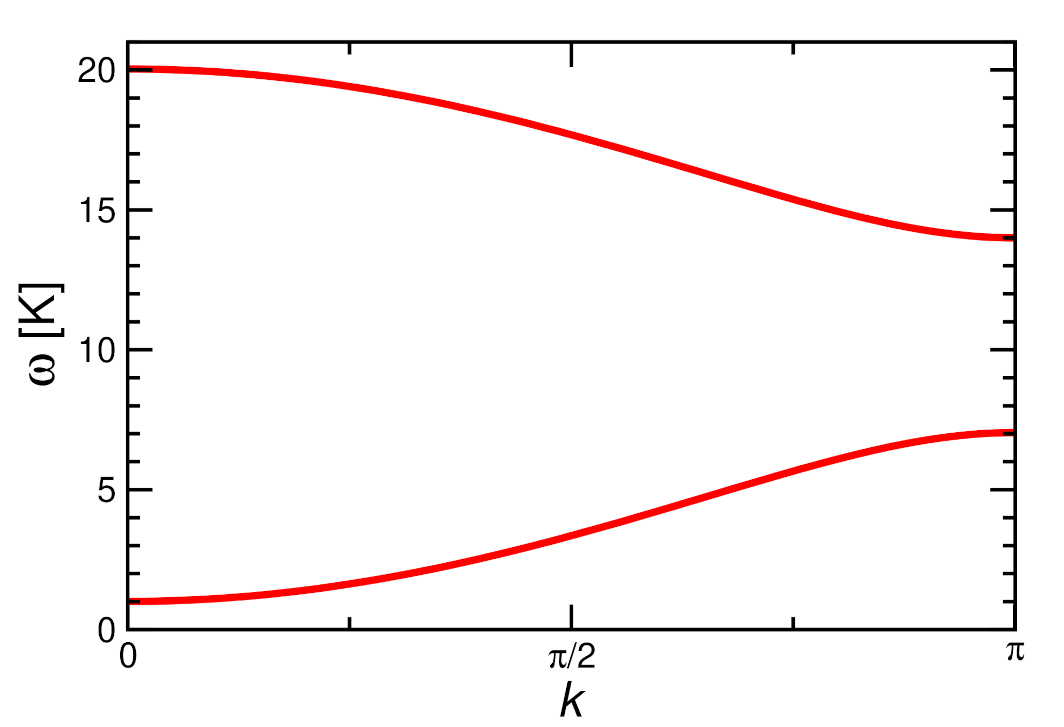
Appendix A. One-Magnon Dispersion
Appendix B. Details of Self-Consistency Procedure in QMC

Appendix C. Single-Site Mean-Field Approximation
Appendix C.1. Phase Diagram
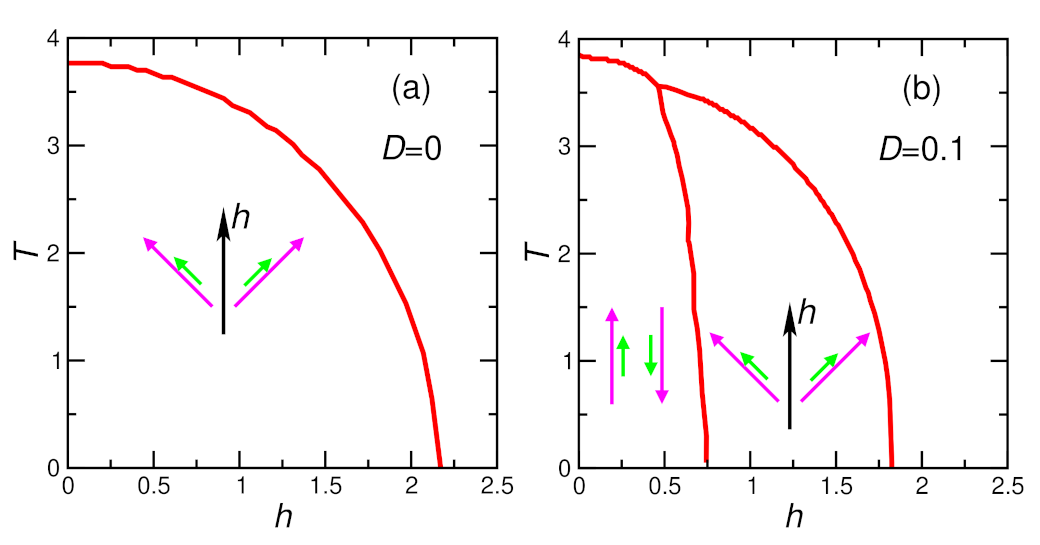
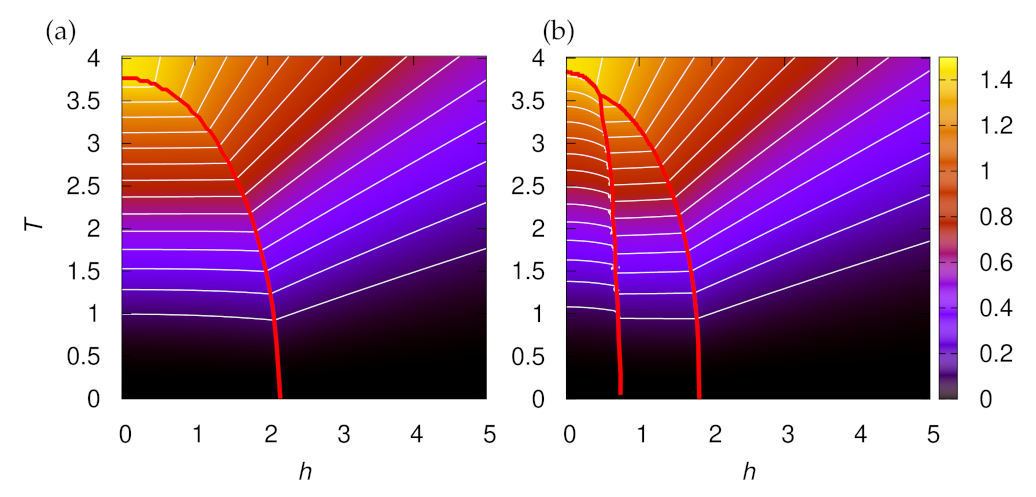
Appendix C.2. Entropy and Magnetocaloric Effect
References
- Mikeska, H.-J.; Kolezhuk, A.K. One-dimensional magnetism. In Quantum Magnetism; Schollwöck, U., Richter, J., Farnell, D.J.J., Bishop, R.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–83. [Google Scholar] [CrossRef]
- Dender, D.C.; Hammar, P.R.; Reich, D.H.; Broholm, C.; Aeppli, G. Direct Observation of Field-Induced Incommensurate Fluctuations in a One-Dimensional S = 1/2 Antiferromagnet. Phys. Rev. Lett. 1997, 79, 1750–1753. [Google Scholar] [CrossRef]
- Oshikawa, M.; Affleck, I. Field-Induced Gap in S = 1/2 Antiferromagnetic Chains. Phys. Rev. Lett. 1997, 79, 2883–2886. [Google Scholar] [CrossRef]
- Essler, F.H.L.; Tsvelik, A.M. Dynamical magnetic susceptibilities in copper benzoate. Phys. Rev. B 1998, 57, 10592–10597. [Google Scholar] [CrossRef]
- Zvyagin, S.A.; Kolezhuk, A.K.; Krzystek, J.; Feyerherm, R. Excitation Hierarchy of the Quantum Sine-Gordon Spin Chain in a Strong Magnetic Field. Phys. Rev. Lett. 2004, 93, 027201. [Google Scholar] [CrossRef] [PubMed]
- Tiegel, A.C.; Honecker, A.; Pruschke, T.; Ponomaryov, A.; Zvyagin, S.A.; Feyerherm, R.; Manmana, S.R. Dynamical properties of the sine-Gordon quantum spin magnet Cu-PM at zero and finite temperature. Phys. Rev. B 2016, 93, 104411. [Google Scholar] [CrossRef]
- Hagiwara, M.; Regnault, L.P.; Zheludev, A.; Stunault, A.; Metoki, N.; Suzuki, T.; Suga, S.; Kakurai, K.; Koike, Y.; Vorderwisch, P.; et al. Spin Excitations in an Anisotropic Bond-Alternating Quantum S = 1 Chain in a Magnetic Field: Contrast to Haldane Spin Chains. Phys. Rev. Lett. 2005, 94, 177202. [Google Scholar] [CrossRef]
- Wolfram, T.; Ellialtioglu, S. Neutron Scattering by Magnons of an Antiferromagnet with Modulated Spin Amplitudes. Phys. Rev. Lett. 1980, 44, 1295–1298. [Google Scholar] [CrossRef]
- Bartolomé, F.; Bartolomé, J.; Benelli, C.; Caneschi, A.; Gatteschi, D.; Paulsen, C.; Pini, M.G.; Rettori, A.; Sessoli, R.; Volokitin, Y. Effect of Chiral Domain Walls on the Specific Heat of Gd(hfac)3NITR (R=Ethyl, Isopropyl, Methyl, Phenyl) Molecular Magnetic Chains. Phys. Rev. Lett. 1996, 77, 382–385. [Google Scholar] [CrossRef] [PubMed]
- Drillon, M.; Coronado, E.; Georges, R.; Gianduzzo, J.C.; Curely, J. Ferrimagnetic Heisenberg chains [(1/2-S] (S = 1 to (5/2): Thermal and magnetic properties. Phys. Rev. B 1989, 40, 10992–10998. [Google Scholar] [CrossRef]
- Pati, S.K.; Ramasesha, S.; Sen, D. Low-lying excited states and low-temperature properties of an alternating spin-1–spin-1/2 chain: A density-matrix renormalization-group study. Phys. Rev. B 1997, 55, 8894–8904. [Google Scholar] [CrossRef]
- Pati, S.K.; Ramasesha, S.; Sen, D. A density matrix renormalization group study of low-energy excitations and low-temperature properties of alternating spin systems. J. Phys. Condens. Matter 1997, 9, 8707–8726. [Google Scholar] [CrossRef][Green Version]
- Ivanov, N.B. Magnon dispersions in quantum Heisenberg ferrimagnetic chains at zero temperature. Phys. Rev. B 2000, 62, 3271–3278. [Google Scholar] [CrossRef]
- Kolezhuk, A.K.; Mikeska, H.-J.; Yamamoto, S. Matrix-product-states approach to Heisenberg ferrimagnetic spin chains. Phys. Rev. B 1997, 55, R3336–R3339. [Google Scholar] [CrossRef]
- Yamamoto, S.; Fukui, T. Thermodynamic properties of Heisenberg ferrimagnetic spin chains: Ferromagnetic-antiferromagnetic crossover. Phys. Rev. B 1998, 57, R14008–R14011. [Google Scholar] [CrossRef]
- Yamamoto, S.; Fukui, T.; Maisinger, K.; Schollwöck, U. Combination of ferromagnetic and antiferromagnetic features in Heisenberg ferrimagnets. J. Phys. Condens. Matter 1998, 10, 11033–11048. [Google Scholar] [CrossRef][Green Version]
- Nakanishi, T.; Yamamoto, S. Intrinsic double-peak structure of the specific heat in low-dimensional quantum ferrimagnets. Phys. Rev. B 2002, 65, 214418. [Google Scholar] [CrossRef]
- Yamamoto, S.; Hori, H. Low-temperature thermodynamics of one-dimensional alternating-spin Heisenberg ferromagnets. Phys. Rev. B 2005, 72, 054423. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; Wiley-VCH: New York, NY, USA, 1993. [Google Scholar]
- Caneschi, A.; Gatteschi, D.; Renard, J.P.; Rey, P.; Sessoli, R. Magnetic coupling in zero- and one-dimensional magnetic systems formed by nickel(II) and nitronyl nitroxides. Magnetic phase transition of a ferrimagnetic chain. Inorg. Chem. 1989, 28, 2940–2944. [Google Scholar] [CrossRef]
- Zhou, P.; Makivic, M.; Zuo, F.; Zane, S.; Miller, J.S.; Epstein, A.J. Ferromagnetic behavior and magnetic excitations in a molecular-based alternating-spin chain: Decamethylchromocenium tetracyanoethanide. Phys. Rev. B 1994, 49, R4364–R4367. [Google Scholar] [CrossRef]
- Nishizawa, M.; Shiomi, D.; Sato, K.; Takui, T.; Itoh, K.; Sawa, H.; Kato, R.; Sakurai, H.; Izuoka, A.; Sugawara, T. Evidence for the Breakdown of Simple Classical Pictures of Organic Molecule-Based Ferrimagnetics: Low-Temperature Crystal Structure and Single-Crystal ESR Studies of an Organic Heterospin System. J. Phys. Chem. B 2000, 104, 503–509. [Google Scholar] [CrossRef]
- Yao, M.-X.; Zheng, Q.; Cai, X.-M.; Li, Y.-Z.; Song, Y.; Zuo, J.-L. Chiral Cyanide-Bridged CrIII–MnIII Heterobimetallic Chains Based on [(Tp)Cr(CN)3]−: Synthesis, Structures, and Magnetic Properties. Inorg. Chem. 2012, 51, 2140–2149. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Shi, W.; Cheng, P. Magnetism in one-dimensional metal-nitronyl nitroxide radical system. Coord. Chem. Rev. 2019, 378, 134–150. [Google Scholar] [CrossRef]
- Thorarinsdottir, A.E.; Harris, T.D. Metal-Organic Framework Magnets. Chem. Rev. 2020, 120, 8716–8789. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, H.; Okita, T.; Iwasaki, Y.; Kono, Y.; Hosokoshi, Y.; Kida, T.; Matsuo, A.; Kawakami, T.; Hagiwara, M. Magnetic Properties of a Mixed Spin-(1/2,5/2) Chain in (4-Cl-o-MePy-V)FeCl4. J. Phys. Soc. Jpn. 2021, 90, 064707. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Furuya, S.C.; Morota, S.; Shimono, S.; Kawakami, T.; Kusanose, Y.; Shimura, Y.; Nakano, K.; Hosokoshi, Y. Observation of thermodynamics originating from a mixed-spin ferromagnetic chain. Phys. Rev. B 2022, 106, L100404. [Google Scholar] [CrossRef]
- Fukushima, N.; Honecker, A.; Wessel, S.; Brenig, W. Thermodynamic properties of ferromagnetic mixed-spin chain systems. Phys. Rev. B 2004, 69, 174430. [Google Scholar] [CrossRef]
- Fukushima, N.; Honecker, A.; Wessel, S.; Grossjohann, S.; Brenig, W. Specific heat and magnetic susceptibility of ferromagnetic mixed-spin chain systems. Physica B 2005, 359–361, 1409–1411. [Google Scholar] [CrossRef]
- Abouie, J.; Ghasemi, S.A.; Langari, A. Thermodynamic properties of ferrimagnetic spin chains in the presence of a magnetic field. Phys. Rev. B 2006, 73, 014411. [Google Scholar] [CrossRef]
- Boyarchenkov, A.S.; Bostrem, I.G.; Ovchinnikov, A.S. Quantum magnetization plateau and sign change of the magnetocaloric effect in a ferrimagnetic spin chain. Phys. Rev. B 2007, 76, 224410. [Google Scholar] [CrossRef]
- Yuan, C.; Ying, X.; Chuang-Chuang, S. Magnetic Properties of One-Dimensional Ferromagnetic Mixed-Spin Model within Tyablikov Decoupling Approximation. Commun. Theor. Phys. 2010, 54, 747–752. [Google Scholar] [CrossRef]
- Hu, A.-Y.; Wu, Z.-M.; Cui, Y.-T.; Qin, G.-P. The paramagnetic properties of ferromagnetic mixed-spin chain system. J. Magn. Magn. Mater. 2015, 374, 539–543. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, Z.-G.; Su, G. Combined study of Schwinger-boson mean-field theory and linearized tensor renormalization group on Heisenberg ferromagnetic mixed spin (S,σ) chains. AIP Adv. 2015, 5, 077183. [Google Scholar] [CrossRef]
- Da Silva, W.M.; Montenegro-Filho, R.R. Role of density-dependent magnon hopping and magnon-magnon repulsion in ferrimagnetic spin-(1/2, S) chains in a magnetic field. Phys. Rev. B 2021, 103, 054432. [Google Scholar] [CrossRef]
- Takahashi, M. Thermodynamics of One-Dimensional Solvable Models; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Dembiński, S.T.; Wydro, T. Linear quantum-classical Heisenberg model. Phys. Status Solidi (B) 1975, 67, K123–K126. [Google Scholar] [CrossRef]
- Hagiwara, M.; Minami, K.; Narumi, Y.; Tatani, K.; Kindo, K. Magnetic Properties of a Quantum Ferrimagnet: NiCu(pba)(D2O)3·2D2O. J. Phys. Soc. Jpn. 1998, 67, 2209–2211. [Google Scholar] [CrossRef]
- Hagiwara, M.; Narumi, Y.; Minami, K.; Tatani, K.; Kindo, K. Magnetization Process of the S = 1/2 and 1 Ferrimagnetic Chain and Dimer. J. Phys. Soc. Jpn. 1999, 68, 2214–2217. [Google Scholar] [CrossRef]
- Fujiwara, N.; Hagiwara, M. Low energy spin dynamics of a quantum ferrimagnetic chain, NiCu(pba)(H2O)32H2O. Solid State Commun. 2000, 113, 433–436. [Google Scholar] [CrossRef]
- Wynn, C.M.; Gîrţu, M.A.; Miller, J.S.; Epstein, A.J. Lattice- and spin-dimensionality crossovers in a linear-chain-molecule-based ferrimagnet with weak spin anisotropy. Phys. Rev. B 1997, 56, 315–320. [Google Scholar] [CrossRef]
- Affronte, M.; Caneschi, A.; Cucci, C.; Gatteschi, D.; Lasjaunias, J.C.; Paulsen, C.; Pini, M.G.; Rettori, A.; Sessoli, R. Low-temperature thermodynamic properties of molecular magnetic chains. Phys. Rev. B 1999, 59, 6282–6293. [Google Scholar] [CrossRef]
- Gîrţu, M.A.; Wynn, C.M.; Zhang, J.; Miller, J.S.; Epstein, A.J. Magnetic properties and critical behavior of Fe(tetracyanoethylene)2·x(CH2Cl2): A high-Tc molecule-based magnet. Phys. Rev. B 2000, 61, 492–500. [Google Scholar] [CrossRef]
- Lascialfari, A.; Ullu, R.; Affronte, M.; Cinti, F.; Caneschi, A.; Gatteschi, D.; Rovai, D.; Pini, M.G.; Rettori, A. Specific heat and μ+SR measurements in Gd(hfac)3NITiPr molecular magnetic chains: Indications for a chiral phase without long-range helical order. Phys. Rev. B 2003, 67, 224408. [Google Scholar] [CrossRef]
- Gillon, B.; Mathonière, C.; Ruiz, E.; Alvarez, S.; Cousson, A.; Rajendiran, T.M.; Kahn, O. Spin Densities in a Ferromagnetic Bimetallic Chain Compound: Polarized Neutron Diffraction and DFT Calculations. J. Am. Chem. Soc. 2002, 124, 14433–14441. [Google Scholar] [CrossRef] [PubMed]
- Kahn, O.; Bakalbassis, E.; Mathonière, C.; Hagiwara, M.; Katsumata, K.; Ouahab, L. Metamagnetic Behavior of the Novel Bimetallic Ferromagnetic Chain Compound MnNi(NO2)4(en)2 (en = Ethylenediamine). Inorg. Chem. 1997, 36, 1530–1531. [Google Scholar] [CrossRef] [PubMed]
- Feyerherm, R.; Mathonière, C.; Kahn, O. Magnetic anisotropy and metamagnetic behaviour of the bimetallic chain MnNi(NO2)4(en)2 (en = ethylenediamine). J. Phys. Condens. Matter 2001, 13, 2639–2650. [Google Scholar] [CrossRef]
- Kreitlow, J.; Mathonière, C.; Feyerherm, R.; Süllow, S. Pressure response of the bimetallic chain compound MnNi(NO2)4(en)2; en=ethylenediamine. Polyhedron 2005, 24, 2413–2416. [Google Scholar] [CrossRef]
- Troyer, M.; Ammon, B.; Heeb, E. Parallel Object Oriented Monte Carlo Simulations. Lect. Notes Comput. Sci. 1998, 1505, 191–198. [Google Scholar] [CrossRef]
- Albuquerque, A.F.; Alet, F.; Corboz, P.; Dayal, P.; Feiguin, A.; Fuchs, S.; Gamper, L.; Gull, E.; Gürtler, S.; Honecker, A.; et al. The ALPS project release 1.3: Open-source software for strongly correlated systems. J. Magn. Magn. Mater. 2007, 310, 1187–1193. [Google Scholar] [CrossRef]
- Alet, F.; Wessel, S.; Troyer, M. Generalized directed loop method for quantum Monte Carlo simulations. Phys. Rev. E 2005, 71, 036706. [Google Scholar] [CrossRef]
- Todo, S.; Kato, K. Cluster Algorithms for General-S Quantum Spin Systems. Phys. Rev. Lett. 2001, 87, 047203. [Google Scholar] [CrossRef]
- Syljuåsen, O.F.; Sandvik, A.W. Quantum Monte Carlo with directed loops. Phys. Rev. E 2002, 66, 046701. [Google Scholar] [CrossRef]
- Bauer, B.; Carr, L.D.; Evertz, H.G.; Feiguin, A.; Freire, J.; Fuchs, S.; Gamper, L.; Gukelberger, J.; Gull, E.; Guertler, S.; et al. The ALPS project release 2.0: Open source software for strongly correlated systems. J. Stat. Mech. Theor. Exp. 2011, 2011, P05001. [Google Scholar] [CrossRef]
- Matsumoto, M.; Nishimura, T. Mersenne Twister: A 623-dimensionally Equidistributed Uniform Pseudo-random Number Generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- Gvozdikova, M.V.; Ziman, T.; Zhitomirsky, M.E. Helicity, anisotropies, and their competition in a multiferroic magnet: Insight from the phase diagram. Phys. Rev. B 2016, 94, R020406. [Google Scholar] [CrossRef]
- Schulz, H.J. Dynamics of Coupled Quantum Spin Chains. Phys. Rev. Lett. 1996, 77, 2790–2793. [Google Scholar] [CrossRef]
- Cavadini, N.; Rüegg, C.; Henggeler, W.; Furrer, A.; Güdel, H.-U.; Krämer, K.; Mutka, H. Temperature renormalization of the magnetic excitations in S=1/2 KCuCl3. Eur. Phys. J. B 2000, 18, 565–571. [Google Scholar] [CrossRef]
- Todo, S.; Shibasaki, A. Improved chain mean-field theory for quasi-one-dimensional quantum magnets. Phys. Rev. B 2008, 78, 224411. [Google Scholar] [CrossRef]
- Fazekas, P. Lecture Notes on Electron Correlation and Magnetism; World Scientific: Singapore, 1999. [Google Scholar] [CrossRef]
- Grossjohann, S.-N. Stochastic Series Expansion an niedrigdimensionalen Quanten-Spin-Systemen. Diploma Thesis, TU Braunschweig, Braunschweig, Germany, 2004. [Google Scholar]
- Trippe, C.; Honecker, A.; Klümper, A.; Ohanyan, V. Exact calculation of the magnetocaloric effect in the spin-1/2XXZ chain. Phys. Rev. B 2010, 81, 054402. [Google Scholar] [CrossRef]
- Landau, L.D. On the theory of phase transitions I. Zh. Eksp. Teor. Fiz. 1937, 7, 19–32. [Google Scholar] [CrossRef]
- Wolf, B.; Honecker, A.; Hofstetter, W.; Tutsch, U.; Lang, M. Cooling through quantum criticality and many-body effects in condensed matter and cold gases. Int. J. Mod. Phys. B 2014, 28, 1430017. [Google Scholar] [CrossRef]
- Konieczny, P.; Sas, W.; Czernia, D.; Pacanowska, A.; Fitta, M.; Pełka, R. Magnetic cooling: A molecular perspective. Dalton Trans. 2022, 51, 12762–12780. [Google Scholar] [CrossRef]
- Junger, I.J.; Ihle, D.; Richter, J. Thermodynamics of S≥1 ferromagnetic Heisenberg chains with uniaxial single-ion anisotropy. Phys. Rev. B 2005, 72, 064454. [Google Scholar] [CrossRef]
- Tiwari, M. Mean-field theory for quantum spin systems and the magnetocaloric effect. Ph.D. Thesis, CY Cergy Paris Université, Cergy-Pontoise, France, 2022. [Google Scholar]
- Weiss, P. L’hypothèse du champ moléculaire et la propriété ferromagnétique. J. Phys. Theor. Appl. 1907, 6, 661–690. [Google Scholar] [CrossRef]
- Blundell, S. Magnetism in Condensed Matter; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Pires, A.S.T. The Heisenberg model. In Theoretical Tools for Spin Models in Magnetic Systems; IOP Publishing: Bristol, UK, 2021; pp. 1-1–1-16. [Google Scholar] [CrossRef]
- Melchy, P.-É.; Zhitomirsky, M.E. Interplay of anisotropy and frustration: Triple transitions in a triangular-lattice antiferromagnet. Phys. Rev. B 2009, 80, 064411. [Google Scholar] [CrossRef]
- Zhitomirsky, M.E.; Nikuni, T. Magnetization curve of a square-lattice Heisenberg antiferromagnet. Phys. Rev. B 1998, 57, 5013–5016. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133–1136. [Google Scholar] [CrossRef]
- Fisher, M.E. Theory of multicritical transitions and the spin-flop bicritical point. AIP Conf. Proc. 1975, 24, 273–280. [Google Scholar] [CrossRef]
- Landau, D.P.; Binder, K. Phase diagrams and multicritical behavior of a three-dimensional anisotropic Heisenberg antiferromagnet. Phys. Rev. B 1978, 17, 2328–2342. [Google Scholar] [CrossRef]
- Hassani, Y. Magnetic Phase Diagram of the Two-Dimensional Heisenberg Spin One-Half Canted Antiferromagnet Ethyl-Ammonium Tetrabromocuprate(II). Master’s Thesis, Montana State University, Bozeman, MT, USA, 1988. [Google Scholar]
- Selke, W.; Bannasch, G.; Holtschneider, M.; McCulloch, I.P.; Peters, D.; Wessel, S. Classical and quantum anisotropic Heisenberg antiferromagnets. Condens. Matter Phys. 2009, 12, 547–558. [Google Scholar] [CrossRef][Green Version]
- Tishin, A.M.; Spichkin, Y.I. The Magnetocaloric Effect and Its Applications; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]
- Heydarinasab, F.; Abouie, J. Mixed-spin system with supersolid phases: Magnetocaloric effect and thermal properties. J. Phys. Condens. Matter 2020, 32, 165804. [Google Scholar] [CrossRef]
- Palacios, E.; Sáez-Puche, R.; Romero, J.; Doi, Y.; Hinatsu, Y.; Evangelisti, M. Large magnetocaloric effect in EuGd2O4 and EuDy2O4. J. Alloys Compd. 2022, 890, 161847. [Google Scholar] [CrossRef]
- Liu, W.; Bykov, E.; Taskaev, S.; Bogush, M.; Khovaylo, V.; Fortunato, N.; Aubert, A.; Zhang, H.; Gottschall, T.; Wosnitza, J.; et al. A study on rare-earth Laves phases for magnetocaloric liquefaction of hydrogen. Appl. Mat. Today 2022, 29, 101624. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Honecker, A.; Brenig, W.; Tiwari, M.; Feyerherm, R.; Bleckmann, M.; Süllow, S. Numerical Interchain Mean-Field Theory for the Specific Heat of the Bimetallic Ferromagnetically Coupled Chain Compound MnNi(NO2)4(en)2 (en = Ethylenediamine). Molecules 2022, 27, 6546. https://doi.org/10.3390/molecules27196546
Honecker A, Brenig W, Tiwari M, Feyerherm R, Bleckmann M, Süllow S. Numerical Interchain Mean-Field Theory for the Specific Heat of the Bimetallic Ferromagnetically Coupled Chain Compound MnNi(NO2)4(en)2 (en = Ethylenediamine). Molecules. 2022; 27(19):6546. https://doi.org/10.3390/molecules27196546
Chicago/Turabian StyleHonecker, Andreas, Wolfram Brenig, Maheshwor Tiwari, Ralf Feyerherm, Matthias Bleckmann, and Stefan Süllow. 2022. "Numerical Interchain Mean-Field Theory for the Specific Heat of the Bimetallic Ferromagnetically Coupled Chain Compound MnNi(NO2)4(en)2 (en = Ethylenediamine)" Molecules 27, no. 19: 6546. https://doi.org/10.3390/molecules27196546
APA StyleHonecker, A., Brenig, W., Tiwari, M., Feyerherm, R., Bleckmann, M., & Süllow, S. (2022). Numerical Interchain Mean-Field Theory for the Specific Heat of the Bimetallic Ferromagnetically Coupled Chain Compound MnNi(NO2)4(en)2 (en = Ethylenediamine). Molecules, 27(19), 6546. https://doi.org/10.3390/molecules27196546