The Cis-Effect Explained Using Next-Generation QTAIM
Abstract
1. Introduction
2. Theoretical Background and Computational Details
2.1. Theoretical Background
2.2. Computational Details
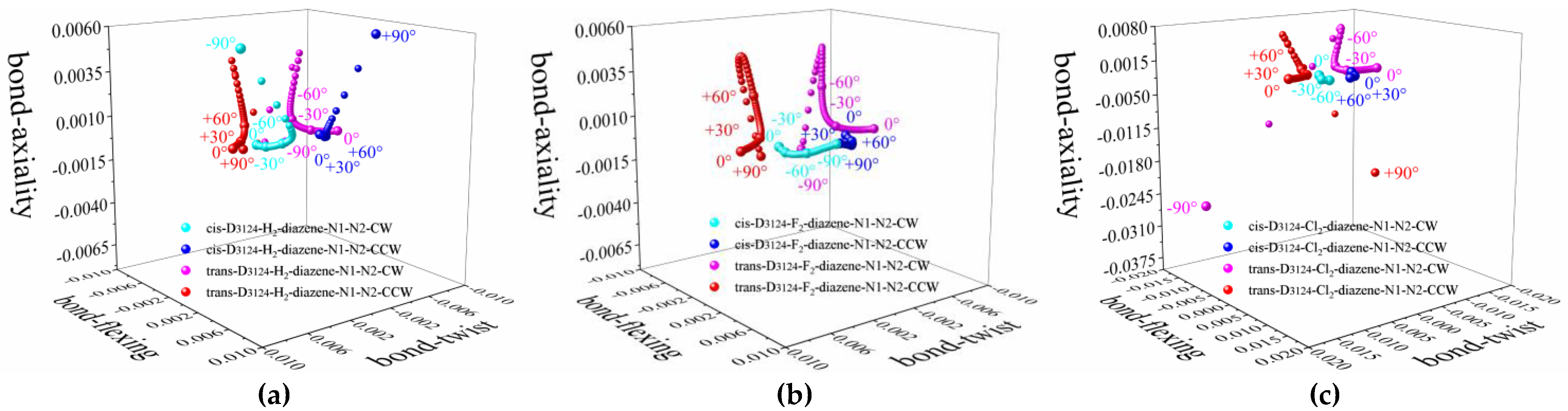
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Garcia-Fernandez, P.; Liu, Y.; Bersuker, I.B.; Boggs, J.E. Pseudo Jahn–Teller Origin of Cis–Trans and Other Conformational Changes. The Role of Double Bonds. Phys. Chem. Chem. Phys. 2011, 13, 3502–3513. [Google Scholar] [CrossRef] [PubMed]
- Feller, D.; Peterson, K.A.; Dixon, D.A. Ab Initio Coupled Cluster Determination of the Heats of Formation of C2H2F2, C2F2, and C2F4. J. Phys. Chem. A 2011, 115, 1440–1451. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T.; Kaneno, D.; Tomoda, S. The Origin of Cis Effect in 1,2-Dihaloethenes: The Quantitative Comparison of Electron Delocalizations and Steric Exchange Repulsions. Bull. Chem. Soc. Jpn. 2008, 81, 1415–1422. [Google Scholar] [CrossRef]
- Zhao, D.B.; Rong, C.Y.; Jenkins, S.; Kirk, S.R.; Yin, D.L.; Liu, S.B. Origin of the Cis-Effect: A Density Functional Theory Study of Doubly Substituted Ethylenes. Acta Phys. Chim. Sin. 2013, 29, 43–54. [Google Scholar] [CrossRef]
- Banerjee, D.; Ghosh, A.; Chattopadhyay, S.; Ghosh, P.; Chaudhuri, R.K. Revisiting the ‘ Cis- Effect’ in 1,2-Difluoro Derivatives of Ethylene and Diazene Using Ab Initio Multireference Methods. Mol. Phys. 2014, 112, 3206–3224. [Google Scholar] [CrossRef]
- Tavanaei, L.; Nori-Shargh, D. New Insights into the Origin of the Cis-Configuration Preferences in 1,2-Dihaloethenes: The Importance of the Bonding Orbital Deviations. Aust. J. Chem. 2018, 71, 1–13. [Google Scholar] [CrossRef]
- Pasto, D.J.; Trobe, M.; Dobrounig, P.; Breinbauer, R. Potassium Azodicarboxylate. In Encyclopedia of Reagents for Organic Synthesis; e-EROS; Wiley: New York, NY, USA, 2001; pp. 1–5. ISBN 978-0-471-93623-7. [Google Scholar]
- Craig, N.C.; Piper, L.G.; Wheeler, V.L. Thermodynamics of Cis-Trans Isomerizations. II. 1-Chloro-2-Fluoroethylenes, 1,2-Difluorocyclopropanes, and Related Molecules. J. Phys. Chem. 1971, 75, 1453–1460. [Google Scholar] [CrossRef]
- Craig, N.C.; Entemann, E.A. Thermodynamics of Cis-Trans Isomerizations. The 1,2-Difluoroethylenes. J. Am. Chem. Soc. 1961, 83, 3047–3050. [Google Scholar] [CrossRef]
- Craig, N.C.; Overend, J. Vibrational Assignments and Potential Constants for Cis- and Trans-1,2-Difluoroethylenes and Their Deuterated Modifications. J. Chem. Phys. 1969, 51, 1127–1142. [Google Scholar] [CrossRef]
- Craig, N.C.; Chen, A.; Suh, K.H.; Klee, S.; Mellau, G.C.; Winnewisser, B.P.; Winnewisser, M. Complete Structure of the Anti Rotamer of 1,2-Difluoroethane from High-Resolution Infrared Spectroscopy. J. Phys. Chem. A 1997, 101, 9302–9308. [Google Scholar] [CrossRef]
- Craig, N.C.; Lo, Y.S.; Piper, L.G.; Wheeler, J.C. Vibrational Assignments and Potential Constants for Cis- and Trans-1-Chloro-2-Fluoroethylenes and Their Deuterated Modifications. J. Phys. Chem. 1970, 74, 1712–1727. [Google Scholar] [CrossRef]
- Wood, R.E.; Stevenson, D.P. The Energy of Isomerization of Cis- and Trans-Dichloroethylene. J. Am. Chem. Soc 2002, 63, 1650–1653. [Google Scholar] [CrossRef]
- Gardner, D.V.; McGreer, D.E. Influence of Steric and Polar Effects in Determining the Equilibrium Position for Cis-Trans-Olefin Pairs. Can. J. Chem. 1970, 48, 2104. [Google Scholar] [CrossRef]
- Craig, N.C.; Brandon, D.W.; Stone, S.C.; Lafferty, W.J. Partial Structure for Trans-1,2-Difluoroethylene from High-Resolution Infrared Spectroscopy. J. Phys. Chem. 1992, 96, 1598–1605. [Google Scholar] [CrossRef]
- Waldron, J.T.; Snyder, W.H. Thermodynamics of Cis-Trans Isomerizations. Relative Stabilities of the 1,2-Dimethoxyethylenes. J. Am. Chem. Soc. 1973, 95, 5491–5495. [Google Scholar] [CrossRef]
- Tokuhashi, K.; Uchimaru, T.; Takizawa, K.; Kondo, S. Rate Constants for the Reactions of OH Radicals with the (E)/(Z) Isomers of CFCl=CFCl and (E)-CHF=CHF. J. Phys. Chem. A 2019, 123, 4834–4843. [Google Scholar] [CrossRef]
- Jenkins, S.; Kirk, S.R.; Rong, C.; Yin, D. The Cis-Effect Using the Topology of the Electronic Charge Density. Mol. Phys. 2012, 111, 1–13. [Google Scholar] [CrossRef]
- Kirk, S.R.; Jenkins, S. Beyond Energetic and Scalar Measures: Next Generation Quantum Theory of Atoms in Molecules. WIREs Computational Molecular Science 2022, Early View, e1611. [Google Scholar] [CrossRef]
- Li, Z.; Xu, T.; Früchtl, H.; van Mourik, T.; Kirk, S.R.; Jenkins, S. Chiral and Steric Effects in Ethane: A next Generation QTAIM Interpretation. Chem. Phys. Lett. 2022, 800, 139669. [Google Scholar] [CrossRef]
- Xu, T.; Nie, X.; Li, S.; Yang, Y.; Früchtl, H.; Mourik, T.; Kirk, S.R.; Paterson, M.J.; Shigeta, Y.; Jenkins, S. Chirality without Stereoisomers: Insight from the Helical Response of Bond Electrons. ChemPhysChem 2021, 22, 1989–1995. [Google Scholar] [CrossRef]
- Xing, H.; Azizi, A.; Momen, R.; Xu, T.; Kirk, S.R.; Jenkins, S. Chirality–Helicity of Cumulenes: A Non-Scalar Charge Density Derived Perspective. Int. J. Quantum Chem. 2022, 122, e26884. [Google Scholar] [CrossRef]
- Hu, M.X.; Xu, T.; Momen, R.; Azizi, A.; Kirk, S.R.; Jenkins, S. The Normal Modes of Vibration of Benzene from the Trajectories of Stress Tensor Eigenvector Projection Space. Chem. Phys. Lett. 2017, 677, 156–161. [Google Scholar] [CrossRef]
- Huang, W.J.; Xu, T.; Kirk, S.R.; Filatov, M.; Jenkins, S. QTAIM and Stress Tensor Bond-Path Framework Sets for the Ground and Excited States of Fulvene. Chem. Phys. Lett. 2018, 713, 125–131. [Google Scholar] [CrossRef]
- Li, J.H.; Huang, W.J.; Xu, T.; Kirk, S.R.; Jenkins, S. Stress Tensor Eigenvector Following with Next-Generation Quantum Theory of Atoms in Molecules. Int. J. Quantum Chem. 2018, 119, e25847. [Google Scholar] [CrossRef]
- Guo, H.; Morales-Bayuelo, A.; Xu, T.; Momen, R.; Wang, L.; Yang, P.; Kirk, S.R.; Jenkins, S. Distinguishing and Quantifying the Torquoselectivity in Competitive Ring-Opening Reactions Using the Stress Tensor and QTAIM. J. Comput. Chem. 2016, 37, 2722–2733. [Google Scholar] [CrossRef]
- Yang, P.; Xu, T.; Momen, R.; Azizi, A.; Kirk, S.R.; Jenkins, S. Fatigue and Photochromism S1 Excited State Reactivity of Diarylethenes from QTAIM and the Stress Tensor. Int. J. Quantum Chem. 2018, 118, e25565. [Google Scholar] [CrossRef]
- Xu, T.; Wang, L.; Ping, Y.; van Mourik, T.; Früchtl, H.; Kirk, S.R.; Jenkins, S. Quinone-Based Switches for Candidate Building Blocks of Molecular Junctions with QTAIM and the Stress Tensor. Int. J. Quantum Chem. 2018, 118, e25676. [Google Scholar] [CrossRef]
- Xu, T.; Farrell, J.; Momen, R.; Azizi, A.; Kirk, S.R.; Jenkins, S.; Wales, D.J. A Stress Tensor Eigenvector Projection Space for the (H2O)5 Potential Energy Surface. Chem. Phys. Lett. 2017, 667, 25–31. [Google Scholar] [CrossRef]
- Bader, R.F.W. Quantum Topology of Molecular Charge Distributions. III. The Mechanics of an Atom in a Molecule. J. Chem. Phys. 1980, 73, 2871–2883. [Google Scholar] [CrossRef]
- Anderson, J.S.M.; Ayers, P.W.; Hernandez, J.I.R. How Ambiguous Is the Local Kinetic Energy?†. J. Phys. Chem. A 2010, 114, 8884–8895. [Google Scholar] [CrossRef]
- Anderson, J.S.M.; Ayers, P.W. Quantum Theory of Atoms in Molecules: Results for the SR-ZORA Hamiltonian. J. Phys. Chem. A 2011, 115, 13001–13006. [Google Scholar] [CrossRef] [PubMed]
- Keith, T.A. AIMAll (19.10.12), TK Gristmill Software, Overland Park KS, USA 2019. Available online: Http://Aim.Tkgristmill.Com (accessed on 9 August 2022).
- Xu, T.; Kirk, S.R.; Jenkins, S. A Comparison of QTAIM and the Stress Tensor for Chirality-Helicity Equivalence in S and R Stereoisomers. Chem. Phys. Lett. 2020, 738, 136907. [Google Scholar] [CrossRef]
- Szarek, P.; Sueda, Y.; Tachibana, A. Electronic Stress Tensor Description of Chemical Bonds Using Nonclassical Bond Order Concept. J. Chem. Phys. 2008, 129, 094102. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.J.; Taylor, P.R. A Diagnostic for Determining the Quality of Single-Reference Electron Correlation Methods. Int. J. Quantum Chem. 1989, 36, 199–207. [Google Scholar] [CrossRef]
- Hegarty, D.; Robb, M.A. Application of Unitary Group Methods to Configuration Interaction Calculations. Mol. Phys. 1979, 38, 1795–1812. [Google Scholar] [CrossRef]
- Robb, M.A.; Niazi, U. The Unitary Group Approach to Electronic Structure Computations. In Reports in Molecular Theory; Weinstein, H., Náray-Szabó, G., Eds.; CRC Press: Boca Raton, FL, USA, 1990; Volume 1, pp. 23–55. [Google Scholar]
- Michael, J.F.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision E.01 2009.
- Brémond, É.; Tognetti, V.; Chermette, H.; Sancho-García, J.C.; Joubert, L.; Adamo, C. Electronic Energy and Local Property Errors at QTAIM Critical Points While Climbing Perdew’s Ladder of Density-Functional Approximations. J. Chem. Theory Comput. 2022, 18, 293–308. [Google Scholar] [CrossRef]
- Yamamoto, T.; Kaneno, D.; Tomoda, S. The Importance of Lone Pair Delocalizations: Theoretical Investigations on the Stability of Cis and Trans Isomers in 1,2-Halodiazenes. J. Org. Chem. 2008, 73, 5429–5435. [Google Scholar] [CrossRef]
- Schneider, S.; Gerken, M.; Haiges, R.; Schroer, T.; Boatz, J.A.; Dixon, D.A.; Grant, D.J.; Christe, K.O. Synthesis and Characterization of Silyldichloramines, Their Reactions with F- Ions, Instability of N2Cl2 and NCl2-, and Formation of NCl3. Inorg. Chem. 2007, 46, 93–102. [Google Scholar] [CrossRef]
- Kirk, S.R.; Jenkins, S. QuantVec. 2021. Available online: https://zenodo.org/record/5553687#.YybZHrRBxPY (accessed on 9 August 2022).
- Li, Z.; Xu, T.; Früchtl, H.; van Mourik, T.; Kirk, S.R.; Jenkins, S. Mixed Chiral and Achiral Character in Substituted Ethane: A Next Generation QTAIM Perspective. Chem. Phys. Lett. 2022, 803, 139762. [Google Scholar] [CrossRef]
- Hanson, R.M.; Musacchio, S.; Mayfield, J.W.; Vainio, M.J.; Yerin, A.; Redkin, D. Algorithmic Analysis of Cahn–Ingold–Prelog Rules of Stereochemistry: Proposals for Revised Rules and a Guide for Machine Implementation. J. Chem. Inf. Model. 2018, 58, 1755–1765. [Google Scholar] [CrossRef]
- Li, Z.; Nie, X.; Xu, T.; Li, S.; Yang, Y.; Früchtl, H.; van Mourik, T.; Kirk, S.R.; Paterson, M.J.; Shigeta, Y.; et al. Control of Chirality, Bond Flexing and Anharmonicity in an Electric Field. Int. J. Quantum Chem. 2021, 121, e26793. [Google Scholar] [CrossRef]
- Bader, R.F.W. A Bond Path: A Universal Indicator of Bonded Interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar] [CrossRef]
- Bader, R.F.W. Bond Paths Are Not Chemical Bonds. J. Phys. Chem. A 2009, 113, 10391–10396. [Google Scholar] [CrossRef] [PubMed]
- Nakatsuji, H. Common Nature of the Electron Cloud of a System Undergoing Change in Nuclear Configuration. J. Am. Chem. Soc. 1974, 96, 24–30. [Google Scholar] [CrossRef]
- Bone, R.G.A.; Bader, R.F.W. Identifying and Analyzing Intermolecular Bonding Interactions in van Der Waals Molecules. J. Phys. Chem. 1996, 100, 10892–10911. [Google Scholar] [CrossRef]
- Jenkins, S.; Heggie, M.I. Quantitative Analysis of Bonding in 90o Partial Dislocation in Diamond. J. Phys. Condens. Matter 2000, 12, 10325–10333. [Google Scholar] [CrossRef]
- Ayers, P.W.; Jenkins, S. An Electron-Preceding Perspective on the Deformation of Materials. J. Chem. Phys. 2009, 130, 154104. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, S.; Morrison, I. The Chemical Character of the Intermolecular Bonds of Seven Phases of Ice as Revealed by Ab Initio Calculation of Electron Densities. Chem. Phys. Lett. 2000, 317, 97–102. [Google Scholar] [CrossRef]
- Jenkins, S.; Maza, J.R.; Xu, T.; Jiajun, D.; Kirk, S.R. Biphenyl: A Stress Tensor and Vector-Based Perspective Explored within the Quantum Theory of Atoms in Molecules. Int. J. Quantum Chem. 2015, 115, 1678–1690. [Google Scholar] [CrossRef]
- Wyatt, R.E. Quantum Dynamics with Trajectories; Interdisciplinary Applied Mathematics, 1st ed.; Springer: Dordrecht, The Netherlands, 2006; ISBN 978-0-387-28145-2. [Google Scholar]
- Xu, T.; Momen, R.; Azizi, A.; van Mourik, T.; Früchtl, H.; Kirk, S.R.; Jenkins, S. The Destabilization of Hydrogen Bonds in an External E-Field for Improved Switch Performance. J. Comput. Chem. 2019, 40, 1881–1891. [Google Scholar] [CrossRef] [PubMed]
- Tian, T.; Xu, T.; van Mourik, T.; Früchtl, H.; Kirk, S.R.; Jenkins, S. Next Generation QTAIM for the Design of Quinone-Based Switches. Chem. Phys. Lett. 2019, 722, 110–118. [Google Scholar] [CrossRef]
- Yang, W.; Zurbenko, I. Kolmogorov–Zurbenko Filters. WIREs Comp. Stat. 2010, 2, 340–351. [Google Scholar] [CrossRef]
- Tian, T.; Xu, T.; Kirk, S.R.; Rongde, I.T.; Tan, Y.B.; Manzhos, S.; Shigeta, Y.; Jenkins, S. Intramolecular Mode Coupling of the Isotopomers of Water: A Non-Scalar Charge Density-Derived Perspective. Phys. Chem. Chem. Phys. 2020, 22, 2509–2520. [Google Scholar] [CrossRef] [PubMed]


| {Tσ, Fσ} | |
|---|---|
| H2 | |
| D3125 {−0.00096[Rσ], 0.00023[Sσ]} D3126 {0.00003[Sσ], 0.00006[Sσ]} D4125 {0.00560[Sσ], 0.00013[Sσ]} D4126 {0.00017[Sσ], −0.00012[Rσ]} | |
| ∑{Tσ, Fσ} | |
| {0.00483[Sσ], 0.00030[Sσ]} | |
| cis-ethene | trans-ethene |
| {Tσ, Fσ} | {Tσ, Fσ} |
| F2 | |
| D3125 {0.00056[Sσ], −0.00190[Rσ]} | {0.01731[Rσ], 0.00000[Qσ]} |
| D3126 {−0.01339[Rσ], 0.00004[Sσ]} | {0.00111[Sσ], 0.00026[Sσ]} |
| D4125 {0.00002[Sσ], −0.00149[Rσ]} | {−0.00030[Rσ], 0.00028[Sσ]} |
| D4126 {0.00143[Sσ], −0.00158[Rσ]} | {−0.00060[Rσ], −0.00011[Rσ]} |
| ∑{Tσ, Fσ} | ∑{Tσ, Fσ} |
| {−0.01138[Rσ], −0.00493[Rσ]} | {−0.01710[Rσ], 0.00043[Sσ]} |
| Cl2 | |
| D3125 {0.14080[Sσ], 0.95259[Sσ]} | {0.00009[Sσ], 0.00022[Sσ]} |
| D3126 {−0.00093[Rσ], 0.00088[Sσ]} | {−0.40475[Rσ], 0.19420[Sσ]} |
| D4125 {-0.00093[Rσ], −0.00001[Rσ]} | {0.00017[Sσ], −0.00091[Rσ]} |
| D4126 {−0.38727[Rσ], 0.11232[Sσ]} | {0.00033[Sσ], 0.00001[Sσ]} |
| ∑{Tσ, Fσ} | ∑{Tσ, Fσ} |
| {−0.24833[Rσ], 1.06578[Sσ]} | {−0.40417[Rσ], 0.19351[Sσ]} |
| cis-diazene | trans-diazene |
| {Tσ, Fσ} | {Tσ, Fσ} |
| H2 | |
| {0.00812[Sσ], 0.00016[Sσ]} | {−0.00176[Rσ]}, {0.00070[Sσ]} |
| F2 | |
| {−0.01077[Rσ], −0.00886[Rσ]} | {0.00023[Sσ]}, {0.00014[Sσ]} |
| Cl2 | |
| {0.00020[Sσ], 0.00672[Sσ]} | {−0.00022[Rσ]}, {−0.00402[Rσ]} |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Yu, W.; Feng, X.; Xu, T.; Früchtl, H.; van Mourik, T.; Kirk, S.R.; Jenkins, S. The Cis-Effect Explained Using Next-Generation QTAIM. Molecules 2022, 27, 6099. https://doi.org/10.3390/molecules27186099
Peng Y, Yu W, Feng X, Xu T, Früchtl H, van Mourik T, Kirk SR, Jenkins S. The Cis-Effect Explained Using Next-Generation QTAIM. Molecules. 2022; 27(18):6099. https://doi.org/10.3390/molecules27186099
Chicago/Turabian StylePeng, Yuting, Wenjing Yu, Xinxin Feng, Tianlv Xu, Herbert Früchtl, Tanja van Mourik, Steven R. Kirk, and Samantha Jenkins. 2022. "The Cis-Effect Explained Using Next-Generation QTAIM" Molecules 27, no. 18: 6099. https://doi.org/10.3390/molecules27186099
APA StylePeng, Y., Yu, W., Feng, X., Xu, T., Früchtl, H., van Mourik, T., Kirk, S. R., & Jenkins, S. (2022). The Cis-Effect Explained Using Next-Generation QTAIM. Molecules, 27(18), 6099. https://doi.org/10.3390/molecules27186099