Prediction of pH Value of Aqueous Acidic and Basic Deep Eutectic Solvent Using COSMO-RS σ Profiles’ Molecular Descriptors
Abstract
:1. Introduction
2. Results and Discussion
2.1. DES Characteristics: Experimental pH Values and σ Profiles
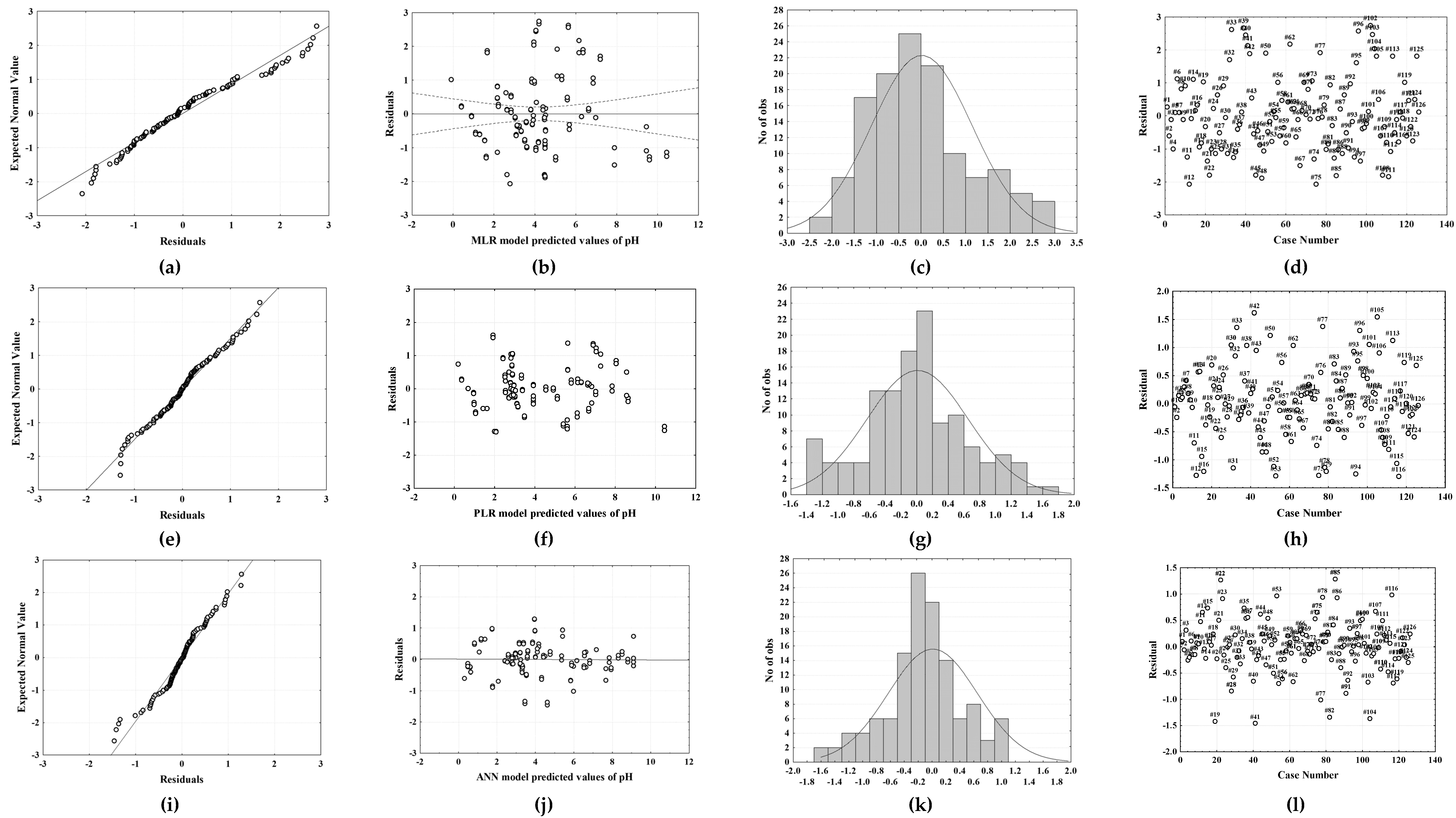
2.2. Multiple Linear Regression and Piecewise Linear Regression
2.3. Artificial Neural Network Modelling
2.4. MLR, PLR, and ANN Models’ Independent Validation
3. Materials and Methods
3.1. Materials
3.2. Methods
3.2.1. DES Preparation
3.2.2. pH Value Measurement
3.2.3. Calculation of DES Constituents’ σ Profiles and Descriptors
3.2.4. Calculation of DES Descriptors
3.2.5. Modeling of Correlation between pH and Descriptors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Appendix A
| Intervals | B Betaine | ChCl Choline Chloride | Pro LDproline | CA Citric Acid | MA Malic Acid | OxA Oxalic Acid | U Urea | H2O | ||
|---|---|---|---|---|---|---|---|---|---|---|
| σ-profile | [−0.025; −0.02] | 1 | 0 | 0 | 0.506 | 4.861 | 3.5955 | 0 | 0 | 0 |
| [−0.02; −0.015] | 2 | 0 | 0 | 5.186 | 14.9695 | 10.5215 | 7.5105 | 6.35 | 6.35 | |
| [−0.015; −0.01] | 3 | 11.869 | 16.1615 | 6.9485 | 13.5665 | 9.368 | 20.482 | 10.027 | 10.027 | |
| [−0.01; −0.005] | 4 | 59.1185 | 66.196 | 17.199 | 29.212 | 28.535 | 9.0145 | 3.5195 | 3.5195 | |
| [−0.005; 0.0] | 5 | 36.625 | 34.4875 | 60.605 | 29.3465 | 23.3925 | 7.9265 | 2.1635 | 2.1635 | |
| [0.0; 0.005] | 6 | 4.5285 | 5.6435 | 21.7815 | 23.467 | 18.1455 | 13.051 | 2.8725 | 2.8725 | |
| [0.005; 0.01] | 7 | 3.2405 | 6.6525 | 10.6 | 37.877 | 25.726 | 7.606 | 4.055 | 4.055 | |
| [0.01; 0.015] | 8 | 7.719 | 18.3 | 17.614 | 38.933 | 30.6435 | 11.679 | 5.2285 | 5.2285 | |
| [0.015; 0.02] | 9 | 22.3525 | 30.0465 | 5.2065 | 1.0135 | 2.3845 | 13.8265 | 8.2765 | 8.2765 | |
| [0.02; 0.025] | 10 | 8.202 | 0.0525 | 1.3475 | 0 | 0 | 0 | 0.172 | 0.5775 | |
| Intervals | EG ethylene glycol | Sol sorbitol | Gly glycerol | Xyol xylitol | Fru Dfructose | Glc Dglucose | Suc sucrose | Xyl Dxylose | ||
| σ-profile | [−0.025; −0.02] | 1 | 0 | 0.1725 | 0.013 | 0.037 | 0.1655 | 0.213 | 0.108 | 0.037 |
| [−0.02; −0.015] | 2 | 3.8055 | 15.884 | 7.828 | 9.216 | 11.8325 | 23.022 | 11.1905 | 8.7015 | |
| [−0.015; −0.01] | 3 | 7.638 | 20.8955 | 11.4065 | 15.941 | 16.9895 | 28.444 | 14.5935 | 12.9035 | |
| [−0.01; −0.005] | 4 | 20.2675 | 41.5705 | 19.6085 | 43.0415 | 36.2095 | 61.232 | 35.406 | 34.6755 | |
| [−0.005; 0.0] | 5 | 28.038 | 30.5525 | 34.6465 | 35.965 | 39.319 | 54.567 | 28.5165 | 45.0735 | |
| [0.0; 0.005] | 6 | 9.973 | 18.7645 | 15.0725 | 19.083 | 19.565 | 29.1605 | 15.066 | 17.7475 | |
| [0.005; 0.01] | 7 | 7.9725 | 21.5775 | 10.103 | 20.848 | 19.4555 | 26.6145 | 20.4555 | 17.2715 | |
| [0.01; 0.015] | 8 | 10.5605 | 28.283 | 17.194 | 28.977 | 30.9465 | 47.3685 | 29.0795 | 23.517 | |
| [0.015; 0.02] | 9 | 9.6155 | 20.752 | 10.7865 | 10.9745 | 11.901 | 26.0425 | 8.4485 | 12.688 | |
| [0.02; 0.025] | 10 | 0.0035 | 0.15 | 0.0115 | 0 | 0 | 1.082 | 0 | 0.005 | |
References
- Anastas, P.T.; Beach, E.S. Green Chemistry: The Emergence of a Transformative Framework. Green Chem. Lett. Rev. 2008, 1, 9–24. [Google Scholar] [CrossRef] [Green Version]
- Cvjetko Bubalo, M.; Vidović, S.; Radojčić Redovniković, I.; Jokić, S. Green Solvents for Green Technologies. J. Chem. Technol. Biotechnol. 2015, 90, 1631–1639. [Google Scholar] [CrossRef]
- Lanza, V.; Vecchio, G. New Conjugates of Superoxide Dismutase/Catalase Mimetics with Cyclodestrins. J. Inorg. Biochem. 2009, 103, 381–388. [Google Scholar] [CrossRef] [PubMed]
- Abbott, A.P.; Capper, G.; Davies, D.L.; Rasheed, R.K.; Tambyrajah, V. Novel Solvent Properties of Choline Chloride/Urea Mixtures. Chem. Commun. 2003, 10, 70–71. [Google Scholar] [CrossRef] [Green Version]
- Martins, M.A.R.; Pinho, S.P.; Coutinho, J.A.P. Insights into the Nature of Eutectic and Deep Eutectic Mixtures. J. Solut. Chem. 2019, 48, 962–982. [Google Scholar] [CrossRef] [Green Version]
- Paiva, A.; Matias, A.A.; Duarte, A.R.C. How Do We Drive Deep Eutectic Systems towards an Industrial Reality? Curr. Opin. Green Sustain. Chem. 2018, 11, 81–85. [Google Scholar] [CrossRef] [Green Version]
- Mitar, A.; Panić, M.; Prlić Kardum, J.; Halambek, J.; Sander, A.; Zagajski Kučan, K.; Radojčić Redovniković, I.; Radošević, K. Physicochemical Properties, Cytotoxicity, and Antioxidative Activity of Natural Deep Eutectic Solvents Containing Organic Acid. Chem. Biochem. Eng. Q. 2019, 33, 1–18. [Google Scholar] [CrossRef]
- Abbott, A.P.; Alabdullah, S.S.M.; Al-Murshedi, A.Y.M.; Ryder, K.S. Brønsted Acidity in Deep Eutectic Solvents and Ionic Liquids. Faraday Discuss. 2017, 206, 365–377. [Google Scholar] [CrossRef]
- Farias, F.O.; Passos, H.; Coutinho, J.A.P.; Mafra, M.R. PH Effect on the Formation of Deep-Eutectic-Solvent-Based Aqueous Two-Phase Systems. Ind. Eng. Chem. Res. 2018, 57, 16917–16924. [Google Scholar] [CrossRef]
- Klamt, A.; Jonas, V.; Bürger, T.; Lohrenz, J.C.W. Refinement and Parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. [Google Scholar] [CrossRef]
- Benguerba, Y.; Alnashef, I.M.; Erto, A.; Balsamo, M.; Ernst, B. A Quantitative Prediction of the Viscosity of Amine Based DESs Using Sσ-Profile Molecular Descriptors. J. Mol. Struct. 2019, 1184, 357–363. [Google Scholar] [CrossRef]
- Lemaoui, T.; Hammoudi, N.E.H.; Alnashef, I.M.; Balsamo, M.; Erto, A.; Ernst, B.; Benguerba, Y. Quantitative Structure Properties Relationship for Deep Eutectic Solvents Using Sσ-Profile as Molecular Descriptors. J. Mol. Liq. 2020, 309, 113165. [Google Scholar] [CrossRef]
- Lemaoui, T.; Abu Hatab, F.; Darwish, A.S.; Attoui, A.; Hammoudi, N.E.H.; Almustafa, G.; Benaicha, M.; Benguerba, Y.; Alnashef, I.M. Molecular-Based Guide to Predict the PH of Eutectic Solvents: Promoting an Efficient Design Approach for New Green Solvents. ACS Sustain. Chem. Eng. 2021, 9, 5783–5808. [Google Scholar] [CrossRef]
- Silva, L.P.; Fernandez, L.; Conceiçao, J.H.F.; Martins, M.A.R.; Sosa, A.; Ortega, J.; Pinho, S.P.; Coutinho, J.A.P. Design and Characterization of Sugar-Based Deep Eutectic Solvents Using Conductor-like Screening Model for Real Solvents. ACS Sustain. Chem. Eng. 2018, 6, 10724–10734. [Google Scholar] [CrossRef] [Green Version]
- Hayyan, A.; Mjalli, F.S.; Alnashef, I.M.; Al-Wahaibi, T.; Al-Wahaibi, Y.M.; Hashim, M.A. Fruit Sugar-Based Deep Eutectic Solvents and Their Physical Properties. Thermochim. Acta 2012, 541, 70–75. [Google Scholar] [CrossRef]
- Cheng, C.L.; Shalabh; Garg, G. Coefficient of Determination for Multiple Measurement Error Models. J. Multivar. Anal. 2014, 126, 137–152. [Google Scholar] [CrossRef] [Green Version]
- Le Man, H.; Behera, S.K.; Park, H.S. Optimization of Operational Parameters for Ethanol Production from Korean Food Waste Leachate. Int. J. Environ. Sci. Technol. 2009, 7, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Feng, C.; Feng, C.; Li, L.; Sadeghpour, A. A Comparison of Residual Diagnosis Tools for Diagnosing Regression Models for Count Data. BMC Med. Res. Methodol. 2020, 20, 175. [Google Scholar] [CrossRef]
- Matešić, N.; Jurina, T.; Benković, M.; Panić, M.; Valinger, D.; Gajdoš Kljusurić, J.; Jurinjak Tušek, A. Microwave-Assisted Extraction of Phenolic Compounds from Cannabis Sativa L.: Optimization and Kinetics Study. Sep. Sci. Technol. 2020, 56, 2047–2060. [Google Scholar] [CrossRef]
- Greenland, S.; Senn, S.J.; Rothman, K.J.; Carlin, J.B.; Poole, C.; Goodman, S.N.; Altman, D.G. Statistical Tests, P Values, Confidence Intervals, and Power: A Guide to Misinterpretations. Eur. J. Epidemiol. 2016, 31, 337–350. [Google Scholar] [CrossRef] [Green Version]
- Abranches, D.O.; Larriba, M.; Silva, L.P.; Melle-Franco, M.; Palomar, J.F.; Pinho, S.P.; Coutinho, J.A.P. Using COSMO-RS to Design Choline Chloride Pharmaceutical Eutectic Solvents. Fluid Phase Equilibria 2019, 497, 71–78. [Google Scholar] [CrossRef] [Green Version]
- Jurinjak Tušek, A.; Jurina, T.; Benković, M.; Valinger, D.; Belščak-Cvitanović, A.; Kljusurić, J.G. Application of Multivariate Regression and Artificial Neural Network Modelling for Prediction of Physical and Chemical Properties of Medicinal Plants Aqueous Extracts. J. Appl. Res. Med. Aromat. Plants 2020, 16, 100229. [Google Scholar] [CrossRef]

| DES | Abbreviation | Molar Ratio | wH2O [%] | pH (20 °C) ± st.dev. |
|---|---|---|---|---|
| Betaine:citric acid | B:CA | 1:1 | 30 | 2.46 ± 0.04 |
| 50 | 2.46 ± 0.02 | |||
| Betaine:ethylene glycol | B:EG | 1:2 | 30 | 6.86 ± 0.00 |
| Betaine:glucose | B:Glc | 1:1 | 10 | 6.64 ± 0.35 |
| Betaine:glycerol | B:Gly | 1:2 | 30 | 6.77 ± 0.04 |
| 50 | 6.38 ± 0.07 | |||
| Betaine:oxalic acid:glycerol | B:OxA:Gly | 1:2:1 | 30 | 2.91 ± 0.05 |
| Betaine:malic acid | B:Ma | 1:1 | 30 | 2.98 ± 0.01 |
| 50 | 2.92 ± 0.01 | |||
| Betaine:sucrose | B:Suc | 4:1 | 30 | 7.85 ± 0.11 |
| Choline chloride:citric acid | Ch:CA | 2:1 | 30 | 0.34 ± 0.04 |
| 50 | 0.71 ± 0.00 | |||
| Choline chloride:ethylene glycol | ChCl:EG | 1:2 | 10 | 6.19 ± 0.01 |
| 30 | 6.60 ± 0.57 | |||
| 50 | 4.58 ± 0.14 | |||
| 80 | 4.41 ± 0.00 | |||
| Choline chloride:fructose | ChCl:Fru | 1:1 | 30 | 3.51 ± 0.05 |
| 50 | 3.35 ± 0.03 | |||
| Choline chloride:glucose | ChCl:Glc | 1:1 | 30 | 4.83 ± 0.06 |
| 50 | 3.56 ± 0.01 | |||
| Choline chloride:glycerol | ChCl:Gly | 1:2 | 30 | 3.71 ± 0.06 |
| 50 | 2.67 ± 0.11 | |||
| 80 | 3.06 ± 0.01 | |||
| Choline chloride:malic acid | ChCl:MA | 1:1 | 30 | 0.63 ± 0.01 |
| 50 | 1.03 ± 0.00 | |||
| Choline chloride:proline:malic acid | ChCl:Pro:MA | 1:1:1 | 10 | 3.23 ± 0.00 |
| 30 | 2.82 ± 0.01 | |||
| 50 | 2.63 ± 0.03 | |||
| Choline chloride:sorbitol | ChCl:Sol | 1:1 | 50 | 4.92 ± 0.04 |
| 80 | 3.80 ± 0.08 | |||
| Choline chloride:urea | ChCl:U | 1:2 | 10 | 9.26 ± 0.08 |
| 30 | 8.85 ± 0.06 | |||
| 50 | 8.23 ± 0.04 | |||
| Choline chloride:urea:ethylene glycol | ChCl:U:EG | 1:2:2 | 10 | 8.29 ± 0.07 |
| Choline chloride:urea:glycerol | ChCl:U:Gly | 1:2:2 | 10 | 8.72 ± 0.05 |
| Choline chloride:xylose | ChCl:Xyl | 2:1 | 30 | 2.86 ± 0.04 |
| 50 | 3.32 ± 0.03 | |||
| 80 | 3.93 ± 0.01 | |||
| Choline chloride:xylitol | ChCl:Xyol | 5:2 | 30 | 6.90 ± 0.06 |
| 50 | 6.50 ± 0.01 | |||
| 80 | 6.03 ± 0.06 | |||
| Choline chloride:fructose | ChCl:Fru | 1:1 | 30 | 3.51 ± 0.05 |
| 50 | 3.35 ± 0.03 | |||
| Citric acid:glucose | CA:Glc | 1:1 | 30 | 0.53 ± 0.04 |
| Citric acid:sucrose | CA:Suc | 1:1 | 30 | 0.83 ± 0.00 |
| Fructose:ethylene glycol | Fru:EG | 1:2 | 30 | 5.31 ± 0.09 |
| Fructose:glucose:ethylene glycol | Fru:Glc:EG | 1:1:2 | 50 | 3.67 ± 0.06 |
| Fructose:glucose:sucrose | Fru:Glc:Suc | 1:1:1 | 50 | 2.63 ± 0.03 |
| 80 | 2.99 ± 0.01 | |||
| Fructose:glucose:urea | Fru:Glc:U | 1:1 | 30 | 8.22 ± 0.06 |
| Glucose:ethylene glycol | Glc:EG | 1:2 | 50 | 4.03 ± 0.02 |
| Glucose:glycerol | Glc:Gly | 1:2 | 50 | 4.33 ± 0.04 |
| Malic acid:fructose | MA:Fru | 1:1 | 30 | 0.77 ± 0.01 |
| Malic acid:fructose:glycerol | MA:Fru:Gly | 1:1 | 30 | 2.77 ± 0.01 |
| Malic acid:glucose | MA:Glc | 1:1 | 30 | 0.83 ± 0.01 |
| Malic acid:glucose:glycerol | MA:Glc:Gly | 1:1:1 | 10 | 0.92 ± 0.00 |
| Malic acid:sucrose | MA:Suc | 2:1 | 30 | 0.66 ± 0.01 |
| Proline:malic acid | Pro:MA | 1:1 | 10 | 2.63 ± 0.01 |
| 30 | 2.78 ± 0.02 | |||
| 50 | 2.73 ± 0.03 | |||
| Sucrose:ethylene glycol | Suc:EG | 1:2 | 30 | 6.05 ± 0.06 |
| Sucrose:glucose:urea | Suc:Glc:U | 1:1 | 30 | 8.14 ± 0.25 |
| Xylose:ethylene glycol | Xyl:EG | 1:2 | 30 | 4.57 ± 0.06 |
| MLR | PLR | |||
|---|---|---|---|---|
| Regression Coeff. ± st. Error | p-Value | Regression Coeff. ± st. Error | p-Value | |
| Break point | 4.1246 ± 0.3292 | 0.0021 | ||
| b0 | −13.4623 ± 4.9782 | 0.0078 | −1.9449 ± 0.1556 −80.4560 ± 10.6436 | 0.0001 |
| b1 (S1mix) | 16.4623 ± 5.1388 | 0.0022 | 14.8847 ± 2.1908 −23.1982 ± 1.8558 | 0.0001 |
| b2 (S2mix) | 9.1349 ± 2.4418 | 0.0003 | 10.2415 ± 2.3918 27.8095 ± 2.2247 | 0.0001 |
| b3 (S3mix) | 9.7560 ± 2.5748 | 0.0002 | 9.1933 ± 1.7354 35.1992 ± 2.8159 | <0.0001 |
| b4 (S4mix) | 4.2440 ± 1.1602 | 0.0004 | 4.8581 ± 1.1221 11.2879 ± 1.1902 | <0.0001 |
| b5 (S5mix) | 2.2980 ± 0.6482 | 0.0006 | 2.5621 ± 0.1188 10.1747 ± 1.3976 | <0.0001 |
| b6 (S6mix) | −0.9176 ± 1.0696 | 0.3927 | −2.4281 ± 0.8779 −14.7126 ± 1.1770 | 0.2666 |
| b7 (S7mix) | −4.5381 ± 1.1435 | 0.0020 | −4.1497 ± 0.6632 −9.6777 ± 0.7742 | <0.0001 |
| b8 (S8mix) | −8.9573 ± 1.9634 | <0.0001 | −9.2237 ± 1.6373 −25.6581 ± 2.0526 | <0.0001 |
| b9 (S9mix) | −10.0312 ± 2.8589 | 0.0006 | −11.4736 ± 3.6473 −32.0013 ± 2.5601 | 0.0001 |
| b10 (S10mix) | −12.9604 ± 3.6943 | 0.0006 | −13.9250 ± 4.4560 −42.7492 ± 3.4199 | 0.0001 |
| R2 | 0.7758 | 0.9654 | ||
| R2adj | 0.7564 | 0.9624 | ||
| RMSE | 1.1865 | 0.6558 | ||
| F value | 39.8120 | 39.8120 | ||
| p-value | <0.0001 | <0.0001 | ||
| Network Name | Training Perf./ Training Error | Test Perf./ Test Error | Validation Perf./ Validation Error | Hidden Activation | Output Activation |
|---|---|---|---|---|---|
| MLP 10-13-1 | 0.9734, 0.0021 | 0.9751, 0.0031 | 0.9578, 0.0042 | Logistic | Logistic |
| MLP 10-11-1 | 0.9812, 0.0013 | 0.9802, 0.0018 | 0.9794, 0.0018 | Tanh | Exponential |
| MLP 10-10-1 | 0.9803, 0.0013 | 0.9827, 0.0016 | 0.9788, 0.0019 | Tanh | Tanh |
| MLP 10-10-1 | 0.9808, 0.0017 | 0.9806, 0.0021 | 0.9716, 0.0019 | Tanh | Logistic |
| MLP 10-5-1 | 0.9868, 0.0011 | 0.9799, 0.0012 | 0.9797, 0.0012 | Tanh | Logistic |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panić, M.; Radović, M.; Cvjetko Bubalo, M.; Radošević, K.; Rogošić, M.; Coutinho, J.A.P.; Radojčić Redovniković, I.; Jurinjak Tušek, A. Prediction of pH Value of Aqueous Acidic and Basic Deep Eutectic Solvent Using COSMO-RS σ Profiles’ Molecular Descriptors. Molecules 2022, 27, 4489. https://doi.org/10.3390/molecules27144489
Panić M, Radović M, Cvjetko Bubalo M, Radošević K, Rogošić M, Coutinho JAP, Radojčić Redovniković I, Jurinjak Tušek A. Prediction of pH Value of Aqueous Acidic and Basic Deep Eutectic Solvent Using COSMO-RS σ Profiles’ Molecular Descriptors. Molecules. 2022; 27(14):4489. https://doi.org/10.3390/molecules27144489
Chicago/Turabian StylePanić, Manuela, Mia Radović, Marina Cvjetko Bubalo, Kristina Radošević, Marko Rogošić, João A. P. Coutinho, Ivana Radojčić Redovniković, and Ana Jurinjak Tušek. 2022. "Prediction of pH Value of Aqueous Acidic and Basic Deep Eutectic Solvent Using COSMO-RS σ Profiles’ Molecular Descriptors" Molecules 27, no. 14: 4489. https://doi.org/10.3390/molecules27144489
APA StylePanić, M., Radović, M., Cvjetko Bubalo, M., Radošević, K., Rogošić, M., Coutinho, J. A. P., Radojčić Redovniković, I., & Jurinjak Tušek, A. (2022). Prediction of pH Value of Aqueous Acidic and Basic Deep Eutectic Solvent Using COSMO-RS σ Profiles’ Molecular Descriptors. Molecules, 27(14), 4489. https://doi.org/10.3390/molecules27144489







