3.1. HOOH
The computed rovibrational spectra for HOOH in this work provide reference benchmarks to show spectral differences between it and the sulfur analogs. As seen in
Table 1, F12-TZ surprisingly outperforms CcCR by producing the more accurate rotational constants compared to experiment. F12-TZ’s
value of 26,171.3 MHz is lower than the experimental [
51] value of 26,194.08965 MHz by 22.8 MHz, an error of 0.09%. In contrast, the
rotational constant computed via the CcCR QFF method is 82.1 MHz higher than the experimental value with the
following suit, having a difference of 169.2 MHz. This, however, is not surprising, as previous computational studies [
52] on this molecule also fail to capture accurate rotational constants possibly due to the large amplitude motion of the torsion. Regardless, the difference between CcCR and the experiment for the
and
constants are 0.31% and 0.67% in error, respectively.
With regard to most vibrational frequencies, the present work agrees well with both the previous theory and experiment, as shown in
Table 2. The fundamental frequencies produced by the F12-TZ method compares well with the gas-phase experiment [
57] with the
frequency, the symmetric H–O–O bend at 1393.9 cm
, being 0.4 cm
higher than the experimental fundamental of 1393.5 cm
. CcCR compares similarly with the
frequency, the O–O stretch with a fundamental of 878.4 cm
, being 0.5 cm
higher than gas-phase value of 877.93 cm
. The worst agreement is the
frequency, the torsion, with F12-TZ and CcCR being 51.5 and 56.2 cm
lower than experiment, respectively. Once again, as discussed in previous literature [
52], this may be attributed to the large amplitude motion of the torsion. A previous theoretical study [
52] utilizes a similar QFF method also employing the CCSD(T)-F12/cc-pVTZ-F12 level of theory, but the previous work uses a different fitting model than the present work and does not mention the inclusion of resonance polyads in the VPT2 corrections. To that end, the difference between the previous theoretical study and the present work is to be expected with most fundamental frequencies being within 0.5 cm
, and the worst agreement being the
fundamental with less than an 8.0 cm
difference.
The inaccuracies in both the rotational constants and the anharmonic vibrational frequencies for
warrant an investigation of the potential well for this torsional motion of HOOH. As seen in
Figure 2A, a relaxed scan of the torsional angle produces an extremely flat potential well with a torsional trans-barrier of 371.9 cm
(1.06 kcal/mol). A previous theoretical study [
60] also investigated the trans-barrier height, seen in
Figure 2A, and calculates the trans-barrier 1.17 kcal/mol higher than the current work at 2.23 kcal/mol (∼780 cm
). However, a previous experimental value [
61] for the trans-barrier at 387.07 cm
is closer to the present work’s trans-barrier than previous theory. The previous theory utilizes the HF/STO level of theory so the inaccuracy compared to the experiment is to be expected. In any case, a molecule with a mode that exhibits a flat potential can be notorious for its inability to be accurately modeled with VPT2 corrections as used in the present work. As stated previously, CcCR QFF methods generally provide more accurate ground state rotational constants. However, due to the composite nature of the method, there are conflicting minima for the potential energy surface, thus introducing additional inaccuracy. This same inaccuracy has been seen as well for [Al, N, C, O] isomers [
62]. While there is still considerable accuracy to experiment for the remainder of the fundamentals, the large amplitude motion of the torsion decreases the overall accuracy of the ground state rotational constants, seemingly preventing the accurate rovibrational modeling of this molecule.
Further, several two-quanta vibrational overtones and combination bands for HOOH have not been reported in the current literature. In order to assist in further potential astrophysical observation, the present work introduces the missing overtones and combination bands for HOOH, as seen in
Table 3. In current literature, two previous studies attribute the same value of 7041.8 cm
to either the 2
or
two-quanta band, Halonen [
63] and Redington et al. [
64], respectively. The present work’s F12-TZ value for the
combination band is 7034.3 cm
falling in a similar region with the value attributed to the value from Redington et al. [
64] with only a difference of 7.5 cm
. Another previous experimental value, from Dzugan et al. [
65], for the
combination band, at 7050 cm
, also falls within the same region as the present work’s theoretical value along the work from both Halonen [
63] and Redington et al. [
64]. Based on the agreement between the present work’s value and each of the previous studies values for the band in question, this band is attributed to the
combination band for HOOH.
With regard to other two-quanta modes, previous gas-phase experimental work is available for comparison [
64]. The previous experimental
combination band, at 4827.49, does not compare favorably to the present F12-TZ value of 4873.8, or a 46.3 cm
difference. Both the
and
two-quanta bands from the previous gas-phase experiment [
64], however, compare exceptionally well to the present theoretical study. The previous gas-phase
value of 4982.57 cm
is 0.8 cm
higher than the present F12-TZ combination band. Similarly, the previous gas-phase
value of 4487.27 cm
is 2.4 cm
higher than the present CcCR value of 4484.9 cm
. While some two-quanta modes compare well to experiment, the slight inaccuracy compared to the experiment for the other two-quanta bands is not unexpected as the available previous gas-phase experiment was conducted in 1962. Therefore, the present work’s theoretical values will serve as a benchmark for any further laboratory analysis, even for the overtones and combination bands.
Analysis of the computed two-quanta mode intensities show far weaker transitions than the anharmonic vibrational frequencies with the brightest two transitions, the and combination bands, at a mere 5.0 km/mol. Outside of these modes, no two-quanta modes are present that exhibit intensities greater than 1.0 km/mol. Though these transitions are weak, the and band fall within the elusive, and consequently understudied, near- to mid-IR spectrum, 1.4 m and 3.7 m range, respectively. With the recently launched James Webb Space Telescope (JWST), the proper instrumentation to analyze this region of the IR spectrum is now achievable with its near infrared spectrograph. Since these fall within the region of the IR dominated by polycyclic aromatic hydrocarbons (PAHs), the data provided in this work will be instrumental in identifying molecules in this region that are unrelated to these PAHs but have yet to be identified.
3.2. HOSH
Considering HOSH’s analogous nature and similar geometry to HOOH, a potential energy scan of the torsional motion for this molecule is also investigated. In
Figure 2B, a considerably deeper potential well, with a trans-barrier height of 1536.4 cm
for the torsion, is seen compared to the potential well for HOOH. With this deeper well, the rovibrational spectra of HOSH will not suffer from the same inaccuracies in its VPT2 corrections. For this reason, the geometrical parameters and rotational constants, given in
Table 4, show a much higher accuracy compared to experiment than that of HOOH. The CcCR value for
of 15,299.9 MHz is in good agreement with the experimental gas-phase value of 15,282 MHz [
67], giving a difference of only 17.9 MHz, which is only an error of 0.12% [
29]. The F12-TZ value is less accurate, as expected, with a difference of ∼40 MHz, an error of 0.26%, further supporting the accuracy of rotational constants computed using CcCR versus F12-TZ when compared to the experiment. Similarly, the
rotational constant shares a 20.4 MHz difference, 0.14% error, between the CcCR value and the previous experimental value of 14,840 MHz, while the F12-TZ
value is 34.7 MHz lower than the experimental method, an error of 0.23%. A previous theoretical study [
68], however, performs more accurately when compared to the experiment and calculates rotational constants at the CCSD(T, full)/cc-pwCVQZ level with vibration–rotation corrections from the CCSD(T)/cc-pV(T+d)Z level of theory and finds the
and
to be within 7.0 and 3.0 MHz, respectively. The difference in accuracy for these rotational constants may largely be due to the previous computational study’s implementation of the CCSD(T, full)/cc-pwCVQZ level of theory with vibrational corrections at the CCSD(T)/cc-pV(T+d)Z level, which is considered to be a more theoretically rigorous composite method.
Additionally, a previous theoretical study [
71] simulates the full rotational line spectrum of HOSH at the CCSD(T)/aug-cc-pV(Q+d) level of theory through the use of the TROVE program [
72]. While the present study utilizes VPT2 to generate accurate rovibrational constants and fundamental frequencies, TROVE implements a variational method for generating accurate rotational energies. The present CcCR
rotational constant of 15,299.9 MHz is 16.1 MHz higher than the previous theory’s
of 15,283.8 MHz, which is only in error of 0.11%. The comparable ground state rotational constants are derived from the rotational energies provided in the previous study. Furthermore, the CcCR
value of 14,860.4 MHz is 22.1 MHz greater than the previous theoretical
value of 14,838.3, only a 0.15% error. While the previous theoretical ground state rotational constants are more accurate compared to experiment, the small margin of error between the present and previous methods still suggests the validity and accuracy of the current VPT2 methodology for generating accurate rotational constants for systems of this type.
Presently, HOSH only has two observed fundamental frequencies by previous gas-phase experiment [
73], as seen in
Table 5: the O–H stretch at 3625.6 cm
and the, tentatively assigned, S–H stretch at 2538 cm
. The present F12-TZ
fundamental of 3626.7 cm
compares favorably with the gas-phase value of 3625.6 cm
. Both the present work and previous theory compare similarly with the gas-phase
fundamental at 2538 cm
with the F12-TZ fundamental being 6.9 cm
higher than experiment, and previous theory at 4.7 cm
lower than the experimental value.
In a previous experimental work conducted by Beckers et al. [
73], the IR spectrum of the S–H stretch was investigated and shown to be just above the
combination band from the SO
byproduct from the experiment. Due to the overlap from this combination band on the lower J branches, the previous work was unable to confirm the full assignment of this fundamental mode. In 2009, Yurchenko et al. [
74] simulated an IR spectrum for the S–H stretching region, utilizing the TROVE program at the aug-cc-pV(Q+d)Z level of theory, to explain perturbations found in the experimental S–H stretching frequency. The previous simulated spectrum is in good qualitative agreement with the region around the band center of the S–H stretching region, but lacks any comparison to the lower or higher frequency bands. The present study provides a simulated IR spectrum generated through PGOPHER’s [
75] vibrational spectrum simulation software. In
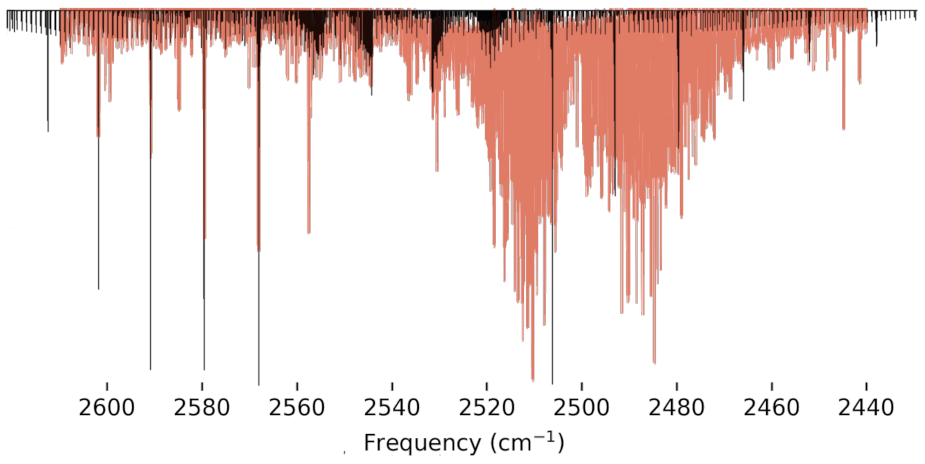
Figure 3, the S–H stretching fundamental frequency is centered on the previous experiment’s fundamental at 2538 cm
in order to compare the overall rovibrational structure from the presently-computed vibrationally excited rotational constants provided by the use of the VPT2 methodology in this work with that from the previously reported laboratory spectrum. The bands align closely with the lower J bands of the previous experimental IR spectrum, only deviating after the third band. These deviations from higher frequencies can be attributed to the present work’s rotational constants being lower than experiment, which is expected.
Moving toward detectability, the anharmonic intensities, seen in
Table 5, show two relatively high intensity vibrational transitions. HOSH’s most intense transition is, again, the
torsion at 72 km/mol, while the second is the
, O–H stretch, fundamental transition at 67 km/mol. Compared to what is considered the intense transition of the anti-symmetric stretch of water at 70 km/mol, the two aforementioned transitions of HOSH are of similar intensity suggesting these are readily detectable. An additional benefit of the use of the QFF methods in this work is their ability to produce not only highly accurate ground vibrational state rotational constants, but also vibrationally excited rotational constants. The present work introduces such rotational constants for multiple fundamentals that serve to assist in accurate rovibrational modeling of HOSH as is discussed above for
. These models are constructed to support further laboratory analysis or potential astronomical observation through the use of vibrationally excited rotational spectroscopy as is the case for the detection of vibrationally excited states of the SiS [
76] and C
H [
77] molecules observed in IRC+10216.
Similar to HOOH, the current literature discussing the two-quanta vibrational overtones and combination bands for HOSH is limited. To aid in this regard, the present work introduces such two-quanta modes for the purpose of benchmarking, assistance in potential astrophysical detection, and further laboratory analysis, as seen in in
Table 6. Comparing to previous literature, a previous theoretical value [
74] for the first overtone of the torsional motion, 2
846.269 cm
, is only 7.2 cm
higher the the present work’s CcCR value of 839.1 cm
. This further suggests the reliability of the present theoretical methodology for generating two-quanta bands for molecules of this type. With regard to the detectability of these two-quanta transitions, much like in HOOH, the relative intensities are exceptionally lower than that of the anharmonic vibrational frequencies. The brightest transitions are the first overtone of both the O–H stretch and the O–S–H bend at 5 km/mol and 4 km/mol, respectively. Once again, these two-quanta modes fall within the near- to short-wavelength mid-IR spectrum that the JWST will be able to probe more efficiently. Thus, the present work provides the necessary benchmark data for the potential astrophysical detection of HOSH via investigation of its overtones and combination bands.
3.3. HSSH
For much of the same reason as HOSH, a potential energy scan of the torsion for HSSH is investigated to probe viability with the current QFF methods. In
Figure 2C, an even deeper potential well for this motion is shown compared to both HOSH and HOOH. This comparison can be clearly seen in
Figure 2C where the torsional PES scans of all three molecules are given. The trans-barrier height of 2026.6 cm
is the highest seen for each of the three molecules investigated in this work and is considerably higher than the HOOH trans-barrier height of 371.9 cm
. That being said, as with HOSH, the current rovibrational spectrum for this molecule should not suffer from the inaccuracies in the VPT2 corrections that are a byproduct of the shallow potential well.
With regard to the rotational constants of HSSH, provided in
Table 7, considerable agreement is demonstrated in the present study’s F12-TZ
rotational constant of 6979.5 MHz being only 9.0 MHz above the gas-phase value, an error of 0.13% [
78]. The same agreement is not present for the CcCR method’s value of 7010.6 MHz being nearly 40.0 MHz above previous gas-phase experiment; nevertheless this difference is only 0.58% in error. With regard to the
rotational constant, the CcCR method produces a value of 6938.1 MHz which is only 30.0 MHz below the 6967.68832 MHz gas-phase constant. The F12-TZ
does not fare similarly, however, with its computed value being nearly 74.0 MHz lower than that from gas-phase experiment. As expected, the CcCR method produces a more accurate
value only in error of 0.42%, while the F12-TZ value is in error of roughly 1.1%. Additionally, the current QFF methodology provides the computation of the vibrationally excited rotational constants that have not been previously investigated possibly offering
supplemental data that may be necessary in the potential detection of this molecule rotationally or rovibrationally in the infrared.
Shown in
Table 8, exceptional agreement can be seen between the two present QFF methods for the anharmonic vibrational frequencies of HSSH. The S−S stretch, fundamental
, shows the best agreement between the computational values with F12-TZ’s value of 516.8 cm
being within 2.0 cm
of CcCR. All fundamentals for HSSH are within 4.0 cm
between QFF methods, except for the CcCR torsional motion of
being 11.0 cm
below that of the F12-TZ method. When comparing to experiment, F12-TZ performs better with the best agreement being the H–S–S anti-symmetric bend,
, at 886.1 cm
, being less than 0.2 cm
above previous gas-phase experiment
[
85]. There is also considerable agreement between the previous gas-phase experiment’s S−S stretching frequency and that from F12-TZ being within 0.9 cm
of one another. The same agreement with the experiment is not suggested with regard to CcCR as almost every mode differs by more than 10.0 cm
, save for the
mode with a difference of 2.0 cm
. The difference between the CcCR QFF and experiment re-illustrates the high accuracy of the F12-TZ QFF method for anharmonic fundamental vibrational frequencies molecules of this type.
The anharmonic intensities of the vibrational transitions for HSSH are reported in
Table 8. While the highest intensity transition, such as HOSH, is the torsion, HSSH has by far the lowest intense of the molecules investigated in this work. HSSH’s torsional motion has a calculated intensity of 14 km/mol, while it is second highest intensity transition is the
S−S–H bend at 2.0 km/mol. These are glaringly less intense than HOSH’s 72 km/mol intensity for its
, torsional, transition suggesting that HSSH is not nearly as observable via IR spectroscopy. Both the gas-phase experiment or theoretical study appear to be lacking with regard to the dipole moment. For this reason, while the present computed dipole moment of HSSH (1.15 D) is relatively small compared to the other sulfur-analog investigated in this work, it should nonetheless serve as a basis for potential radio-astronomical observation.
Furthermore, the present work introduces calculated two-quanta vibrational overtones and combination bands that appear to be missing from the current literature, as seen in
Table 9. There is previous experimental work [
78] for the first overtone of the torsional motion, 2
808.0 cm
, that is only 3.8 cm
lower than the present work’s F12-TZ value. Unlike HOOH and HOSH, HSSH exhibits no overtone or combination band transitions that have intensities over 1.0 km/mol potentially reducing its chance of detection through the use of IR spectroscopy and explaining why sulfur-containing molecules may be underdetected in astrophysical sources. Nonetheless, the present work’s introduction of the two-quanta modes provides reference data for further laboratory benchmarking or potential astrophysical detection.