Parameter Reliability and Understanding Enzyme Function
Abstract
1. Introduction
- Designing appropriate enzyme assay procedures
- Competition between different enzymes for a single substrate
- Competition between substrates for a single enzyme
- Understanding the effects of pH on enzymes
- Determination of enzyme-catalysed reaction mechanisms
- Assessment of inhibition and its effects
- Calculation of reaction equilibria under defined conditions
- The effects of temperature on enzyme activity
- Deterministic systems modelling (simulation)
2. Sources of Parameters
3. Selecting Appropriate Assay Conditions
4. Simple Questions That Have to Be Asked
5. What Effective Parameters Might Be Needed
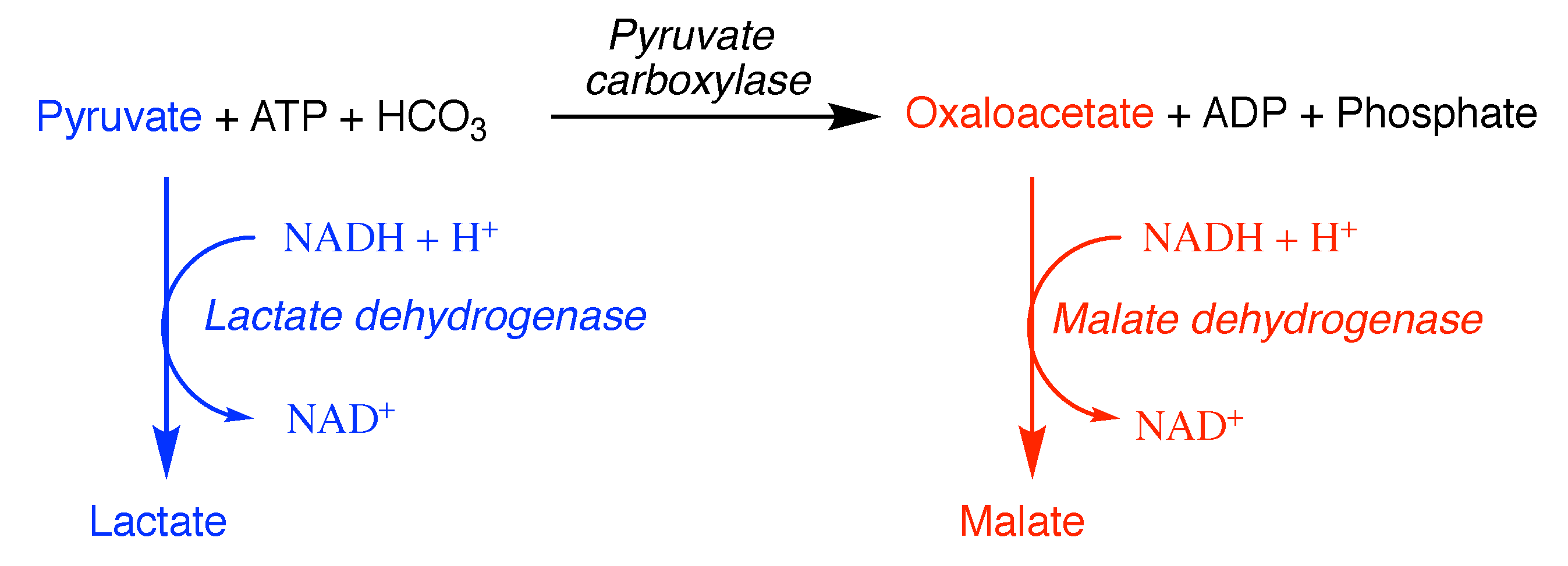
6. Pitfalls of Using Data from Purified Enzymes
7. Approximating the Activity within the Cell
8. Obtaining Reliable Data
8.1. Curve Fitting
8.2. The Importance of Zero
8.3. Progress-Curve Analysis
9. Apparent Cooperativity
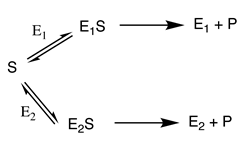 where the rate of the overall reaction () will be given by the sum of the velocities of the reactions catalysed by E and E ( and , respectively)
where the rate of the overall reaction () will be given by the sum of the velocities of the reactions catalysed by E and E ( and , respectively)
10. Statistical Considerations
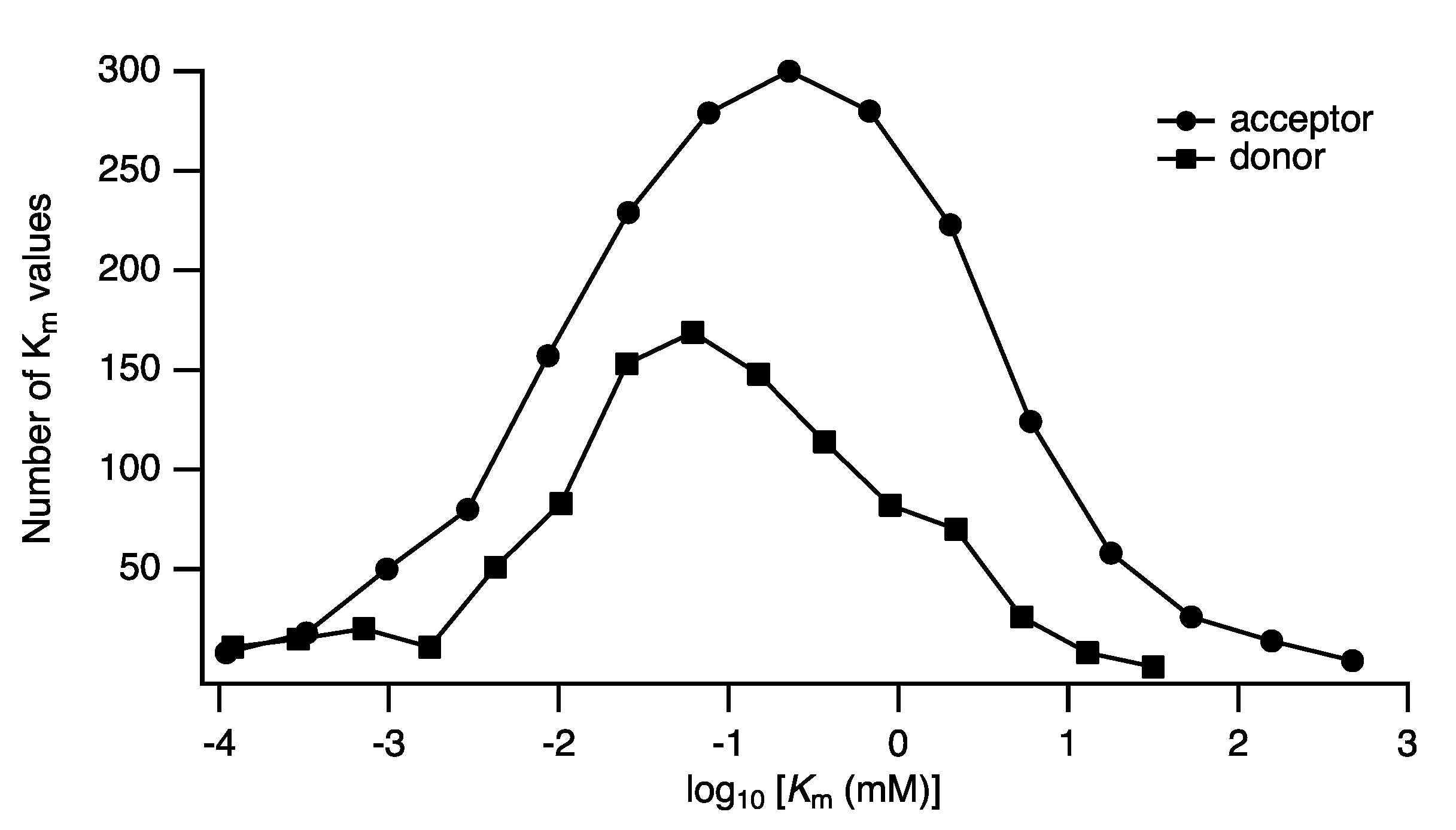
Distributions of Parameters
11. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Segel, I.H. Enzyme Kinetics: Behaviour and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1975. [Google Scholar]
- Cleland, W.W. Enzyme Kinetics. Annu. Rev. Biochem. 1967, 36, 77–112. [Google Scholar] [CrossRef] [PubMed]
- Dalziel, K. The interpretation of kinetic data for enzyme-catalysed reactions involving three substrates. Biochem. J. 1969, 114, 547–556. [Google Scholar] [CrossRef]
- Fromm, H.J. Summary of kinetic reaction mechanisms. In Methods Enzymology; Elsevier: Amsterdam, The Netherlands, 1979; Volume 63, pp. 42–53. [Google Scholar] [CrossRef]
- McDonald, A.G.; Tipton, K.F. Kinetics of Catalyzed Reactions—Biological. In Encyclopedia of Catalysis; Horváth, I.T., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Hofmeyr, J.H.S.; Cornish-Bowden, H. The reversible Hill equation: How to incorporate cooperative enzymes into metabolic models. Bioinformatics 1997, 13, 377–385. [Google Scholar] [CrossRef]
- Najdi, T.S.; Yang, C.R.; Shapiro, B.E.; Hatfield, G.W.; Mjolsness, E.D. Application of a generalized MWC model for the mathematical simulation of metabolic pathways regulated by allosteric enzymes. J. Bioinform. Comput. Biol. 2006, 4, 335–355. [Google Scholar] [CrossRef]
- Heijnen, J.J. Approximative kinetic formats used in metabolic network modeling. Biotechnol. Bioeng. 2005, 91, 534–545. [Google Scholar] [CrossRef]
- Rizzi, M.; Baltes, M.; Theobald, U.; Reuss, M. In vivo analysis of metabolic dynamics in Saccharomyces cerevisiae: II. Mathematical model. Biotechnol. Bioeng. 1997, 55, 592–608. [Google Scholar] [CrossRef]
- Chang, A.; Jeske, L.; Ulbrich, S.; Hofmann, J.; Koblitz, J.; Schomburg, I.; Neumann-Schaal, M.; Jahn, D.; Schomburg, D. BRENDA, the ELIXIR core data resource in 2021: New developments and updates. Nucleic Acids Res. 2021, 49, D498–D508. [Google Scholar] [CrossRef] [PubMed]
- Wittig, U.; Rey, M.; Weidemann, A.; Kania, R.; Müller, W. SABIO-RK: An updated resource for manually curated biochemical reaction kinetics. Nucleic Acids Res. 2018, 46, D656–D660. [Google Scholar] [CrossRef]
- Swainston, N.; Baici, A.; Bakker, B.M.; Cornish-Bowden, A.; Fitzpatrick, P.F.; Halling, P.; Leyh, T.S.; O’Donovan, C.; Raushel, F.M.; Reschel, U.; et al. STRENDA DB: Enabling the validation and sharing of enzyme kinetics data. FEBS J. 2018, 285, 2193–2204. [Google Scholar] [CrossRef]
- McDonald, A.G.; Boyce, S.; Tipton, K.F. ExplorEnz: The primary source of the IUBMB enzyme list. Nucleic Acids Res. 2009, 37, D593–D597. [Google Scholar] [CrossRef]
- Pietruszko, R. Polymorphism of horse liver alcohol dehydrogenase. Biochem. Biophys. Res. Commun. 1974, 60, 687–694. [Google Scholar] [CrossRef]
- Pietruszko, R.; Ryzewski, C.N. A new subunit of horse liver alcohol dehydrogenase and subunit composition of the polymorphic form. Biochem. J. 1976, 153, 249–257. [Google Scholar] [CrossRef]
- Ninio, J. Connections between translation, transcription and replication error-rates. Biochimie 1991, 73, 1517–1523. [Google Scholar] [CrossRef]
- Boyce, S.; Tipton, K.F.; McDonald, A.G. Extending enzyme classification with metabolic and kinetic data: Some difficulties to be resolved. In Proceedings of the 1st International Beilstein Workshop on Experimental Standard Conditions of Enzyme Characterizations; Hicks, M.G., Kettner, C., Eds.; Beilstein Institut: Frankfurt, Germany, 2004; pp. 17–43. [Google Scholar]
- Markovicč, O.; Theorell, H.; Rao, S.; Omfeldt, M.; Lagerlund, I.; Ehrenberg, L. Rat Liver Alcohol Dehydrogenase. Purification and Properties. Acta Chem. Scand. 1971, 25, 195–205. [Google Scholar] [CrossRef]
- McDonald, A.G.; Tipton, K.F.; Boyce, S. Tracing metabolic pathways from enzyme data. Biochim. Biophys. Acta Proteins Proteom. 2009, 1794, 1364–1371. [Google Scholar] [CrossRef] [PubMed]
- Tipton, K.F. 90 years of monoamine oxidase: Some progress and some confusion. J. Neural Transm. 2018, 125, 1519–1551. [Google Scholar] [CrossRef]
- Orsi, B.A.; Cleland, W.W. Inhibition and kinetic mechanism of rabbit muscle glyceraldehyde-3-phosphate dehydrogenase. Biochemistry 1972, 11, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Ganson, N.J.; Fromm, H.J. Initial rate and isotope exchange studies of rat skeletal muscle hexokinase. J. Biol. Chem. 1985, 260, 12099–12105. [Google Scholar] [CrossRef]
- Storer, A.C.; Cornish-Bowden, A. Kinetics of rat liver glucokinase. Co-operative interactions with glucose at physiologically significant concentrations. Biochem. J. 1976, 159, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Wong, M.; Khirich, G.; Loria, J.P. What’s in Your Buffer? Solute Altered Millisecond Motions Detected by Solution NMR. Biochemistry 2013, 52, 6548–6558. [Google Scholar] [CrossRef]
- García-Contreras, R.; Vos, P.; Westerhoff, H.V.; Boogerd, F.C. Why in vivo may not equal in vitro—New effectors revealed by measurement of enzymatic activities under the same in vivo-like assay conditions. FEBS J. 2012, 279, 4145–4159. [Google Scholar] [CrossRef]
- Glusker, J.P. Cation-activated enzymes. In Encyclopedia of Inorganic and Bioinorganic Chemistry; Scott, R.A., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; p. eibc0037. [Google Scholar] [CrossRef]
- Spina, J.; Bright, H.J.; Rosenbloom, J. Purification and properties of l-malic enzyme from Escherichia coli. Biochemistry 1970, 9, 3794–3801. [Google Scholar] [CrossRef]
- Motherway, M.; Tipton, K.F.; McCarthy, A.D.; Couée, I.; Irwin, J. Purification of glutamate dehydrogenase from liver and brain. Curr. Protoc. Protein Sci. 2002, 29, 1.4.1–1.4.34. [Google Scholar] [CrossRef]
- Lund, P.; Wiggins, D. Inhibition of carbamoyl-phosphate synthase (ammonia) by Tris and Hepes. Effect on Ka for N-acetylglutamate. Biochem. J. 1987, 243, 273–276. [Google Scholar] [CrossRef]
- Van Eunen, K.; Bouwman, J.; Daran-Lapujade, P.; Postmus, J.; Canelas, A.B.; Mensonides, F.I.C.; Orij, R.; Tuzun, I.; van den Brink, J.; Smits, G.J.; et al. Measuring enzyme activities under standardized in vivo-like conditions for systems biology: Standardized enzyme assays for systems biology. FEBS J. 2010, 277, 749–760. [Google Scholar] [CrossRef]
- Balut, C.; vandeVen, M.; Despa, S.; Lambrichts, I.; Ameloot, M.; Steels, P.; Smets, I. Measurement of cytosolic and mitochondrial pH in living cells during reversible metabolic inhibition. Kidney Int. 2008, 73, 226–232. [Google Scholar] [CrossRef] [PubMed]
- Kresnowati, M.; Suarez-Mendez, C.; van Winden, W.; van Gulik, W.; Heijnen, J. Quantitative physiological study of the fast dynamics in the intracellular pH of Saccharomyces cerevisiae in response to glucose and ethanol pulses. Metab. Eng. 2008, 10, 39–54. [Google Scholar] [CrossRef]
- Nicholls, R.; Jerfy, A.; Roy, A. The determination of the initial velocity of enzyme-catalysed reactions. Anal. Biochem. 1974, 61, 93–100. [Google Scholar] [CrossRef]
- Kimmel, J.R.; Smith, E.L. Crystalline papain. I. Preparation, specificity, and activation. J. Biol. Chem. 1954, 207, 515–531. [Google Scholar] [CrossRef]
- Seydoux, F.; Malhotra, O.P.; Bernhard, S.A.; Stark, G. Half-Site Reactivity. Crit. Rev. Biochem. 1974, 2, 227–257. [Google Scholar] [CrossRef]
- Dixon, M.; Webb, E.C.; Thorne, C.J.R.; Tipton, K.F. Enzymes; Longman: London, UK, 1979. [Google Scholar]
- Elliott, K.R.F.; Tipton, K.F. Kinetic studies of bovine liver carbamoyl phosphate synthetase. Biochem. J. 1974, 141, 807–816. [Google Scholar] [CrossRef][Green Version]
- Fersht, A. Enzyme Structure and Mechanism, 2nd ed.; W.H. Freeman: New York, USA, 1985. [Google Scholar]
- Eisenthal, R.; Danson, M.J.; Hough, D.W. Catalytic efficiency and kcat/KM: A useful comparator? Trends Biotechnol. 2007, 25, 247–249. [Google Scholar] [CrossRef]
- Duggleby, R.G. Estimation of the initial velocity of enzyme-catalysed reactions by non-linear regression analysis of progress curves. Biochem. J. 1985, 228, 55–60. [Google Scholar] [CrossRef]
- Crompton, I.E.; Waley, S.G. The determination of specificity constants in enzyme-catalysed reactions. Biochem. J. 1986, 239, 221–224. [Google Scholar] [CrossRef]
- Houslay, M.D.; Tipton, K.F. Amine competition for oxidation by rat liver mitochondrial monoamine oxidase. Biochem. Pharmacol. 1975, 24, 627–631. [Google Scholar] [CrossRef]
- Sevilla, C.L.; Fischer, E.H. Purification and properties of rat muscle glycogen phosphorylase. Biochemistry 1969, 8, 2161–2171. [Google Scholar] [CrossRef]
- Nimmo, H.; Tipton, K. Fructose-bisphosphatase from ox liver. In Methods Enzymology; Elsevier: Amsterdam, The Netherlands, 1982; Volume 90, pp. 330–334. [Google Scholar] [CrossRef]
- Garfinkel, L.; Kohn, M.C.; Garfinkel, D. Computer simulation of the fructose bisphosphatase/phosphofructokinase couple in rat liver. Eur. J. Biochem. 1979, 96, 183–192. [Google Scholar] [CrossRef]
- McCarthy, A.D.; Walker, J.M.; Tipton, K.F. Purification of glutamate dehydrogenase from ox brain and liver. Evidence that commercially available preparations of the enzyme from ox liver have suffered proteolytic cleavage. Biochem. J. 1980, 191, 605–611. [Google Scholar] [CrossRef]
- Couée, I.; Tipton, K.F. The sulphydryl groups of ox brain and liver glutamate dehydrogenase preparations and the effects of oxidation on their inhibitor sensitivities. Neurochem. Res. 1991, 16, 773–780. [Google Scholar] [CrossRef]
- Johnson, D.R.; Lambright, D.G.; Wong, S.S. Lactose synthase: Effect of α-lactalbumin on substrate activity of N-acylglucosamines. Biochim. Biophys. Acta Protein Struct. Mol. Enzymol. 1985, 832, 373–377. [Google Scholar] [CrossRef]
- Rimmer, M.A.; Nadeau, O.W.; Artigues, A.; Carlson, G.M. Structural characterization of the catalytic γ and regulatory β subunits of phosphorylase kinase in the context of the hexadecameric enzyme complex: Structure of β and γ Subunits of Phosphorylase Kinase. Protein Sci. 2018, 27, 485–497. [Google Scholar] [CrossRef]
- Funk, M.A.; Judd, E.T.; Marsh, E.N.G.; Elliott, S.J.; Drennan, C.L. Structures of benzylsuccinate synthase elucidate roles of accessory subunits in glycyl radical enzyme activation and activity. Proc. Natl. Acad. Sci. USA 2014, 111, 10161–10166. [Google Scholar] [CrossRef] [PubMed]
- Yee, A.; Wu, L.; Liu, L.; Kobayashi, R.; Xiong, Y.; Hall, F.L. Biochemical characterization of the human cyclin-dependent protein kinase activating kinase. Identification of p35 as a novel regulatory subunit. J. Biol. Chem. 1996, 271, 471–477. [Google Scholar] [CrossRef] [PubMed]
- Uemura, S.; Kihara, A.; Inokuchi, J.I.; Igarashi, Y. Csg1p and newly identified Csh1p function in mannosylinositol phosphorylceramide synthesis by interacting with Csg2p. J. Biol. Chem. 2003, 278, 45049–45055. [Google Scholar] [CrossRef]
- Wendeler, M.; Werth, N.; Maier, T.; Schwarzmann, G.; Kolter, T.; Schoeniger, M.; Hoffmann, D.; Lemm, T.; Saenger, W.; Sandhoff, K. The enzyme-binding region of human GM2-activator protein. FEBS J. 2006, 273, 982–991. [Google Scholar] [CrossRef]
- Skropeta, D. The effect of individual N-glycans on enzyme activity. Bioorg. Med. Chem. 2009, 17, 2645–2653. [Google Scholar] [CrossRef]
- Shauchuk, A.; Szulc, B.; Maszczak-Seneczko, D.; Wiertelak, W.; Skurska, E.; Olczak, M. N-glycosylation of the human β1,4-galactosyltransferase 4 is crucial for its activity and Golgi localization. Glycoconj. J. 2020, 37, 577–588. [Google Scholar] [CrossRef]
- Yang, C.; Wang, Q.; Ding, W. Recent progress in the imaging detection of enzyme activities in vivo. RSC Adv. 2019, 9, 25285–25302. [Google Scholar] [CrossRef]
- Speers, A.E.; Cravatt, B.F. Profiling Enzyme Activities In Vivo Using Click Chemistry Methods. Chem. Biol. 2004, 11, 535–546. [Google Scholar] [CrossRef]
- dos Santos, M.M.; Gombert, A.K.; Christensen, B.; Olsson, L.; Nielsen, J. Identification of in vivo enzyme activities in the cometabolism of glucose and acetate by Saccharomyces cerevisiae by using 13C-labeled substrates. Eukaryot. Cell 2003, 2, 599–608. [Google Scholar] [CrossRef]
- Ishihama, Y.; Schmidt, T.; Rappsilber, J.; Mann, M.; Hartl, F.U.; Kerner, M.J.; Frishman, D. Protein abundance profiling of the Escherichia coli cytosol. BMC Genomics 2008, 9, 102. [Google Scholar] [CrossRef]
- White, C.A.; Oey, N.; Emili, A. Global Quantitative Proteomic Profiling through 18O-Labeling in Combination with MS/MS Spectra Analysis. J. Proteome Res. 2009, 8, 3653–3665. [Google Scholar] [CrossRef]
- Fortelny, N.; Overall, C.M.; Pavlidis, P.; Freue, G.V.C. Can we predict protein from mRNA levels? Nature 2017, 547, E19–E20. [Google Scholar] [CrossRef]
- Yu, X.; Wallstrom, G.; Magee, D.M.; Qiu, J.; Mendoza, D.E.A.; Wang, J.; Bian, X.; Graves, M.; LaBaer, J. Quantifying antibody binding on protein microarrays using microarray nonlinear calibration. Biotechniques 2013, 54, 257–264. [Google Scholar] [CrossRef]
- Gomez, N.; Unzeta, M.; Tipton, K.F.; Anderson, M.C.; O’Carroll, A.M. Determination of monoamine oxidase concentrations in rat liver by inhibitor binding. Biochem. Pharmacol. 1986, 35, 4467–4472. [Google Scholar] [CrossRef]
- McDonald, A.G.; Keith, K.F. Enzymes: Irreversible Inhibition. In Encyclopedia of the Life Sciences (eLS), 1st ed.; John Wiley & Sons, Ltd., Ed.; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Hanson, A.D.; McCarty, D.R.; Henry, C.S.; Xian, X.; Joshi, J.; Patterson, J.A.; García-García, J.D.; Fleischmann, S.D.; Tivendale, N.D.; Millar, A.H. The number of catalytic cycles in an enzyme’s lifetime and why it matters to metabolic engineering. Proc. Natl. Acad. Sci. USA 2021, 118, e2023348118. [Google Scholar] [CrossRef] [PubMed]
- van Eunen, K.; Bakker, B.M. The importance and challenges of in vivo-like enzyme kinetics. Perspect. Sci. 2014, 1, 126–130. [Google Scholar] [CrossRef]
- Tipton, K. Principles of enzyme assay and kinetic studies. In Enzyme Assays: A Practical Approach, 2nd ed.; Eisenthal, R.A., Danson, M.J., Eds.; Number 257 in the Practical Approach Series; Oxford University Press: Oxford, UK, 2002; pp. 1–47. [Google Scholar]
- Warren, G.B.; Tipton, K.F. Pig liver pyruvate carboxylase. Purification, properties and cation specificity. Biochem. J. 1974, 139, 297–310. [Google Scholar] [CrossRef] [PubMed]
- Warren, G.B.; Tipton, K.F. Pig liver pyruvate carboxylase. The reaction pathway for the carboxylation of pyruvate. Biochem. J. 1974, 139, 311–320. [Google Scholar] [CrossRef] [PubMed]
- Mitchison, T.J. Colloid osmotic parameterization and measurement of subcellular crowding. Mol. Biol. Cell 2019, 30, 173–180. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.Q.; Zhong, W.Z. Diffusion-Controlled Reactions of Enzymes: A Comparison between Chou’s Model and Alberty-Hammes-Eigen’s Model. Eur. J. Biochem. 2005, 128, 383–387. [Google Scholar] [CrossRef]
- Fersht, A. Measurement and magnitude of enzymatic rate constants. In Enzyme Structure and Mechanism; W. H. Freeman: New York, NY, USA, 1984; pp. 147–154. [Google Scholar]
- Jevtic, S.; Anders, J. A qualitative quantum rate model for hydrogen transfer in soybean lipoxygenase. J. Chem. Phys. 2017, 147, 114108. [Google Scholar] [CrossRef] [PubMed]
- Shahid, S.; Hassan, M.I.; Islam, A.; Ahmad, F. Size-dependent studies of macromolecular crowding on the thermodynamic stability, structure and functional activity of proteins: In vitro and in silico approaches. Biochim. Biophys. Acta Gen. Subj. 2017, 1861, 178–197. [Google Scholar] [CrossRef] [PubMed]
- Pastor, I.; Pitulice, L.; Balcells, C.; Vilaseca, E.; Madurga, S.; Isvoran, A.; Cascante, M.; Mas, F. Effect of crowding by Dextrans in enzymatic reactions. Biophys. Chem. 2014, 185, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Wilcox, X.E.; Chung, C.B.; Slade, K.M. Macromolecular crowding effects on the kinetics of opposing reactions catalyzed by alcohol dehydrogenase. Biochem. Biophys. Rep. 2021, 26, 100956. [Google Scholar] [CrossRef]
- Balbo, J.; Mereghetti, P.; Herten, D.P.; Wade, R. The Shape of Protein Crowders is a Major Determinant of Protein Diffusion. Biophys. J. 2013, 104, 1576–1584. [Google Scholar] [CrossRef]
- Vogel, K.; Greinert, T.; Reichard, M.; Held, C.; Harms, H.; Maskow, T. Thermodynamics and Kinetics of Glycolytic Reactions. Part II: Influence of Cytosolic Conditions on Thermodynamic State Variables and Kinetic Parameters. Int. J. Mol. Sci. 2020, 21, 7921. [Google Scholar] [CrossRef] [PubMed]
- Poggi, C.G.; Slade, K.M. Macromolecular crowding and the steady-state kinetics of malate dehydrogenase. Biochemistry 2015, 54, 260–267. [Google Scholar] [CrossRef]
- Peters, T. Serum Albumin. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1985; Volume 37, pp. 161–245. [Google Scholar] [CrossRef]
- Liu, B.; Poolman, B.; Boersma, A.J. Ionic Strength Sensing in Living Cells. ACS Chem. Biol. 2017, 12, 2510–2514. [Google Scholar] [CrossRef] [PubMed]
- Altamash, T.; Ahmed, W.; Rasool, S.; Biswas, K.H. Intracellular Ionic Strength Sensing Using NanoLuc. Int. J. Mol. Sci. 2021, 22, 677. [Google Scholar] [CrossRef] [PubMed]
- Castañeda Agulló, M.; del Castillo, L.M.; Whitaker, J.R.; Tappel, A.L. Effect of Ionic Strength on the Kinetics of Trypsin and Alpha Chymotrypsin. J. Gen. Physiol. 1961, 44, 1103–1120. [Google Scholar] [CrossRef] [PubMed]
- Nørby, J.G.; Esmann, M. The Effect of Ionic Strength and Specific Anions on Substrate Binding and Hydrolytic Activities of Na,K-ATPase. J. Gen. Physiol. 1997, 109, 555–570. [Google Scholar] [CrossRef]
- Neville, W.M.; Eyring, H. Hydrostatic Pressure and Ionic Strength Effects on the Kinetics of Lysozyme. Proc. Natl. Acad. Sci. USA 1972, 69, 2417–2419. [Google Scholar] [CrossRef]
- Epstein, W. The roles and regulation of potassium in bacteria. In Progress in Nucleic Acid Research and Molecular Biology; Elsevier: Amsterdam, The Netherlands, 2003; Volume 75, pp. 293–320. [Google Scholar] [CrossRef]
- Brooks, S.; Storey, K. Where is the glycolytic complex? A critical evaluation of present data from muscle tissue. FEBS Lett. 1991, 278, 135–138. [Google Scholar] [CrossRef]
- Haldane, J.B.S. Graphical Methods in Enzyme Chemistry. Nature 1957, 179, 832. [Google Scholar] [CrossRef]
- Dowd, J.E.; Riggs, D.S. A comparison of estimates of Michaelis-Menten kinetic constants from various linear transformations. J. Biol. Chem. 1965, 240, 863–869. [Google Scholar] [CrossRef]
- De Miguel Merino, F. A new method for determining the Michaelis constant. Biochem. J. 1974, 143, 93–95. [Google Scholar] [CrossRef] [PubMed]
- Eisenthal, R.; Cornish-Bowden, A. The direct linear plot. A new graphical procedure for estimating enzyme kinetic parameters. Biochem. J. 1974, 139, 715–720. [Google Scholar] [CrossRef] [PubMed]
- Cornish-Bowden, A.; Eisenthal, R. Statistical considerations in the estimation of enzyme kinetic parameters by the direct linear plot and other methods. Biochem. J. 1974, 139, 721–730. [Google Scholar] [CrossRef]
- Wilkinson, G. Statistical estimations in enzyme kinetics. Biochem. J. 1961, 80, 324–332. [Google Scholar] [CrossRef]
- Cleland, W.W. Computer Programmes for Processing Enzyme Kinetic Data. Nature 1963, 198, 463–465. [Google Scholar] [CrossRef] [PubMed]
- Atkins, G.L.; Nimmo, I.A. A comparison of seven methods for fitting the Michaelis-Menten equation. Biochem. J. 1975, 149, 775–777. [Google Scholar] [CrossRef]
- Cornish-Bowden, A. Detection of Errors of Interpretation in Experiments in Enzyme Kinetics. Methods 2001, 24, 181–190. [Google Scholar] [CrossRef] [PubMed]
- Selwyn, M. Michaelis-Menten data: Misleading textbook examples. Biochem. Educ. 1995, 23, 138–141. [Google Scholar] [CrossRef]
- Orsi, B.A.; Tipton, K.F. [8] Kinetic analysis of progress curves. In Methods Enzymology; Elsevier: Amsterdam, The Netherlands, 1979; Volume 63, pp. 159–183. [Google Scholar] [CrossRef]
- Goudar, C.T.; Sonnad, J.R.; Duggleby, R.G. Parameter estimation using a direct solution of the integrated Michaelis-Menten equation. Biochim. Biophys. Acta 1999, 1429, 377–383. [Google Scholar] [CrossRef]
- Schnell, S.; Mendoza, C. Closed Form Solution for Time-dependent Enzyme Kinetics. J. Theoret. Biol. 1997, 187, 207–212. [Google Scholar] [CrossRef]
- Zavrel, M.; Kochanowski, K.; Spiess, A.C. Comparison of different approaches and computer programs for progress curve analysis of enzyme kinetics. Eng. Life Sci. 2010, 10, 191–200. [Google Scholar] [CrossRef]
- Gadagkar, S.R.; Call, G.B. Computational tools for fitting the Hill equation to dose–response curves. J. Pharmacol. Toxicol. Methods 2015, 71, 68–76. [Google Scholar] [CrossRef] [PubMed]
- Kirtley, M.E.; Koshland, D.E. Models for cooperative effects in proteins containing subunits. Effects of two interacting ligands. J. Biol. Chem. 1967, 242, 4192–4205. [Google Scholar] [CrossRef]
- Bardsley, W.G.; Childs, R.E. Sigmoid curves, non-linear double-reciprocal plots and allosterism. Biochem. J. 1975, 149, 313–328. [Google Scholar] [CrossRef]
- Solano-Muñoz, F.; Bardsley, W.G.; Indge, K.J. The probability that complex enzyme kinetic curves can be caused by activators or inhibitors. Biochem. J. 1981, 195, 589–601. [Google Scholar] [CrossRef]
- Storer, A.C.; Cornish-Bowden, A. Concentration of MgATP2- and other ions in solution. Calculation of the true concentrations of species present in mixtures of associating ions. Biochem. J. 1976, 159, 1–5. [Google Scholar] [CrossRef]
- Cleland, W. [7] Kinetic method for determination of dissociation constants nucleotide complexes. In Methods Enzymology; Elsevier: Amsterdam, The Netherlands, 1995; Volume 249, pp. 181–188. [Google Scholar] [CrossRef]
- Elliott, K.R.F.; Tipton, K.F. A kinetic analysis of enzyme systems involving four substrates. Biochem. J. 1974, 141, 789–805. [Google Scholar] [CrossRef]
- Levitzki, A.; Koshland, D. The Role of Negative Cooperativity and Half-of-the-Sites Reactivity in Enzyme Regulation. In Current Topics in Cellular Regulation; Elsevier: Amsterdam, The Netherlands, 1976; Volume 10, pp. 1–40. [Google Scholar] [CrossRef]
- Dixon, H.B.F.; Tipton, K.F. Negatively co-operative ligand binding. Biochem. J. 1973, 133, 837–842. [Google Scholar] [CrossRef]
- Trowbridge, C.G.; Krehbiel, A.; Laskowski, M. Substrate Activation of Trypsin. Biochemistry 1963, 2, 843–850. [Google Scholar] [CrossRef]
- Spears, G.; Sneyd, J.G.T.; Loten, E.G. A method for deriving kinetic constants for two enzymes acting on the same substrate. Biochem. J. 1971, 125, 1149–1151. [Google Scholar] [CrossRef]
- Holt, A. On the practical aspects of characterising monoamine oxidase inhibition in vitro. J. Neural Transm. 2018, 125, 1685–1705. [Google Scholar] [CrossRef] [PubMed]
- Vaux, D.L. Know when your numbers are significant. Nature 2012, 492, 180–181. [Google Scholar] [CrossRef]
- Vaux, D.L. Basic Statistics in Cell Biology. Annu. Rev. Cell Dev. Biol. 2014, 30, 23–37. [Google Scholar] [CrossRef]
- Halling, P.; Fitzpatrick, P.F.; Raushel, F.M.; Rohwer, J.; Schnell, S.; Wittig, U.; Wohlgemuth, R.; Kettner, C. An empirical analysis of enzyme function reporting for experimental reproducibility: Missing/incomplete information in published papers. Biophys. Chem. 2018, 242, 22–27. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McDonald, A.G.; Tipton, K.F. Parameter Reliability and Understanding Enzyme Function. Molecules 2022, 27, 263. https://doi.org/10.3390/molecules27010263
McDonald AG, Tipton KF. Parameter Reliability and Understanding Enzyme Function. Molecules. 2022; 27(1):263. https://doi.org/10.3390/molecules27010263
Chicago/Turabian StyleMcDonald, Andrew G., and Keith F. Tipton. 2022. "Parameter Reliability and Understanding Enzyme Function" Molecules 27, no. 1: 263. https://doi.org/10.3390/molecules27010263
APA StyleMcDonald, A. G., & Tipton, K. F. (2022). Parameter Reliability and Understanding Enzyme Function. Molecules, 27(1), 263. https://doi.org/10.3390/molecules27010263





