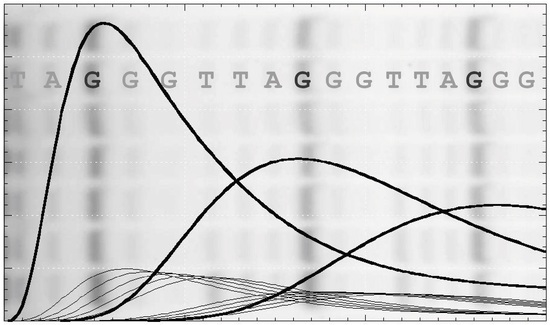
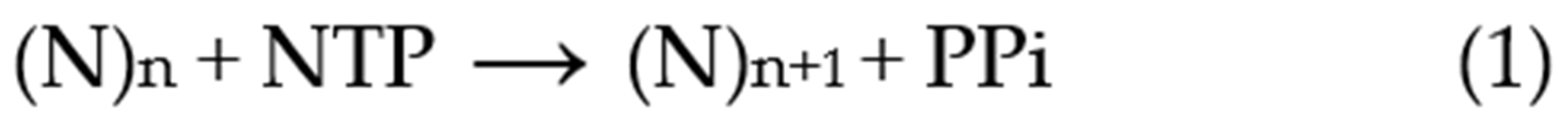2.1. Primer Extension Assays
Before discussing the analysis of simulated data, it is useful to review the nature of the experimental approaches and their variations. A typical primer extension assay involves adding telomerase to the primer DNA (e.g., the 18-mer (TTAGGG)
3), followed by addition of the nucleotide substrates (dATP, dGTP and dTTP in the case of human telomerase). After an appropriate incubation time, the reaction is stopped by the addition of EDTA and SDS, phenol-chloroform extracted and the DNA precipitated with ethanol, prior to separation by gel electrophoresis [
6,
7,
12]. If the DNA primer is radiolabeled, then the radioactivity in each band, whose molecular weight is increased by one nucleotide addition, is directly proportional to its concentration (
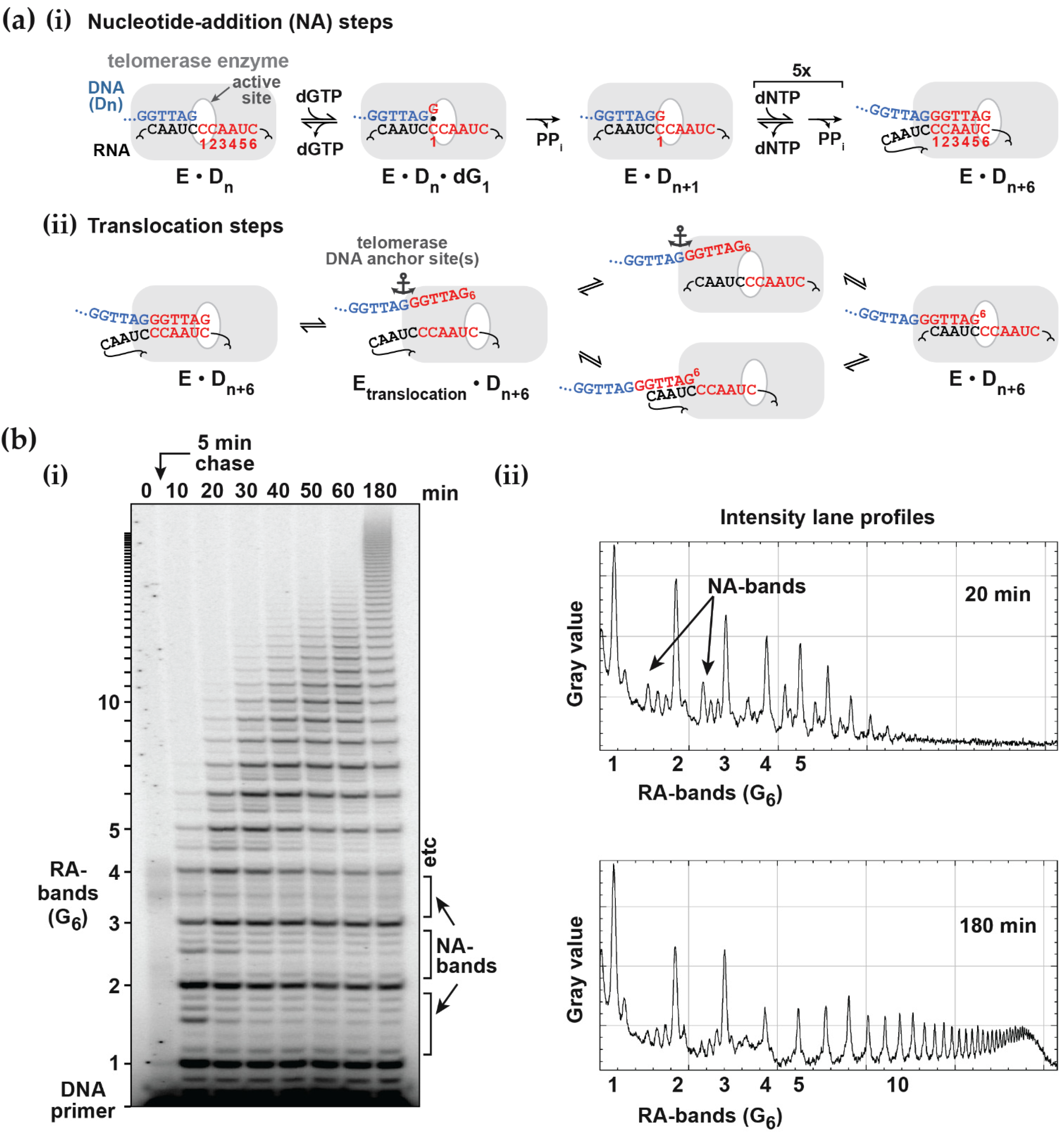
Figure 1b). Alternatively, one of the deoxynucleotides may be radiolabeled, which has the advantage that more counts will appear in the higher molecular weight bands. This compensates for their lower concentration at the extremity of the DNA product exponential distribution. In this case, the product concentration in terms of DNA molecules needs to be adjusted according to the number of labeled nucleotides in the extended sequence. While advantageous in terms of signal strength, this approach may limit the molar concentration of the labeled nucleotide used in the assay to ensure a reasonable fraction of the counts are incorporated. Furthermore, this procedure complicates the assessment of the contribution from the unresolved bands, which is necessary for some analytical procedures discussed below. One problem in both assays is the potential for dissociated products to rebind and undergo further elongation. This can be minimized by restricting the analysis to early time points, such that the labeled primer remains in large excess. A better solution is to add a large excess of unlabeled primer soon after the assay is initiated (a pulse-chase assay) to limit the rebinding of all labeled species.
Following electrophoresis, the gel is typically analyzed using a phosphorimager. In order to retrieve data of sufficient quality to warrant quantitative analysis, a number of procedures are incorporated to minimize random and systematic errors. During phenol/chloroform extraction, the volume of the aqueous layer is increased so that any denatured protein at the interface is not carried over to the gel where it might interfere with DNA migration. With this precaution, the number of counts remaining in the well is < 0.5% that of the resolved bands and there is no evidence of smearing of intensity beneath the wells. Variations arising from pipetting errors and extraction efficiencies, which typically span about 10%, can be accommodated by normalizing the total counts of each lane. The total counts should also be examined to make sure there is no systematic error across lanes that might reflect differential extraction of low and high molecular weight DNA products. The relative product concentrations are determined from the counts in each band and, in some cases, are calibrated absolutely using the labeled primer intensity as a standard (see below).
The intensity and resolution of the bands become progressively lower with increasing molecular weight. Telomerases present a further challenge in that the 5 NA-bands between each pair of RA-bands are an order of magnitude weaker in intensity and often ignored in the analysis. NA-bands are poorly resolved beyond about the 5th RA-band, while the RA-bands themselves may be analyzed up to around 20 to 25 repeats (equivalent to 120 to 150 total added nucleotides:
Figure 1b and
Figure S1a). Analysis of gel band intensity can be performed with various degrees of sophistication from manual definition of peak boundaries using a tool such as the Analyze Gel option in ImageJ (
https://imagej.nih.gov/ij/ accessed on 7 December 2021) to least-squares fitting to a series of Lorentzian line shapes [
18,
19,
20]. Ultimately, the analysis is limited by insufficient resolution of the high molecular weight bands and uncertainty in the baseline counts. However, in some procedures it is important to estimate the net contribution from the unresolved bands.
2.2. Analysis of Processivity from the “End-Point” Product Distribution
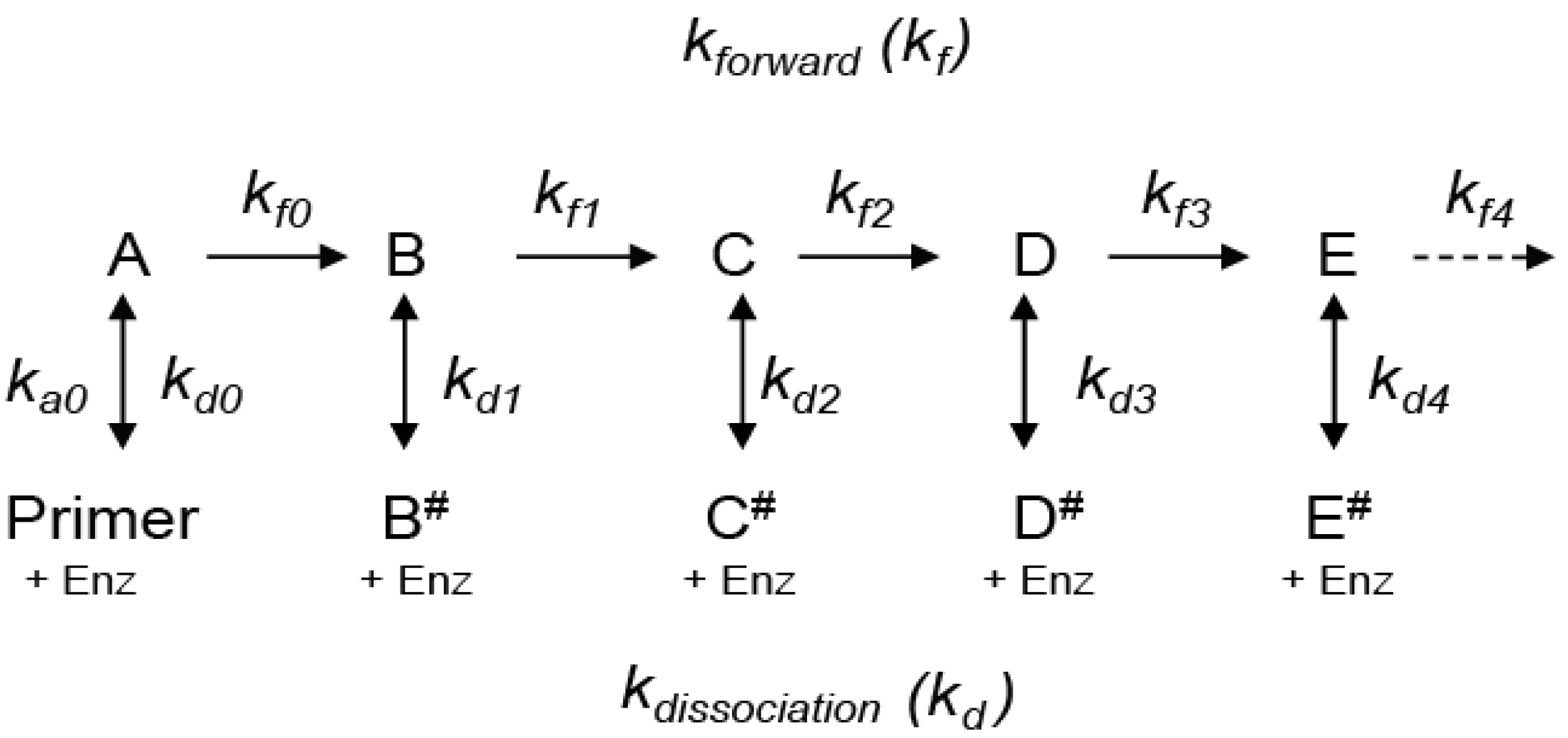
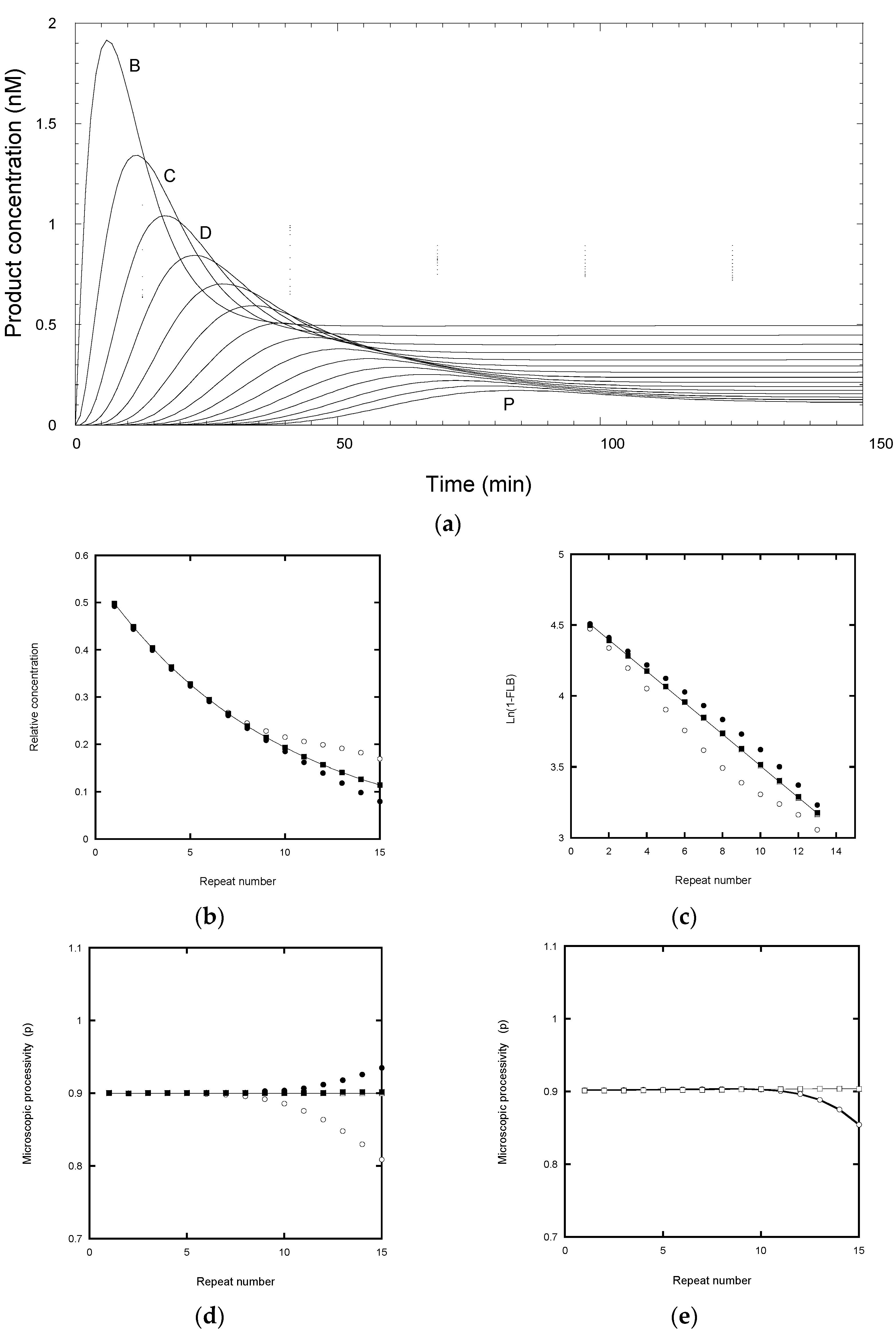
We start by considering a simplified mechanism, where the microscopic processivity is the same at each step of the reaction (p = P), in order to explore the systematic distortions of the data that arise during various analytical procedures. (
Table 1).
Scheme 2 can be used to analyze RA- to RA-band transitions, where the NA-steps are ignored. With constant
kf and
kd values, the RA-product concentrations show a discrete exponential distribution as the reaction approaches equilibrium. For example, with P = 0.9 for RAP, 90% of the product undergoes further extension in units of the hexanucleotide repeat while 10% dissociates at each RA-step (
Table 2). Consequently, after seven repeats, the product is reduced in concentration to 0.9
7 = 0.478, which is close to the median product length expressed in terms of number of repeats until the [product] is reduced to 50% (R
1/2 = 0.69).
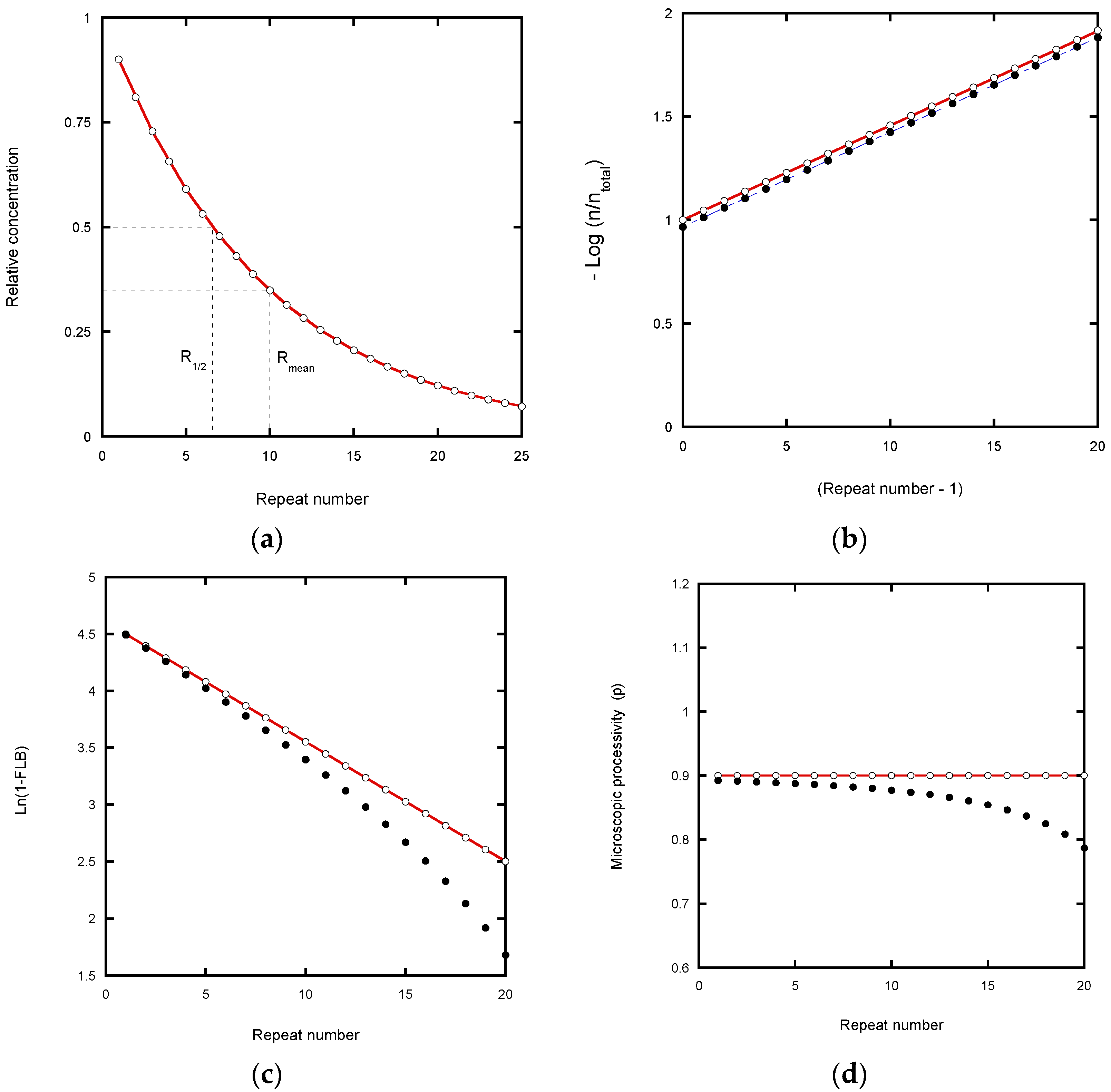
Fitting a continuous exponential decay function to the product distribution provides a direct method for defining the processivity (
Figure 2a: decay constant = 0.105 per repeat). From this decay constant, R
1/2 equals Ln(2)/decay constant and the macroscopic processivity, P equals e
(−decay constant). Variations of this method involve taking the logarithm of the product concentration which gives a linear plot, but this can distort the analysis. Linear transformation prior to data fitting biases the result due to distortion of the error distribution [
21,
22]. In addition, it weights the fit towards higher repeat numbers where the relative experimental error is larger because of low intensity and poor resolution from neighboring bands.
In the case of the von Hippel plot, −Log(I
n/I
total) versus repeat number [
4], the intensity of a band at position n (I
n) is normalized with a constant denominator, I
total, the total intensity. Note that von Hippel et al. applied their equation to DNA polymerases and not telomerases, but the analysis is included here to compare with the logarithmic plot of Latrick and Cech [
7] which has different characteristics. In the von Hippel plot, errors in the total intensity due to truncation of the analyzed gel area (
Figure 2b) cause a small shift in the intercept value, but not the slope. The latter therefore potentially yields an accurate processivity estimation (apart from the error weighting problem of log plots referred to above), as confirmed in
Figure 2b. Note that in the original article [
4], processivities were given in terms of the mean number of repeats, R
mean (=1/decay constant;
Figure 2a) rather than R
1/2.
In the Latrick and Cech plot [
7], the data are transformed by normalizing to the Fraction Left Behind (FLB:
Table 1). This plot is based on a cumulative normalized exponential function which smooths out local variations in the microscopic processivity values. While this appears to assist in determining a macroscopic processivity value, P, it can also introduce systematic error. Any underestimate in the total concentration due to analyzing a finite number of bands causes the plot to curve at high repeat numbers and to under-estimate the processivity (
Figure 2c). In the case of experiments using a labeled primer, the error is readily corrected by adding the contribution from the unresolved peaks in the normalization process. This contribution can be estimated from the relative area (pixel count) of the unresolved peaks in the gel scan compared with the resolved peaks which are included in the analysis (
Figure S1a).
The analysis of microscopic processivity by the method of Peng et al. [
5], also involves normalization to a running accumulated product intensity. This plot likewise suffers from curvature if only a limited number of bands are included in the normalization (
Figure 2d). However, the correction for the total product concentration returns the input P = p = 0.9 at each step of the reaction.
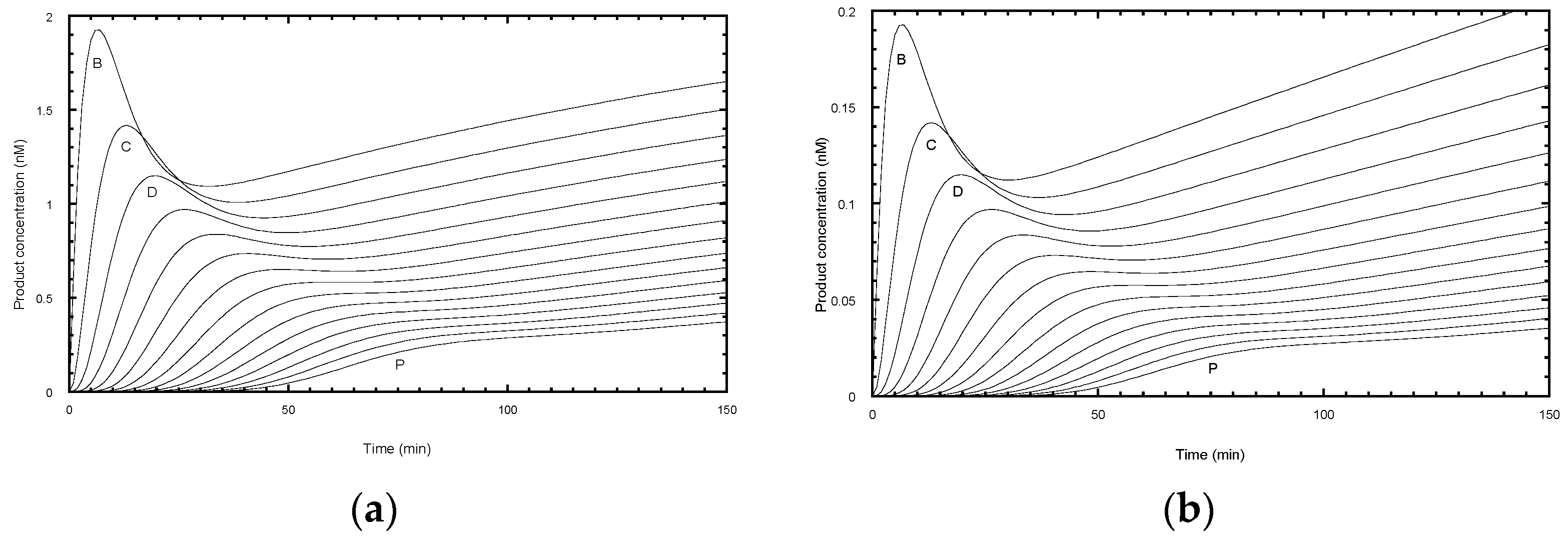
2.3. Errors due to Incomplete Equilibration
An exponential distribution of product concentrations arises only when the reaction nears its “end-point” value. This refers to the equilibrium concentration for a pulse-chase experiment where all the labeled products dissociate and are prevented from further extension by the large excess of unlabeled primer. Experimentally, the time to reach a near end-point distribution is determined empirically from the incubation period where no further change in the resolvable product band intensities is detected. This time may be incorporated into a standard protocol but its validity is not always checked for different experimental conditions or number of bands analyzed. To determine the effect of incomplete equilibration on the analysis of processivity, a reaction was simulated according to
Scheme 2 with k
f = 0.18 min
−1 and k
d = 0.02 min
−1 at each step in the reaction, corresponding to a processivity of 0.9. The values for the rate constants were chosen to roughly match the time course of product formation in telomerase assays under the conditions used by Jansson et al. [
12]. In this simulation, 5 nM telomerase was mixed with 50 nM labeled primer DNA and, after a short time interval (5 min in the simulation analyzed in
Figure 3), 10 μM cold primer was added.
It can be seen that each product reached its peak concentration at intervals of about 5.5 min (
Figure 3a), controlled by its mean lifetime (=1/
kf). For subsequent analysis, samples were analyzed every 10 min for a total incubation time of 200 min (
Figure 3a), in line with a typical experimental protocol. After about 120 min the products corresponding to the first 15 repeats had fully dissociated and showed an exponential distribution with respect to repeat number (
Figure 3b). The decay constant of 0.105 repeat
−1 corresponds to the input processivity of 0.9 and matches that of the equilibrium analysis in
Figure 2a. However, after 90 min incubation (85 min after chase), the total product distribution deviates from a single exponential function from about the 9th repeat (RA-band J) onwards (
Figure 3b, open circles). The curve falls above the exponential function because some product remains bound to the telomerase, so increasing the total product concentration for those species. In some experimental protocols [
23], the incubation mix is subject to a separation step before gel electrophoresis, so that the bands represent the free rather than total product. This procedure reduced the deviation, but now the data fell below exponential function from about the 11th repeat (
Figure 3b solid circles). This simulation indicates that the best approach is to wait for the reaction (>120 min for 15 RA-bands) to reach a stationary end-point, after which the total product equals free product and avoids the need for a separation step. The latter may itself cause problems if the bound product dissociates on the time scale of the separation procedure.
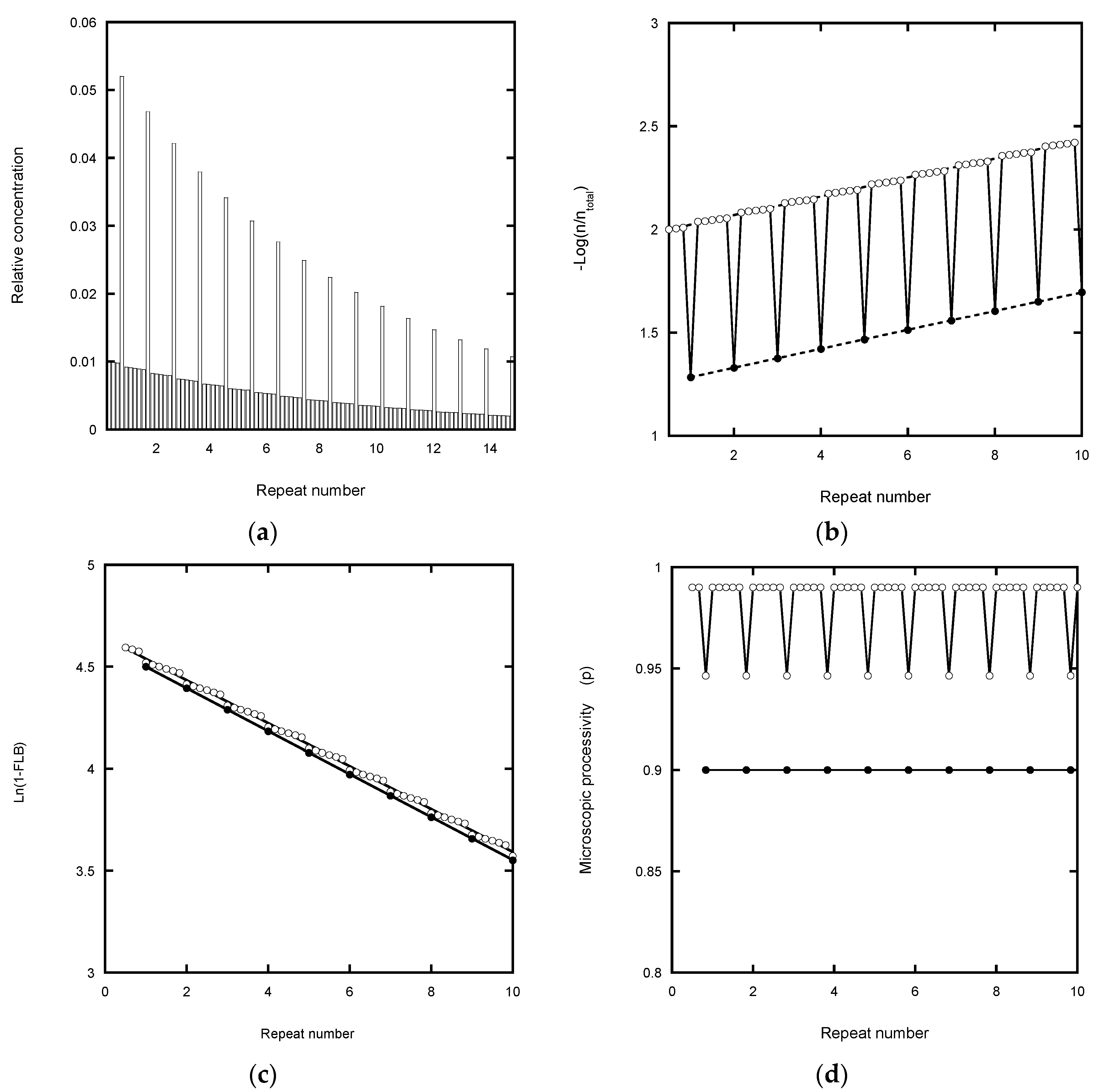
Analyzing the same data using the Latrick and Cech procedure [
7] for the first 15 repeats, with correction for the truncation error discussed above, gave a linear plot for the product distribution at 200 min and a derived P = 0.89, close to the input value (
Figure 3c). However, the distribution at 90 min gave a non-linear plot, although the initial slopes for the total and free product yielded P = 0.87 and 0.91, respectively, which are reasonably close to the input P value. Note that the deviation from linearity is seen by the 2nd repeat because the smoothing effect of a cumulative plot mixes “good” data (bands B to H) with the “bad” (bands J to P).
Peng plots [
5] yielded the correct microscopic processivity values for the 200 min data, but progressively deviated from about the ninth repeat for the 90 min data (
Figure 3d). In particular, the total product underestimates the microscopic processivity. This is a consequence of the contribution from the bound product, most of which would continue to elongate rather than dissociate. On the other hand, the free products at 90 min overestimated the processivity beyond the 11th repeat because the dissociated products have not risen to their final values.
Finally, an attempt was made to fit the complete time series at 10 min sampling intervals by global fitting using numerical methods [
12,
16,
17] to determine
kf and
kd at each step of the reaction for the first 15 repeats. When the dataset included data up to 200 min, the estimated
kf and
kd values were accurate and defined the microscopic processivity,
kf/(
kf +
kd) = 0.90. When the data only extended to 90 min, the estimated processivity deviated from about repeat 11. Note the slight improvement in the microscopic processivity estimates for the 90 min data compared with Peng analysis (
Figure 3d) for the total product intensity. This arises because the kinetic information allows an estimate of the partitioning of the total product between free and bound states between the ninth and 11th repeat but, beyond the 11th repeat, insufficient dissociation occurs to allow an accurate estimate of the
kd value. In practice, it is better to solve this problem by obtaining data at longer incubation times or restricting rigorous analysis to low repeat numbers, where the products have fully dissociated. We show below that the deviations, which arise from ignoring or incompletely resolving the NA-bands can give rise to systematic errors in the fit, and therefore it is better to determine end-point concentrations experimentally rather than relying on the extrapolation of a kinetic model.
2.4. Errors Arising from Analysis of Steady-State Distributions
The time course of primer extension assays, in the absence of a chase with excess unlabeled primer, give more complex profiles (
Figure 4). Each product showed a lag phase depending on the repeat number, a burst phase dominated by bound product, followed by a near-linear steady-state phase as the free product accumulated.
An experimental protocol invariably requires a compromise in selecting an optimal incubation time. Long incubations are required for the later products to appear during which time the early products may rebind and invalidate the assumption of “single hit conditions” required for an accurate assessment of the processivity. A rule of thumb is sometimes used that the primer should not be depleted by more than 10% during the assay. Analysis of simulated profiles confirms these complications. Under the same conditions as used for the simulation in
Figure 3a, but without the chase, the reaction barely reached a steady-state as evident from the curvature of the final phase of early products (
Figure 4a). This arises because of the relatively high ratio of telomerase (5 nM) to labelled primer (50 nM), which caused depletion of the primer to 68% of the starting concentration by 150 min. The curvature arose from products rebinding in competition with the primer. In the simulation, the rate constant for product rebinding was the same as initial primer binding (0.1 nM
−1 min
−1) and therefore degree of competition was proportional to the relative concentration of each species. While the product distribution at 200 min follows an exponential function, the extracted processivity, P = 0.91 (R
1/2 = 7.5 repeats) slightly overestimates the processivity. Kinetic analysis using DynaFit, assuming a similar association rate constants for all species, provided a better estimate of the true processivity (P = 0.890 to 0.904) because it modeled the contribution from product rebinding. In practice, the association rate constants for each product are unknown, thus limiting the value of this approach
Reducing the telomerase ten-fold to 0.5 nM overcomes the multiple hit problem, so that the free product is formed linearly (
Figure 4b). Here, the primer concentration was 96% of the starting value at 150 min. However, the signal intensity was reduced ten-fold and would require higher specific labeling of the primer or longer exposure time to compensate. While the product distribution at 200 min followed an exponential decay, the calculated processivity now slightly under-estimated the processivity (P = 0.88, R
1/2 = 5.7 repeats). These systematic errors can be accounted for as follows. In the case of primer depletion, products have a second chance to rebind and become extended and hence increase the apparent processivity. In the case of single hit conditions, the early repeat products have a head-start in accumulation compared with later repeats and hence are overrepresented in the processivity calculation, leading to a decrease in the apparent processivity. For a fixed number of bands,
n, under analysis, longer incubation times would reduce this error, but then the chances of multiple hits increase. In conclusion, the use of an unlabeled primer chase is the best solution as it avoids these ambiguities.
The ratio of primer to telomerase of 10 used in the simulation in
Figure 4a is higher than many experimental protocols but is close to that used by Jansson et al. [
12]. While this ratio results in departure from single hit conditions, the burst in primer binding provides a sensitive measure of telomerase active site concentration which is generally not well-defined by the protein concentration.
2.5. Analysis of Nucleotide Addition Processivity (NAP)
Scheme 2 was also used to model the intervening NA-transitions with the appropriate assignment of the microscopic processivity values at each step. In primer extension assays (
Figure 1b), the NA-bands are typically about 10 to 20% of the intensity of the adjacent RA-bands for 10 μM dNTP concentrations [
12]. This indicates that processivity associated with NAP is significantly higher for RAP. In the following simulations, we assigned a microscopic processivity = 0.99 for all NA-transitions in order to determine any systematic deviations of the extracted processivity values. To aid comparison with the RAP-only simulations above, the processivity of the G6 to G1-transition was set to 0.9464, so that the overall RAP = 0.9, when analyzed as a single step. This value was derived from the cumulative relationship of the processivity: (i.e., 0.99
5 × 0.9464 = 0.90). Note that a RA-band, as defined here, requires the preceding NA-step (the incorporation of G6) in order for it to be visible on a gel, while the stalling due to the translocation steps slows the incorporation of the next G1.
Figure 5a shows the expected product distribution when the reaction approaches equilibrium, calculated for 1000 steps with P
NAP = 0.99 and P
RAP = 0.9464. Fitting the intensity of the RA-bands only to an exponential function gave a decay constant of 0.1 repeat
−1, corresponding to an overall processivity of 0.90. Plotting the same data according to von Hippel [
4] yielded P
NAP = 0.99 and P
RAP = 0.945 from the intercept values, while the slope gave the cumulative processivity of the combined NA- and RA-events = 0.90 (
Figure 5b). When intensities corresponding to the NA- and RA-products were plotted according to Latrick and Cech [
7], the transitions between the NA- and RA-events were greatly smoothed. Small discontinuities were observed at each RA-step, but the overall trend was linear with a gradient of −0.1 repeat
−1 (
Figure 5c). The same gradient was observed when the intensities for the RA-bands alone were plotted and yielded a processivity of 0.90. A Peng plot (
Figure 5d) of the NA- and RA-bands yielded the input microscopic processivities of p
NAP = P
NAP = 0.99 and p
RAP = P
RAP = 0.9464. When the RA-bands were analyzed as a single transition, the observed p = P = 0.90, regardless of whether the intensity was based on that of the RA-bands alone, or that summed with the adjacent NA-bands to retain conservation of mass.
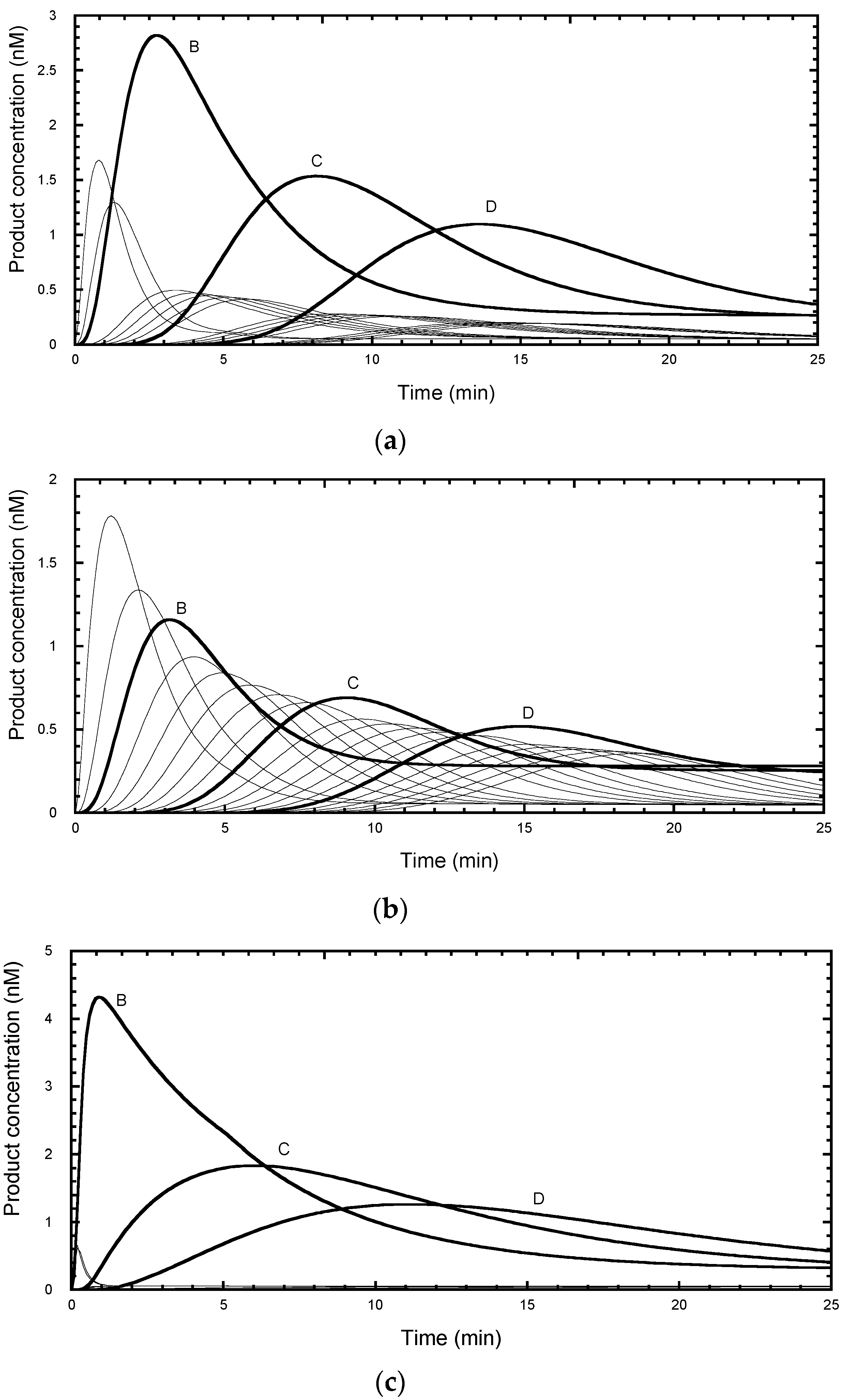
The increased processivity of NAP relative to the RAP could arise from changes in kf and/or kd. Three models were considered (i) kd remained similar and the reduced band intensities for NAP reflects the shorter transition time to the next intermediate because of an increased kf (ii) kf remains similar and the reduced band intensity for the NA-bands arises from a smaller kd (iii) both kf and kd are higher for the NA-transitions, but kf is most affected to give a higher processivity. These scenarios showed different kinetics but, with the appropriate selection of rate constants, the end-point product distributions can be identical. Hence, data obtained just from near end-point assays cannot distinguish these mechanisms.
Rate constants for the simulations were selected such that the processivity at each step matched those of the equilibrium models discussed above (i.e., P
NAP = 0.99 and P
RAP = 0.9464) while the overall transit time between RA-bands was comparable to that of the RAP-only model (1/0.18 = 5.5 min) of
Figure 3. The resultant schemes are shown in
Figure 6. Simulations of these mechanisms showed clear differences (
Figure 7). When
kd was similar for the NA- and RA-transitions, the NA-product concentrations remained at a near constant ratio (15 to 20%) compared with the neighboring RA-products throughout the time course (
Figure 7a). When
kf was similar for the NA- and RA-transitions, the NA-product concentrations showed transient values which were comparable to the peak RA-products (
Figure 7b). When
kf and
kd were larger for the NA-transitions, the NA-product concentrations reached their near-end point values without any transient phase, apart from the small peaks for the NA-transitions before the first RA-transition (
Figure 7c). The time courses reported by Jansson et al. [
12] and
Figure 1b most closely followed the model of
Figure 7a, indicative of the slowing of the forward transitions associated with the RA-transition, while the dissociation rate constants were less affected. The latter observation indicates that the anchor site is effective at retaining the DNA on the telomerase during the translocation steps.
A challenge for the analysis of experimental data is that the NA-bands are only well-resolved between early RA-bands (typically up to about the 5th or 6th repeat) and, beyond the 10th repeat, quantification of NA-bands is difficult (
Figure 1b and
Figure S1). The low intensities and poor resolution of the NA-bands lead to large relative errors in their estimated contribution, particularly for high molecular weight products. In the analysis of experimental data, the NA-band intensities can be ignored, pooled with adjacent RA-bands, pooled with adjacent NA-bands or subject to full analysis. Analysis of simulated data provides an assessment of the potential errors introduced by these approaches. For this purpose, the scheme of
Figure 6b, with NA-events k
f = 1.98 min
−1, RA-events k
f = 0.353 min
−1 and k
d = 0.02 min
−1, was subject to further analysis. Following the simulation as shown in
Figure 7a (determined with a numerical time increment of 0.00002 min), the data set was reduced by taking concentration values at 5 min intervals from 0 to 40 min following the chase, to make the set comparable to experimental sampling times. With this limited data set, DynaFit returned accurate rate constant values for both NA- and RA-steps for the first three RA-steps and the intervening NA-steps (deviation from input values was <1%:
Figure S2a, Table S1). To simulate the experimental noise and distortion of NA-band intensity by adjacent dominant RA-bands, a random factor was added to or subtracted from each band concentration with a value up to 10% of the summed concentration of the band with its neighbors (
Figure S2b). In this way an error in defining the boundary between a RA-band and the adjacent NA-band would distort the latter to a greater relative extent, as might occur in the experimental analysis of gel intensities. In this case, the deviations in returned rate constants for NA-steps k
f and k
d were <40% of the input values while for RA-steps
kf and
kd they were <20% (
Table S1). Note that the estimates of the rate constants for the first 3 NA-steps prior to the first RA-transition had a large error because these steps were largely complete by the first time point in the simulation (5 min after mixing when the chase was initiated). These simulations indicate that rate constants can be determined for the individual NA-transitions provided the NA-band intensities can be estimated with high accuracy, but this condition is unlikely to be met with experimental data beyond the first few repeats (cf.
Figure 1b and
Figure S1a).
For later repeats, where the NA-bands are poorly resolved, the intensity of the NA-bands between each pair of RA-bands can be summed and the NA-transitions modelled as a single elementary step. This approximation leads to a systematic deviation of the fit whose magnitude was ascertained by simulation. In the example in
Figure S2c,d, the five sequential NA-transitions, each with a rate constant of 1.98 min
−1, are reduced to a single step with an apparent rate constant ≈ 0.39 min
−1 (
Table S2). When simulated data were analyzed using DynaFit, the returned values of
kf and
kd for the first 7 RA-transitions deviate from the input values (0.353 min
−1 and 0.02 min
−1 respectively) by <10% and <20% respectively (
Table S2). These deviations are of the same order as the likely random experimental error and similar to the reported standard errors in the fit. However, the deviations are systematic and increase with the RA repeat number. They also depend on the precise time intervals over which the reaction is sampled. Fits to early RA-transitions place more emphasis on the end-point concentrations compared with later transitions, when sampled over the same intervals.
A further simplification can be made by pooling the NA-band intensities with the adjacent RA-band, which allows analysis of a large number of RA-steps. Again, the effect of this approximation was ascertained by analysis of simulated data (
Figure S2e). In the example analyzed, the NA- and RA-transitions have constant input rate constants and consequently it makes little difference (apart from the first transition) whether the NA-intensities are summed with the preceding or trailing RA-intensities or split between the two. The latter is the most practical method for high repeat numbers when only RA-bands can be resolved and was used in the analysis here. As discussed above, 5 consecutive NA-transitions with
kf = 1.98 min
−1 coupled with 1 RA-transition with
kf = 0.353 min
−1 approximates to a single transition with
kf ≈ 0.18 min
−1 (
Figure 6a). The fitted values of
kf and
kd for the 2nd to 7th RA-transition deviate by <25% and <40% respectively from the expected input values (
Table S3). Monte-Carlo analysis shows that
kf and
kd were covariant so that the deviations of the calculated microscopic processivity values from the input value (=0.9) is substantially less (<3%). Again, the estimated rate constants show systematic deviations from the true values for the same reasons as discussed above. The reported standard errors in the DynaFit estimates encompass the absolute deviations of the output which arise from lumping the NA-products with the adjacent RA-products. Ignoring the NA-products completely (
Figure S2f) is the poorest approximation (
Table S3), as well as presenting a practical challenge for high repeat numbers where the resolution of the NA-bands from the RA-bands is poor. Nevertheless, the extracted microscopic processivity values are still within 6% of the expected value.
For the analysis of experimental data, the above simulations suggest the following strategies: (i) When NA-bands are sufficiently resolved, it is best to include them in the analysis. Even if the estimated rate constants for the NA-transitions have a large error (as indicated by the standard error of the fit or confidence interval from Monte Carlo analysis), the rate constants for the RA-transitions (G6 to G1) are subject to minimal systematic error; (ii) If analysis extends into regions where NA-bands are poorly resolved, they are best treated as a single species (i.e., lump the 5 NA-band intensities into one); (iii) At high repeat numbers where NA-bands cannot be distinguished from the RA-bands, then the estimated RA-band intensities necessarily include the unresolved NA-intensities. When analyzing data using a simple processive model of RA-transitions (
Figure 6a), the intensities of the partially-resolved NA-bands at lower repeat numbers should be added to the adjacent RA-intensities rather than ignored (cf.
Figure S2e,f). The latter results in the failure to conserve mass and introduces the largest systematic error.