Combining Isotope Dilution and Standard Addition—Elemental Analysis in Complex Samples
Abstract
1. Introduction
2. Theoretical Methods
3. Materials and Experimental Methods
4. Results and Discussion
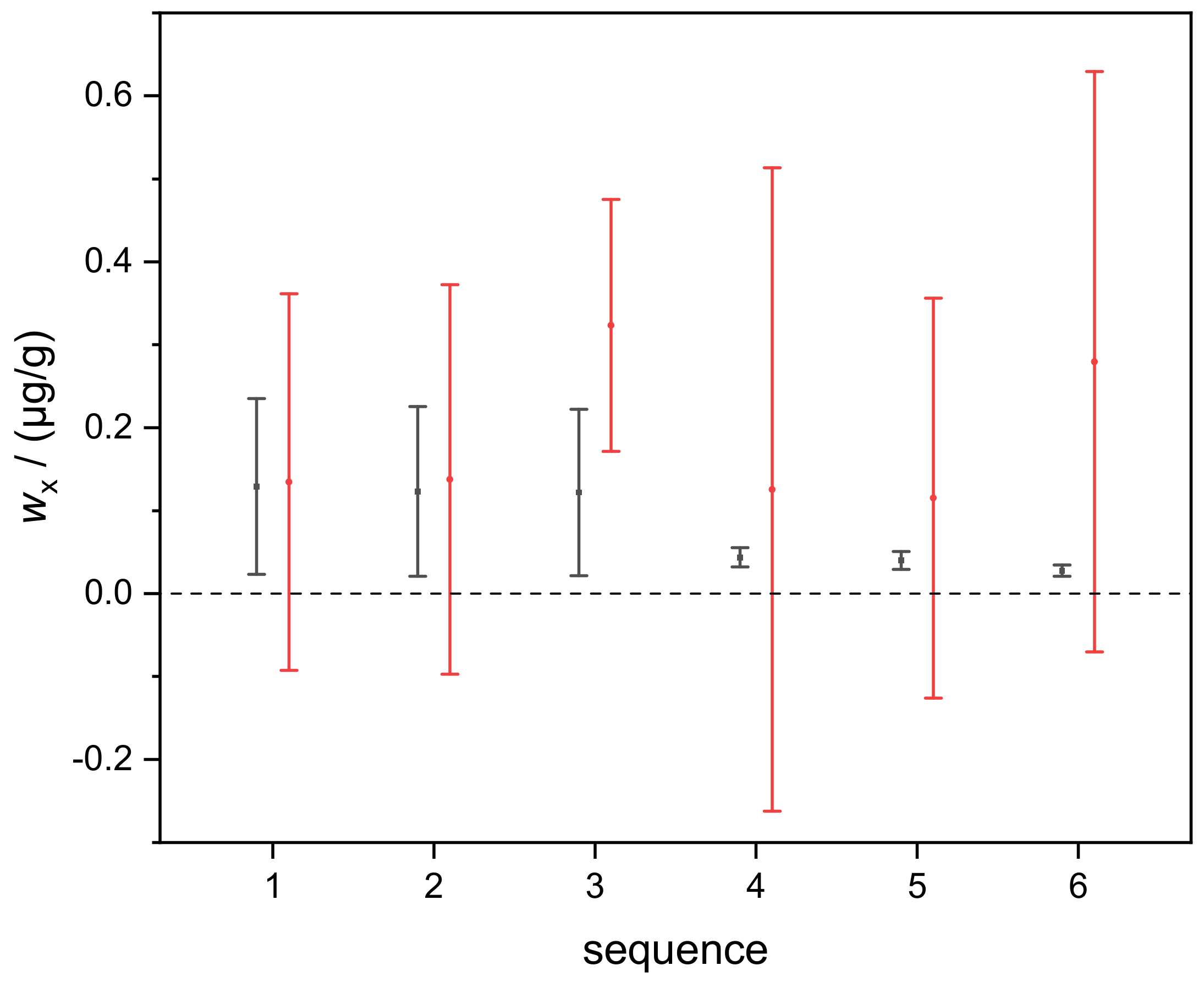
4.1. Silicon in Aqueous TMAH
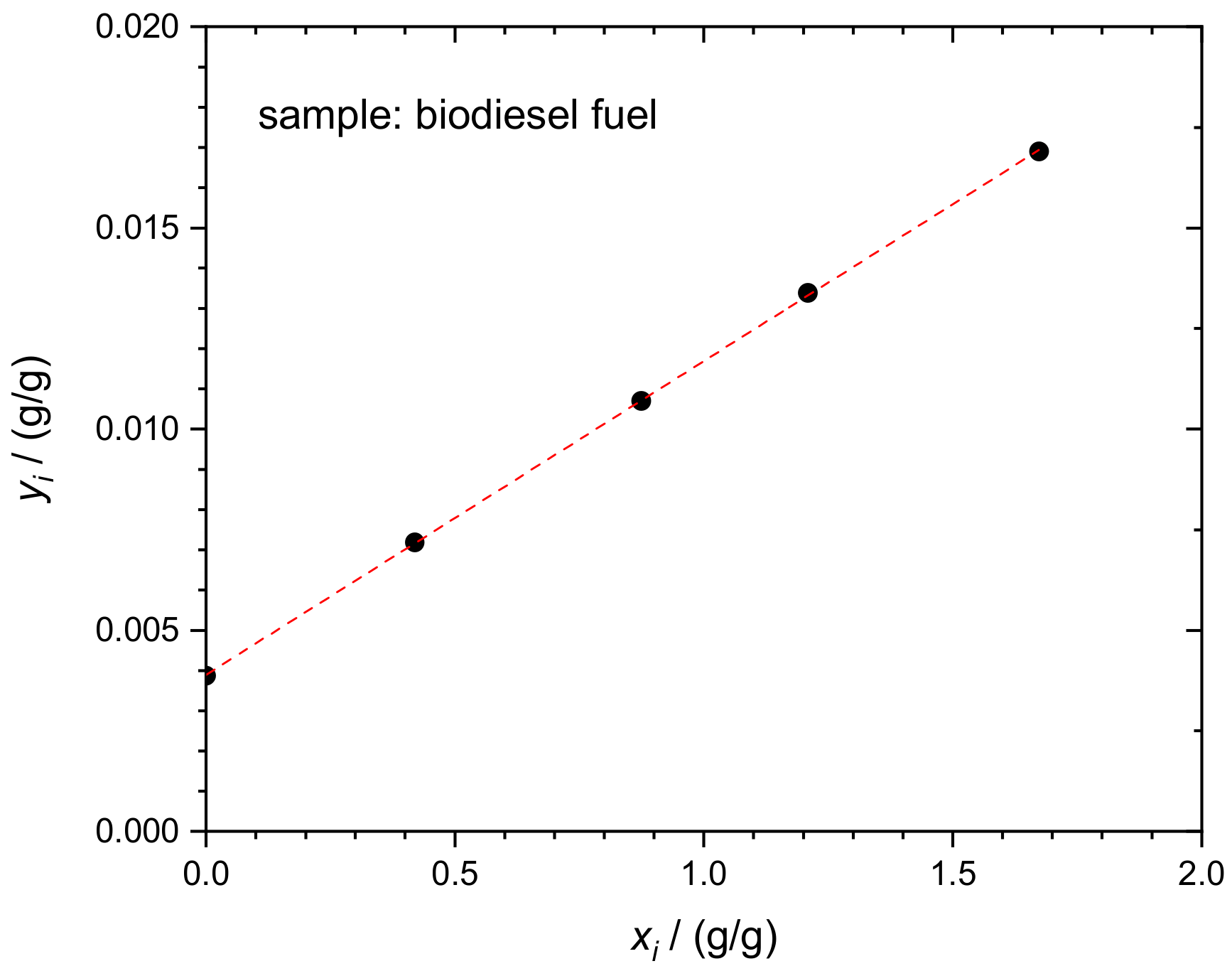
4.2. Sulfur in Biodiesel Fuel (BDF)
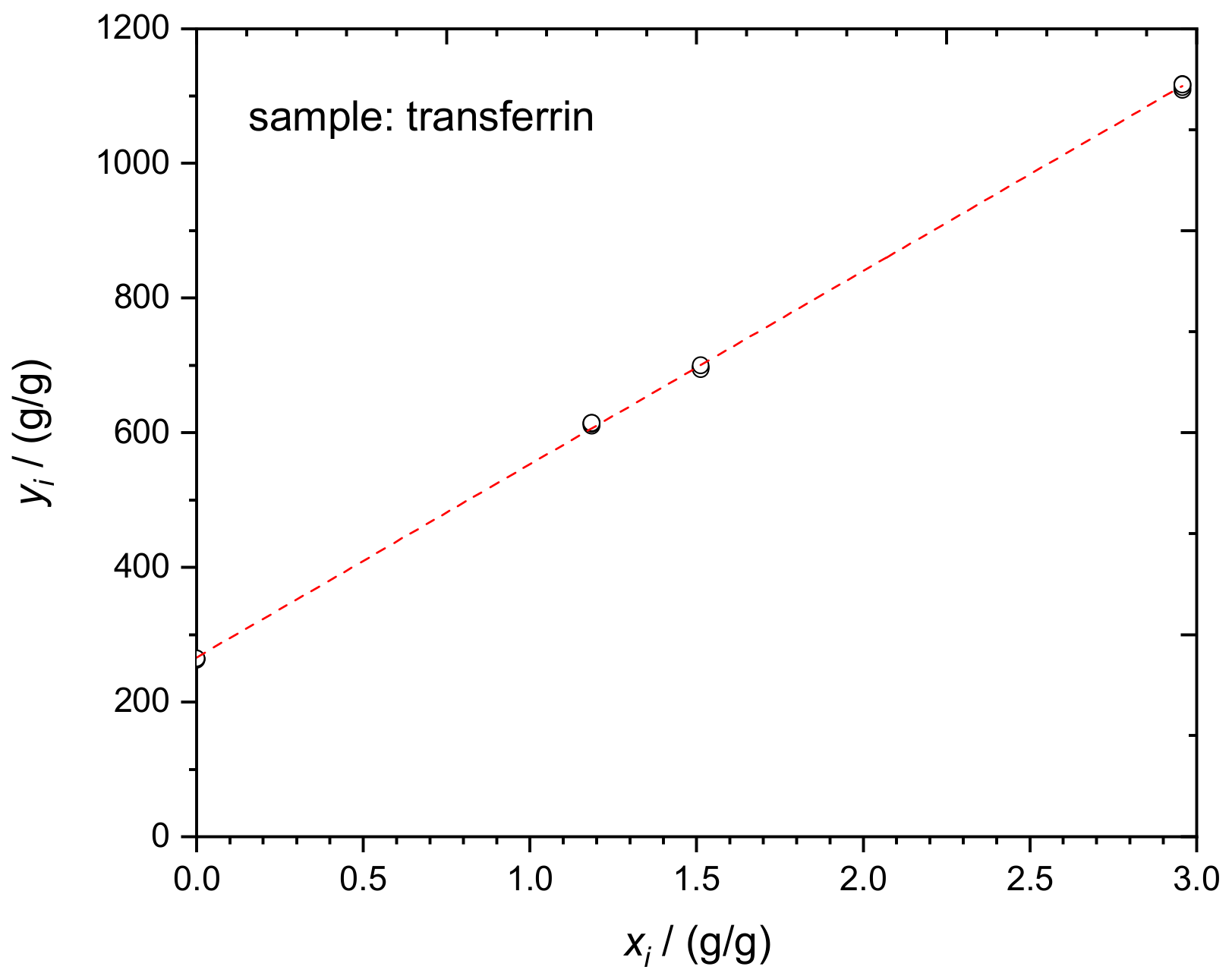
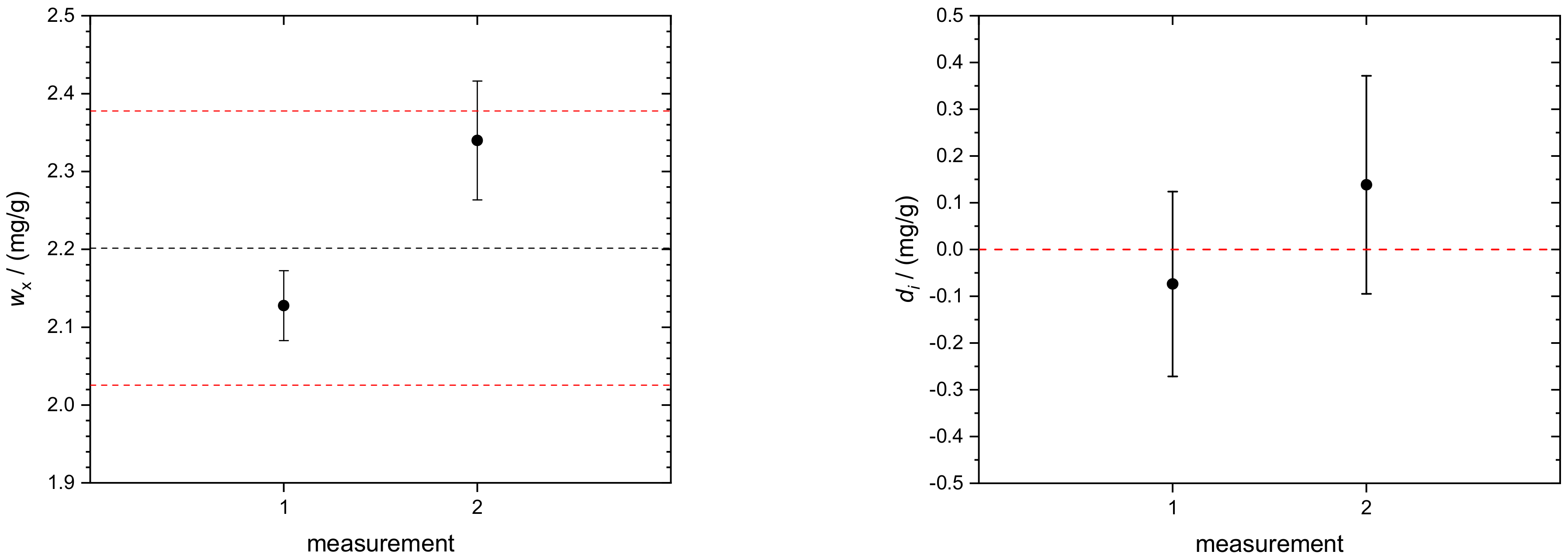
4.3. Transferrin in Human Serum
4.4. Comparison of Linear Regression (This Work) and Analytical Solution (Pagliano and Meija)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Pagliano, E.; Meija, J. Reducing the matrix effects in chemical analysis: Fusion of isotope dilution and standard addition methods. Metrologia 2016, 53, 829–834. [Google Scholar] [CrossRef]
- Sargent, M.; Goenaga-Infante, H.; Inagaki, K.; Ma, L.; Meija, J.; Pramann, A.; Rienitz, O.; Sturgeon, R.; Vogl, J.; Wang, J.; et al. The role of ICP-MS in inorganic chemical metrology. Metrologia 2019, 56, 1–32. [Google Scholar] [CrossRef]
- Vanhaecke, F.; Degryse, P. MC-ICP-MS in Isotopic Analysis: Fundamentals and Applications Using ICP-MS; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Yang, L. Accurate and precise determination of isotopic ratios by MC-ICP-MS: A review. Mass Spectrom. Rev. 2009, 28, 990–1011. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Tong, S.; Zhou, Z.; Hu, Z.; Mester, Z.; Meija, J. A critical review on isotopic fractionation correction methods for accurate isotope amount ratio measurements by MC-ICP-MS. J. Anal. At. Spectrom. 2018, 33, 1849–1861. [Google Scholar] [CrossRef]
- Andrén, H.; Rodushkin, I.; Stenberg, A.; Malinovskiy, D.; Baxter, D.C. Sources of mass bias and isotope ratio variation in multi-collector ICP-MS: Optimization of instrumental parameters based on experimental observations. J. Anal. At. Spectrom. 2004, 19, 1217–1224. [Google Scholar] [CrossRef]
- Pramann, A.; Rienitz, O.; Schiel, D.; Güttler, B.; Valkiers, S. Novel concept for the mass spectrometric determination of absolute isotopic abundances with improved measurement uncertainty: Part 3—Molar mass of silicon highly enriched in 28Si. Int. J. Mass Spectrom. 2011, 305, 58–68. [Google Scholar] [CrossRef]
- Vogl, J. Calibration strategies and quality assurance. In Inductively Coupled Plasma Mass Spectrometry Handbook; Nelms, S.M., Ed.; Blackwell Publishing Ltd: Oxford, UK, 2005; pp. 147–181. [Google Scholar]
- Working Group 1 of the Joint Committee for Guides in Metrology (JCGM/WG 1). JCGM 100:2008. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; JCGM: Sevres, France, 2008. [Google Scholar]
- Heumann, K.G. Isotope-dilution mass spectrometry of inorganic and organic substances. Fresenius Z. Anal. Chem. 1986, 325, 661–666. [Google Scholar] [CrossRef]
- De Bièvre, P. Isotope dilution mass spectrometry: What can it contribute to accuracy in trace analysis? Fresenius Z. Anal. Chem. 1990, 327, 766–771. [Google Scholar] [CrossRef]
- Heumann, K.G. Isotope dilution mass spectrometry (IDMS) of the elements. Mass Spectrom. Rev. 1992, 11, 41–67. [Google Scholar] [CrossRef]
- Sargent, M.; Harrington, C.; Harte, R. Guidelines for Achieving High Accuracy in Isotope Dilution Mass Spectrometry (IDMS); LGC Ltd: Cambridge, MA, USA, 2002. [Google Scholar]
- Vogl, J. Measurement uncertainty in single, double, and triple isotope dilution mass spectrometry. Rapid Comm. Mass Spectrom. 2012, 26, 275–281. [Google Scholar] [CrossRef]
- Frank, C.; Rienitz, O.; Swart, C.; Schiel, D. Improving species-specific IDMS: The advantages of triple IDMS. Anal. Bioanal. Chem. 2013, 405, 1913–1919. [Google Scholar] [CrossRef]
- Hauswaldt, A.-L.; Rienitz, O.; Jährling, R.; Fischer, N.; Schiel, D.; Labarraque, G.; Magnusson, B. Uncertainty of standard addition experiments: A novel approach to include the uncertainty associated with the standard in the model equation. Accred. Qual. Assur. 2012, 17, 129–138. [Google Scholar] [CrossRef]
- Rienitz, O.; Hauswaldt, A.-L.; Jährling, R. Standard addition challenge. Anal. Bioanal. Chem. 2012, 403, 2461–2462. [Google Scholar] [CrossRef] [PubMed]
- Rienitz, O.; Hauswaldt, A.-L.; Jährling, R. Solution to standard addition challenge. Anal. Bioanal. Chem. 2012, 404, 2117–2118. [Google Scholar] [CrossRef] [PubMed]
- Fujii, K.; Bettin, H.; Becker, P.; Massa, E.; Rienitz, O.; Pramann, A.; Nicolaus, A.; Kuramoto, N.; Busch, I.; Borys, M. Realization of the kilogram by the XRCD method. Metrologia 2016, 53, A19–A45. [Google Scholar] [CrossRef]
- Pramann, A.; Lee, K.S.; Noordmann, J.; Rienitz, O. Probing the homogeneity of the isotopic composition and molar mass of the ‘Avogadro’-crystal. Metrologia 2015, 52, 800–810. [Google Scholar] [CrossRef]
- Bartl, G.; Becker, P.; Beckhoff, B.; Bettin, H.; Beyer, E.; Borys, M.; Busch, I.; Cibik, L.; D’Agostino, G.; Darlatt, E.; et al. A new 28Si single crystal: Counting the atoms for the new kilogram definition. Metrologia 2017, 54, 693–715. [Google Scholar] [CrossRef]
- Güttler, B.; Rienitz, O.; Pramann, A. The avogadro constant for the definition and realization of the mole. Ann. Phys. 2018, 1800292. [Google Scholar] [CrossRef]
- Kuroiwa, T.; Zhu, Y.; Inagaki, K.; Long, S.E.; Christopher, S.J.; Puelles, M.; Borinsky, M.; Hatamleh, N.; Murby, J.; Merrick, J.; et al. Report of the CCQM-K123: Trace elements in biodiesel fuel. Metrologia 2017, 54, 08008. [Google Scholar] [CrossRef]
- Jou, Y.J.; Lin, C.D.; Lai, C.H.; Chen, C.H.; Kao, J.Y.; Chen, S.Y.; Tsai, M.H.; Huang, S.H.; Lin, C.W. Proteomic identification of salivary transferrin as a biomarker for early detection of oral cancer. Anal. Chim. Acta 2010, 681, 41–48. [Google Scholar] [CrossRef]
- Deutsches Ärzteblatt. Neufassung der Richtlinie der Bundesärztekammer zur Qualitätssicherung laboratoriumsmedizinischer Untersuchungen—Rili-BÄK. Dtsch. Arztebl. 2019, 116, A-2422 / B-1990 / C-1930. [Google Scholar]
- Feng, L.; Zhang, D.; Wang, J.; Li, H. Simultaneous quantification of proteins in human serum via sulfur and iron using HPLC coupled to post-column isotope dilution mass spectrometry. Anal. Methods 2014, 6, 7655–7662. [Google Scholar] [CrossRef]
- Larios, R.; Del Castillo Busto, M.E.; Garcia-Sar, D.; Ward-Deitrich, C.; Goenaga-Infante, H. Accurate quantification of carboplatin adducts with serum proteins by monolithic chromatography coupled to ICPMS with isotope dilution analysis. J. Anal. At. Spectrom. 2019, 34, 729–740. [Google Scholar] [CrossRef]
- Mana, G.; Rienitz, O. The calibration of Si-isotope ratio measurements. Int. J. Mass Spectrom. 2010, 291, 55–60. [Google Scholar] [CrossRef]
- Rienitz, O.; Pramann, A.; Vogl, J.; Lee, K.-S.; Yim, Y.-H.; Malinovskiy, D.; Hill, S.; Dunn, P.; Goenaga-Infante, H.; Ren, T.; et al. The comparability of the determination of the molar mass of silicon highly enriched in 28Si: Results of the CCQM-P160 interlaboratory comparison and additional external measurements. Metrologia 2020, 57, 1–13. [Google Scholar] [CrossRef]
- D’Agostino, G.; Di Luzio, M.; Mana, G.; Oddone, M.; Pramann, A.; Prata, M. 30Si mole fraction of a silicon material highly enriched in 28si determined by instrumental neutron activation analysis. Anal. Chem. 2015, 87, 5716–5722. [Google Scholar] [CrossRef]
- Kaltenbach, A.; Noordmann, J.; Görlitz, V.; Pape, C.; Richter, S.; Kipphardt, H.; Kopp, G.; Jährling, R.; Rienitz, O.; Güttler, B. Gravimetric preparation and characterization of primary reference solutions of molybdenum and rhodium. Anal. Bioanal. Chem. 2015, 407, 3093–3102. [Google Scholar] [CrossRef]
- Paris, G.; Sessions, A.L.; Subhas, A.V.; Adkins, J.F. MC-ICP-MS measurement of δ34S and ∆33S in small amounts of dissolved sulfate. Chem. Geol. 2013, 345, 50–61. [Google Scholar] [CrossRef]
- Deutsches Ärzteblatt. Neufassung der Richtlinie der Bundesärztekammer zur Qualitätssicherung laboratoriumsmedizinischer Untersuchungen—Rili-BÄK. Dtsch. Arztebl. 2014, 111, A-1583/B-1363/C-1295. [Google Scholar]
- Del Castillo Busto, M.E.; Montes-Bayón, M.; Sans-Mendel, A. Accurate determination of human serum transferrin isoforms: Exploring metal-specific isotope dilution analysis as a quantitative proteomic tool. Anal. Chem. 2006, 78, 8218–8226. [Google Scholar] [CrossRef]
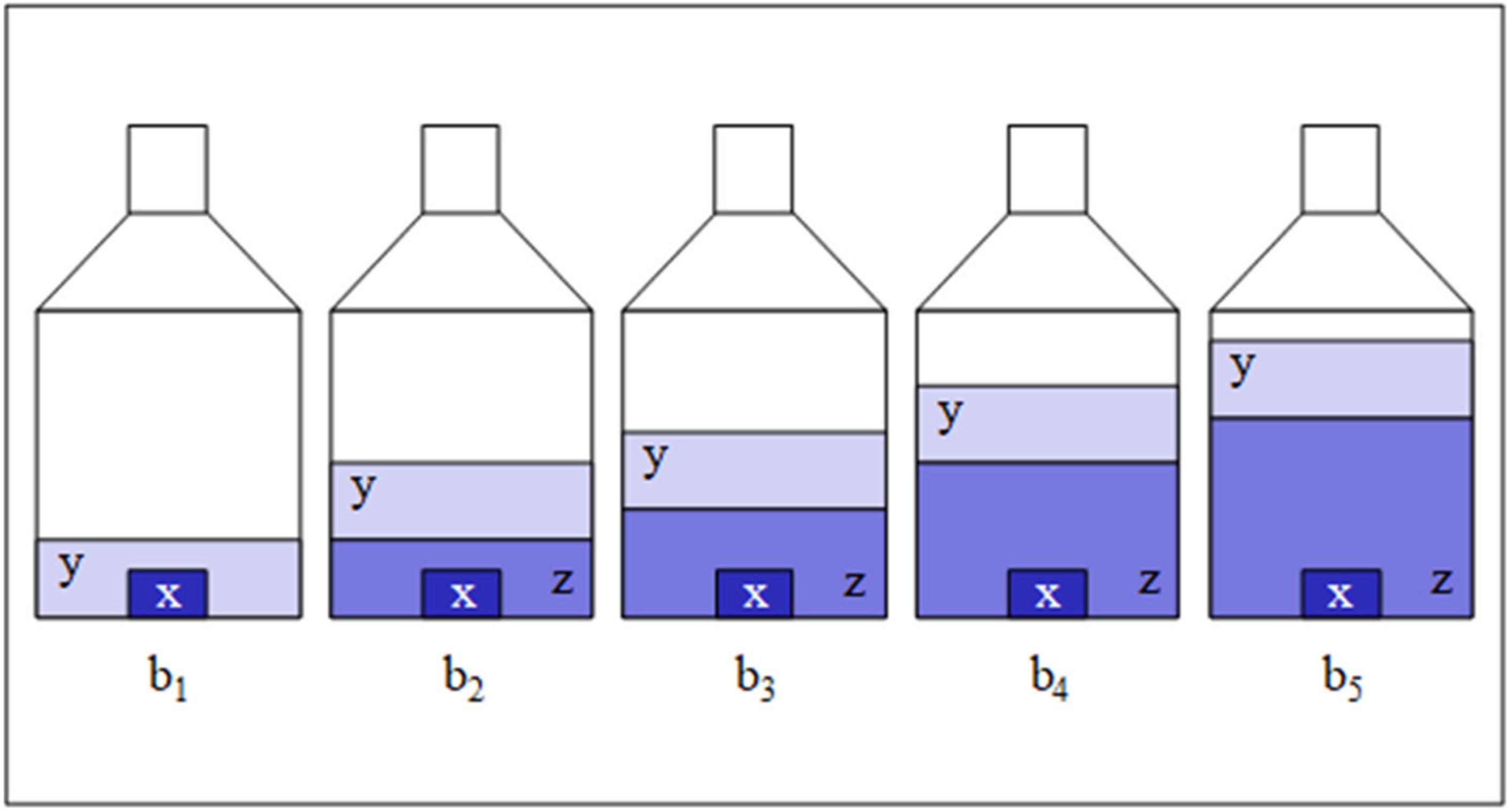
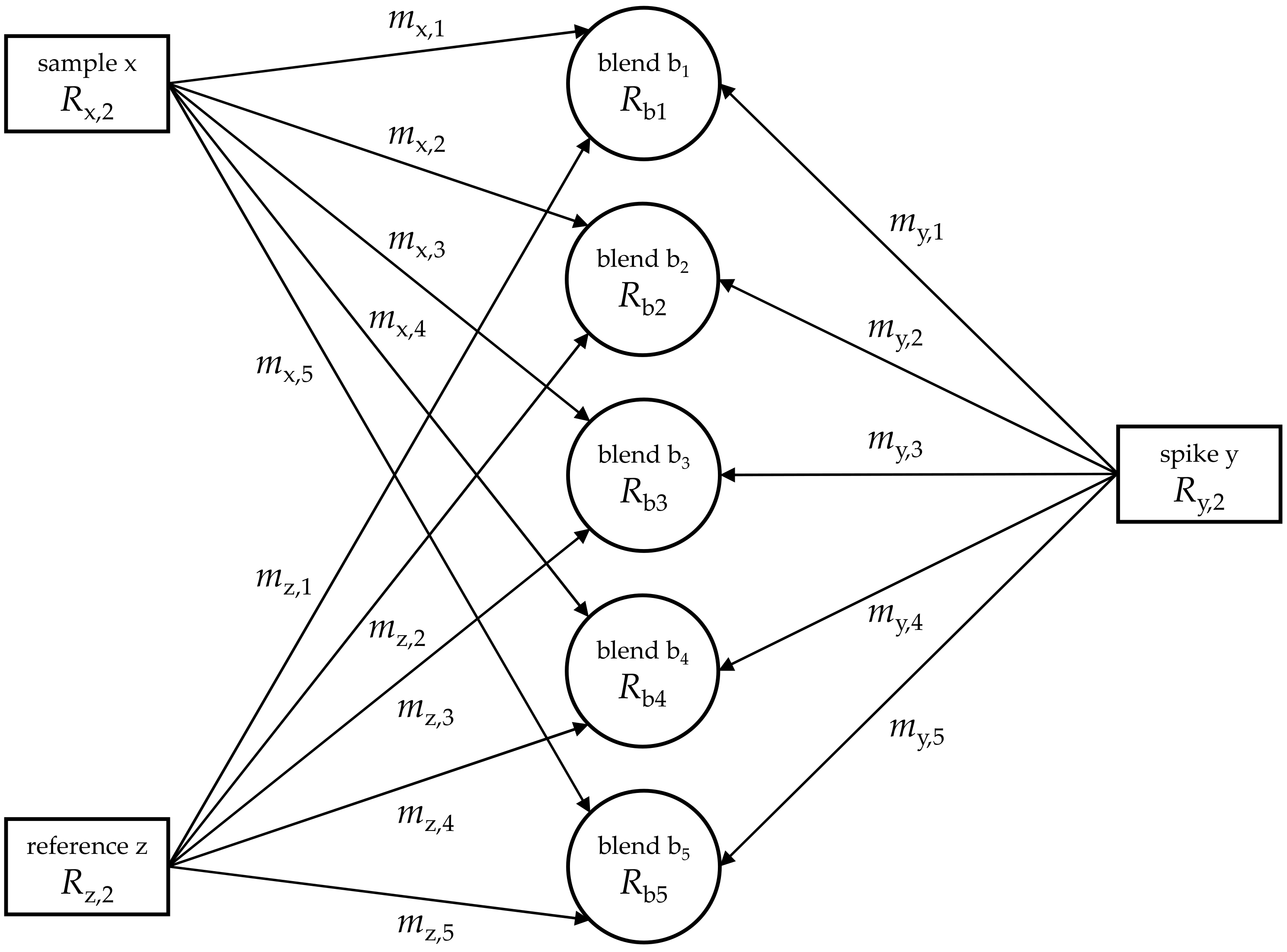


| Sample/Matrix | Silicon/TMAH | Sulfur/Biodiesel Fuel | TRF/Human Serum |
|---|---|---|---|
| Laboratory | PTB | BAM | PTB |
| Instrument | Thermo MC–ICP–MS Neptune | Thermo MC-ICP-MS Neptune Plus | Agilent 8900 ICP-QQQ-MS |
| Sample Introduction | PFA nebulizer 100 µL/min PEEK/PFA cyclonic + Scott chamber sapphire torch + injector BN shield Ni sampler + Ni X-skimmer | Aridus II desolvating system PFA nebulizer 100 µL/min Aridus PFA spray chamber standard torch and injector quartz shieldNi sampler + Ni H-skimmer | PFA MicroFlow nebulizer 700 µL, Scott chamber at 3 °C torch with 1 mm injector Pt shield Pt sampler and skimmer |
| Gas Flow Rates (Ar) | cooling: 16 L min−1 auxiliary: 0.8 L min−1 sample: 1.0 L min−1 | cooling: 16 L min−1 auxiliary: 0.9 L min−1 sample: 0.85 L min−1 | cooling: 15 L min−1 auxiliary: 0.9 L min−1 nebulizer gas: 0.8 L min−1 reaction gas (H2): 6.1 mL min−1 |
| Machine Parameters | high resolution (M/∆M = 8000) RF power 1180 W integration time 4.194 s idle time 3 s number of blocks 6 cycles/block 3 rotating amplifiers: yes Faraday cups: L3(28Si), C(29Si), H3(30Si) | high resolution (M/∆M = 8000) RF power 1200 W integration time 4.194 s idle time 3 s number of blocks 1 cycles/block 40 rotating amplifiers: no Faraday cups: L3(32S), C(33S), H3(34S) | MS/MS mode RF power 1550 W Sample depth 8.0 mm x-lens configuration integration time 0.1 s m/z 53, 54, 56, 57, 58, 60 |
| Sequence Settings | rinse time 120 s take-up time 60 s measured samples/sequence b1, b2, b3, b4, b5 (4 times each) | rinse time 30 s take-up time 80 s measured samples/sequence b1, b2, b3, b4, b5 (3 times each, separated by a block of 5 standards) | rinse time + take-up not applicable: HPLC separationmeasured samples/sequence b1, b2, b3, b4, blank, SP, K, blank (4 times) |
| Separation Settings | Agilent Bioinert 1260 HPLC system Column: MonoQ® GL 5/50 from GE Healthcare (Uppsala, Sweden) Mobile phase A: 12.5 mmol/L Tris at pH = 6.4 Mobile phase B: 12.5 mmol/L Tris + 125 mmol/L NH4Ac at pH = 6.4 Flow: 0.5 mL min−1 Gradient: 0 min → 0% B, 20 min → 100% B, 27 min → 100% B Column oven 30 °C Injection volume: 10 µL MWD 254 nm, 280 nm |
| x | z | y | ||||||
|---|---|---|---|---|---|---|---|---|
| bi | TMAHaq | WASO04 | “Si30” | Rb,i | Rx,i | Ry,i | ||
| i | mx,i | mz,i | my,i | I(30Si)/I(28Si) | xi | yi | I(30Si)/I(28Si) | I(30Si)/I(28Si) |
| g | g | g | V/V | g/g | g/g | V/V | mol/mol | |
| 1 | 10.0863 | 0.0000 | 22.8557 | 113.77732 | 0.0000 | 1.80 | 0.03353 | 204.19578 |
| 2 | 9.7836 | 7.8858 | 22.7577 | 1.59655 | 0.8060 | 301.51 | 0.03353 | 204.19578 |
| 3 | 9.6700 | 10.5255 | 22.3198 | 1.18847 | 1.0885 | 405.71 | 0.03353 | 204.19578 |
| 4 | 11.3192 | 15.3000 | 22.4864 | 0.83531 | 1.3517 | 503.86 | 0.03353 | 204.19578 |
| 5 | 10.0440 | 22.4061 | 22.7651 | 0.61405 | 2.2308 | 794.84 | 0.03353 | 204.19578 |
| a1 | a0 | wx | ||||||
| (g/g)/(g/g) | (g/g) | µg/g | ||||||
| 356.10062 | 11.474 | 0.13 |
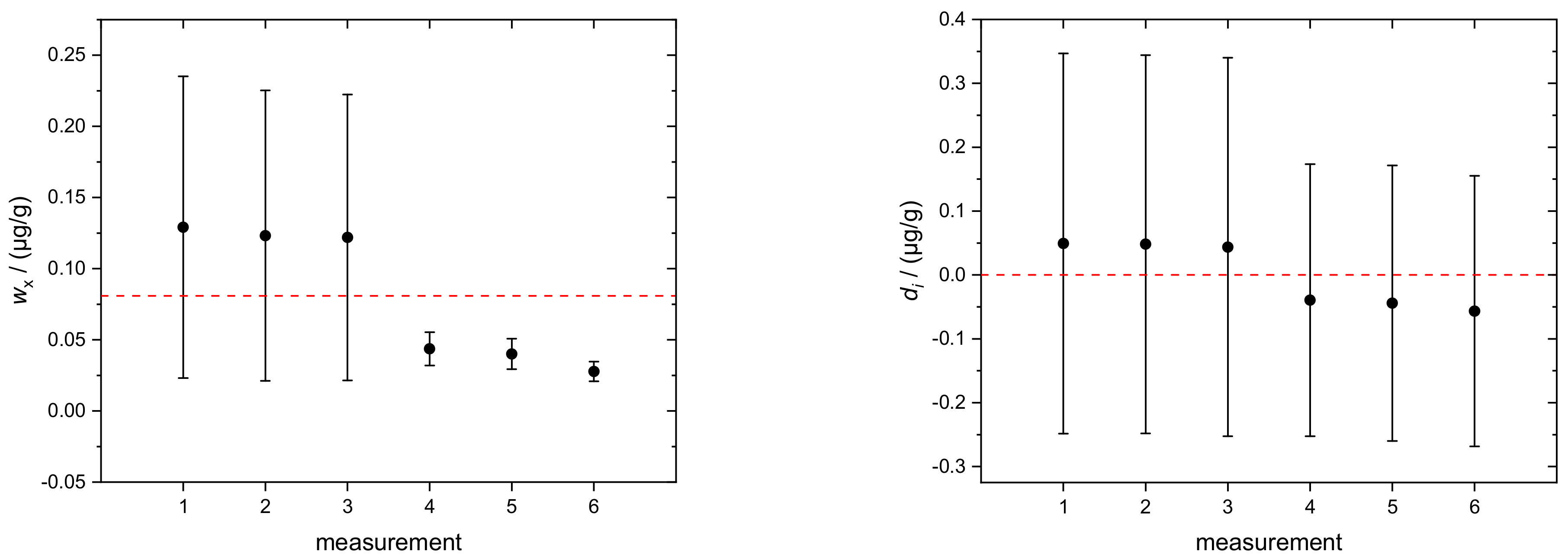
| Run | wx (Si) | u(wx (Si)) |
|---|---|---|
| µg/g | µg/g | |
| 1 | 0.13 | 0.11 |
| 2 | 0.12 | 0.10 |
| 3 | 0.12 | 0.10 |
| 4 | 0.044 | 0.012 |
| 5 | 0.040 | 0.011 |
| 6 | 0.028 | 0.007 |
| average | 0.081 | 0.073 |
| x | z | y | ||||||
|---|---|---|---|---|---|---|---|---|
| bi | BDF | NIST SRM 3154 | BAM S-34 | Rb,i | Rx,i | Ry,i | ||
| i | mx,i | mz,i | my,i | I(32S)/I(34S) | xi | yi | I(32S)/I(34S) | I(32S)/I(34S) |
| g | g | g | V/V | g/g | g/g | V/V | mol/mol | |
| 1 | 0.23748 | 0.00000 | 0.09670 | 0.20030 | 0.00000 | 0.00387 | 21.16643 | 0.00099 |
| 2 | 0.24149 | 0.10125 | 0.09843 | 0.36731 | 0.41927 | 0.00718 | 21.16643 | 0.00099 |
| 3 | 0.23819 | 0.20828 | 0.10899 | 0.48453 | 0.87443 | 0.01070 | 21.16643 | 0.00099 |
| 4 | 0.25126 | 0.30375 | 0.10631 | 0.64994 | 1.20891 | 0.01339 | 21.16643 | 0.00099 |
| 5 | 0.24311 | 0.40679 | 0.09966 | 0.83887 | 1.67328 | 0.01690 | 21.16643 | 0.00099 |
| a1 | a0 | wx | wx,corr | |||||
| (g/g)/(g/g) | g/g | µg/g | µg/g | |||||
| 0.007797 | 0.003894 | 8.063 | 7.36 |
| Run | wx,corr(S) | u(wx,corr(S)) |
|---|---|---|
| µg/g | µg/g | |
| 1 | 7.36 | 0.13 |
| 2 | 7.36 | 0.13 |
| 3 | 7.358 | 0.079 |
| average | 7.36 | 0.11 |
| x | z | y | ||||||
|---|---|---|---|---|---|---|---|---|
| bi | SeronormTM Immuno-Protein Lyo L-1 | ERM®-DA470k/IFCC | In-House Prepared TRF Spike | Rb,i | Rx,i | Ry,i | ||
| i | mx,i | mz,i | my,i | R(54Fe/56Fe) | xi | yi | R(54Fe/56Fe) | R(54Fe/56Fe) |
| g | g | g | mol/mol | g/g | g/g | mol/mol | mol/mol | |
| 1 | 0.04848 | 0.00000 | 0.15104 | 3.01104 | 0.00000 | 262.4 | 0.063703 | 251.22 |
| 2 | 2.99958 | 0.00000 | 263.4 | |||||
| 3 | 2.99154 | 0.00000 | 264.1 | |||||
| 4 | 2.98887 | 0.00000 | 264.4 | |||||
| 5 | 0.04923 | 0.05834 | 0.15123 | 1.31282 | 1.18510 | 614.6 | ||
| 6 | 1.32126 | 1.18510 | 610.5 | |||||
| 7 | 1.31656 | 1.18510 | 612.8 | |||||
| 8 | 1.31365 | 1.18510 | 614.2 | |||||
| 9 | 0.04910 | 0.07424 | 0.14909 | 1.15279 | 1.51220 | 697.3 | ||
| 10 | 1.15426 | 1.51220 | 696.3 | |||||
| 11 | 1.15733 | 1.51220 | 694.4 | |||||
| 12 | 1.14892 | 1.51220 | 699.8 | |||||
| 13 | 0.04923 | 0.14561 | 0.14951 | 0.74959 | 2.95788 | 1109.1 | ||
| 14 | 0.74722 | 2.95788 | 1113.0 | |||||
| 15 | 0.74440 | 2.95788 | 1117.6 | |||||
| 16 | 0.74494 | 2.95788 | 1116.7 | |||||
| a1 | a0 | wx | ||||||
| (g/g)/(g/g) | g/g | mg/g | ||||||
| 287.078 | 266.04 | 2.128 |
| This Work | Approach of [1] |
|---|---|
| blends | blends |
| b1, b2, b3, b4, b5 | b1, b2, b3 |
| wx(Si) | wx(Si) |
| µg/g | µg/g |
| 0.1292 | −0.5004 |
| Quantity | Unit | Best Estimate (Value) | Standard Uncertainty | Sensitivity Coefficient | Index |
|---|---|---|---|---|---|
| Xi | [Xi] | xi | u(xi) | ci | |
| wz | µg/g | 4.00694 | 6.01 × 10−3 | 0.031 | 0.0% |
| my1 | g | 22.49660 | 1.00 × 10−3 | 2.2 | 0.0% |
| mz2 | g | 10.31270 | 1.00 × 10−3 | 11 | 0.0% |
| my3 | g | 22.26850 | 1.00 × 10−3 | 2.8 | 0.0% |
| Rb2 | V/V | 1.23933 | 3.62 × 10−3 | 92 | 74.4% |
| Rz2 | V/V | 0.033527 | 335 × 10−6 | ||
| Rb3 | V/V | 0.88472 | 1.50 × 10−3 | −73 | 8.0% |
| Rb1 | V/V | 1.68846 | 5.46 × 10−3 | −30 | 17.5% |
| my2 | g | 22.43470 | 1.00 × 10−3 | −5.0 | 0.0% |
| mz3 | g | 14.57170 | 1.00 × 10−3 | −4.2 | 0.0% |
| mz1 | g | 7.46840 | 1.00 × 10−3 | −6.4 | 0.0% |
| mx2 | g | 9.22730 | 1.00 × 10−3 | 0.33 | 0.0% |
| Rx2 | V/V | 0.033527 | 335 × 10−6 | 10 | 0.0% |
| mx3 | g | 9.79000 | 1.00 × 10−3 | −0.13 | 0.0% |
| mx1 | g | 9.46490 | 1.00 × 10−3 | −0.20 | 0.0% |
| wx | g | 0.125 | 0.388 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brauckmann, C.; Pramann, A.; Rienitz, O.; Schulze, A.; Phukphatthanachai, P.; Vogl, J. Combining Isotope Dilution and Standard Addition—Elemental Analysis in Complex Samples. Molecules 2021, 26, 2649. https://doi.org/10.3390/molecules26092649
Brauckmann C, Pramann A, Rienitz O, Schulze A, Phukphatthanachai P, Vogl J. Combining Isotope Dilution and Standard Addition—Elemental Analysis in Complex Samples. Molecules. 2021; 26(9):2649. https://doi.org/10.3390/molecules26092649
Chicago/Turabian StyleBrauckmann, Christine, Axel Pramann, Olaf Rienitz, Alexander Schulze, Pranee Phukphatthanachai, and Jochen Vogl. 2021. "Combining Isotope Dilution and Standard Addition—Elemental Analysis in Complex Samples" Molecules 26, no. 9: 2649. https://doi.org/10.3390/molecules26092649
APA StyleBrauckmann, C., Pramann, A., Rienitz, O., Schulze, A., Phukphatthanachai, P., & Vogl, J. (2021). Combining Isotope Dilution and Standard Addition—Elemental Analysis in Complex Samples. Molecules, 26(9), 2649. https://doi.org/10.3390/molecules26092649








