Cross-Talk between Overlap Interactions in Biomolecules: A Case Study of the β-Turn Motif
Abstract
1. Introduction
2. Results
2.1. Identifying Overlap-Based Interactions in -Turns of Proteins
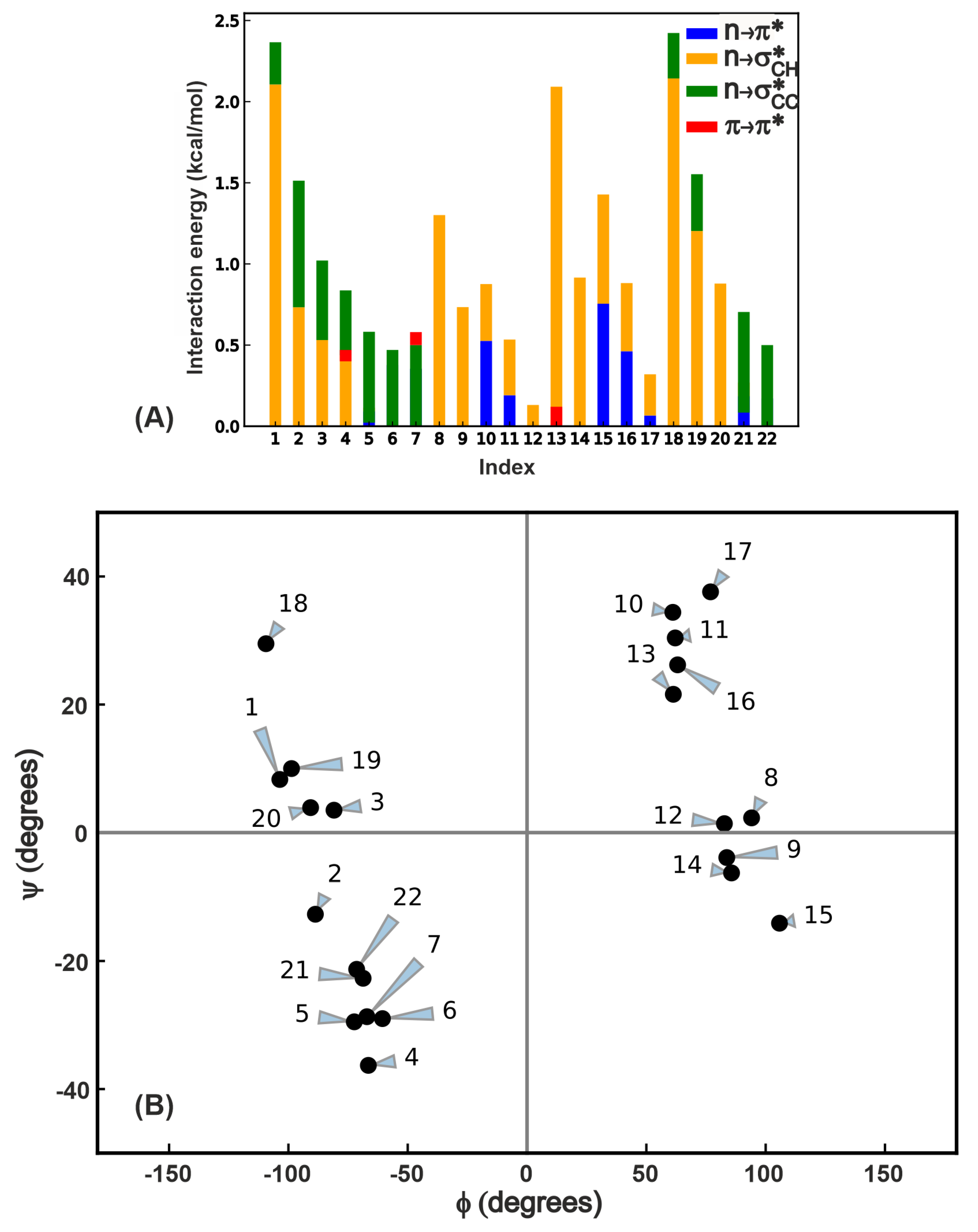
2.2. Analysis of NCIs in -Turns in Terms of Structure and Interaction Energy
2.3. Prevalence of NCIs in -Turns of PDB Structures
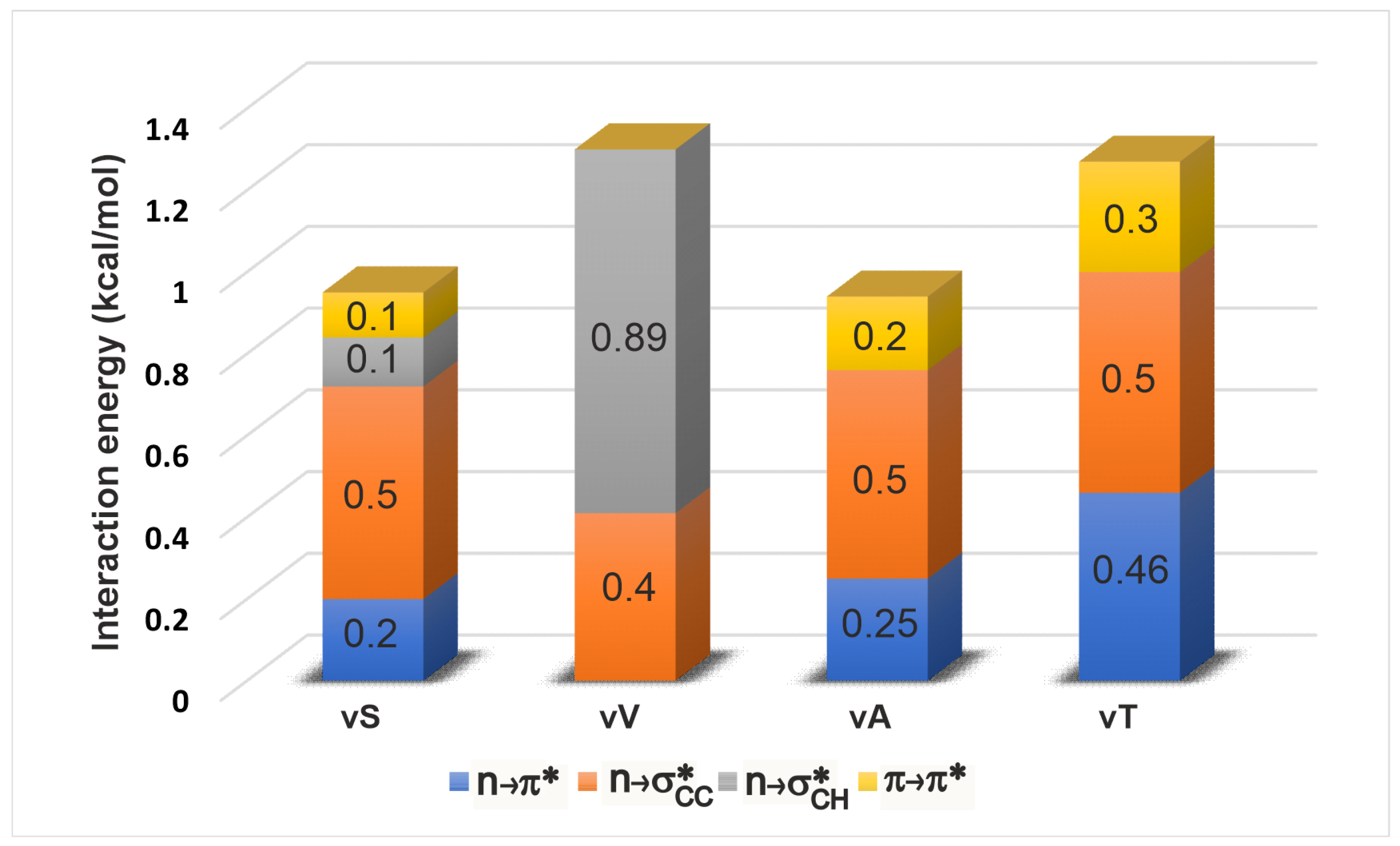
2.3.1. Energetics
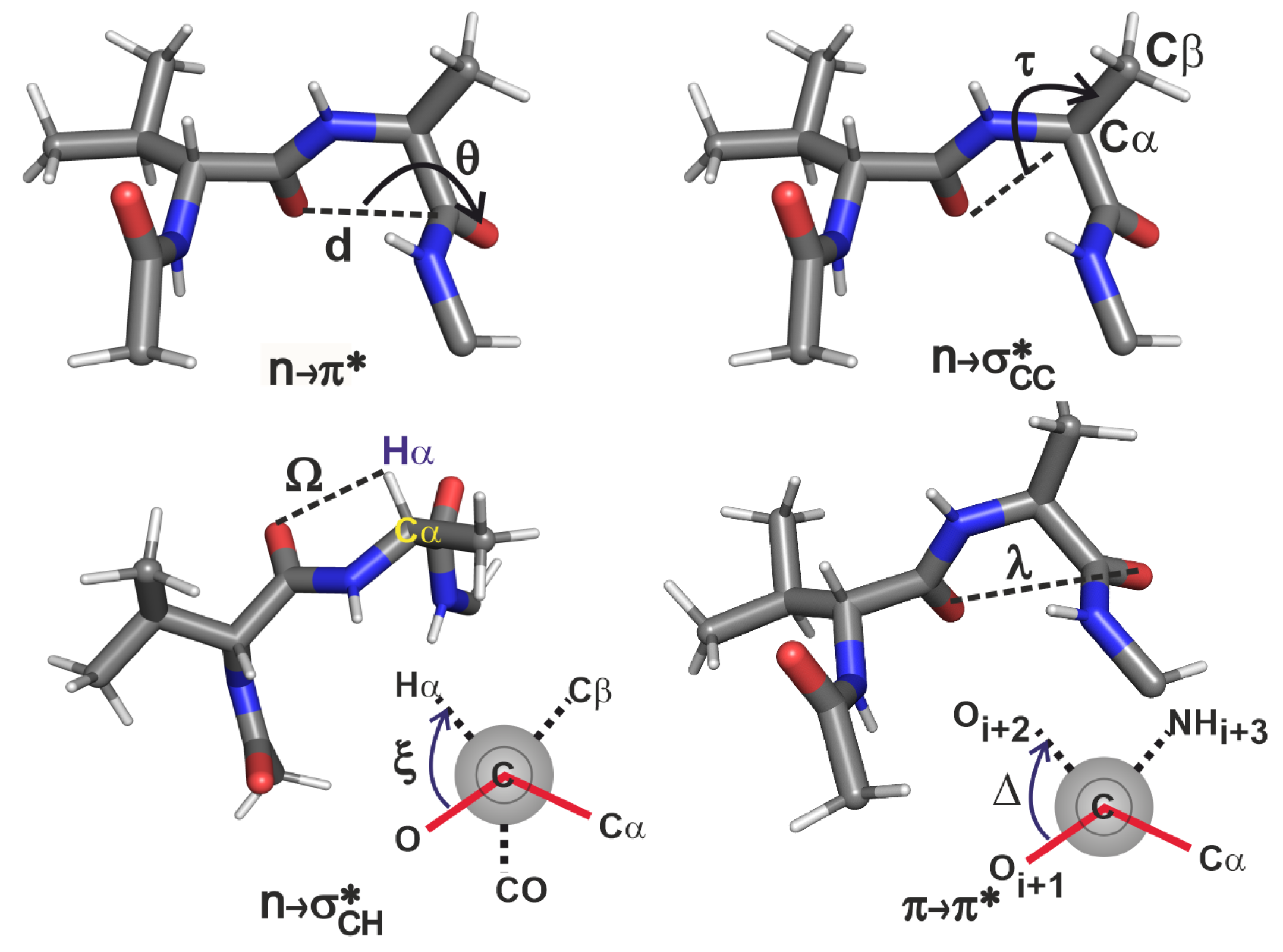
2.3.2. Geometric Criteria Based on Variations in -Turn Sidechain Structure
- As increases, decreases in strength. A small value of this coordinate is more important than the dihedral in order for the interaction to materialise. From this analysis, it is clear that this interaction exists when 0 Å Å and .
- The strength of the interaction decreases as deviates from , suggesting that this interaction is likely to be present when . Though the lower limit of has emerged from the current analysis of only 22 proteins, it is apparent that the extent of overlap will go to zero as we approach or lower.
- The presents two possible scenarios for its existence. The orbital can overlap with the n orbital either when C=O and are on the same side of the peptide backbone, or on the opposite sides of the backbone because of the cylindrical nature of the orbital. Therefore this interaction is possible when (a) Å Å and , and (b) Å Å and . Though the latter case was not seen in the GB1 variants, the PDB analysis shows that these interactions can occur in more than one orientation. Note that this is in contrast to expecting this interaction to exist simply based on the distance being less than sum of van der Waals radii of and , and an exhaustive NBO analysis was essential to establish the criterion for the existence of even when is large.
2.3.3. Analysis
3. Discussion
4. Methods
4.1. Natural Bond Order Analysis
4.2. Solvent Model
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pauling, L. The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules. J. Am. Chem. Soc. 1931, 53, 1367–1400. [Google Scholar] [CrossRef]
- Wintjens, R.; Liévin, J.; Rooman, M.; Buisine, E. Contribution of cation-π interactions to the stability of protein-DNA complexes. J. Mol. Biol. 2000, 302, 393–408. [Google Scholar] [CrossRef] [PubMed]
- Gallivan, J.P.; Dougherty, D.A. Cation-π interactions in structural biology. Proc. Natl. Acad. Sci. USA 1999, 96, 9459–9464. [Google Scholar] [CrossRef] [PubMed]
- Purich, D.L. Enzyme catalysis: A new definition accounting for noncovalent substrate-and product-like states. Trends Biochem. Sci. 2001, 26, 417–421. [Google Scholar] [CrossRef]
- Cooper, G.M. The Chemistry of Cells: The Central Role of Enzymes as Biological Catalysts; Sinauer Associates: Sunderland, MA, USA, 2000. [Google Scholar]
- Hudson, K.L.; Bartlett, G.J.; Diehl, R.C.; Agirre, J.; Gallagher, T.; Kiessling, L.L.; Woolfson, D.N. Carbohydrate–aromatic interactions in proteins. J. Am. Chem. Soc. 2015, 137, 15152–15160. [Google Scholar] [CrossRef] [PubMed]
- Spiwok, V. CH/π interactions in carbohydrate recognition. Molecules 2017, 22, 1038. [Google Scholar] [CrossRef]
- Vernon, R.M.; Chong, P.A.; Tsang, B.; Kim, T.H.; Bah, A.; Farber, P.; Lin, H.; Forman-Kay, J.D. Pi-Pi contacts are an overlooked protein feature relevant to phase separation. eLife 2018, 7, e31486–e31534. [Google Scholar] [CrossRef] [PubMed]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Pauling, L.; Corey, R.B.; Branson, H.R. The structure of proteins: Two hydrogen-bonded helical configurations of the polypeptide chain. Proc. Natl. Acad. Sci. USA 1951, 37, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Iwaoka, M.; Takemoto, S.; Tomoda, S. Statistical and theoretical investigations on the directionality of nonbonded S⋯O interactions. Implications for molecular design and protein engineering. J. Am. Chem. Soc. 2002, 124, 10613–10620. [Google Scholar] [CrossRef]
- Burgi, H.; Dunitz, J.; Shefter, E. Geometrical reaction coordinates. II. Nucleophilic addition to a carbonyl group. J. Am. Chem. Soc. 1973, 95, 5065–5067. [Google Scholar] [CrossRef]
- Bürgi, H.; Dunitz, J.; Shefter, E. Chemical reaction paths. IV. Aspects of O⋯C= O interactions in crystals. Acta Crystall. B-Struct. 1974, 30, 1517–1527. [Google Scholar] [CrossRef]
- Sahariah, B.; Sarma, B.K. Relative orientation of the carbonyl groups determines the nature of orbital interactions in carbonyl–carbonyl short contacts. Chem. Sci. 2019, 10, 909–917. [Google Scholar] [CrossRef]
- Singh, S.K.; Kumar, S.; Das, A. Competition between n →π Ar* and conventional hydrogen bonding (N–H-N) interactions: An ab initio study of the complexes of 7-azaindole and fluorosubstituted pyridines. Phys. Chem. Chem. Phys. 2014, 16, 8819–8827. [Google Scholar] [CrossRef]
- Bartlett, G.J.; Newberry, R.W.; VanVeller, B.; Raines, R.T.; Woolfson, D.N. Interplay of hydrogen bonds and n →π* interactions in proteins. J. Am. Chem. Soc. 2013, 135, 18682–18688. [Google Scholar] [CrossRef]
- Allen, F.; Baalham, C.A.; Lommerse, J.; Raithby, P. Carbonyl–carbonyl interactions can be competitive with hydrogen bonds. Acta Crystall. B-Struct. 1998, 54, 320–329. [Google Scholar] [CrossRef]
- Frontera, A.; Quiñonero, D.; Costa, A.; Ballester, P.; Deyà, P.M. MP2 study of cooperative effects between cation–π, anion–π and π–π interactions. New J. Chem. 2007, 31, 556–560. [Google Scholar] [CrossRef]
- Jeffrey, G.A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer-Verlag: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Newberry, R.W.; Raines, R.T. Secondary forces in protein folding. ACS Chem. Biol. 2019, 14, 1677–1686. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, R. Cooperative hydrogen bonding in amides and peptides. J. Mol. Liq. 2000, 84, 65–75. [Google Scholar] [CrossRef]
- Shishkin, O.V.; Gorb, L.; Leszczynski, J. Modeling of the hydration shell of uracil and thymine. Int. J. Mol. Sci. 2000, 1, 17–27. [Google Scholar] [CrossRef]
- Robertson, A.D.; Murphy, K.P. Protein structure and the energetics of protein stability. Chem. Rev. 1997, 97, 1251–1268. [Google Scholar] [CrossRef]
- Weinhold, F. Nature of H-bonding in clusters, liquids, and enzymes: An ab initio, natural bond orbital perspective. J. Mol. Struct. Theochem. 1997, 398, 181–197. [Google Scholar] [CrossRef]
- Hinderaker, M.P.; Raines, R.T. An electronic effect on protein structure. Prot. Sci. 2003, 12, 1188–1194. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, G.J.; Choudhary, A.; Raines, R.T.; Woolfson, D.N. n →π* interactions in proteins. Nat. Chem. Biol. 2010, 6, 615–620. [Google Scholar] [CrossRef] [PubMed]
- Sahariah, B.; Sarma, B.K. Spectroscopic evidence of n →π* interactions involving carbonyl groups. Phys. Chem. Chem. Phys. 2020, 22, 26669–26681. [Google Scholar] [CrossRef] [PubMed]
- Deb, P.; Jin, G.Y.; Singh, S.K.; Moon, J.; Kwon, H.; Das, A.; Bagchi, S.; Kim, Y.S. Interconverting Hydrogen-Bonding and Weak n →π* Interactions in Aqueous Solution: A Direct Spectroscopic Evidence. J. Phys. Chem. Lett. 2018, 9, 5425–5429. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.K.; Mishra, K.K.; Sharma, N.; Das, A. Direct spectroscopic evidence for an n →π* interaction. Angew. Chem. Int. Ed. 2016, 55, 7801–7805. [Google Scholar] [CrossRef] [PubMed]
- Khatri, B.; Majumder, P.; Nagesh, J.; Penmatsa, A.; Chatterjee, J. Increasing protein stability by engineering the n-→π* interaction at the β-turn. Chem. Sci. 2020, 11, 9480–9487. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom disperson corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision D. 01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 6.0: Natural bond orbital analysis program. J. Comput. Chem. 2013, 34, 1429–1437, Erratum in 2013, 34, 2134. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation theory approach to intermolecular potential energy surfaces of van der Waals complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, R.; Li, P.; Zhang, H. On the properties of S⋯O and S⋯π noncovalent interactions: The analysis of geometry, interaction energy and electron density. New J. Chem. 2015, 39, 1611–1618. [Google Scholar] [CrossRef]
- Jakobsche, C.E.; Choudhary, A.; Miller, S.J.; Raines, R.T. n →π* Interaction and n)(π Pauli repulsion are antagonistic for protein stability. J. Am. Chem. Soc. 2010, 132, 6651–6653. [Google Scholar] [CrossRef]
- Dill, K.A. Dominant forces in protein folding. Biochemistry 1990, 29, 7133–7155. [Google Scholar] [CrossRef]
- Honig, B.; Yang, A.S. Free energy balance in protein folding. Adv. Protein Chem. 1995, 46, 27–58. [Google Scholar]
- Mahadevi, A.S.; Sastry, G.N. Cooperativity in noncovalent interactions. Chem. Rev. 2016, 116, 2775–2825. [Google Scholar] [CrossRef]
- Chawla, M.; Chermak, E.; Zhang, Q.; Bujnicki, J.M.; Oliva, R.; Cavallo, L. Occurrence and stability of lone pair–π stacking interactions between ribose and nucleobases in functional RNAs. Nucleic Acids Res. 2017, 45, 11019–11032. [Google Scholar] [CrossRef] [PubMed]
- Poater, J.; Swart, M.; Bickelhaupt, F.M.; Guerra, C.F. B-DNA structure and stability: The role of hydrogen bonding, π–π stacking interactions, twist-angle, and solvation. Org. Biomol. Chem. 2014, 12, 4691–4700. [Google Scholar] [CrossRef]
- Hunter, C.A. Sequence-dependent DNA structure: The role of base stacking interactions. J. Mol. Biol. 1993, 230, 1025–1054. [Google Scholar] [CrossRef] [PubMed]
- Cooper, V.R.; Thonhauser, T.; Puzder, A.; Schröder, E.; Lundqvist, B.I.; Langreth, D.C. Stacking interactions and the twist of DNA. J. Am. Chem. Soc. 2008, 130, 1304–1308. [Google Scholar] [CrossRef] [PubMed]
- Murthy, A.C.; Dignon, G.L.; Kan, Y.; Zerze, G.H.; Parekh, S.H.; Mittal, J.; Fawzi, N.L. Molecular interactions underlying liquid- liquid phase separation of the FUS low-complexity domain. Nat. Struct. Mol. Biol. 2019, 26, 637–648. [Google Scholar] [CrossRef]
- Nott, T.J.; Petsalaki, E.; Farber, P.; Jervis, D.; Fussner, E.; Plochowietz, A.; Craggs, T.D.; Bazett-Jones, D.P.; Pawson, T.; Forman-Kay, J.D.; et al. Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles. Mol. Cell 2015, 57, 936–947. [Google Scholar] [CrossRef] [PubMed]
- Weinhold, F. Natural bond orbital methods. Encycl. Comput. Chem. 1998, 3, 1792–1811. [Google Scholar]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Von Hopffgarten, M.; Frenking, G. Energy decomposition analysis. WIREs Comput. Mol. Sci. 2018, 8, e1345. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic population analysis on LCAO–MO molecular wave functions. I. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef]
- Mayer, I. Charge, bond order and valence in the AB initio SCF theory. Chem. Phys. Lett. 1983, 97, 270–274. [Google Scholar] [CrossRef]
- Khaliullin, R.Z.; Cobar, E.A.; Lochan, R.C.; Bell, A.T.; Head-Gordon, M. Unravelling the origin of intermolecular interactions using absolutely localized molecular orbitals. J. Phys. Chem. A 2007, 111, 8753–8765. [Google Scholar] [CrossRef] [PubMed]
- Weiner, P.K.; Langridge, R.; Blaney, J.M.; Schaefer, R.; Kollman, P.A. Electrostatic potential molecular surfaces. Proc. Natl. Acad. Sci. USA 1982, 79, 3754–3758. [Google Scholar] [CrossRef] [PubMed]
- Carlson, B.; Keller, J.M. Eigenvalues of density matrices. Phys. Rev. 1961, 121, 659–661. [Google Scholar] [CrossRef]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry: An Introduction to Advanced Electronic Structure Theory; Dover Publications: Mineola, NY, USA, 1989. [Google Scholar]
- Scalmani, G.; Frisch, M.J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110-1–114110-15. [Google Scholar] [CrossRef] [PubMed]
- Ponce, M.; van Zon, R.; Northrup, S.; Gruner, D.; Chen, J.; Ertinaz, F.; Fedoseev, A.; Groer, L.; Mao, F.; Mundim, B.C.; et al. Deploying a Top-100 Supercomputer for Large Parallel Workloads: The Niagara Supercomputer. In Proceedings of the Practice and Experience in Advanced Research Computing on Rise of the Machines (Learning) (PEARC’19); Association for Computing Machinery: New York, NY, USA, 2019. [Google Scholar]
- Loken, C.; Gruner, D.; Groer, L.; Peltier, R.; Bunn, N.; Craig, M.; Henriques, T.; Dempsey, J.; Yu, C.H.; Chen, J.; et al. SciNet: Lessons Learned from Building a Power-efficient Top-20 System and Data Centre. J. Phys. Conf. Ser. 2010, 256, 012026. [Google Scholar] [CrossRef]
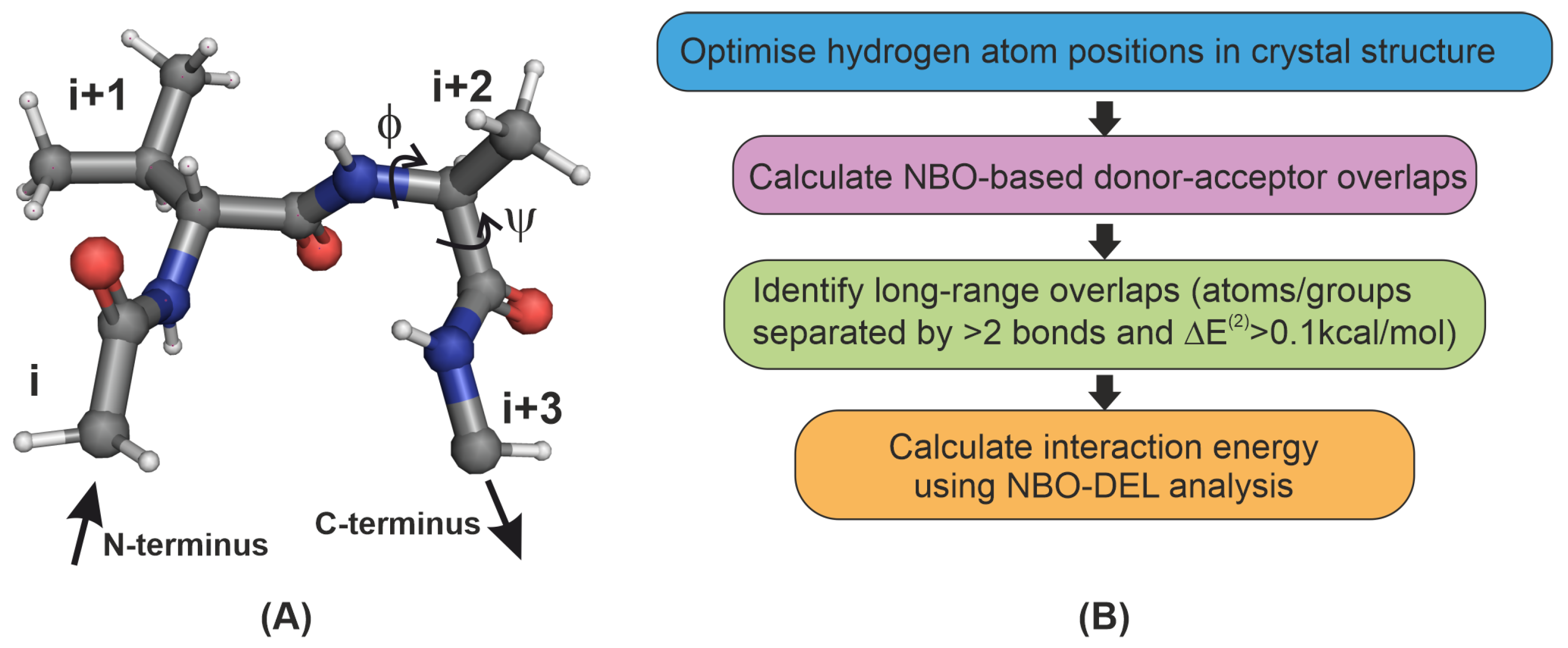
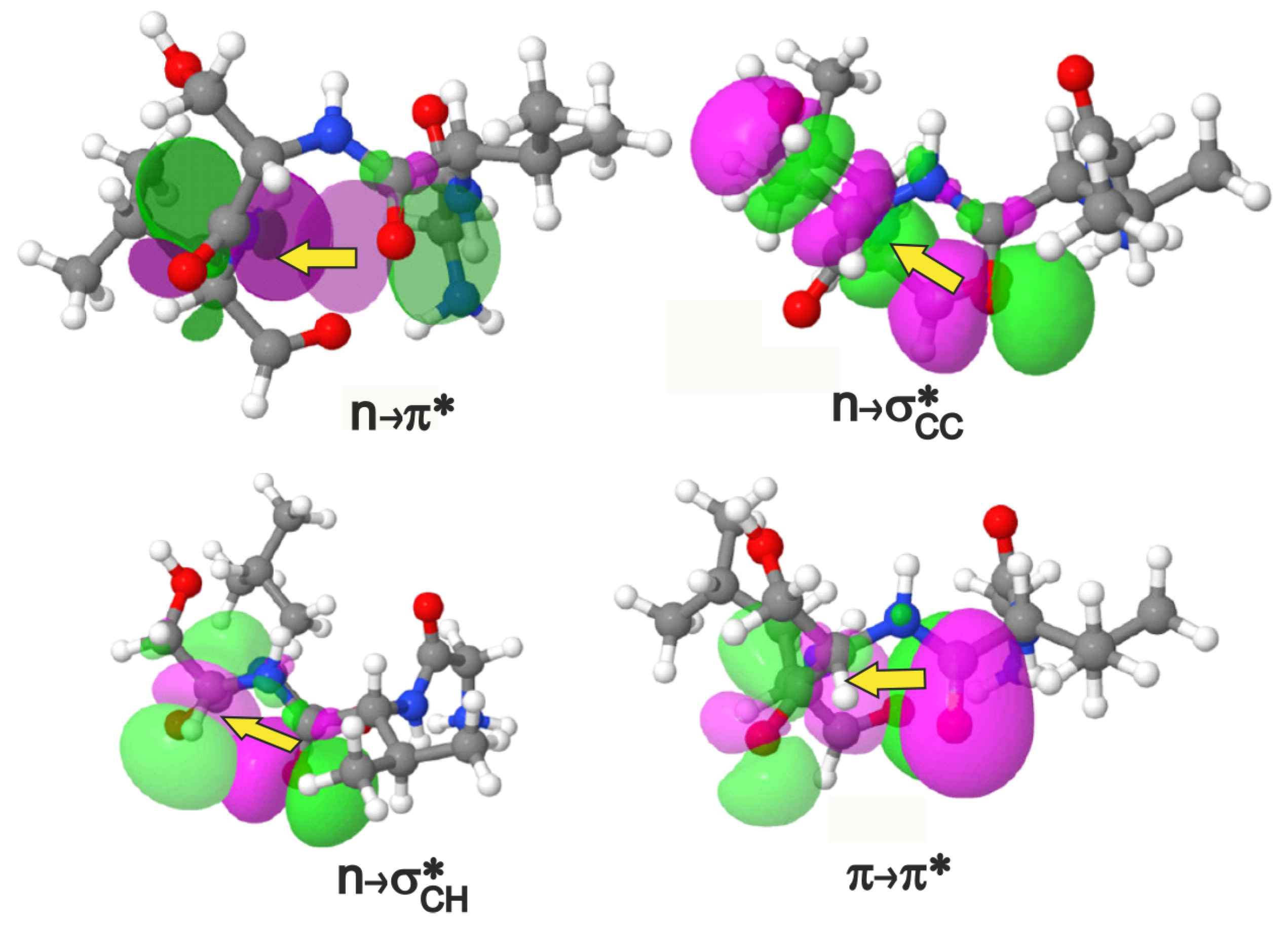
| Interaction | Donor () | Acceptor () | Covalent Bond | ||
|---|---|---|---|---|---|
| Atom(s) | Orbital | Atom(s) | Orbital | Separation | |
| O | n | C=O | 4 | ||
| O | n | - | 3 | ||
| O | n | - | 3 | ||
| C=O | C=O | 3 | |||
| -Variant | (,) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d(Å) | () | (Å) | () | () | (Å) | () | ||||||
| vT | (−58.8,−46.6) | 2.9 | 97.6 | 0.46 | 2.6 | 51.2 | - | 163.6 | 0.54 | 3.3 | 13.2 | 0.27 |
| vA | (−59.7,−42.2) | 3.0 | 102.2 | 0.25 | 2.7 | 44.6 | - | 163.6 | 0.51 | 3.5 | 15.4 | 0.18 |
| vS | (−66.3,−28.9) | 3.0 | 112.2 | 0.20 | 2.5 | 43.1 | 0.12 | 162.2 | 0.52 | 3.7 | 21.2 | 0.11 |
| vV | (−85.1,−12.4) | 3.3 | 122.8 | - | 2.4 | 24.5 | 0.89 | 150.1 | 0.41 | 4.2 | 15.8 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagesh, J. Cross-Talk between Overlap Interactions in Biomolecules: A Case Study of the β-Turn Motif. Molecules 2021, 26, 1533. https://doi.org/10.3390/molecules26061533
Nagesh J. Cross-Talk between Overlap Interactions in Biomolecules: A Case Study of the β-Turn Motif. Molecules. 2021; 26(6):1533. https://doi.org/10.3390/molecules26061533
Chicago/Turabian StyleNagesh, Jayashree. 2021. "Cross-Talk between Overlap Interactions in Biomolecules: A Case Study of the β-Turn Motif" Molecules 26, no. 6: 1533. https://doi.org/10.3390/molecules26061533
APA StyleNagesh, J. (2021). Cross-Talk between Overlap Interactions in Biomolecules: A Case Study of the β-Turn Motif. Molecules, 26(6), 1533. https://doi.org/10.3390/molecules26061533






