Solubility of Cinnarizine in (Transcutol + Water) Mixtures: Determination, Hansen Solubility Parameters, Correlation, and Thermodynamics
Abstract
1. Introduction
2. Results and Discussion
2.1. Mole Fraction Solubility Data of CNZ
2.2. Hansen Solubility Parameters (HSPs)
2.3. Cosolvency-Based Mathematical Models for CNZ Solubility Correlation
2.4. Apparent Thermodynamic Parameters for CNZ
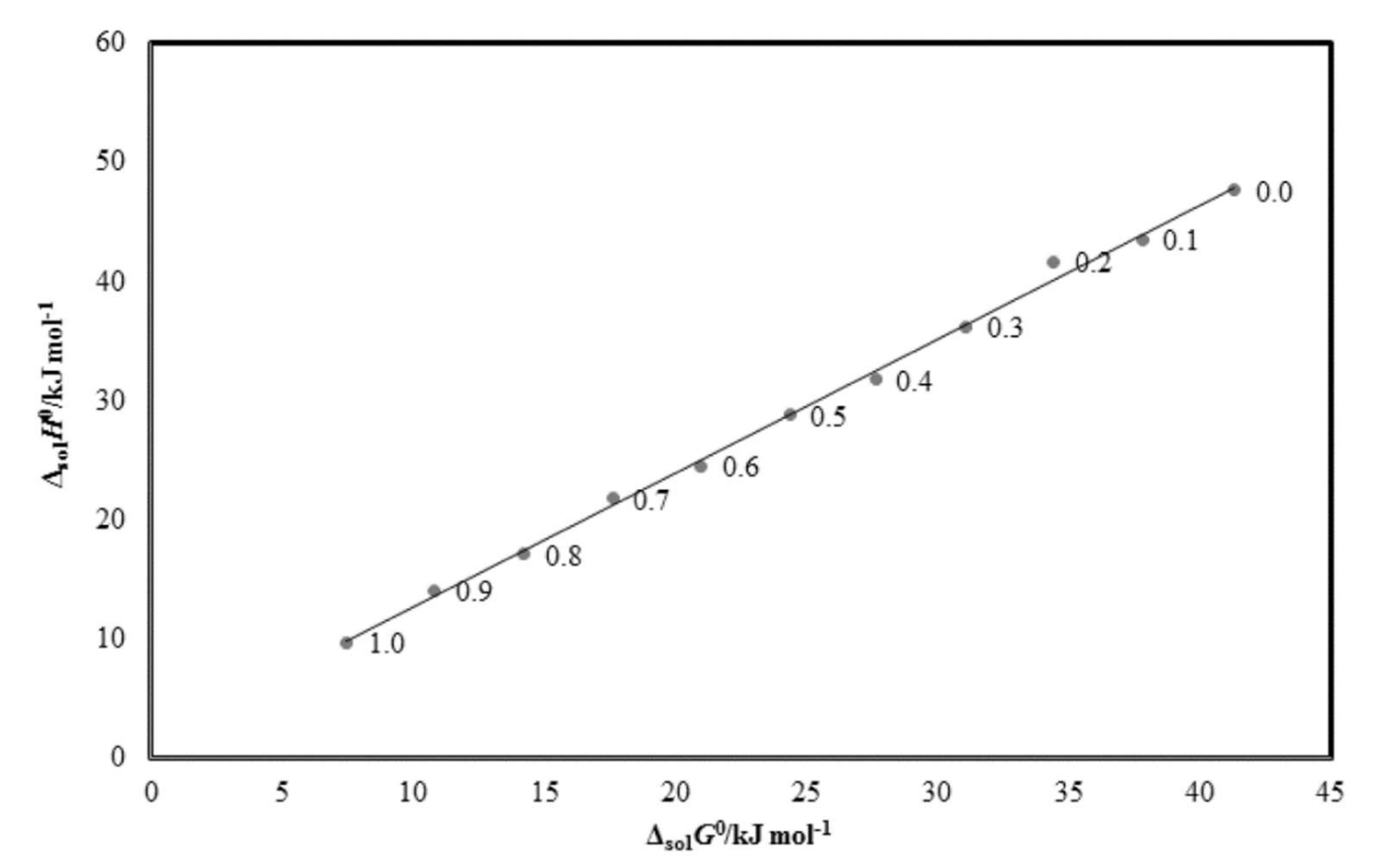
2.5. Enthalpy–Entropy Compensation Analysis
3. Materials and Methods
3.1. Materials
3.2. CNZ (3) Solubility Determination in Binary {TP (1) + Water (2)} Combinations
3.3. HSPs of CNZ and Various {TP (1) + Water (2)} Mixtures
3.4. Cosolvency-Based Mathematical Models for CNZ Solubility Correlation
3.5. Apparent Thermodynamic Parameters for CNZ
3.6. Enthalpy–Entropy Compensation Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Paus, R.; Hart, E.; Ji, Y.; Sadowski, G. Solubility and caloric properties of cinnarizine. J. Chem. Eng. Data 2015, 60, 2256–2261. [Google Scholar] [CrossRef]
- Raghuvanshi, S.; Pathak, K. Recent advances in drug delivery systems and therapeutics of cinnarizine: A poorly water soluble drug with absorption window in stomach. J. Drug Deliv. 2014, 2014, 479246. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Chen, H.; Lin, X.; Tang, X. Pharmacokinetics, tissue distribution and safety of cinnarizine delivered in lipid emulsion. Int. J. Pharm. 2010, 383, 264–270. [Google Scholar] [CrossRef]
- Amidon, G.L.; Lennernas, H.; Shah, V.P.; Crison, J.R. A theoretical basis for a biopharmaceutic drug classification-the correlation of in-vitro drug product dissolution and in-vivo bioavailability. Pharm. Res. 1995, 12, 413–420. [Google Scholar] [CrossRef]
- Loftsson, T.; Hreinsdóttir, D.; Másson, M. Evaluation of cyclodextrin solubilization of drugs. Int. J. Pharm. 2005, 302, 18–28. [Google Scholar] [CrossRef] [PubMed]
- Sassene, P.J.; Knopp, M.M.; Hesselkilde, J.Z.; Koradia, V.; Larsen, A.; Rades, T.; Mullertz, A. Precipitation of a poorly soluble model drug during in vitro lipolysis: Characterization and dissolution of the precipitate. J. Pharm. Sci. 2010, 99, 4982–4991. [Google Scholar] [CrossRef] [PubMed]
- Larsen, A.T.; Ogbonna, A.; Abu-Rmaileh, R.; Abrahamsson, B.; Østergaard, J.; Mullertz, A. SNEDDS containing poorly water soluble cinnarizine; development and in vitro characterization of dispersion, digestion and solubilization. Pharmaceutics 2012, 4, 641–655. [Google Scholar] [CrossRef]
- Shahba, A.A.-W.; Mohsin, K.; Alanazi, F.K. Novel self-nanoemulsifying drug delivery system (SNEDDS) for oral delivery cinnarizine: Design, optimization, and in-vitro assessment. AAPS PharmSciTech. 2012, 13, 967–977. [Google Scholar] [CrossRef] [PubMed]
- Rai, S.; Yasir, M. Cinnarizine-loaded lipid based system: Preparation, optimization, and in-vitro evaluation. IOSR J. Pharm. 2012, 2, 47–56. [Google Scholar] [CrossRef]
- Larsen, A.T.; Ohlsson, A.G.; Polentarutti, B.; Barker, R.A.; Phillips, A.R.; Abu-Rmaileh, R.; Dickinson, P.A.; Abrahamsson, B.; Østergaard, J.; Mullertz, A. Oral bioavailability of cinnarizine in dogs: Relation to SNEDDS droplet size, drug solubility and in vitro precipitation. Eur. J. Pharm. Sci. 2013, 48, 339–350. [Google Scholar] [CrossRef]
- Shahba, A.A.-W.; Mohsin, K.; Alanazi, F.K.; Abdel-Rahman, S.I. Optimization of self-nanoemulsifying formulations for weakly basic lipophilic drugs: Role of acidification and experimental design. Br. J. Pharm. Sci. 2016, 52, 654–667. [Google Scholar] [CrossRef][Green Version]
- Jørgensen, S.D.S.; Rades, T.; Mu, H.; Graeser, K.; Mullertz, A. Exploring the utility of the chasing principle: Influence of drug-free SNEDDS composition on solubilization of carvedilol, cinnarizine and R3040 in aqueous suspension. Acta Pharm. Sin. B. 2019, 9, 194–201. [Google Scholar] [CrossRef]
- Ilie, A.-R.; Griffin, B.T.; Vertzoni, M.; Kuentz, M.; Kolakovic, R.; Prudic-Paus, A.; Malash, A.; Bohets, H.; Herman, J.; Holm, R. Exploring precipitation inhibitors to improve in vivo absorption of cinnarizine from supersaturated lipid-based drug delivery systems. Eur. J. Pharm. Sci. 2021, 159, 105691. [Google Scholar] [CrossRef] [PubMed]
- Shahba, A.A.; Tashish, A.Y.; Alanazi, F.K.; Kazi, M. Combined self-nanoemulsifying and solid dispersion systems showed enhanced cinnarizine release in hypochlorhydria/achlorhydria dissolution model. Pharmaceutics 2021, 13, 627. [Google Scholar] [CrossRef] [PubMed]
- Ruether, F.; Sadowski, G. Modeling the solubility of pharmaceuticals in pure solvents and solvent mixtures for drug process design. J. Pharm. Sci. 2009, 98, 4205–4215. [Google Scholar] [CrossRef]
- Blagden, N.; De Matas, M.; Gavan, P.; York, P. Crystal engineering of active pharmaceutical ingredients to improve solubility and dissolution rates. Adv. Drug Deliv. Rev. 2007, 59, 617–630. [Google Scholar] [CrossRef]
- Kazi, M.; Alhajri, A.; Alshehri, S.M.; Elzayat, E.M.; Al Meanazel, O.T.; Shakeel, F.; Noman, O.; Altamimi, M.A.; Alanazi, F.K. Enhancing oral bioavailability of apigenin using a bioactive self-nanoemulsifying drug delivery system (Bio-SNEDDS): In vitro, in vivo and stability evaluations. Pharmaceutics 2020, 12, 749. [Google Scholar] [CrossRef] [PubMed]
- Alshehri, S.; Shakeel, F. Solubility determination, various solubility parameters and solution thermodynamics of sunitinib malate in some cosolvents, water and various (Transcutol + water) mixtures. J. Mol. Liq. 2020, 307, 112970. [Google Scholar] [CrossRef]
- Shakeel, F.; Alshehri, S. Solubilization, Hansen solubility parameters, solution thermodynamics and solvation behavior of flufenamic acid in (Carbitol + water) mixtures. Processes 2020, 8, 1204. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Alanazi, F.K.; Alanazi, S.A.; Alsarra, I.A. Solubility of sinapic acid in various (Carbitol + water) systems: Computational modeling and solution thermodynamics. J. Thermal Anal. Calorim. 2020, 142, 1437–1446. [Google Scholar] [CrossRef]
- Jouyban, A.; Acree, W.E., Jr.; Martinez, F. Preferential solvation of apremilast in some (Transcutol® + water) mixtures. J. Mol. Liq. 2020, 316, 113905. [Google Scholar] [CrossRef]
- Barzegar-Jalali, M.; Agha, E.M.H.; Adibkia, K.; Martinez, F.; Jouyban, A. The solubility of ketoconazole in binary carbitol + water mixtures at T = (293.2313.2) K. J. Mol. Liq. 2020, 297, 111756. [Google Scholar] [CrossRef]
- Osoria, I.P.; Martinez, F.; Pena, M.A.; Jouyban, A.; Acree, W.E., Jr. Solubility of sulphadiazine in some {Carbitol® (1) + water (2)} mixtures: Determination, correlation, and preferential solvation. Phys. Chem. Liq. 2021, 59, 890–906. [Google Scholar] [CrossRef]
- Apelblat, A.; Manzurola, E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic and p-toluic acid and magnesium-DL-aspartate in water from T = (278–348) K. J. Chem. Thermodyn. 1999, 31, 85–91. [Google Scholar] [CrossRef]
- Manzurola, E.; Apelblat, A. Solubilities of L-glutamic acid, 3-nitrobenzoic acid, acetylsalicylic, p-toluic acid, calcium-L-lactate, calcium gluconate, magnesium-DL-aspartate, and magnesium-L-lactate in water. J. Chem. Thermodyn. 2002, 34, 1127–1136. [Google Scholar] [CrossRef]
- Yalkowsky, S.H.; Roseman, T.J. Solubilization of drugs by cosolvents. In Techniques of Solubilization of Drugs; Yalkowsky, S.H., Ed.; Marcel Dekker Inc.: New York, NY, USA, 1981; pp. 91–134. [Google Scholar]
- Akay, S.; Kayan, B.; Jouyban, A.; Martinez, F.; Acree, W.E., Jr. Equilibrium solubility vanillin in some (ethanol + water) mixtures: Determination, correlation, thermodynamics and preferential solvation. J. Mol. Liq. 2021, 342, 117529. [Google Scholar] [CrossRef]
- Ruidiaz, M.A.; Delgado, D.R.; Martínez, F.; Marcus, Y. Solubility and preferential solvation of indomethacin in 1,4-dioxane + water solvent mixtures. Fluid Phase Equilib. 2010, 299, 259–265. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Alshehri, S. Solubility data of the bioactive compound piperine in (Transcutol + water) mixtures: Computational modeling, Hansen solubility parameters and mixing thermodynamic properties. Molecules 2020, 25, 2743. [Google Scholar] [CrossRef]
- Shakeel, F.; Alshehri, S.; Haq, N.; Elzayat, E.; Ibrahim, M.; Altamimi, M.A.; Mohsin, K.; Alanazi, F.K.; Alsarra, I.A. Solubility determination and thermodynamic data of apigenin in binary {Transcutol® + water} mixtures. Ind. Crops Prod. 2018, 116, 56–63. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Alanazi, F.K.; Alsarra, I.A. Solubility and thermodynamic function of apremilast in different (Transcutol + water) cosolvent mixtures: Measurement, correlation and molecular interactions. J. Ind. Eng. Chem. 2017, 56, 99–107. [Google Scholar] [CrossRef]
- Higuchi, T.; Connors, K.A. Phase-solubility techniques. Adv. Anal. Chem. Inst. 1965, 4, 117–122. [Google Scholar]
- Shakeel, F.; Haq, N.; Salem-Bekhit, M.M.; Raish, M. Solubility and dissolution thermodynamics of sinapic acid in (DMSO + water) binary solvent mixtures at different temperatures. J. Mol. Liq. 2017, 225, 833–839. [Google Scholar] [CrossRef]
- Zhu, Q.N.; Wang, Q.; Hu, Y.B.; Abliz, X. Practical determination of the solubility parameters of 1-alkyl-3-methylimidazolium bromide ([CnC1im]Br, n = 5, 6, 7, 8) ionic liquids by inverse gas chromatography and the Hansen solubility parameter. Molecules 2019, 24, 1346. [Google Scholar] [CrossRef] [PubMed]
- Alanazi, A.; Alshehri, S.; Altamimi, M.; Shakeel, F. Solubility determination and three dimensional Hansen solubility parameters of gefitinib in different organic solvents: Experimental and computational approaches. J. Mol. Liq. 2020, 299, 112211. [Google Scholar] [CrossRef]
- Kalam, M.A.; Alshamsan, A.; Alkholief, M.; Alsarra, I.A.; Ali, R.; Haq, N.; Anwer, M.K.; Shakeel, F. Solubility measurement and various solubility parameters of glipizide in different neat solvents. ACS Omega 2020, 5, 1708–1716. [Google Scholar] [CrossRef] [PubMed]
- Anwer, M.K.; Muqtader, M.; Iqbal, M.; Ali, R.; Almutairy, B.K.; Alshetaili, A.; Alshahrani, S.M.; Aldawsari, M.F.; Alalaiwe, A.; Shakeel, F. Estimating the solubility, solution thermodynamics, and molecular interactions of aliskiren hemifumarate in alkyl imidazolium based ionic liquids. Molecules 2019, 24, 2807. [Google Scholar] [CrossRef]
- Wan, Y.; He, H.; Huang, Z.; Zhang, P.; Sha, J.; Li, T.; Ren, B. Solubility, thermodynamic modeling and Hansen solubility parameter of 5-norbornene-2,3-dicarboximide in three binary solvents (methanol, ethanol, ethyl acetate + DMF) from 278.15 K to 323.15 K. J. Mol. Liq. 2020, 300, E112097. [Google Scholar] [CrossRef]
- Mondal, P.; Roy, S.; Loganathan, G.; Mandal, B.; Dharumadurai, D.; Akbarsha, M.A.; Sengupta, P.S.; Chattopadhyay, S.; Guin, P.S. 1-Amino-4-hydroxy-9,10-anthraquinone—An analogue of anthracycline anticancer drugs, interacts with DNA and induces apoptosis in human MDA-MB-231 breast adinocarcinoma cells: Evaluation of structure–activity relationship using computational, spectroscopic and biochemical studies. Biochem. Biophys. Rep. 2015, 4, 321–323. [Google Scholar]
- Banerjee, S.; Roy, S.; Datta, A.; Mondal, P.; Mishra, M.; Perumalsamy, B.; Thirmurugan, R.; Dharumadurai, D.; Das, S.; Guin, P.S. Solubilization of sodium 3-amino-2-hydroxyanthraquinone-1-sulfonate in sodium dodecyl sulfate micelles explains its permeation in A549 human lung cancer cell. J. Chin. Chem. Soc. 2021, 68, 250–262. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.S. Enthalpy-entropy compensation. 2. Separation of the chemical from the statistic effect. J. Phys. Chem. 1976, 80, 2341–2351. [Google Scholar] [CrossRef]
- Holguín, A.R.; Rodríguez, G.A.; Cristancho, D.M.; Delgado, D.R.; Martínez, F. Solution thermodynamics of indomethacin in propylene glycol + water mixtures. Fluid Phase Equilib. 2012, 314, 134–139. [Google Scholar] [CrossRef]
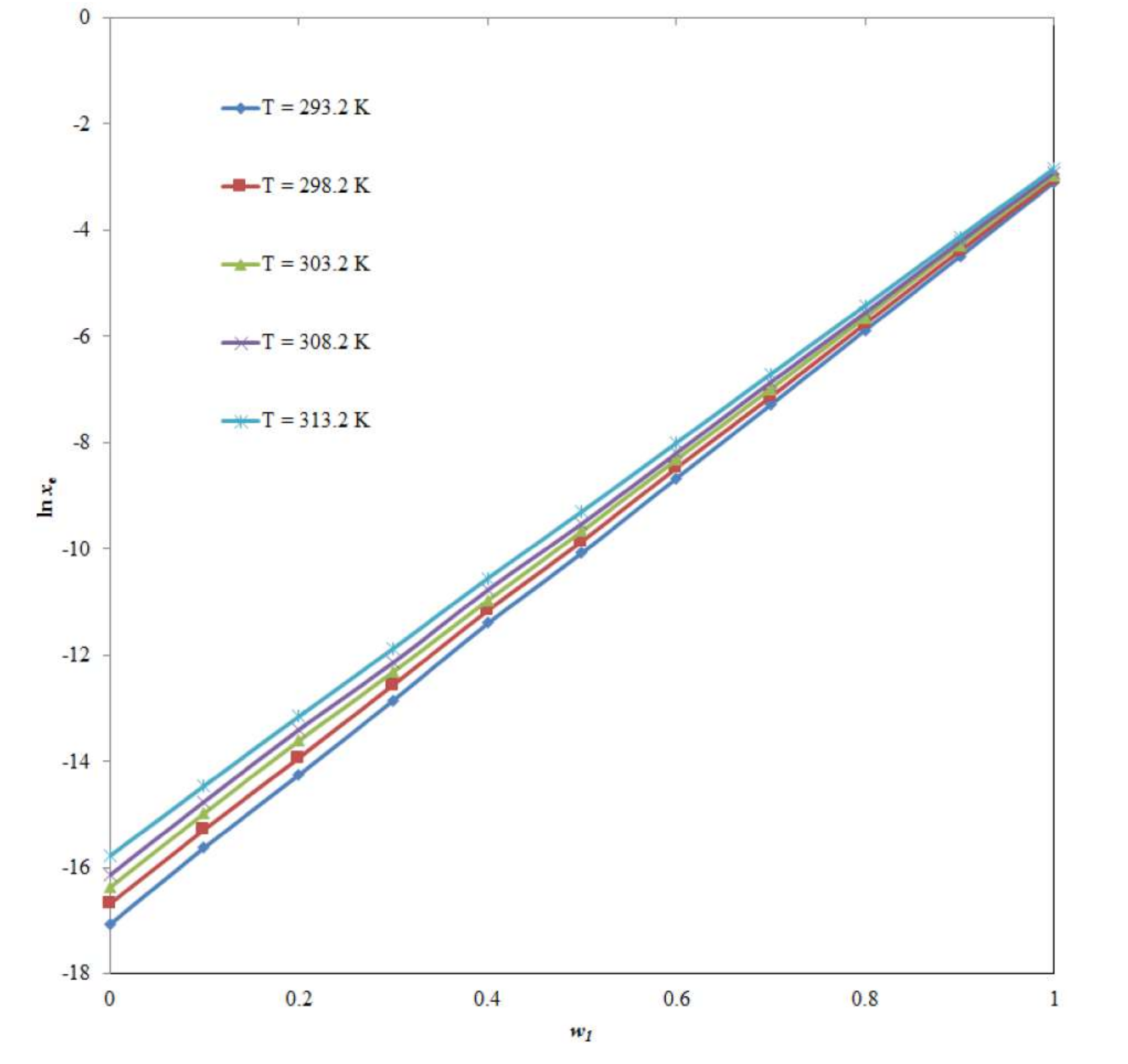

| w1a | xeb | ||||
|---|---|---|---|---|---|
| T = 293.2 K | T = 298.2 K | T = 303.2 K | T = 308.2 K | T = 313.2 K | |
| 0.0 | 3.91 × 10−8 | 5.67 × 10−8 | 7.82 × 10−8 | 9.78 × 10−8 | 1.42 × 10−7 |
| 0.1 | 1.66 × 10−7 | 2.30 × 10−7 | 3.16 × 10−7 | 3.91 × 10−7 | 5.30 × 10−7 |
| 0.2 | 6.50 × 10−7 | 8.87 × 10−7 | 1.23 × 10−6 | 1.51 × 10−6 | 1.95 × 10−6 |
| 0.3 | 2.64 × 10−6 | 3.50 × 10−6 | 4.49 × 10−6 | 5.35 × 10−6 | 7.00 × 10−6 |
| 0.4 | 1.12 × 10−5 | 1.42 × 10−5 | 1.72 × 10−5 | 2.09 × 10−5 | 2.62 × 10−5 |
| 0.5 | 4.24 × 10−5 | 5.26 × 10−5 | 6.34 × 10−5 | 7.33 × 10−5 | 9.22 × 10−5 |
| 0.6 | 1.73 × 10−4 | 2.10 × 10−4 | 2.44 × 10−4 | 2.77 × 10−4 | 3.36 × 10−4 |
| 0.7 | 6.89 × 10−4 | 8.00 × 10−4 | 9.22 × 10−4 | 1.05 × 10−3 | 1.23 × 10−3 |
| 0.8 | 2.81 × 10−3 | 3.17 × 10−3 | 3.53 × 10−3 | 3.90 × 10−3 | 4.43 × 10−3 |
| 0.9 | 1.12 × 10−2 | 1.25 × 10−2 | 1.38 × 10−2 | 1.48 × 10−2 | 1.62 × 10−2 |
| 1.0 | 4.52 × 10−2 | 4.78 × 10−2 | 5.08 × 10−2 | 5.44 × 10−2 | 5.83 × 10−2 |
| w1 | A | B | C | R2 | MPD (%) |
|---|---|---|---|---|---|
| 0.0 | 224.09 | −15741 | −32.997 | 0.9956 | - |
| 0.1 | 286.07 | −18057 | −42.264 | 0.9979 | - |
| 0.2 | 442.94 | −24887 | −65.536 | 0.9980 | - |
| 0.3 | 211.39 | −13815 | −31.176 | 0.9969 | - |
| 0.4 | −25.275 | −2611.0 | 4.0112 | 0.9988 | - |
| 0.5 | 8.3136 | −3761.7 | −0.97648 | 0.9957 | 2.27 |
| 0.6 | 53.365 | −5294.9 | −7.7389 | 0.9956 | - |
| 0.7 | −72.315 | 715.43 | 11.018 | 0.9955 | - |
| 0.8 | −46.705 | 101.83 | 7.1263 | 0.9981 | - |
| 0.9 | 127.04 | −7373.2 | −18.728 | 0.9994 | - |
| 1.0 | −132.56 | 4855.2 | 19.875 | 0.9998 | - |
| w1 | a | b | R2 | MPD (%) |
|---|---|---|---|---|
| 0.0 | 2.5154 | −5733.0 | 0.9947 | |
| 0.1 | 2.2793 | −5240.5 | 0.9967 | |
| 0.2 | 2.8838 | −5015.9 | 0.9953 | |
| 0.3 | 2.0440 | −4360.6 | 0.9959 | |
| 0.4 | 1.6487 | −3824.2 | 0.9987 | |
| 0.5 | 1.7473 | −3462.8 | 0.9954 | 5.15 |
| 0.6 | 1.3939 | −2946.3 | 0.9952 | |
| 0.7 | 1.6646 | −2623.1 | 0.9993 | |
| 0.8 | 1.1397 | −2057.0 | 0.9978 | |
| 0.9 | 1.2918 | −1694.4 | 0.9973 | |
| 1.0 | 0.88450 | −1169.3 | 0.9960 |
| w1 | log xYal | MPD (%) | ||||
|---|---|---|---|---|---|---|
| T = 293.2 K | T = 298.2 K | T = 303.2 K | T = 308.2 K | T = 313.2 K | - | |
| 0.1 | −6.80 | −6.65 | −6.52 | −6.43 | −6.28 | - |
| 0.2 | −6.19 | −6.06 | −5.94 | −5.86 | −5.72 | - |
| 0.3 | −5.58 | −5.46 | −5.36 | −5.28 | −5.16 | - |
| 0.4 | −4.98 | −4.87 | −4.78 | −4.71 | −4.60 | 24.76 |
| 0.5 | −4.37 | −4.28 | −4.20 | −4.13 | −4.04 | - |
| 0.6 | −3.77 | −3.69 | −3.61 | −3.56 | −3.47 | - |
| 0.7 | −3.16 | −3.09 | −3.03 | −2.98 | −2.91 | - |
| 0.8 | −2.55 | −2.50 | −2.45 | −2.41 | −2.35 | - |
| 0.9 | −1.95 | −1.91 | −1.87 | −1.83 | −1.79 | - |
| w1 | ΔsolnH°/kJ mol−1 | ΔsolnG°/kJ mol−1 | ΔsolnS°/J mol−1 K−1 | R2 |
|---|---|---|---|---|
| 0.0 | 47.65 | 41.32 | 20.48 | 0.994 |
| 0.1 | 43.56 | 37.82 | 18.92 | 0.996 |
| 0.2 | 41.69 | 34.43 | 23.94 | 0.995 |
| 0.3 | 36.24 | 31.10 | 16.96 | 0.995 |
| 0.4 | 31.78 | 27.64 | 13.68 | 0.998 |
| 0.5 | 28.78 | 24.38 | 14.50 | 0.995 |
| 0.6 | 24.49 | 20.98 | 11.57 | 0.995 |
| 0.7 | 21.80 | 17.61 | 13.82 | 0.999 |
| 0.8 | 17.09 | 14.23 | 9.464 | 0.997 |
| 0.9 | 14.08 | 10.83 | 10.72 | 0.997 |
| 1.0 | 9.719 | 7.492 | 7.346 | 0.996 |
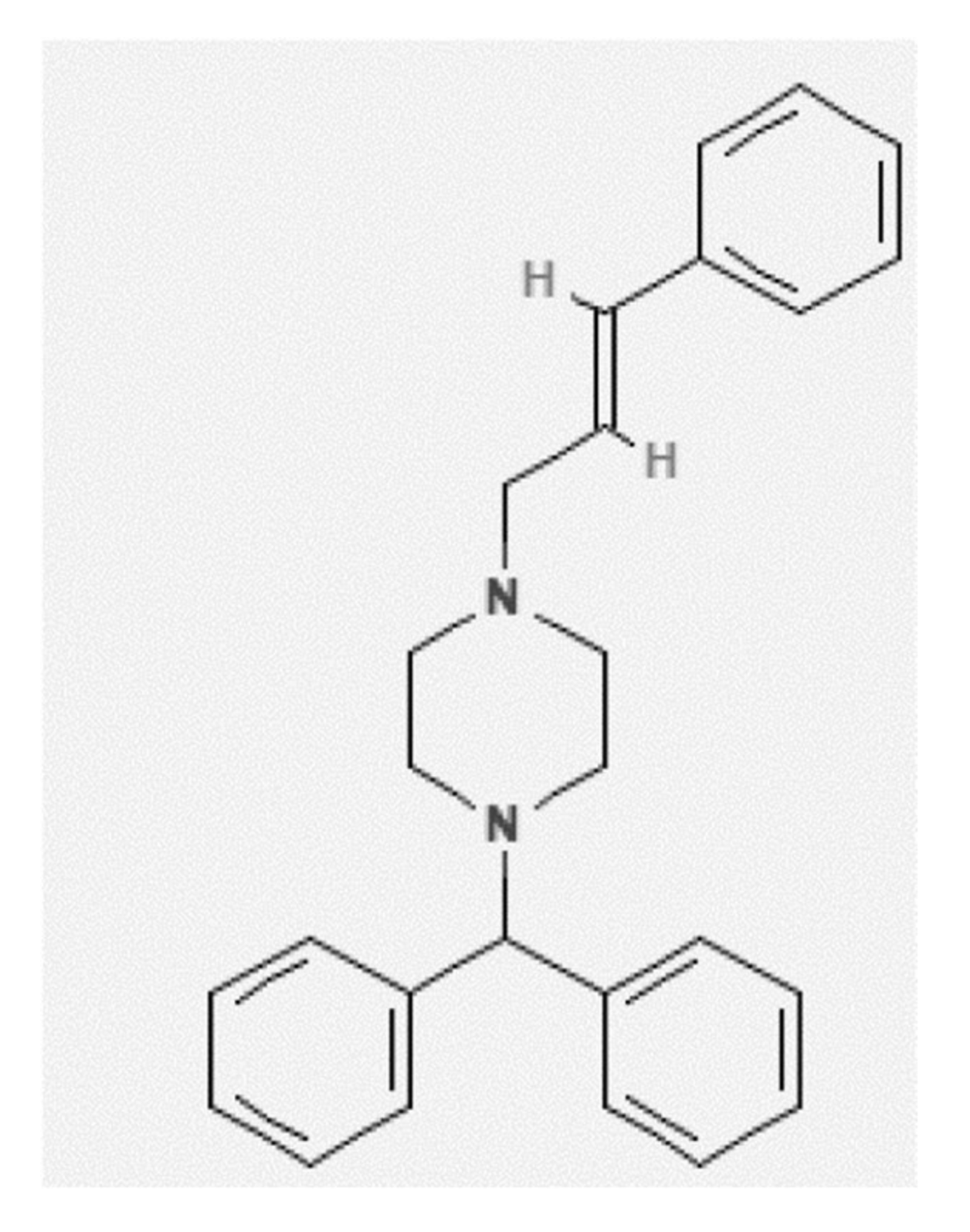
| Material | Molecular Formula | Molar Mass (g mol−1) | CAS RN | Purification Method | Mass Fraction Purity | Analysis Method | Source |
|---|---|---|---|---|---|---|---|
| CNZ | C26H28N2 | 368.50 | 298-57-7 | None | >0.99 | HPLC | FDC Ltd. |
| TP | C6H14O3 | 134.17 | 111-90-0 | None | >0.99 | GC | Gattefosse |
| Water | H2O | 18.07 | 7732-18-5 | None | - | - | Milli-Q |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakeel, F.; Kazi, M.; Alanazi, F.K.; Alam, P. Solubility of Cinnarizine in (Transcutol + Water) Mixtures: Determination, Hansen Solubility Parameters, Correlation, and Thermodynamics. Molecules 2021, 26, 7052. https://doi.org/10.3390/molecules26227052
Shakeel F, Kazi M, Alanazi FK, Alam P. Solubility of Cinnarizine in (Transcutol + Water) Mixtures: Determination, Hansen Solubility Parameters, Correlation, and Thermodynamics. Molecules. 2021; 26(22):7052. https://doi.org/10.3390/molecules26227052
Chicago/Turabian StyleShakeel, Faiyaz, Mohsin Kazi, Fars K. Alanazi, and Prawez Alam. 2021. "Solubility of Cinnarizine in (Transcutol + Water) Mixtures: Determination, Hansen Solubility Parameters, Correlation, and Thermodynamics" Molecules 26, no. 22: 7052. https://doi.org/10.3390/molecules26227052
APA StyleShakeel, F., Kazi, M., Alanazi, F. K., & Alam, P. (2021). Solubility of Cinnarizine in (Transcutol + Water) Mixtures: Determination, Hansen Solubility Parameters, Correlation, and Thermodynamics. Molecules, 26(22), 7052. https://doi.org/10.3390/molecules26227052









