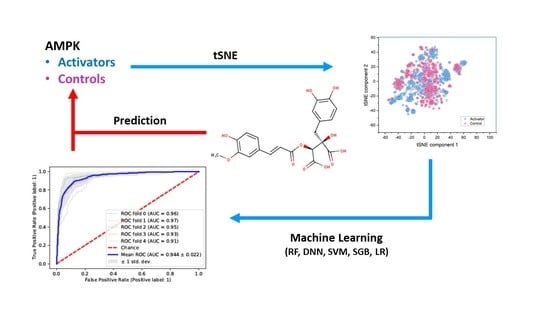
Modeling Structure–Activity Relationship of AMPK Activation
Abstract
:1. Introduction
2. Results
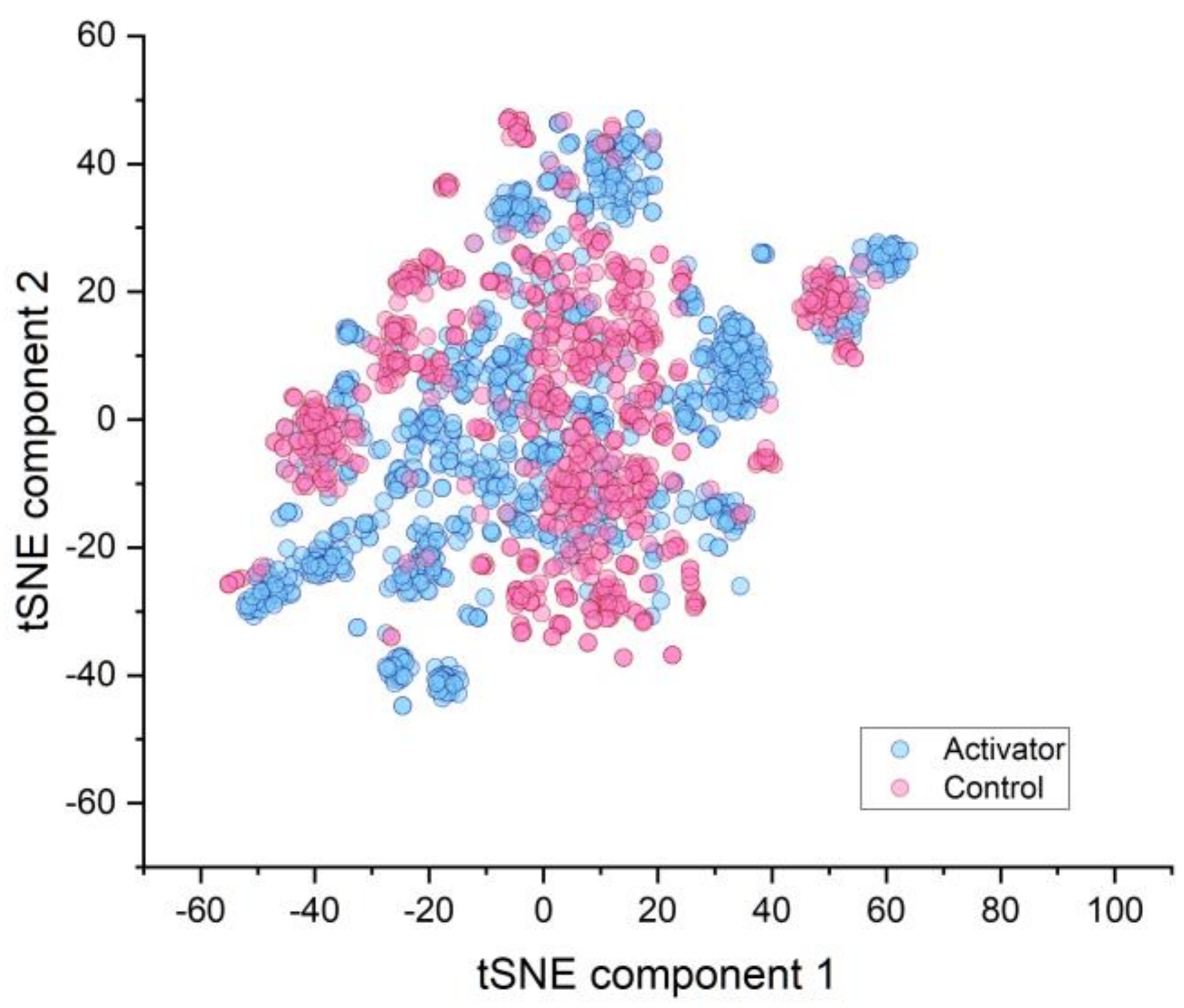
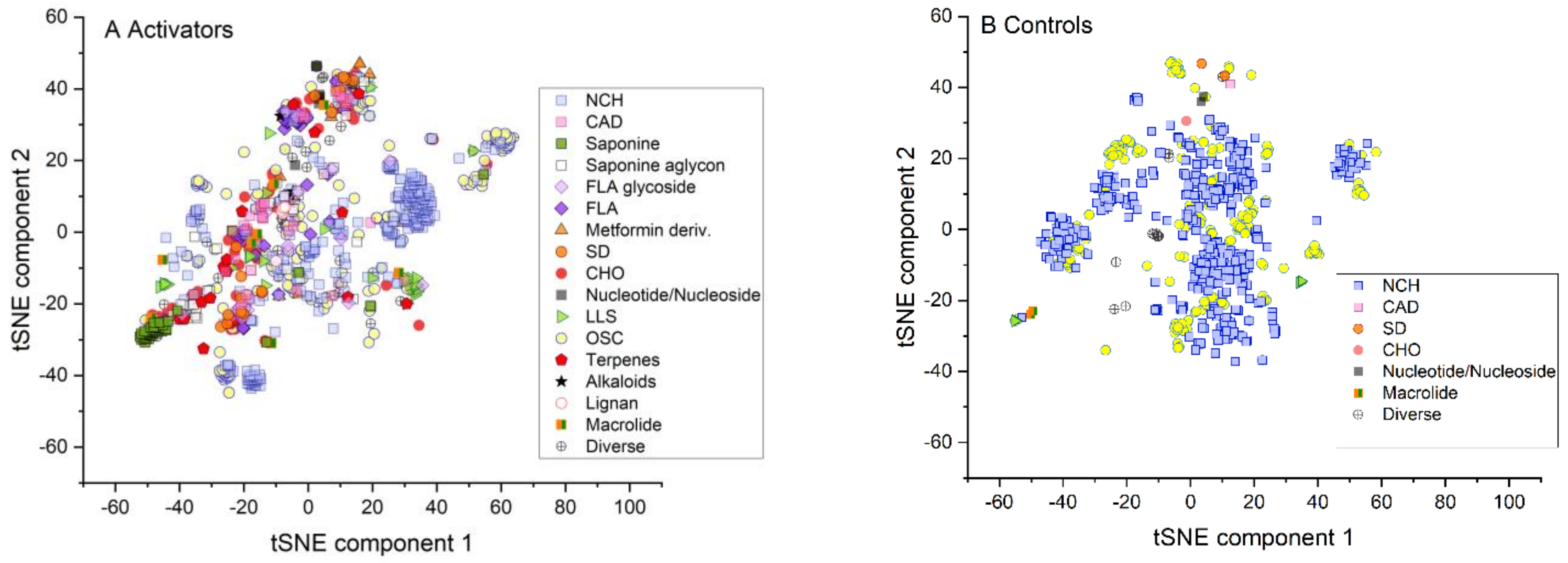
2.1. Similarity of Groups
2.2. Statistical Comparison of Datasets
2.3. Random Forest Classification (RFC)
2.4. Support Vector Machine Classification (SVM-C)
2.5. Stochastic Gradient Boosting (SGB) Analysis
2.6. Logistic Regression Classification (LRC)
2.7. Deep Neural Network (DNN) Analysis
2.8. Test Performance
3. Discussion
4. Materials and Methods
4.1. Data
- “AMPK AND activation”
- “AMPK AND inhibition”
4.2. Data Preprocessing
- with their names, smiles codes, PubChem IDs, and PubMed IDs (Compounds.csv); and
- with all calculated PaDel descriptors (Data.csv) in https://github.com/cptbern/QSAR_AMPK, accessed on 27 October 2021.
4.3. Validation
4.4. Similarity
4.5. Machine Learning Models
4.6. Random Forest Classification (RFC)
4.7. Stochastic Gradient Boosting Classification (SGB)
4.8. Support Vector Machine Classification (SVM-C)
4.9. Logistic Regression Classification (LRC)
4.10. Deep Learning Neural Network (DNN)
4.11. Model Evaluation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Hardie, D.G.; Carling, D. The AMP-activated protein kinase—Fuel gauge of the mammalian cell? Eur. J. Biochem. FEBS 1997, 246, 259–273. [Google Scholar] [CrossRef]
- Hardie, D.G.; Ross, F.A.; Hawley, S.A. AMPK: A nutrient and energy sensor that maintains energy homeostasis. Nat. Rev. Mol. Cell Biol. 2012, 13, 251–262. [Google Scholar] [CrossRef] [Green Version]
- Hardie, D.G. Adenosine Monophosphate-Activated Protein Kinase: A Central Regulator of Metabolism with Roles in Diabetes, Cancer, and Viral Infection. Cold Spring Harb. Symp. Quant. Biol. 2011, 76, 155–164. [Google Scholar] [CrossRef] [Green Version]
- López, M.; Seoane, L.; Tovar, S.; Senaris, R.M.; Diéguez, C. Thyroid status regulates CART but not AgRP mRNA levels in the rat hypothalamus. Neuroreport 2002, 13, 1775–1779. [Google Scholar] [CrossRef]
- Blanco Martínez de Morentin, P.; González, C.R.; Saha, A.K.; Martins, L.; Diéguez, C.; Vidal-Puig, A.; Tena-Sempere, M.; López, M. Hypothalamic AMP-activated protein kinase as a mediator of whole body energy balance. Rev. Endocr. Metab. Disord. 2011, 12, 127–140. [Google Scholar] [CrossRef]
- López, M.; Nogueiras, R.; Tena-Sempere, M.; Dieguez, C. Hypothalamic AMPK: A canonical regulator of whole-body energy balance. Nat. Rev. 2016, 12, 421–432. [Google Scholar] [CrossRef]
- Merchenthaler, I.; Lane, M.V.; Numan, S.; Dellovade, T.L. Distribution of estrogen receptor alpha and beta in the mouse central nervous system: In vivo autoradiographic and immunocytochemical analyses. J. Comp. Neurol. 2004, 473, 270–291. [Google Scholar] [CrossRef] [PubMed]
- American Diabetes Association. 9. Pharmacologic Approaches to Glycemic Treatment: Standards of Medical Care in Diabetes-2019. Diabetes Care 2019, 42, S90–S102. [Google Scholar] [CrossRef] [Green Version]
- Shackelford, D.B.; Shaw, R.J. The LKB1-AMPK pathway: Metabolism and growth control in tumour suppression. Nat. Rev. Cancer 2009, 9, 563–575. [Google Scholar] [CrossRef]
- Zhuang, Y.; Miskimins, W.K. Cell cycle arrest in Metformin treated breast cancer cells involves activation of AMPK, downregulation of cyclin D1, and requires p27Kip1 or p21Cip1. J. Mol. Signal 2008, 3, 18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ben Sahra, I.; Laurent, K.; Loubat, A.; Giorgetti-Peraldi, S.; Colosetti, P.; Auberger, P.; Tanti, J.F.; Le Marchand-Brustel, Y.; Bost, F. The antidiabetic drug metformin exerts an antitumoral effect in vitro and in vivo through a decrease of cyclin D1 level. Oncogene 2008, 27, 3576–3586. [Google Scholar] [CrossRef] [Green Version]
- Ben Sahra, I.; Le Marchand-Brustel, Y.; Tanti, J.F.; Bost, F. Metformin in cancer therapy: A new perspective for an old antidiabetic drug? Mol. Cancer Ther. 2010, 9, 1092–1099. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Li, S.; Wang, F.; Xin, F. Structural and biochemical insights into the allosteric activation mechanism of AMP-activated protein kinase. Chem. Biol. Drug Des. 2017, 89, 663–669. [Google Scholar] [CrossRef] [PubMed]
- Sharma, H.; Kumar, S. Natural AMPK Activators: An Alternative Approach for the Treatment and Management of Metabolic Syndrome. Curr. Med. Chem. 2017, 24, 1007–1047. [Google Scholar] [CrossRef] [PubMed]
- Moser, C.; Vickers, S.P.; Brammer, R.; Cheetham, S.C.; Drewe, J. Antidiabetic effects of the Cimicifuga racemosa extract Ze 450 in vitro and in vivo in ob/ob mice. Phytomedicine 2014, 21, 1382–1389. [Google Scholar] [CrossRef]
- Hammann, F.; Gutmann, H.; Vogt, N.; Helma, C.; Drewe, J. Prediction of adverse drug reactions using decision tree modeling. Clin. Pharm. 2010, 88, 52–59. [Google Scholar] [CrossRef]
- Schöning, V.; Hammann, F.; Peinl, M.; Drewe, J. Identification of any structure-specific hepatotoxic potential of different pyrrolizidine alkaloids using Random Forests and artificial Neural Networks. Toxicol. Sci. 2017, 160, 361–370. [Google Scholar] [CrossRef]
- Schöning, V.; Krähenbühl, S.; Drewe, J. The hepatotoxic potential of protein kinase inhibitors predicted with Random Forest and Artificial Neural Networks. Toxicol. Lett. 2018, 299, 145–148. [Google Scholar] [CrossRef]
- Hammann, F.; Schöning, V.; Drewe, J. Prediction of clinically relevant drug-induced liver injury from structure using machine learning. J. Appl. Toxicol 2019, 39, 412–419. [Google Scholar] [CrossRef]
- Helma, C.; Schöning, V.; Drewe, J.; Boss, P. A comparison of nine machine learning mutagenicity models and their application for predicting pyrrolizidine alkaloids. Front. Pharmacol. 2021, 12, 1–15. [Google Scholar] [CrossRef]
- Hammann, F.; Gutmann, H.; Jecklin, U.; Maunz, A.; Helma, C.; Drewe, J. Development of decision tree models for substrates, inhibitors, and inducers of p-glycoprotein. Curr. Drug Metab. 2009, 10, 339–346. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Z.; Yang, J.; Tian, G.; Liu, F.; Wen, H.; Peng, L.; Chen, M.; Xiang, J.; Peng, L. Revealing Drug-Target Interactions with Computational Models and Algorithms. Molecules 2019, 24, 1714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tejera, E.; Munteanu, C.R.; Lopez-Cortes, A.; Cabrera-Andrade, A.; Perez-Castillo, Y. Drugs Repurposing Using QSAR, Docking and Molecular Dynamics for Possible Inhibitors of the SARS-CoV-2 M(pro) Protease. Molecules 2020, 25, 5172. [Google Scholar] [CrossRef]
- Balaramnavar, V.M.; Srivastava, R.; Rahuja, N.; Gupta, S.; Rawat, A.K.; Varshney, S.; Chandasana, H.; Chhonker, Y.S.; Doharey, P.K.; Kumar, S.; et al. Identification of novel PTP1B inhibitors by pharmacophore based virtual screening, scaffold hopping and docking. Eur. J. Med. Chem. 2014, 87, 578–594. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Yang, Z.; Li, J.; Han, L.; Zhang, Y.; Wang, T. Discovery of natural adenosine monophosphateactivated protein kinase activators through virtual screening and activity verification studies. Mol. Med. Rep. 2021, 23, 203. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Peng, J.; Li, P.; Du, H.; Li, Y.; Liu, X.; Zhang, L.; Wang, L.L.; Zuo, Z. Identification of potential AMPK activator by pharmacophore modeling, molecular docking and QSAR study. Comput. Biol. Chem. 2019, 79, 165–176. [Google Scholar] [CrossRef]
- Nanduri, R.; Kalra, R.; Bhagyaraj, E.; Chacko, A.P.; Ahuja, N.; Tiwari, D.; Kumar, S.; Jain, M.; Parkesh, R.; Gupta, P. AutophagySMDB: A curated database of small molecules that modulate protein targets regulating autophagy. Autophagy 2019, 15, 1280–1295. [Google Scholar] [CrossRef]
- Ramesh, M.; Vepuri, S.B.; Oosthuizen, F.; Soliman, M.E. Adenosine Monophosphate-Activated Protein Kinase (AMPK) as a Diverse Therapeutic Target: A Computational Perspective. Appl. Biochem. Biotechnol. 2016, 178, 810–830. [Google Scholar] [CrossRef]
- Shi, Q.; Pei, F.; Silverman, G.A.; Pak, S.C.; Perlmutter, D.H.; Liu, B.; Bahar, I. Mechanisms of Action of Autophagy Modulators Dissected by Quantitative Systems Pharmacology Analysis. Int. J. Mol. Sci. 2020, 21, 2855. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Huo, J.; Sun, L.; Wang, Y.; Jin, H.; Yu, H.; Zhang, L.; Zhou, L. Computer-aided drug design for AMP-activated protein kinase activators. Curr. Comput.-Aided Drug Des. 2011, 7, 214–227. [Google Scholar] [CrossRef]
- Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef]
- OECD. OECD Environment Health and Safety Publications Series on Testing and Assessment No. 49. ENV/JM/MONO(2004)24. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.136.7793&rep=rep1&type=pdf (accessed on 22 October 2004).
- Tropsha, A. Best Practices for QSAR Model Development, Validation, and Exploitation. Mol. Inform. 2010, 29, 476–488. [Google Scholar] [CrossRef]
- Van der Maaten, L.J.P.; Hinton, G.E. Visualizing high-dimensional data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; pp. 278–282. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Math. Intell. 2005, 27, 83–85. [Google Scholar] [CrossRef]
- Fan, R.-E.; Chang, K.-W.; Hsieh, C.J.; Wang, X.-R.; Lin, C.-J. LIBLINEAR: A Library for Large Linear Classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Tolles, J.; Meurer, W.J. Logistic Regression: Relating Patient Characteristics to Outcomes. JAMA 2016, 316, 533–534. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Universal Approximation Properties and Depth. In Deep Learning; MIT Press: Cambridge, UK; London, UK, 2016. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]

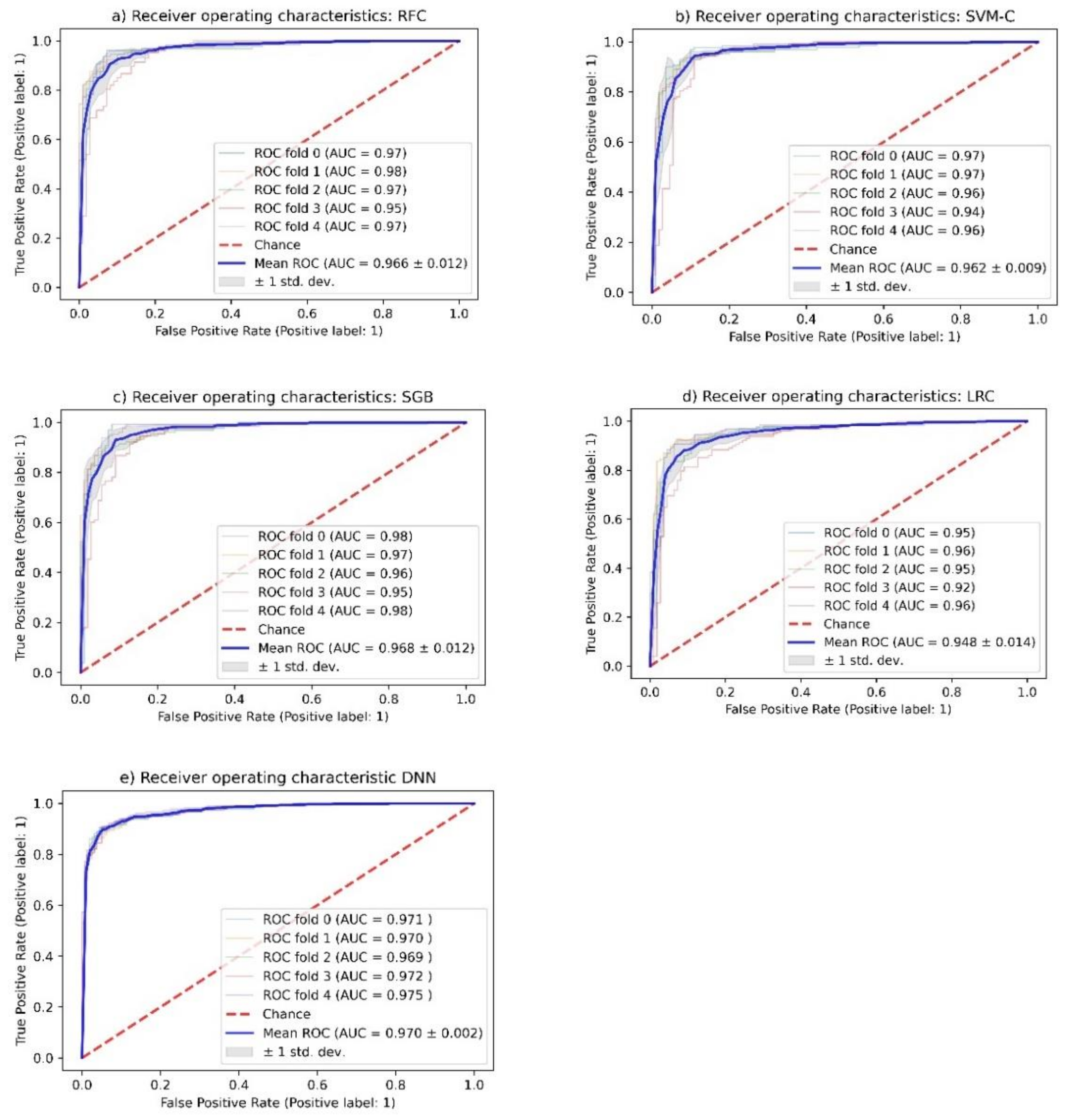

| Method | Training Accuracy (%) | Test Accuracy (%) | Y-Randomization ** (%) | Test Precision (%) | Sensitivity (%) | Specificity (%) | AUC * |
|---|---|---|---|---|---|---|---|
| RFC | 91.6 | 92.6 | 52.7 ± 2.3 | 90.3 | 91.2 | 94.0 | 0.968 ± 0.013 |
| SVM-C | 91.0 | 93.0 | 53.2 ± 2.2 | 90.1 | 93.5 | 92.4 | 0.962 ± 0.009 |
| SGB | 91.3 | 93.0 | 52.8 ± 2.2 | 90.7 | 92.0 | 94.0 | 0.968 ± 0.012 |
| LRC | 90.8 | 91.0 | 52.6 ± 2.1 | 89.2 | 97.4 | 94.8 | 0.948 ± 0.014 |
| DNN | 91.6 | 90.6 | 53.0 ± 1.8 | 87.6 | 90.2 | 91.1 | 0.970 ± 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drewe, J.; Küsters, E.; Hammann, F.; Kreuter, M.; Boss, P.; Schöning, V. Modeling Structure–Activity Relationship of AMPK Activation. Molecules 2021, 26, 6508. https://doi.org/10.3390/molecules26216508
Drewe J, Küsters E, Hammann F, Kreuter M, Boss P, Schöning V. Modeling Structure–Activity Relationship of AMPK Activation. Molecules. 2021; 26(21):6508. https://doi.org/10.3390/molecules26216508
Chicago/Turabian StyleDrewe, Jürgen, Ernst Küsters, Felix Hammann, Matthias Kreuter, Philipp Boss, and Verena Schöning. 2021. "Modeling Structure–Activity Relationship of AMPK Activation" Molecules 26, no. 21: 6508. https://doi.org/10.3390/molecules26216508
APA StyleDrewe, J., Küsters, E., Hammann, F., Kreuter, M., Boss, P., & Schöning, V. (2021). Modeling Structure–Activity Relationship of AMPK Activation. Molecules, 26(21), 6508. https://doi.org/10.3390/molecules26216508