Design Principles of Large Cation Incorporation in Halide Perovskites
(This article belongs to the Section Electrochemistry)
Abstract
:1. Introduction
2. Results and Discussion
2.1. Ionic Size
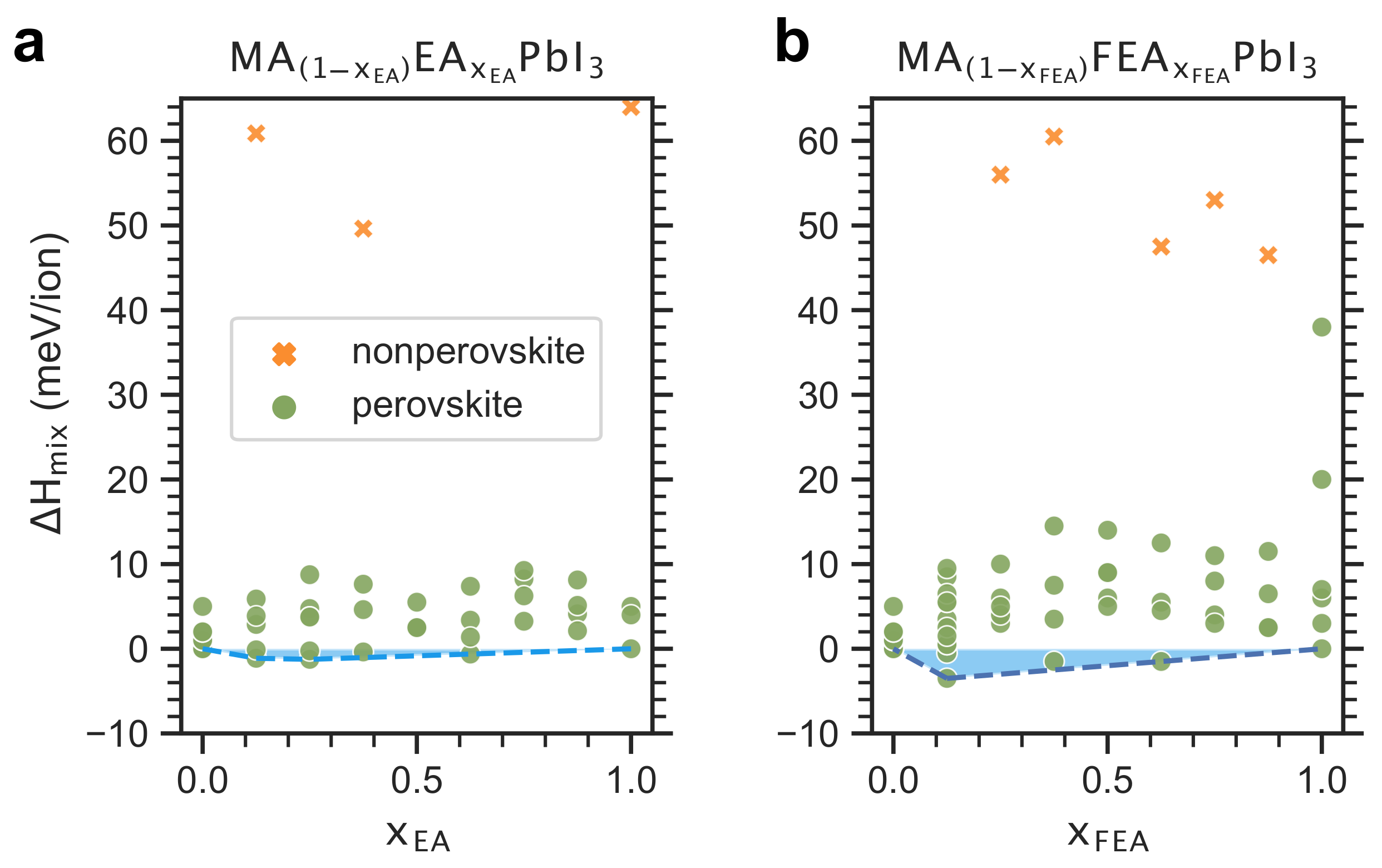
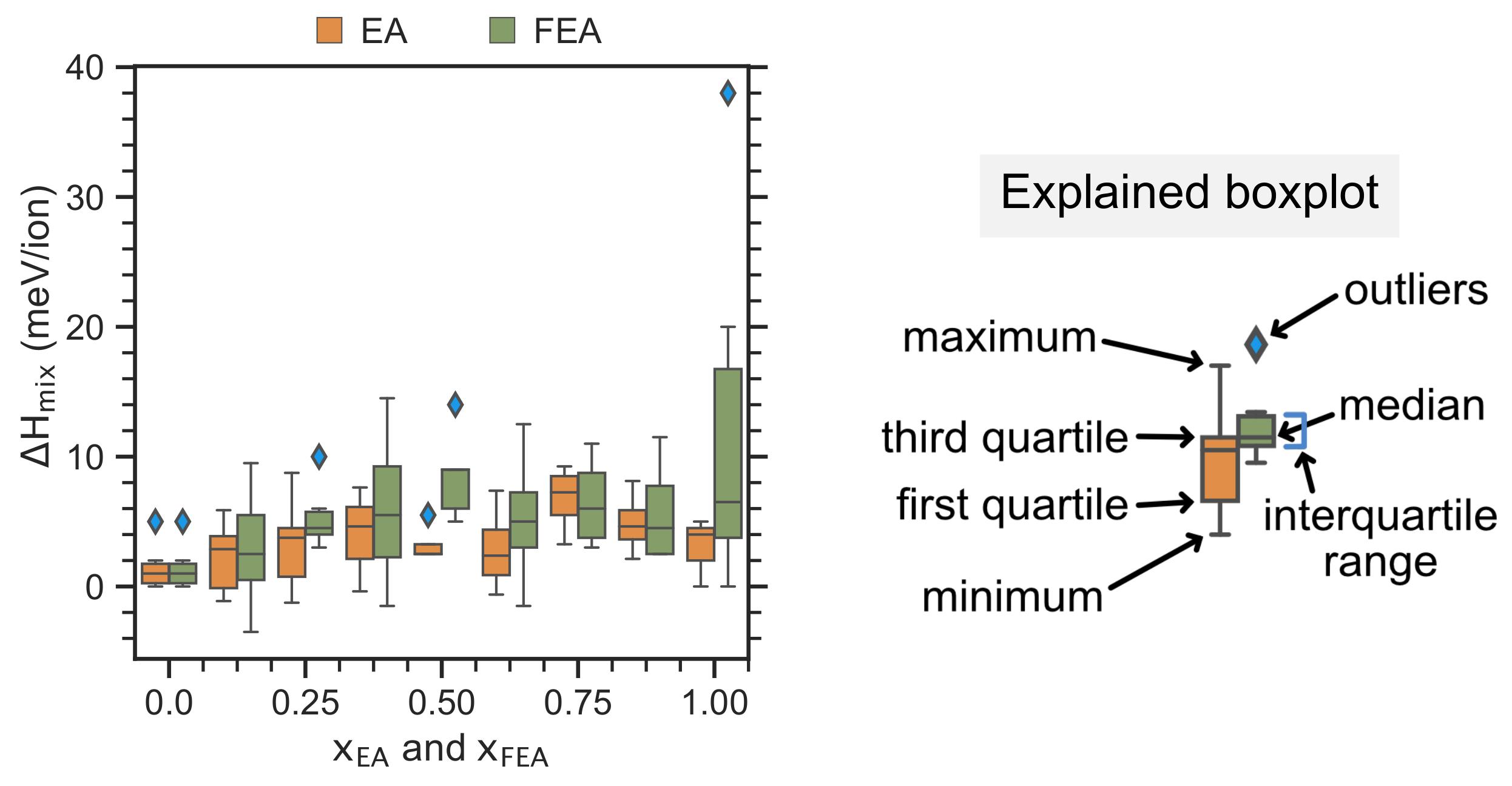
2.2. Enthalpy of Cation Mixing
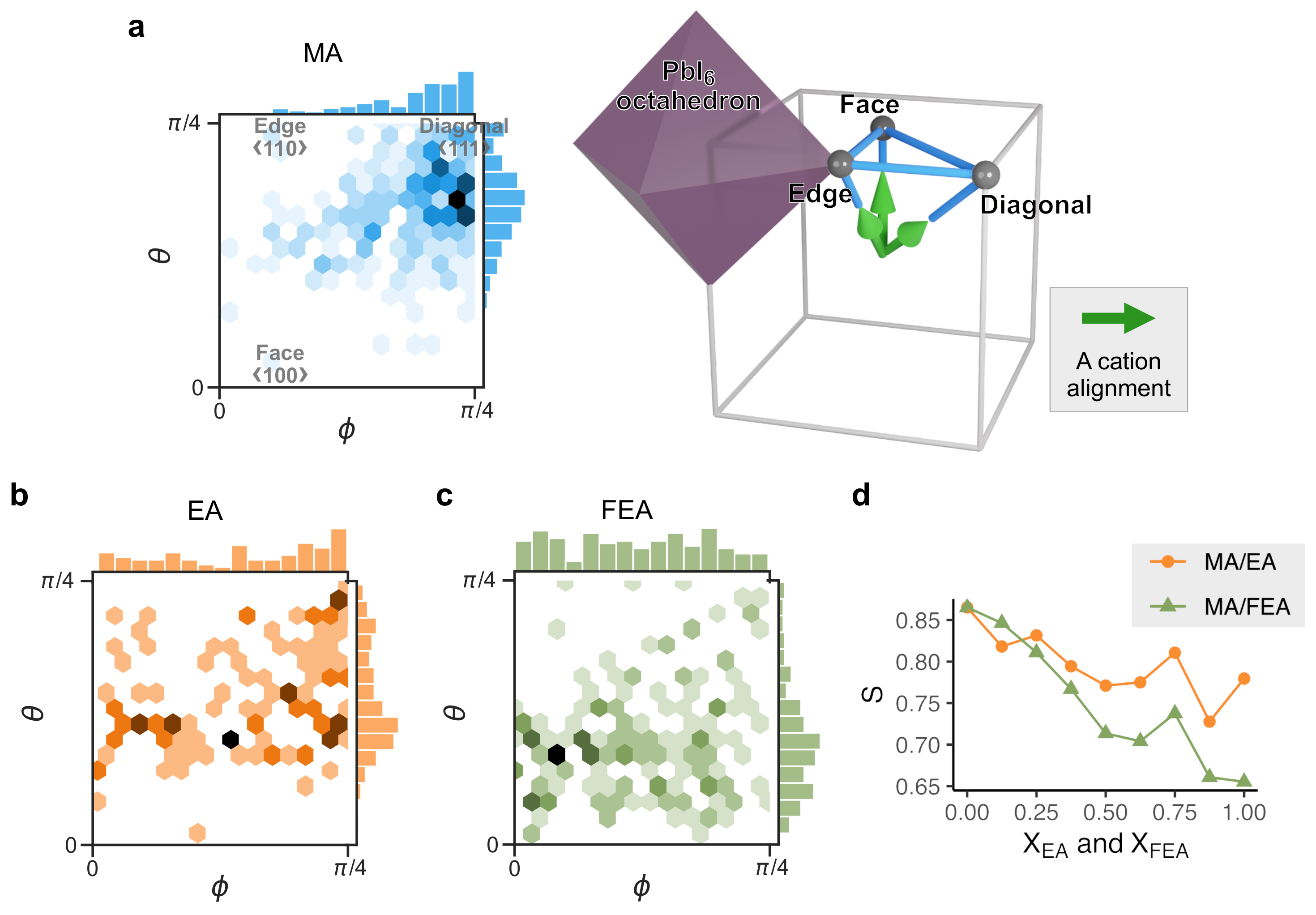
2.3. Cation Alignment
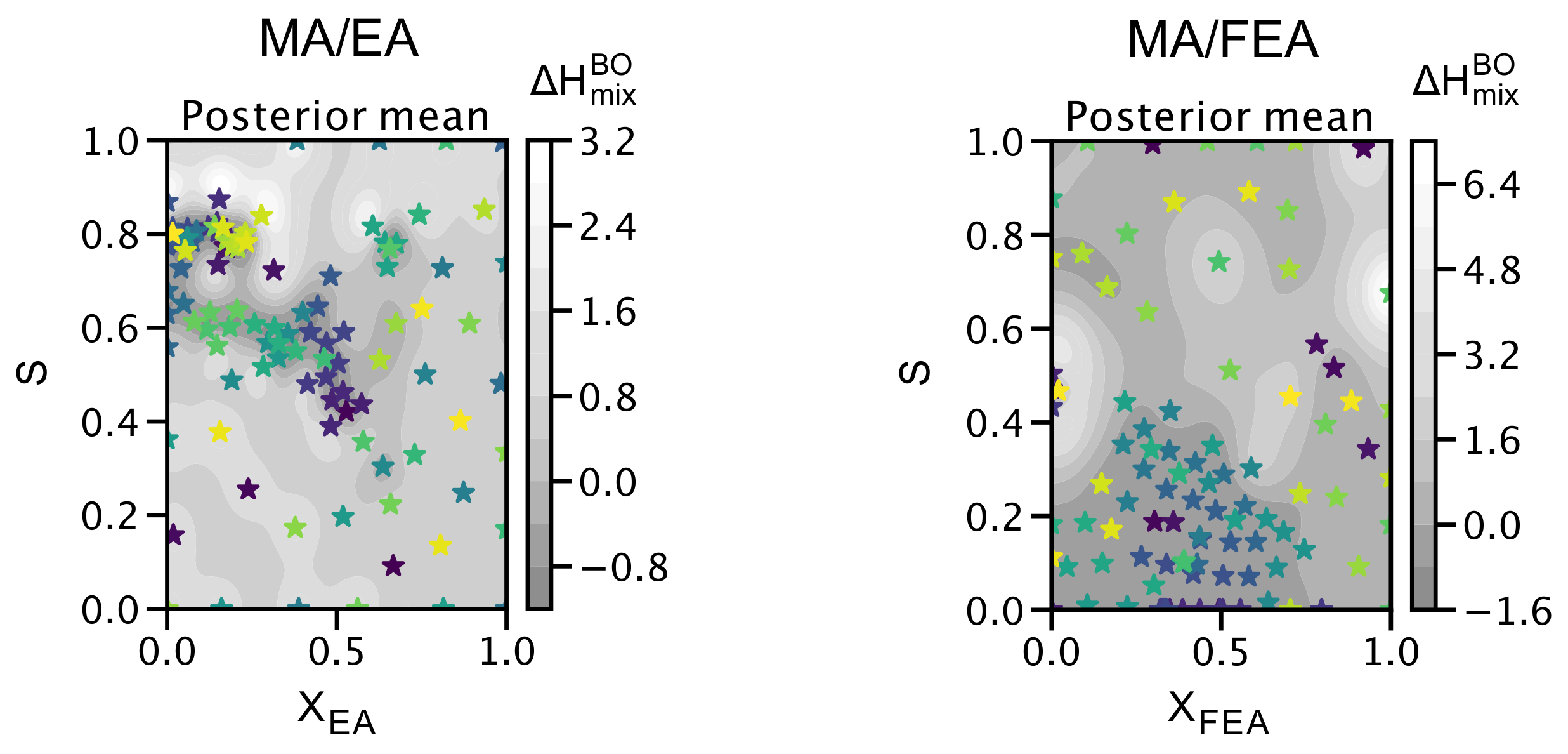
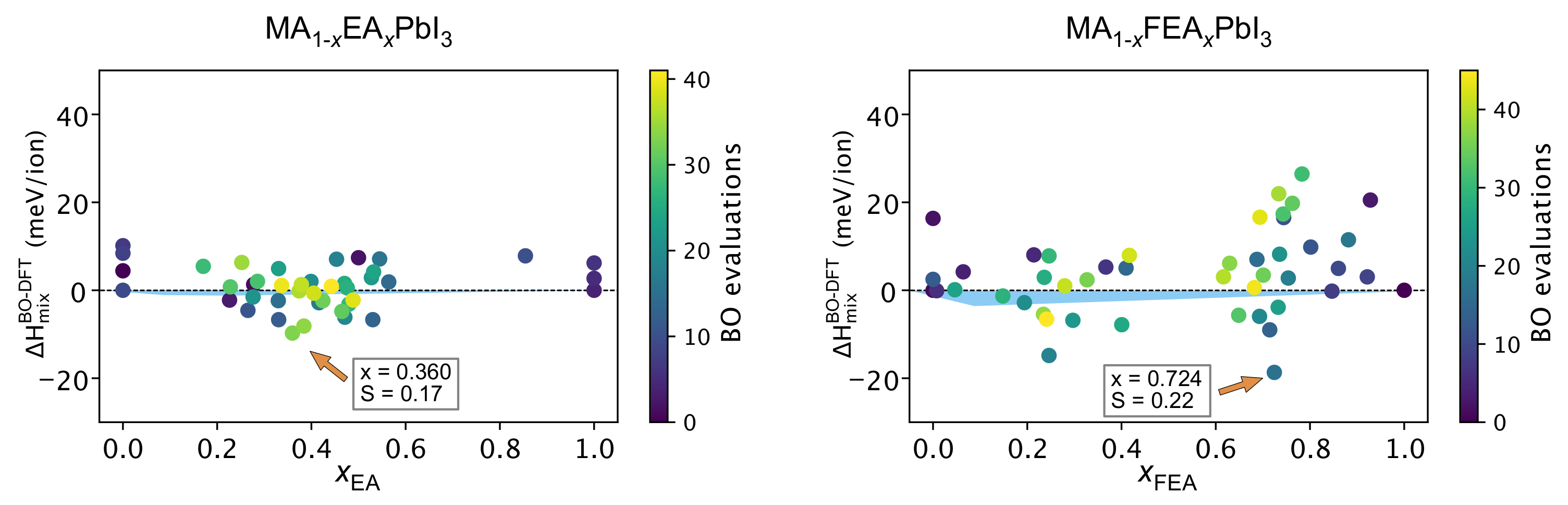
2.4. The Search for Optimal Concentration of Large Cation Replacement of MA: Bayesian Optimization Aided Design
2.5. DFT Workflow Automation Aided by Bayesian Optimization
3. Computational Methods
3.1. Dft Calculation Methods
3.2. Bayesian Optimization Methodology
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jeon, N.J.; Noh, J.H.; Yang, W.S.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S.I. Compositional engineering of perovskite materials for high-performance solar cells. Nature 2015, 517, 476. [Google Scholar] [CrossRef]
- Yin, W.J.; Yang, J.H.; Kang, J.; Yan, Y.; Wei, S.H. Halide perovskite materials for solar cells: A theoretical review. J. Mater. Chem. A 2015, 3, 8926–8942. [Google Scholar] [CrossRef]
- Walsh, A. Principles of chemical bonding and band gap engineering in hybrid organic–inorganic halide perovskites. J. Phys. Chem. C 2015, 119, 5755–5760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- An, Y.; Hidalgo, J.; Perini, C.A.R.; Castro-Méndez, A.F.; Vagott, J.N.; Bairley, K.; Wang, S.; Li, X.; Correa-Baena, J.P. Structural Stability of Formamidinium-and Cesium-Based Halide Perovskites. ACS Energy Lett. 2021, 6, 1942–1969. [Google Scholar] [CrossRef]
- Kanhere, P.; Chen, Z. A review on visible light active perovskite-based photocatalysts. Molecules 2014, 19, 19995–20022. [Google Scholar] [CrossRef] [Green Version]
- Frost, J.M.; Butler, K.T.; Brivio, F.; Hendon, C.H.; Van Schilfgaarde, M.; Walsh, A. Atomistic origins of high-performance in hybrid halide perovskite solar cells. Nano Lett. 2014, 14, 2584–2590. [Google Scholar] [CrossRef] [Green Version]
- Park, N.G. Perovskite solar cells: An emerging photovoltaic technology. Mater. Today 2015, 18, 65–72. [Google Scholar] [CrossRef]
- Best Research-Cell Efficiency Chart. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 25 May 2021).
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Hao, X. Solar cell efficiency tables (version 56). Prog. Photovolt. Res. Appl. 2020, 28, 629–638. [Google Scholar] [CrossRef]
- Yin, W.J.; Shi, T.; Yan, Y. Unique properties of halide perovskites as possible origins of the superior solar cell performance. Adv. Mater. 2014, 26, 4653–4658. [Google Scholar] [CrossRef]
- Chen, Q.; De Marco, N.; Yang, Y.M.; Song, T.B.; Chen, C.C.; Zhao, H.; Hong, Z.; Zhou, H.; Yang, Y. Under the spotlight: The organic–inorganic hybrid halide perovskite for optoelectronic applications. Nano Today 2015, 10, 355–396. [Google Scholar] [CrossRef] [Green Version]
- Song, Z.; Watthage, S.C.; Phillips, A.B.; Heben, M.J. Pathways toward high-performance perovskite solar cells: Review of recent advances in organo-metal halide perovskites for photovoltaic applications. J. Photonics Energy 2016, 6, 022001. [Google Scholar] [CrossRef]
- Sunghak, P.; Je Chang, W.; Woo Lee, C.; Sangbaek, P.; Hyo-Yong, A.; Tae Nam, K. Photocatalytic hydrogen generation from hydriodic acid using methylammonium lead iodide in dynamic equilibrium with aqueous solution. Nat. Energy 2016, 2, 16185. [Google Scholar] [CrossRef]
- Bresolin, B.M.; Park, Y.; Bahnemann, D.W. Recent Progresses on Metal Halide Perovskite-Based Material as Potential Photocatalyst. Catalysts 2020, 10, 709. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, L.; Song, T.; Mudryi, A.; Li, Y.; Chen, Q. Recent Progress in Designing Halide-Perovskite-Based System for the Photocatalytic Applications. Front. Chem. 2021, 8, 1178. [Google Scholar] [CrossRef]
- Romani, L.; Malavasi, L. Solar-Driven Hydrogen Generation by Metal Halide Perovskites: Materials, Approaches, and Mechanistic View. ACS Omega 2020, 5, 25511–25519. [Google Scholar] [CrossRef]
- Huang, H.; Pradhan, B.; Hofkens, J.; Roeffaers, M.B.J.; Steele, J.A. Solar-Driven Metal Halide Perovskite Photocatalysis: Design, Stability, and Performance. ACS Energy Lett. 2020, 5, 1107–1123. [Google Scholar] [CrossRef]
- Chen, P.; Ong, W.J.; Shi, Z.; Zhao, X.; Li, N. Pb-Based Halide Perovskites: Recent Advances in Photo (electro) catalytic Applications and Looking Beyond. Adv. Funct. Mater. 2020, 30, 1909667. [Google Scholar] [CrossRef]
- Ju, D.; Zheng, X.; Liu, J.; Chen, Y.; Zhang, J.; Cao, B.; Xiao, H.; Mohammed, O.F.; Bakr, O.M.; Tao, X. Reversible Band Gap Narrowing of Sn-Based Hybrid Perovskite Single Crystal with Excellent Phase Stability. Angew. Chem. Int. Ed. 2018, 57, 14868–14872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pisanu, A.; Speltini, A.; Quadrelli, P.; Drera, G.; Sangaletti, L.; Malavasi, L. Enhanced air-stability of Sn-based hybrid perovskites induced by dimethylammonium (DMA): Synthesis, characterization, aging and hydrogen photogeneration of the MA1-xDMAxSnBr3 system. J. Mater. Chem. C 2019, 7, 7020–7026. [Google Scholar] [CrossRef]
- Ding, L.; Shen, C.; Zhao, Y.; Chen, Y.; Yuan, L.; Yang, H.; Liang, X.; Xiang, W.; Li, L. CsPbBr3 nanocrystals glass facilitated with Zn ions for photocatalytic hydrogen production via H2O splitting. Mol. Catal. 2020, 483, 110764. [Google Scholar] [CrossRef]
- Koh, T.M.; Fu, K.; Fang, Y.; Chen, S.; Sum, T.C.; Mathews, N.; Mhaisalkar, S.G.; Boix, P.P.; Baikie, T. Formamidinium-containing metal-halide: An alternative material for near-IR absorption perovskite solar cells. J. Phys. Chem. C 2014, 118, 16458–16462. [Google Scholar] [CrossRef]
- Mozur, E.M.; Neilson, J.R. Cation Dynamics in Hybrid Halide Perovskites. Annu. Rev. Mater. Res. 2021, 51, 269–291. [Google Scholar] [CrossRef]
- Fu, Y.; Jiang, X.; Li, X.; Traoré, B.; Spanopoulos, I.; Katan, C.; Even, J.; Kanatzidis, M.G.; Harel, E. Cation Engineering in Two-Dimensional Ruddlesden–Popper Lead Iodide Perovskites with Mixed Large A-Site Cations in the Cages. J. Am. Chem. Soc. 2020, 142, 4008–4021. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wu, Z.; Dou, Y.; Zhang, J.; Bu, T.; Zhang, K.; Fang, D.; Ku, Z.; Huang, F.; Cheng, Y.B.; et al. Formamidinium-Based Perovskite Solar Cells with Enhanced Moisture Stability and Performance via Confined Pressure Annealing. J. Phys. Chem. C 2020, 124, 12249–12258. [Google Scholar] [CrossRef]
- Hui, W.; Chao, L.; Lu, H.; Xia, F.; Wei, Q.; Su, Z.; Niu, T.; Tao, L.; Du, B.; Li, D.; et al. Stabilizing black-phase formamidinium perovskite formation at room temperature and high humidity. Science 2021, 371, 1359–1364. [Google Scholar] [CrossRef]
- Park, B.W.; Kwon, H.W.; Lee, Y.; Lee, D.Y.; Kim, M.G.; Kim, G.; Kim, K.J.; Kim, Y.K.; Im, J.; Shin, T.J.; et al. Stabilization of formamidinium lead triiodide α-phase with isopropylammonium chloride for perovskite solar cells. Nat. Energy 2021, 6, 419–428. [Google Scholar] [CrossRef]
- Ono, L.K.; Juarez-Perez, E.J.; Qi, Y. Progress on perovskite materials and solar cells with mixed cations and halide anions. ACS Appl. Mater. Interfaces 2017, 9, 30197–30246. [Google Scholar] [CrossRef] [Green Version]
- Maheshwari, S.; Patwardhan, S.; Schatz, G.C.; Renaud, N.; Grozema, F.C. The effect of the magnitude and direction of the dipoles of organic cations on the electronic structure of hybrid halide perovskites. Phys. Chem. Chem. Phys. 2019, 21, 16564–16572. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.M.; Ahmed, A.; Ge, C.y.; Singh, R.; Yoo, K.; Sandhu, S.; Kim, S.; Lee, J.J. Trimethylsulfonium lead triiodide (TMSPbI3) for moisture-stable perovskite solar cells. Sustain. Energy Fuels 2021, 5, 4327–4335. [Google Scholar] [CrossRef]
- Parashar, M.; Singh, R.; Yoo, K.; Lee, J.J. Formation of 1-D/3-D Fused Perovskite for Efficient and Moisture Stable Solar Cells. ACS Appl. Energy Mater. 2021, 4, 2751–2760. [Google Scholar] [CrossRef]
- Yi, C.; Luo, J.; Meloni, S.; Boziki, A.; Ashari-Astani, N.; Grätzel, C.; Zakeeruddin, S.M.; Röthlisberger, U.; Grätzel, M. Entropic stabilization of mixed A-cation ABX3 metal halide perovskites for high performance perovskite solar cells. Energy Environ. Sci. 2016, 9, 656–662. [Google Scholar] [CrossRef]
- Huang, S.; Huang, P.; Wang, L.; Han, J.; Chen, Y.; Zhong, H. Halogenated-Methylammonium Based 3D Halide Perovskites. Adv. Mater. 2019, 31, 1903830. [Google Scholar] [CrossRef]
- Lefler, B.M.; May, S.J.; Fafarman, A.T. Role of fluoride and fluorocarbons in enhanced stability and performance of halide perovskites for photovoltaics. Phys. Rev. Mater. 2020, 4, 120301. [Google Scholar] [CrossRef]
- Lermer, C.; Birkhold, S.T.; Moudrakovski, I.L.; Mayer, P.; Schoop, L.M.; Schmidt-Mende, L.; Lotsch, B.V. Toward Fluorinated Spacers for MAPI-Derived Hybrid Perovskites: Synthesis, Characterization, and Phase Transitions of (FC2H4NH3)2PbCl4. Chem. Mater. 2016, 28, 6560–6566. [Google Scholar] [CrossRef] [Green Version]
- El-Mellouhi, F.; Rashkeev, S.N.; Marzouk, A.; Kabalan, L.; Belaidi, A.; Merzougui, B.; Tabet, N.; Alharbi, F.H. Intrinsic stability enhancement and ionic migration reduction by fluorinated cations incorporated in hybrid lead halide perovskites. J. Mater. Chem. C 2019, 7, 5299–5306. [Google Scholar] [CrossRef]
- Chu, L.L.; Zhang, T.; Gao, Y.F.; Zhang, W.Y.; Shi, P.P.; Ye, Q.; Fu, D.W. Fluorine Substitution in Ethylamine Triggers Second Harmonic Generation in Noncentrosymmetric Crystalline [NH3CH2CH2F]3BiCl6. Chem. Mater. 2020, 32, 6968–6974. [Google Scholar] [CrossRef]
- Haruyama, J.; Sodeyama, K.; Han, L.; Tateyama, Y. First-principles study of ion diffusion in perovskite solar cell sensitizers. J. Am. Chem. Soc. 2015, 137, 10048–10051. [Google Scholar] [CrossRef]
- Tong, C.J.; Geng, W.; Prezhdo, O.V.; Liu, L.M. Role of Methylammonium Orientation in Ion Diffusion and Current–Voltage Hysteresis in the CH3NH3PbI3 Perovskite. ACS Energy Lett. 2017, 2, 1997–2004. [Google Scholar] [CrossRef]
- Garoufalis, C.S.; Galanakis, I.; Zeng, Z.; Hayrapetyan, D.B.; Baskoutas, S. Structural and Electronic Properties of Small Perovskite Nanoparticles of the Form ABX3 (A = MA, DEA, FA, GA, B = Pb, Sn, X = Cl, Br, I). Electron. Mater. 2021, 2, 26. [Google Scholar] [CrossRef]
- Koliogiorgos, A.; Garoufalis, C.S.; Galanakis, I.; Baskoutas, S. Electronic and Optical Properties of Ultrasmall ABX3 (A = Cs, CH3NH3/B = Ge, Pb, Sn, Ca, Sr/X = Cl, Br, I) Perovskite Quantum Dots. ACS Omega 2018, 3, 18917–18924. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Mall, R.; Alharbi, F.H.; Sanvito, S.; Tabet, N.; Bensmail, H.; El-Mellouhi, F. Exploring new approaches towards the formability of mixed-ion perovskites by DFT and machine learning. Phys. Chem. Chem. Phys. 2019, 21, 1078–1088. [Google Scholar] [CrossRef]
- Park, H.; Mall, R.; Alharbi, F.H.; Sanvito, S.; Tabet, N.; Bensmail, H.; El-Mellouhi, F. Learn-and-Match Molecular Cations for Perovskites. J. Phys. Chem. A 2019, 123, 7323–7334. [Google Scholar] [CrossRef]
- Ali, A.; Park, H.; Mall, R.; Aïssa, B.; Sanvito, S.; Bensmail, H.; Belaidi, A.; El-Mellouhi, F. Machine Learning Accelerated Recovery of the Cubic Structure in Mixed-Cation Perovskite Thin Films. Chem. Mater. 2020, 32, 2998–3006. [Google Scholar] [CrossRef]
- Park, H.; Mall, R.; Ali, A.; Sanvito, S.; Bensmail, H.; El-Mellouhi, F. Importance of structural deformation features in the prediction of hybrid perovskite bandgaps. Comput. Mater. Sci. 2020, 184, 109858. [Google Scholar] [CrossRef]
- Park, H.; Ali, A.; Mall, R.; Bensmail, H.; Sanvito, S.; El-Mellouhi, F. Data-driven enhancement of cubic phase stability in mixed-cation perovskites. Mach. Learn. Sci. Technol. 2021, 2, 025030. [Google Scholar] [CrossRef]
- Jodlowski, A.D.; Roldán-Carmona, C.; Grancini, G.; Salado, M.; Ralaiarisoa, M.; Ahmad, S.; Koch, N.; Camacho, L.; Miguel, G.D.; Nazeeruddin, M.K. Large guanidinium cation mixed with methylammonium in lead iodide perovskites for 19% efficient solar cells. Nat. Energy 2017, 2, 972–979. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Xie, J.; Cheng, G.; Xiang, Y.; Zhu, H.; Guo, W.; Wang, H.; Qin, M.; Lu, X.; Qu, J.; et al. General Nondestructive Passivation by 4-Fluoroaniline for Perovskite Solar Cells with Improved Performance and Stability. Small 2018, 14, 1803350. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Wu, C.; Jha, S.K.; Li, Z.; Zhu, K.; Priya, S. Improved Phase Stability of Formamidinium Lead Triiodide Perovskite by Strain Relaxation. ACS Energy Lett. 2016, 1, 1014–1020. [Google Scholar] [CrossRef]
- Correa-Baena, J.P.; Luo, Y.; Brenner, T.M.; Snaider, J.; Sun, S.; Li, X.; Jensen, M.A.; Hartono, N.T.P.; Nienhaus, L.; Wieghold, S.; et al. Homogenized halides and alkali cation segregation in alloyed organic-inorganic perovskites. Science 2019, 363, 627–631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knight, A.J.; Borchert, J.; Oliver, R.D.J.; Patel, J.B.; Radaelli, P.G.; Snaith, H.J.; Johnston, M.B.; Herz, L.M. Halide Segregation in Mixed-Halide Perovskites: Influence of A-Site Cations. ACS Energy Lett. 2021, 6, 799–808. [Google Scholar] [CrossRef]
- Waskom, M.L. Seaborn: Statistical data visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Mozur, E.M.; Maughan, A.E.; Cheng, Y.; Huq, A.; Jalarvo, N.; Daemen, L.L.; Neilson, J.R. Orientational Glass Formation in Substituted Hybrid Perovskites. Chem. Mater. 2017, 29, 10168–10177. [Google Scholar] [CrossRef]
- Sahayaraj, S.; Radicchi, E.; Ziółek, M.; Ścigaj, M.; Tamulewicz-Szwajkowska, M.; Serafińczuk, J.; De Angelis, F.; Wojciechowski, K. Combination of a large cation and coordinating additive improves carrier transport properties in quasi-2D perovskite solar cells. J. Mater. Chem. A 2021, 9, 9175–9190. [Google Scholar] [CrossRef]
- Dunn, A.; Brenneck, J.; Jain, A. Rocketsled: A software library for optimizing high-throughput computational searches. J. Phys. Mater. 2019, 2, 034002. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Chen, W.; Medasani, B.; Qu, X.; Kocher, M.; Brafman, M.; Petretto, G.; Rignanese, G.M.; Hautier, G.; et al. FireWorks: A dynamic workflow system designed for high-throughput applications. Concur. Comp.-Pract. E. 2015, 27, 5037–5059. [Google Scholar] [CrossRef] [Green Version]
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. [Google Scholar] [CrossRef] [Green Version]
- Barca, G.M.J.; Bertoni, C.; Carrington, L.; Datta, D.; De Silva, N.; Deustua, J.E.; Fedorov, D.G.; Gour, J.R.; Gunina, A.O.; Guidez, E.; et al. Recent developments in the general atomic and molecular electronic structure system. J. Chem. Phys. 2020, 152, 154102. [Google Scholar] [CrossRef] [Green Version]
- Kieslich, G.; Sun, S.; Cheetham, A.K. Solid-state principles applied to organic–inorganic perovskites: New tricks for an old dog. Chem. Sci. 2014, 5, 4712–4715. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
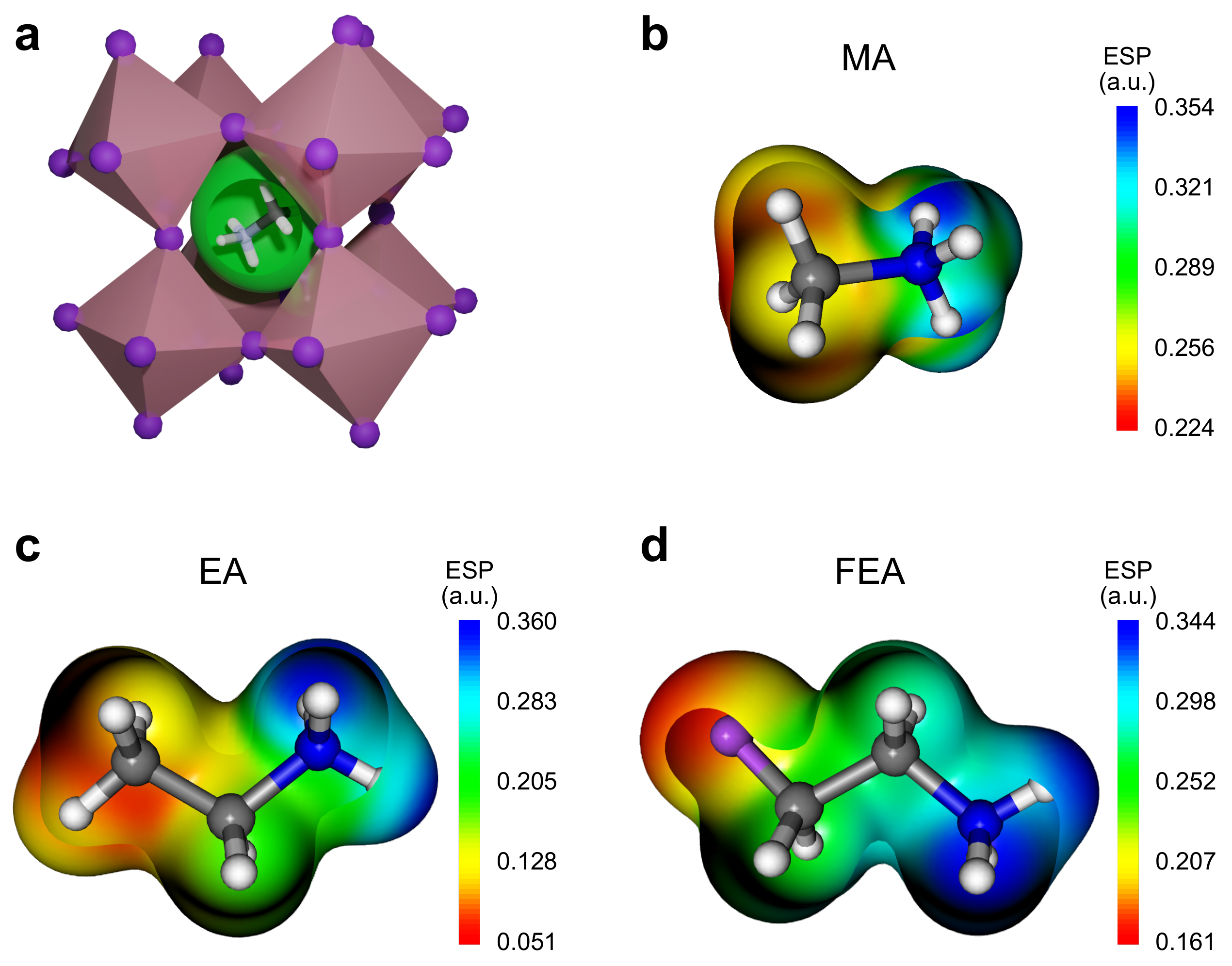

| Cation | Formula | Ionic Radius (pm) | Dipole Moment (Debye) | |
|---|---|---|---|---|
| MA | [CH3NH3]+ | 217 | 2.20 | 0.91 |
| EA | [CH3CH2NH3]+ | 274 | 3.85 | 1.03 |
| FEA | [CH2FCH2NH3]+ | 338 | 9.17 | 1.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, H.; Kumar, S.; Chawla, S.; El-Mellouhi, F. Design Principles of Large Cation Incorporation in Halide Perovskites. Molecules 2021, 26, 6184. https://doi.org/10.3390/molecules26206184
Park H, Kumar S, Chawla S, El-Mellouhi F. Design Principles of Large Cation Incorporation in Halide Perovskites. Molecules. 2021; 26(20):6184. https://doi.org/10.3390/molecules26206184
Chicago/Turabian StylePark, Heesoo, Syam Kumar, Sanjay Chawla, and Fedwa El-Mellouhi. 2021. "Design Principles of Large Cation Incorporation in Halide Perovskites" Molecules 26, no. 20: 6184. https://doi.org/10.3390/molecules26206184
APA StylePark, H., Kumar, S., Chawla, S., & El-Mellouhi, F. (2021). Design Principles of Large Cation Incorporation in Halide Perovskites. Molecules, 26(20), 6184. https://doi.org/10.3390/molecules26206184






