Brief Overview of Ice Nucleation
Abstract
1. Introduction
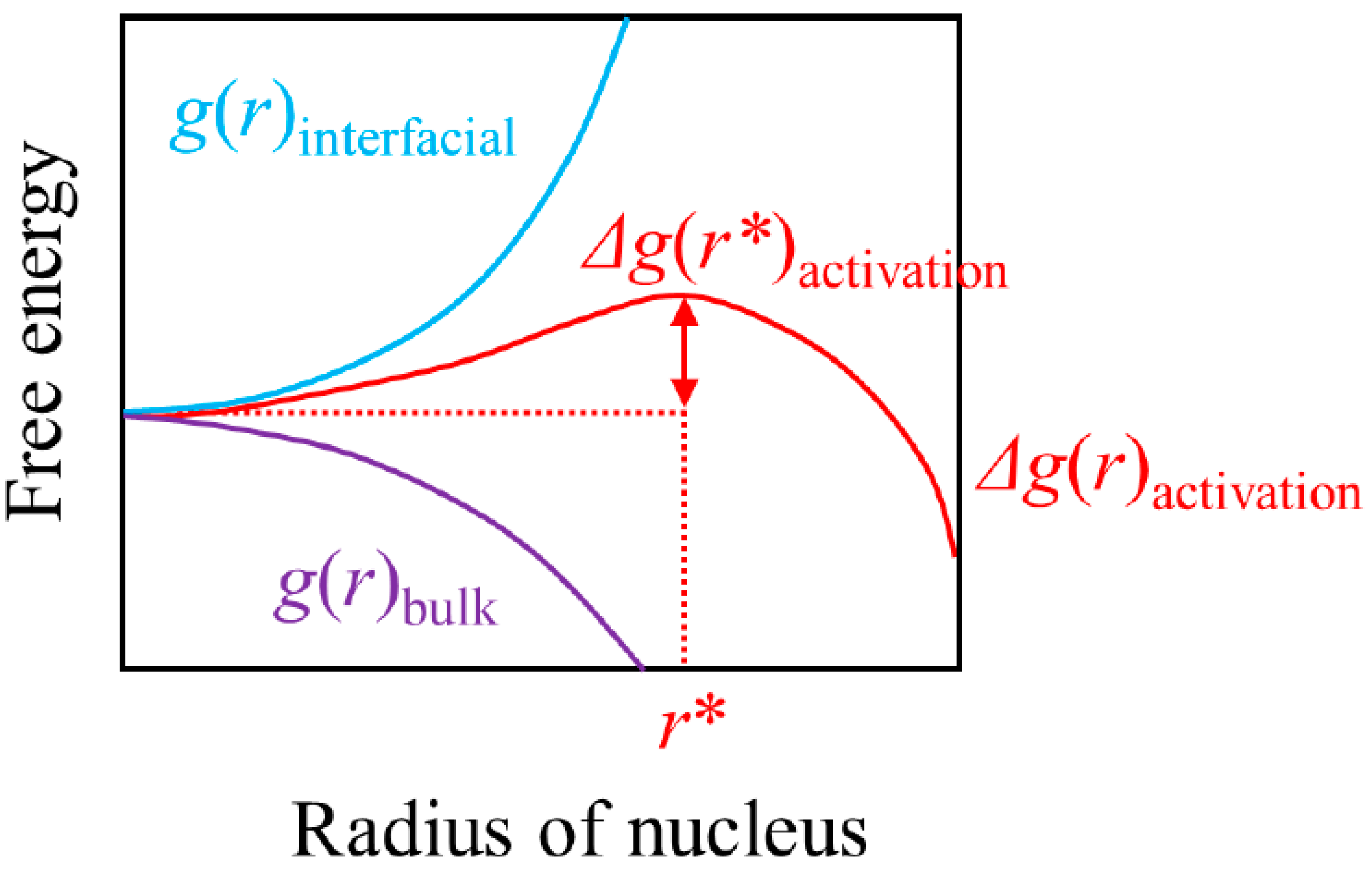
2. Nucleation and Classical Nucleation Theory
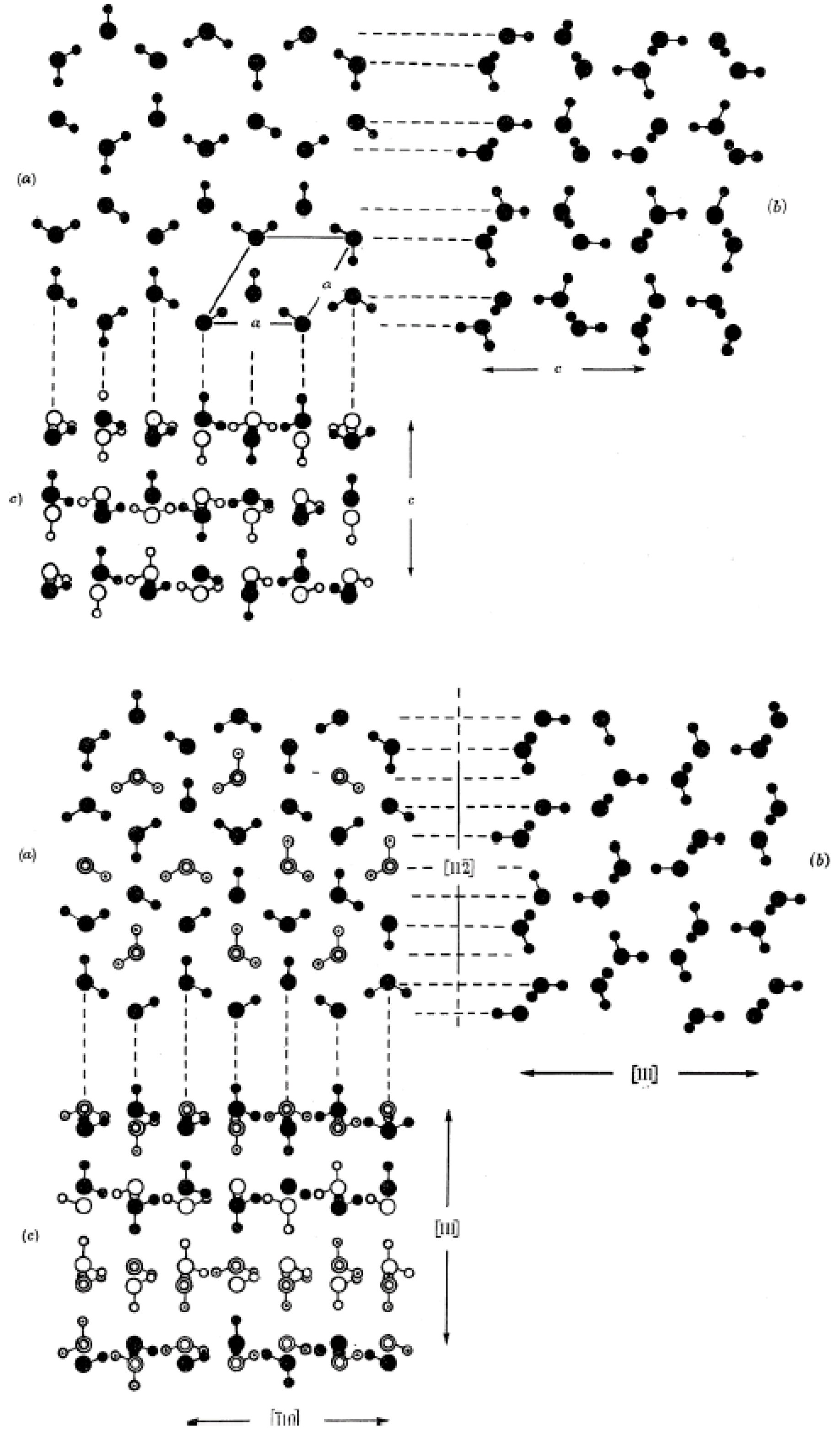
3. Nucleation of Ice from Liquid Water
4. Organic Ice Nucleation Promoters
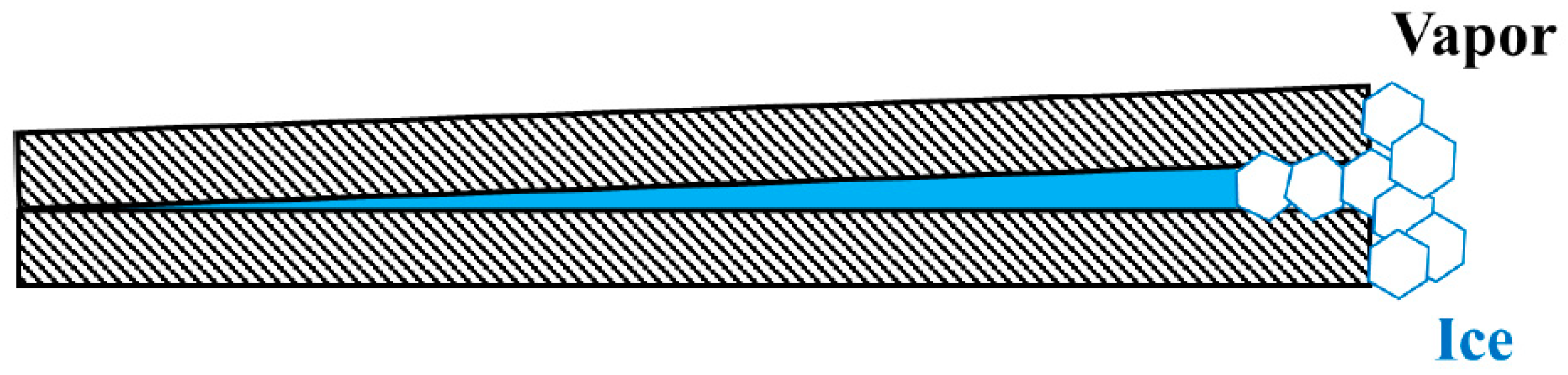
5. Nucleation of Ice from Water Vapor
6. System Size Dependence
7. Size Distributions of Ice Particles in the Atmosphere
8. The Memory Effect in Ice Nucleation
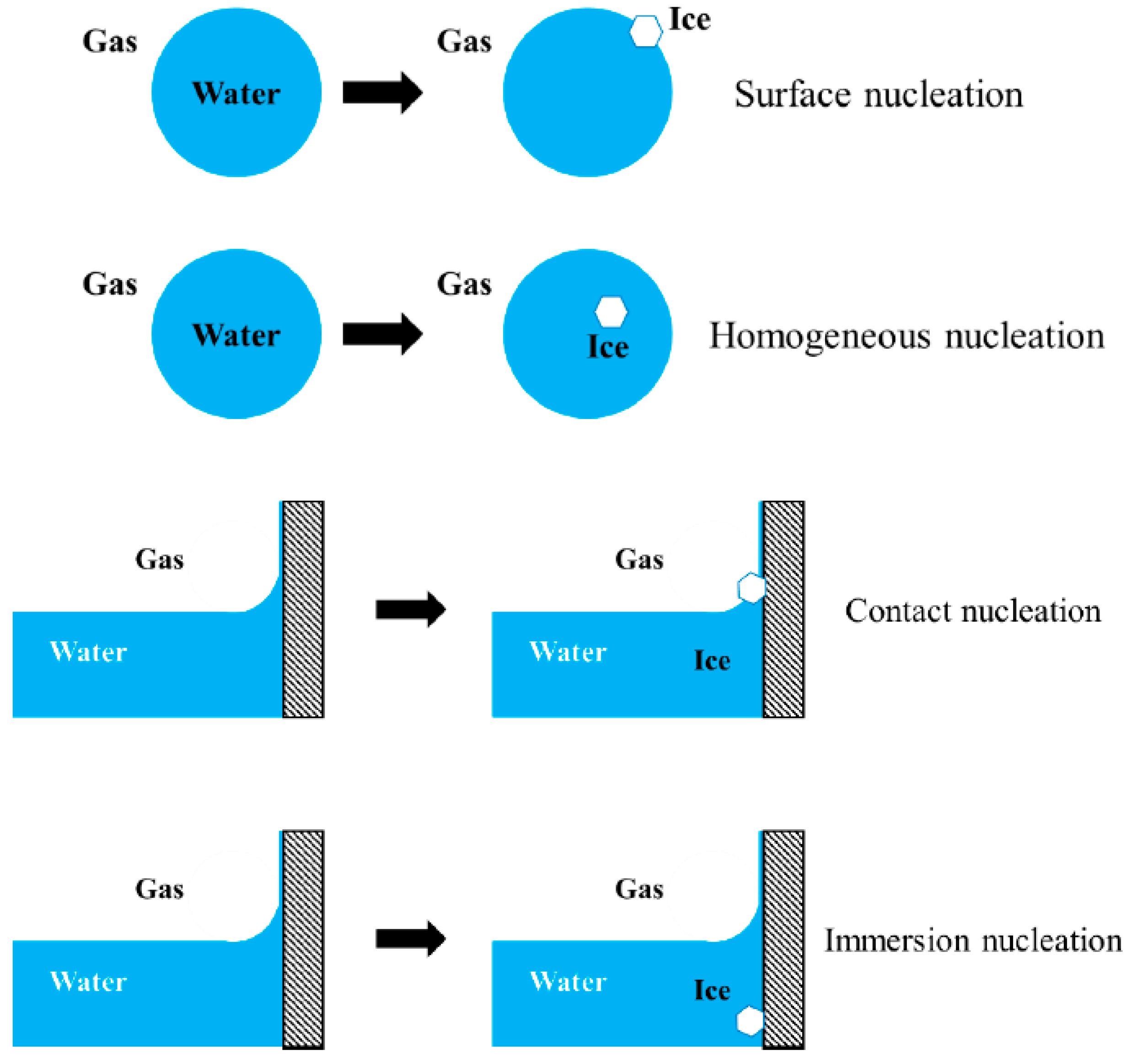
9. Surface Nucleation and Contact Nucleation
10. Concluding Remarks
Funding
Conflicts of Interest
Nomenclature
| J | nucleation rate |
| A | a kinetic constant that includes the attachment frequency of monomer molecules |
| N0 | the concentration of potential nucleation sites |
| Δg | the height of the activation barrier |
| k | the Boltzmann constant |
| T | the absolute temperature |
| g(r)bulk | the free energy of forming a new phase at a constant temperature in the absence of an interface |
| g(r)interfacial | the interfacial free energy between the new phase and the old phase at a constant temperature |
| Δg(r)activation | the height of the activation barrier at a constant temperature, which is the sum of g(r)bulk and g(r)interfacial |
| r | the radius of the nucleus |
| P | the actual vapor pressure |
| P0 | the saturation vapor pressure |
| γ | the specific interfacial free energy |
| vm | the molecular volume |
| rK | the Kelvin radius. For a spherical nucleus, r = 2rK |
| n | number of molecules in a nucleus |
| n* | number of molecules in a critically sized nucleus |
| θ | the contact angle of a spherical cap–shaped nucleus that forms on the substrate in the metastable parent phase |
| W(n) | nucleation work, which is a function of the size of the nucleus |
References
- Assegehegn, G.; Brito-de la Fuente, E.; Franco, J.M.; Gallegos, C. The Importance of Understanding the Freezing Step and Its Impact on Freeze-Drying Process Performance. J. Pharm. Sci. 2019, 108, 1378–1395. [Google Scholar] [CrossRef]
- Gao, D.; Critser, J.K. Mechanisms of cryoinjury in living cells. ILAR J. 2000, 41, 187–196. [Google Scholar] [CrossRef]
- Griffith, M.; Ewart, K.V. Antifreeze proteins and their potential use in frozen foods. Biotechnol. Adv. 1995, 13, 375–402. [Google Scholar] [CrossRef]
- Leygonie, C.; Britz, T.J.; Hoffman, L.C. Impact of freezing and thawing on the quality of meat: Review. Meat Sci. 2012, 91, 93–98. [Google Scholar] [CrossRef]
- Li, D.-Z.; Pritchard, H.W. The science and economics of ex situ plant conservation. Trends Plant Sci. 2009, 14, 614–621. [Google Scholar] [CrossRef]
- Ciftci, H.B.; Aygun, A. Poultry semen cryopreservation technologies. Worlds Poult. Sci. J. 2018, 74, 699–709. [Google Scholar] [CrossRef]
- Maity, T.; Saxena, A.; Raju, P.S. Use of hydrocolloids as cryoprotectant for frozen foods. Crit. Rev. Food Sci. Nutr. 2018, 58, 420–435. [Google Scholar] [CrossRef]
- Moore, S.G.; Hasler, J.F. A 100-Year Review: Reproductive technologies in dairy science. J. Dairy Sci. 2017, 100, 10314–10331. [Google Scholar] [CrossRef]
- Naing, A.H.; Kim, C.K. A brief review of applications of antifreeze proteins in cryopreservation and metabolic genetic engineering. 3 Biotech 2019, 9, 329. [Google Scholar] [CrossRef]
- Popova, E.; Shukla, M.; Kim, H.-H.; Saxena, P.K. Root cryobanking: An important tool in plant cryopreservation. Plant Cell Tissue Organ Cult. 2020. [Google Scholar] [CrossRef]
- Suris-Valls, R.; Voets, I.K. Peptidic Antifreeze Materials: Prospects and Challenges. Int. J. Mol. Sci. 2019, 20, 5149. [Google Scholar] [CrossRef]
- Ugur, M.R.; Abdelrahman, A.S.; Evans, H.C.; Gilmore, A.A.; Hitit, M.; Arifiantini, R.I.; Purwantara, B.; Kaya, A.; Memili, E. Advances in Cryopreservation of Bull Sperm. Front. Vet. Sci. 2019, 6, 268. [Google Scholar] [CrossRef]
- Aguiar, F.L.N.; Gastal, G.D.A.; Alves, K.A.; Alves, B.G.; Figueiredo, J.R.; Gastal, E.L. Supportive techniques to investigate in vitro culture and cryopreservation efficiencies of equine ovarian tissue: A review. Theriogenology 2020, 156, 296–309. [Google Scholar] [CrossRef]
- Meneghel, J.; Kilbride, P.; Morris, G.J. Cryopreservation as a Key Element in the Successful Delivery of Cell-Based Therapies-A Review. Front. Med. 2020, 7. [Google Scholar] [CrossRef]
- Ullah, I.; Subbarao, R.B.; Rho, G.J. Human mesenchymal stem cells—Current trends and future prospective. Biosci. Rep. 2015, 35. [Google Scholar] [CrossRef]
- Bragg, M.B.; Broeren, A.P.; Blumenthal, L.A. Iced-airfoil aerodynamics. Prog. Aerosp. Sci. 2005, 41, 323–362. [Google Scholar] [CrossRef]
- Lynch, F.T.; Khodadoust, A. Effects of ice accretions on aircraft aerodynamics. Prog. Aerosp. Sci. 2001, 37, 669–767. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Cao, Y.; Xin, M. Numerical Simulation of Supercooled Large Droplet Icing Phenomenon: A Review. Arch. Comput. Methods Eng. 2020, 27, 1231–1265. [Google Scholar] [CrossRef]
- Shen, Y.; Wu, X.; Tao, J.; Zhu, C.; Lai, Y.; Chen, Z. Icephobic materials: Fundamentals, performance evaluation, and applications. Prog. Mater. Sci. 2019, 103, 509–557. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, Q.; Lin, T.; Cheng, P. A review of recent literature on icing phenomena: Transport mechanisms, their modulations and controls. Int. J. Heat Mass Transf. 2020, 159, 120074. [Google Scholar] [CrossRef]
- Parent, O.; Ilinca, A. Anti-icing and de-icing techniques for wind turbines: Critical review. Cold Reg. Sci. Technol. 2011, 65, 88–96. [Google Scholar] [CrossRef]
- Andreae, M.O.; Rosenfeld, D. Aerosol-cloud-precipitation interactions. Part 1. The nature and sources of cloud-active aerosols. Earth-Sci. Rev. 2008, 89, 13–41. [Google Scholar] [CrossRef]
- Despres, V.R.; Huffman, J.A.; Burrows, S.M.; Hoose, C.; Safatov, A.S.; Buryak, G.; Froehlich-Nowoisky, J.; Elbert, W.; Andreae, M.O.; Poeschl, U.; et al. Primary biological aerosol particles in the atmosphere: A review. Tellus Ser. B Chem. Phys. Meteorol. 2012, 64, 15598. [Google Scholar] [CrossRef]
- Hoose, C.; Moehler, O. Heterogeneous ice nucleation on atmospheric aerosols: A review of results from laboratory experiments. Atmos. Chem. Phys. 2012, 12, 9817–9854. [Google Scholar] [CrossRef]
- Murray, B.J.; O’Sullivan, D.; Atkinson, J.D.; Webb, M.E. Ice nucleation by particles immersed in supercooled cloud droplets. Chem. Soc. Rev. 2012, 41, 6519–6554. [Google Scholar] [CrossRef]
- Tao, W.-K.; Chen, J.-P.; Li, Z.; Wang, C.; Zhang, C. Impact of aerosols on convective clouds and precipitation. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.-M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. Clouds and Aerosols; Cambridge University Press: Cambridge, UK, 2014; pp. 571–657. [Google Scholar]
- Bartels-Rausch, T. Ten things we need to know about ice and snow. Nature 2013, 494, 27–29. [Google Scholar] [CrossRef]
- Cantrell, W.; Heymsfield, A. Production of ice in tropospheric clouds—A review. Bull. Am. Meteorol. Soc. 2005, 86, 795–807. [Google Scholar] [CrossRef]
- Kashchiev, D. Nucleation; Elsevier: Oxford, UK, 2000. [Google Scholar]
- Dash, J.G. Surface Melting. Contemp. Phys. 1989, 30, 89–100. [Google Scholar] [CrossRef]
- Dash, J.G.; Fu, H.Y.; Wettlaufer, J.S. The Premelting of Ice and Its Environmental Consequences. Rep. Prog. Phys. 1995, 58, 115–167. [Google Scholar] [CrossRef]
- Maeda, N. Nucleation of Gas Hydrates, 1st ed.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Debenedetti, P.G. Supercooled and glassy water. J. Phys. Condes. Matter 2003, 15, R1669–R1726. [Google Scholar] [CrossRef]
- Maeda, N. Nucleation curves of methane hydrate from constant cooling ramp methods. Fuel 2018, 223, 286–293. [Google Scholar] [CrossRef]
- Reif, F. Fundamentals of Statistical and Thermal Physics; McGraw-Hill Book Co: Singapore, 1965. [Google Scholar]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces, 6th ed.; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Maxwell, J.C. Capillary Action. In Encyclopaedia Britannica, 9th ed.; A & C Black: London, UK, 1875; pp. 56–71. [Google Scholar]
- Wulff, G. On the question of speed of growth and dissolution of crystal surfaces. Z. Kryst. Mineral. 1901, 34, 449–530. [Google Scholar] [CrossRef]
- Zhou, W.; Yan, B.; Cheng, C.; Cong, C.; Hu, H.; Fan, H.; Yu, T. Facile synthesis and shape evolution of highly symmetric 26-facet polyhedral microcrystals of Cu2O. CrystEngComm 2009, 11, 2291–2296. [Google Scholar] [CrossRef]
- Angell, C.A. Supercooled Water. Annu. Rev. Phys. Chem. 1983, 34, 593–630. [Google Scholar] [CrossRef]
- Polen, M.; Lawlis, E.; Sullivan, R.C. The unstable ice nucleation properties of Snomax (R) bacterial particles. J. Geophys. Res. Atmos. 2016, 121, 11666–11678. [Google Scholar] [CrossRef]
- Franks, F. Nucleation of ice and its management in ecosystems. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 557–574. [Google Scholar] [CrossRef]
- Sciortino, F.; Geiger, A.; Stanley, H.E. Effect of defects on molecular mobility in liquid water. Nature 1991, 354, 218–221. [Google Scholar] [CrossRef]
- Hare, D.E.; Sorensen, C.M. Raman-spectroscopic study of bulk water supercooled to −33 °C. J. Chem. Phys. 1990, 93, 25–33. [Google Scholar] [CrossRef]
- Rice, S.A.; Sceats, M.G. A random network model for water. J. Phys. Chem. 1981, 85, 1108–1119. [Google Scholar] [CrossRef]
- Xie, Y.L.; Ludwig, K.F.; Morales, G.; Hare, D.E.; Sorensen, C.M. Noncritical behavior of density-fluctuations in supercooled water. Phys. Rev. Lett. 1993, 71, 2050–2053. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.H.; Spah, A.; Pathak, H.; Perakis, F.; Mariedahl, D.; Amann-Winkel, K.; Sellberg, J.A.; Lee, J.H.; Kim, S.; Park, J.; et al. Maxima in the thermodynamic response and correlation functions of deeply supercooled water. Science 2017, 358, 1589–1593. [Google Scholar] [CrossRef] [PubMed]
- Palmer, J.C.; Poole, P.H.; Sciortino, F.; Debenedetti, P.G. Advances in Computational Studies of the Liquid-Liquid Transition in Water and Water-Like Models. Chem. Rev. 2018, 118, 9129–9151. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, A.; Pettersson, L.G.M. The structural origin of anomalous properties of liquid water. Nat. Commun. 2015, 6, 1–11. [Google Scholar] [CrossRef]
- Moore, E.B.; Molinero, V. Growing correlation length in supercooled water. J. Chem. Phys. 2009, 130, 244505. [Google Scholar] [CrossRef] [PubMed]
- Bullock, G.; Molinero, V. Low-density liquid water is the mother of ice: On the relation between mesostructure, thermodynamics and ice crystallization in solutions. Faraday Discuss. 2013, 167, 371–388. [Google Scholar] [CrossRef]
- Sellberg, J.A.; Huang, C.; McQueen, T.A.; Loh, N.D.; Laksmono, H.; Schlesinger, D.; Sierra, R.G.; Nordlund, D.; Hampton, C.Y.; Starodub, D.; et al. Ultrafast X-ray probing of water structure below the homogeneous ice nucleation temperature. Nature 2014, 510, 381–384. [Google Scholar] [CrossRef]
- Matsumoto, M.; Saito, S.; Ohmine, I. Molecular dynamics simulation of the ice nucleation and growth process leading to water freezing. Nature 2002, 416, 409–413. [Google Scholar] [CrossRef]
- Ediger, M.D. Spatially heterogeneous dynamics in supercooled liquids. Annu. Rev. Phys. Chem. 2000, 51, 99–128. [Google Scholar] [CrossRef]
- Fitzner, M.; Sosso, G.C.; Cox, S.J.; Michaelides, A. Ice is born in low-mobility regions of supercooled liquid water. Proc. Natl. Acad. Sci. USA 2019, 116, 2009–2014. [Google Scholar] [CrossRef] [PubMed]
- Russo, J.; Tanaka, H. Understanding water’s anomalies with locally favoured structures. Nat. Comm. 2014, 5, 1–11. [Google Scholar] [CrossRef]
- Conrad, P.; Ewing, G.E.; Karlinsey, R.L.; Sadtchenko, V. Ice nucleation on BaF2(111). J. Chem. Phys. 2005, 122, 064709. [Google Scholar] [CrossRef] [PubMed]
- Sadtchenko, V.; Ewing, G.E.; Nutt, D.R.; Stone, A.J. Instability of ice films. Langmuir 2002, 18, 4632–4636. [Google Scholar] [CrossRef]
- Fletcher, N.H. Entropy Effect in Ice Crystal Nucleation. J. Chem. Phys. 1959, 30, 1476–1482. [Google Scholar] [CrossRef]
- Cox, S.J.; Kathmann, S.M.; Slater, B.; Michaelides, A. Molecular simulations of heterogeneous ice nucleation. I. Controlling ice nucleation through surface hydrophilicity. J. Chem. Phys. 2015, 142, 184704. [Google Scholar] [CrossRef]
- Lata, N.N.; Zhou, J.; Hamilton, P.; Larsen, M.; Sarupria, S.; Cantrell, W. Multivalent Surface Cations Enhance Heterogeneous Freezing of Water on Muscovite Mica. J. Phys. Chem. Lett. 2020, 11, 8682–8689. [Google Scholar] [CrossRef]
- Turnbull, D. Kinetics of Heterogeneous Nucleation. J. Chem. Phys. 1950, 18, 198–203. [Google Scholar] [CrossRef]
- Head, R.B. Steroids as Ice Nucleators. Nature 1961, 191, 1058–1059. [Google Scholar] [CrossRef]
- Pummer, B.G.; Budke, C.; Augustin-Bauditz, S.; Niedermeier, D.; Felgitsch, L.; Kampf, C.J.; Huber, R.G.; Liedl, K.R.; Loerting, T.; Moschen, T.; et al. Ice nucleation by water-soluble macromolecules. Atmos. Chem. Phys. 2015, 15, 4077–4091. [Google Scholar] [CrossRef]
- Fukuta, N.; Mason, B.J. Epitaxial Growth of Ice on Organic Crystals. J. Phys. Chem. Solids 1963, 24, 715–718. [Google Scholar] [CrossRef]
- Maki, L.R.; Galyan, E.L.; Chang-Chien, M.M.; Caldwell, D.R. Ice nucleation induced by pseudomonas-syringae. Appl. Microbiol. 1974, 28, 456–459. [Google Scholar] [CrossRef] [PubMed]
- Pandey, R.; Usui, K.; Livingstone, R.A.; Fischer, S.A.; Pfaendtner, J.; Backus, E.H.G.; Nagata, Y.; Froehlich-Nowoisky, J.; Schmueser, L.; Mauri, S.; et al. Ice-nucleating bacteria control the order and dynamics of interfacial water. Sci. Adv. 2016, 2, e1501630. [Google Scholar] [CrossRef] [PubMed]
- Fukuta, N. Experimental studies of organic ice nuclei. J. Atmos. Sci. 1966, 23, 191–196. [Google Scholar] [CrossRef][Green Version]
- Popovitzbiro, R.; Wang, J.L.; Majewski, J.; Shavit, E.; Leiserowitz, L.; Lahav, M. Induced freezing of supercooled water into ice by self-assembled crystalline monolayers of amphiphilic alcohols at the air-water-interface. J. Am. Chem. Soc. 1994, 116, 1179–1191. [Google Scholar] [CrossRef]
- Majewski, J.; Popovitzbiro, R.; Kjaer, K.; Alsnielsen, J.; Lahav, M.; Leiserowitz, L. Toward a determination of the critical size of ice nuclei—A demonstration by grazing-incidence x-ray-diffraction of epitaxial-growth of ice under the c31h63oh alcohol monolayer. J. Phys. Chem. 1994, 98, 4087–4093. [Google Scholar] [CrossRef]
- Evans, L.F. 2-dimensional nucleation of ice. Nature 1967, 213, 384. [Google Scholar] [CrossRef]
- Qiu, Y.; Odendahl, N.; Hudait, A.; Mason, R.; Bertram, A.K.; Paesani, F.; DeMott, P.J.; Molinero, V. Ice Nucleation Efficiency of Hydroxylated Organic Surfaces Is Controlled by Their Structural Fluctuations and Mismatch to Ice. J. Am. Chem. Soc. 2017, 139, 3052–3064. [Google Scholar] [CrossRef]
- Fitzner, M.; Sosso, G.C.; Cox, S.J.; Michaelides, A. The Many Faces of Heterogeneous Ice Nucleation: Interplay between Surface Morphology and Hydrophobicity. J. Am. Chem. Soc. 2015, 137, 13658–13669. [Google Scholar] [CrossRef]
- Andreae, M.O.; Gelencser, A. Black carbon or brown carbon? The nature of light-absorbing carbonaceous aerosols. Atmos. Chem. Phys. 2006, 6, 3131–3148. [Google Scholar] [CrossRef]
- DeMott, P.J.; Chen, Y.; Kreidenweis, S.M.; Rogers, D.C.; Sherman, D.E. Ice formation by black carbon particles. Geophys. Res. Lett. 1999, 26, 2429–2432. [Google Scholar] [CrossRef]
- Jacobson, M.Z. Climate response of fossil fuel and biofuel soot, accounting for soot’s feedback to snow and sea ice albedo and emissivity. J. Geophys. Res. Atmos. 2004, 109, D21201. [Google Scholar] [CrossRef]
- Lupi, L.; Hudait, A.; Molinero, V. Heterogeneous Nucleation of Ice on Carbon Surfaces. J. Am. Chem. Soc. 2014, 136, 3156–3164. [Google Scholar] [CrossRef] [PubMed]
- Suzanne, J.; Ferry, D.; Popovitcheva, O.; Shonija, N.K. Ice nucleation by kerosene soot under upper tropospheric conditions. Can. J. Phys. 2003, 81, 423–429. [Google Scholar] [CrossRef]
- Wu, S.; He, Z.; Zang, J.; Jin, S.; Wang, Z.; Wang, J.; Yao, Y.; Wang, J. Heterogeneous ice nucleation correlates with bulk-like interfacial water. Sci. Adv. 2019, 5, eaat9825. [Google Scholar] [CrossRef]
- Mochizuki, K.; Qiu, Y.; Molinero, V. Promotion of Homogeneous Ice Nucleation by Soluble Molecules. J. Am. Chem. Soc. 2017, 139, 17003–17006. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R. Radiative forcing and climate response. J. Geophys. Res. Atmos. 1997, 102, 6831–6864. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D.; Boucher, O. A satellite view of aerosols in the climate system. Nature 2002, 419, 215–223. [Google Scholar] [CrossRef]
- Lohmann, U.; Feichter, J. Global indirect aerosol effects: A review. Atmos. Chem. Phys. 2005, 5, 715–737. [Google Scholar] [CrossRef]
- Ramanathan, V.; Cess, R.D.; Harrison, E.F.; Minnis, P.; Barkstrom, B.R.; Ahmad, E.; Hartmann, D. Cloud-radiative forcing and climate—Results from the earth radiation budget experiment. Science 1989, 243, 57–63. [Google Scholar] [CrossRef]
- Ramanathan, V.; Crutzen, P.J.; Kiehl, J.T.; Rosenfeld, D. Atmosphere—Aerosols, climate, and the hydrological cycle. Science 2001, 294, 2119–2124. [Google Scholar] [CrossRef] [PubMed]
- Twomey, S. Pollution and planetary albedo. Atmos. Environ. 1974, 8, 1251–1256. [Google Scholar] [CrossRef]
- Kovacs, T.; Christenson, H.K. A two-step mechanism for crystal nucleation without supersaturation. Faraday Discuss. 2012, 159, 123–138. [Google Scholar] [CrossRef]
- David, R.O.; Marcolli, C.; Fahrni, J.; Qiu, Y.; Sirkin, Y.A.P.; Molinero, V.; Mahrt, F.; Bruhwiler, D.; Lohmann, U.; Kanji, Z.A. Pore condensation and freezing is responsible for ice formation below water saturation for porous particles. Proc. Natl. Acad. Sci. USA 2019, 116, 8184–8189. [Google Scholar] [CrossRef] [PubMed]
- Christenson, H.K. Two-step crystal nucleation via capillary condensation. CrystEngComm 2013, 15, 2030–2039. [Google Scholar] [CrossRef]
- Kovacs, T.; Meldrum, F.C.; Christenson, H.K. Crystal Nucleation without Supersaturation. J. Phys. Chem. Lett. 2012, 3, 1602–1606. [Google Scholar] [CrossRef]
- Campbell, J.M.; Christenson, H.K. Nucleation- and Emergence-Limited Growth of Ice from Pores. Phys. Rev. Lett. 2018, 120, 165701. [Google Scholar] [CrossRef]
- Campbell, J.M.; Meldrum, F.C.; Christenson, H.K. Observing the formation of ice and organic crystals in active sites. Proc. Natl. Acad. Sci. USA 2017, 114, 810–815. [Google Scholar] [CrossRef]
- Christenson, H.K. Liquid capillary condensates below the freezing-point. Phys. Rev. Lett. 1995, 74, 4675–4678. [Google Scholar] [CrossRef]
- Maeda, N.; Christenson, H. Direct observation of surface effects on the freezing and melting of an n-alkane. Colloids Surf. A 1999, 159, 135–148. [Google Scholar] [CrossRef]
- Li, T.; Donadio, D.; Galli, G. Ice nucleation at the nanoscale probes no man’s land of water. Nat. Comm. 2013, 4, 1–6. [Google Scholar] [CrossRef]
- Bai, G.; Gao, D.; Liu, Z.; Zhou, X.; Wang, J. Probing the critical nucleus size for ice formation with graphene oxide nanosheets. Nature 2019, 576, 437–441. [Google Scholar] [CrossRef] [PubMed]
- Oxtoby, D.W. Crystal nucleation in simple and complex fluids. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2003, 361, 419–427. [Google Scholar] [CrossRef] [PubMed]
- Bartell, L.S.; Huang, J.F. Supercooling of water below the anomalous range near 226 k. J. Phys. Chem. 1994, 98, 7455–7457. [Google Scholar] [CrossRef]
- Huang, J.F.; Bartell, L.S. Kinetics of Homogeneous Nucleation in the Freezing of Large Water Clusters. J. Phys. Chem. 1995, 99, 3924–3931. [Google Scholar] [CrossRef]
- Mayer, E.; Hallbrucker, A. Cubic ice from liquid water. Nature 1987, 325, 601–602. [Google Scholar] [CrossRef]
- Keyser, L.F.; Leu, M.T. Morphology of nitric-acid and water ice films. Microsc. Res. Tech. 1993, 25, 434–438. [Google Scholar] [CrossRef]
- Riikonen, M.; Sillanpaa, M.; Virta, L.; Sullivan, D.; Moilanen, J.; Luukkonen, I. Halo observations provide evidence of airborne cubic ice in the Earth’s atmosphere. Appl. Opt. 2000, 39, 6080–6085. [Google Scholar] [CrossRef]
- Goodman, J.; Toon, O.B.; Pueschel, R.F.; Snetsinger, K.G.; Verma, S. Antarctic stratospheric ice crystals. J. Geophys. Res. Atmos. 1989, 94, 16449–16457. [Google Scholar] [CrossRef]
- Suzuki, Y.; Duran, H.; Steinhart, M.; Kappl, M.; Butt, H.-J.; Floudas, G. Homogeneous Nucleation of Predominantly Cubic Ice Confined in Nanoporous Alumina. Nano Lett. 2015, 15, 1987–1992. [Google Scholar] [CrossRef]
- Lonsdale, K. The structure of ice. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1958, 247, 424–434. [Google Scholar]
- Naberukhin, Y.I.; Voloshin, V.P. Structure of ice Ih and ice Ic as described in the language of Delaunay simplices. Acta Crystallogr. Sect. A 2011, 67, 507–511. [Google Scholar] [CrossRef] [PubMed]
- Malkin, T.L.; Murray, B.J.; Salzmann, C.G.; Molinero, V.; Pickering, S.J.; Whale, T.F. Stacking disorder in ice I. Phys. Chem. Chem. Phys. 2015, 17, 60–76. [Google Scholar] [CrossRef] [PubMed]
- Lupi, L.; Hudait, A.; Peters, B.; Grunwald, M.; Mullen, R.G.; Nguyen, A.H.; Molinero, V. Role of stacking disorder in ice nucleation. Nature 2017, 551, 218–222. [Google Scholar] [CrossRef] [PubMed]
- Heymsfield, A.J.; Platt, C.M.R. A parameterization of the particle-size spectrum of ice clouds in terms of the ambient-temperature and the ice water-content. J. Atmos. Sci. 1984, 41, 846–855. [Google Scholar] [CrossRef]
- Korolev, A.; Leisner, T. Review of experimental studies of secondary ice production. Atmos. Chem. Phys. 2020, 20, 11767–11797. [Google Scholar] [CrossRef]
- Tobo, Y.; Adachi, K.; DeMott, P.J.; Hill, T.C.J.; Hamilton, D.S.; Mahowald, N.M.; Nagatsuka, N.; Ohata, S.; Uetake, J.; Kondo, Y.; et al. Glacially sourced dust as a potentially significant source of ice nucleating particles. Nat. Geosci. 2019, 12, 253–258. [Google Scholar] [CrossRef]
- Roberts, P.; Hallett, J. A laboratory study of ice nucleating properties of some mineral particulates. Q. J. R. Meteorol. Soc. 1968, 94, 25–34. [Google Scholar] [CrossRef]
- Edwards, G.R.; Evans, L.F. Mechanism of activation of ice nuclei. J. Atmos. Sci. 1971, 28, 1443–1447. [Google Scholar] [CrossRef]
- Edwards, G.R.; Evans, L.F.; Zipper, A.F. 2-dimensional phase changes in water adsorbed on ice-nucleating substrates. Trans. Faraday Soc. 1970, 66, 220–234. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation; Reidel: Dordrecht, The Netherlands, 1978. [Google Scholar]
- CRC Handbook of Chemistry and Physics, 95th ed.; CRC Press: Boca Raton, FL, USA, 2014–2015.
- Rosinski, J. Latent ice-forming nuclei in the Pacific Northwest. Atmos. Res. 1991, 26, 509–523. [Google Scholar] [CrossRef]
- Rosinski, J.; Morgan, G. Cloud condensation nuclei as a source of ice-forming nuclei in clouds. J. Aerosol Sci. 1991, 22, 123–133. [Google Scholar] [CrossRef]
- Seeley, L.H.; Seidler, G.T. Preactivation in the nucleation of ice by Langmuir films of aliphatic alcohols. J. Chem. Phys. 2001, 114, 10464–10470. [Google Scholar] [CrossRef]
- Marcolli, C.; Nagare, B.; Welti, A.; Lohmann, U. Ice nucleation efficiency of AgI: Review and new insights. Atmos. Chem. Phys. 2016, 16, 8915–8937. [Google Scholar] [CrossRef]
- Fukuta, N. Study of mechanism of contact ice nucleation. J. Atmos. Sci. 1975, 32, 1597–1603. [Google Scholar] [CrossRef]
- Shaw, R.A.; Durant, A.J.; Mi, Y. Heterogeneous surface crystallization observed in undercooled water. J. Phys. Chem. B 2005, 109, 9865–9868. [Google Scholar] [CrossRef]
- Gurganus, C.; Kostinski, A.B.; Shaw, R.A. High-Speed Imaging of Freezing Drops: Still No Preference for the Contact Line. J. Phys. Chem. C 2013, 117, 6195–6200. [Google Scholar] [CrossRef]
- Gurganus, C.W.; Charnawskas, J.C.; Kostinski, A.B.; Shaw, R.A. Nucleation at the Contact Line Observed on Nanotextured Surfaces. Phys. Rev. Lett. 2014, 113, 235701. [Google Scholar] [CrossRef]
- Djikaev, Y.S.; Ruckenstein, E. Thermodynamics of Heterogeneous Crystal Nucleation in Contact and Immersion Modes. J. Phys. Chem. A 2008, 112, 11677–11687. [Google Scholar] [CrossRef]
- Djikaev, Y.S.; Tabazadeh, A.; Hamill, P.; Reiss, H. Thermodynamic conditions for the surface-stimulated crystallization of atmospheric droplets. J. Phys. Chem. A 2002, 106, 10247–10253. [Google Scholar] [CrossRef]
- Sear, R.P. Nucleation at contact lines where fluid-fluid interfaces meet solid surfaces. J. Phys. Condes. Matter 2007, 19, 466106. [Google Scholar] [CrossRef]
- Whale, T.F.; Holden, M.A.; Wilson, T.W.; O’Sullivan, D.; Murray, B.J. The enhancement and suppression of immersion mode heterogeneous ice-nucleation by solutes. Chem. Sci. 2018, 9, 4142–4151. [Google Scholar] [CrossRef]
- Tabazadeh, A.; Djikaev, Y.S.; Reiss, H. Surface crystallization of supercooled water in clouds. Proc. Natl. Acad. Sci. USA 2002, 99, 15873–15878. [Google Scholar] [CrossRef]
- Mendez-Villuendas, E.; Bowles, R.K. Surface nucleation in the freezing of gold nanoparticles. Phys. Rev. Lett. 2007, 98, 185503. [Google Scholar] [CrossRef]
- Durant, A.J.; Shaw, R.A. Evaporation freezing by contact nucleation inside-out. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Yang, F.; Cantrell, W.H.; Kostinski, A.B.; Shaw, R.A.; Vogelmann, A.M. Is Contact Nucleation Caused by Pressure Perturbation? Atmosphere 2020, 11, 1. [Google Scholar] [CrossRef]
- Duft, D.; Leisner, T. Laboratory evidence for volume-dominated nucleation of ice in supercooled water microdroplets. Atmos. Chem. Phys. 2004, 4, 1997–2000. [Google Scholar] [CrossRef]
- Ocko, B.M.; Wu, X.Z.; Sirota, E.B.; Sinha, S.K.; Gang, O.; Deutsch, M. Surface freezing in chain molecules: Normal alkanes. Phys. Rev. E 1997, 55, 3164–3182. [Google Scholar] [CrossRef]
- Gang, O.; Wu, X.Z.; Ocko, B.M.; Sirota, E.B.; Deutsch, M. Surface freezing in chain molecules. II. Neat and hydrated alcohols. Phys. Rev. E 1998, 58, 6086–6100. [Google Scholar] [CrossRef]
- Maeda, N.; Yaminsky, V. Surface supercooling and stability of n-alkane films. Phys. Rev. Lett. 2000, 84, 698–700. [Google Scholar] [CrossRef]
- Merkl, C.; Pfohl, T.; Riegler, H. Influence of the molecular ordering on the wetting of SiO2/air interfaces by alkanes. Phys. Rev. Lett. 1997, 79, 4625–4628. [Google Scholar] [CrossRef]
- Maeda, N.; Kohonen, M.M.; Christenson, H.K. Phase behavior of long-chain n-alkanes at one and between two mica surfaces. J. Phys. Chem. B 2001, 105, 5906–5913. [Google Scholar] [CrossRef]
- Navascues, G.; Tarazona, P. Line Tension Effects in Heterogeneous Nucleation Theory. J. Chem. Phys. 1981, 75, 2441–2446. [Google Scholar] [CrossRef]
- Chatain, D.; Wynblatt, P. Anisotropy of Wetting of Pb Crystals by Their Own Melt and by Liquid Ga-Pb Alloys; Springer: Boston, MA, USA, 1997; pp. 53–58. [Google Scholar]
- Bradley, R.S.; Shellard, A.D. The Rate of Evaporation of Droplets. III. Vapour Pressures and Rates of Evaporation of Straight-Chain Paraffin Hydrocarbons. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1949, 198, 239–251. [Google Scholar] [CrossRef]
- Elbaum, M.; Lipson, S.G.; Dash, J.G. Optical study of surface melting on ice. J. Cryst. Growth 1993, 129, 491–505. [Google Scholar] [CrossRef]
- Slater, B.; Michaelides, A. Surface premelting of water ice. Nat. Rev. Chem. 2019, 3, 172–188. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maeda, N. Brief Overview of Ice Nucleation. Molecules 2021, 26, 392. https://doi.org/10.3390/molecules26020392
Maeda N. Brief Overview of Ice Nucleation. Molecules. 2021; 26(2):392. https://doi.org/10.3390/molecules26020392
Chicago/Turabian StyleMaeda, Nobuo. 2021. "Brief Overview of Ice Nucleation" Molecules 26, no. 2: 392. https://doi.org/10.3390/molecules26020392
APA StyleMaeda, N. (2021). Brief Overview of Ice Nucleation. Molecules, 26(2), 392. https://doi.org/10.3390/molecules26020392




