Spectroscopic and Structural Study of a New Conducting Pyrazolium Salt
Abstract
:1. Introduction
2. Results and Discussions
2.1. Crystallographic Investigations
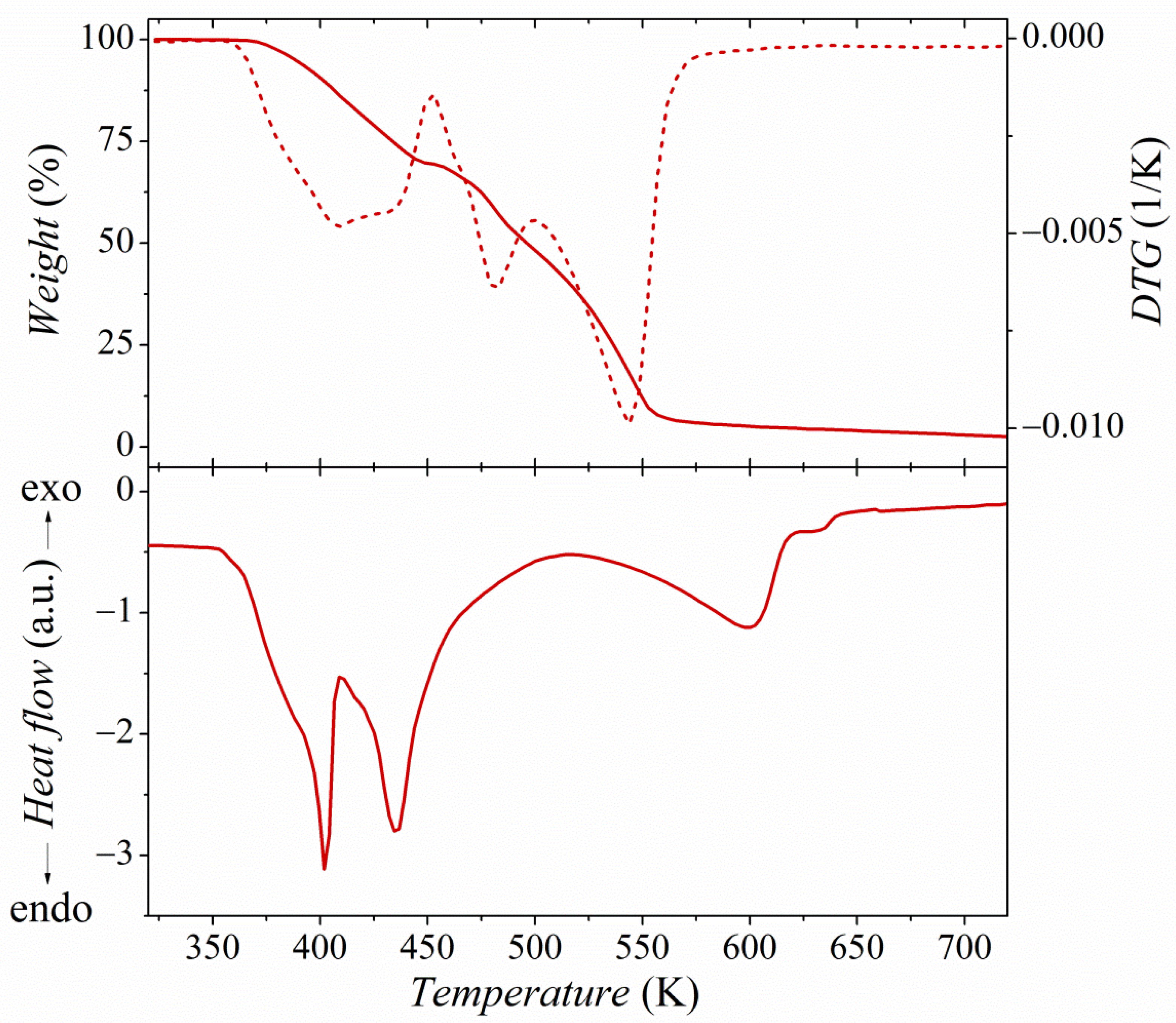
2.2. Thermal Properties Analysis
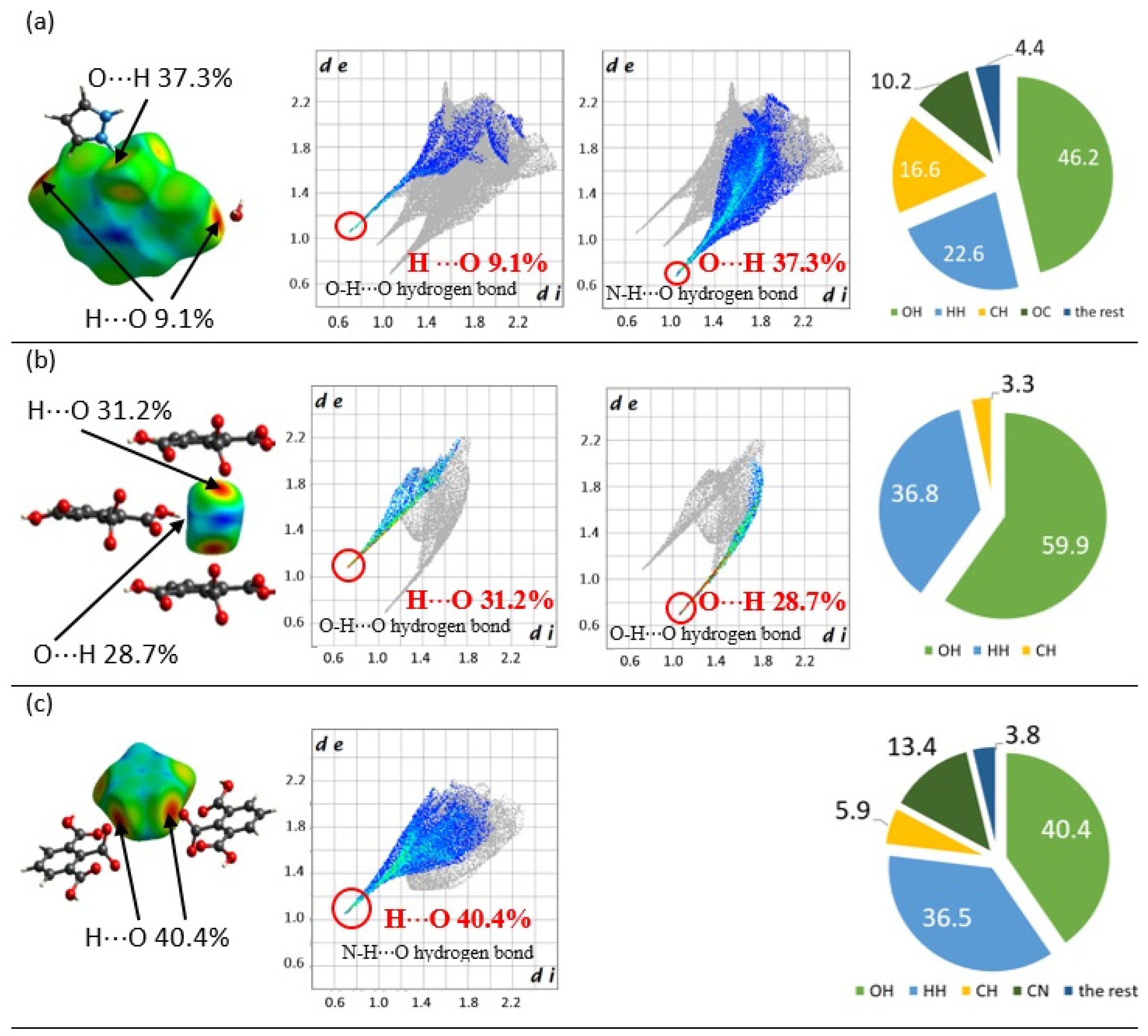
2.3. Intermolecular Interactions Analysis
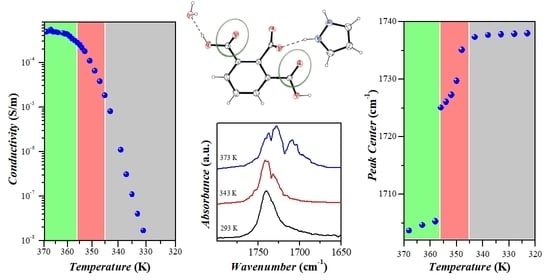
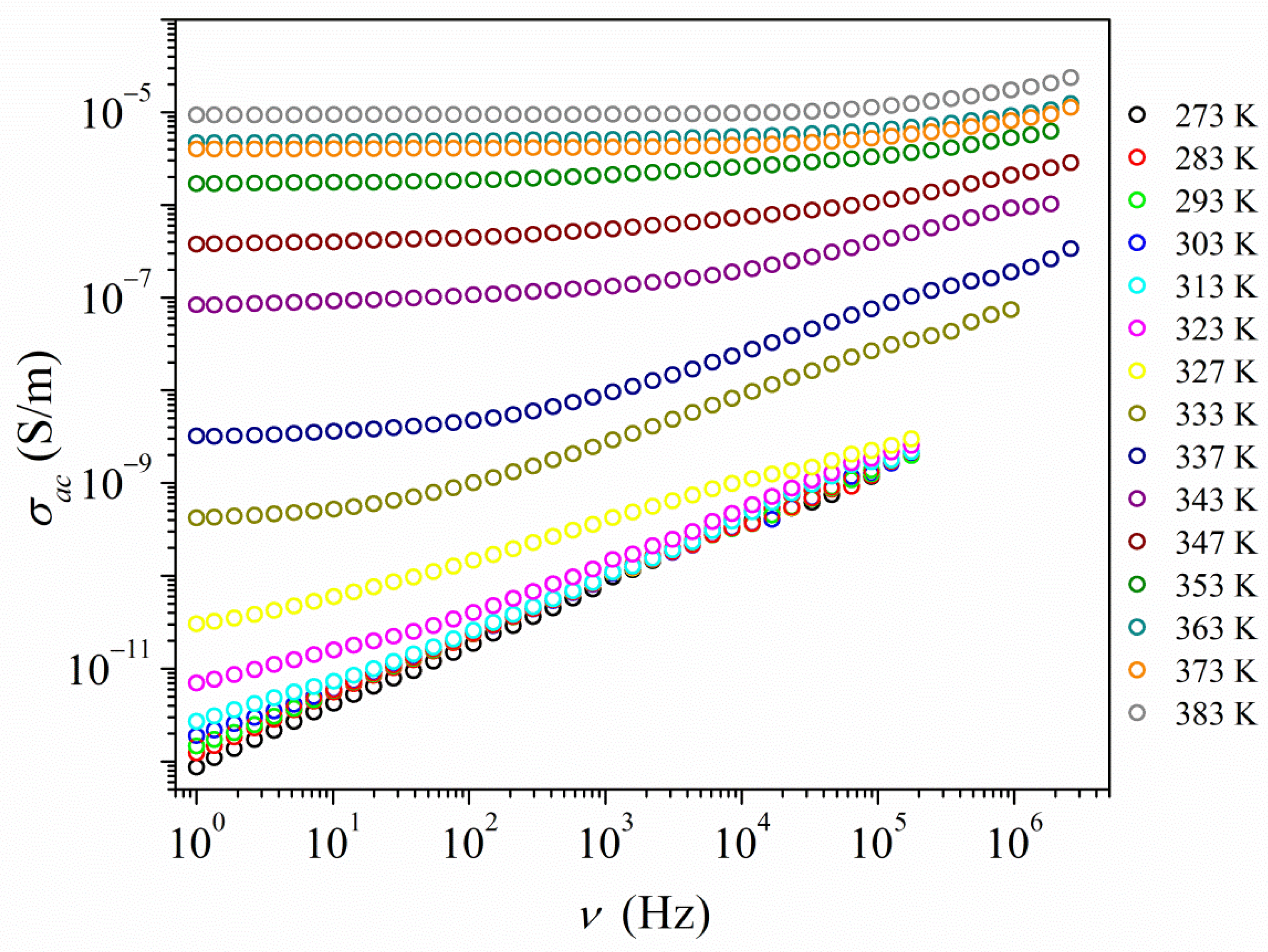
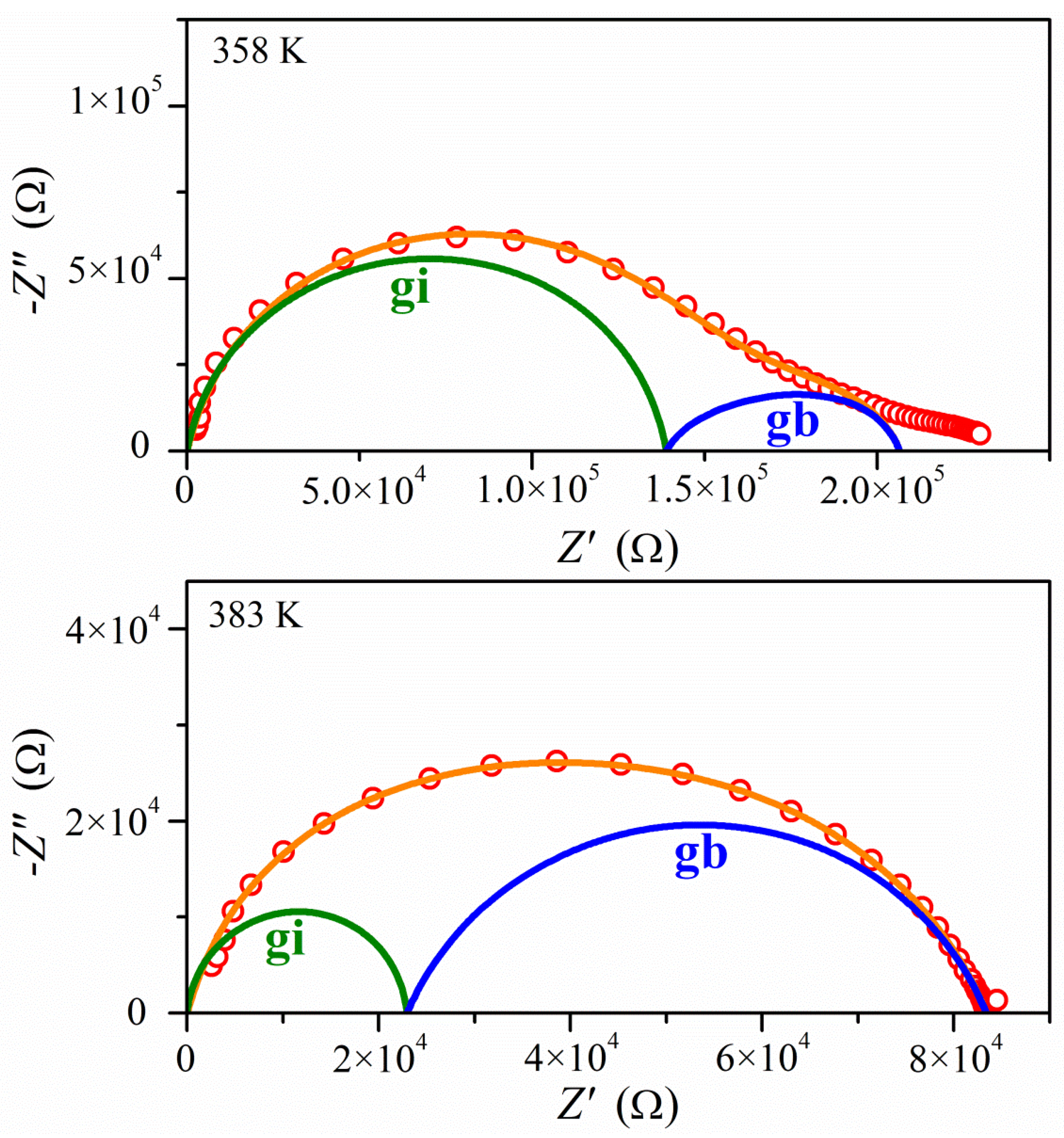
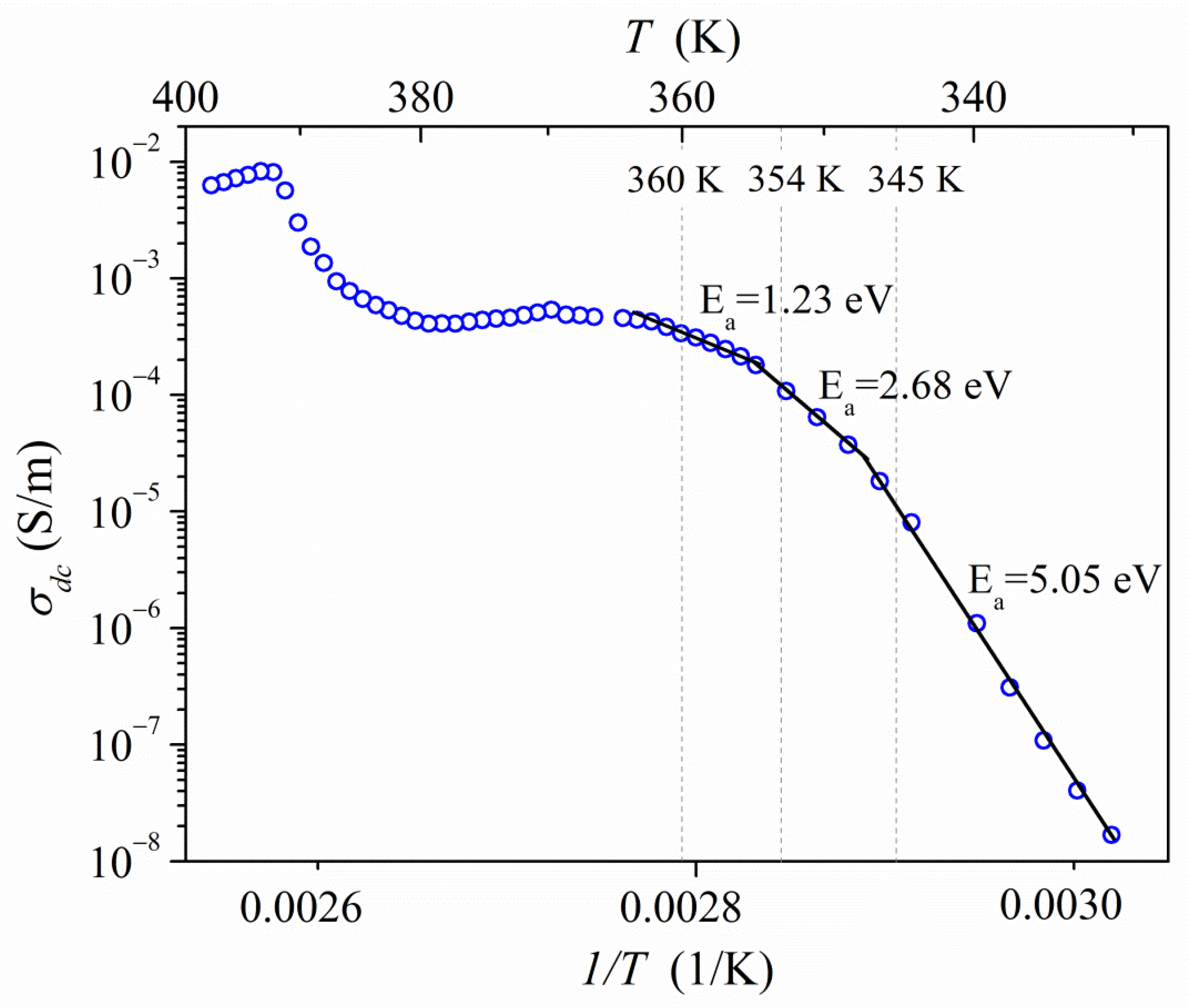
2.4. Electrical Properties Analysis
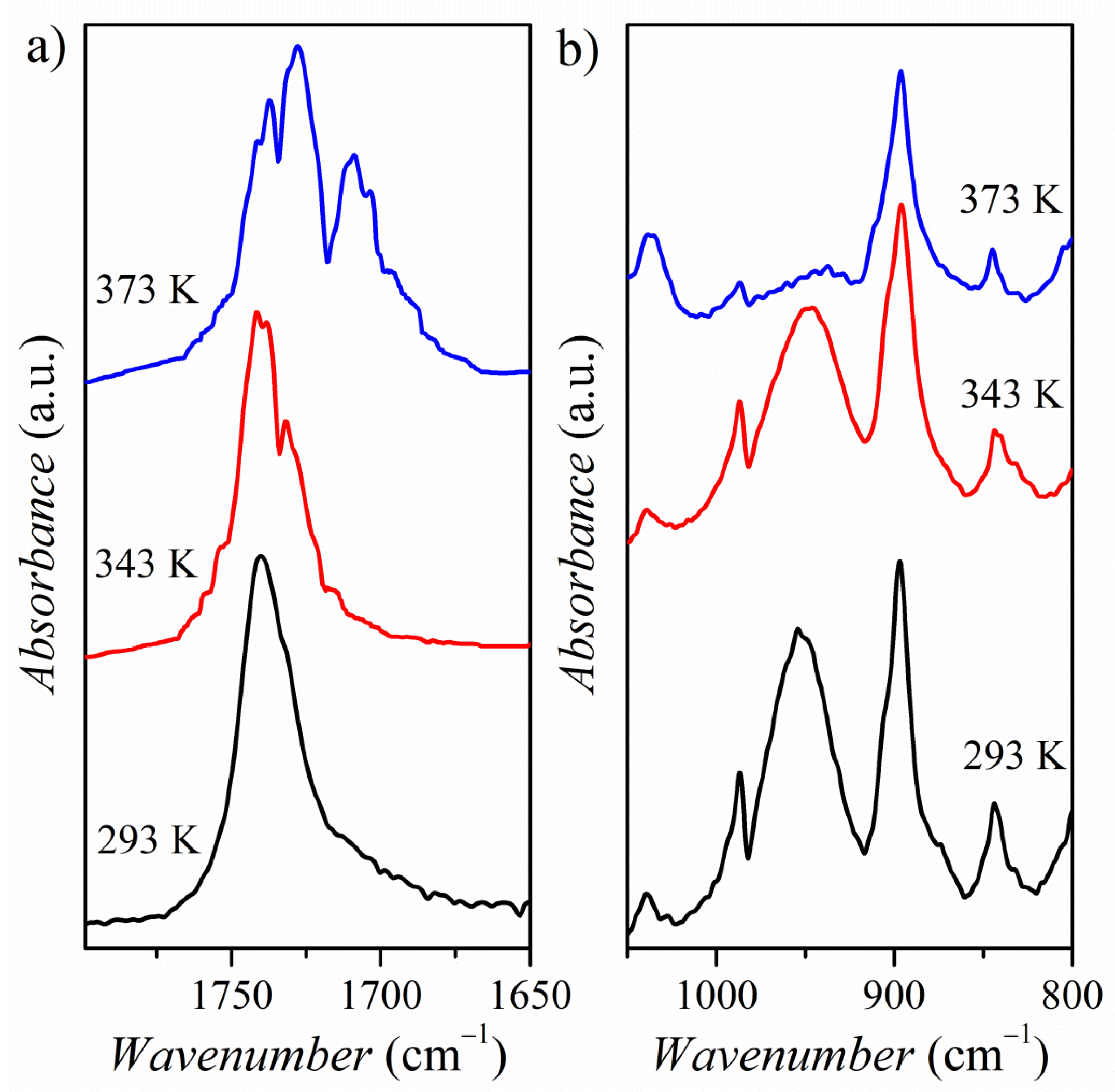
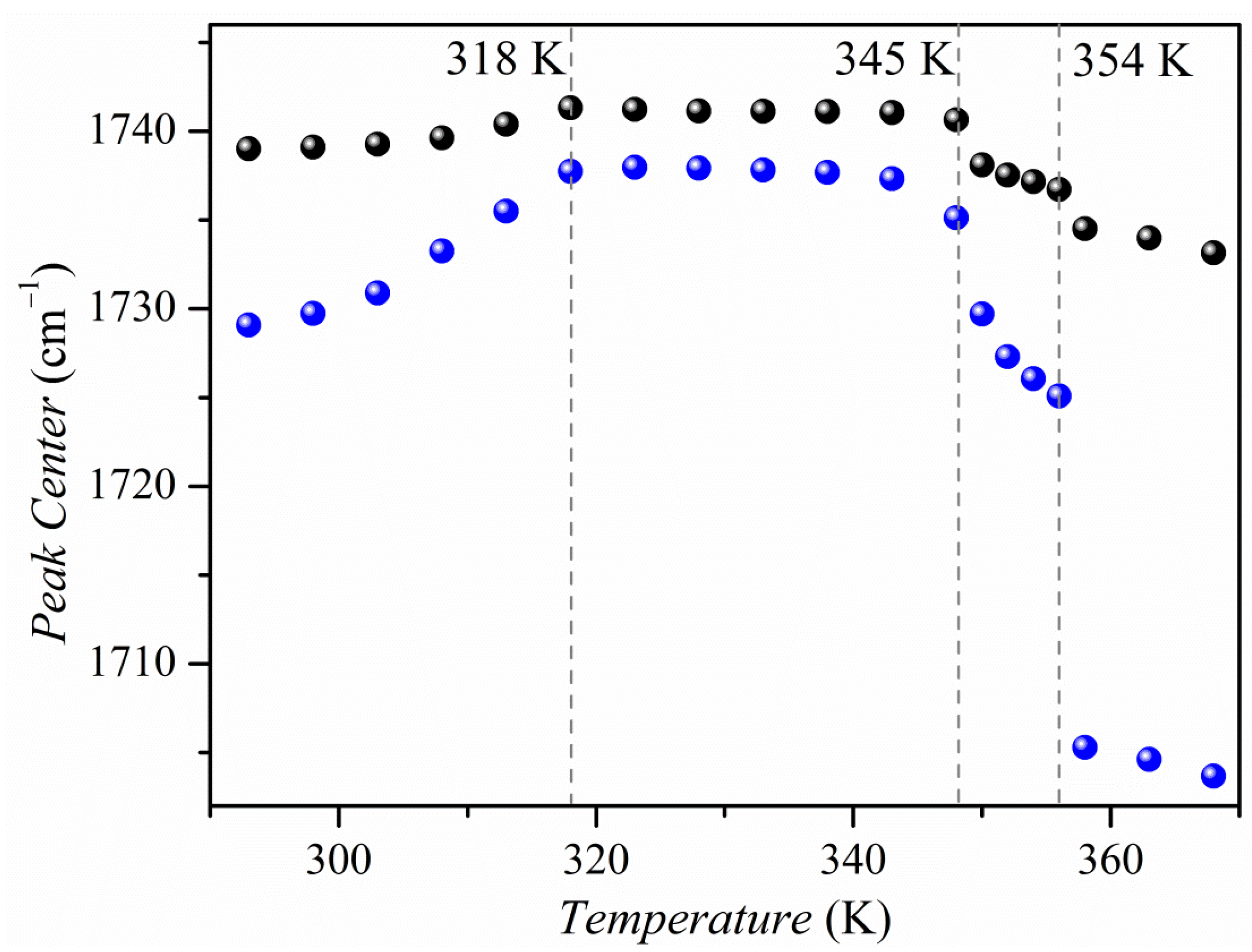
2.5. Vibrational Analysis
3. Materials and Methods
3.1. Experimental Section
3.1.1. Synthesis
3.1.2. Crystal Structure Determination
3.1.3. DSC/TGA Analysis
3.1.4. FT-IR and Raman Spectroscopy
3.1.5. Impedance Spectroscopy
3.2. Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Wang, Y.; Chen, K.S.; Mishler, J.; Chan Cho, S.; Adroher, X.C. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research. Appl. Energy 2011, 88, 981–1007. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Aili, D.; Savinell, R.F.; Jensen, J.O. Acid–Base Chemistry and Proton Conductivity. In High-Temperature Polymer Electrolyte Membrane Fuel Cells; Springer: Cham, Switzerland, 2016; pp. 37–57. [Google Scholar]
- Haile, S.M. Fuel cell materials and components. Acta Mater. 2003, 51, 5981–6000. [Google Scholar] [CrossRef]
- Ma, N.; Kosasang, S.; Yoshida, A.; Horike, S. Proton-conductive coordination polymer glass for solid-state anhydrous proton batteries. Chem. Sci. 2021, 12, 5818–5824. [Google Scholar] [CrossRef]
- Sunairi, Y.; Ueda, A.; Yoshida, J.; Suzuki, K.; Mori, H. Anisotropic Proton Conductivity Arising from Hydrogen-Bond Patterns in Anhydrous Organic Single Crystals, Imidazolium Carboxylates. J. Phys. Chem. C 2018, 122, 11623–11632. [Google Scholar] [CrossRef]
- Kreuer, K.D.; Fuchs, A.; Ise, M.; Spaeth, M.; Maier, J. Imidazole and pyrazole-based proton conducting polymers and liquids. J. Electrochim. Acta 1998, 43, 1281–1288. [Google Scholar] [CrossRef]
- Haile, S.M.; Boysen, D.A.; Chisholm, C.R.I.; Merle, R.B. Solid acids as fuel cell electrolytes. Nature 2001, 410, 910–913. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhang, Y.; Ribeiorinha, P.; Li, H.; Kong, X.; Boaventura, M. A proton conductor electrolyte based on molten CsH5(PO4)2 for intermediate-temperature fuel cells. RSC Adv. 2018, 8, 5225–5232. [Google Scholar] [CrossRef] [Green Version]
- Schmidt-Rohr, K.; Chen, Q. Parallel cylindrical water nanochannels in Nafion fuel-cell membranes. Nat. Mater. 2008, 7, 75–83. [Google Scholar] [CrossRef]
- Grubb, W.T.; Niedrach, L.W. Batteries with Solid Ion-Exchange Membrane Electrolytes: II. Low-Temperature Hydrogen-Oxygen Fuel Cells. J. Electrochem. Soc. 1960, 107, 131. [Google Scholar] [CrossRef]
- Mauritz, K.A.; Moore, R.B. State of Understanding of Nafion. Chem. Rev. 2004, 104, 4535–4586. [Google Scholar] [CrossRef]
- Pogorzelec-Glaser, K.; Garbarczyk, J.; Pawlaczyk, C.; Markiewicz, E. Electrical conductivity in new imidazolium salts of dicarboxylic acids. Mater. Sci. Pol. 2006, 24, 245. [Google Scholar]
- Higashino, T.; Ueda, A.; Yoshida, J.; Mori, H. Improved stability of a metallic state in benzothienobenzothiophene-based molecular conductors: An effective increase of dimensionality with hydrogen bonds. Chem. Commun. 2017, 53, 3426–3429. [Google Scholar] [CrossRef]
- Zięba, S.; Dubis, A.; Ławniczak, P.; Gzella, A.; Pogorzelec-Glaser, K.; Łapiński, A. Effect of counter ions on physical properties of imidazole-based proton conductors. Electrochim. Acta 2019, 306, 575–589. [Google Scholar] [CrossRef]
- Zięba, S.; Dubis, A.T.; Gzella, A.K.; Ławniczak, P.; Pogorzelec-Glaser, K.; Łapiński, A. Toward a new type of proton conductor based on imidazole and aromatic acids. Phys. Chem. Chem. Phys. 2019, 21, 17152–17162. [Google Scholar] [CrossRef] [PubMed]
- Farrington, G.C.; Briant, J.L. Fast Ionic Transport in Solids. Science 1979, 204, 1371–1379. [Google Scholar] [CrossRef] [PubMed]
- Howe, A.T.; Shilton, M.G. Studies of layered uranium(VI) compounds. I. High proton conductivity in polycrystalline hydrogen uranyl phosphate tetrahydrate. J. Solid Stare Chem. 1979, 28, 345–361. [Google Scholar] [CrossRef]
- Krishtalik, L.I. The mechanism of the proton transfer: An outline. BBA-Bioenerg. 2000, 1458, 6–27. [Google Scholar] [CrossRef] [Green Version]
- Widelicka, M.; Pogorzelec-Glaser, K.; Pietraszko, A.; Ławniczak, P.; Pankiewicz, R.; Łapiński, A. Order–disorder phase transition in an anhydrous pyrazole-based proton conductor: The enhancement of electrical transport properties. Phys. Chem. Chem. Phys. 2017, 19, 25653. [Google Scholar] [CrossRef] [Green Version]
- Zięba, S.; Mizera, A.; Pogorzelec-Glaser, K.; Łapiński, A. Proton conducting system (ImH2)2SeO4·2H2O investigated with vibrational spectroscopy. Spectrochim. Acta Part A 2017, 180, 224–233. [Google Scholar] [CrossRef] [PubMed]
- Phair, J.W.; Badwal, S.P.S. Review of proton conductors for hydrogen separation. Ionics 2006, 12, 103–115. [Google Scholar] [CrossRef] [Green Version]
- Vairam, S.; Govindarajan, S. New hydrazinium salts of benzene tricarboxylic and tetracarboxylic acids-preparation and their thermal studies. Thermochim. Acta 2004, 414, 263–270. [Google Scholar] [CrossRef]
- Gao, L.; Hu, Y.; Zhang, H.; Liu, Y.; Song, Z.; Dai, Y. DFT computational study on decarboxylation mechanism of salicylic acid and its derivatives in the anionic state. J. Mol. Struct. 2016, 1116, 56–61. [Google Scholar] [CrossRef]
- Spackman, M.A.; McKinnon, J.J. Fingerprinting intermolecular interactions in molecular crystals. CrystEngComm 2002, 4, 378–392. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules A Quantum Theory; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Matta, C.; Boyd, R.J. Quantum Theory of Atoms in Molecule: Recent Progress in Theory and Application; Wiley-VCH: New York, NY, USA, 2007. [Google Scholar]
- Koch, U.; Popelier, P.L.A. Characterization of C‒H‒O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
- Rozas, I.; Alkorta, I.; Elguero, J. Behavior of ylides containing N, O, and C atoms as hydrogen bond acceptors. J. Am. Chem. Soc. 2000, 122, 11154–11161. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. Chemical Bonds without Bonding Electron Density—Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem. Int. Ed. Engl. 1984, 23, 627. [Google Scholar] [CrossRef]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Grabowski, S.J. Hydrogen bonding strength—measures based on geometric and topological parameters. J. Phys. Org. Chem. 2004, 17, 18–31. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R.J. (Eds.) Impedance Spectroscopy Theory, Experiment and Applications; Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Dijk, T.; Burggraaf, A.J. Grain boundary effects on ionic conductivity in ceramic GdxZr1–xO2–(x/2) solid solutions. Phys. Stat. Sol. (A) 1981, 63, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Baran, J.; Czapla, Z.; Ilczyszyn, M.M.; Ratajczak, H. The infrared and polarized Raman spectra of ferroelectric RbHSeO4. Acta Phys. Pol. A 1981, 59, 753–764. [Google Scholar]
- Baran, J.; Czapla, Z.; Ratajczak, H. Polarized infrared spectra of ferroelectric RbHSeO4 single crystal. Acta Phys. Pol. A 1986, 70, 389–402. [Google Scholar]
- Baran, J.; Barnes, A.J.; Marchewka, M.K.; Pietraszko, A.; Ratajczak, H. Structure and vibrational spectra of the bis(betaine)-selenic acid molecular crystal. J. Mol. Struct. 1997, 416, 33–42. [Google Scholar] [CrossRef]
- Fillaux, F.; Marchon, B.; Novak, A.; Tomkinson, J. Proton dynamics in the hydrogen bond. Inelastic neutron scattering by single crystals of CsH2PO4 at 20 K. Chem. Phys. 1989, 130, 257–270. [Google Scholar] [CrossRef]
- Grabowski, S.J. Hydrogen Bonding-New Insights; Springer: Dordrecht,.The Netherlands, 2006. [Google Scholar]
- CrysAlis PRO, Version 1.171.38.46; Rigaku Oxford Diffraction: Yarnton, UK, 2015.
- Sheldrick, G.M. A short history of SHELX. Acta Cryst. 2008, 64, 112–122. [Google Scholar] [CrossRef] [Green Version]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Farrugia, L.J. WinGX and ORTEP for windows: An update. J. Appl. Cryst. 2012, 45, 849–854. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Spek, A.L. Structure validation in chemical crystallography. Acta Cryst. D 2009, 65, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Wolff, S.K.; Grimwood, D.J.; McKinnon, J.J.; Turner, M.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer 3.1; University of Western Australia: Perth, Australia, 2012. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Chai, J.D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef] [PubMed]
- Todd, A.; Keith, T.K. AIMALL, Version 10.05.04; Gristmill Software: Overland Park, KS, USA, 2017. [Google Scholar]
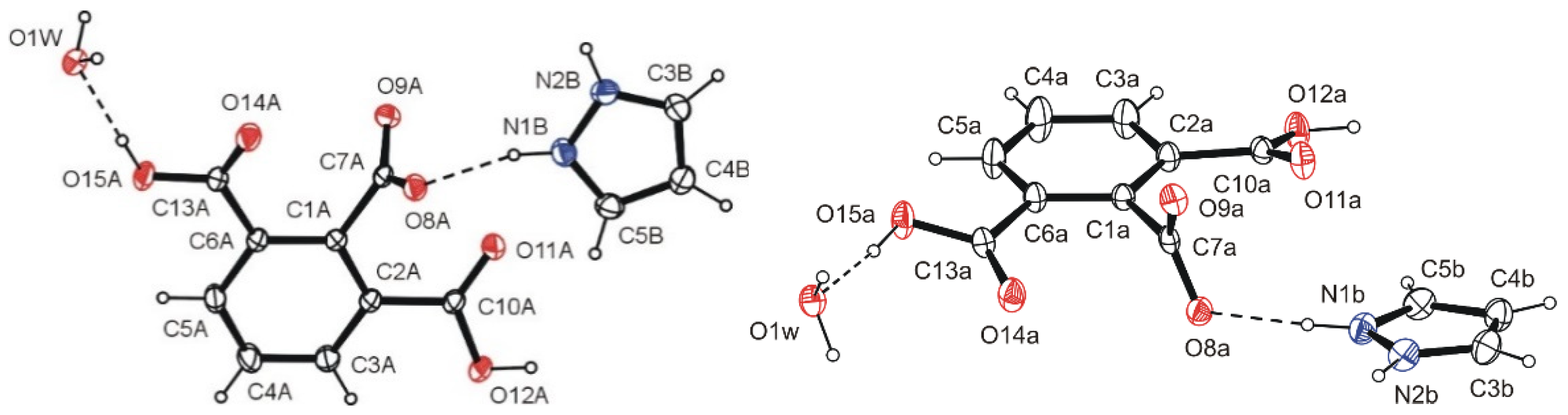





| D—H∙∙∙A | D—H | H∙∙∙A | D∙∙∙A | D—H∙∙∙A |
|---|---|---|---|---|
| N1b—H1b∙∙∙O8a | 0.89(2) | 1.85(2) | 2.7137(17) | 165(2) |
| N2b—H2b∙∙∙O9a i | 0.91(2) | 1.87(2) | 2.7581(17) | 165(2) |
| O12a—H12a∙∙∙O1w ii | 0.90(2) | 1.82(2) | 2.7217(15) | 175(3) |
| O15a—H15a∙∙∙O1w | 0.90(3) | 1.83(2) | 2.7164(15) | 172(3) |
| O1w—H1wA∙∙∙O9a iv | 0.92(3) | 1.86(3) | 2.7695(16) | 171(3) |
| O1w—H1wB∙∙∙O8a iii | 0.92(3) | 1.86(3) | 2.7695(16) | 171(3) |
| C3b—H3b∙∙∙O14a i | 0.93 | 2.46 | 3.057(2) | 122 |
| C3b—H3b∙∙∙O14a v | 0.93 | 2.55 | 3.072(2) | 116 |
| C5b—H5b∙∙⋅O11a | 0.93 | 2.56 | 3.032(2) | 112 |
| C5b—H5b∙∙O11a vi | 0.93 | 2.35 | 3.071(2) | 134 |
| D‒H…A | D-H…A | |||||||
|---|---|---|---|---|---|---|---|---|
| N35—H⸱⸱⸱O30 | 1.862 | 164.8 | 0.918 | 0.0305 | 0.1106 | 0.0262 | −0.0250 | 0.0014 |
| N33—H⸱⸱⸱O29 | 1.851 | 164.1 | 0.886 | 0.0315 | 0.1202 | 0.0283 | −0.0266 | 0.0017 |
| O1—H⸱⸱⸱O29 | 1.875 | 175.8 | 0.900 | 0.0296 | 0.1087 | 0.0258 | −0.0243 | 0.0014 |
| O4—H⸱⸱⸱O30 | 1.857 | 171.1 | 0.919 | 0.0307 | 0.1106 | 0.0265 | −0.0253 | 0.0012 |
| O40—H⸱⸱⸱O5 | 1.804 | 172.6 | 0.918 | 0.0340 | 0.1262 | 0.0309 | −0.0302 | 0.0007 |
| O53—H⸱⸱⸱O38 | 1.815 | 174.5 | 0.911 | 0.0333 | 0.1241 | 0.0302 | −0.0293 | 0.0009 |
| C58—H⸱⸱⸱O51 | 2.457 | 122.3 | 0.931 | 0.0099 | 0.0375 | 0.0077 | −0.0061 | 0.0016 |
| C57—H⸱⸱⸱O57 | 2.556 | 112.2 | 0.929 | 0.0089 | 0.0346 | 0.0071 | −0.0056 | 0.0015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zięba, S.; Piotrowska, A.; Mizera, A.; Ławniczak, P.; Markiewicz, K.H.; Gzella, A.; Dubis, A.T.; Łapiński, A. Spectroscopic and Structural Study of a New Conducting Pyrazolium Salt. Molecules 2021, 26, 4657. https://doi.org/10.3390/molecules26154657
Zięba S, Piotrowska A, Mizera A, Ławniczak P, Markiewicz KH, Gzella A, Dubis AT, Łapiński A. Spectroscopic and Structural Study of a New Conducting Pyrazolium Salt. Molecules. 2021; 26(15):4657. https://doi.org/10.3390/molecules26154657
Chicago/Turabian StyleZięba, Sylwia, Agata Piotrowska, Adam Mizera, Paweł Ławniczak, Karolina H. Markiewicz, Andrzej Gzella, Alina T. Dubis, and Andrzej Łapiński. 2021. "Spectroscopic and Structural Study of a New Conducting Pyrazolium Salt" Molecules 26, no. 15: 4657. https://doi.org/10.3390/molecules26154657
APA StyleZięba, S., Piotrowska, A., Mizera, A., Ławniczak, P., Markiewicz, K. H., Gzella, A., Dubis, A. T., & Łapiński, A. (2021). Spectroscopic and Structural Study of a New Conducting Pyrazolium Salt. Molecules, 26(15), 4657. https://doi.org/10.3390/molecules26154657