Formulation Improvements in the Applications of Surfactant–Oil–Water Systems Using the HLDN Approach with Extended Surfactant Structure
Abstract
:1. Introduction
| Extended Surfactant 1 | σ | k | SCPN = σ/k * | Author and Year | Ref. |
|---|---|---|---|---|---|
| S/12/6/2/SO4 | −1.43 | 0.075 | −19.1 | Miñana-Perez, 1995 | [13] |
| S/12/10/2/SO4 | −0.3 | 0.11 | −2.7 | Miñana-Perez, 1995 | [13] |
| S/12/14/2/SO4 | 1.21 | 0.16 | 7.6 | Miñana-Perez, 1995 | [13] |
| A/14−15/8/0/SO4 | 0.16 | 0.13 | 1.2 | Witthayapanyanon, 2006 | [30] |
| A/10/18/2/SO4 | 0.57 | 0.053 | 10.8 | Do, 2009 | [39] |
| A/14−15/4/0/SO4 | −0.18 | 0.11 | −1.6 | Velásquez, 2010 | [24] |
| A/16−17/4/0/SO4 | −0.29 | 0.11 | −2.6 | Velásquez, 2010 | [24] |
| A/12−13/8/0/SO4 | −0.52 | 0.08 | −6.5 | Velásquez, 2010 | [24] |
| A/12−13/4/0/SO4 | −0.98 | 0.11 | −8.9 | Velásquez, 2010 | [24] |
| Chen/8/9/3/SO4 | −0.39 | 0.17 | −2.3 | Chen, 2019 | [40] |
| A/12−13/4/0/SO4 | −1.55 | 0.049 | −31.6 | Wang, 2019 | [41] |
| He/13/2/0/SO4 | −1.8 | 0.056 | −32.1 | He, 2019 | [42] |
| A/10/4/0/SO4 | −2.24 | 0.053 | −42.3 | Phaodee, 2020 | [43] |
2. Historical Introduction on Formulation Concepts
The Unidimensional Scan of a Formulation Variable
3. Multivariable Scans and Generalized HLD Expression for Optimum Formulation
3.1. The Normalized Hydrophilic Lipophilic Deviation (HLDN) Equation
3.2. The Normalized Surfactant Characteristic Parameter (SCPN)
4. Performance Issues
4.1. Attaining a High Performance through a Double Formulation Change at Both Sides of the Interface
4.2. Attaining a High Performance through a Double Formulation Change at One Side of the Interface
4.3. Additional Strategies to Increase Performance
5. Lipophilic and Hydrophilic Linkers, and Extended Surfactants
5.1. The Lipophilic Linker
5.2. The Hydrophilic Linker
5.3. The Extended Surfactant with an Intramolecular PO Extension
5.4. The Increased Performance of Extended Surfactant Systems with Polar Oils and Crude Oils
5.5. The Application of the HLDN in Extended Surfactant Systems
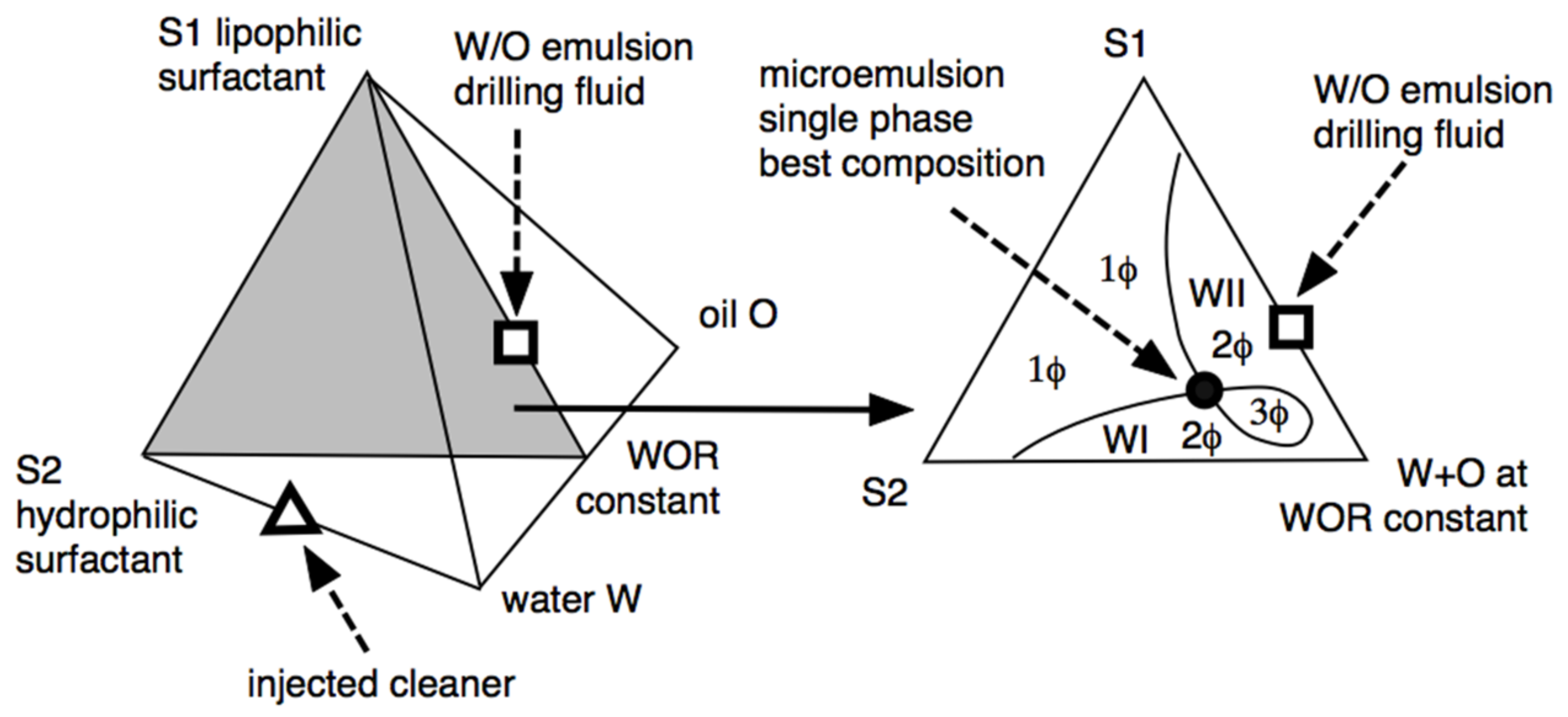
6. Extended Surfactants for Drilling Fluids Applications
6.1. Best Solubilization Drilling Fluid Cleaning through Single-Phase Wiping (at Optimum)
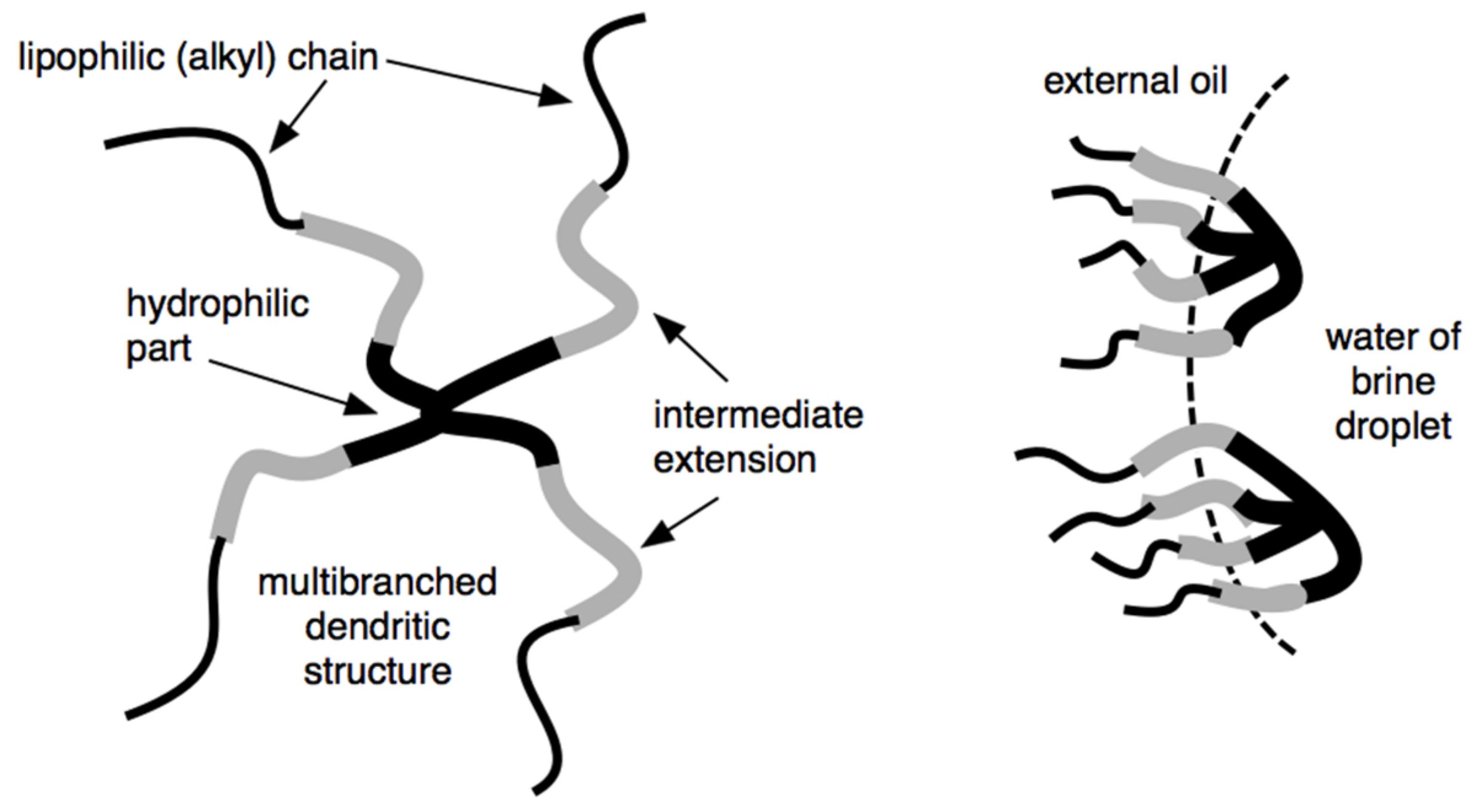
6.2. Extended Dendritic Surfactant for the Formulation of Oil-Based Muds and for Their Removal from the Well by Using a Fluid with a More Hydrophilic Extended Surfactant
7. Improved Performance and Robustness in Crude Oil Dewatering and Dehydration
7.1. The Application of Extended Surfactants for Efficient Breaking of Crude Oil in Water Emulsions
7.2. Extended Surfactants Robust Systems to Decrease Interfacial Elasticity at Low Demulsifier Concentration
8. Future Perspective
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salager, J.-L.; Antón, R.E.; Sabatini, D.A.; Harwell, J.H.; Acosta, E.; Tolosa, L.I. Enhancing solubilization in microemulsions-State of the art and current trends. J. Surfactants Deterg. 2005, 8, 3. [Google Scholar] [CrossRef]
- Salager, J.-L.; Forgiarini, A.; Marquez, R. Extended Surfactants Including an Alkoxylated Central Part Intermediate Producing a Gradual Polarity Transition—A Review of the Properties Used in Applications Such as Enhanced Oil Recovery and Polar Oil Solubilization in Microemulsions. J. Surfactants Deterg. 2019, 22. [Google Scholar] [CrossRef]
- Bourrel, M.; Lipow, A.M.; Wade, W.H.; Schechter, R.S.; Salager, J.-L. Properties Of Amphiphile/Oil/Water Systems At An Optimum Formulation For Phase Behavior. In Proceedings of the SPE Annual Fall Technical Conference and Exhibition, Houston, TX, USA, 1–3 October 1978. [Google Scholar]
- Doe, P.; El-Emary, M.; Wade, W.H.; Schechter, R.S. Surfactants for producing low interfacial tensions I: Linear alkyl benzene sulfonates. J. Am. Oil Chem. Soc. 1977, 54, 570–577. [Google Scholar] [CrossRef]
- Salager, J.-L. Physico-Chemical Properties of Surfactant-Water-Oil Mixtures: Phase Behavior, Micro-Emulsion Formation and Interfacial Tension. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1977. [Google Scholar]
- Carmona, I.; Schechter, R.S.; Wade, W.H.; Weerasooriya, U. Ethoxylated Oleyl Sulfonates As Model Compounds for Enhanced Oil Recovery. Soc. Pet. Eng. J. 1985, 25, 351–357. [Google Scholar] [CrossRef]
- Abe, M.; Schechter, D.; Schechter, R.S.; Wade, W.H.; Weerasooriya, U.; Yiv, S. Microemulsion formation with branched tail polyoxyethylene sulfonate surfactants. J. Colloid Interface Sci. 1986, 114, 342–356. [Google Scholar] [CrossRef]
- Maerker, J.M.; Gale, W.W. Surfactant flood process design for Loudon. SPE Reserv. Eng. 1992, 7, 36–44. [Google Scholar] [CrossRef]
- Salager, J.-L. A normalized Hydrophilic-Lipophilic Deviation expression HLDN is necessary to avoid confusions close to the optimum formulation of Surfactant-Oil-Water systems. J. Surfactants Deterg. 2021. [Google Scholar] [CrossRef]
- Salager, J.-L.; Forgiarini, A.M.; Bullón, J.; Marquez, R.; Alvarado, J.G. A Review on the Surfactant Characteristic Parameter used in Enhanced Oil Recovery, Crude Oil Dehydration and Other Formulation Applications. FIRP Booklet E729B. 2014. Available online: https://es.firp-ula.org/wp-content/uploads/2020/05/E719B.pdf (accessed on 20 May 2021).
- Salager, J.-L.; Antón, R.E.; Bullón, J.; Forgiarini, A.; Marquez, R. How to Use the Normalized Hydrophilic-Lipophilic Deviation (HLDN) Concept for the Formulation of Equilibrated and Emulsified Surfactant-Oil-Water Systems for Cosmetics and Pharmaceutical Products. Cosmetics 2020, 7, 57. [Google Scholar] [CrossRef]
- Baran, J.R.; Pope, G.A.; Wade, W.H.; Weerasooriya, V. Phase Behavior of Water/Perchloroethylene/Anionic Surfactant Systems. Langmuir 1994, 10, 1146–1150. [Google Scholar] [CrossRef]
- Miñana-Perez, M.; Graciaa, A.; Lachaise, J.; Salager, J.-L. Solubilization of polar oils with extended surfactants. Colloids Surf. A Physicochem. Eng. Asp. 1995, 100, 217–224. [Google Scholar] [CrossRef]
- Aoudia, M.; Wade, W.H.; Weerasooriya, V. Optimum microemulsions formulated with propoxylated Guerbet alcohol and propoxylated tridecyl alcohol sodium sulfates. J. Dispers. Sci. Technol. 1995, 16, 115–135. [Google Scholar] [CrossRef]
- Minana-Perez, M.; Graciaa, A.; Lachaise, J.; Salager, J.L. Systems containing mixtures of extended surfactants and conventional nonionics. Phase behavior and solubilization in microemulsion. In Proceedings of the 4th World Surfactants Congress, Barcelona, Spain, 3–7 June 1996; Volume 2, pp. 226–234. [Google Scholar]
- Pérez, M.M.; Salager, J.-L.; Graciaa, A.; Lachaise, J. Solubilization of polar oils in microemulsion systems. Trends Colloid Interface Sci. IX 1995, 177–179. [Google Scholar] [CrossRef]
- Scorzza, C.; Godé, P.; Goethals, G.; Martin, P.; Miñana-Pérez, M.; Salager, J.L.; Usubillaga, A.; Villa, P. Another new family of “extended” glucidoamphiphiles. Synthesis and surfactant properties for different sugar head groups and spacer arm lengths. J. Surfactants Deterg. 2002, 5, 337–343. [Google Scholar] [CrossRef]
- Scorzza, C.; Godé, P.; Martin, P.; Miñana-Pérez, M.; Salager, J.L.; Villa, P.; Goethals, G. Synthesis and surfactant properties of a new “extended” glucidoamphiphile made from D-glucose. J. Surfactants Deterg. 2002, 5, 331–335. [Google Scholar] [CrossRef]
- Goethals, G.; Fernández, A.; Martin, P.; Miñana-Pérez, M.; Scorzza, C.; Villa, P.; Godé, P. Spacer arm influence on glucidoamphiphile compound properties. Carbohydr. Polym. 2001, 45, 147–154. [Google Scholar] [CrossRef]
- Salager, J.; Scorzza, C.; Forgiarini, A.; Arandia, M.A.; Pietrangeli, G.; Manchego, L.; Vejar, F. Amphiphilic Mixtures versus Surfactant Structures with Smooth Polarity Transition across Interface to Improve Solubilization Performance. In Proceedings of the CESIO 2008—7th World Surfactant Congress Paris Session: Design and Analisis—Paper Number O-A17, Paris, France, 22–25 June 2008; pp. 1–9. [Google Scholar]
- Fernández, A.; Scorzza, C.; Usubillaga, A.; Salager, J.-L. Synthesis of new extended surfactants containing a carboxylate or sulfate polar group. J. Surfactants Deterg. 2005, 8, 187–191. [Google Scholar] [CrossRef]
- Fernández, A.; Scorzza, C.; Usubillaga, A.; Salager, J. Synthesis of new extended surfactants containing a xylitol polar group. J. Surfactants Deterg. 2005, 8, 193–198. [Google Scholar] [CrossRef]
- Illous, E.; Ontiveros, J.F.; Lemahieu, G.; Lebeuf, R.; Aubry, J.M. Amphiphilicity and salt-tolerance of ethoxylated and propoxylated anionic surfactants. Colloids Surf. A Physicochem. Eng. Asp. 2020, 601, 124786. [Google Scholar] [CrossRef]
- Velásquez, J.; Scorzza, C.; Vejar, F.; Forgiarini, A.M.; Antón, R.E.; Salager, J.L. Effect of temperature and other variables on the optimum formulation of anionic extended surfactant-alkane-brine systems. J. Surfactants Deterg. 2010, 13, 69–73. [Google Scholar] [CrossRef]
- Arandia, M.A.; Forgiarini, A.M.; Salager, J.-L. Resolving an enhanced oil recovery challenge: Optimum formulation of a surfactant-oil-water system made insensitive to dilution. J. Surfactants Deterg. 2010, 13, 119–126. [Google Scholar] [CrossRef]
- Forgiarini, A.M.; Scorzza, C.; Velásquez, J.; Vejar, F.; Zambrano, E.; Salager, J. Influence of the mixed propoxy/ethoxy spacer arrangement order and of the ionic head group nature on the adsorption and aggregation of extended surfactants. J. Surfactants Deterg. 2010, 13, 451–458. [Google Scholar] [CrossRef]
- Solairaj, S.; Britton, C.; Lu, J.; Kim, D.H.; Weerasooriya, U.; Pope, G.A. New correlation to predict the optimum surfactant structure for EOR. In Proceedings of the SPE—DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 14–18 April 2012; Volume 2, pp. 1390–1399. [Google Scholar] [CrossRef]
- Yang, H.; Britton, C.; Liyanage, P.J.; Solairaj, S.; Kim, D.H.; Nguyen, Q.; Weerasooriya, U.; Pope, G.A. Low-cost, high-performance chemicals for enhanced oil recovery. Proceedings SPE—DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 24–28 April 2010; Volume 2, pp. 1474–1497. [Google Scholar] [CrossRef]
- Phaodee, P.; Sabatini, D.A. Effect of Surfactant Systems, Alcohol Types, and Salinity on Cold-Water Detergency of Triacylglycerol Semisolid Soil. Part II. J. Surfactants Deterg. 2020, 23, 423–432. [Google Scholar] [CrossRef]
- Witthayapanyanon, A.; Acosta, E.; Harwell, J.H.; Sabatini, D.A. Formulation of ultralow interfacial tension systems using extended surfactants. J. Surfactants Deterg. 2006, 9, 331–339. [Google Scholar] [CrossRef]
- Salager, J.L.; Forgiarini, A.M.; Antón, R.E.; Quintero, L. Available know-how in transforming an emulsified drilling fluid to be removed from an unwanted location into a low-viscosity single-phase system. Energy Fuels 2012, 26, 4078–4085. [Google Scholar] [CrossRef]
- Quintero, L.; Clark, D.E.; Salager, J.; Forgiarini, A. Mesophase Fluids with Extended Chain Surfactants for Downhole Treatments. US Patent Office US8235120B2, 7 August 2012. [Google Scholar]
- Quintero, L.; Clark, D.E.; Cardenas, A.E.; Salager, J.; Forgiarini, A.; Bahsas, A.H. Dendritic Surfactants and Extended Surfactants for Drilling Fluid Formulations. US Patent Office US20120241220A1, 27 September 2012. [Google Scholar]
- Delgado-Linares, J.G.; Pereira, J.C.; Rondón, M.; Bullón, J.; Salager, J.L. Breaking of Water-in-Crude Oil Emulsions. 6. Estimating the Demulsifier Performance at Optimum Formulation from Both the Required Dose and the Attained Instability. Energy Fuels 2016, 30, 5483–5491. [Google Scholar] [CrossRef]
- Pereira, J.C.; Delgado-Linares, J.; Scorzza, C.; Rondón, M.; Rodríguez, S.; Salager, J.-L. Breaking of Water-in-Crude Oil Emulsions. 4. Estimation of the Demulsifier Surfactant Performance To Destabilize the Asphaltenes Effect. Energy Fuels 2011, 25, 1045. [Google Scholar] [CrossRef]
- Marquez, R.; Forgiarini, A.; Langevin, D.; Salager, J.-L. Breaking of Water-In-Crude Oil Emulsions. Part 9. New Interfacial Rheology Characteristics Measured Using a Spinning Drop Rheometer at Optimum Formulation. Energy Fuels 2019, 33, 8151–8164. [Google Scholar] [CrossRef]
- Han, X.; Lu, M.; Fan, Y.; Li, Y.; Holmberg, K. Recent Developments on Surfactants for Enhanced Oil Recovery. Tenside Surfactants Deterg. 2021, 58, 164–176. [Google Scholar] [CrossRef]
- Gagnon, Y.; Mhemdi, H.; Delbecq, F.; Van Hecke, E. Extended surfactants and their tailored applications for vegetable oils extraction: An overview. OCL Oilseeds Fats Crop. Lipids 2021, 28. [Google Scholar] [CrossRef]
- Do, L.; Witthayapanyanon, A.; Harwell, J.H.; Sabatini, D.A. Environmentally friendly Vegetable oil Microemulsion using Extended Surfactants and Linkers. J. Surfactants Deterg. 2009, 12, 91. [Google Scholar] [CrossRef]
- Chen, J.; Hu, X.Y.; Fang, Y.; Liu, H.H.; Xia, Y.M. Comparative Study of Conventional/Ethoxylated/Extended n-Alkylsulfate Surfactants. Langmuir 2019, 35, 3116–3125. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Chen, C.; Yuan, N.; Ma, Y.; Ogbonnaya, O.I.; Shiau, B.; Harwell, J.H. Design of extended surfactant-only EOR formulations for an ultrahigh salinity oil field by using hydrophilic lipophilic deviation (HLD) approach: From laboratory screening to simulation. Fuel 2019, 254. [Google Scholar] [CrossRef]
- He, W.; Ge, J.; Zhang, G.; Jiang, P.; Jin, L. Effects of Extended Surfactant Structure on the Interfacial Tension and Optimal Salinity of Dilute Solutions. ACS Omega 2019, 4, 12410–12417. [Google Scholar] [CrossRef] [Green Version]
- Phaodee, P.; Harwell, J.H.; Sabatini, D.A. Correlation between Detergency of Different Oily and Solid Non-Particulate Soils and Hydrophilic–Lipophilic Deviation. J. Surfactants Deterg. 2020, 23, 953–962. [Google Scholar] [CrossRef]
- Roon, L.; Oesper, R.E. A Contribution to the Theory of Emulsification Based on Pharmaceutical Practice. Ind. Eng. Chem. 1917, 9, 156–161. [Google Scholar] [CrossRef] [Green Version]
- Crockett, W.G.; Oesper, R.E. A Contribution to the Theory of Emulsification Based on Pharmaceutical Practice-II. Ind. Eng. Chem. 1917, 9, 967–969. [Google Scholar] [CrossRef]
- Harkins, W.D.; McLaughlin, H.M. The structure of films of water on salt solutions I. Surface tension and adsorption for aqueous solutions of sodium chloride. J. Am. Chem. Soc. 1925, 47, 2083–2089. [Google Scholar] [CrossRef]
- Griffin, W. Classification of surface-active agents by “HLB”. J. Soc. Cosmet. Chem. 1949, 1, 311–326. [Google Scholar]
- Griffin, W. Calculation of HLB Values of Non-ionic Surfactants. J. Soc. Cosmet. Chem. 1954, 5, 249. [Google Scholar]
- Becher, P. Emulsions: Theory and Practice; Oxford University Press: New York, NY, USA, 2001; ISBN 0-8412-3496-5. [Google Scholar]
- Winsor, P. Hydrotropy, solubilisation and related emulsification processes. Trans. Faraday Soc. 1948, 44, 376–398. [Google Scholar] [CrossRef]
- Winsor, P. Solvent Properties of Amphiphilic Compounds; Butterworths Scientific Publications: Oxford, UK, 1954. [Google Scholar]
- Winsor, P. Binary and multicomponent solutions of amphiphilic compounds. Solubilization and the formation, structure, and theoretical significance of liquid crystalline solutions. Chem. Rev. 1968, 68, 1–40. [Google Scholar] [CrossRef]
- Bourrel, M.; Verzaro, F.; Chambu, C. Effect of Oil Type on Solubilization by Amphiphiles. SPE Reserv. Eng. 1987, 2, 41–53. [Google Scholar] [CrossRef]
- Bourrel, M.; Schechter, R.S. Microemulsions and Related Systems: Formulation, Solvency, and Physical Properties; Editions Technip: Paris, France, 2010; ISBN 2710809567. [Google Scholar]
- Salager, J.-L.; Forgiarini, A.M.; Bullón, J. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 1. Optimum formulation for simple surfactant-oil-water ternary systems. J. Surfactants Deterg. 2013, 16, 449–472. [Google Scholar] [CrossRef]
- Ghosh, S.; Johns, R.T. Dimensionless Equation of State to Predict Microemulsion Phase Behavior. Langmuir 2016, 32, 8969–8979. [Google Scholar] [CrossRef]
- Fotland, P.; Skange, A. Ultralow Interfacial Tension as a Function of Pressure. J. Dispers. Sci. Technol. 1986, 7, 563. [Google Scholar] [CrossRef]
- Austad, T.; Strand, S. Chemical flooding of oil reservoirs 4. Effects of temperature and pressure on the middle phase solubilization parameters close to optimum flood conditions. Colloids Surf. A Physicochem. Eng. Asp. 1996, 108, 243–252. [Google Scholar] [CrossRef]
- Scriven, L.E. Equilibrium bicontinuous structure. Nature 1976, 263, 123–125. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Taupin, C. Microemulsions and the flexibility of oil/water interfaces. J. Phys. Chem. 1982, 86, 2294–2304. [Google Scholar] [CrossRef]
- Scriven, L.E. Equilibrium bicontinuous structures. In Micellization, Solubilization, and Microemulsions; Mittal, K.L., Ed.; Springer: Berlin/Heidelberg, Germany, 1977; pp. 877–893. [Google Scholar]
- Langevin, D. Emulsions, Microemulsions and Foams; Springer: Cham, Switzerland, 2020; ISBN 978-3-030-55681-5. [Google Scholar]
- Salager, J.-L. Quantifying the concept of physico-chemical formulation in surfactant-oil-water systems—State of the art. Prog. Colloid Polym. Sci. 1996, 100, 137–142. [Google Scholar] [CrossRef]
- Salager, J.-L.; Antón, R.E.; Anderez, J.M.; Aubry, J.-M. Formulation des micro-émulsions par la méthode HLD. Techniques de l’Ingénieur 2001, 157, 1–16. [Google Scholar]
- Shah, D.O.; Schechter, R.S. Improved Oil Recovery by Surfactant and Polymer Flooding; Elsevier: Amsterdam, The Netherlands, 1977; ISBN 978-0-12-641750-0. [Google Scholar]
- Huh, C. Interfacial tensions and solubilizing ability of a microemulsion phase that coexists with oil and brine. J. Colloid Interface Sci. 1979, 71, 408–426. [Google Scholar] [CrossRef]
- Shinoda, K.; Arai, H. The Correlation between Phase Inversion Temperature in Emulsion and Cloud Point in Solutions of Nonionic Emulsifier. J. Phys. Chem. 1964, 68, 3485–3490. [Google Scholar] [CrossRef]
- Bourrel, M.; Graciaa, A.; Schechter, R.S.; Wade, W.H. The relation of emulsion stability to phase behavior and interfacial tension of surfactant systems. J. Colloid Interface Sci. 1979, 72, 161. [Google Scholar] [CrossRef]
- Salager, J.-L.; Quintero, L.; Ramos, E.; Anderez, J.M. Properties of surfactant/oil/water emulsified systems in the neighborhood of the three-phase transition. J. Colloid Interface Sci. 1980, 77. [Google Scholar] [CrossRef]
- Vinatieri, J.E. Correlation of emulsion stability with phase behavior in surfactant systems for tertiary oil recovery. Soc. Pet. Eng. J. 1980, 20, 402–406. [Google Scholar] [CrossRef]
- Salager, J.-L.; Miñana-Pérez, M.; Pérez-Sánchez, M.; Ramírez-Gouveia, M.; Rojas, C. Surfactant-Oil-Water Systems near the Affinity Inversion Part III: The Two Kinds of Emulsion Inversion. J. Dispers. Sci. Technol. 1983, 4, 313. [Google Scholar] [CrossRef]
- Marquez, R.; Forgiarini, A.M.; Fernández, J.; Langevin, D.; Salager, J.-L. New Interfacial Rheology Characteristics Measured using a Spinning-Drop Rheometer at the Optimum Formulation of a Simple Surfactant–Oil–Water System. J. Surfactants Deterg. 2018, 21. [Google Scholar] [CrossRef]
- Marquez, R.; Forgiarini, A.M.; Langevin, D.; Salager, J.-L. Instability of Emulsions Made with Surfactant–Oil–Water Systems at Optimum Formulation with Ultralow Interfacial Tension. Langmuir 2018, 34, 9252–9263. [Google Scholar] [CrossRef] [PubMed]
- Wade, W.; Morgan, J.C.; Schechter, R.S.; Jacobson, J.K.; Salager, J.-L. Interfacial tension and phase behavior of surfactant systems. Soc. Pet. Eng. J. 1978, 18, 242–252. [Google Scholar] [CrossRef]
- Salager, J.-L.; Marquez, N.; Graciaa, A.; Lachaise, J. Partitioning of ethoxylated octylphenol surfactants in microemulsion-oil-water systems: Influence of temperature and relation between partitioning coefficient and physicochemical formulation. Langmuir 2000, 16, 5534–5539. [Google Scholar] [CrossRef]
- Salager, J.-L.; Morgan, J.C.; Schechter, R.S.; Wade, W.H.; Vasquez, E. Optimum formulation of surfactant/water/oil systems for minimum interfacial tension or phase behavior. Soc. Pet. Eng. J. 1979, 19, 107–115. [Google Scholar] [CrossRef]
- Salager, J.L. Quantifying the concept of physico-chemical formulation in surfactant-oil-water systems—state of the art. Trends Colloid Interface Sci. X 1996, 137–142. [Google Scholar] [CrossRef]
- Antón, R.E.; Garcés, N.; Yajure, A. A correlation for three-phase behavior of cationic surfactant-oil-water systems. J. Dispers. Sci. Technol. 1997, 18, 539–555. [Google Scholar] [CrossRef]
- Hammond, C.E.; Acosta, E.J. On the characteristic curvature of alkyl-polypropylene oxide sulfate extended surfactants. J. Surfactants Deterg. 2012, 15, 157–165. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Morgan, C.; Poindexter, L.; Fernandez, J. Application of the Hydrophilic–Lipophilic Deviation Concept to Surfactant Characterization and Surfactant Selection for Enhanced Oil Recovery. J. Surfactants Deterg. 2019, 22, 983–999. [Google Scholar] [CrossRef]
- Barakat, Y.; Fortney, L.N.; Schechter, R.S.; Wade, W.H.; Yiv, S.H.; Graciaa, A. Criteria for structuring surfactants to maximize solubilization of oil and water: II. Alkyl benzene sodium sulfonates. J. Colloid Interface Sci. 1983, 92, 561–574. [Google Scholar] [CrossRef]
- Bourrel, M.; Salager, J.-L.; Schechter, R.S.; Wade, W.H. A correlation for phase behavior of nonionic surfactants. J. Colloid Interface Sci. 1980, 75, 451–461. [Google Scholar] [CrossRef]
- Antón, R.E.; Salager, J.-L. Effect of the Electrolyte Anion on the Salinity Contribution to Optimum Formulation of Anionic Surfactant Microemulsions. J. Colloid Interface Sci. 1990, 140, 75. [Google Scholar] [CrossRef]
- Aubry, J.M.; Ontiveros, J.F.; Salager, J.-L.; Nardello-Rataj, V. Use of the normalized hydrophilic-lipophilic-deviation (HLDN) equation for determining the equivalent alkane carbon number (EACN) of oils and the preferred alkane carbon number (PACN) of nonionic surfactants by the fish-tail method (FTM). Adv. Colloid Interface Sci. 2020, 276. [Google Scholar] [CrossRef]
- Doe, P.H.; El-Emary, M.; Wade, W.H.; Schechter, R.S. Surfactants for producing low interfacial tensions: III. Di and tri n-alkylbenzenesulfonates. J. Am. Oil Chem. Soc. 1978, 55, 513–520. [Google Scholar] [CrossRef]
- Salager, J.-L.; Bourrel, M.; Schechter, R.S.; Wade, W.H. Mixing Rules for Optimum Phase Behavior Formulation of Surfactant-Oil-Water Systems. Soc. Pet. Eng. J. 1979, 19, 271. [Google Scholar] [CrossRef]
- Acosta, E.; Yuan, J.S.; Bhakta, A.S. The characteristic curvature of ionic surfactants. J. Surfactants Deterg. 2008, 11, 145. [Google Scholar] [CrossRef]
- Sottmann, T.; Strey, R. Ultralow interfacial tensions in water-n-alkane-surfactant systems. J. Chem. Phys. 1997, 106, 8606–8615. [Google Scholar] [CrossRef]
- Salager, J.-L.; Manchego, L.; Márquez, L.; Bullón, J.; Forgiarini, A. Trends to attain a lower interfacial tension in a revisited pure alkyl polyethyleneglycol surfactant–alkane–water ternary system. Basic concepts and straightforward guidelines for improving performance in enhanced oil recovery formulations. J. Surfactants Deterg. 2014, 17, 199–213. [Google Scholar] [CrossRef]
- Marquez, N.; Anton, R.E.; Graciaa, A.; Lachaise, J.; Salager, J.L. Partitioning of ethoxylated alkylphenol surfactants in microemulsion-oil-water systems. Colloids Surf. A Physicochem. Eng. Asp. 1995, 100, 225–231. [Google Scholar] [CrossRef]
- Márquez, N.; Anton, R.E.; Graciaa, A.; Lachaise, J.; Salager, J.-L. Partitioning of ethoxylated alkylphenol surfactants in microemulsion- oil-water systems. Part II: Influence of hydrophobe branching. Colloids Surf. A Physicochem. Eng. Asp. 1998, 131, 45–49. [Google Scholar] [CrossRef]
- Bourrel, M.; Chambu, C. The Rules for Achieving High Solubilization of Brine and Oil by Amphiphilic Molecules. Soc. Pet. Eng. J. 1983, 23, 327. [Google Scholar] [CrossRef]
- Bourrel, M.; Schechter, R.S. Microemulsions and Related Systems; Dekker: New York, NY, USA, 1988; ISBN 0824779517. [Google Scholar]
- Graciaa, A.; Barakat, Y.; El-Emary, M.; Fortney, L.; Schechter, R.S.; Yiv, S.; Wade, W.H. HLB, CMC, and phase behavior as related to hydrophobe branching. J. Colloid Interface Sci. 1982, 89, 209–216. [Google Scholar] [CrossRef]
- Wade, W.; Morgan, J.C.; Jacobson, J.K.; Schechter, R.S. Low interfacial tensions involving mixtures of surfactants. Soc. Pet. Eng. J. 1977, 17, 122–128. [Google Scholar] [CrossRef]
- Doe, P.H.; Wade, W.H.; Schechter, R.S. Alkyl benzene sulfonates for producing low interfacial tensions between hydrocarbons and water. J. Colloid Interface Sci. 1977, 59, 525–531. [Google Scholar] [CrossRef]
- Doe, P.H.; El-Emary, M.; Wade, W.H.; Schechter, R.S. Surfactants for producing low interfacial tensions: II. Linear alkylbenzenesulfonates with additional alkyl substituents. J. Am. Oil Chem. Soc. 1978, 55, 505–512. [Google Scholar] [CrossRef]
- Lo, I.; Florence, A.T.; Treguier, J.P.; Seiller, M.; Puisieux, F. The influence of surfactant HLB and the nature of the oil phase on the phase diagrams of nonionic surfactant-oil-water systems. J. Colloid Interface Sci. 1977, 59, 319–327. [Google Scholar] [CrossRef]
- Shinoda, K.; Kunieda, H. Conditions to produce so-called microemulsions: Factors to increase the mutual solubility of oil and water by solubilizer. J. Colloid Interface Sci. 1973, 42, 381–387. [Google Scholar] [CrossRef]
- Magzymov, D.; Qiao, C.; Johns, R.T. Impact of surfactant mixtures on microemulsion phase behavior. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 26–28 September 2016. [Google Scholar] [CrossRef]
- Graciaa, A.; Lachaise, J.; Cucuphat, C.; Bourrel, M.; Salager, J.L. Interfacial Segregation of an Ethyl Oleate/Hexadecane Oil Mixture in Microemulsion Systems. Langmuir 1993, 9, 1473–1478. [Google Scholar] [CrossRef]
- Graciaa, A.; Lachaise, J.; Cucuphat, C.; Bourrel, M.; Salager, J.L. Improving solubilization in microemulsions with additives. 1. The lipophilic linker role. Langmuir 1993, 9, 669–672. [Google Scholar] [CrossRef]
- Graciaa, A.; Lachaise, J.; Cucuphat, C.; Bourrel, M.; Salager, J.L. Improving Solubilization in Microemulsions with Additives. 2. Long Chain Alcohols as Lipophilic Linkers. Langmuir 1993, 9, 3371–3374. [Google Scholar] [CrossRef]
- Salager, J.L.; Graciaa, A.; Lachaise, J. Improving solubilization in microemulsions with additives. Part III: Lipophilic linker optimization. J. Surfactants Deterg. 1998, 1, 403–406. [Google Scholar] [CrossRef]
- Acosta, E.; Do Mai, P.; Harwell, J.H.; Sabatini, D.A. Linker-Modified Microemulsions for a Variety of Oils and Surfactants. J. Surfactants Deterg. 2003, 6, 353–363. [Google Scholar] [CrossRef]
- Quintero, L.; Pietrangeli, G.; Hughes, B.; Salager, J.L.; Forgiarini, A. Optimization of microemulsion formulations with linker molecules. In Proceedings of the SPE–European Formation Damage Conference, EFDC, Noordwijk, The Netherlands, 5–7 June 2013; Volume 2, pp. 1275–1287. [Google Scholar] [CrossRef]
- Acosta, E.; Uchiyama, H.; Sabatini, D.A.; Harwell, J.H. The role of hydrophilic linkers. J. Surfactants Deterg. 2002, 5, 151–157. [Google Scholar] [CrossRef]
- Frank, C.; Frielinghaus, H.; Allgaier, J.; Richter, D. Hydrophilic alcohol ethoxylates as efficiency boosters for Microemulsions. Langmuir 2008, 24, 6036–6043. [Google Scholar] [CrossRef]
- Miñana-Pérez, M. Contribution à la Microémulsification d’huiles Polaires de Synthèse ou Naturelles. Ph.D. Thesis, Universidad de Los Andes—Universite de Pau, Santiago, Chile, 1993. [Google Scholar]
- Salager, J.-L.; Forgiarini, A.M. Extended surfactants A fine tuned structure to improve interfacial performance. In Proceedings of the 101st AOCS Annual Meeting, Phoenix, AZ, USA, 16–19 May 2010. [Google Scholar]
- Salager, J.L.; Scorzza, C.; Fernandez, A.; Antón, R.E.; Miñana-Pérez, M.; Usubillaga, A.; Villa, P. Enhancing Solubilization in Microemulsions: From Classic To Novel “Extended” Surfactant Structures. In Proceedings of the Surfactants in Solution, Barcelona, Spain, 9–14 June 2002. [Google Scholar]
- Salager, J.; Forgiarini, A.; Marquez, L. Understanding of Extended Surfactants Intramolecular Structure to enhance solubilization for a variety of applications. In Proceedings of the 8th World Surfactant Congress CESIO, Vienna, Austria, 6–8 June 2011. [Google Scholar]
- Chen, J.; Hu, X.Y.; Fang, Y.; Jin, G.Y.; Xia, Y.M. What dominates the interfacial properties of extended surfactants: Amphipathicity or surfactant shape? J. Colloid Interface Sci. 2019, 547, 190–198. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Britton, C.; Solairaj, S.; Liyanage, P.J.; Kim, D.H.; Adkins, S.; Arachchilage, G.W.P.; Weerasooriya, U.; Pope, G.A. Novel large-hydrophobe alkoxy carboxylate surfactants for enhanced oil recovery. SPE J. 2014, 19, 1024–1034. [Google Scholar] [CrossRef]
- Ghosh, S.; Johns, R.T. An Equation-of-State Model To Predict Surfactant/Oil/Brine-Phase Behavior. SPE J. 2016, 21, 1106. [Google Scholar] [CrossRef]
- Chung, J.; Holtsclaw, J.; Henderson, T.C.; Everett, T.A.; Schultheiss, N.C.; Boudouris, B.W.; Franses, E.I. Relationship of Various Interfacial Tensions of Surfactants/Brine/Oil Formulations to Oil Recovery Efficiency. Energy Fuels 2021, 35, 7768–7777. [Google Scholar] [CrossRef]
- Antón, R.E.; Graciaa, A.; Lachaise, J.; Salager, J.L. Surfactant-Oil-Water Systems Near the Affinity Inversion, Part VIII: Optimum Formulation and Phase Behavior of Mixed Anionic-Nonionic Systems Versus Temperature. J. Dispers. Sci. Technol. 1992, 13, 565–579. [Google Scholar] [CrossRef]
- Acosta, E.; Bhakta, A.S. The HLD-NAC model for mixtures of ionic and nonionic surfactants. J. Surfactants Deterg. 2009, 12, 7–19. [Google Scholar] [CrossRef]
- Salager, J.-L.; Forgiarini, A.M.; Rondón, M.J. How to Attain an Ultralow Interfacial Tension and a Three-Phase Behavior with a Surfactant Formulation for Enhanced Oil Recovery: A Review—Part 3. Practical Procedures to Optimize the Laboratory Research according to the Current State of the Art in Surf. J. Surfactants Deterg. 2017, 20, 3. [Google Scholar] [CrossRef]
- Darley, H. Composition and Properties of Drilling Fluids and Completion Fluids; Gulf Professional Publishing: Houston, TX, USA, 1983; ISBN 0-87201-147-X. [Google Scholar]
- Quintero, L. An overview of surfactant applications in drilling fluids for the petroleum industry. J. Dispers. Sci. Technol. 2002, 23, 393–404. [Google Scholar] [CrossRef]
- Caenn, R.; Chillingar, G.V. Drilling fluids: State of the art. J. Pet. Sci. Eng. 1996, 14, 221–230. [Google Scholar] [CrossRef]
- Audibert-Hayet, A.; Dalmazzone, C. Surfactant system for water-based well fluids. Colloids Surf. A Physicochem. Eng. Asp. 2006, 288, 113–120. [Google Scholar] [CrossRef]
- Skalli, L.; Buckley, J.S.; Zhang, Y.; Morrow, N.R. Surface and core wetting effects of surfactants in oil-based drilling fluids. J. Pet. Sci. Eng. 2006, 52, 253–260. [Google Scholar] [CrossRef]
- Christian, C.F.; Quintero, L.; Clark, D.E.; Jones, T.A. Production enhancement of cased-hole wells using mesophase fluids. In Proceedings of the Society of Petroleum Engineers—SPE Saudi Arabia Section Technical Symposium, Al-Khobar, Saudi Arabia, 9–11 May 2009. [Google Scholar] [CrossRef]
- Brege, J.; El Sherbeny, W.; Quintero, L.; Jones, T. Using microemulsion technology to remove oil-based mud in wellbore displacement and remediation applications. In Proceedings of the Society of Petroleum Engineers—North Africa Technical Conference Exhibition, Cairo, Egypt, 20–22 February 2012; Volume 1, pp. 323–330. [Google Scholar] [CrossRef]
- Quintero, L.; Jones, T.A.; Pietrangeli, P.A. Proper design criteria of microemulsion treatment fluids for enhancing well production (SPE 154451). In Proceedings of the 74th EAGE Conference and Exhibition Incorporating EUROPEC 2012. European Association of Geoscientists & Engineers, Copenhagen, Denmark, 4–7 June 2012; pp. 571–581. [Google Scholar]
- Salager, J.; Antón, R.; Forgiarini, A.; Scorzza, C.; Tolosa, L.; Vejar, F. Microemulsiones para fluidos espaciadores en completación de pozos. Ciencia Ingenieria 2007, 30, 72–79. [Google Scholar]
- Salager, J.L.; Forgiarini, A.; Marquez, L.; Pena, A.; Pizzino, A.; Rodriguez, M.P.; Rondon-Gonzalez, M. Using emulsion inversion in industrial processes. Adv. Colloid Interface Sci. 2004, 108, 259–272. [Google Scholar] [CrossRef] [PubMed]
- Rondón, M.; Bouriat, P.; Lachaise, J.; Salager, J.-L. Breaking of water-in-crude oil emulsions. 1. Physicochemical phenomenology of demulsifier action. Energy Fuels 2006, 20, 1600. [Google Scholar] [CrossRef]
- Rondón, M.; Pereira, J.C.; Bouriat, P.; Graciaa, A.; Lachaise, J.; Salager, J.-L. Breaking of water-in-crude-oil emulsions. 2. Influence of asphaltene concentration and diluent nature on demulsifier action. Energy Fuels 2008, 22, 702–707. [Google Scholar] [CrossRef]
- Salager, J.-L. Fundamental basis for the action of a chemical dehydrant. Influence of the physical and chemical formulation on the stability of an emulsion. Int. Chem. Eng. 1990, 30, 103–116. [Google Scholar]
- Langevin, D.; Argillier, J.-F. Interfacial behavior of asphaltenes. Adv. Colloid Interface Sci. 2016, 233, 83–93. [Google Scholar] [CrossRef]
- Freer, E.; Svitova, T.; Radke, C.J. The role of Interfacial Rheology in reservoir mixed Wettability. J. Pet. Sci. Eng. 2003, 39, 137. [Google Scholar] [CrossRef]
- Mullins, O.C.; Sabbah, H.; Eyssautier, J.; Pomerantz, A.E.; Barré, L.; Andrews, A.B.; Ruiz-Morales, Y.; Mostowfi, F.; McFarlane, R.; Goual, L. Advances in asphaltene science and the Yen–Mullins model. Energy Fuels 2012, 26, 3986–4003. [Google Scholar] [CrossRef]
- Alvarado, J.G.; Delgado-Linares, J.G.; Forgiarini, A.M.; Salager, J.-L.J.L. Breaking of Water-in-Crude Oil Emulsions. 8. Demulsifier Performance at Optimum Formulation Is Significantly Improved by a Small Aromatic Content of the Oil. Energy Fuels 2019, 33, 1928–1936. [Google Scholar] [CrossRef]
- Alvarez, G.; Poteau, S.; Argillier, J.-F.; Langevin, D.; Salager, J.-L. Heavy oil− water interfacial properties and emulsion stability: Influence of dilution. Energy Fuels 2009, 23, 294–299. [Google Scholar] [CrossRef]
- Goldszal, A.; Bourrel, M. Demulsification of crude oil emulsions: Correlation to microemulsion phase behavior. Ind. Eng. Chem. Res. 2000, 39, 2746–2751. [Google Scholar] [CrossRef]
- Salager, J.-L.; Bullón, J.; Pizzino, A.; Rondón-González, M.; Tolosa, L.; Somasundaran, P. Emulsion formulation engineering for the practitioner. In Encyclopedia of Surface and Colloid Science; Somasundaran, P., Ed.; Taylor & Francis: New York, NY, USA, 2010; Volume 1, pp. 1–6. [Google Scholar]
- Marquez, R.; Meza, L.; Alvarado, J.; Johnny, B.; Langevin, D.; Forgiarini, A.; Salager, J.-L. Interfacial rheology measured with a spinning drop interfacial rheometer: More realistic surfactant-oil-water systems close to optimum formulation at HLDN = 0. J. Surfactants Deterg. 2021. [Google Scholar] [CrossRef]
- Marfisi, S.; Rodríguez, M.P.; Alvarez, G.; Celis, M.-T.; Forgiarini, A. Complex Emulsion Inversion Pattern associated with the Partitioning of Nonionic Surfactant Mixtures in the presence of alcohol cosurfactant. Langmuir 2005, 21, 6712. [Google Scholar] [CrossRef]
- Fillous, L.; Cárdenas, A.; Rouvière, J.; Salager, J.-L. Interfacial Mass Transfer versus Formulation in Multiple Phase Anionic Surfactant-Oil-Water Systems. J. Surfactants Deterg. 1999, 2, 303–307. [Google Scholar] [CrossRef]
- Cardenas, A.; Fillous, L.; Rouviere, J.; Salager, J. An experimental method to estimate the mass transfer through the interfacial region of liquid membrane systems. Ciencia 2001, 9, 70–76. [Google Scholar]
- Kim, Y.-H.; Wasan, D.T.; Breen, P.J. A study of dynamic interfacial mechanisms for demulsification of water-in-oil emulsions. Colloids Surf. A Physicochem. Eng. Asp. 1995, 95, 235–247. [Google Scholar] [CrossRef]
- Kim, Y.H.; Wasan, D.T. Effect of Demulsifier Partitioning on the Destabilization of Water-in-Oil Emulsions. Ind. Eng. Chem. Res. 1996, 35, 1141–1149. [Google Scholar] [CrossRef]
- Delgado-Linares, J.G.; Alvarado, J.G.; Véjar, F.; Bullón, J.; Forgiarini, A.M.; Salager, J.L. Breaking of Water-in-Crude Oil Emulsions. 7. Demulsifier Performance at Optimum Formulation for Various Extended Surfactant Structures. Energy Fuels 2016, 30, 7065–7071. [Google Scholar] [CrossRef]
- Salager, J.-L.; Antón, R.E.; Arandia, M.A.; Forgiarini, A.M. How to attain ultralow interfacial tension and three-phase behavior with surfactant formulation for enhanced oil recovery: A review. Part 4: Robustness of the optimum formulation zone through the insensibility to some variables and the occurrence of compl. J. Surfactants Deterg. 2017, 20, 987–1018. [Google Scholar] [CrossRef]
- Salager, J.-L.; Forgiarini, A.M.; Márquez, L.; Manchego, L.; Bullón, J.; Marquez, L.; Manchego, L.; Bullon, J. How to Attain an Ultralow Interfacial Tension and a Three-Phase Behavior with a Surfactant Formulation for Enhanced Oil Recovery: A Review. Part 2. Performance Improvement Trends from Winsor’s Premise to Currently Proposed Inter- and Intra-Molecular Mixtu. J. Surfactants Deterg. 2013, 16, 631–663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zamora, J.M.; Marquez, R.; Forgiarini, A.M.; Langevin, D.; Salager, J.L. Interfacial rheology of low interfacial tension systems using a new oscillating spinning drop method. J. Colloid Interface Sci. 2018, 519, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Marquez, R.; Antón, R.; Vejar, F.; Salager, J.L.; Forgiarini, A.M. New Interfacial Rheology Characteristics Measured Using a Spinning Drop Rheometer at the Optimum Formulation. Part 2. Surfactant–Oil–Water Systems with a High Volume of Middle-Phase Microemulsion. J. Surfactants Deterg. 2019, 22, 177–188. [Google Scholar] [CrossRef]
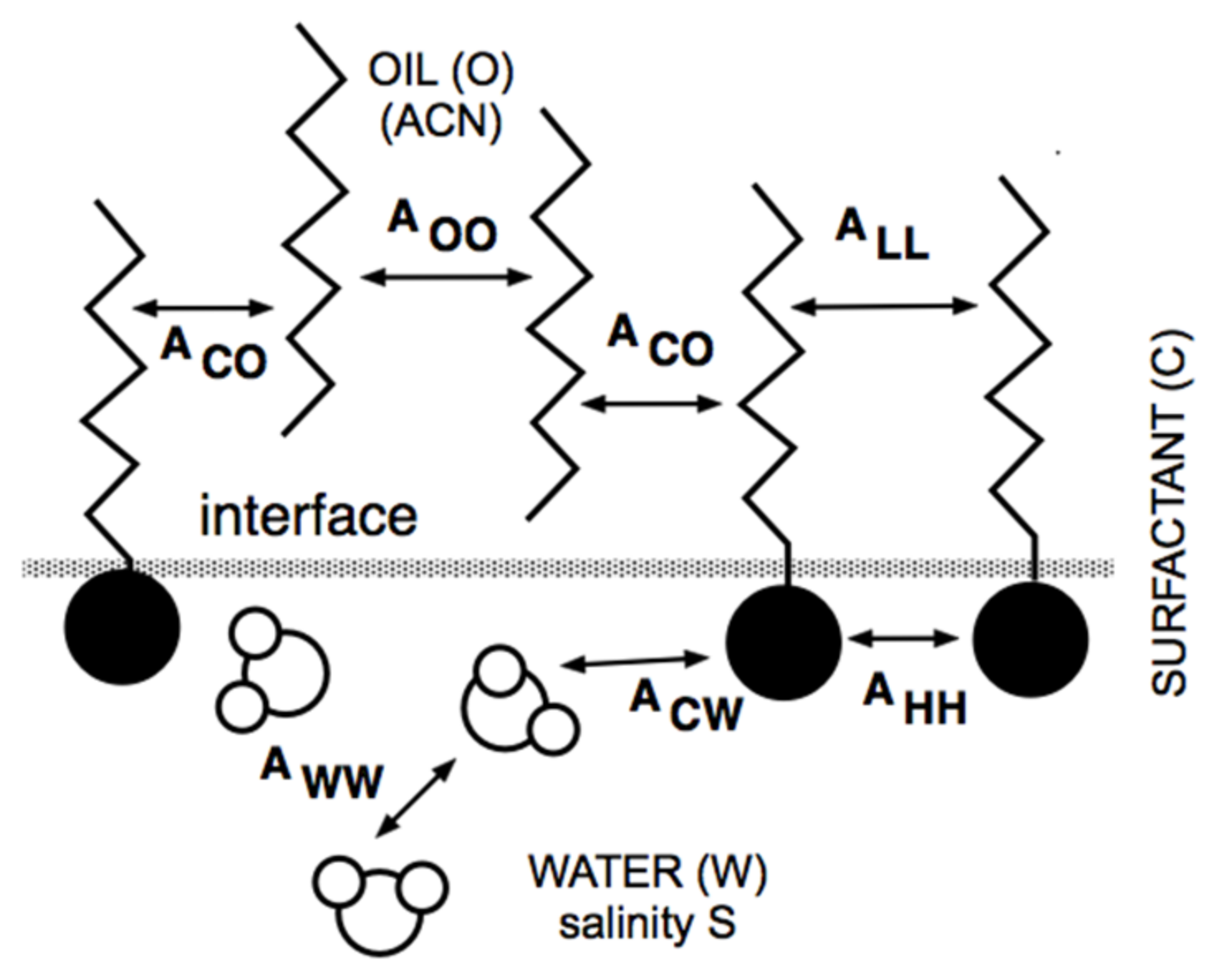
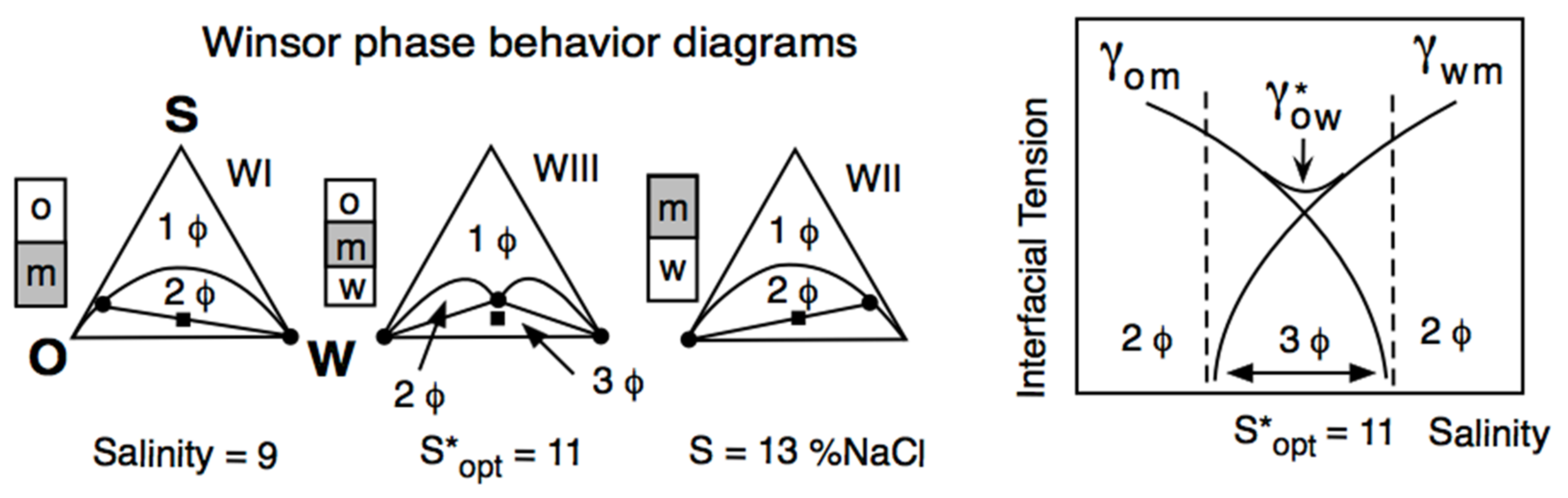
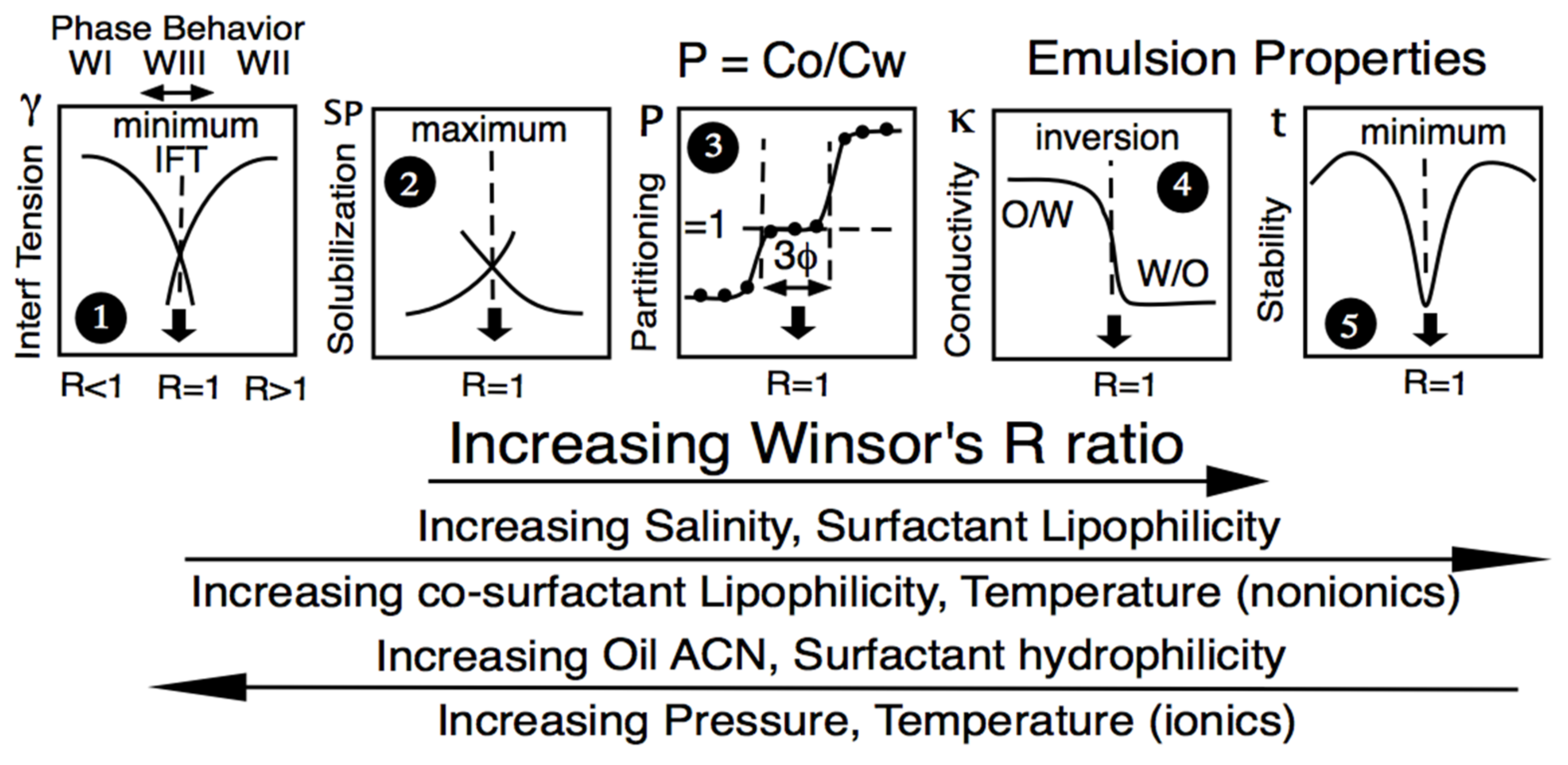


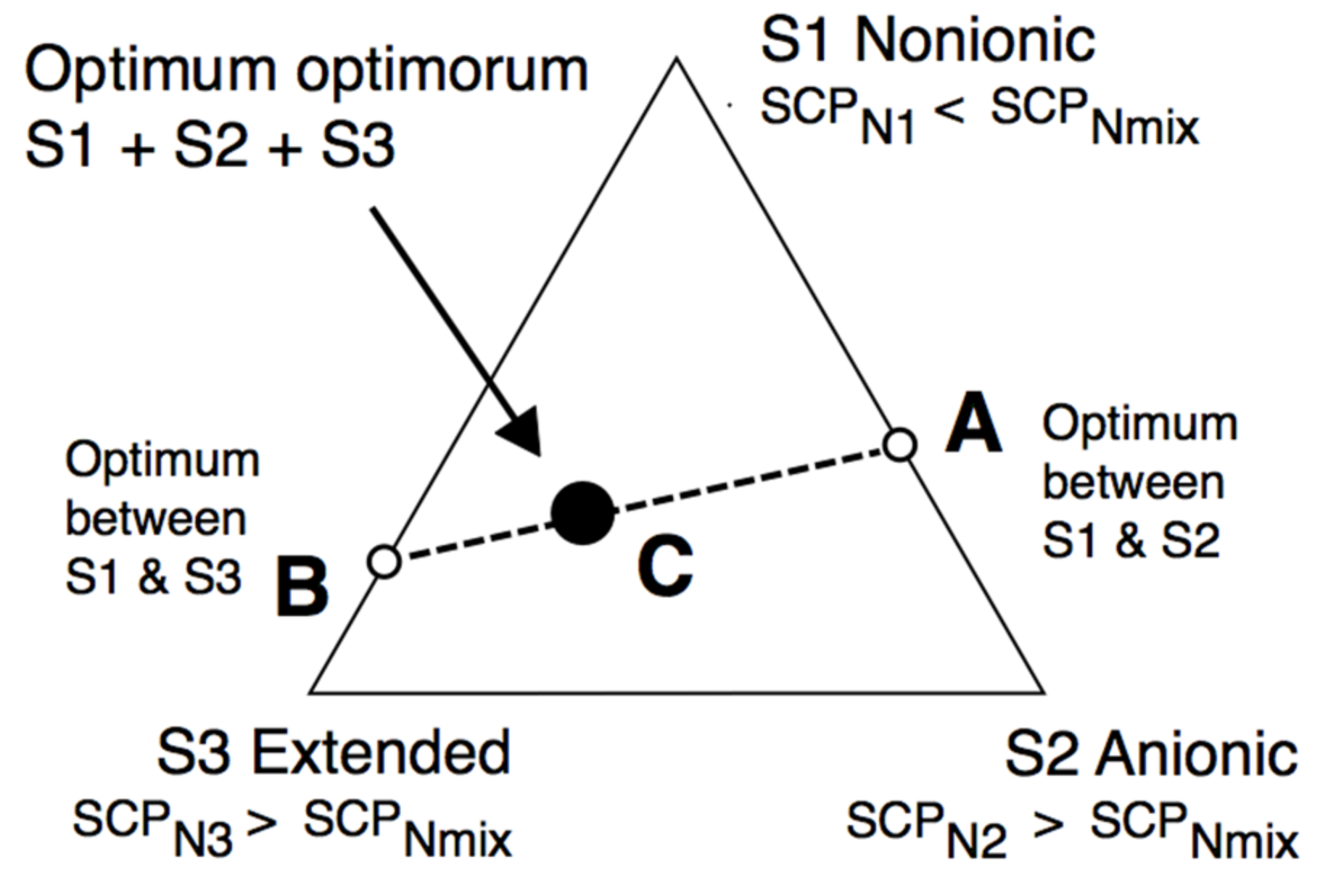


| HLD Equation–Surfactant Type |
|---|
| ΔHLD1 = ΔLnS − 0.16 ΔACN = 0 for alkylbenzene sulfonates ΔHLD2 = ΔLnS − 0.19 ΔACN = 0 for alkyltrimethyl ammonium chlorides ΔHLD3 = ΔLnS − 0.07 ΔACN = 0 for alkyl hexapropyleneoxide diethylenoxide sulfates ΔHLD4 = 0.33 ΔSAT − ΔEON = 0 for ethoxylated n-alcohol with EON~5 and T~25 °C ΔHLD5 = 0.13 ΔS − ΔEON = 0 for ethoxylated n-alcohol with EON~5 and T~25 °C ΔHLD6 = 2.25 ΔSAT − ΔACN = 0 for ethoxylated n-alcohol with EON~5 ΔHLD7 = − 0.24 ΔACN − ΔEON = 0 for ethoxylated n-alcohol with EON~5 ΔHLD8 = − ΔT − 20 ΔACN = 0 for n-alkyl sulfates ΔHLD9 = − ΔT − 14.3 ΔACN = 0 for alkylbenzene sulfonates ΔHLD10 = ΔT − 4 ΔACN = 0 for ethoxylated nonionic (EON~5–6 & T~20–30 °C) ΔHLD11 = ΔT − 1.4 ΔACN = 0 for ethoxylated nonionic (EON~8–9 & T~70 °C) ΔHLD12 = ΔT − 0.90 ΔACN = 0 for ethoxylated nonionic (EON~10–11 & T~80–90 °C) ΔHLD13 = − ΔGN − 0.12 ΔACN = 0 for polyglyceryl monolaurate (GN~5–6) ΔHLD14 = ΔLnS − 0.14 ΔPON = 0 for alkyl polypropyleneoxide diethylenoxide sulfates |
| HLDN Equation−Surfactant Type |
|---|
| ΔHLDN1 = 6.25 ΔLnS − ΔACN = 0 for alkylbenzene sulfonates ΔHLDN2 = 5.26 ΔLnS − ΔACN = 0 for alkyltrimethyl ammonium chlorides ΔHLDN3 = 14.3 ΔLnS − ΔACN = 0 for alkyl hexapropyleneoxide diethylenoxide sulf. ΔHLDN4 = 1.4 ΔSAT − 4.2 ΔEON = 0 for ethoxylated n-alcohol (EON~5 & T~25 °C) ΔHLDN5 = 0.55 ΔS − 4.2 ΔEON = 0 for ethoxylated n-alcohol (EON~5 & T~25 °C) ΔHLDN6 = 2.25 ΔSAT − ΔACN = 0 for ethoxylated n-alcohol with EON~5 ΔHLDN7 = − 4.2 ΔEON − ΔACN = 0 for ethoxylated n-alcohol with EON~5 ΔHLDN8 = − 0.05 ΔT − ΔACN = 0 for n-alkyl sulfates ΔHLDN9 = − 0.07 ΔT − ΔACN = 0 for alkylbenzene sulfonates ΔHLDN10 = 0.25 ΔT − ΔACN = 0 for ethoxylated nonionic (EON~5–6 & T~20–30 °C) ΔHLDN11 = 0.70 ΔT − ΔACN = 0 for ethoxylated nonionic (EON~8–9 & T~70 °C) ΔHLDN12 = 1.1 ΔT − ΔACN = 0 for ethoxylated nonionic (EON~11 & T~80–90 °C) ΔHLDN13 = − 8.3 ΔGN − ΔACN = 0 for polyglyceryl monolaurate (GN~5–6) ΔHLDN14 = 1.2 ΔPON − ΔACN = 0 for alkyl polypropyleneoxide PON sulfates |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forgiarini, A.M.; Marquez, R.; Salager, J.-L. Formulation Improvements in the Applications of Surfactant–Oil–Water Systems Using the HLDN Approach with Extended Surfactant Structure. Molecules 2021, 26, 3771. https://doi.org/10.3390/molecules26123771
Forgiarini AM, Marquez R, Salager J-L. Formulation Improvements in the Applications of Surfactant–Oil–Water Systems Using the HLDN Approach with Extended Surfactant Structure. Molecules. 2021; 26(12):3771. https://doi.org/10.3390/molecules26123771
Chicago/Turabian StyleForgiarini, Ana M., Ronald Marquez, and Jean-Louis Salager. 2021. "Formulation Improvements in the Applications of Surfactant–Oil–Water Systems Using the HLDN Approach with Extended Surfactant Structure" Molecules 26, no. 12: 3771. https://doi.org/10.3390/molecules26123771
APA StyleForgiarini, A. M., Marquez, R., & Salager, J.-L. (2021). Formulation Improvements in the Applications of Surfactant–Oil–Water Systems Using the HLDN Approach with Extended Surfactant Structure. Molecules, 26(12), 3771. https://doi.org/10.3390/molecules26123771









