Porosity at Different Structural Levels in Human and Yak Belly Hair and Its Effect on Hair Dyeing
Abstract
1. Introduction
2. Results
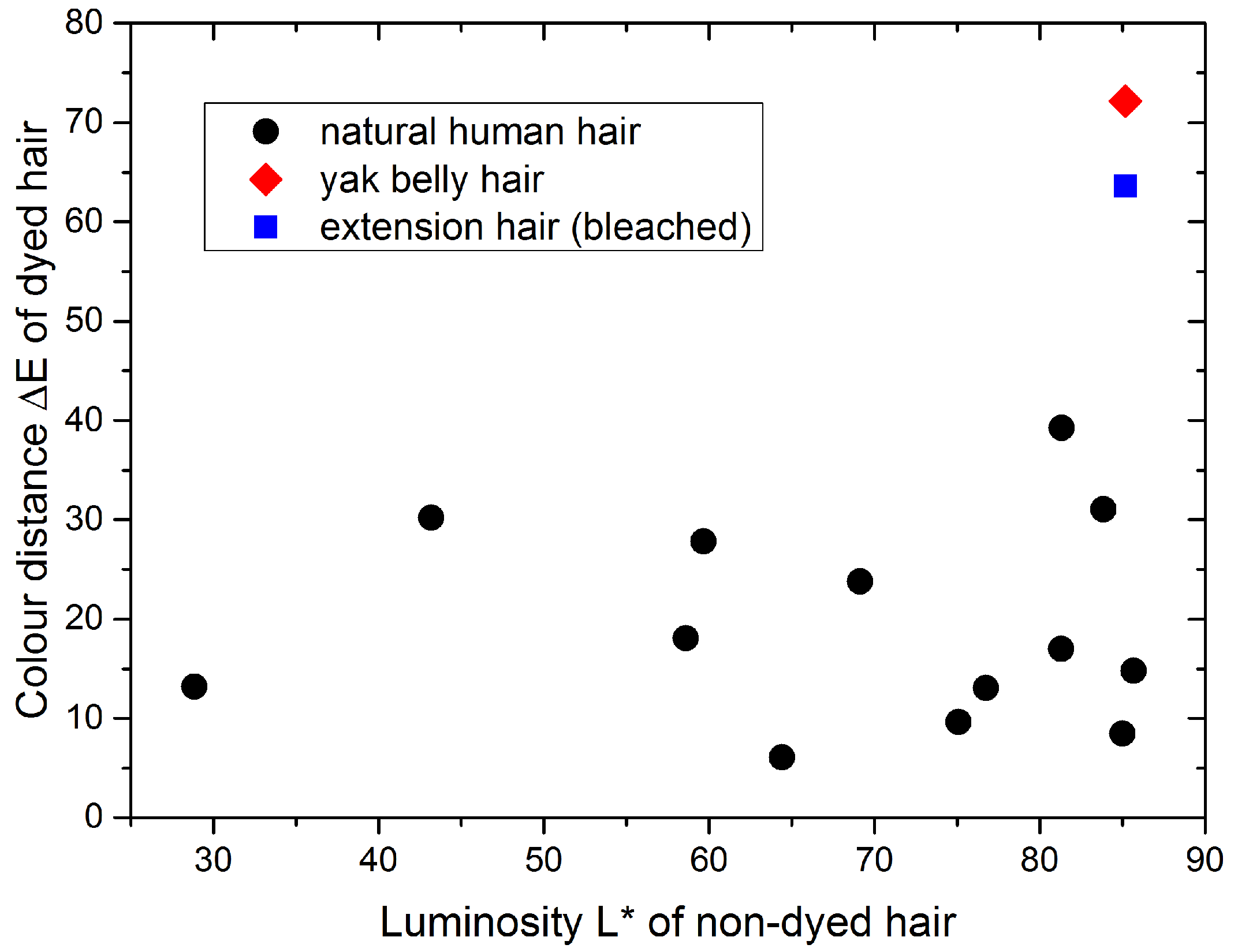
2.1. Colorimetry
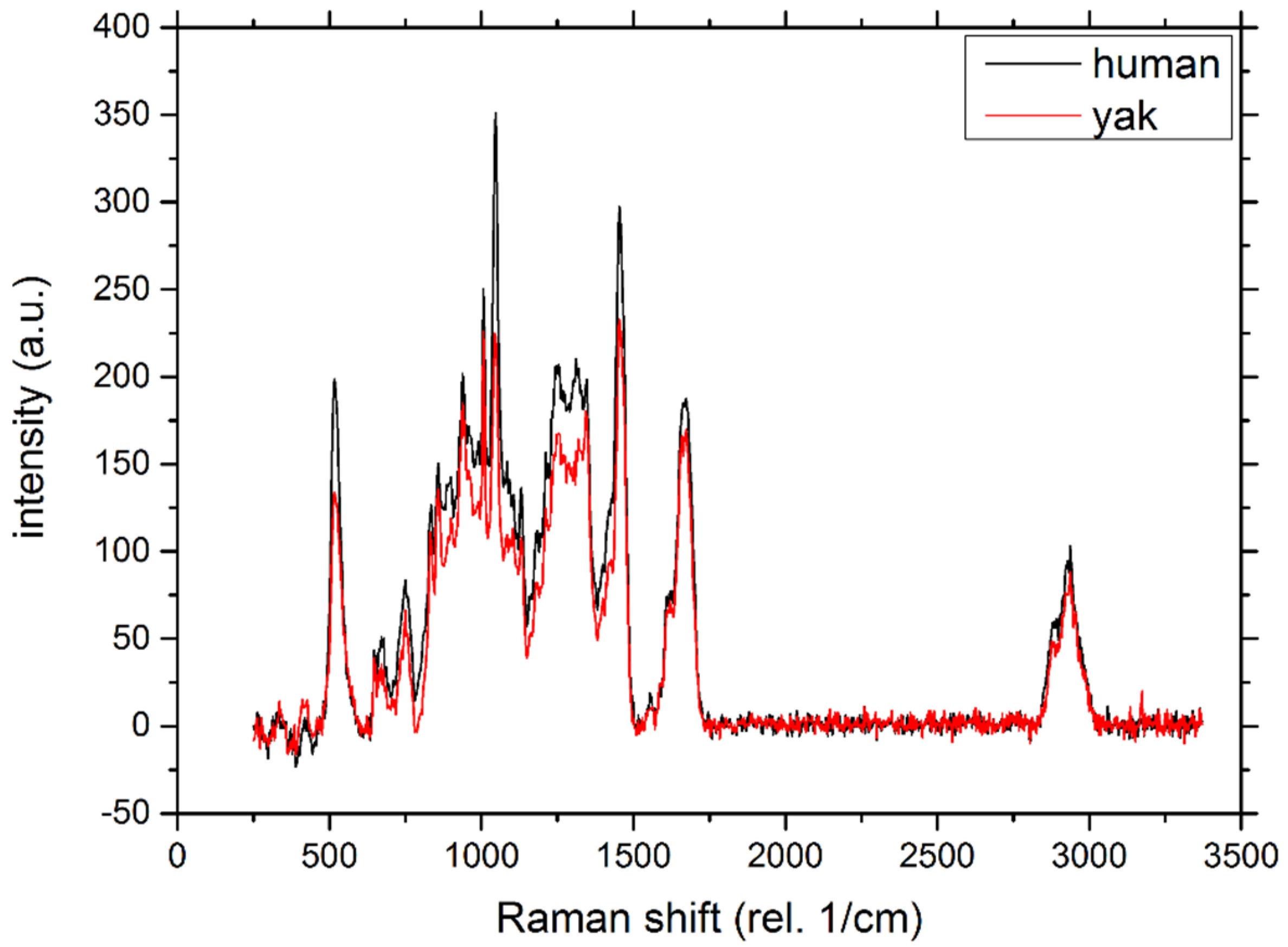
2.2. Raman Spectroscopy
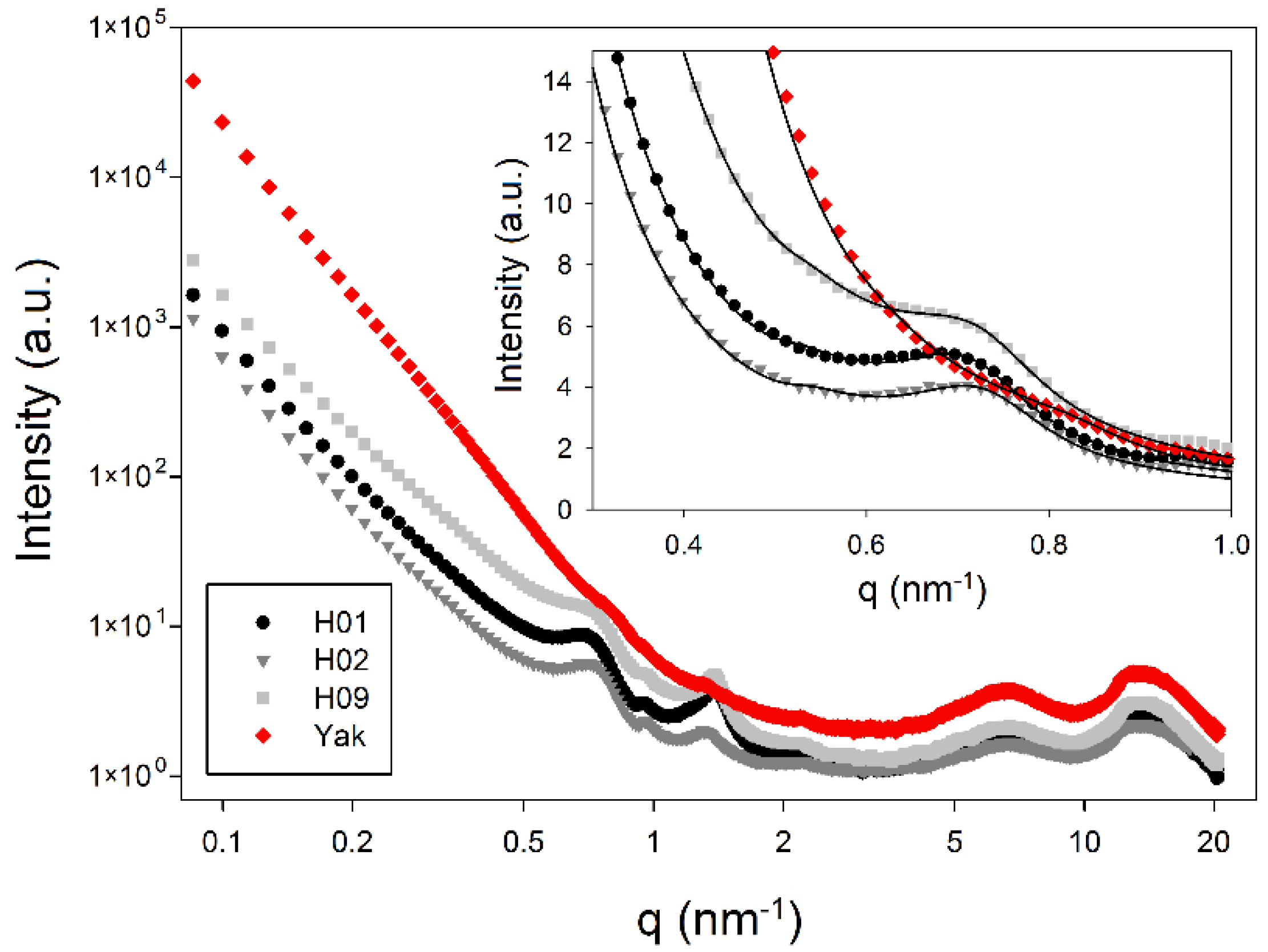
2.3. Nanostructure from Small-Angle X-ray Scattering (SAXS)
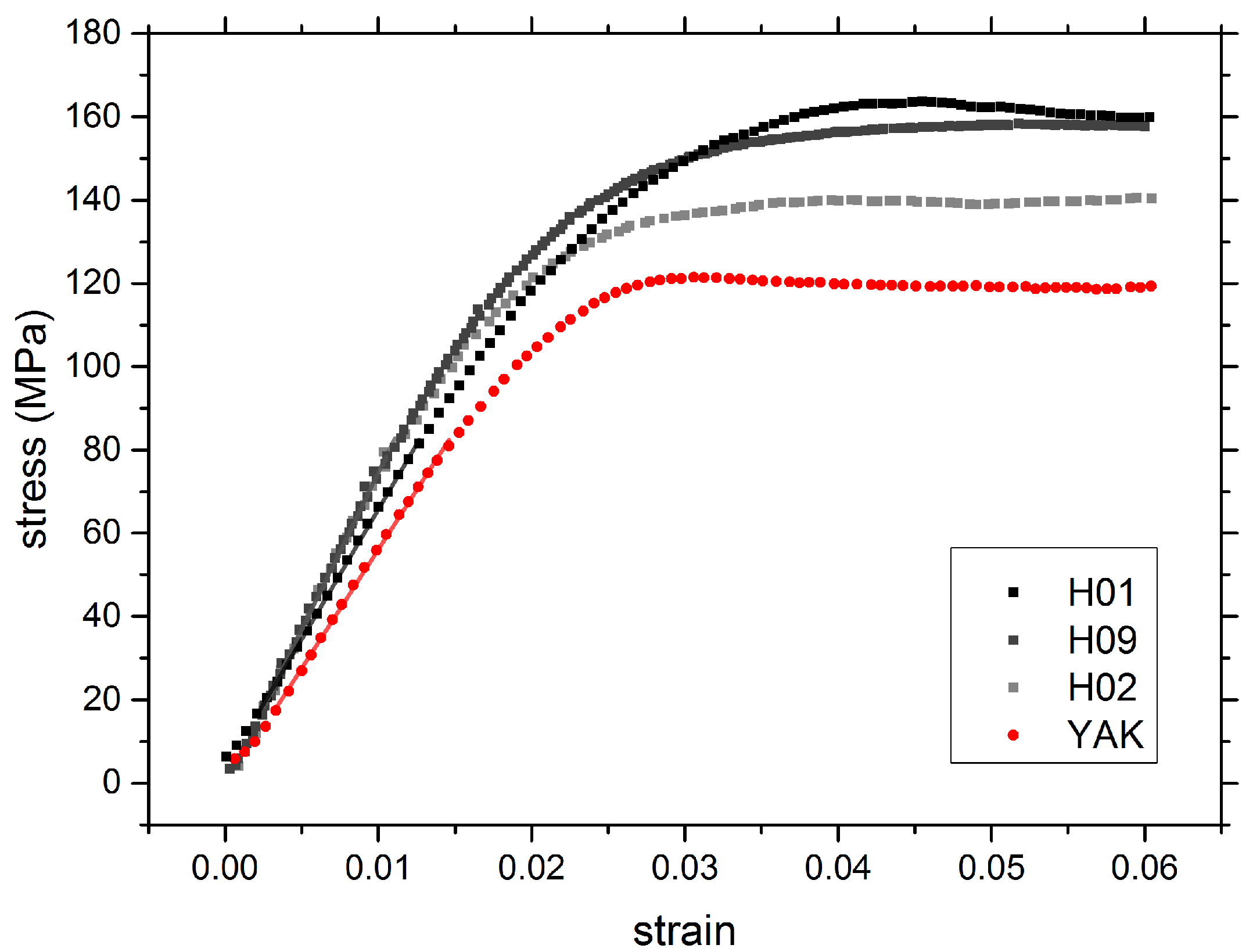
2.4. Mechanical Properties
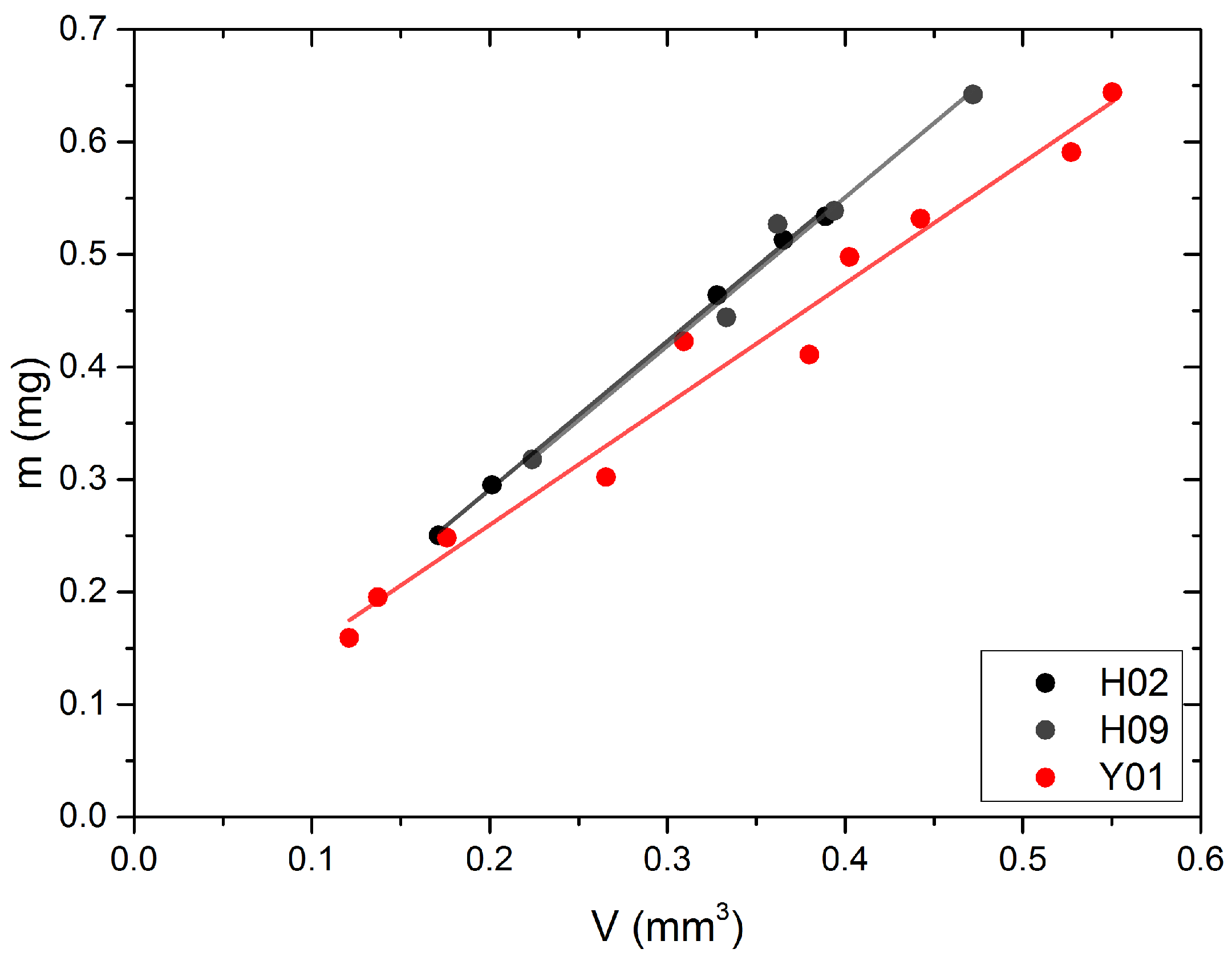
2.5. Density
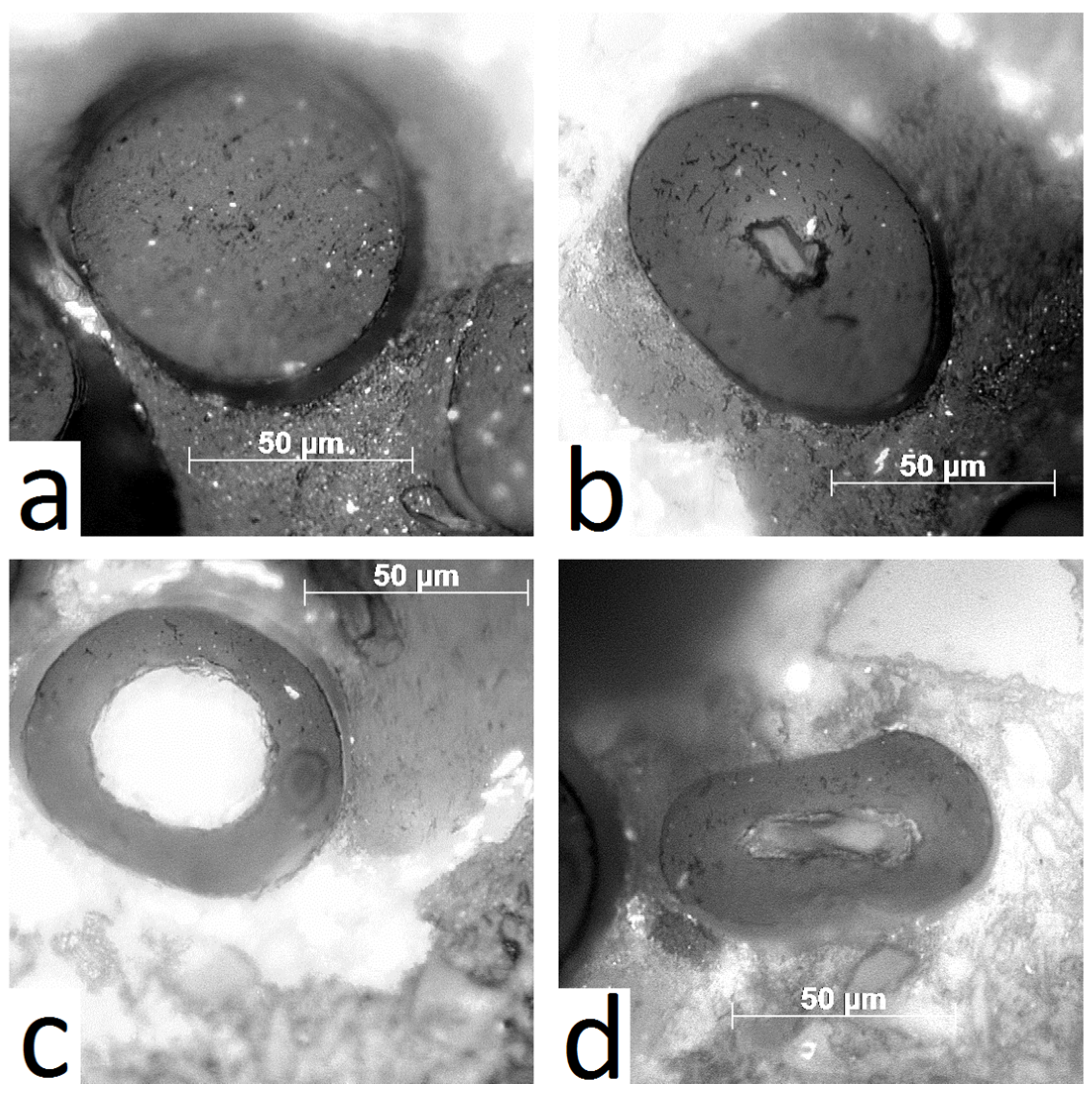
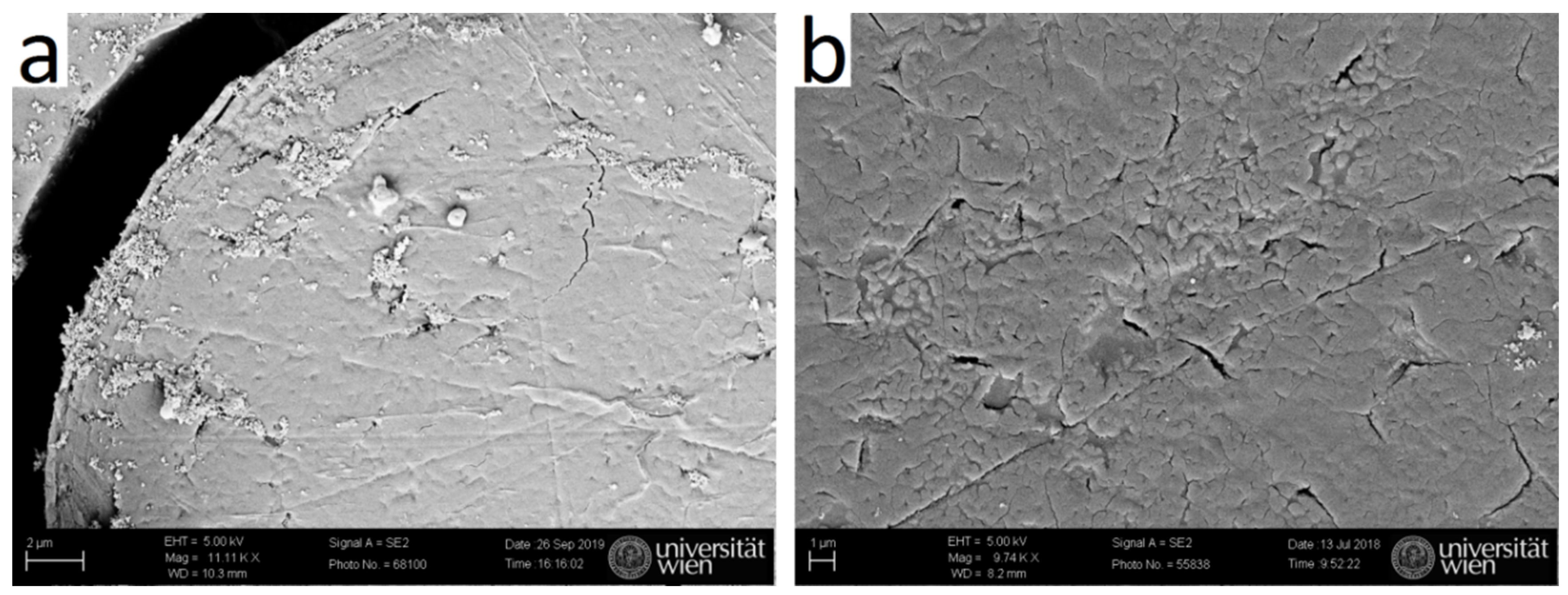
2.6. Optical Microscopy (OM) and Scanning Electron Microscopy (SEM)
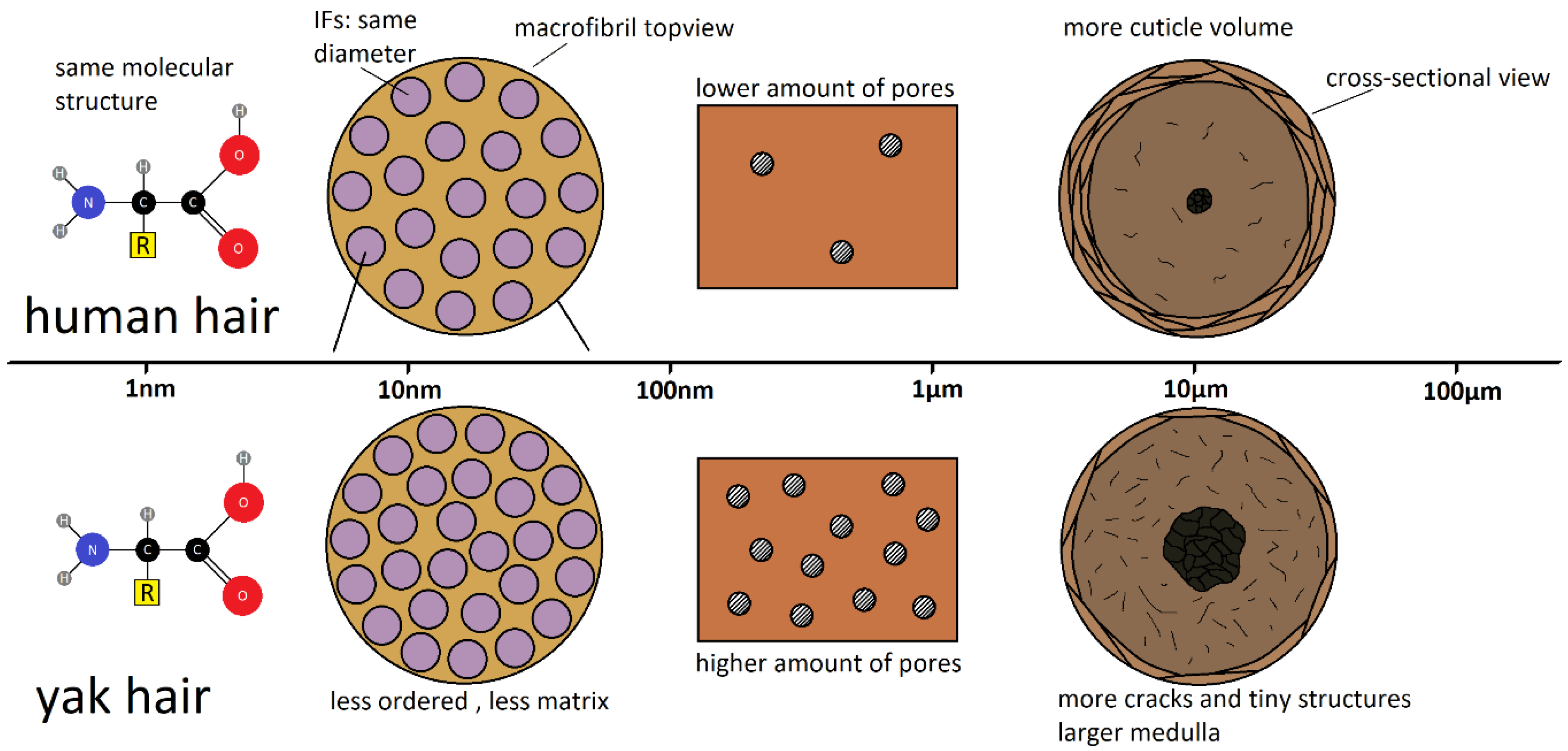
3. Discussion and Conclusions
4. Materials and Methods
4.1. Preparation
4.2. Colorimetry
4.3. Raman Spectroscopy
4.4. SAXS and WAXS
4.5. Tensile Tests
4.6. Density
4.7. SEM
Author Contributions
Funding
Conflicts of Interest
References
- Gottschaldt, K.-M.; Iggo, A.; Young, D.W. Functional characteristics of mechanoreceptors in sinus hair follicles of the cat. J. Physiol. 1973, 235, 287–315. [Google Scholar] [CrossRef] [PubMed]
- Metwally, S.; Comesana, S.M.; Zarzyka, M.; Szewczyk, P.K.; Karbowniczek, J.E.; Stachewicz, U. Thermal insulation design bioinspired by microstructure study of penguin feather and polar bear hair. Acta Biomater. 2019, 91, 270–283. [Google Scholar] [CrossRef] [PubMed]
- Catania, K.C. No taming the shrew. Nat. Hist. 2008, 117, 56–60. [Google Scholar]
- Amador, G.J.; Hu, D.L. Cleanliness is next to godliness: Mechanisms for staying clean. J. Exp. Biol. 2015, 218, 3164–3174. [Google Scholar] [CrossRef]
- Popescu, C.; Höcker, H. Hair—The most sophisticated biological composite material. Chem. Soc. Rev. 2007, 36, 1282–1291. [Google Scholar] [CrossRef]
- Bartman, E. Hair and the artifice of Roman female adornment. Am. J. Archaeol. 2001, 105, 1–25. [Google Scholar] [CrossRef]
- Pudney, P.D.A.; Bonnist, E.Y.M.; Mutch, K.J.; Nicholls, R.; Rieley, H.; Stanfield, S. Confocal raman spectroscopy of whole hairs. Appl. Spectrosc. 2013, 67, 1408–1416. [Google Scholar] [CrossRef]
- Chen, N.; Bhushan, B. Morphological, nanomechanical and cellular structural characterization of human hair and conditioner distribution using torsional resonance mode with an atomic force microscope. J. Microsc. 2005, 220, 96–112. [Google Scholar] [CrossRef]
- Paquin, R.; Colomban, P. Nanomechanics of single keratin fibres: A Raman study of the alphahelix → beta-sheet transition and the effect of water. J. Raman Spectrosc. 2007, 38, 504–514. [Google Scholar] [CrossRef]
- Kuzuhara, A.; Fujiwara, N.; Hori, T. Analysis of internal structure changes in black human hair keratin fibers with aging using raman spectroscopy. Biopolymers 2007, 87, 134–140. [Google Scholar] [CrossRef]
- Fraser, R.D.B.; Macrae, T.P.; Parry, D.A.D.; Suzuki, E. Intermediate filaments in a-keratins. Proc. Natl. Acad. Sci. USA 1986, 83, 1179–1183. [Google Scholar] [CrossRef] [PubMed]
- Parry, D.A.D.; Steinert, P.M. Intermediate filaments: Molecular architecture, assembly, dynamics and polymorphism. Q. Rev. Biophys. 1999, 32, 99–187. [Google Scholar] [CrossRef] [PubMed]
- Fraser, R.D.B.; Parry, D.A.D. The three-dimensional structure of trichocyte (hard α-) keratin intermediate filaments: Features of the molecular packing deduced from the sites of induced crosslinks. J. Struct. Biol. 2005, 151, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Fraser, R.D.B.; Parry, D.A.D. The three-dimensional structure of trichocyte (hard α-) keratin intermediate filaments: The nature of the repeating unit. J. Struct. Biol. 2006, 155, 375–378. [Google Scholar] [CrossRef]
- Fraser, R.D.B.; Parry, D.A.D. The role of disulfide bond formation in the structural transition observed in the intermediate filaments of developing hair. J. Struct. Biol. 2012, 180, 117–124. [Google Scholar] [CrossRef]
- Harland, D.P.; Walls, R.J.; Vernon, J.A.; Dyer, J.M.; Woods, J.L.; Bell, F. Three-dimensional architecture of macrofibrils in the human scalp hair cortex. J. Struct. Biol. 2014, 185, 397–404. [Google Scholar] [CrossRef]
- Wade, M.; Tucker, I.; Cunningham, P.; Skinner, R.; Bell, F.; Lyons, T.; Patten, K.; Gonzalez, L.; Wess, T. Investigating the origins of nanostructural variations in differential ethnic hair types using X-ray scattering techniques. Int. J. Cosmet. Sci. 2013, 35, 430–441. [Google Scholar] [CrossRef]
- Coderch, L.; Méndez, S.; Barba, C.; Pons, R.; Martí, M.; Parra, J.L. Lamellar rearrangement of internal lipids from human hair. Chem. Phys. Lipids 2008, 155, 1–6. [Google Scholar] [CrossRef]
- Stanić, V.; Bettini, J.; Montoro, F.E.; Stein, A.; Evans-Lutterodt, K. Local structure of human hair spatially resolved by sub-micron X-ray beam. Sci. Rep. 2015, 5, 17347. [Google Scholar] [CrossRef]
- Bornschlögl, T.; Bildstein, L.; Thibaut, S.; Santoprete, R.; Fiat, F.; Luengo, G.S.; Doucet, J.; Bernard, B.A.; Baghdadli, N. Keratin network modifications lead to the mechanical stiffening of the hair follicle fiber. Proc. Natl. Acad. Sci. USA 2016, 113, 5940–5945. [Google Scholar] [CrossRef]
- Kreplak, L.; Doucet, J.; Dumas, P.; Briki, F. New aspects of the α-helix to β-sheet transition in stretched hard α-keratin fibers. Biophys. J. 2004, 87, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Yang, W.; Wang, B.; Meyers, M.A. Structure and mechanical behavior of human hair. Mater. Sci. Eng. C 2017, 73, 152–163. [Google Scholar] [CrossRef] [PubMed]
- Bhushan, B.; Chen, N. AFM studies of environmental effects on nanomechanical properties and cellular structure of human hair. Ultramicroscopy 2006, 106, 755–764. [Google Scholar] [CrossRef] [PubMed]
- Bloch, L.D.; Goshiyama, A.M.; Dario, M.F.; Escudeiro, C.C.; Sarruf, F.D.; Velasco, M.V.R.; Valente, N.Y.S. Chemical and physical treatments damage Caucasian and Afro-ethnic hair fibre: Analytical and image assays. J. Eur. Acad. Dermatol. Venereol. 2019, 33, 2158–2167. [Google Scholar] [CrossRef]
- Scanavez, C.; Zoega, M.; Barbosa, A.; Joekes, I. Scanavez diffuse reflectance spectrophotometry.pdf. J. Cosmet. Sci. 2000, 51, 289–302. [Google Scholar]
- Essendoubi, M.; Meunier, M.; Scandolera, A.; Gobinet, C.; Manfait, M.; Lambert, C.; Auriol, D.; Reynaud, R.; Piot, O. Conformation changes in human hair keratin observed using confocal Raman spectroscopy after active ingredient application. Int. J. Cosmet. Sci. 2019, 41, 203–212. [Google Scholar] [CrossRef]
- Er Rafik, M.; Doucet, J.; Briki, F. The intermediate filament architecture as determined by x-ray diffraction modeling of hard α-keratin. Biophys. J. 2004, 86, 3893–3904. [Google Scholar] [CrossRef]
- Kreplak, L.; Franbourg, A.; Briki, F.; Leroy, F.; Dalle, D.; Doucet, J. A new deformation model of hard α-keratin fibers at the nanometer scale: Implications for hard α-keratin intermediate filament mechanical properties. Biophys. J. 2002, 82, 2265–2274. [Google Scholar] [CrossRef][Green Version]
- Busson, B.; Engström, P.; Doucet, J. Existence of various structural zones in keratinous tissues revealed by X-ray microdiffraction. J. Synchrotron Radiat. 1999, 6, 1021–1030. [Google Scholar] [CrossRef]
- Hosemann, R. Crystalline and paracrystalline order in high polymers. J. Appl. Phys. 1963, 34, 25–41. [Google Scholar] [CrossRef]
- Busson, B.; Doucet, J. Distribution and interference function for two-dimensional hexagonal paracrystals. Acta Crystallogr. Sect. A Found. Crystallogr. 2000, A56, 68–72. [Google Scholar] [CrossRef] [PubMed]
- Briki, F.; Busson, B.; Doucet, J. Organization of microfibrils in keratin fibers studied by X-ray scattering: Modelling using the paracrystal concept. Biochim. Biophys. Acta 1998, 1429, 57–68. [Google Scholar] [CrossRef]
- Hashimoto, T.; Kawamura, T.; Harada, M.; Tanaka, H. Small-angle scattering from hexagonally packed cylindrical particles with paracrystalline distortion. Macromolecules 1994, 27, 3063–3072. [Google Scholar] [CrossRef]
- Marx, A.; Pless, J.; Mandelkow, E.M.; Mandelkow, E. On the rigidity of the cytoskeleton: Are MAPs crosslinkers or spacers of microtubules? Cell. Mol. Biol. 2000, 46, 949–965. [Google Scholar] [PubMed]
- Fraser, R.; Macrae, T. Structural implications of the equatorial X-ray diffraction pattern of α-keratin. Biochim. Biophys. Acta 1958, 29, 229–240. [Google Scholar] [CrossRef]
- Parry, D.A.D. Hard α-keratin intermediate filaments: An alternative interpretation of the low-angle equatorial X-ray diffraction pattern, and the axial disposition of putative disulphide bonds in the intra- and inter protofilamentous networks. Int. J. Biol. Macromol. 1996, 19, 45–50. [Google Scholar] [CrossRef]
- Gourrier, A.; Wagermaier, W.; Burghammer, M.; Lammie, D.; Gupta, H.S.; Fratzl, P.; Riekel, C.; Wess, T.J.; Paris, O. Scanning X-ray imaging with small-angle scattering. J. Appl. Crystallogr. 2007, 40, s78–s82. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds (human hair as received and with dye, yak hair as received and with dye) are available from the authors. |




| Measured Values | Human Hair | Yak Hair |
|---|---|---|
| Lattice parameter d (nm) | 8.37 ± 0.10 | 7.27 ± 0.08 |
| IF distance <a> (nm) | 9.66 ± 0.11 | 8.40 ± 0.10 |
| Core radius R (nm) | 3.40 ± 0.09 | 3.54 ± 0.12 |
| Matrix thickness m (nm) | 2.86 ± 0.15 | 1.32 ± 0.15 |
| Axial stagger distance (nm) | 6.54 ± 0.05 | 6.65 ± 0.05 |
| Lipid layer distance (nm) | 4.62 ± 0.14 | 4.74 ± 0.10 |
| Power law background n | 2.9 ± 0.1 | 4 |
| Measured Value | Human (GPa) | Yak (GPa) |
|---|---|---|
| Young’s modulus | 7.11 ± 0.44 | 5.76 ± 0.04 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müllner, A.R.M.; Pahl, R.; Brandhuber, D.; Peterlik, H. Porosity at Different Structural Levels in Human and Yak Belly Hair and Its Effect on Hair Dyeing. Molecules 2020, 25, 2143. https://doi.org/10.3390/molecules25092143
Müllner ARM, Pahl R, Brandhuber D, Peterlik H. Porosity at Different Structural Levels in Human and Yak Belly Hair and Its Effect on Hair Dyeing. Molecules. 2020; 25(9):2143. https://doi.org/10.3390/molecules25092143
Chicago/Turabian StyleMüllner, Alexander R. M., Ruben Pahl, Doris Brandhuber, and Herwig Peterlik. 2020. "Porosity at Different Structural Levels in Human and Yak Belly Hair and Its Effect on Hair Dyeing" Molecules 25, no. 9: 2143. https://doi.org/10.3390/molecules25092143
APA StyleMüllner, A. R. M., Pahl, R., Brandhuber, D., & Peterlik, H. (2020). Porosity at Different Structural Levels in Human and Yak Belly Hair and Its Effect on Hair Dyeing. Molecules, 25(9), 2143. https://doi.org/10.3390/molecules25092143







