Unsteady Radiative Natural Convective MHD Nanofluid Flow Past a Porous Moving Vertical Plate with Heat Source/Sink
Abstract
1. Introduction
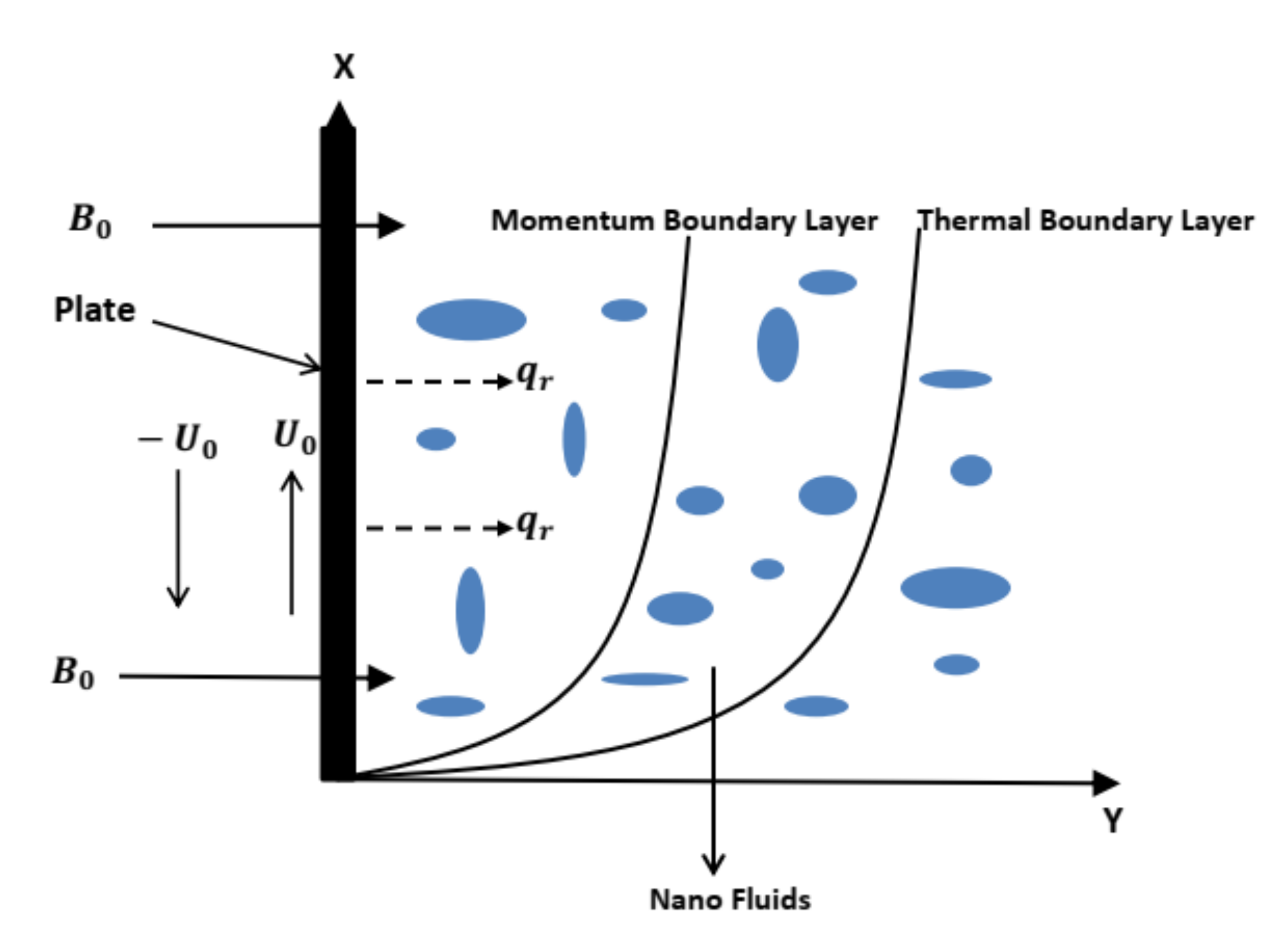
2. Statement of Problem
3. Analytical Solution of Problem
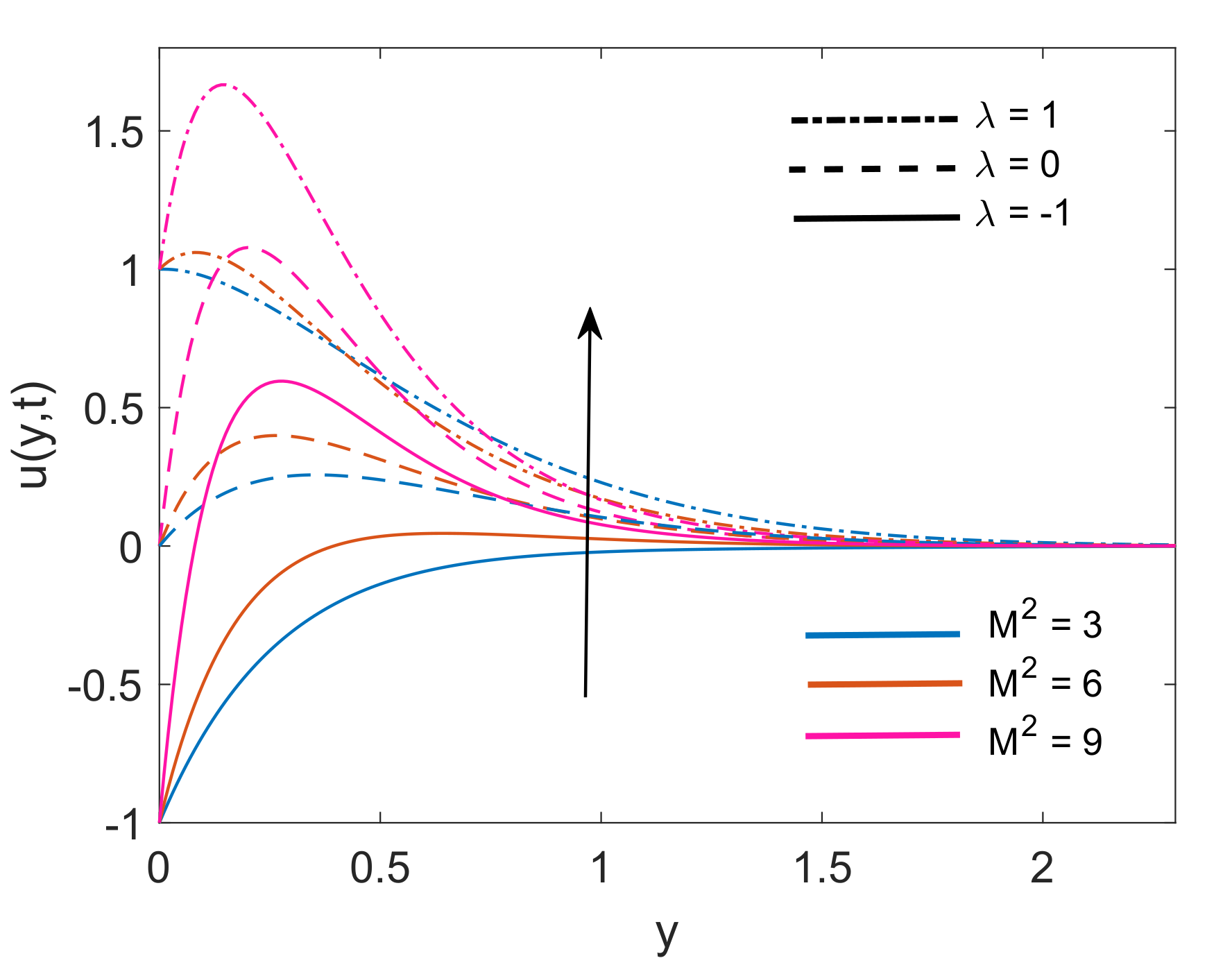
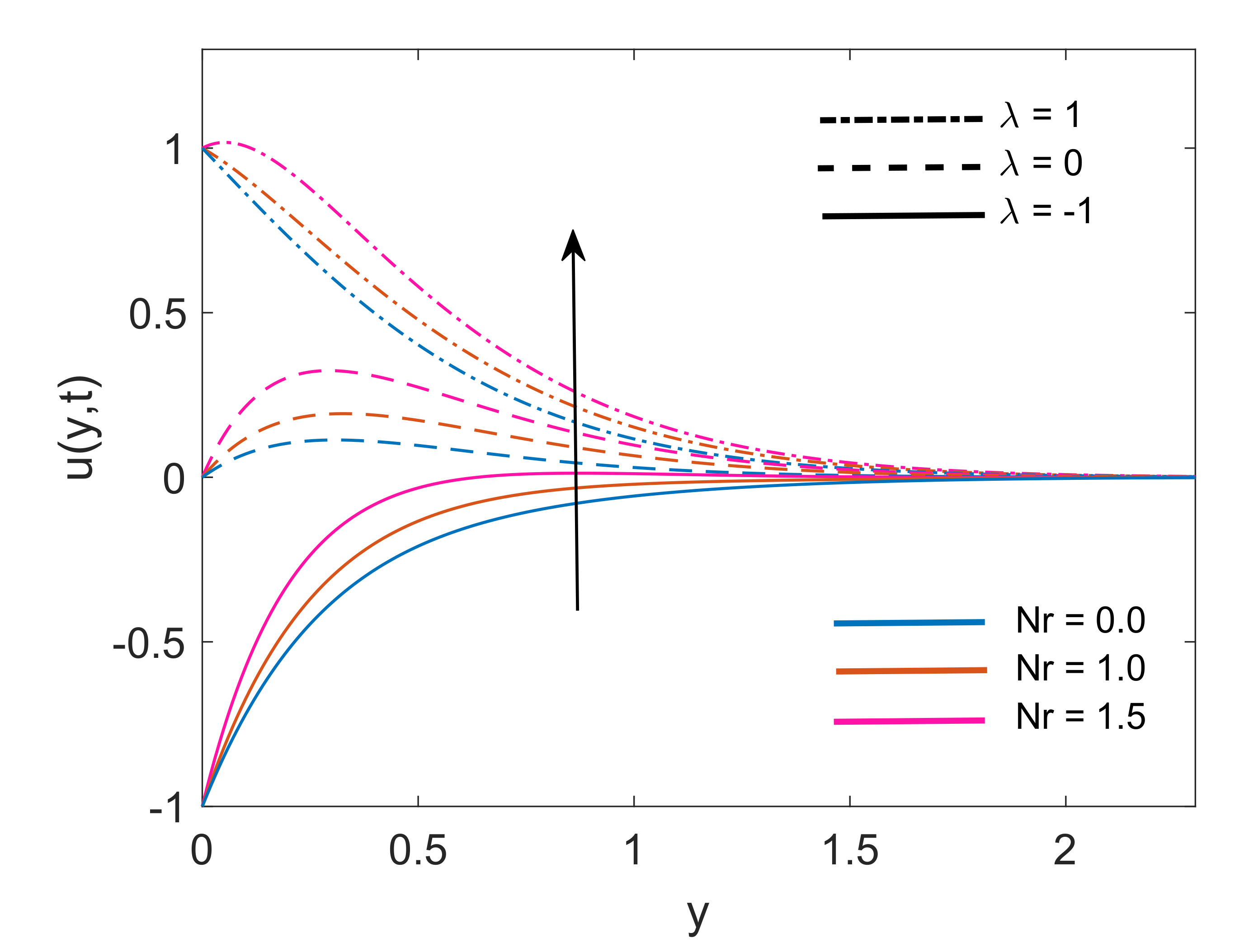
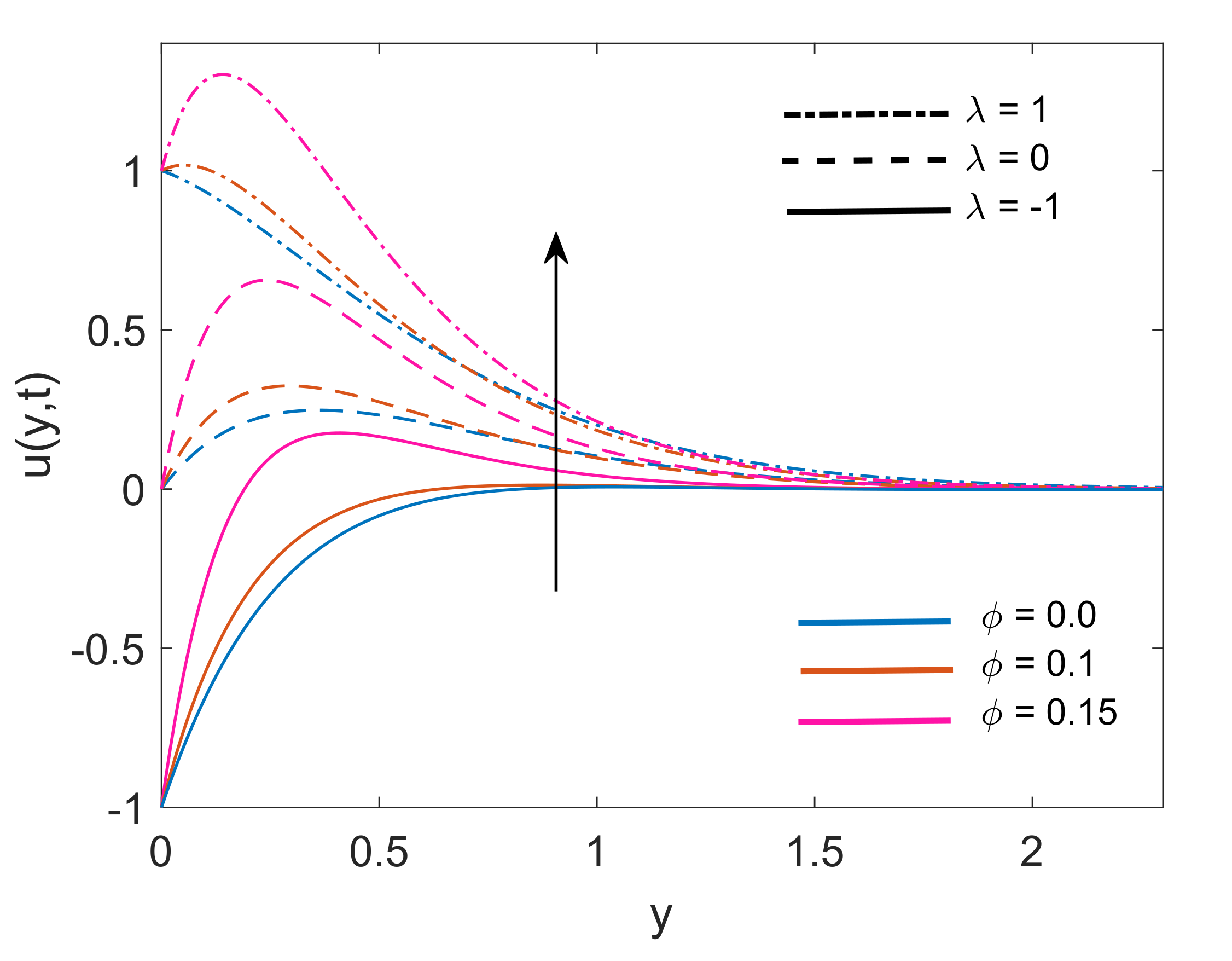
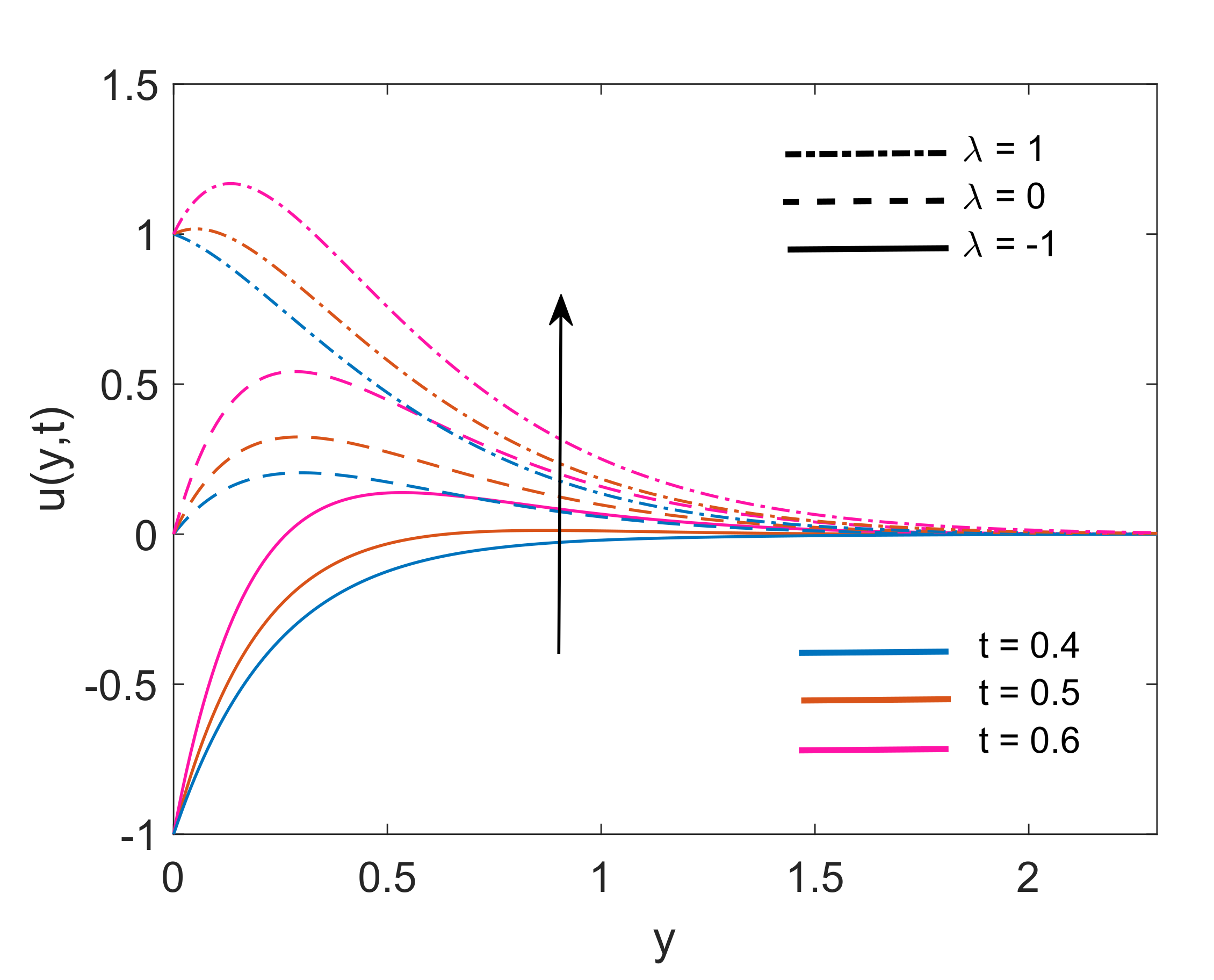
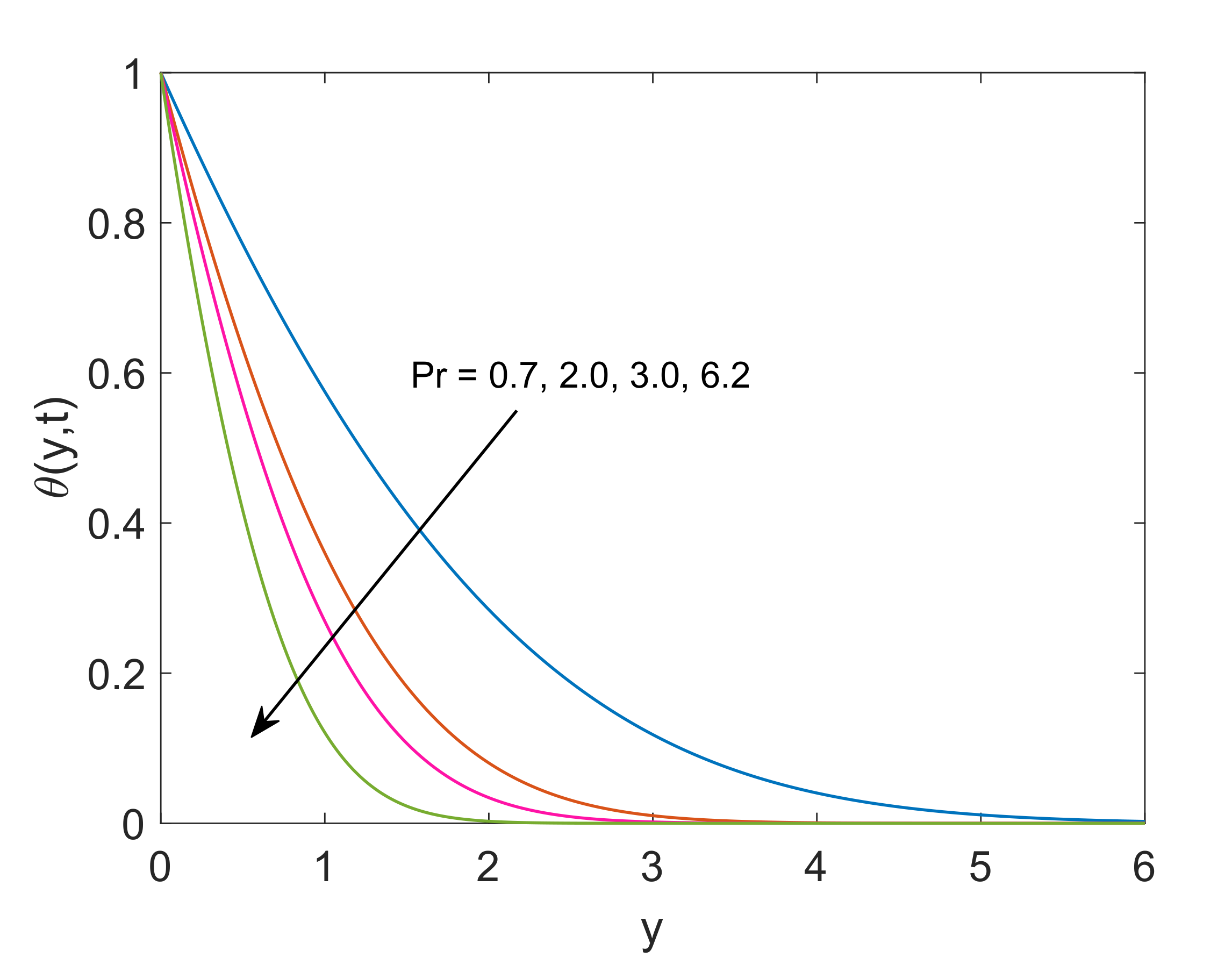
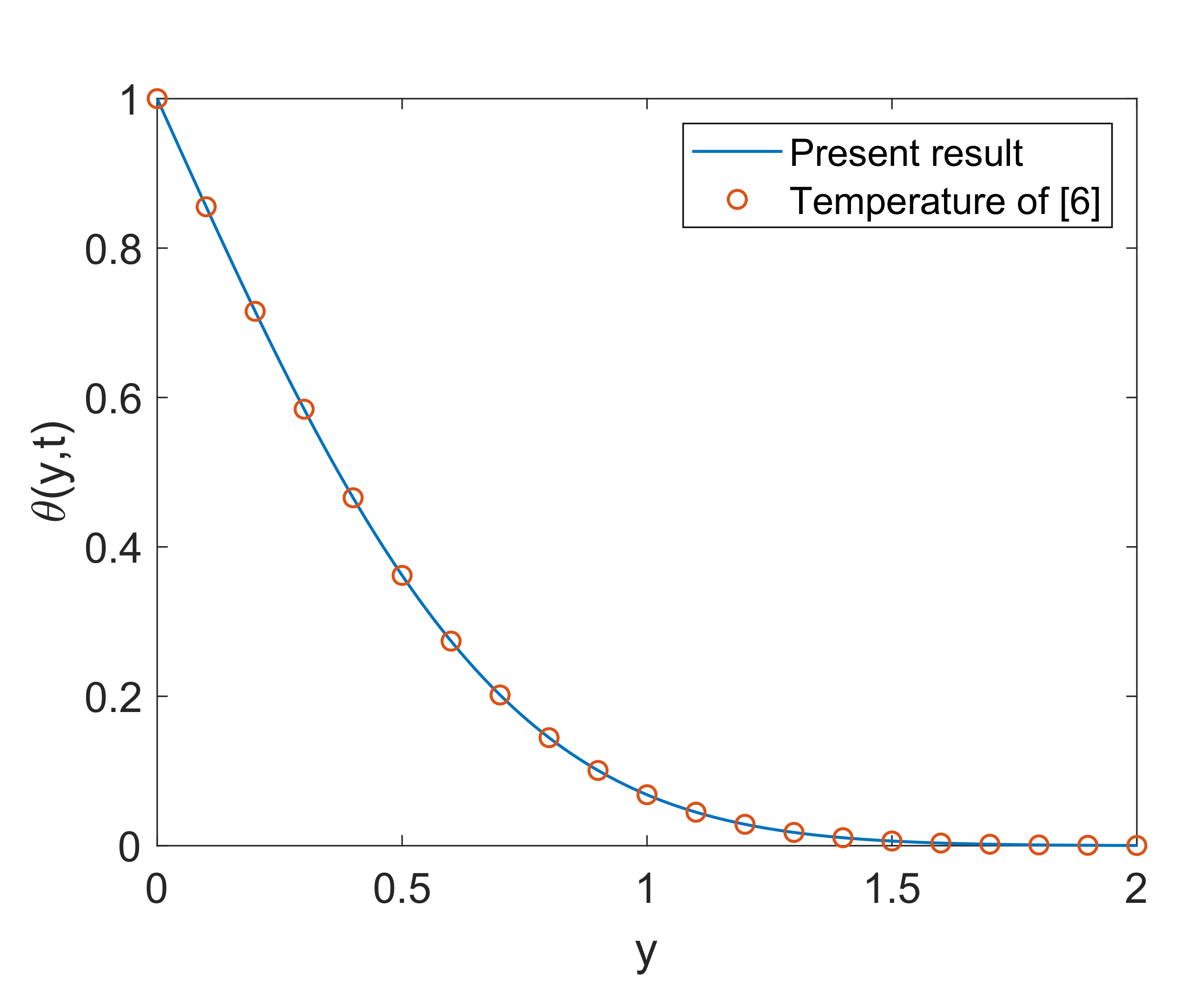
4. Numerical Case Studies
5. Conclusions
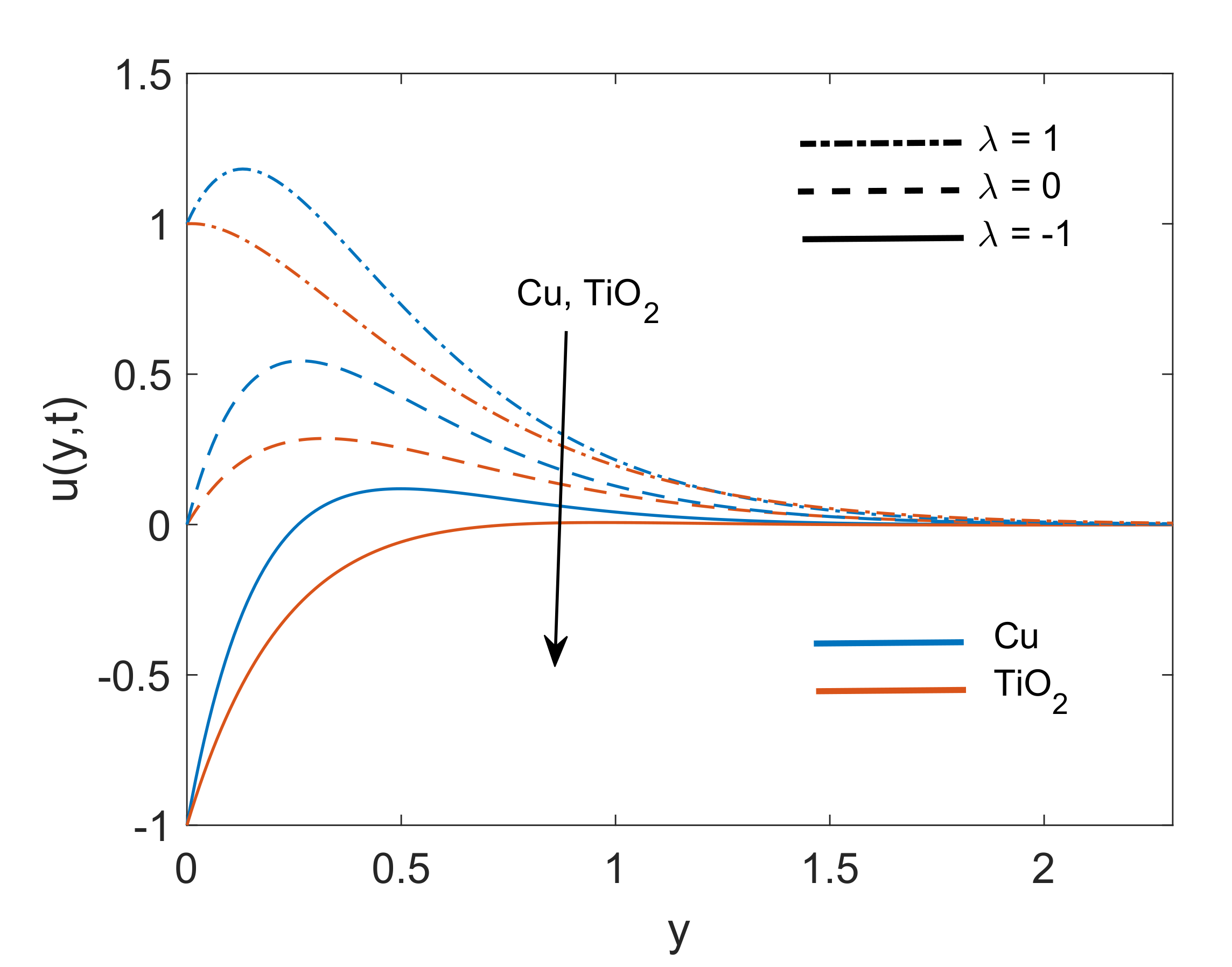
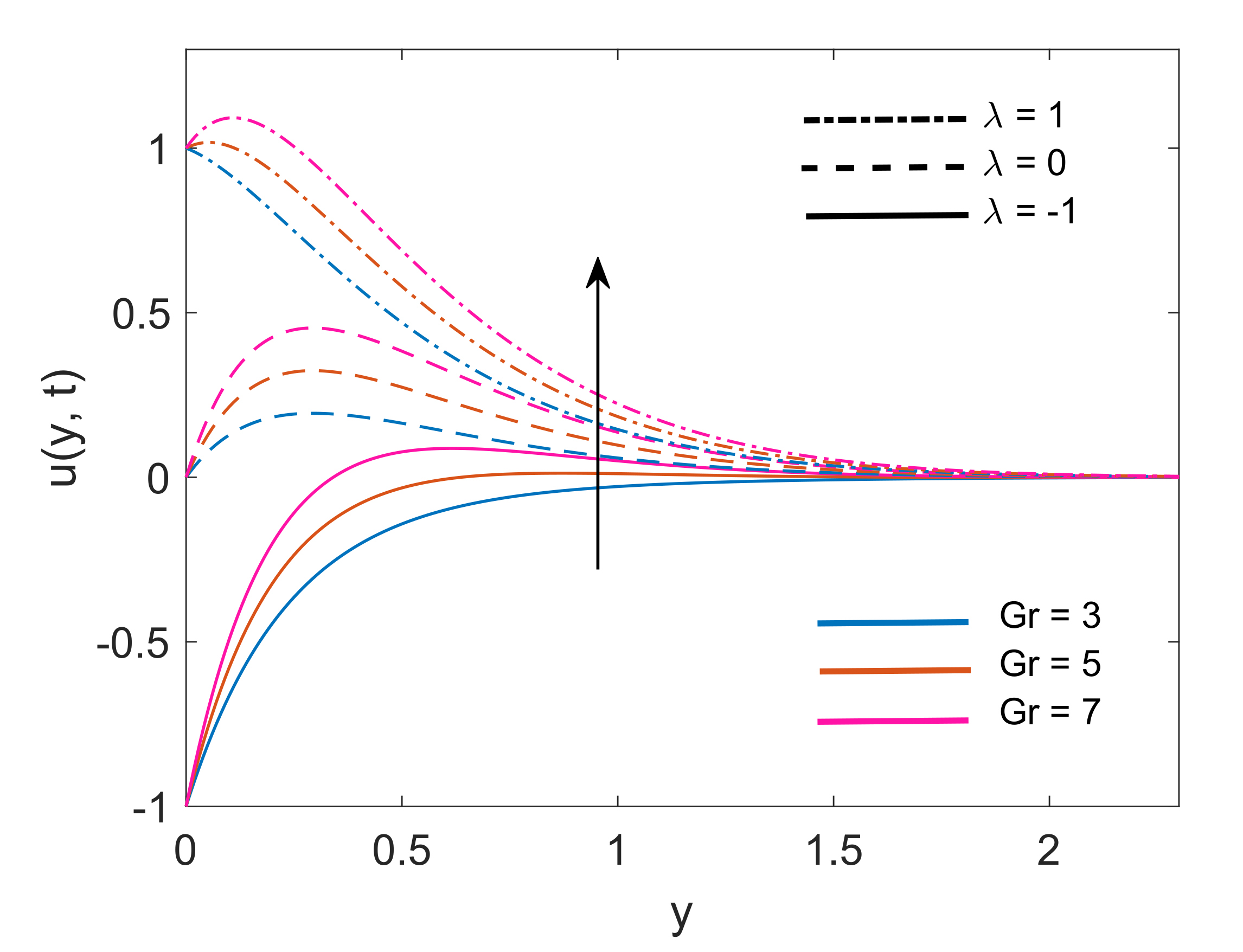
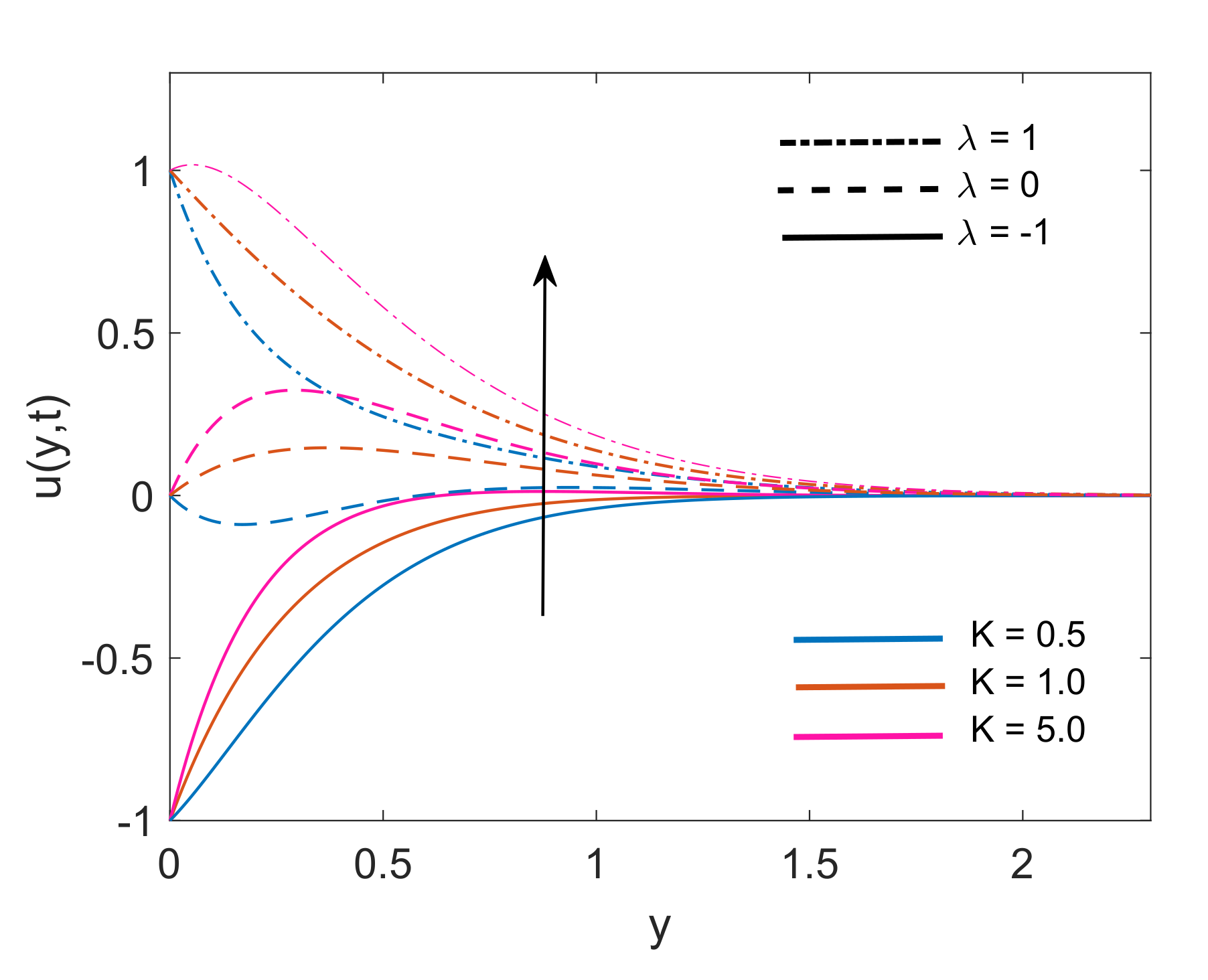
- For both nanofluids, the increase in the porosity parameter, magnetic parameter and Grashof number leads to an increase in the velocity of the fluid.
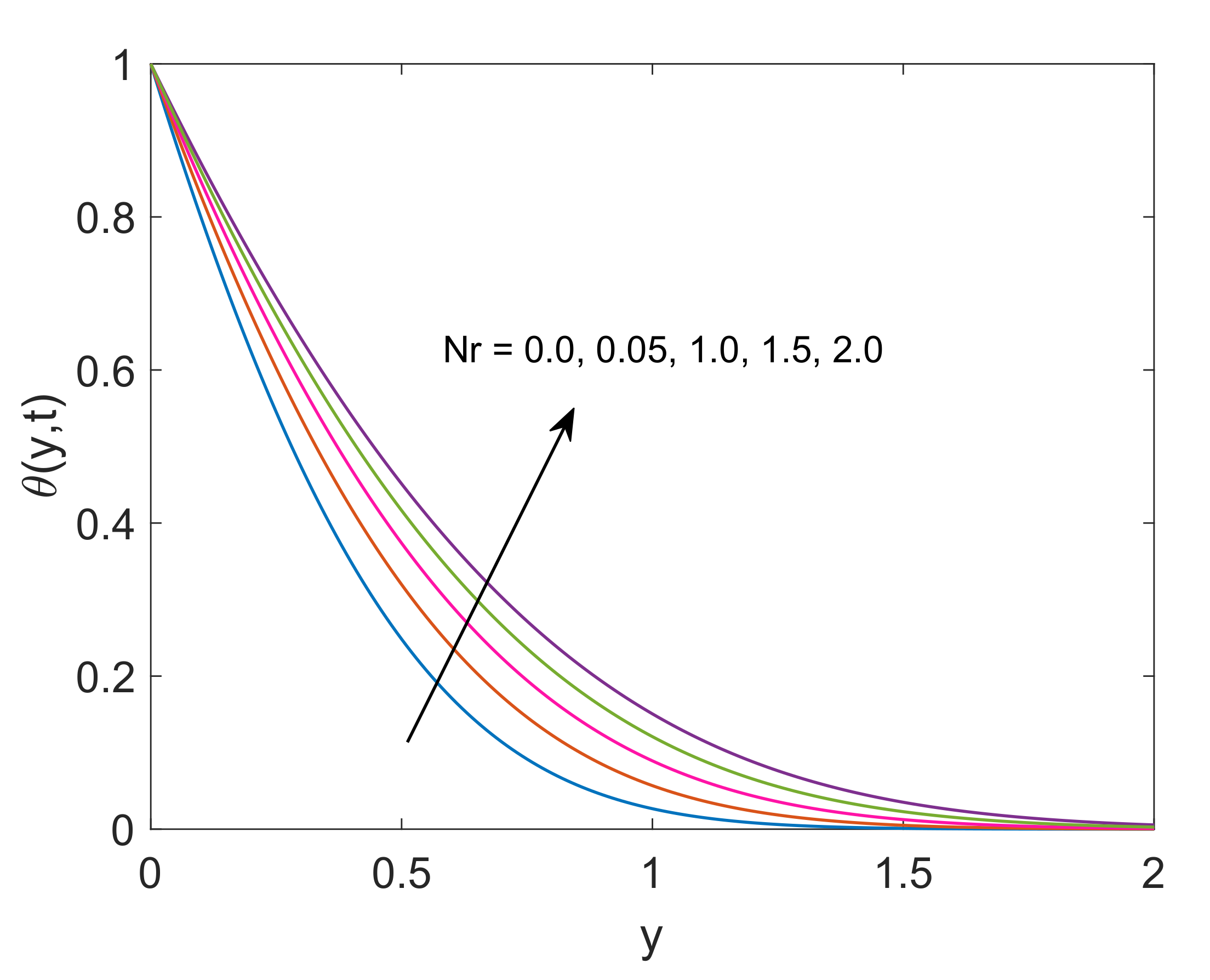
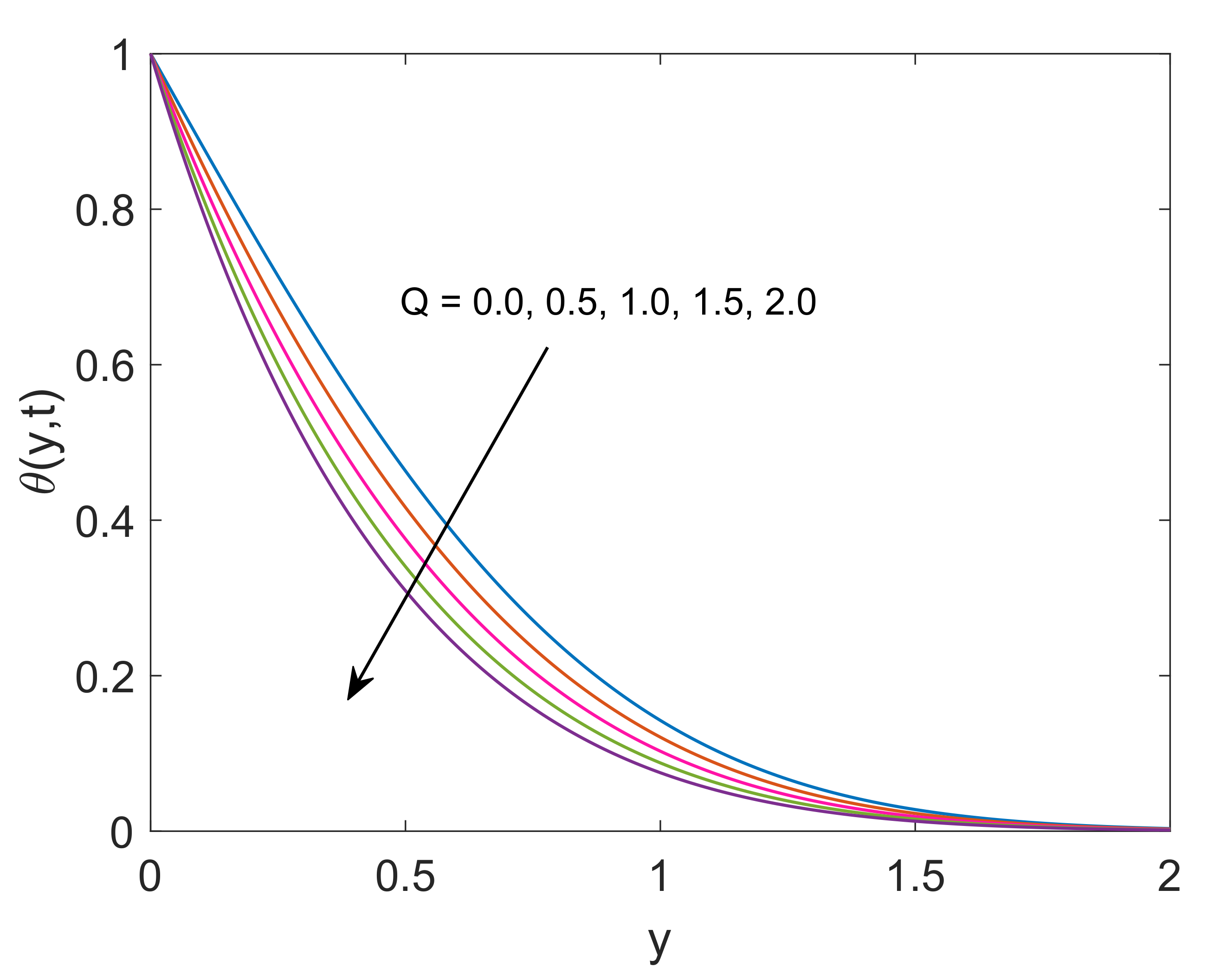
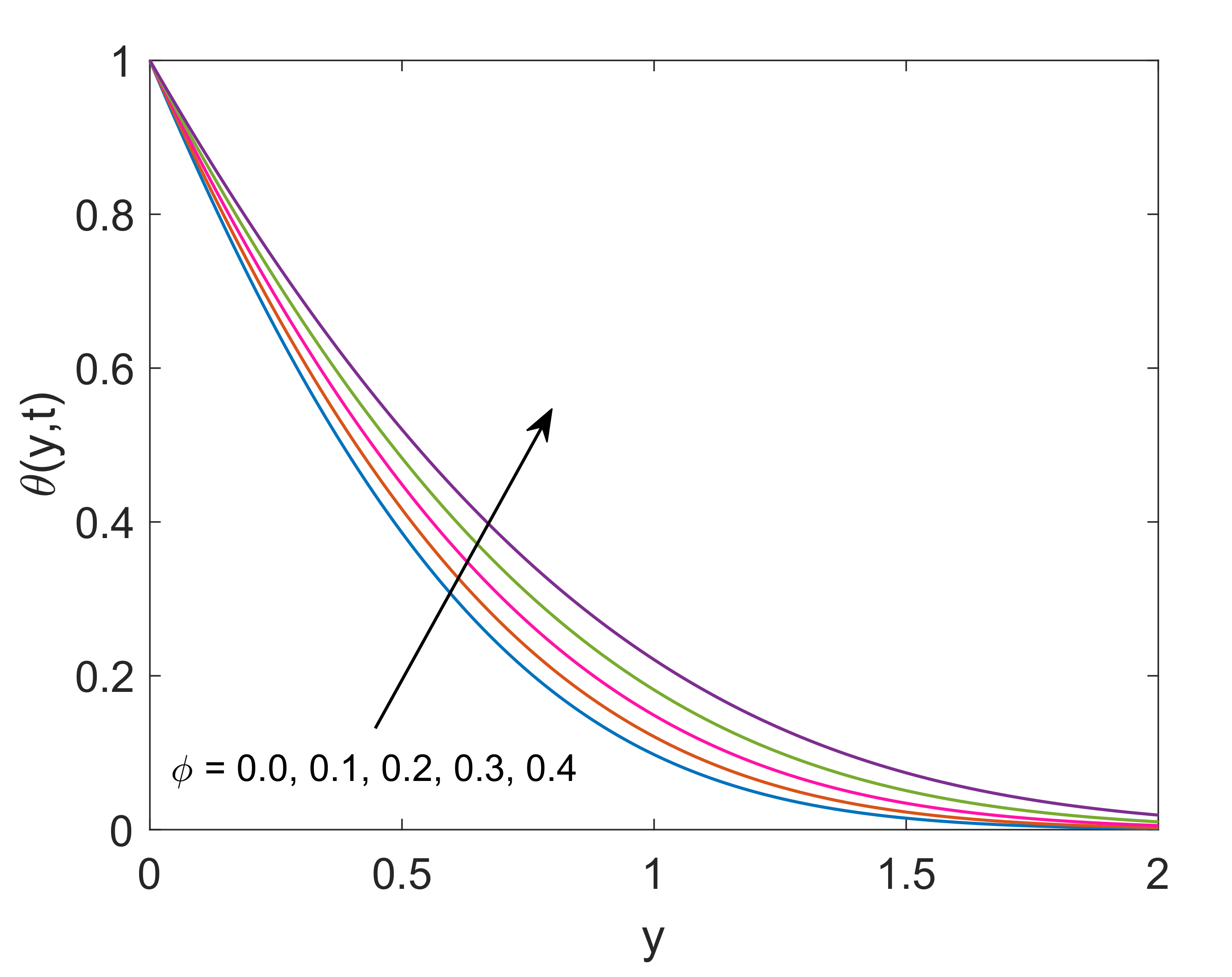
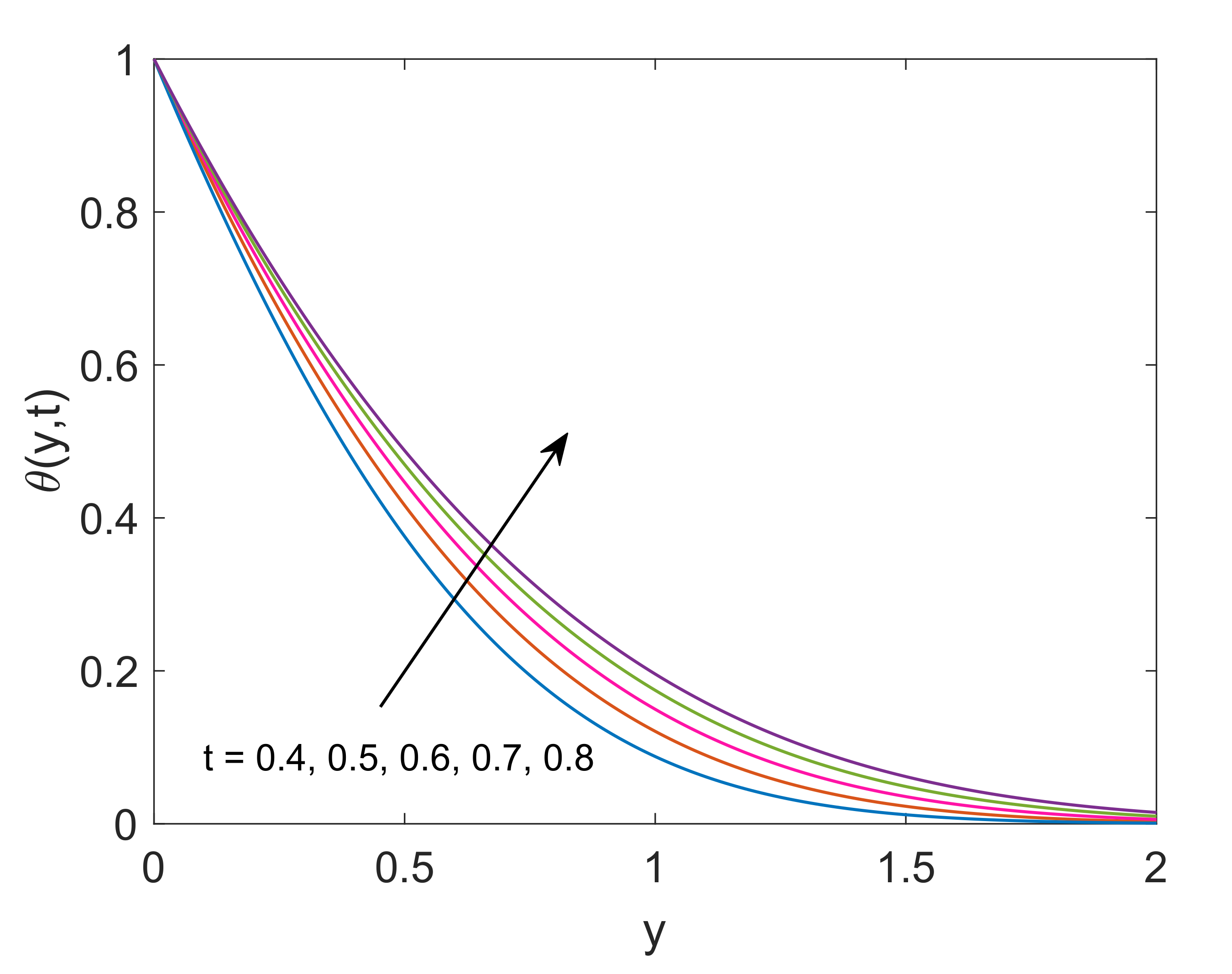
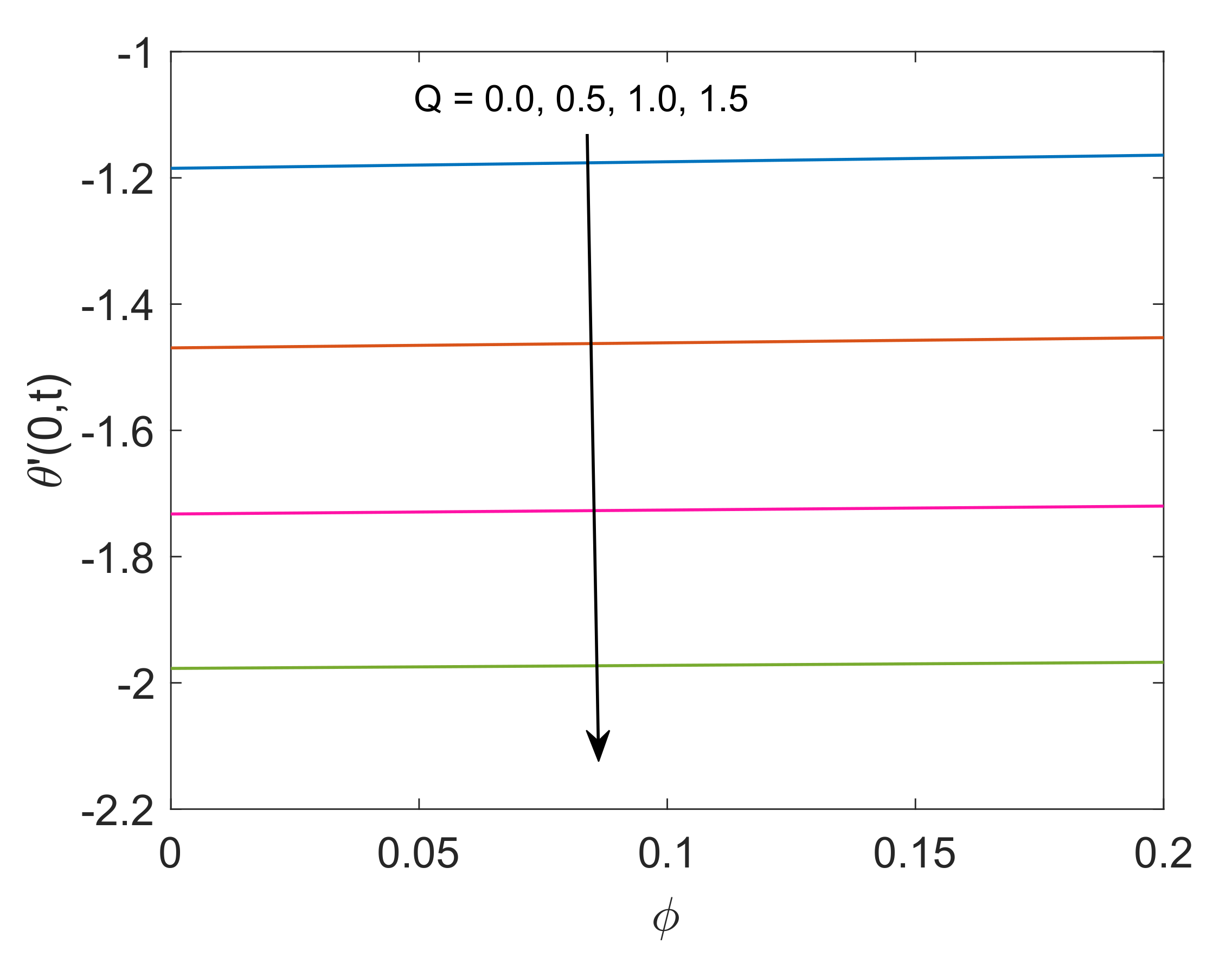
- Temperature of both nanofluids gets elevation with an increase in radiation parameter, while an opposite behavior is noted for increasing values of heat sink parameter.
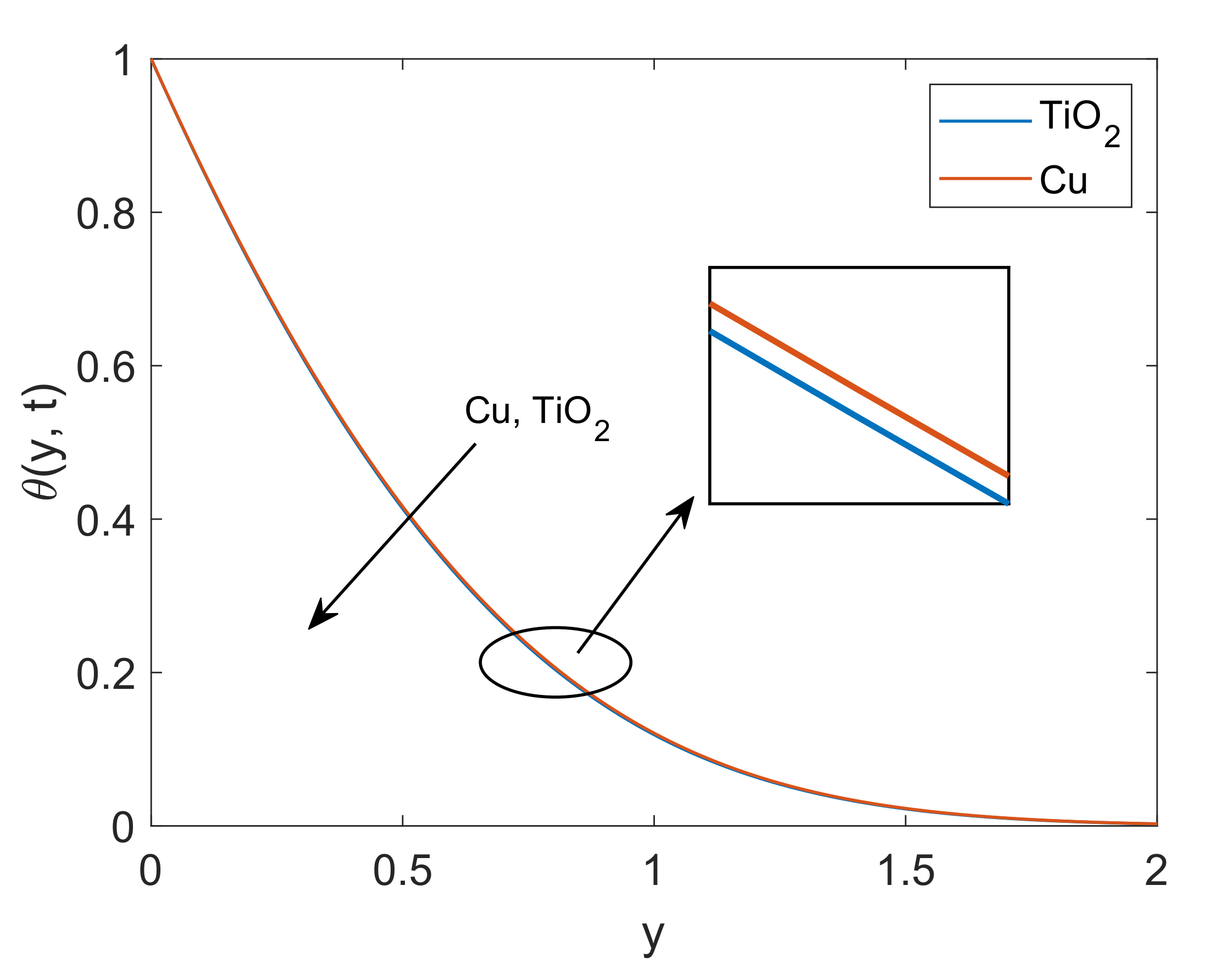
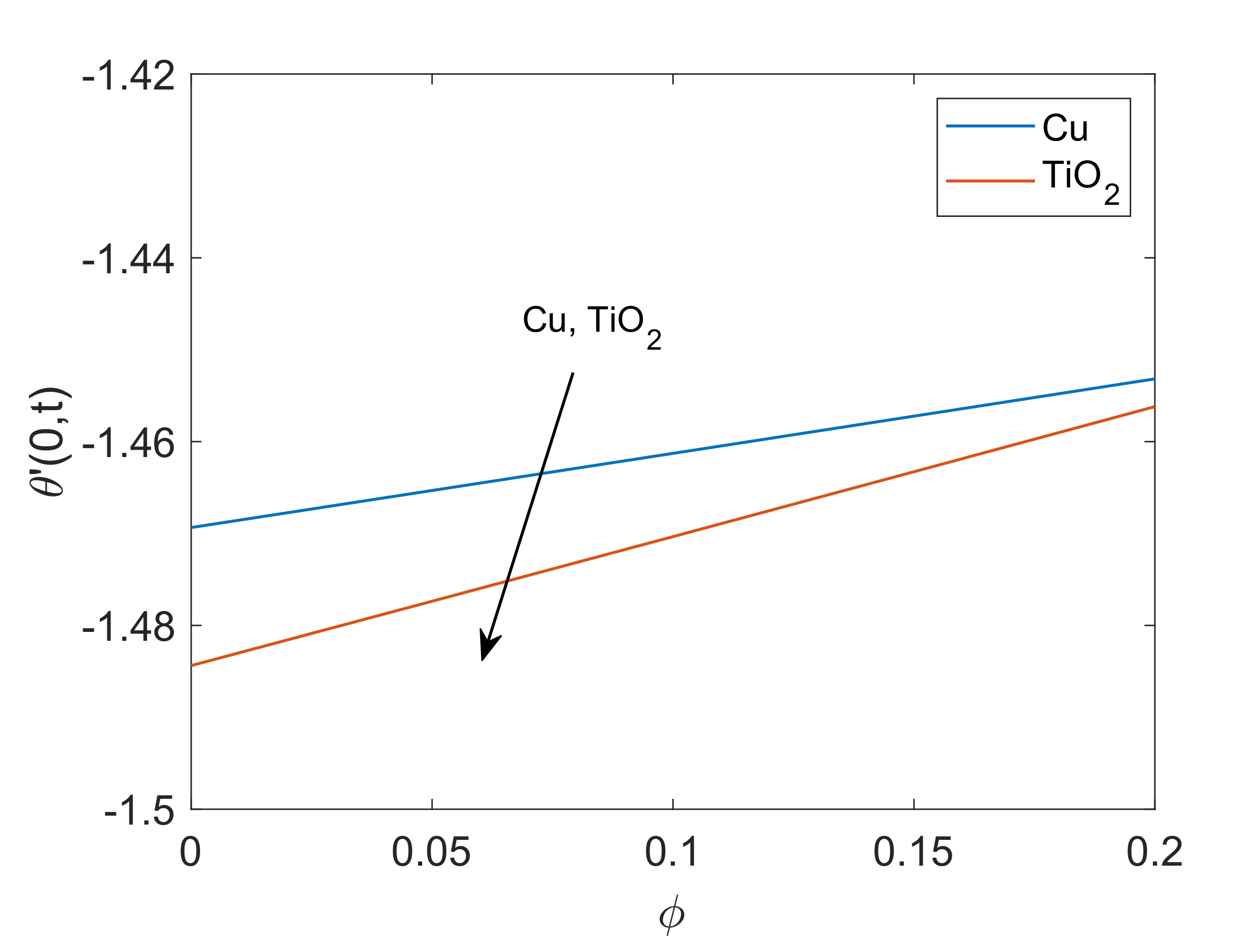
- Cu-water has greater momentum boundary layer thickness than -water nanofluid.
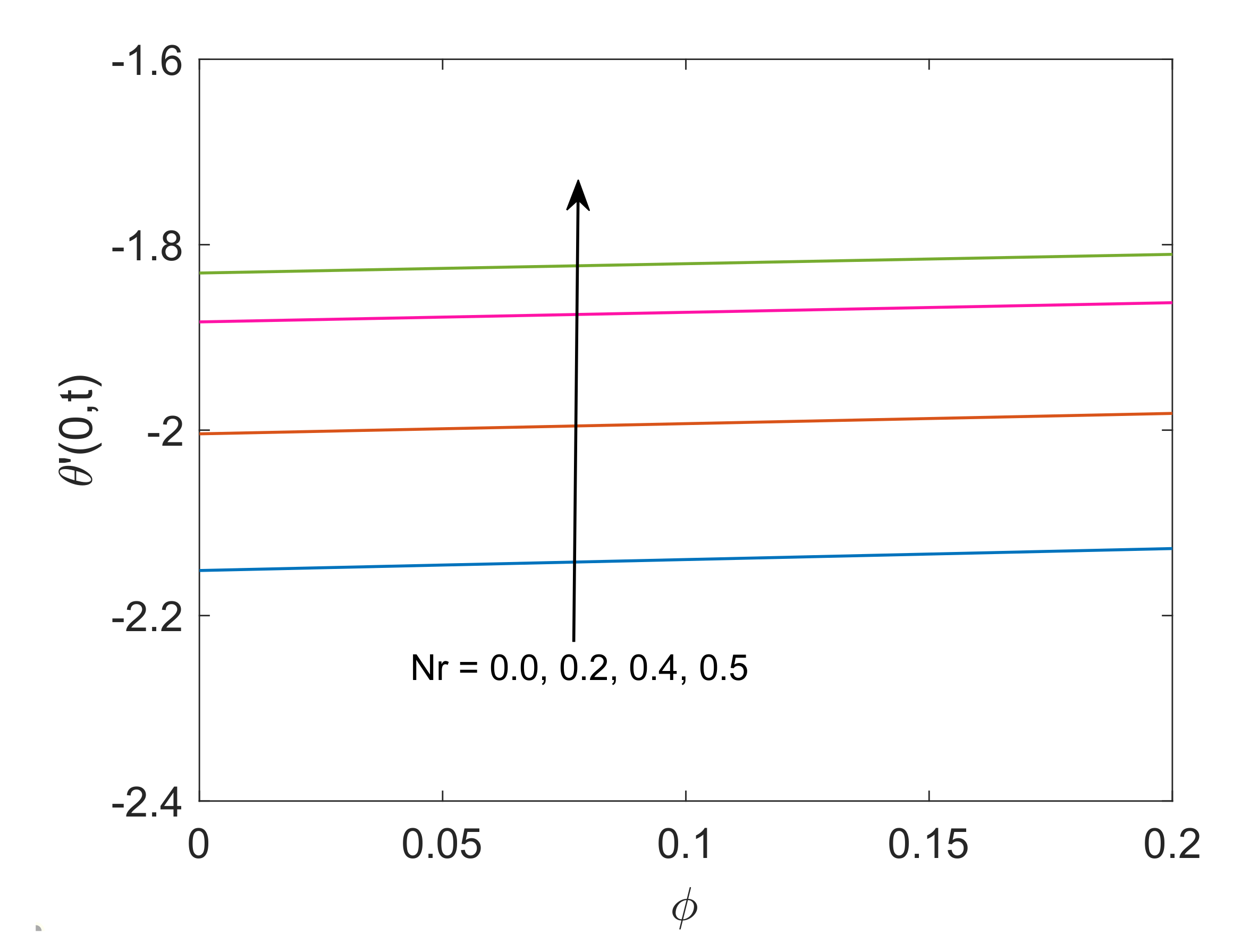
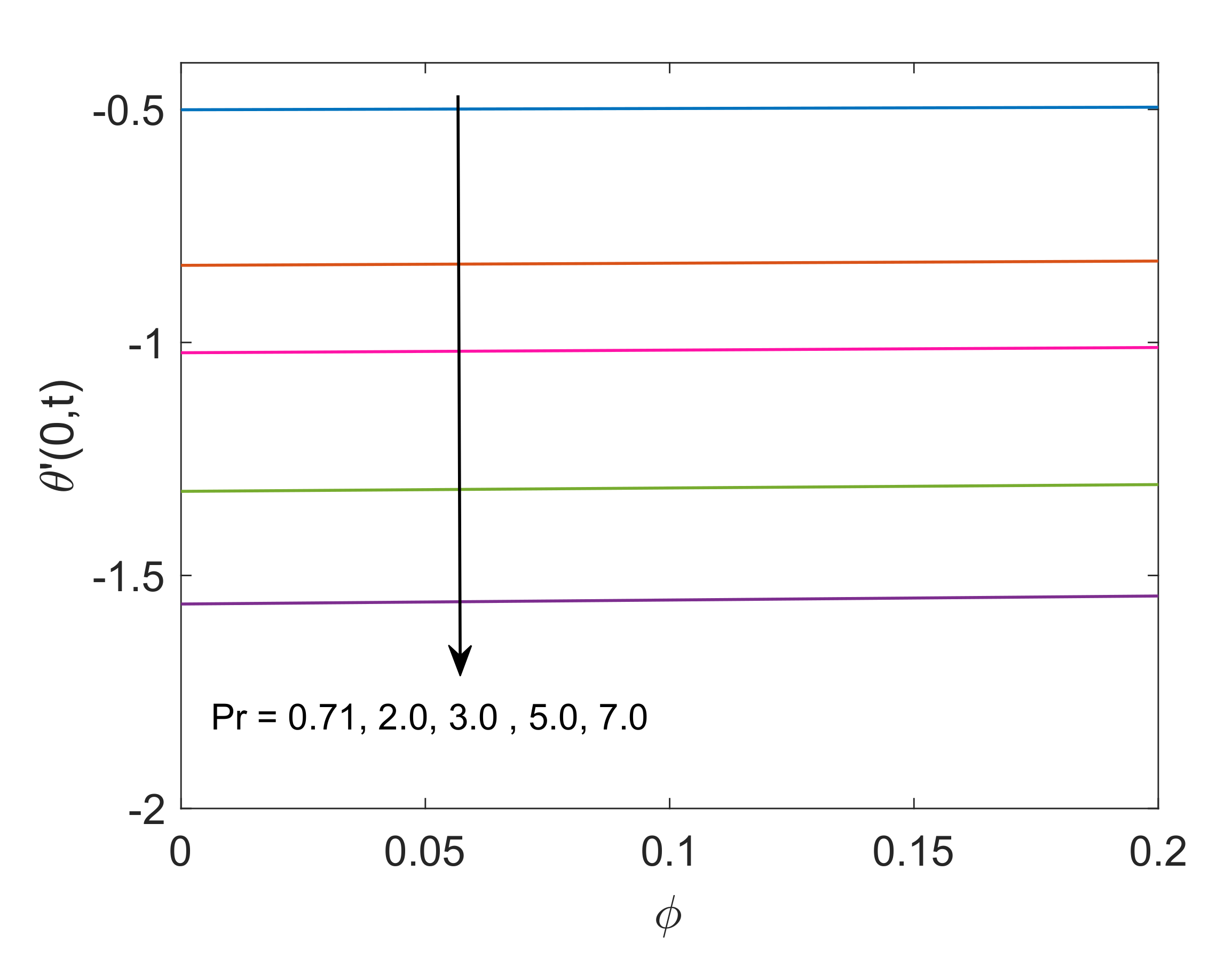
- Rate of heat transfer increases as the radiation parameter increases, while the increase in values of heat sink parameter reduces the rate of heat transfer.
- -water has a lower rate of heat transfer at the wall in contrast to Cu-water.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Gr | Grashof number (-) |
| Pr | Prandtl number (-) |
| Q | Parameter of Heat sink (-) |
| Magnetic parameter (-) | |
| Nr | Radiation parameter (-) |
| Nusselt number (-) | |
| Density of fluid (kgm) | |
| Dynamic viscosity (Kgms) | |
| Electrical conductivity (Sm) | |
| Kinematic Viscosity (ms) | |
| k | Thermal conductivity (W m K) |
| Volume fraction | |
| Heat capacitance (J KgK) | |
| Magnetic field strength (NmA) | |
| Porosity (-) | |
| g | Standard gravity (ms) |
| Velocity (ms) | |
| t | Time (-) |
| y | Spatial variable (m) |
| Temperature (-) | |
| Laplace transform operator | |
| s | Complex Laplace frequency |
| K | Parameter of Porosity (-) |
| Constant ambient temperature (K) | |
| Coefficient of Thermal expansion (K) | |
| Coefficient of Rosseland adsorption (m) | |
| Stefan–Boltzmann constant (WmK) |
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Di Sarli, V.; Landi, G.; Lisi, L.; Di Benedetto, A. Ceria-coated diesel particulate filters for continuous regeneration. AIChE J. 2017, 63, 3442–3449. [Google Scholar] [CrossRef]
- Aaiza, G.; Khan, I.; Shafie, S. Energy transfer in mixed convection MHD flow of nanofluid containing different shapes of nanoparticles in a channel filled with saturated porous medium. Nanoscale Res. Lett. 2015, 10, 490. [Google Scholar] [CrossRef] [PubMed]
- Masuda, H.; Ebata, A.; Teramae, K. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Choi, S.; Zhang, Z.; Yu, W.; Lockwood, F.; Grulke, E. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Das, S.; Jana, R. Natural convective magneto-nanofluid flow and radiative heat transfer past a moving vertical plate. Alex. Eng. J. 2015, 54, 55–64. [Google Scholar] [CrossRef]
- Das, K. Flow and heat transfer characteristics of nanofluids in a rotating frame. Alex. Eng. J. 2014, 53, 757–766. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Asadollahi, A. Peristaltic blood flow of couple stress fluid suspended with nanoparticles under the influence of chemical reaction and activation energy. Symmetry 2019, 11, 276. [Google Scholar] [CrossRef]
- Hussanan, A.; Khan, I.; Hashim, H.; Anuar, M.K.; Ishak, N.; Sarif, N.M.; Salleh, M.Z. Unsteady MHD flow of some nanofluids past an accelerated vertical plate embedded in a porous medium. J. Teknol. 2016, 78, 2. [Google Scholar] [CrossRef]
- Ullah, A.; Shah, Z.; Kumam, P.; Ayaz, M.; Islam, S.; Jameel, M. Viscoelastic MHD Nanofluid Thin Film Flow over an Unsteady Vertical Stretching Sheet with Entropy Generation. Processes 2019, 7, 262. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Ali, F.; Eid, M.R.; Sehaqui, R. Numerical analysis of the unsteady natural convection MHD couette nanofluid flow in the presence of thermal radiation using single and two-phase nanofluid models for Cu–Water nanofluids. Int. J. Appl. Comput. Math. 2018, 4, 81. [Google Scholar] [CrossRef]
- Atif, S.; Hussain, S.; Sagheer, M. Effect of thermal radiation on MHD micropolar Carreau nanofluid with viscous dissipation, Joule heating, and internal heating. Sci. Iran. 2019, 26, 3875–3888. [Google Scholar] [CrossRef]
- Malvandi, A.; Ganji, D. Magnetic field and slip effects on free convection inside a vertical enclosure filled with alumina/water nanofluid. Chem. Eng. Res. Des. 2015, 94, 355–364. [Google Scholar] [CrossRef]
- Mostafazadeh, A.; Toghraie, D.; Mashayekhi, R.; Akbari, O.A. Effect of radiation on laminar natural convection of nanofluid in a vertical channel with single-and two-phase approaches. J. Therm. Anal. Calorim. 2019, 138, 779–794. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.W. Recent developments in numerical modelling of heating and cooling processes in the food industry—A review. Trends Food Sci. Technol. 2003, 14, 408–423. [Google Scholar] [CrossRef]
- Soomro, F.A.; Haq, R.U.; Al-Mdallal, Q.M.; Zhang, Q. Heat generation/absorption and nonlinear radiation effects on stagnation point flow of nanofluid along a moving surface. Results Phys. 2018, 8, 404–414. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Aly, A. MHD free convection flow of a nanofluid past a vertical plate in the presence of heat generation or absorption effects. Chem. Eng. Commun. 2010, 198, 425–441. [Google Scholar] [CrossRef]
- Ameen, I.; Shah, Z.; Islam, S.; Nasir, S.; Khan, W.; Kumam, P.; Thounthong, P. Hall and ion-slip effect on CNTS nanofluid over a porous extending surface through heat generation and absorption. Entropy 2019, 21, 801. [Google Scholar] [CrossRef]
- O Alzahrani, E.; Shah, Z.; Alghamdi, W.; Zaka Ullah, M. Darcy–Forchheimer Radiative Flow of Micropoler CNT Nanofluid in Rotating Frame with Convective Heat Generation/Consumption. Processes 2019, 7, 666. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Darcy-Forchheimer flow of nanofluid in a rotating frame. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 2895–2915. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A. On the performance of heat absorption/generation and thermal stratification in mixed convective flow of an Oldroyd-B fluid. Nucl. Eng. Technol. 2017, 49, 1645–1653. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Rikhtegar, F.; Sabaghan, A.; Roohi, E. Heat transfer and entropy generation in a microchannel with longitudinal vortex generators using nanofluids. Energy 2016, 101, 190–201. [Google Scholar] [CrossRef]
- Nisa, Z.U.; Hajizadeh, A.; Nazar, M. Free convection flow of nanofluid over infinite vertical plate with damped thermal flux. Chin. J. Phys. 2019, 59, 175–188. [Google Scholar] [CrossRef]
- Beckermann, C.; Ramadhyani, S.; Viskanta, R. Natural convection flow and heat transfer between a fluid layer and a porous layer inside a rectangular enclosure. J. Heat Transf. 1987, 109, 363–370. [Google Scholar] [CrossRef]
- Mharzi, M.; Daguenet, M.; Daoudi, S. Thermosolutal natural convection in a vertically layered fluid-porous medium heated from the side. Energy Convers. Manag. 2000, 41, 1065–1090. [Google Scholar] [CrossRef]
- Gobin, D.; Goyeau, B.; Neculae, A. Convective heat and solute transfer in partially porous cavities. Int. J. Heat Mass Transf. 2005, 48, 1898–1908. [Google Scholar] [CrossRef]
- Chen, F.; Chen, C. Convection in superposed fluid and porous layers. J. Fluid Mech. 1992, 234, 97–119. [Google Scholar] [CrossRef]
- Kim, S.J.; Choi, C.Y. Convective heat transfer in porous and overlying fluid layers heated from below. Int. J. Heat Mass Transf. 1996, 39, 319–329. [Google Scholar] [CrossRef]
- Singh, A.; Paul, T.; Thorpe, G. Natural convection due to heat and mass transfer in a composite system. Heat Mass Transf. 1999, 35, 39–48. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: Berlin, Germany, 2006; Volume 3. [Google Scholar]
- Umavathi, J.; Hemavathi, K. Flow and heat transfer of composite porous medium saturated with nanofluid. Propuls. Power Res. 2019, 8, 173–181. [Google Scholar] [CrossRef]
- Amhalhel, G.; Furmański, P. Problems of modeling flow and heat transfer in porous media. J. Power Technol. 1997, 85, 55–88. [Google Scholar]
- Khan, U.; Mohyud-Din, S.T.; Bin-Mohsin, B. Convective heat transfer and thermo-diffusion effects on flow of nanofluid towards a permeable stretching sheet saturated by a porous medium. Aerosp. Sci. Technol. 2016, 50, 196–203. [Google Scholar] [CrossRef]
- Raju, C.; Babu, M.J.; Sandeep, N.; Sugunamma, V.; Reddy, J.R. Radiation and Soret effects of MHD nanofluid flow over a moving vertical moving plate in porous medium. Chem. Process. Eng. Res. 2015, 30, 9–21. [Google Scholar]
- AbdEl-Gaied, S.; Hamad, M. MHD forced convection laminar boundary layer flow of alumina-water nanofluid over a moving permeable flat plate with convective surface boundary condition. J. Appl. Math. 2013, 2013, 403210. [Google Scholar] [CrossRef]
- Satya Narayana, P.; Venkateswarlu, B.; Venkataramana, S. Thermal radiation and heat source effects on a MHD nanofluid past a vertical plate in a rotating system with porous medium. Heat Transf. Res. 2015, 44, 1–19. [Google Scholar] [CrossRef]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Mobin, N. Numerical Simulation and Mathematical Modeling of Electro-Osmotic Couette–Poiseuille Flow of MHD Power-Law Nanofluid with Entropy Generation. Symmetry 2019, 11, 1038. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Abuobeida, I.A.A.; Vuthaluru, H.B.; Liu, S. Two-phase forced convection of nanofluids flow in circular tubes using convergent and divergent conical rings inserts. Int. Commun. Heat Mass Transf. 2019, 101, 10–20. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Two-Phase Couette Flow of Couple Stress Fluid with Temperature Dependent Viscosity Thermally Affected by Magnetized Moving Surface. Symmetry 2019, 11, 647. [Google Scholar] [CrossRef]
- Zeeshan, A.; Ellahi, R.; Siddiqui, A.; Rahman, H. An investigation of porosity and magnetohydrodynamic flow of non-Newtonian nanofluid in coaxial cylinders. Int. J. Phys. Sci. 2012, 7, 1353–1361. [Google Scholar] [CrossRef]
- Cramer, K.R.; Pai, S.I. Magnetofluid Dynamics for Engineers and Applied Physicists; MacGraw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Das, S.; Jana, R.; Makinde, O. Transient natural convection in a vertical channel filled with nanofluids in the presence of thermal radiation. Alex. Eng. J. 2016, 55, 253–262. [Google Scholar] [CrossRef]
- Loganathan, P.; Nirmal Chand, P.; Ganesan, P. Radiation effects on an unsteady natural convective flow of a nanofluid past an infinite vertical plate. Nano 2013, 8, 1350001. [Google Scholar] [CrossRef]
- Kakaç, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Rosseland, S. Astrophysik: Auf atomtheoretischer grundlage; Springer: Berlin, Germany, 2013; Volume 11. [Google Scholar]
- Le Page, W.R. Complex Variables and the Laplace Transform for Engineers; Courier Corporation: North Chelmsford, MA, USA, 1980. [Google Scholar]

| Fluid/Nanoparticles | ||||||
| Water | 997.1 | 4179 | 0.613 | 21 | 0.0 | |
| Copper (Cu) | 8933 | 385 | 401 | 1.67 | 0.05 | |
| Titanium Oxide | 4250 | 686.2 | 8.9538 | 0.90 | 0.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anwar, T.; Kumam, P.; Shah, Z.; Watthayu, W.; Thounthong, P. Unsteady Radiative Natural Convective MHD Nanofluid Flow Past a Porous Moving Vertical Plate with Heat Source/Sink. Molecules 2020, 25, 854. https://doi.org/10.3390/molecules25040854
Anwar T, Kumam P, Shah Z, Watthayu W, Thounthong P. Unsteady Radiative Natural Convective MHD Nanofluid Flow Past a Porous Moving Vertical Plate with Heat Source/Sink. Molecules. 2020; 25(4):854. https://doi.org/10.3390/molecules25040854
Chicago/Turabian StyleAnwar, Talha, Poom Kumam, Zahir Shah, Wiboonsak Watthayu, and Phatiphat Thounthong. 2020. "Unsteady Radiative Natural Convective MHD Nanofluid Flow Past a Porous Moving Vertical Plate with Heat Source/Sink" Molecules 25, no. 4: 854. https://doi.org/10.3390/molecules25040854
APA StyleAnwar, T., Kumam, P., Shah, Z., Watthayu, W., & Thounthong, P. (2020). Unsteady Radiative Natural Convective MHD Nanofluid Flow Past a Porous Moving Vertical Plate with Heat Source/Sink. Molecules, 25(4), 854. https://doi.org/10.3390/molecules25040854








