Excited State Dynamics of 8-Vinyldeoxyguanosine in Aqueous Solution Studied by Time-Resolved Fluorescence Spectroscopy and Quantum Mechanical Calculations
Abstract
1. Introduction
2. Material and Methods
2.1. Experimental Details
2.1.1. Steady-Stated Spectroscopy
2.1.2. Time-Resolved Fluorescence Spectroscopy
2.2. Computational Details
2.2.1. Models
2.2.2. Methods
2.2.3. Solvation Models
3. Results
3.1. Steady-State Spectroscopy
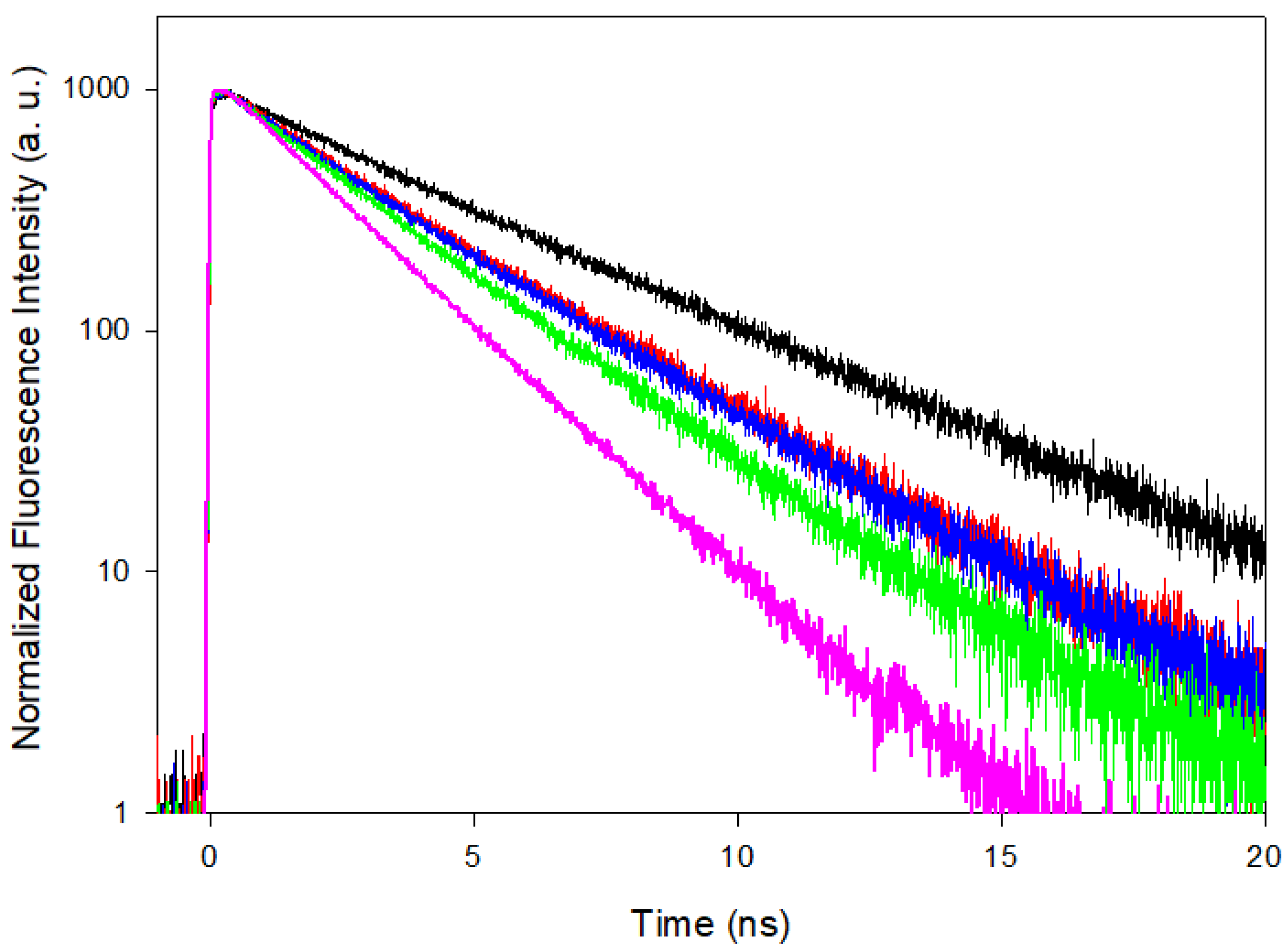
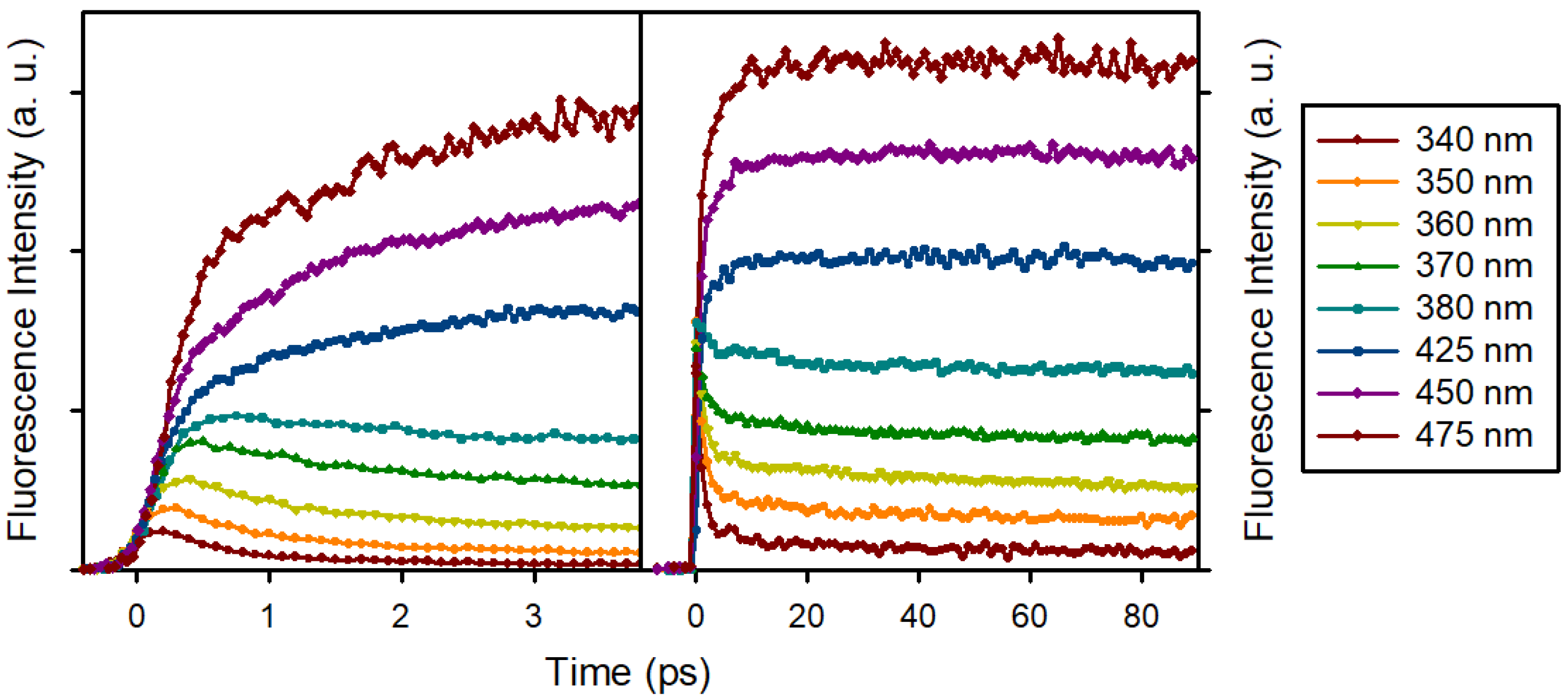
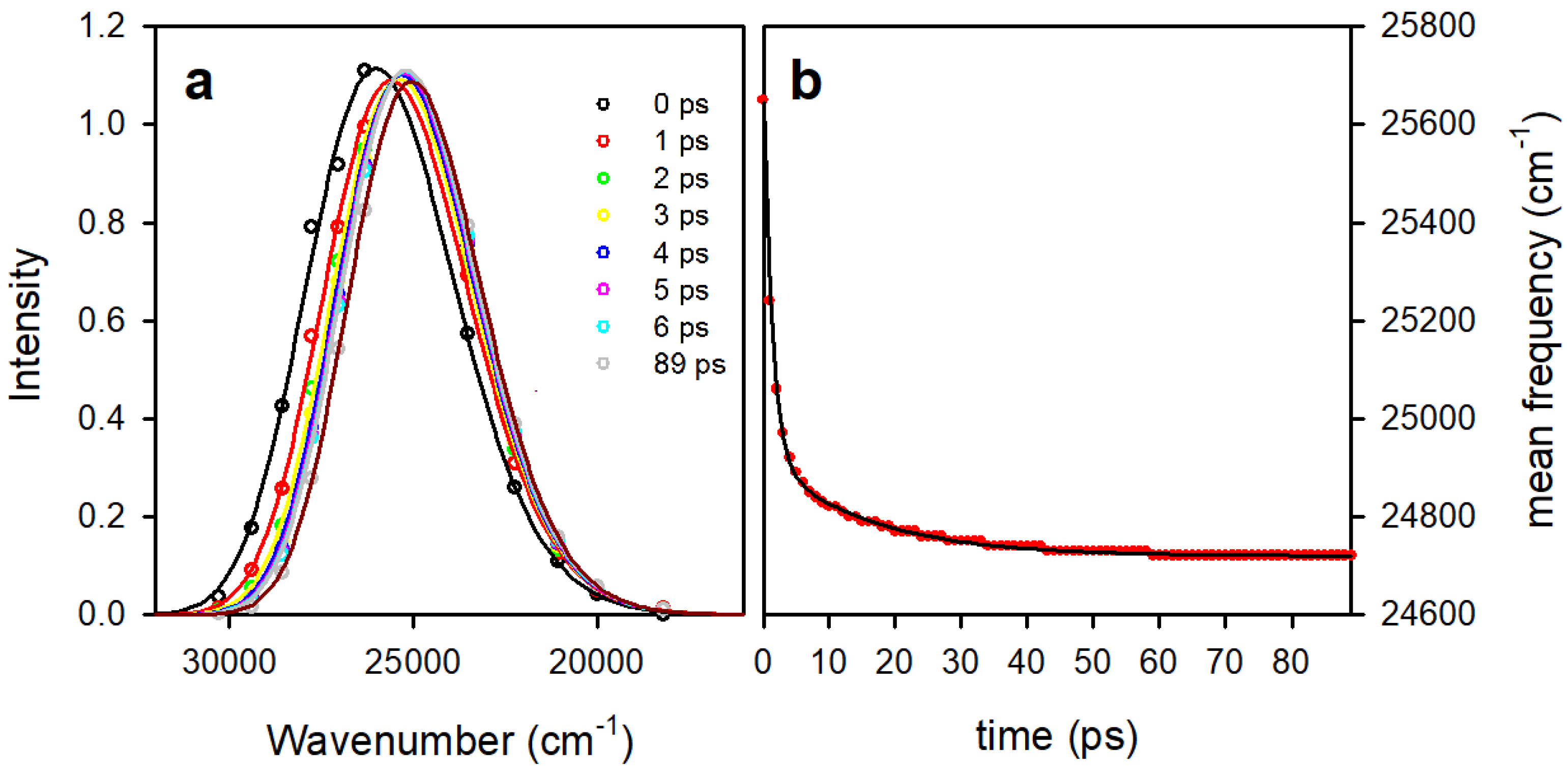
3.2. Time Resolved Fluorescence Spectroscopy
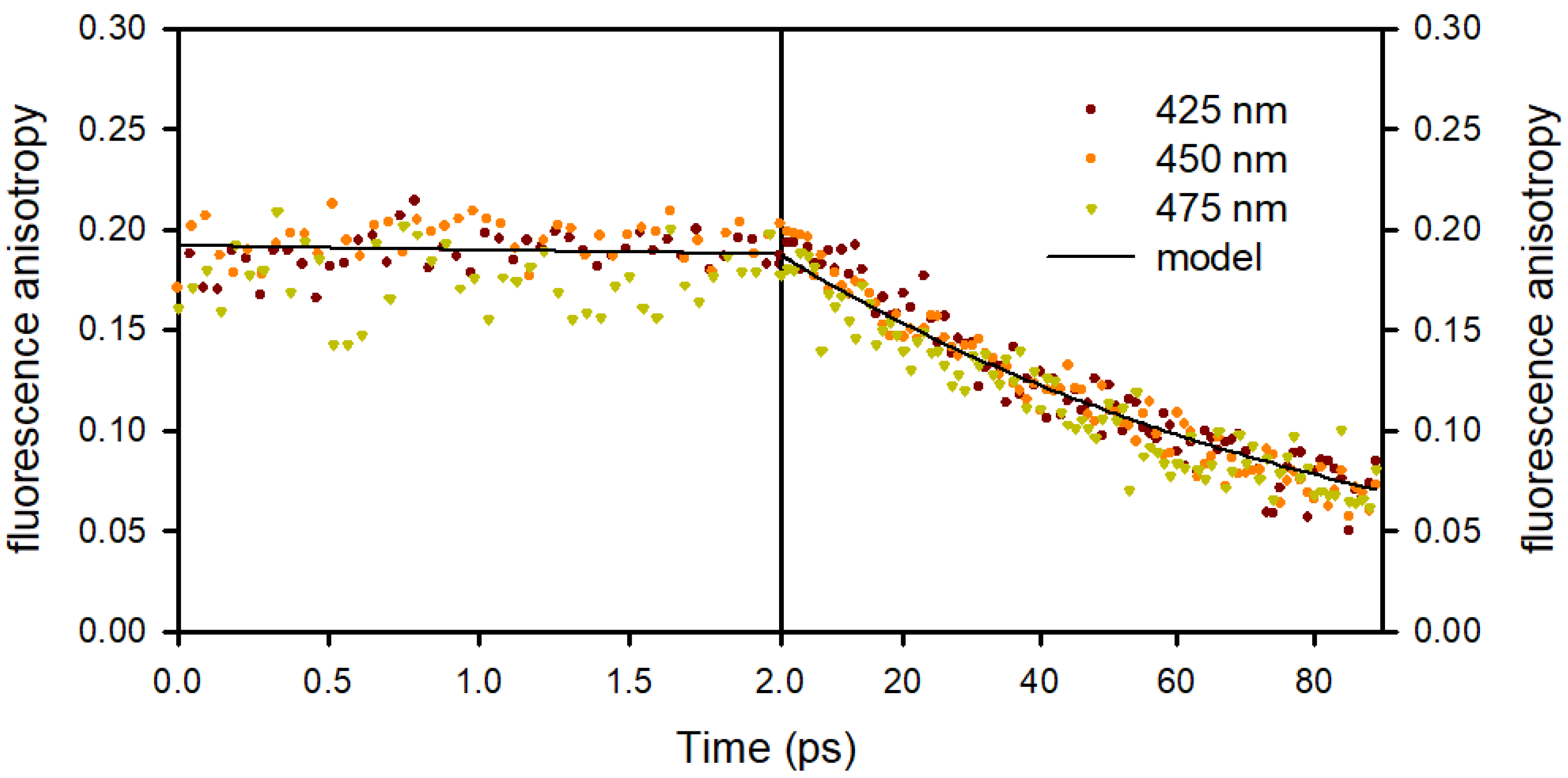
Fluorescence Anisotropy Decays
3.3. Computational Results
3.3.1. Ground State Equilibria
3.3.2. The Excited States in the Franck-Condon Region.
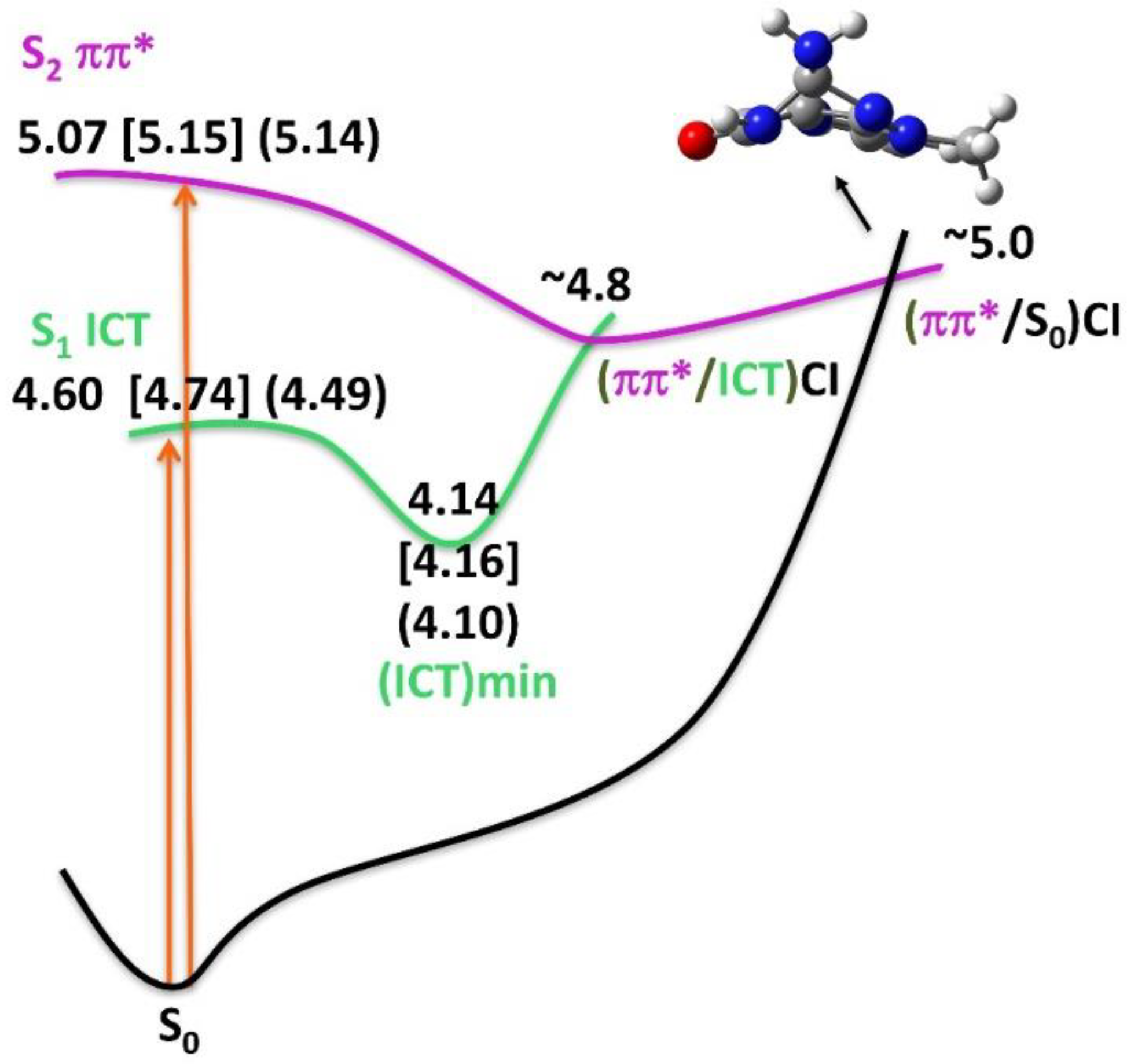
3.3.3. Excited State Optimization and Emission
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Plenum Press: New York, NY, USA, 2006. [Google Scholar]
- Sinkeldam, R.W.; Greco, N.J.; Tor, Y. Fluorescent Analogs of Biomolecular Building Blocks: Design, Properties and Applications. Chem. Rev. 2010, 110, 2579–2619. [Google Scholar] [CrossRef] [PubMed]
- Onidas, D.; Markovitsi, D.; Marguet, S.; Sharonov, A.; Gustavsson, T. Fluorescence properties of DNA nucleosides and nucleotides: A refined steady-state and femtosecond investigation. J. Phys. Chem. B 2002, 106, 11367–11374. [Google Scholar] [CrossRef]
- Markovitsi, D.; Gustavsson, T.; Banyasz, A. DNA Fluorescence. In Handbook of Organic Photochemistry and Photobiology; Griesbeck, A., Ghetti, F., Oelgemoeller, M., Eds.; Taylor and Francis: Boca Raton, FL, USA, 2012; pp. 1057–1079. [Google Scholar]
- Markovitsi, D.; Gustavsson, T.; Banyasz, A. Absorption of UV radiation by DNA: Spatial and temporal features. Mutat. Res.-Rev. Mutat. Res. 2010, 704, 21–28. [Google Scholar] [CrossRef] [PubMed]
- Wilhelmsson, L.M. Fluorescent nucleic acid base analogues. Q. Rev. Biophys. 2010, 43, 159–183. [Google Scholar] [CrossRef] [PubMed]
- Rachofsky, E.L.; Osman, R.; Ross, J.B.A. Probing structure and dynamics of DNA with 2-aminopurine: Effects of local environment on fluorescence. Biochemistry 2001, 40, 946–956. [Google Scholar] [CrossRef]
- Serrano-Andres, L.; Merchán, M.; Borin, A.C. Adenine and 2-aminopurine: Paradigms of modern theoretical photochemistry. Proc. Natl. Acad. Sci. USA 2006, 103, 8691–8696. [Google Scholar] [CrossRef]
- Liang, J.X.; Matsika, S. Pathways for Fluorescence Quenching in 2-Aminopurine pi-Stacked with Pyrimidine Nucleobases. J. Am. Chem. Soc. 2011, 133, 6799–6808. [Google Scholar] [CrossRef]
- Holz, B.; Weinhold, E.; Klimasauskas, S.; Serva, S. 2-Aminopurine as a fluorescent probe for DNA base flipping by methyltransferases. Nucleic Acids Res. 1998, 26, 1076–1083. [Google Scholar] [CrossRef]
- Reha-Krantz, L.J.; Hariharan, C.; Subuddhi, U.; Xia, S.; Zhao, C.; Beckman, J.; Christian, T.; Konigsberg, W. Structure of the 2-aminopurine-cytosine base pair formed in the polymerase active site of the RB69 Y567A-DNA polymerase. Biochemistry 2011, 50, 10136–10149. [Google Scholar] [CrossRef][Green Version]
- Pitsikas, P.; Patapas, J.M.; Cupples, C.G. Mechanism of 2-aminopurine-stimulated mutagenesis in Escherichia coli. Mutat. Res. Fundam. Mol. Mech. Mutagenes. 2004, 550, 25–32. [Google Scholar] [CrossRef]
- Dallmann, A.; Dehmel, L.; Peters, T.; Mugge, C.; Griesinger, C.; Tuma, J.; Ernsting, N.P. 2-Aminopurine Incorporation Perturbs the Dynamics and Structure of DNA. Angew. Chem. Int. Ed. 2010, 49, 5989–5992. [Google Scholar] [CrossRef] [PubMed]
- Lang, P.; Gerez, C.; Tritsch, D.; Fontecave, M.; Biellmann, J.-F.; Burger, A. Synthesis of 8-vinyladenosine 5′-di- and 5′-triphosphate: Evaluation of the diphosphate compound on ribonucleotide reductase. Tetrahedron 2003, 59, 7315–7322. [Google Scholar] [CrossRef]
- Ben Gaied, N.; Glasser, N.; Ramalanjaona, N.; Beltz, H.; Wolff, P.; Marquet, R.; Burger, A.; Mély, Y. 8-vinyl-deoxyadenosine, an alternative fluorescent nucleoside analog to 2′-deoxyribosyl-2-aminopurine with improved properties. Nucleic Acids Res. 2005, 33, 1031–1039. [Google Scholar] [CrossRef] [PubMed]
- Kenfack, C.A.; Piemont, E.; Ben Gaied, N.; Burger, A.; Mely, Y. Time-resolved fluorescent properties of 8-vinyl-deoxyadenosine and 2-amino-deoxyribosylpurine exhibit different sensitivity to their opposite base in duplexes. J. Phys. Chem. B 2008, 112, 9736–9745. [Google Scholar] [CrossRef]
- Matsika, S. Modified Nucleobases. In Photoinduced Phenomena in Nucleic Acids I: Nucleobases in the Gas Phase and in Solvents; Barbatti, M., Borin, A.C., Ullrich, S., Eds.; Springer-Verlag Berlin: Berlin, Germany, 2015; Volume 355, pp. 209–244. [Google Scholar]
- Kenfack, C.A.; Burger, A.; Mely, Y. Excited-state properties and transitions of fluorescent 8-vinyl adenosine in DNA. J. Phys. Chem. B 2006, 110, 26327–26336. [Google Scholar] [CrossRef]
- Kodali, G.; Kistler, K.A.; Narayanan, M.; Matsika, S.; Stanley, R.J. Change in Electronic Structure upon Optical Excitation of 8-Vinyladenosine: An Experimental and Theoretical Study. J. Phys. Chem. A 2010, 114, 256–267. [Google Scholar] [CrossRef]
- Narayanan, M.; Kodali, G.; Singh, V.R.; Velvadapu, V.; Stanley, R.J. Oxidation and reduction potentials of 8-vinyladenosine measured by cyclic voltammetry: Implications for photoinduced electron transfer quenching of a fluorescent adenine analog. J. Photochem. Photobiol. A Chem. 2012, 249, 9–14. [Google Scholar] [CrossRef]
- Nadler, A.; Strohmeier, J.; Diederichsen, U. 8-Vinyl-2′-deoxyguanosine as a Fluorescent 2′-Deoxyguanosine Mimic for Investigating DNA Hybridization and Topology. Angew. Chem. Int. Ed. 2011, 50, 5392–5396. [Google Scholar] [CrossRef]
- Holzberger, B.; Strohmeier, J.; Siegmund, V.; Diederichsen, U.; Marx, A. Enzymatic synthesis of 8-vinyl- and 8-styryl-2′-deoxyguanosine modified DNA-novel fluorescent molecular probes. Bioorg. Med. Chem. Lett. 2012, 22, 3136–3139. [Google Scholar] [CrossRef]
- Mullar, S.; Strohmeier, J.; Diederichsen, U. 8-Vinylguanine Nucleo Amino Acid: A Fluorescent PNA Building Block. Org. Lett. 2012, 14, 1382–1385. [Google Scholar] [CrossRef]
- Kochman, M.A.; Pola, M.; Miller, R.J.D. Theoretical Study of the Photophysics of 8-Vinylguanine, an Isomorphic Fluorescent Analogue of Guanine. J. Phys. Chem. A 2016, 120, 6200–6215. [Google Scholar] [CrossRef] [PubMed]
- Markovitsi, D.; Onidas, D.; Talbot, F.; Marguet, S.; Gustavsson, T.; Lazzarotto, E. UVB/UVC induced processes in model DNA helices studied by time-resolved spectroscopy: Pitfalls and tricks. J. Photochem. Photobiol. A 2006, 183, 1–8. [Google Scholar] [CrossRef]
- Gustavsson, T.; Banyasz, A.; Lazzarotto, E.; Markovitsi, D.; Scalmani, G.; Frisch, M.J.; Barone, V.; Improta, R. Singlet excited-state behavior of uracil and thymine in aqueous solution: A combined experimental and computational study of 11 uracil derivatives. J. Am. Chem. Soc. 2006, 128, 607–619. [Google Scholar] [CrossRef] [PubMed]
- Maroncelli, M.; Fleming, G.R. Picosecond solvation dynamics of coumarin 153: The importance of molecular aspects of solvation. J. Chem. Phys. 1987, 86, 6221–6239. [Google Scholar] [CrossRef]
- Yanai, T. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Martinez-Fernandez, L.; Pepino, A.J.; Segarra-Marti, J.; Jovaisaite, J.; Vaya, I.; Nenov, A.; Markovitsi, D.; Gustavsson, T.; Banyasz, A.; Garavelli, M.; et al. Photophysics of Deoxycytidine and 5-Methyldeoxycytidine in Solution: A Comprehensive Picture by Quantum Mechanical Calculations and Femtosecond Fluorescence Spectroscopy. J. Am. Chem. Soc. 2017, 139, 7780–7791. [Google Scholar] [CrossRef]
- Improta, R.; Santoro, F.; Blancafort, L. Quantum Mechanical Studies on the Photophysics and the Photochemistry of Nucleic Acids and Nucleobases. Chem. Rev. 2016, 116, 3540–3593. [Google Scholar] [CrossRef]
- Improta, R.; Barone, V. Excited States Behavior of Nucleobases in Solution: Insights from Computational Studies. In Photoinduced Phenomena in Nucleic Acids I; Barbatti, M., Borin, A., Ullrich, S., Eds.; Springer International Publishing: Cham, Switzerland, 2014; Volume 355, pp. 329–357. [Google Scholar]
- Levine, B.G.; Ko, C.; Quenneville, J.; Martinez, T.J. Conical intersections and double excitations in time-dependent density functional theory. Mol. Phys. 2006, 104, 1039–1051. [Google Scholar] [CrossRef]
- Gonzalez, L.; Escudero, D.; Serrano-Andres, L. Progress and Challenges in the Calculation of Electronic Excited States. ChemPhysChem 2012, 13, 28–51. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999. [Google Scholar] [CrossRef]
- Miertus, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum—A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Banyasz, A.; Martinez-Fernandez, L.; Ketola, T.M.; Munoz-Losa, A.; Esposito, L.; Markovitsi, D.; Improta, R. Excited State Pathways Leading to Formation of Adenine Dimers. J. Phys. Chem. Lett. 2016, 7, 2020–2023. [Google Scholar] [CrossRef] [PubMed]
- Improta, R.; Barone, V.; Scalmani, G.; Frisch, M.J. A state-specific polarizable continuum model time dependent density functional theory method for excited state calculations in solution. J. Chem. Phys. 2006, 125, 054103. [Google Scholar] [CrossRef] [PubMed]
- Improta, R.; Scalmani, G.; Frisch, M.J.; Barone, V. Toward effective and reliable fluorescence energies in solution by a new state specific polarizable continuum model time dependent density functional theory approach. J. Chem. Phys. 2007, 127, 074504. [Google Scholar] [CrossRef]
- Frisch, M.J.T.G.W.; Trucks, G.W.S.H.B.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. Gaussian 09 Revision A.1; Gaussian Inc.: Wellington, CT, USA, 2009. [Google Scholar]
- Jimenez, R.; Fleming, G.R.; Kumar, P.V.; Maroncelli, M. Femtosecond solvation dynamics of water. Nature 1994, 369, 471–473. [Google Scholar] [CrossRef]
- Miannay, F.A.; Gustavsson, T.; Banyasz, A.; Markovitsi, D. Excited-State Dynamics of dGMP Measured by Steady-State and Femtosecond Fluorescence Spectroscopy. J. Phys. Chem. A 2010, 114, 3256–3263. [Google Scholar] [CrossRef]
- Karunakaran, V.; Kleinermanns, K.; Improta, R.; Kovalenko, S.A. Photoinduced Dynamics of Guanosine Monophosphate in Water from Broad-Band Transient Absorption Spectroscopy and Quantum-Chemical Calculations. J. Am. Chem. Soc. 2009, 131, 5839–5850. [Google Scholar] [CrossRef]
- Dudycz, L.; Stolarski, R.; Pless, R.; Shugar, D. A 1H NMR Study of the Syn-Anti Dynamic Equilibrium in Adenine Nucleosides and Nucleotides with the Aid of Some Synthetic Model Analogues with Fixed Conformations. Z. Naturforsch. C 1979, 34, 359–373. [Google Scholar] [CrossRef]
- Stolarski, R.; Dudycz, L.; Shugar, D. NMR Studies on the syn-anti Dynamic Equilibrium in Purine Nucleosides and Nucleotides. Eur. J. Biochem. 1980, 108, 111–121. [Google Scholar] [CrossRef]
- Improta, R.; Barone, V.; Santoro, F. Accurate Steady-State and Zero-Time Fluorescence Spectra of Large Molecules in Solution by a First-Principle Computational Method. J. Phys. Chem. B 2007, 111, 14080–14082. [Google Scholar] [CrossRef]
- Ferrer, F.J.A.; Improta, R.; Santoro, F.; Barone, V. Computing the inhomogeneous broadening of electronic transitions in solution: A first-principle quantum mechanical approach. Phys. Chem. Chem. Phys. 2011, 13, 17007–17012. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Sample of 8-vinyl-deoxyguanosine (8vdG) is available from the authors (UD). |
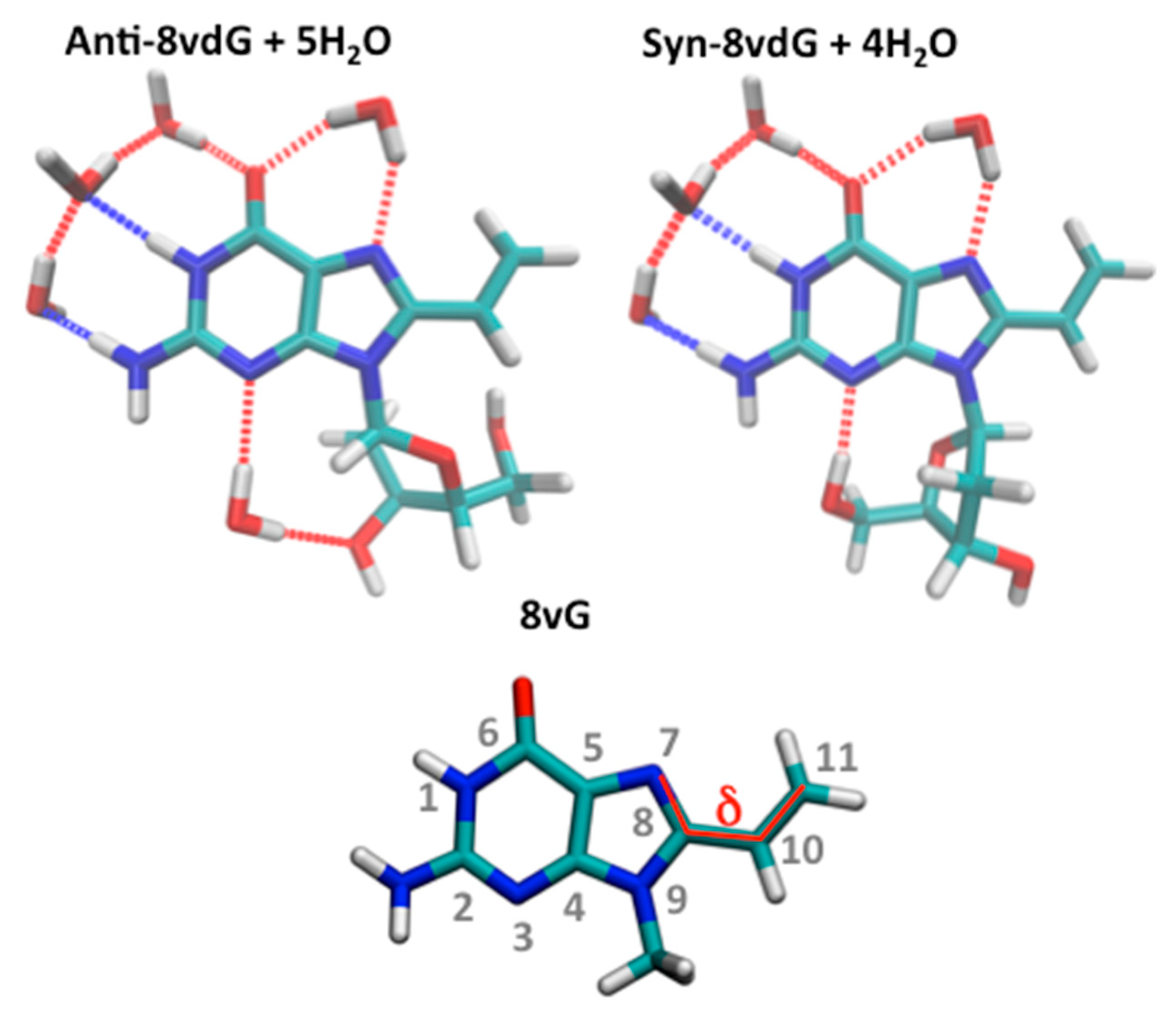
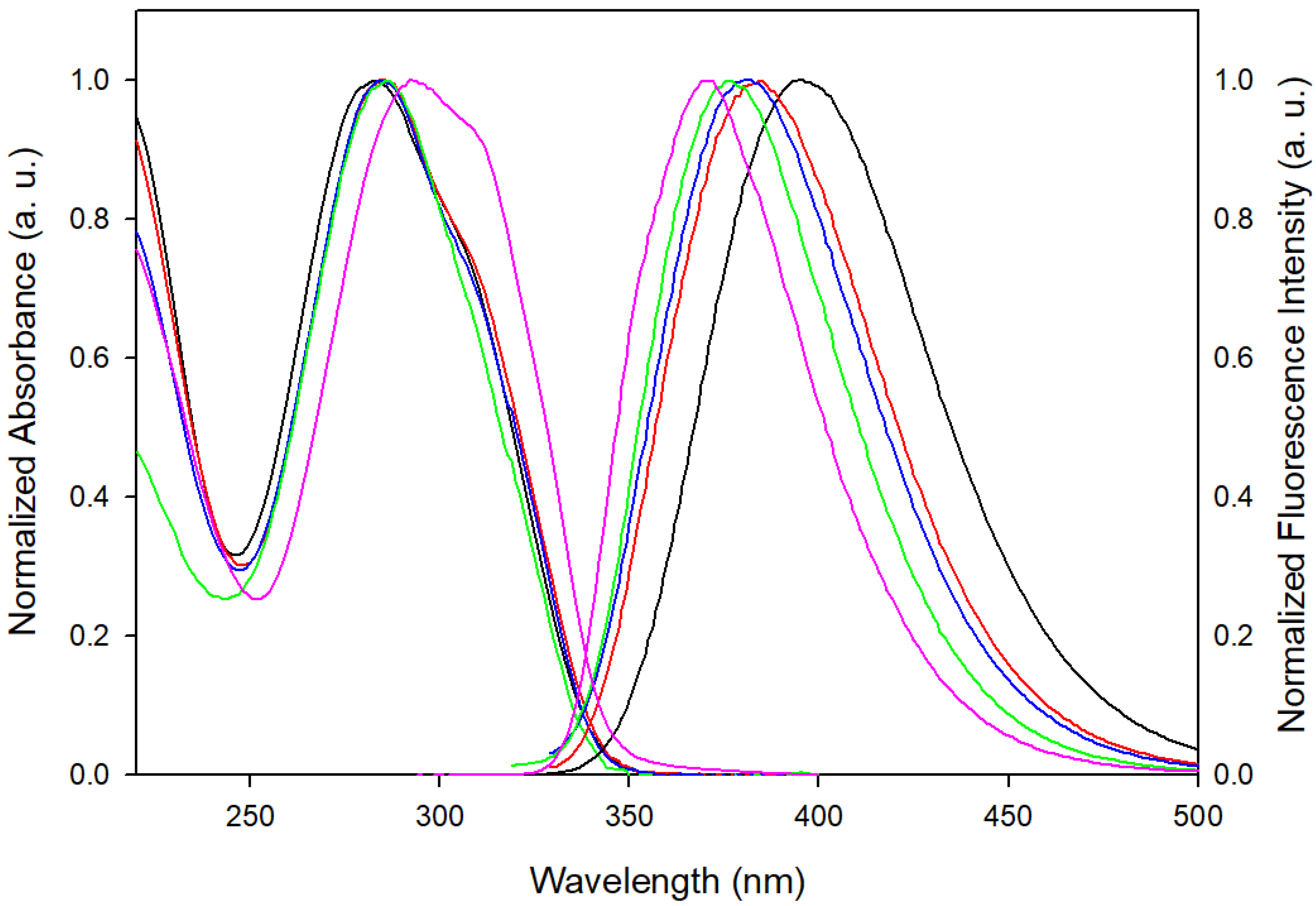
| THF | MeCN | EtOH | MeOH | H2O | |
|---|---|---|---|---|---|
| Absorption max (nm) | 293 | 286 | 284 | 284 | 283 |
| Absorption max (103 cm−1) | 34.1 | 34.9 | 35.2 | 35.2 | 35.4 |
| Fluorescence max (nm) | 370 | 376 | 380 | 384 | 396 |
| Fluorescence max (103 cm−1) a | 26.9 | 26.3 | 26.0 | 25.8 | 24.8 |
| τF (at fluo-max) (ns) | 2.07 | 2.73 | 3.10 | 3.17 | 4.35 |
| τ1 | a1 | τ2 | a2 | τ3 | a3 | |
|---|---|---|---|---|---|---|
| 330 nm | 0.836 | 0.832 | 6.74 | 0.116 | (4350) | 0.0528 |
| 340 nm | 1.09 | 0.810 | 19.0 | 0.101 | (4350) | 0.0890 |
| 350 nm | 1.20 | 0.694 | 23.5 | 0.104 | (4350) | 0.203 |
| 360 nm | 1.36 | 0.532 | 41.5 | 0.125 | (4350) | 0.343 |
| 370 nm | 1.66 | 0.294 | 21.5 | 0.104 | (4350) | 0.601 |
| 380 nm | 1.00 | 0.153 | 14.2 | 0.0890 | (4350) | 0.758 |
| 425 nm | 0.486 | −0.194 | 4.82 | −0.219 | (4350) | 1.41 |
| 450 nm | 1.62 | −0.390 | 11.7 | −0.141 | (4350) | 1.53 |
| 475 nm | 2.52 | −0.360 | 10.6 | −0.105 | (4350) | 1.47 |
| 500 nm | 0.935 | −0.155 | 6.18 | −0.248 | (4350) | 1.40 |
| 550 nm | 2.40 | 0.232 | (4350) | 0.768 |
| 8vdG-anti | 8vdG-syn | 8vG | |||||
|---|---|---|---|---|---|---|---|
| H2O | (+5H2O) | (+4H2O) | (+5H2O) | ||||
| ΔE | f | ΔE | f | ΔE | f | ||
| S1 | π(G)-π*(V) [ICT] | 4.74 [262] 4.70 | 0.4855 | 4.60 [269] 4.54 | 0.5100 | 4.49 [276] 4.45 | 0.5164 |
| S2 | π(G)-π*(G) [Lb] | 5.15 [240] 5.22 | 0.2702 | 5.07 [244] 5.15 | 0.2693 | 5.14 [241] 5.22 | 0.2858 |
| MeCN | |||||||
| ΔE | f | ΔE | f | ΔE | f | ||
| S1 | π(G)-π*(V) [ICT] | 4.64 [267] 4.57 | 0.5983 | 4.64 [267] 4.58 | 0.6033 | 4.58 [270] 4.52 | 0.5946 |
| S2 | π(G)-π*(G) [Lb] | 5.10 [243] 5.17 | 0.1590 | 5.08 [244] 5.14 | 0.1669 | 5.14 [241] 5.22 | 0.1907 |
| THF | |||||||
| S1 | π(G)-π*(V) [ICT] | 4.64 [267] 4.60 | 0.6266 | 4.64 [267] 4.60 | 0.6315 | 4.58 [270] 4.53 | 0.6214 |
| S2 | π(G)-π*(G) [Lb] | 5.09 [244] 5.14 | 0.1409 | 5.07 [244] 5.12 | 0.1568 | 5.13 [242] 5.20 | 0.1813 |
| 8vdG-anti | 8vdG-syn | 8vG | 8vdG Exp | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Minima | ΔE | Stokes | R | ΔE | Stokes | r | ΔE | Stokes | r | Stokes | ||
| H2O | ||||||||||||
| FC(ICT)- (ICT)min | 3.69 NE3.64 E3.48 | 1.05 | 0.37 | 0.53 0.86 | 3.73 NE3.68 E3.53 | 0.86 | 0.39 | 0.49 0.80 | 3.71 NE3.66 E3.49 | 0.78 | 0.40 | |
| FC(ππ*)- (ICT)min | 1.46 | 0.17 | 1.34 | 0.11 | 1.43 | 0.11 | 1.44 | |||||
| MeCN | ||||||||||||
| FC(ICT)- (ICT)min | 3.76 NE3.71 E3.57 | 0.88 | 0.36 | 0.43 0.70 | 3.81 NE3.77 E3.64 | 0.83 | 0.40 | 0.40 0.64 | 3.78 NE3.73 E3.57 | 0.80 | 0.40 | |
| FC(ππ*)- (ICT)min | 1.34 | 0.08 | 1.28 | 0.06 | 1.36 | 0.11 | 1.13 | |||||
| THF | ||||||||||||
| FC(ICT)- (ICT)min | 3.76 NE3.75 E3.66 | 0.88 | 0.40 | 0.40 0.64 | 3.80 NE3.81 E3.73 | 0.84 | 0.40 | 0.37 0.58 | 3.78 NE3.77 E3.67 | 0.80 | 0.40 | |
| FC(ππ*)- (ICT)min | 1.33 | 0.04 | 1.27 | 0.04 | 1.35 | 0.09 | 0.98 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez-Fernandez, L.; Gustavsson, T.; Diederichsen, U.; Improta, R. Excited State Dynamics of 8-Vinyldeoxyguanosine in Aqueous Solution Studied by Time-Resolved Fluorescence Spectroscopy and Quantum Mechanical Calculations. Molecules 2020, 25, 824. https://doi.org/10.3390/molecules25040824
Martinez-Fernandez L, Gustavsson T, Diederichsen U, Improta R. Excited State Dynamics of 8-Vinyldeoxyguanosine in Aqueous Solution Studied by Time-Resolved Fluorescence Spectroscopy and Quantum Mechanical Calculations. Molecules. 2020; 25(4):824. https://doi.org/10.3390/molecules25040824
Chicago/Turabian StyleMartinez-Fernandez, Lara, Thomas Gustavsson, Ulf Diederichsen, and Roberto Improta. 2020. "Excited State Dynamics of 8-Vinyldeoxyguanosine in Aqueous Solution Studied by Time-Resolved Fluorescence Spectroscopy and Quantum Mechanical Calculations" Molecules 25, no. 4: 824. https://doi.org/10.3390/molecules25040824
APA StyleMartinez-Fernandez, L., Gustavsson, T., Diederichsen, U., & Improta, R. (2020). Excited State Dynamics of 8-Vinyldeoxyguanosine in Aqueous Solution Studied by Time-Resolved Fluorescence Spectroscopy and Quantum Mechanical Calculations. Molecules, 25(4), 824. https://doi.org/10.3390/molecules25040824





