How do the Hückel and Baird Rules Fade away in Annulenes?
Abstract
1. Introduction
2. Methodology
2.1. Aromaticity Indices
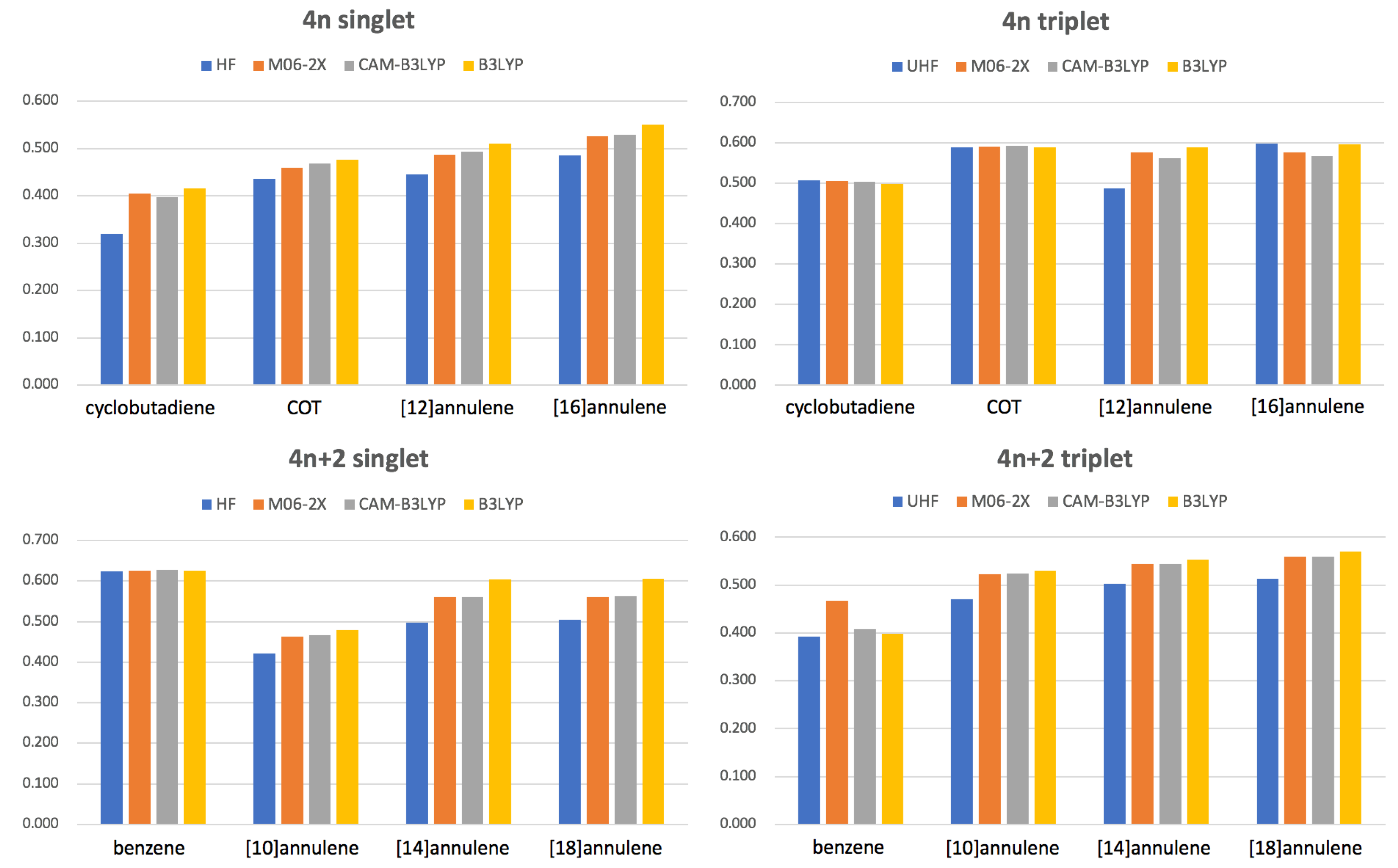
2.1.1. The Aromatic Fluctuation Index: FLU
2.1.2. The Bond-Length and Bond-Order Alternation Indices
2.1.3. A Many-Center Electron Delocalization Index:
2.1.4. AV1245 and
2.2. Hückel Molecular Orbital Method
3. Results
3.1. Aromaticity from the HMO Method
3.2. Geometrical Relaxation
3.2.1. Annulenes
3.2.2. Annulenes
3.3. Aromaticity from DFAs
3.4. The Delocalization Error in DFAs
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AOM | Atomic overlaps matrix |
| AV1245 | Aromaticity index for large rings [55] |
| Minimal value of 12-45 delocalizations [56] | |
| BLA | Bond-length alternation |
| BOA | Bond-order alternation |
| DFA | Density Functional Approximation |
| DI | Delocalization index [28] |
| FLU | Fluctuation aromaticity index [27] |
| HF | Hartree-Fock |
| HMO | Hückel Molecular Orbital |
| HOMA | Harmonic Oscillator Model of Aromaticity [33] |
| LDA | Local density approximation [109] |
| MCI | Multicenter index [43] |
| RE | Resonance energy |
| TREPE | Topological resonance energy per electron |
| Giambiagi’s multicenter index [42] | |
| Approximation to (Equation (8)) |
References
- Von Ragué Schleyer, P.; Jiao, H. What is aromaticity. Pure Appl. Chem. 1996, 68, 209–218. [Google Scholar]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. Quantifying aromaticity with electron delocalisation measures. Chem. Soc. Rev. 2015, 44, 6389–6646. [Google Scholar] [CrossRef] [PubMed]
- Solà, M. Why aromaticity is a suspicious concept? Why? Front. Chem. 2017, 5, 22. [Google Scholar] [CrossRef] [PubMed]
- Boldyrev, A.I.; Wang, L.S. All-metal aromaticity and antiaromaticity. Chem. Rev. 2005, 105, 3716–3757. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. Metalloaromaticity. WIREs Comput. Mol. Sci. 2013, 3, 105–122. [Google Scholar] [CrossRef]
- Wade, K. The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds. J. Chem. Soc. D: Chem. Common. 1971, 792–793. [Google Scholar] [CrossRef]
- Mingos, D.M. Polyhedral Skeletal Electron Pair Approach. Acc. Chem. Res. 1984, 17, 311–319. [Google Scholar] [CrossRef]
- Hirsch, A.; Chen, Z.; Jiao, H. Spherical aromaticity in Ih symmetrical fullerenes: the 2 (N + 1) 2 rule. Angew. Chem. Int. Ed. 2000, 39, 3915–3917. [Google Scholar] [CrossRef]
- Poater, J.; Solà, M. Open-shell spherical aromaticity: The 2N2 + 2N + 1 (with S = N + 1/2) rule. Chem. Commun. 2011, 47, 11647–11649. [Google Scholar] [CrossRef]
- Poater, J.; Solà, M. Open-shell jellium aromaticity in metal clusters. Chem. Commun. 2019, 55, 5559–5562. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. Rules of aromaticity. In Applications of Topological Methods in Molecular Chemistry; Springer: Cham, Switzerland, 2016; pp. 321–335. [Google Scholar]
- Hückel, E. Quantentheoretische Beitraäge zum Benzolproblem, I: Die Elektronenkonfiguration des Benzols und verwandter Verbindungen. Z. Physik 1931, 70, 104–186. [Google Scholar] [CrossRef]
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem, II: Quantentheorie der induzierten Polaritäten. Z. Physik 1931, 72, 310–337. [Google Scholar] [CrossRef]
- Hückel, E. Beiträge zum Problem der aromatischen und ungesättigten Verbingungen. III. Z. Physik 1932, 76, 628–648. [Google Scholar] [CrossRef]
- Hückel, E. Grundzüge der Theorie ungesättigter und aromatischer Verbindungen. Z. Elektrochem. 1937, 43, 752–788, 827–849. [Google Scholar]
- Gellini, C.; Salvi, P.R. Structures of annulenes and model annulene systems in the ground and lowest excited states. Symmetry 2010, 2, 1846–1924. [Google Scholar] [CrossRef]
- Baird, N.C. Quantum organic photochemistry. II. Resonance and aromaticity in the lowest 3. pi.. pi.* state of cyclic hydrocarbons. J. Am. Chem. Soc. 1972, 94, 4941–4948. [Google Scholar] [CrossRef]
- Aihara, J.I. Aromaticity-based theory of pericyclic reactions. Bull. Chem. Soc. Jpn. 1978, 51, 1788–1792. [Google Scholar] [CrossRef]
- Ottosson, H. Organic photochemistry: exciting excited-state aromaticity. Nat. Chem. 2012, 4, 969–971. [Google Scholar] [CrossRef]
- Streifel, B.C.; Zafra, J.L.; Espejo, G.L.; Gómez-García, C.J.; Casado, J.; Tovar, J.D. An Unusually Small Singlet–Triplet Gap in a Quinoidal 1, 6-Methano [10]annulene Resulting from Baird’s 4n π-Electron Triplet Stabilization. Angew. Chem. Int. Ed. 2015, 54, 5888–5893. [Google Scholar] [CrossRef]
- Jorner, K.; Feixas, F.; Ayub, R.; Lindh, R.; Solà, M.; Ottosson, H. Analysis of a compound class with triplet states stabilized by potentially Baird aromatic [10]annulenyl dicationic rings. Chem. Eur. J. 2016, 22, 2793–2800. [Google Scholar] [CrossRef]
- Ueda, M.; Jorner, K.; Sung, Y.M.; Mori, T.; Xiao, Q.; Kim, D.; Ottosson, H.; Aida, T.; Itoh, Y. Energetics of Baird aromaticity supported by inversion of photoexcited chiral [4n] annulene derivatives. Nat. Chem. 2017, 8, 346–354. [Google Scholar] [CrossRef] [PubMed]
- Peeks, M.D.; Claridge, T.D.; Anderson, H.L. Aromatic and antiaromatic ring currents in a molecular nanoring. Nature 2017, 541, 200–205. [Google Scholar] [CrossRef] [PubMed]
- Choi, C.H.; Kertesz, M. Bond length alternation and aromaticity in large annulenes. J. Chem. Phys. 1998, 108, 6681–6688. [Google Scholar] [CrossRef]
- Soncini, A.; Fowler, P.W.; Jenneskens, L.W. Ring currents in large [4n + 2]-annulenes. Phys. Chem. Chem. Phys. 2004, 6, 277–284. [Google Scholar] [CrossRef]
- Wannere, C.S.; Schleyer, P.v.R. How Aromatic Are Large (4n + 2) π Annulenes? Org. Lett. 2003, 5, 865–868. [Google Scholar] [CrossRef]
- Matito, E.; Duran, M.; Solà, M. The aromatic fluctuation index (FLU): A new aromaticity index based on electron delocalization. J. Chem. Phys. 2005, 122, 014109, Erratum in 2006, 125, 059901. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Stephens, M.E. Fluctuation and correlation of electrons in molecular systems. Chem. Phys. Lett. 1974, 26, 445–449. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Stephens, M.E. Spatial localization of the electronic pair and number distributions in molecules. J. Am. Chem. Soc. 1975, 97, 7391–7399. [Google Scholar] [CrossRef]
- Fradera, X.; Austen, M.A.; Bader, R.F.W. The Lewis Model and Beyond. J. Phys. Chem. A 1999, 103, 304–314. [Google Scholar] [CrossRef]
- Matito, E.; Solà, M.; Salvador, P.; Duran, M. Electron sharing indexes at the correlated level. Application to aromaticity calculations. Faraday Discuss. 2007, 135, 325–345. [Google Scholar] [CrossRef]
- Mayer, I. Charge, Bond Order, and Valence in the ab initio SCF Theory. Chem. Phys. Lett. 1983, 97, 270–274. [Google Scholar] [CrossRef]
- Kruszewski, J.; Krygowski, T.M. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyranski, M.K. Structural aspects of aromaticity. Chem. Rev. 2001, 101, 1385–1420. [Google Scholar] [CrossRef] [PubMed]
- Matito, E.; Poater, J.; Duran, M.; Solà, M. An analysis of the changes in aromaticity and planarity along the reaction path of the simplest Diels–Alder reaction. Exploring the validity of different indicators of aromaticity. J. Mol. Struct. (Theochem) 2005, 727, 165–171. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. On the performance of some aromaticity indices: A critical assessment using a test set. J. Comput. Chem. 2008, 29, 1543–1554. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Handgraaf, J.W.; Baerends, E.J.; Bickelhaupt, F.M. Voronoi deformation density (VDD) charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD methods for charge analysis. J. Comput. Chem. 2004, 25, 189–210. [Google Scholar] [CrossRef]
- Matito, E.; Poater, J.; Solà, M.; Duran, M.; Salvador, P. Comparison of the AIM Delocalization Index and the Mayer and Fuzzy Atom Bond Orders. J. Phys. Chem. A 2005, 109, 9904–9910. [Google Scholar] [CrossRef]
- Matito, E.; Solà, M.; Duran, M.; Salvador, P. Aromaticity Measures from Fuzzy-Atom Bond Orders (FBO). The Aromatic Fluctuation (FLU) and the para-Delocalization (PDI) Indexes. J. Phys. Chem. A 2006, 110, 5108–5113. [Google Scholar] [CrossRef]
- Casademont-Reig, I.; Woller, T.; Contreras-García, J.; Alonso, M.; Torrent-Sucarrat, M.; Matito, E. New electron delocalization tools to describe the aromaticity in porphyrinoids. Phys. Chem. Chem. Phys. 2018, 20, 2787–2796. [Google Scholar] [CrossRef]
- Giambiagi, M.; De Giambiagi, M.S.; Mundim, K.C. Definition of a multicenter bond index. Struct. Chem. 1990, 1, 423–427. [Google Scholar] [CrossRef]
- Giambiagi, M.; De Giambiagi, M.S.; Dos Santos Silva, C.D.; De Figuereido, A.P. Multicenter bond indices as a measure of aromaticity. Phys. Chem. Chem. Phys. 2000, 2, 3381–3392. [Google Scholar] [CrossRef]
- Bultinck, P.; Ponec, R.; Van Damme, S. Multicenter bond indices as a new measure of aromaticity in polycyclic aromatic hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. [Google Scholar] [CrossRef]
- Cioslowski, J.; Matito, E.; Solà, M. Properties of Aromaticity Indices Based on the One-electron Density Matrix. J. Phys. Chem. A 2007, 111, 6521–6525. [Google Scholar] [CrossRef] [PubMed]
- Feixas, F.; Jiménez-Halla, J.; Matito, E.; Poater, J.; Solà, M. A Test to Evaluate the Performance of Aromaticity Descriptors in All-Metal and Semimetal Clusters. An Appraisal of Electronic and Magnetic Indicators of Aromaticity. J. Chem. Theory Comput. 2010, 6, 1118–1130. [Google Scholar] [CrossRef]
- Feixas, F.; Vandenbussche, J.; Bultinck, P.; Matito, E.; Solà, M. Electron delocalization and aromaticity in low-lying excited states of archetypal organic compounds. Phys. Chem. Chem. Phys. 2011, 13, 20690–20703. [Google Scholar] [CrossRef]
- Mercero, J.M.; Matito, E.; Ruipérez, F.; Infante, I.; Lopez, X.; Ugalde, J.M. The Electronic Structure of the Anion: Is it Aromatic? Chem. Eur. J. 2015, 21, 9610–9614. [Google Scholar] [CrossRef]
- Fortenberry, R.C.; Novak, C.M.; Layfield, J.P.; Matito, E.; Lee, T.J. Overcoming the Failure of Correlation for Out-of-Plane Motions in a Simple Aromatic: Rovibrational Quantum Chemical Analysis of c-C3H2. J. Chem. Theory Comput. 2018, 14, 2155–2164. [Google Scholar] [CrossRef]
- Grande-Aztatzi, R.; Mercero, J.M.; Matito, E.; Frenking, G.; Ugalde, J.M. The aromaticity of dicupra [10]annulenes. Phys. Chem. Chem. Phys. 2017, 19, 9669–9675. [Google Scholar] [CrossRef]
- López, R.V.; Faza, O.N.; Matito, E.; López, C.S. Cycloreversion of the CO2 trimer: A paradigmatic pseudopericyclic [2+ 2+ 2] cycloaddition reaction. Org. Biomol. Chem. 2017, 15, 435–441. [Google Scholar] [CrossRef]
- Popov, I.A.; Pan, F.X.; You, X.R.; Li, L.J.; Matito, E.; Liu, C.; Zhai, H.J.; Sun, Z.M.; Boldyrev, A.I. Peculiar All-Metal σ-Aromaticity of the [Au2Sb16]4- Anion in the Solid State. Angew. Chem. Int. Ed. 2016, 128, 15570–15572. [Google Scholar] [CrossRef]
- Min, X.; Popov, I.A.; Pan, F.X.; Li, L.J.; Matito, E.; Sun, Z.M.; Wang, L.S.; Boldyrev, A.I. All-Metal Antiaromaticity in Sb4-Type Lanthanocene Anions. Angew. Chem. Int. Ed. 2016, 55, 5531–5535. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Halla, J.O.C.; Matito, E.; Solà, M.; Braunschweig, H.; Hörl, C.; Krummenacher, I.; Wahler, J. A theoretical study of the aromaticity in neutral and anionic borole compounds. Dalton Trans. 2015, 44, 6740–6747. [Google Scholar] [CrossRef] [PubMed]
- Castro, A.C.; Osorio, E.; Cabellos, J.L.; Cerpa, E.; Matito, E.; Solà, M.; Swart, M.; Merino, G. Exploring the Potential Energy Surface of E2P4 Clusters (E= Group 13 Element): The Quest for Inverse Carbon-Free Sandwiches. Chem. Eur. J. 2014, 20, 4583–4590. [Google Scholar] [CrossRef] [PubMed]
- Matito, E. Electronic Aromaticity Index for Large Rings. Phys. Chem. Chem. Phys. 2016, 18, 11839–11846. [Google Scholar] [CrossRef] [PubMed]
- García-Fernández, C.; Sierda, E.; Abadia, M.; Bugenhagen, B.E.C.; Prosenc, M.H.; Wiesendanger, R.; Bazarnik, M.; Ortega, J.E.; Brede, J.; Matito, E.; et al. Exploring the Relation Between Intramolecular Conjugation and Band Dispersion in One-Dimensional Polymers. J. Phys. Chem. C 2017, 121, 27118–27125. [Google Scholar] [CrossRef]
- Gutman, I.; Milun, M.; Trinajstić, N. Graph theory and molecular orbitals. 19. Nonparametric resonance energies of arbitrary conjugated systems. J. Am. Chem. Soc. 1977, 99, 1692–1704. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Solà, M.; Poater, J. Analysis of Hückel’s [4n+2] Rule through Electronic Delocalization Measures. J. Phys. Chem. A 2008, 112, 13231–13238. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Solà, M.; Poater, J. Patterns of π-electron delocalization in aromatic and antiaromatic organic compounds in the light of Hückel’s 4n+2 rule. Phys. Chem. Chem. Phys. 2010, 12, 7126–7137. [Google Scholar] [CrossRef]
- Li, X.; Kuznetsov, A.E.; Zhang, H.F.; Boldyrev, A.I.; Wang, L.S. Observation of all-metal aromatic molecules. Science 2001, 291, 859–861. [Google Scholar] [CrossRef]
- Jiménez-Halla, J.O.C.; Matito, E.; Blancafort, L.; Robles, J.; Solà, M. Tuning aromaticity in trigonal alkaline earth metal clusters and their alkali metal salts. J. Comput. Chem. 2009, 30, 2764–2776. [Google Scholar] [CrossRef]
- Garcia-Borràs, M.; Osuna, S.; Swart, M.; Luis, J.M.; Solà, M. Maximum aromaticity as a guiding principle for the most suitable hosting cages in endohedral metallofullerenes. Angew. Chem. Int. Ed. 2013, 52, 9275–9278. [Google Scholar] [CrossRef]
- Lu, X.; Chen, Z. Curved pi-conjugation, aromaticity, and the related chemistry of small fullerenes. Chem. Rev. 2005, 105, 3643–3696. [Google Scholar] [CrossRef]
- Osuka, A.; Saito, S. Expanded porphyrins and aromaticity. Chem. Commun. 2011, 47, 4330–4339. [Google Scholar] [CrossRef] [PubMed]
- Feixas, F.; Solà, M.; Swart, M. Chemical bonding and aromaticity in metalloporphyrins 1, 2. Can. J. Chem. 2009, 87, 1063–1073. [Google Scholar] [CrossRef]
- Sung, Y.M.; Oh, J.; Cha, W.Y.; Kim, W.; Lim, J.M.; Yoon, M.C.; Kim, D. Control and switching of aromaticity in various all-aza-expanded porphyrins: spectroscopic and theoretical analyses. Chem. Rev. 2017, 117, 2257–2312. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.; Osuka, A. Conjugated porphyrin arrays: synthesis, properties and applications for functional materials. Chem. Soc. Rev. 2015, 44, 943–969. [Google Scholar] [CrossRef] [PubMed]
- Stępień, M.; Latos-Grażyński, L.; Sprutta, N.; Chwalisz, P.; Szterenberg, L. Expanded porphyrin with a split personality: a Hückel–Möbius aromaticity switch. Angew. Chem. Int. Ed. 2007, 46, 7869–7873. [Google Scholar] [CrossRef]
- Marcos, E.; Anglada, J.M.; Torrent-Sucarrat, M. Theoretical study of the switching between Hückel and Möbius topologies for expanded porphyrins. J. Phys. Chem. C 2012, 116, 24358–24366. [Google Scholar] [CrossRef]
- Liu, Z.; Tian, Z.; Li, W.; Meng, S.; Wang, L.; Ma, J. Chiral Interconversions of Pd and/or Au Bis-Metalated [32]Octaphyrins(1,0,1,0,1,0,1,0) Involving Hückel and Möbius Macrocyclic Topologies: A Theoretical Prediction. J. Org. Chem. 2012, 77, 8124–8130. [Google Scholar] [CrossRef]
- Marcos, E.; Anglada, J.M.; Torrent-Sucarrat, M. Effect of the Meso-Substituent in the Hückel-to-Möbius Topological Switches. J. Org. Chem. 2014, 79, 5036–5046. [Google Scholar] [CrossRef]
- Alonso, M.; Geerlings, P.; De Proft, F. Exploring the structure–aromaticity relationship in Hückel and Möbius N-fused pentaphyrins using DFT. Phys. Chem. Chem. Phys. 2014, 16, 14396–14407. [Google Scholar] [CrossRef] [PubMed]
- Alonso, M.; Pinter, B.; Geerlings, P.; De Proft, F. Metalated Hexaphyrins: From Understanding to Rational Design. Chem. Eur. J. 2015, 21, 17631–17638. [Google Scholar] [CrossRef] [PubMed]
- Matito, E.; Feixas, F.; Solà, M. Electron delocalization and aromaticity measures within the Hückel molecular orbital method. J. Mol. Struct. (Theochem) 2007, 811, 3–11. [Google Scholar] [CrossRef]
- Karadakov, P.; Castaño, O.; Ftatev, F.; Enchev, V. Some contributions and generalizations to the electronic theory of even polyenes and annulenes. Chem. Phys. Lett. 1981, 78, 560–565. [Google Scholar] [CrossRef]
- Fratev, F.; Enchev, V.; Polansky, O.; Bonchev, D. A theoretical—information study on the electron delocalization (aromaticity) of annulenes with and without bond alternation. J. Mol. Struct. (Theochem) 1982, 88, 105–118. [Google Scholar] [CrossRef]
- Spitler, E.L.; Johnson, C.A.; Haley, M.M. Renaissance of annulene chemistry. Chem. Rev. 2006, 106, 5344–5386. [Google Scholar] [CrossRef]
- Koseki, S.; Toyota, A. Energy component analysis of the Pseudo-Jahn-Teller effect in the ground and electronically excited states of the cyclic conjugated hydrocarbons: Cyclobutadiene, benzene, and cyclooctatetraene. J. Phys. Chem. A 1997, 101, 5712–5718. [Google Scholar] [CrossRef]
- Papadakis, R.; Ottosson, H. The excited state antiaromatic benzene ring: A molecular Mr Hyde? Chem. Soc. Rev. 2015, 44, 6472–6493. [Google Scholar] [CrossRef]
- Moll, J.F.; Pemberton, R.P.; Gutierrez, M.G.; Castro, C.; Karney, W.L. Configuration change in [14] annulene requires Möbius antiaromatic bond shifting. J. Am. Chem. Soc. 2007, 129, 274–275. [Google Scholar] [CrossRef]
- Wannere, C.S.; Sattelmeyer, K.W.; Schaefer III, H.F.; Schleyer, P.v.R. Aromaticity: The Alternating C-C Bond Length Structures of [14]-, [18]-, and [22] Annulene. Angew. Chem. Int. Ed. 2004, 43, 4200–4206. [Google Scholar] [CrossRef]
- Feixas, F.; Solà, M.; Barroso, J.M.; Ugalde, J.M.; Matito, E. New Approximation to the Third-Order Density. Application to the Calculation of Correlated Multicenter Indices. J. Chem. Theory Comput. 2014, 10, 3055–3065. [Google Scholar] [CrossRef] [PubMed]
- Feixas, F.; Rodríguez-Mayorga, M.; Matito, E.; Solà, M. Three-center bonding analyzed from correlated and uncorrelated third-order reduced density matrices. Comput. Theor. Chem. 2015, 1053, 173–179. [Google Scholar] [CrossRef]
- Mandado, M.; Graña, A.M.; Pérez-Juste, I. Aromaticity in spin-polarized systems: Can rings be simultaneously alpha aromatic and beta antiaromatic? J. Chem. Phys. 2008, 129, 164114. [Google Scholar] [CrossRef]
- Karadakov, P.B. Aromaticity and antiaromaticity in the low-lying electronic states of cyclooctatetraene. J. Phys. Chem. A 2008, 112, 12707–12713. [Google Scholar] [CrossRef] [PubMed]
- Braten, M.N.; Castro, C.; Herges, R.; Köhler, F.; Karney, W.L. The [12]annulene global minimum. J. Org. Chem. 2008, 73, 1532–1535. [Google Scholar] [CrossRef]
- Castro, C.; Karney, W.L. Mechanisms and Möbius strips: Understanding dynamic processes in annulenes. J. Phys. Org. Chem. 2012, 25, 612–619. [Google Scholar] [CrossRef]
- Lee, H.L.; Li, W.K. Computational study on the electrocyclic reactions of [16]annulene. Org. Biomol. Chem. 2003, 1, 2748–2754. [Google Scholar] [CrossRef]
- Arbitman, J.K.; Michel, C.S.; Castro, C.; Karney, W.L. Calculations Predict That Heavy-Atom Tunneling Dominates Möbius Bond Shifting in [12]-and [16] Annulene. Org. Lett. 2019, 21, 8587–8591. [Google Scholar] [CrossRef]
- Merkle, R.; Savin, A.; Preuss, H. Singly ionized first-row dimers and hydrides calculated with the fully-numerical density-functional program numol. J. Chem. Phys. 1992, 97, 9216–9221. [Google Scholar] [CrossRef]
- Savin, A. On degeneracy, near-degeneracy and density functional theory. In Recent Developments of Modern Density Functional Theory; Seminario, J.M., Ed.; Elsevier: Amsterdam, The Netherlands, 1996; p. 327. [Google Scholar]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Insights into Current Limitations of Density Functional Theory. Science 2008, 321, 792–794. [Google Scholar] [CrossRef]
- Sancho-García, J.; Pérez-Jiménez, A. Improved accuracy with medium cost computational methods for the evaluation of bond length alternation of increasingly long oligoacetylenes. Phys. Chem. Chem. Phys. 2007, 9, 5874–5879. [Google Scholar] [CrossRef]
- Torrent-Sucarrat, M.; Navarro, S.; Cossío, F.P.; Anglada, J.M.; Luis, J.M. Relevance of the DFT method to study expanded porphyrins with different topologies. J. Comput. Chem. 2017, 38, 2819–2828. [Google Scholar] [CrossRef] [PubMed]
- Szczepanik, D.W.; Solà, M.; Andrzejak, M.; Pawełek, B.; Dominikowska, J.; Kukułka, M.; Dyduch, K.; Krygowski, T.M.; Szatylowicz, H. The role of the long-range exchange corrections in the description of electron delocalization in aromatic species. J. Comput. Chem. 2017, 38, 1640–1654. [Google Scholar] [CrossRef] [PubMed]
- Peccati, F.; Laplaza, R.; Contreras-García, J. Overcoming Distrust in Solid State Simulations: Adding Error Bars to Computational Data. J. Phys. Chem. C 2019, 123, 4767–4772. [Google Scholar] [CrossRef]
- Sim, E.; Song, S.; Burke, K. Quantifying density errors in DFT. J. Phys. Chem. Lett. 2018, 9, 6385–6392. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Keith, T.A. AIMAll (Version 14.11.23); TK Gristmill Software: Overland Park, KS, USA, 2014. [Google Scholar]
- Matito, E. ESI-3D; IQCC and DIPC: Donostia, Euskadi, Spain, 2015. [Google Scholar]
- Wolfram, S. Mathematica 10; Wolfram Research Inc.: Champaign, IL, USA, 2014. [Google Scholar]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
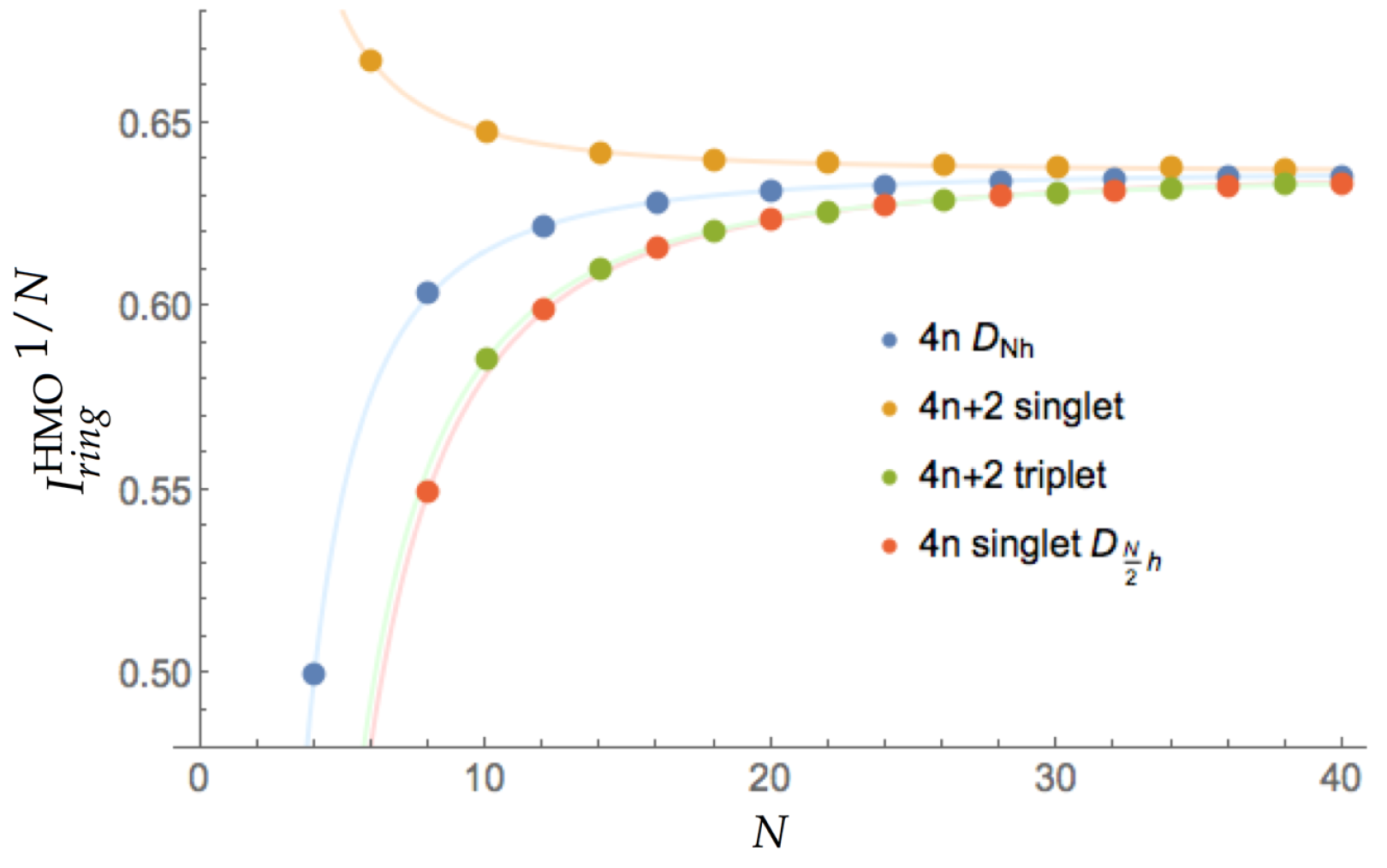
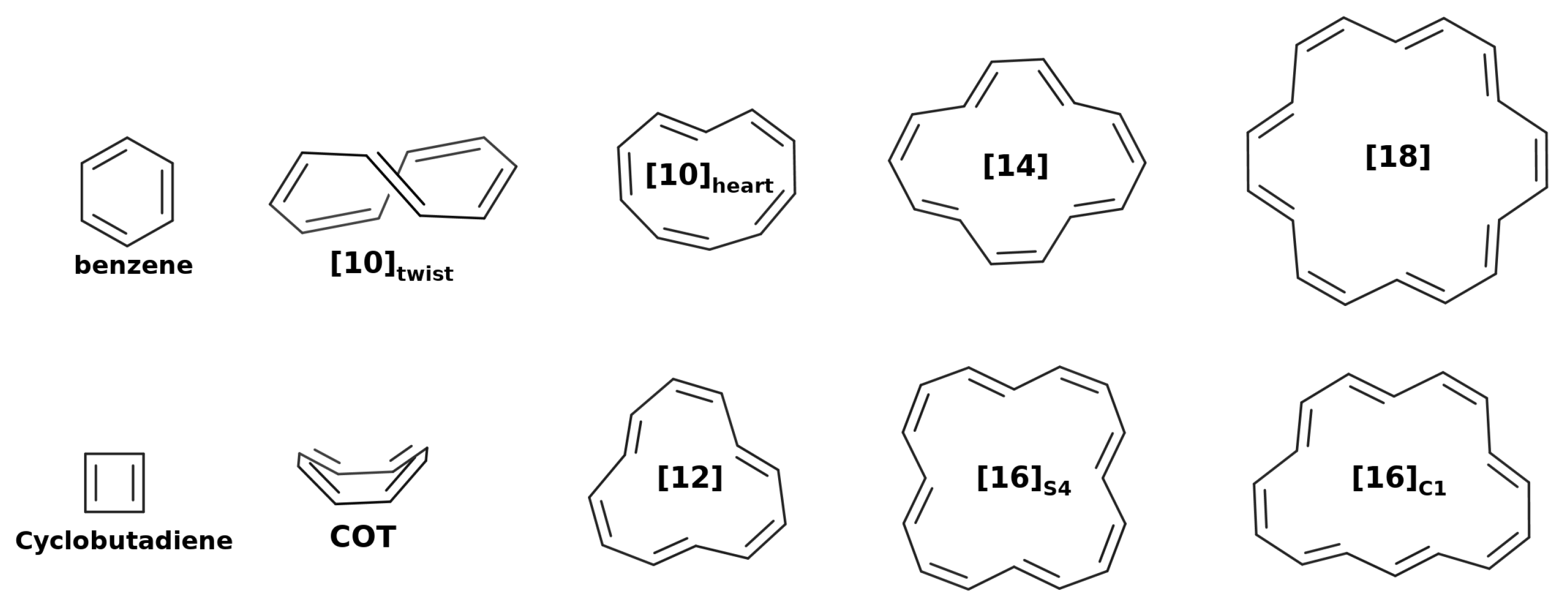
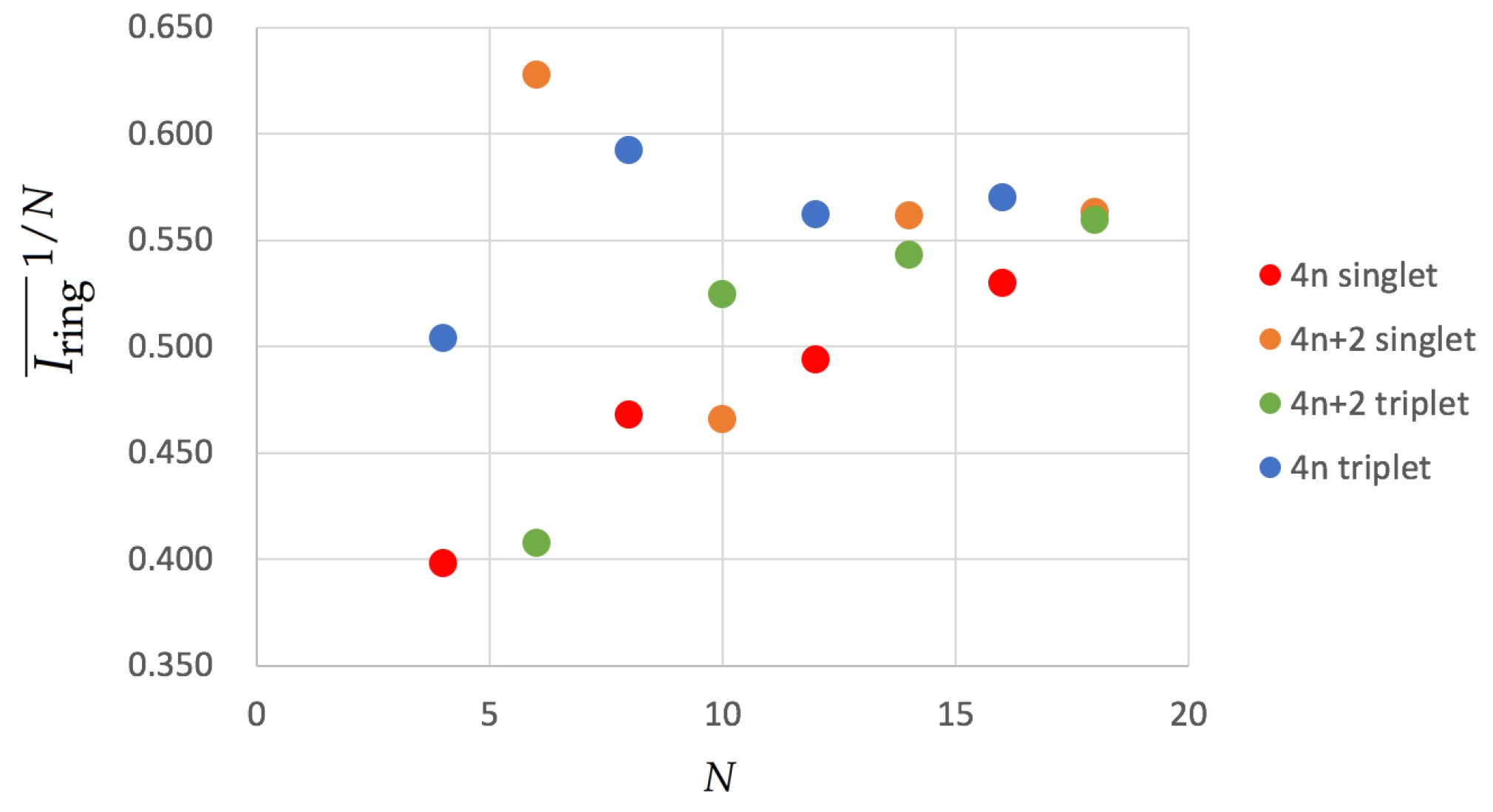
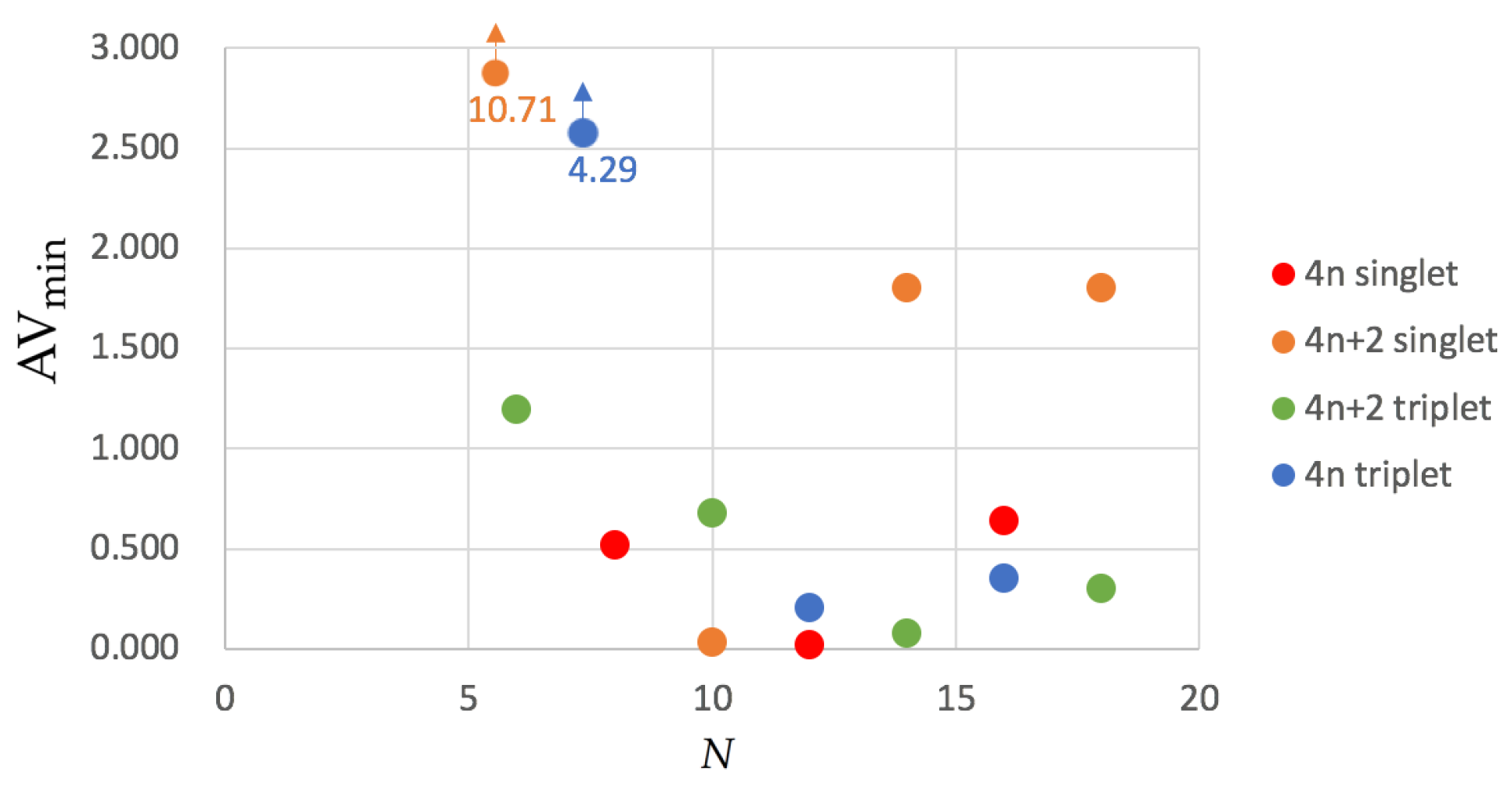
| Structure | Multiplicity | Functional | FLU | 1/N | BOA | BLA | 1/N | | | |
|---|---|---|---|---|---|---|---|---|
| CH | S | HF | 0.000 | 0.624 | 0.000 | 0.000 | 0.597 | 10.25 |
| B3LYP | 0.000 | 0.625 | 0.000 | 0.000 | 0.603 | 10.72 | ||
| CAM-B3LYP | 0.000 | 0.628 | 0.000 | 0.000 | 0.603 | 10.71 | ||
| M06-2X | 0.000 | 0.626 | 0.000 | 0.000 | 0.603 | 10.73 | ||
| CH | T | HF | 0.024 | 0.393 | 0.246 | 0.089 | 0.341 | 0.39 |
| B3LYP | 0.025 | 0.399 | 0.275 | 0.090 | 0.353 | 1.51 | ||
| CAM-B3LYP | 0.025 | 0.408 | 0.276 | 0.091 | 0.363 | 1.20 | ||
| M06-2X | 0.041 | 0.467 | 0.281 | 0.056 | 0.380 | 0.28 | ||
| CH (twist) | S | HF | 0.068 | 0.421 | 0.728 | 0.157 | 0.339 | 0.00 |
| B3LYP | 0.052 | 0.480 | 0.639 | 0.128 | 0.322 | 0.03 | ||
| CAM-B3LYP | 0.059 | 0.466 | 0.677 | 0.137 | 0.341 | 0.03 | ||
| M06-2X | 0.058 | 0.463 | 0.670 | 0.136 | 0.325 | 0.05 | ||
| CH (heart) | S | HF | 0.065 | 0.436 | 0.712 | 0.153 | 0.380 | 0.01 |
| B3LYP | 0.000 | 0.610 | 0.007 | 0.009 | 0.579 | 5.19 | ||
| CAM-B3LYP | 0.000 | 0.614 | 0.009 | 0.010 | 0.579 | 5.13 | ||
| M06-2X | 0.000 | 0.611 | 0.010 | 0.010 | 0.579 | 5.11 | ||
| CH (naphthalene) | T | HF | 0.030 | 0.470 | 0.364 | 0.085 | 0.353 | 0.14 |
| B3LYP | 0.023 | 0.531 | 0.328 | 0.064 | 0.460 | 0.91 | ||
| CAM-B3LYP | 0.027 | 0.524 | 0.364 | 0.072 | 0.446 | 0.68 | ||
| M06-2X | 0.028 | 0.522 | 0.367 | 0.073 | 0.444 | 0.63 | ||
| CH (twist) | T | HF | 0.020 | 0.478 | 0.266 | 0.068 | 0.295 | 0.05 |
| B3LYP | 0.020 | 0.517 | 0.305 | 0.066 | 0.352 | 0.08 | ||
| CAM-B3LYP | 0.022 | 0.513 | 0.324 | 0.071 | 0.347 | 0.07 | ||
| M06-2X | 0.022 | 0.511 | 0.328 | 0.072 | 0.337 | 0.10 | ||
| CH | S | HF | 0.050 | 0.497 | 0.626 | 0.136 | - | 0.49 |
| B3LYP | 0.001 | 0.605 | 0.010 | 0.008 | - | 4.24 | ||
| CAM-B3LYP | 0.026 | 0.561 | 0.449 | 0.091 | - | 1.80 | ||
| M06-2X | 0.025 | 0.561 | 0.438 | 0.088 | - | 1.89 | ||
| CH (TS) | S | CAM-B3LYP | 0.000 | 0.609 | 0.007 | 0.007 | - | 4.29 |
| M06-2X | 0.001 | 0.606 | 0.007 | 0.007 | - | 4.27 | ||
| CH | T | HF | 0.021 | 0.502 | 0.282 | 0.069 | - | 0.01 |
| B3LYP | 0.017 | 0.554 | 0.302 | 0.060 | - | 0.13 | ||
| CAM-B3LYP | 0.023 | 0.544 | 0.348 | 0.071 | - | 0.08 | ||
| M06-2X | 0.022 | 0.544 | 0.349 | 0.071 | - | 0.04 | ||
| CH | S | HF | 0.049 | 0.504 | 0.616 | 0.133 | 0.472 | 0.57 |
| B3LYP | 0.001 | 0.606 | 0.026 | 0.011 | 0.573 | 4.27 | ||
| CAM-B3LYP | 0.026 | 0.563 | 0.446 | 0.090 | 0.530 | 1.80 | ||
| M06-2X | 0.025 | 0.561 | 0.444 | 0.089 | 0.529 | 1.81 | ||
| CH (TS) | S | CAM-B3LYP | 0.001 | 0.609 | 0.022 | 0.010 | 0.572 | 4.29 |
| M06-2X | 0.001 | 0.607 | 0.022 | 0.010 | 0.572 | 4.28 | ||
| CH | T | HF | 0.018 | 0.514 | 0.257 | 0.060 | 0.411 | 0.12 |
| B3LYP | 0.013 | 0.570 | 0.265 | 0.053 | 0.533 | 0.58 | ||
| CAM-B3LYP | 0.019 | 0.559 | 0.324 | 0.066 | 0.513 | 0.30 | ||
| M06-2X | 0.019 | 0.559 | 0.324 | 0.065 | 0.517 | 0.46 |
| Structure | Multiplicity | Method | FLU | 1/N | BOA | BLA | 1/N | | | |
|---|---|---|---|---|---|---|---|---|
| CH | S | HF | 0.101 | 0.391 | 0.888 | 0.249 | 0.262 | - |
| B3LYP | 0.104 | 0.416 | 0.900 | 0.247 | 0.266 | - | ||
| CAM-B3LYP | 0.103 | 0.398 | 0.898 | 0.245 | 0.264 | - | ||
| M06-2X | 0.103 | 0.405 | 0.898 | 0.242 | 0.268 | - | ||
| CH | T | HF | 0.010 | 0.507 | 0.000 | 0.000 | 0.433 | - |
| B3LYP | 0.012 | 0.499 | 0.000 | 0.000 | 0.440 | - | ||
| CAM-B3LYP | 0.011 | 0.504 | 0.000 | 0.000 | 0.439 | - | ||
| M06-2X | 0.011 | 0.505 | 0.000 | 0.000 | 0.438 | - | ||
| CH | S | HF | 0.067 | 0.436 | 0.726 | 0.156 | 0.406 | 0.30 |
| B3LYP | 0.056 | 0.477 | 0.664 | 0.134 | 0.441 | 0.72 | ||
| CAM-B3LYP | 0.061 | 0.468 | 0.693 | 0.140 | 0.428 | 0.52 | ||
| M06-2X | 0.062 | 0.460 | 0.694 | 0.141 | 0.427 | 0.51 | ||
| CH | T | HF | 0.001 | 0.590 | 0.000 | 0.000 | 0.534 | 4.07 |
| B3LYP | 0.001 | 0.589 | 0.000 | 0.000 | 0.540 | 4.31 | ||
| CAM-B3LYP | 0.001 | 0.593 | 0.000 | 0.000 | 0.539 | 4.29 | ||
| M06-2X | 0.001 | 0.591 | 0.000 | 0.000 | 0.539 | 4.29 | ||
| CH | S | HF | 0.063 | 0.445 | 0.698 | 0.153 | - | 0.04 |
| B3LYP | 0.042 | 0.511 | 0.565 | 0.115 | - | 0.01 | ||
| CAM-B3LYP | 0.050 | 0.494 | 0.624 | 0.128 | - | 0.02 | ||
| M06-2X | 0.050 | 0.488 | 0.624 | 0.128 | - | 0.06 | ||
| CH | T | HF | 0.021 | 0.487 | 0.280 | 0.067 | - | 0.07 |
| B3LYP | 0.002 | 0.590 | 0.033 | 0.012 | - | 0.07 | ||
| CAM-B3LYP | 0.015 | 0.562 | 0.288 | 0.056 | - | 0.21 | ||
| M06-2X | 0.008 | 0.577 | 0.208 | 0.039 | - | 0.13 | ||
| CH (S) | S | HF | 0.054 | 0.486 | 0.651 | 0.139 | 0.440 | 0.33 |
| B3LYP | 0.029 | 0.551 | 0.476 | 0.095 | 0.513 | 0.96 | ||
| CAM-B3LYP | 0.041 | 0.529 | 0.564 | 0.113 | 0.484 | 0.64 | ||
| M06-2X | 0.040 | 0.526 | 0.562 | 0.113 | 0.484 | 0.63 | ||
| CH (C) | S | HF | 0.053 | 0.488 | 0.643 | 0.139 | 0.452 | 0.25 |
| B3LYP | 0.029 | 0.548 | 0.474 | 0.096 | 0.512 | 0.78 | ||
| CAM-B3LYP | 0.040 | 0.530 | 0.555 | 0.113 | 0.487 | 0.55 | ||
| M06-2X | 0.039 | 0.526 | 0.553 | 0.112 | 0.487 | 0.58 | ||
| CH (C) | T | HF | 0.001 | 0.598 | 0.013 | 0.005 | - | 1.08 |
| B3LYP | 0.002 | 0.596 | 0.057 | 0.013 | - | 1.16 | ||
| CAM-B3LYP | 0.015 | 0.568 | 0.294 | 0.059 | - | 0.35 | ||
| M06-2X | 0.011 | 0.576 | 0.252 | 0.050 | - | 0.74 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casademont-Reig, I.; Ramos-Cordoba, E.; Torrent-Sucarrat, M.; Matito, E. How do the Hückel and Baird Rules Fade away in Annulenes? Molecules 2020, 25, 711. https://doi.org/10.3390/molecules25030711
Casademont-Reig I, Ramos-Cordoba E, Torrent-Sucarrat M, Matito E. How do the Hückel and Baird Rules Fade away in Annulenes? Molecules. 2020; 25(3):711. https://doi.org/10.3390/molecules25030711
Chicago/Turabian StyleCasademont-Reig, Irene, Eloy Ramos-Cordoba, Miquel Torrent-Sucarrat, and Eduard Matito. 2020. "How do the Hückel and Baird Rules Fade away in Annulenes?" Molecules 25, no. 3: 711. https://doi.org/10.3390/molecules25030711
APA StyleCasademont-Reig, I., Ramos-Cordoba, E., Torrent-Sucarrat, M., & Matito, E. (2020). How do the Hückel and Baird Rules Fade away in Annulenes? Molecules, 25(3), 711. https://doi.org/10.3390/molecules25030711







