Revisiting the Rearrangement of Dewar Thiophenes
Abstract
1. Introduction
2. Computational Details
3. Structures
4. Reaction Profiles and Forces
5. Evolution of Bonding
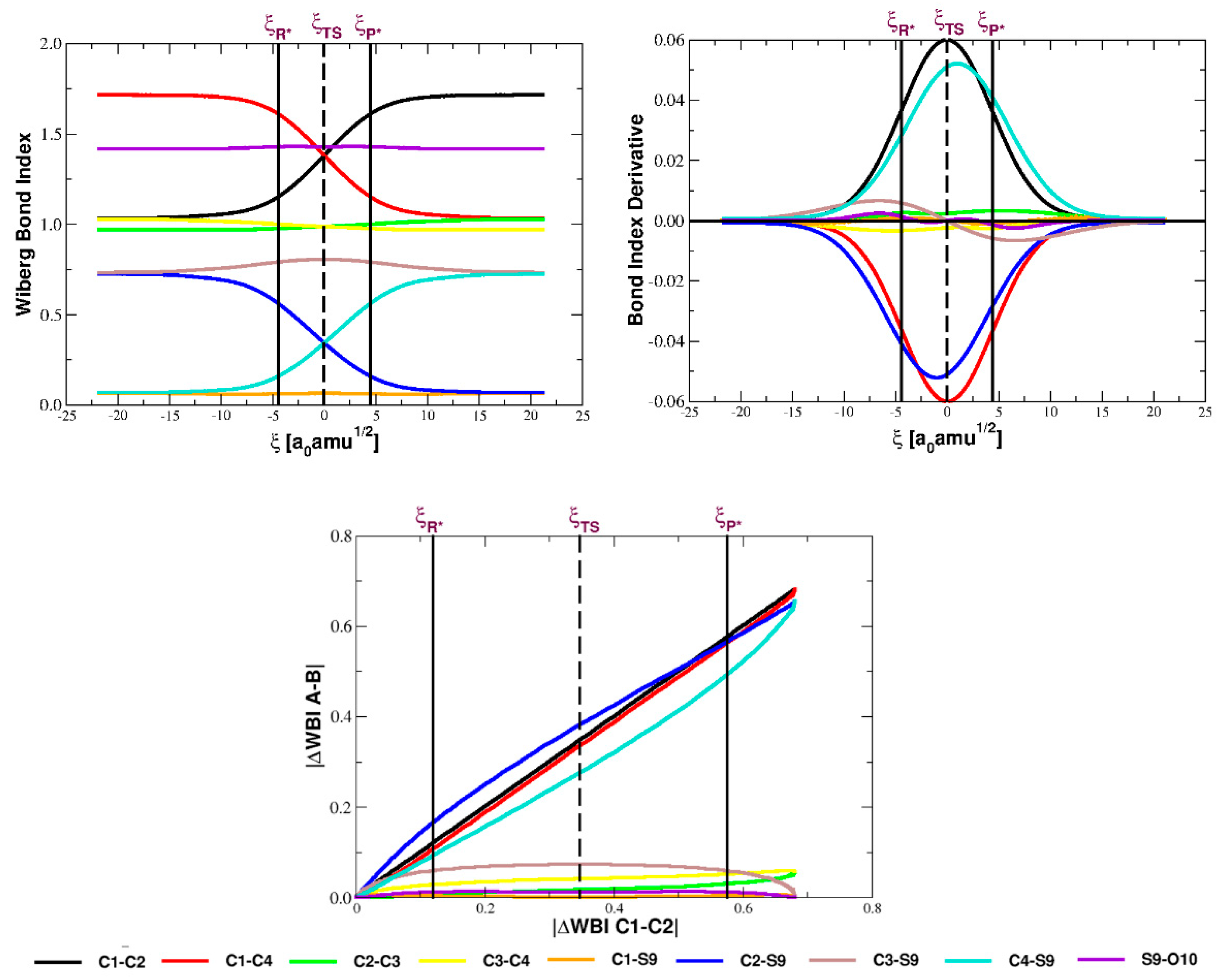
5.1. Bond Orders and Their Derivatives
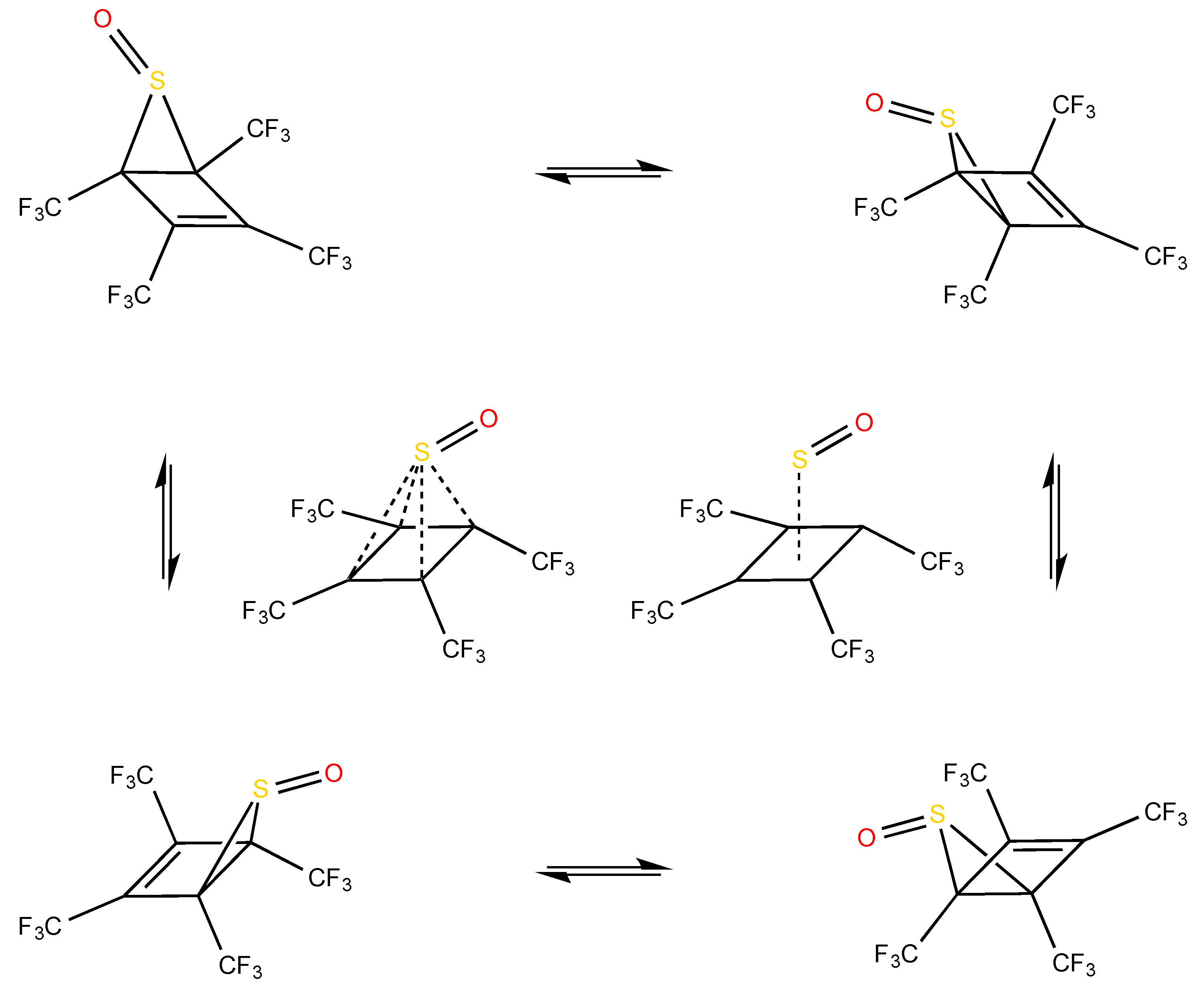
5.2. Evolution of the Dewar Rearrangement in S-oxide Perfluorotetramethyl Thiophene
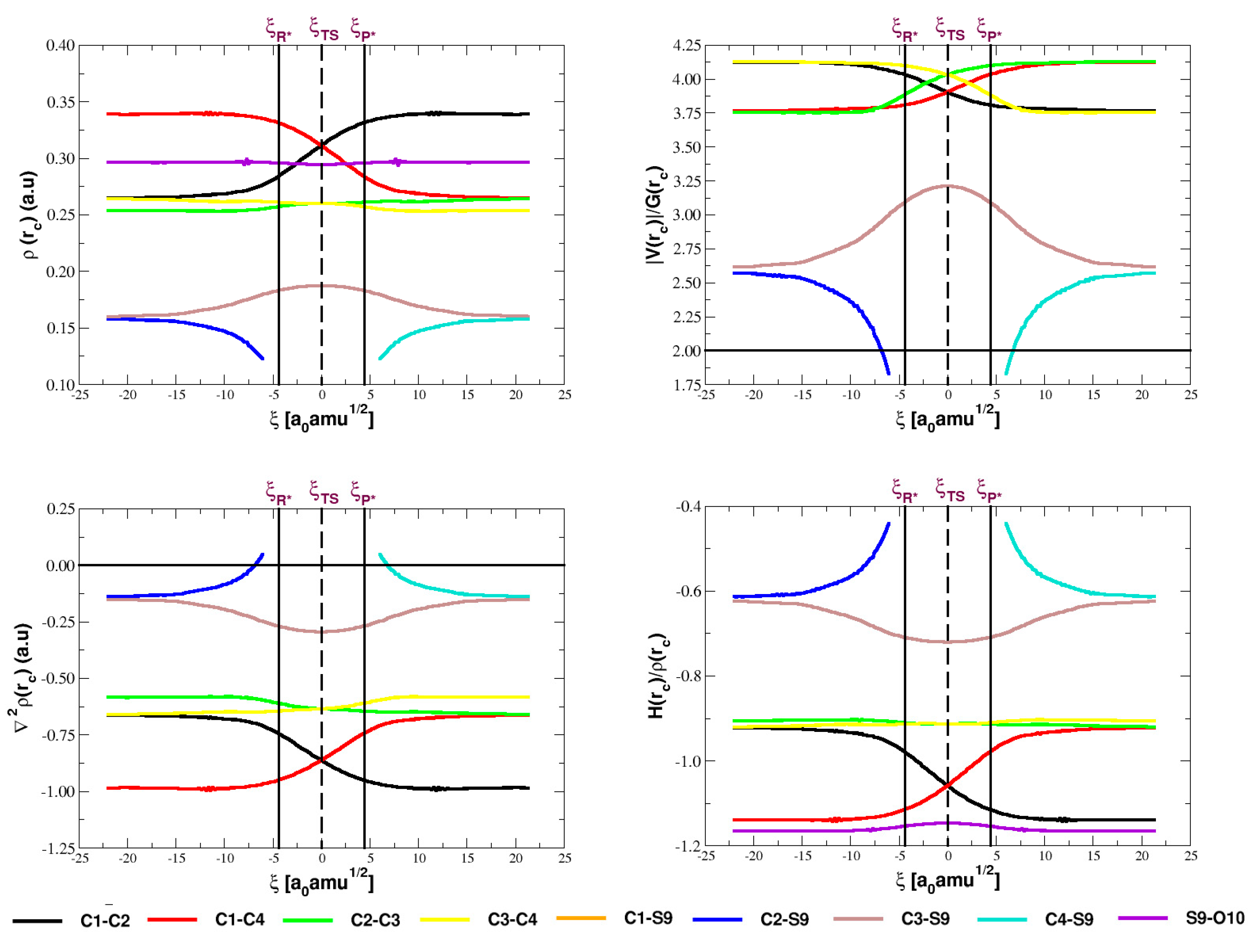
5.3. Analysis of the Electron Densities
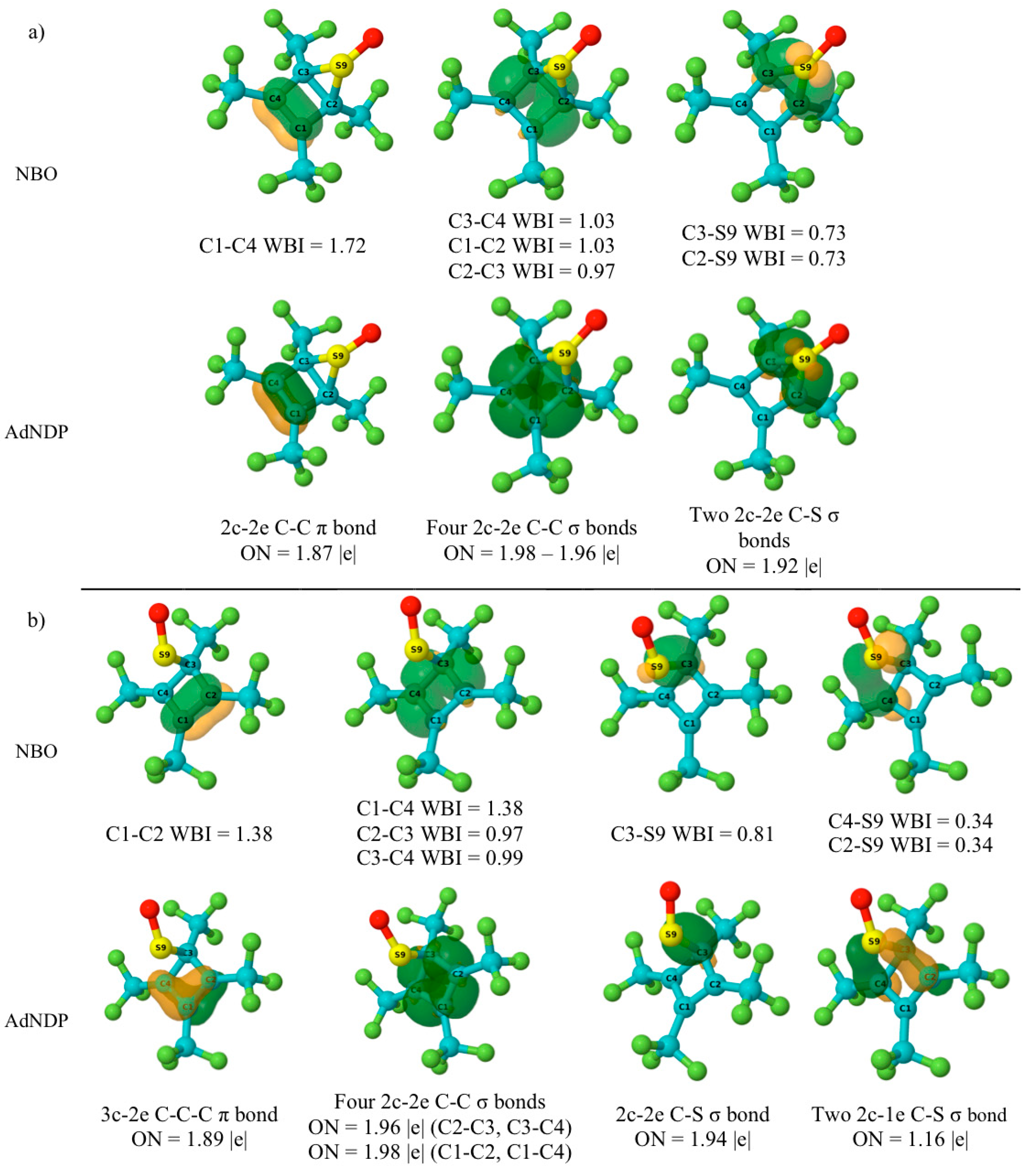
5.4. NBO and AdNDP Analysis
6. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kobayashi, Y.; Kumadaki, I. Heterocycles Dewar and Related Compounds. In Advances in Heterocyclic Chemistry; Elsevier: New York, NY, USA, 1982; Volume 31, p. 169. [Google Scholar]
- Bushweller, C.H.; Ross, J.A.; Lemal, D.M. Automerization of a Dewar thiophene and its exo-S-oxide. A dramatic contrast. J. Am. Chem. Soc. 1977, 99, 629–631. [Google Scholar] [CrossRef]
- Dorogan, I.V.; Minkin, V.I.; Novikova, L.M. Computer simulation of the mechanisms and energetics of circumambulatory rearrangements of Dewar furan, thiophene and selenophene. Mendeleev Commun. 2003, 13, 205–207. [Google Scholar] [CrossRef]
- Martin Birney, D. Theory, experiment and unusual features of potential energy surfaces of pericyclic and pseudopericyclic reactions with sequential transition structures Curr. Org. Chem. 2010, 14, 1658–1668. [Google Scholar]
- Ross, J.A.; Seiders, R.P.; Lemal, D.M. An extraordinarily facile sulfoxide automerization. J. Am. Chem. Soc. 1976, 98, 4325–4327. [Google Scholar] [CrossRef]
- Schleyer, P.V.R.; Wu, J.I.; Cossío, F.P.; Fernández, I. Aromaticity in transition structures. Chem. Soc. Rev. 2014, 43, 4909–4921. [Google Scholar] [CrossRef]
- Jalife, S.; Martínez-Guajardo, G.; Zavala-Oseguera, C.; Fernández-Herrera, M.A.; Schleyer, P.V.R.; Merino, G. Mechanistic elucidation of the 2-norbornyl to 1,3-dimethylcyclopentenyl cation isomerization. Eur. J. Org. Chem. 2014, 35, 7955–7959. [Google Scholar] [CrossRef]
- Jalife, S.; Judy, I.; Wu, C.; Martínez-Guajardo, G.; Schleyer, P.V.R.; Fernández-Herrera, M.A.; Merino, G. The 9-homocubyl cation rearrangement revisited. Chem. Commun. 2015, 51, 5391–5393. [Google Scholar] [CrossRef]
- Jalife, S.; Mondal, S.; Cabellos, J.L.; Martinez-Guajardo, G.; Fernandez-Herrera, M.A.; Merino, G. The cubyl cation rearrangements. Chem. Commun. 2016, 52, 3403–3405. [Google Scholar] [CrossRef] [PubMed]
- Jalife, S.; Mondal, S.; Osorio, E.; Cabellos, J.L.; Martinez-Guajardo, G.; Fernandez-Herrera, M.A.; Merino, G. Nonclassical 21-homododecahedryl cation rearrangement revisited. Org. Lett. 2016, 18, 1140–1142. [Google Scholar] [CrossRef] [PubMed]
- Barroso, J.; Cabellos, J.L.; Pan, S.; Murillo, F.; Zarate, X.; Fernandez-Herrera, M.A.; Merino, G. Revisiting the racemization mechanism of helicenes. Chem. Commun. 2018, 54, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Toro-Labbé, A. Characterization of chemical reactions from the profiles of energy, chemical Potential, and hardness. J. Phys. Chem. A 1999, 103, 4398–4403. [Google Scholar] [CrossRef]
- Toro-Labbé, A.; Gutiérrez-Oliva, S.; Murray, J.; Politzer, P. A new perspective on chemical and physical processes: The reaction force. Mol. Phys. 2007, 105, 2619–2625. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Jaque, P. Perspectives on the reaction force constant. J. Mol. Model. 2013, 19, 4111. [Google Scholar] [CrossRef]
- Fukui, K. The path of chemical reactions—The IRC approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Hargis, J.C.; Vöhringer-Martinez, E.; Woodcock, H.L.; Toro-Labbé, A.; Schaefer III, H.F. Characterizing the mechanism of the double proton transfer in the formamide dimer. J. Phys. Chem. A 2011, 115, 2650–2657. [Google Scholar] [CrossRef]
- Gómez, S.; Guerra, D.; López, J.G.; Toro-Labbé, A.; Restrepo, A. A Detailed Look at the Reaction Mechanisms of Substituted Carbenes with Water. J. Phys. Chem. A 2013, 117, 1991–1999. [Google Scholar] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 (Revision E.01); Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154119. [Google Scholar] [CrossRef] [PubMed]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Landis, C.R.; Weinhold, F. Natural Bond Order 6.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2013. [Google Scholar]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef] [PubMed]
- Zubarev, D.Y.; Boldyrev, A.I. Revealing intuitively assessable chemical bonding patterns in organic aromatic molecules via adaptive natural density partitioning. J. Org. Chem. 2008, 73, 9251–9258. [Google Scholar] [CrossRef] [PubMed]
- Duarte, F.; Toro-Labbé, A. The mechanism of H2 activation by (amino)carbenes. J. Phys. Chem. A 2011, 115, 3050–3059. [Google Scholar] [CrossRef]
- Giraldo, C.; Gómez, S.; Weinhold, F.; Restrepo, A. Insight into the mechanism of the Michael reaction. ChemPhysChem 2016, 17, 2022–2034. [Google Scholar] [CrossRef]
- Bader, R. Atoms in Molecules. A Quantum Theory; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Popelier, P.L.A. On the full topology of the Laplacian of the electron density. Coord. Chem. Rev. 2000, 197, 169–189. [Google Scholar] [CrossRef]
- Popelier, P.L.A. Atoms in Molecules: An Introduction; Prentice Hall: London, UK, 2000. [Google Scholar]
- Bader, R.F.W. The quantum mechanical basis of conceptual chemistry. Monatsh. Chem. 2005, 136, 819–854. [Google Scholar] [CrossRef]
- Becke, A. The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Merino, G.; Vela, A.; Heine, T. Description of electron delocalization via the analysis of molecular fields. Chem. Rev. 2005, 105, 3812–3841. [Google Scholar] [CrossRef]
- Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H⋯F–Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural bond orbital methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 1–42. [Google Scholar] [CrossRef]
- Wiberg, K.B. Application of the Pople-Santry-Segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968, 24, 1083–1096. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
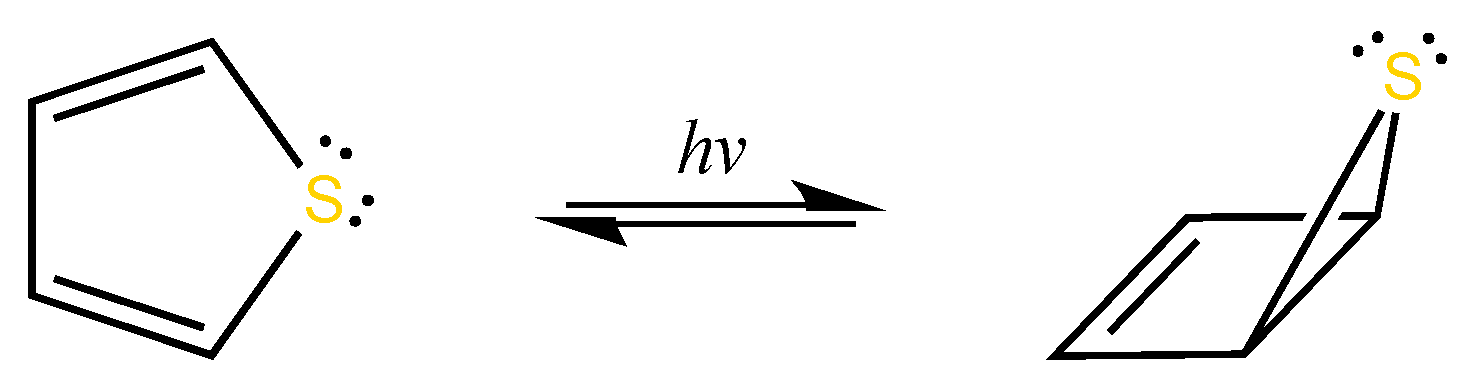
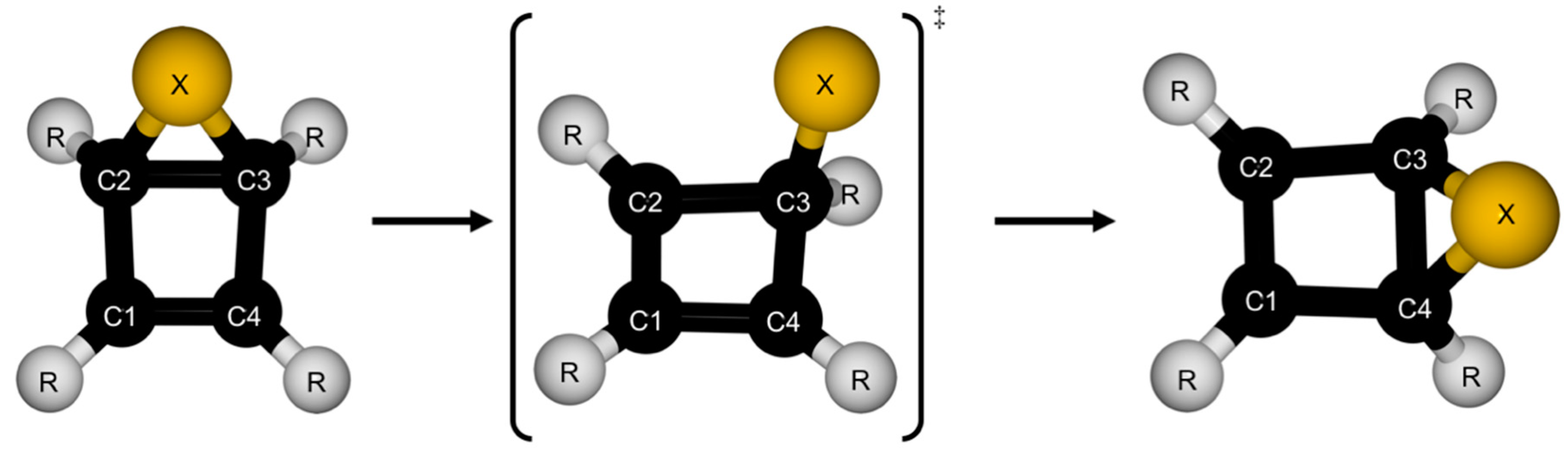
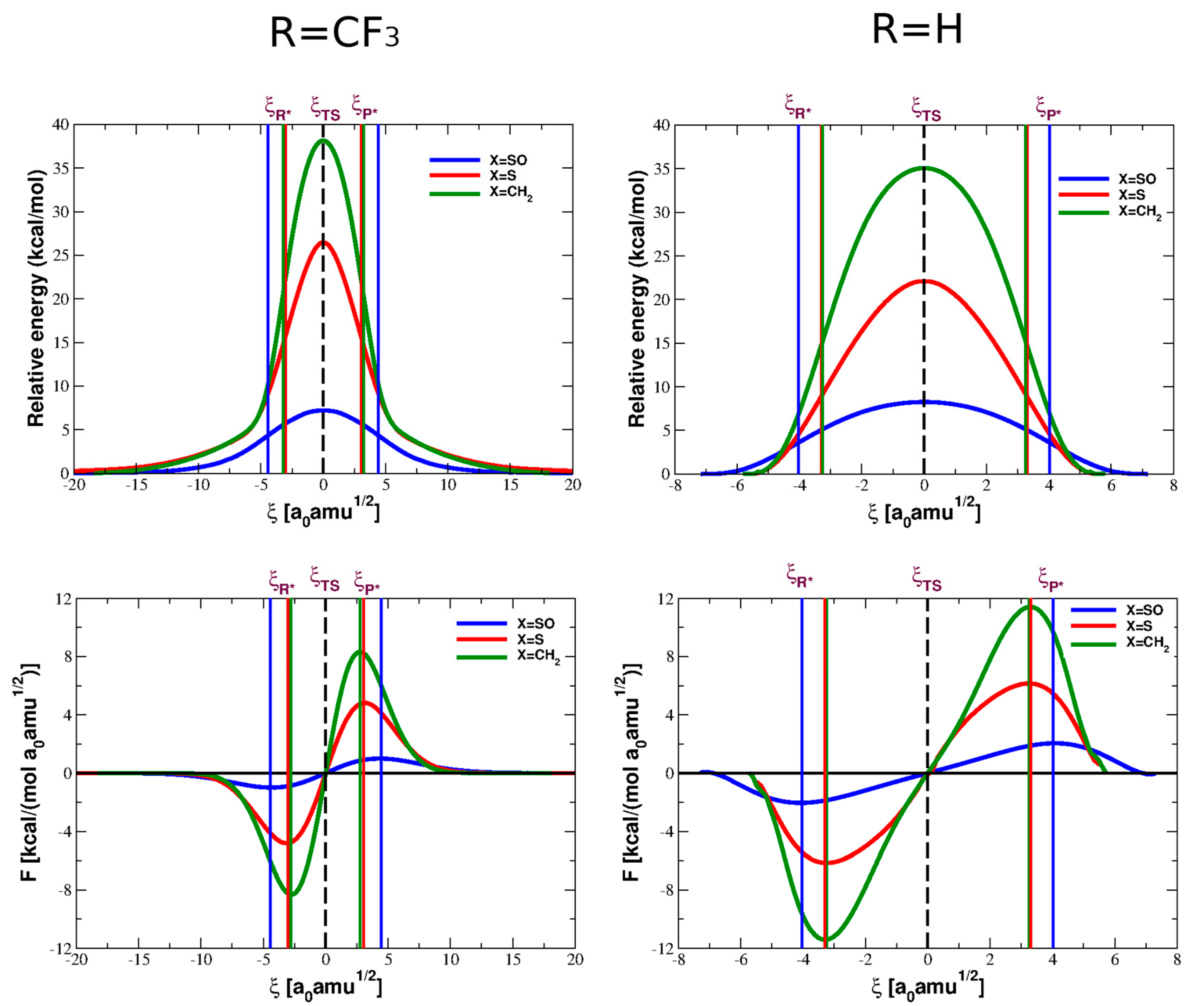
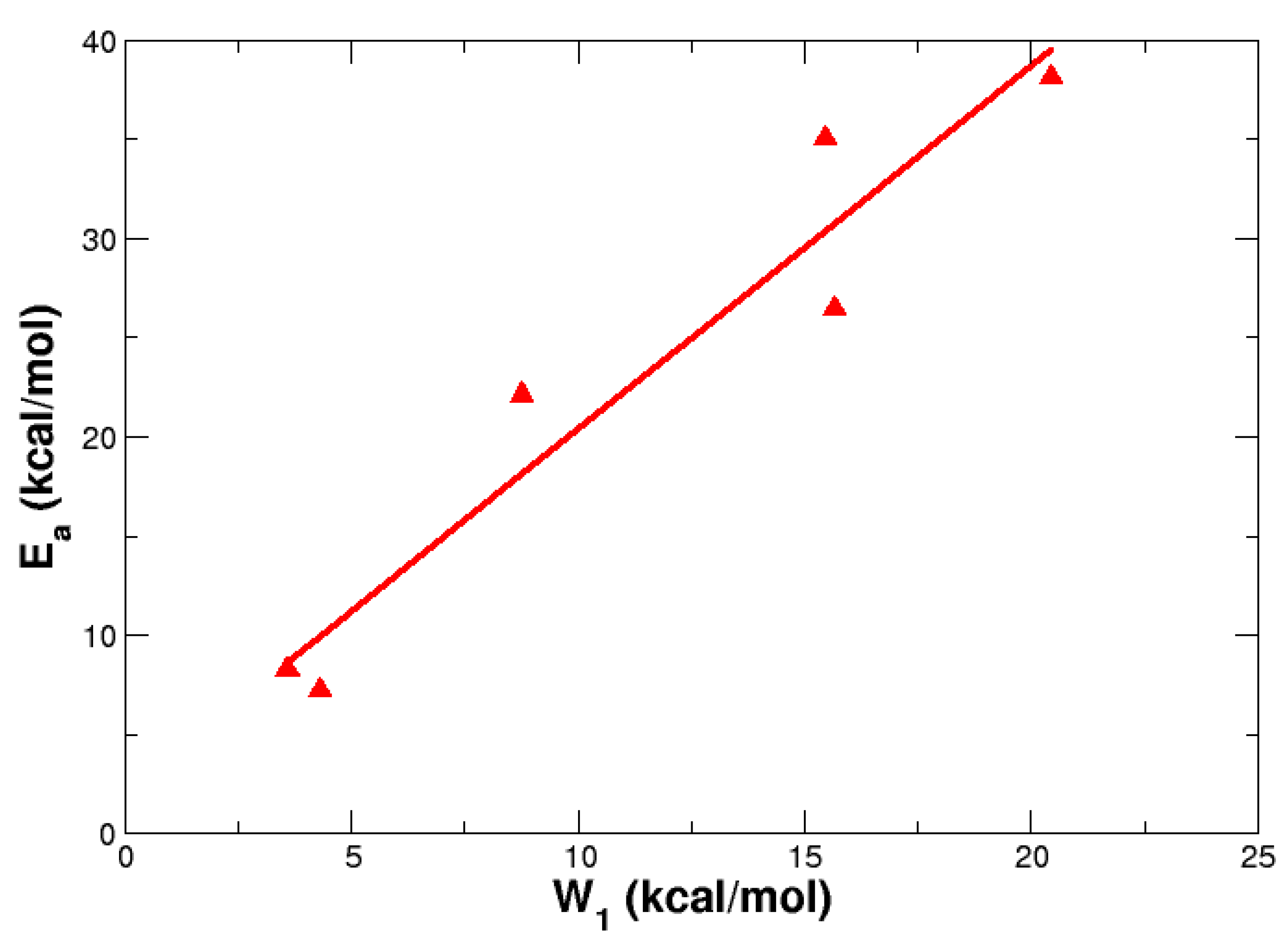
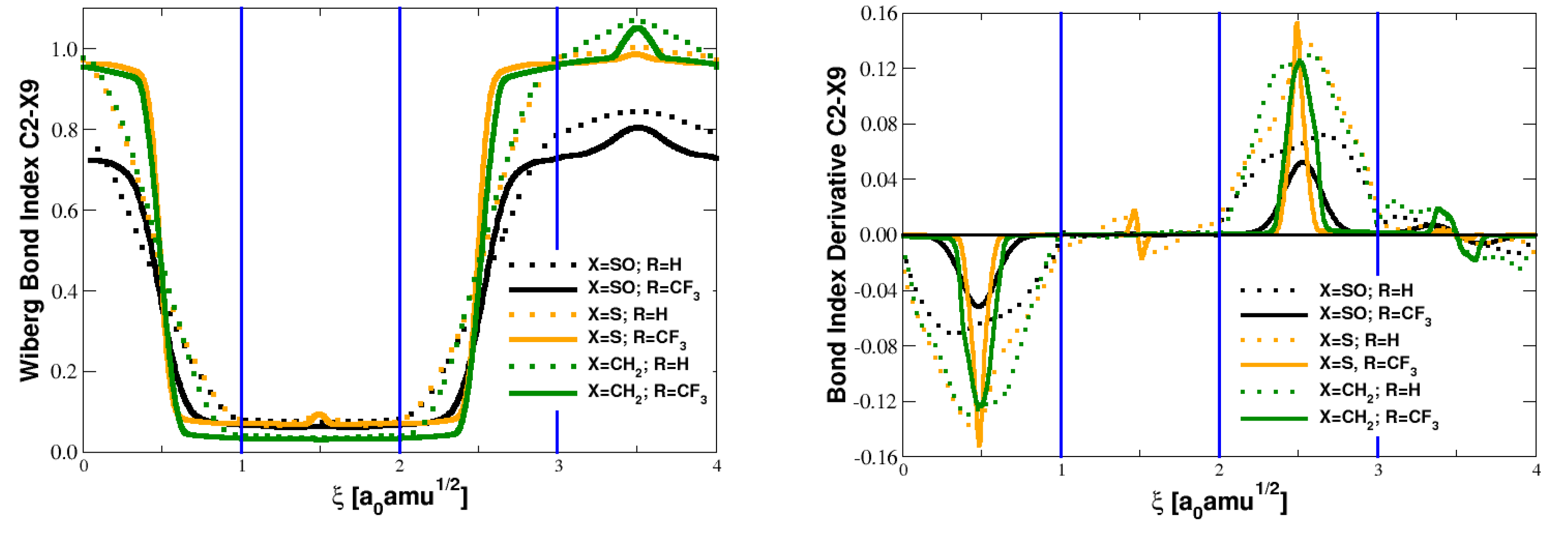
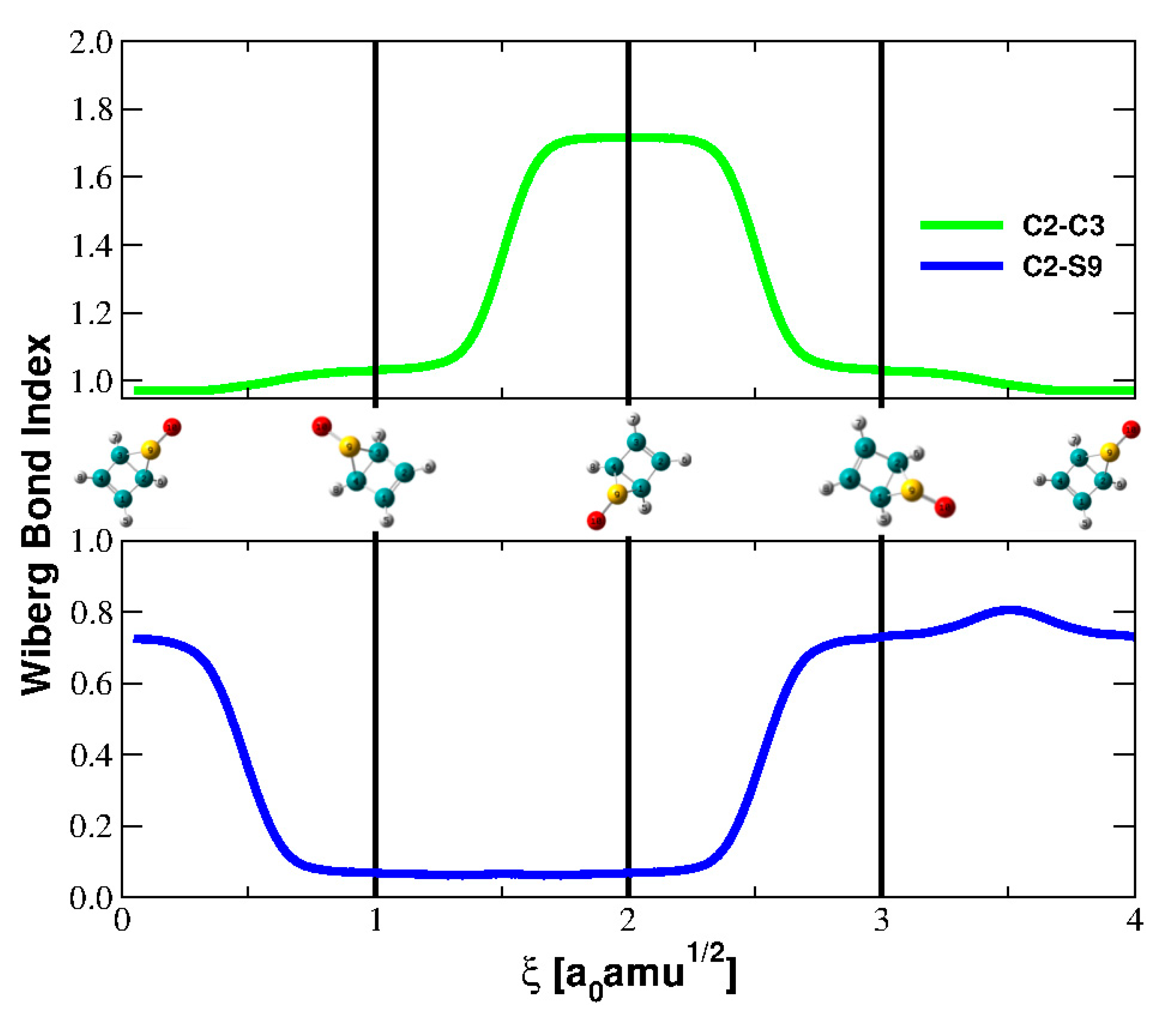
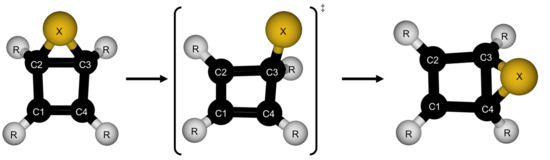
| Parameter | Reactant | TS | Product |
|---|---|---|---|
| Bond Distance | |||
| C1-C2 | 1.48 | 1.40 | 1.35 |
| C1-C4 | 1.35 | 1.40 | 1.48 |
| C2-C3 | 1.50 | 1.49 | 1.49 |
| C3-C4 | 1.49 | 1.49 | 1.5 |
| C1-S9 | 2.62 | 2.69 | 2.62 |
| C2-S9 | 1.89 | 2.31 | 2.61 |
| C3-S9 | 1.88 | 1.81 | 1.88 |
| C4-S9 | 2.61 | 2.31 | 1.89 |
| S9-O10 | 1.45 | 1.45 | 1.45 |
| Dihedral Angles | |||
| dr | 0 | 0 | 0 |
| F3C-C1-C2-C3 | −170 | −171 | −169 |
| F3C-C2-C3-C4 | 143 | 179 | −169 |
| F3C-C3-C4-C1 | 142 | 136 | 140 |
| F3C-C4-C1-C2 | −168 | 179 | 144 |
| X | R | Ea | W1 | W2 | ||
|---|---|---|---|---|---|---|
| Electronic | Gibbs at 157 °C | Gibbs at −135.8 °C | ||||
| S = O | H | 8.26 | 8.25 | 7.79 | 3.58 | 4.68 |
| CF3 | 7.23 | 7.57 | 6.86 | 4.29 | 2.94 | |
| (6.7 ± 0.1) | ||||||
| S | Ha | 22.14 | 21.16 | 21.24 | 8.76 | 13.38 |
| CF3 | 26.46 | 25.06 | 25.35 | 15.64 | 10.82 | |
| (22.1 ± 0.1) | ||||||
| CH2 | H | 35.06 | 32.98 | 33.16 | 15.46 | 19.6 |
| CF3 | 38.13 | 35.73 | 36.4 | 20.42 | 17.71 |
| R = CF3 | R = H | |||
|---|---|---|---|---|
| Atoms | ON | Atoms | ON | |
| X = SO | C2-S9 | 1.16 | C2-S9 | 1.21 |
| C4-S9 | 1.16 | C4-S9 | 1.21 | |
| X = S | C2-S9 | 1.58 | C2-S9 | 1.66 |
| C4-S9 | 1.58 | C4-S9 | 1.66 | |
| X = CH2 | C2-S9 | 1.37 | C2-S9 | 1.48 |
| C4-S9 | 1.37 | C4-S9 | 1.48 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, S.; Osorio, E.; Dzib, E.; Islas, R.; Restrepo, A.; Merino, G. Revisiting the Rearrangement of Dewar Thiophenes. Molecules 2020, 25, 284. https://doi.org/10.3390/molecules25020284
Gómez S, Osorio E, Dzib E, Islas R, Restrepo A, Merino G. Revisiting the Rearrangement of Dewar Thiophenes. Molecules. 2020; 25(2):284. https://doi.org/10.3390/molecules25020284
Chicago/Turabian StyleGómez, Sara, Edison Osorio, Eugenia Dzib, Rafael Islas, Albeiro Restrepo, and Gabriel Merino. 2020. "Revisiting the Rearrangement of Dewar Thiophenes" Molecules 25, no. 2: 284. https://doi.org/10.3390/molecules25020284
APA StyleGómez, S., Osorio, E., Dzib, E., Islas, R., Restrepo, A., & Merino, G. (2020). Revisiting the Rearrangement of Dewar Thiophenes. Molecules, 25(2), 284. https://doi.org/10.3390/molecules25020284