QSAR Model for Predicting the Cannabinoid Receptor 1 Binding Affinity and Dependence Potential of Synthetic Cannabinoids
Abstract
1. Introduction
2. Results and Discussion
2.1. QSAR Modeling for Predicting CB1R Binding Affinity of THC and SCs
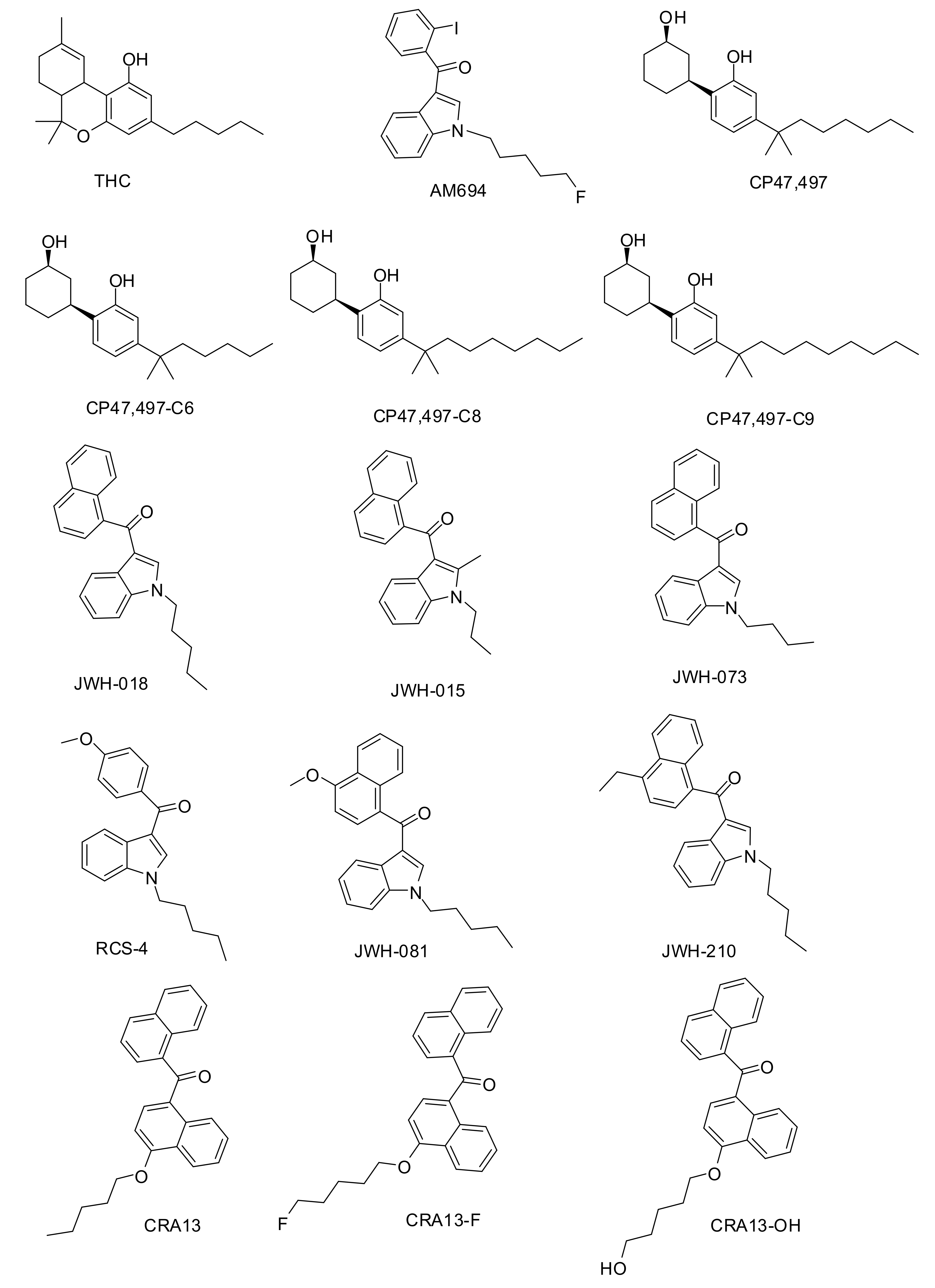
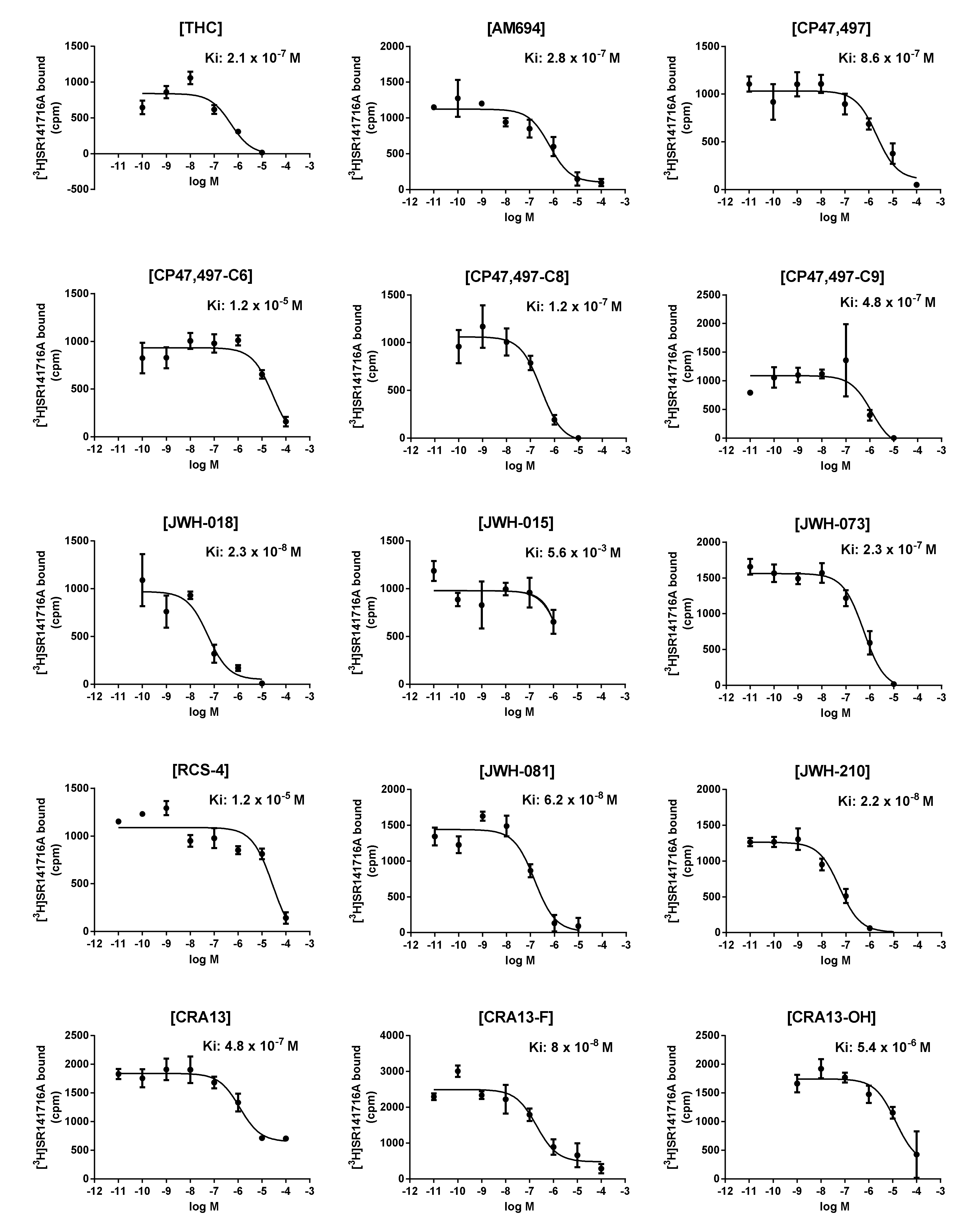
2.1.1. Dataset Compounds
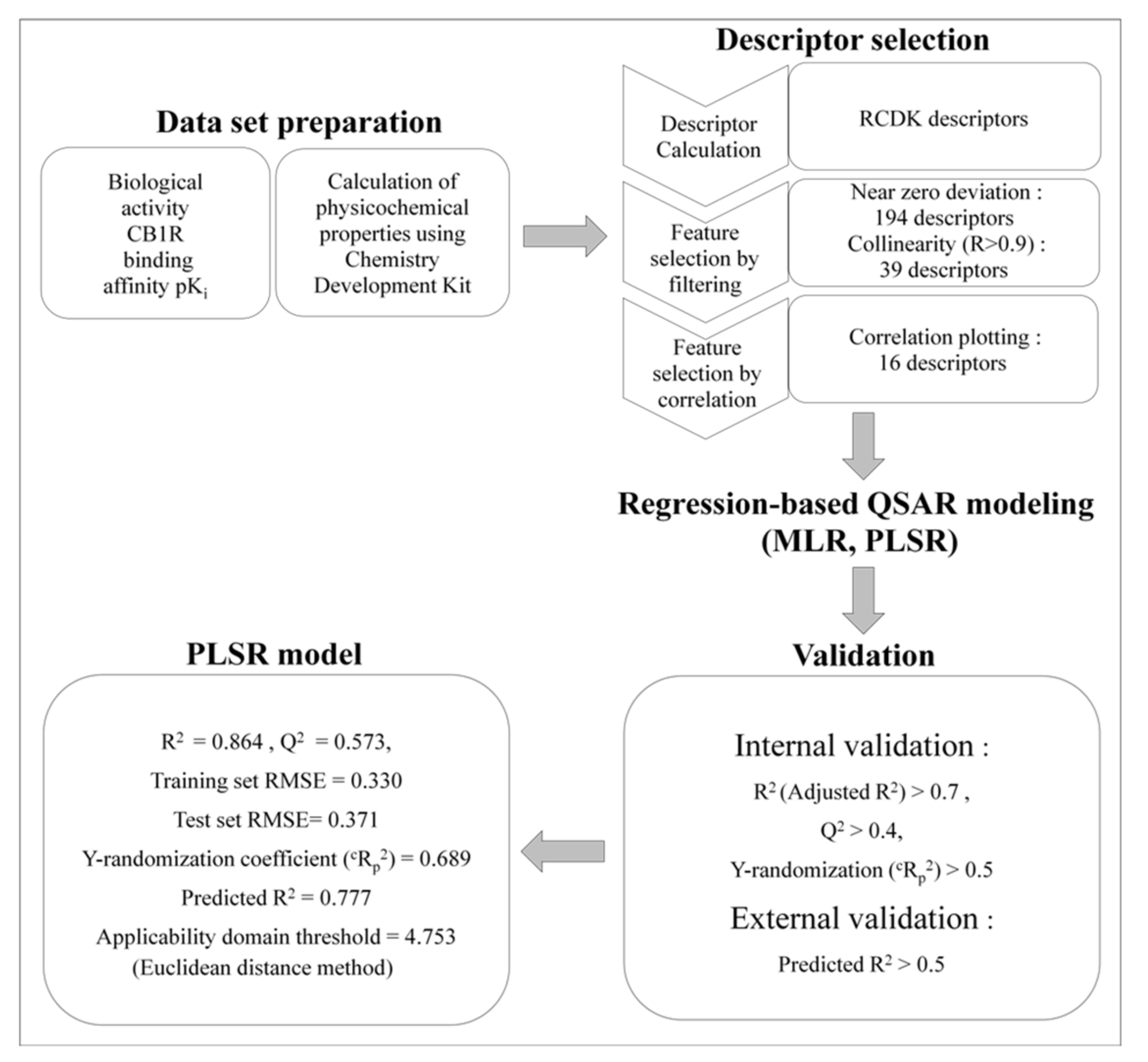
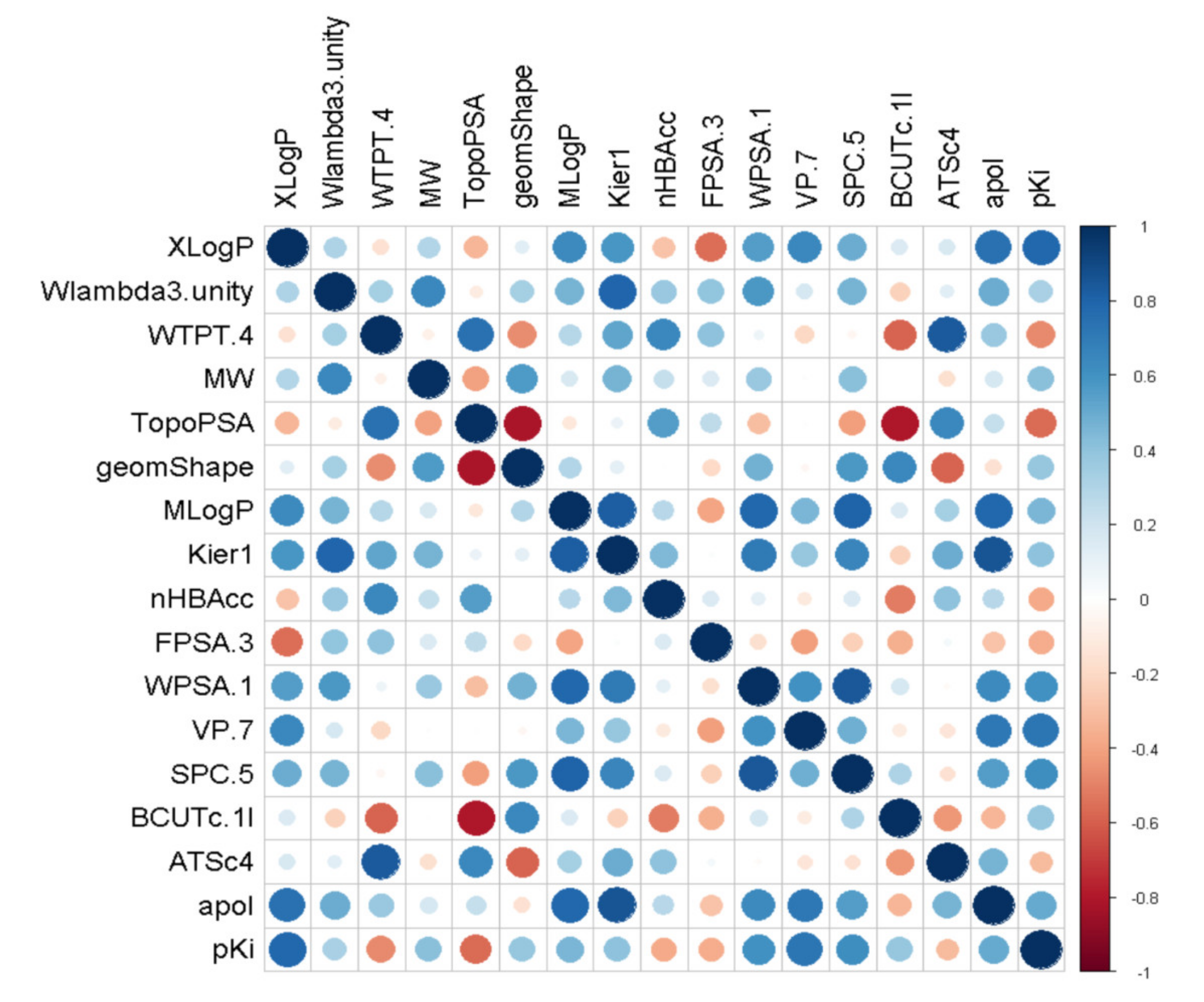
2.1.2. Feature Selection
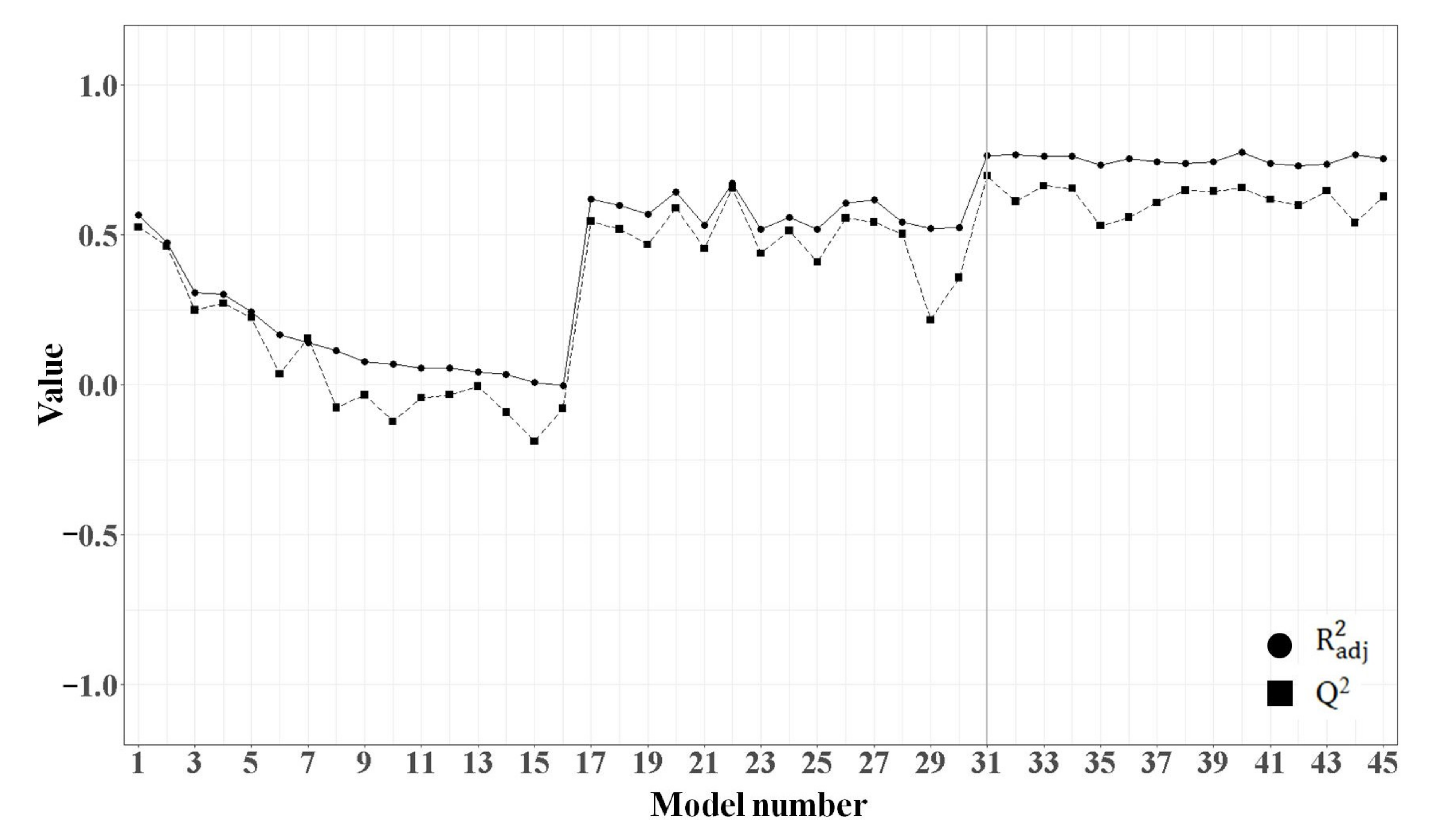
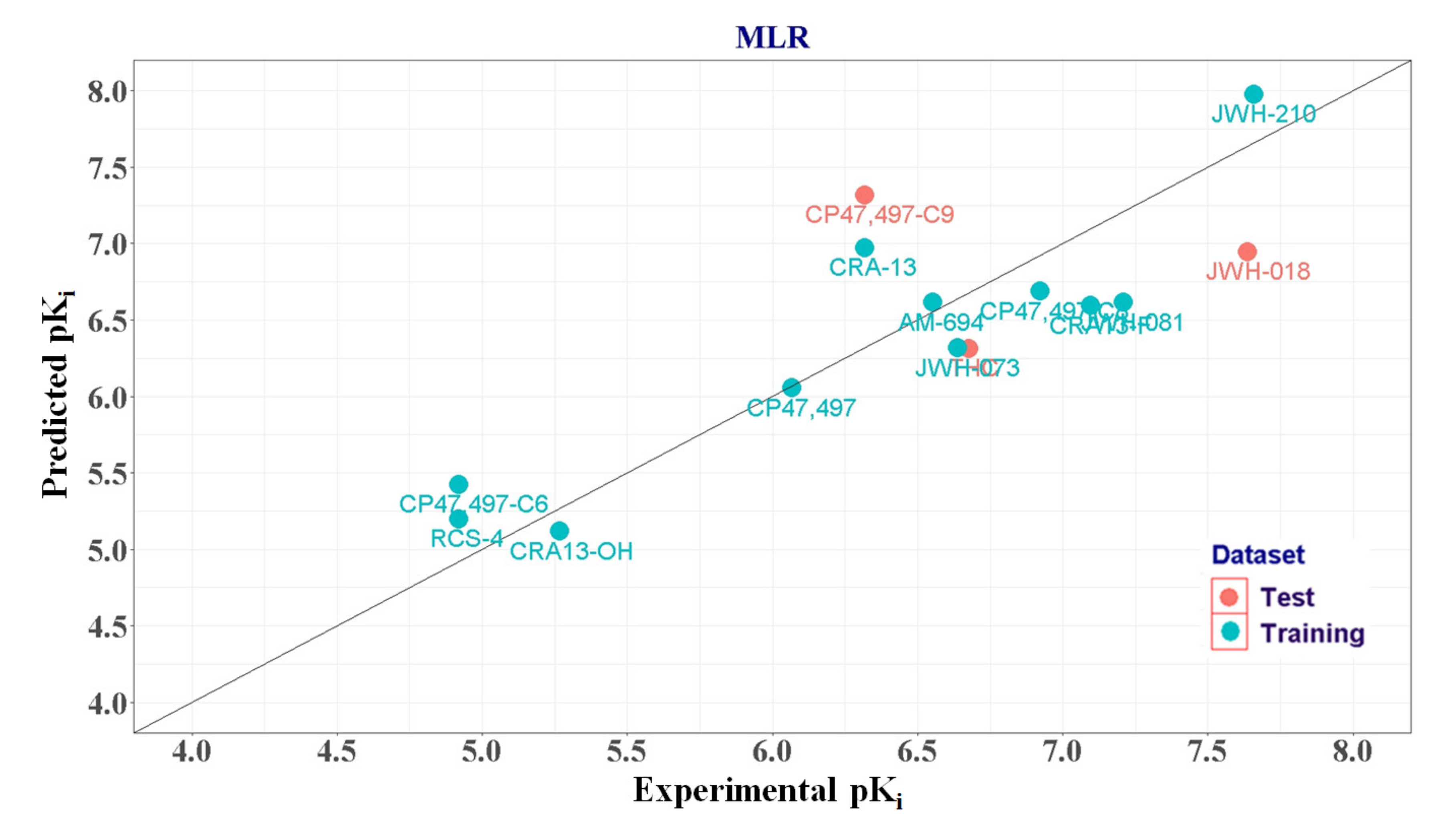
2.1.3. MLR Analysis
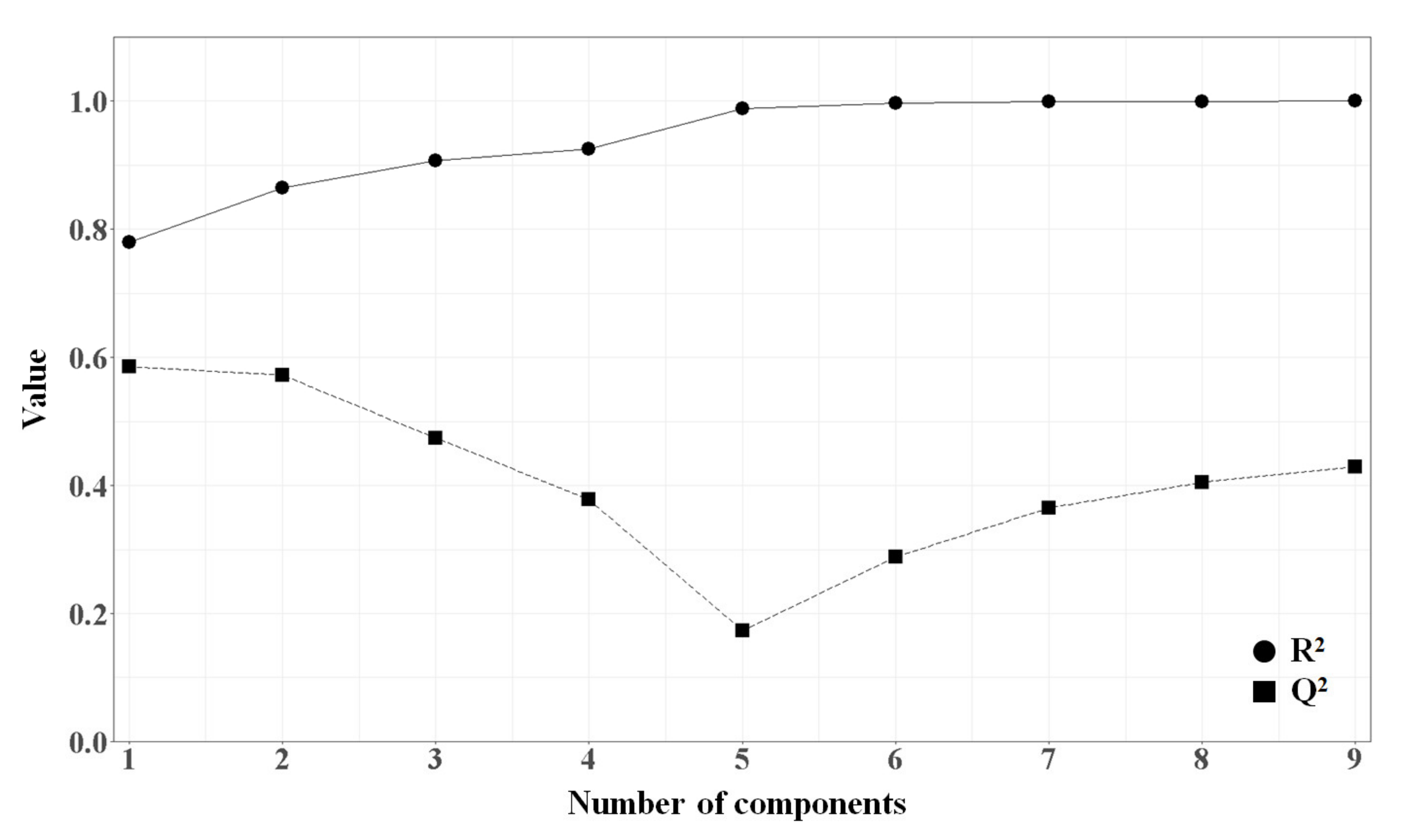
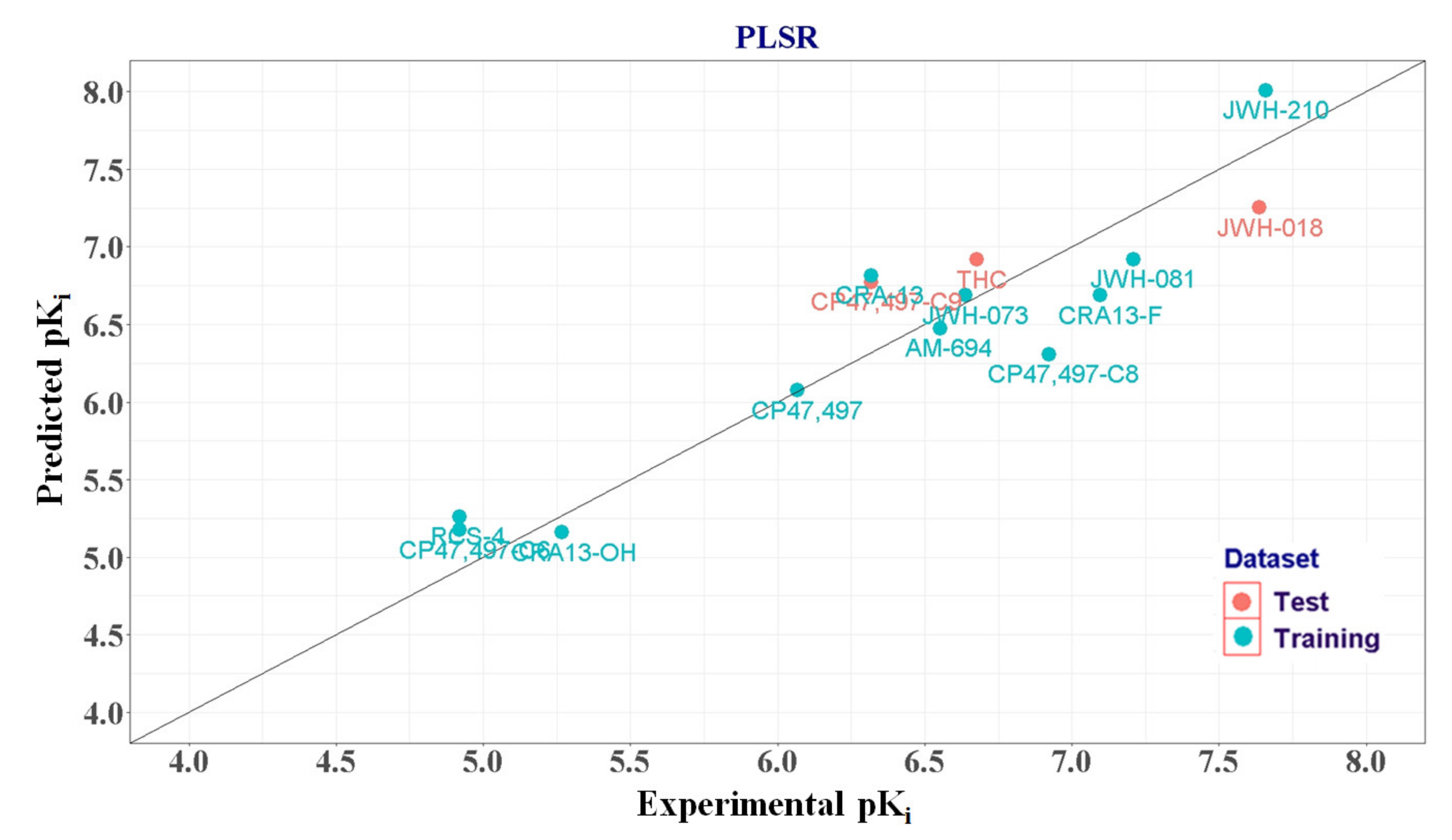
2.1.4. PLSR Analysis
2.1.5. Comparison of the Quality of MLR and PLSR Models
3. Materials and Methods
3.1. Chemistry
3.2. In Vitro CB1R-Binding Assay
3.3. QSAR Modeling
3.3.1. Preparation of Datasets and Calculation of Molecular Descriptors
3.3.2. MLR
3.3.3. PLSR
3.3.4. Model Validation
3.3.5. Applicability Domain of the Model
3.3.6. Validation of PLSR Model Using an External Evaluation Set
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- World Drug Report 2020; Sales No. E.20.XI.6; United Nations Publication: New York, NY, USA, 2020.
- Peacock, A.; Leung, J.; Larney, S.; Colledge, S.; Hickman, M.; Rehm, J.; Giovino, G.A.; West, R.; Hall, W.; Griffiths, P.; et al. Global statistics on alcohol, tobacco and illicit drug use: 2017 status report. Addiction 2018, 113, 1905–1926. [Google Scholar] [CrossRef] [PubMed]
- Corsi, D.J.; Donelle, J.; Sucha, E.; Hawken, S.; Hsu, H.; El-Chaâr, D.; Bisnaire, L.; Fell, D.; Wen, S.W.; Walker, M. Maternal cannabis use in pregnancy and child neurodevelopmental outcomes. Nat. Med. 2020, 26, 1536–1540. [Google Scholar] [CrossRef] [PubMed]
- Hermanns-Clausen, M.; Kithinji, J.; Spehl, M.; Angerer, V.; Franz, F.; Eyer, F.; Auwärter, V. Adverse effects after the use of JWH-210–a case series from the EU Spice II plus project. Drug Test. Anal. 2016, 8, 1030–1038. [Google Scholar] [CrossRef] [PubMed]
- Castellano, C.; Rossi-Arnaud, C.; Cestari, V.; Costanzi, M. Cannabinoids and memory; animal studies. Curr. Drug Targets CNS Neurol. Disord. 2003, 2, 389–402. [Google Scholar] [CrossRef] [PubMed]
- Moreira, F.A.; Lutz, B. The endocannabinoid system: Emotion, learning and addiction. Addict. Biol. 2008, 13, 196–212. [Google Scholar] [CrossRef]
- Puighermanal, E.; Busquets-Garcia, A.; Maldonado, R.; Ozaita, A. Cellular and intracellular mechanisms involved in the cognitive impairment of cannabinoids. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 3254–3263. [Google Scholar] [CrossRef]
- Rodriguez, J.S.; McMahon, L.R. JWH-018 in rhesus monkeys: Differential antagonism of discriminative stimulus, rate-decreasing, and hypothermic effects. Eur. J. Pharmacol. 2014, 740, 151–159. [Google Scholar] [CrossRef]
- Atwood, B.K.; Huffman, J.; Straiker, A.; Mackie, K. JWH018, a common constituent of ‘Spice’herbal blends, is a potent and efficacious cannabinoid CB1 receptor agonist. Br. J. Pharmacol. 2010, 160, 585–593. [Google Scholar] [CrossRef]
- Atwood, B.K.; Lee, D.; Straiker, A.; Widlanski, T.S.; Mackie, K. CP47, 497-C8 and JWH073, commonly found in ‘Spice’herbal blends, are potent and efficacious CB1 cannabinoid receptor agonists. Eur. J. Pharmacol. 2011, 659, 139–145. [Google Scholar] [CrossRef]
- Aung, M.M.; Griffin, G.; Huffman, J.W.; Wu, M.-J.; Keel, C.; Yang, B.; Showalter, V.M.; E Abood, M.; Martin, B.R. Influence of the N-1 alkyl chain length of cannabimimetic indoles upon CB1 and CB2 receptor binding. Drug Alcohol Depend. 2000, 60, 133–140. [Google Scholar] [CrossRef]
- Cha, H.J.; Lee, K.-W.; Song, M.-J.; Hyeon, Y.-J.; Hwang, J.-Y.; Jang, C.-G.; Ahn, J.-I.; Jeon, S.-H.; Kim, H.-U.; Kim, Y.-H.; et al. Dependence potential of the synthetic cannabinoids JWH-073, JWH-081, and JWH-210: In vivo and in vitro approaches. Biomol. Ther. 2014, 22, 363. [Google Scholar] [CrossRef] [PubMed]
- Leonhart, M. Schedules of controlled substances: Placement of five synthetic cannabinoids into Schedule I. Fed. Regist. Drug Enforc. Adm. 2012, 77, 12508–12514. [Google Scholar]
- Afantitis, A.; Melagraki, G.; Sarimveis, H.; Koutentis, P.A.; Markopoulos, J.; Igglessi-Markopoulou, O. Development and evaluation of a QSPR model for the prediction of diamagnetic susceptibility. QSAR Comb. Sci. 2008, 27, 432–436. [Google Scholar] [CrossRef]
- Paulke, A.; Proschak, E.; Sommer, K.; Achenbach, J.; Wunder, C.; Toennes, S.W. Synthetic cannabinoids: In silico prediction of the cannabinoid receptor 1 affinity by a quantitative structure-activity relationship model. Toxicol. Lett. 2016, 245, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Hermanns-Clausen, M.; Kneisel, S.; Szabo, B.; Auwärter, V. Acute toxicity due to the confirmed consumption of synthetic cannabinoids: Clinical and laboratory findings. Addiction 2013, 108, 534–544. [Google Scholar] [CrossRef] [PubMed]
- Badowski, M.E.; Perez, S.E. Clinical utility of dronabinol in the treatment of weight loss associated with HIV and AIDS. HIV/AIDS (Auckland NZ) 2016, 8, 37. [Google Scholar] [CrossRef][Green Version]
- Smith, L.A.; Azariah, F.; Lavender, V.T.; Stoner, N.S.; Bettiol, S. Cannabinoids for nausea and vomiting in adults with cancer receiving chemotherapy. Cochrane Database Syst. Rev. 2015, 2015, CD009464. [Google Scholar] [CrossRef]
- Urits, I.; Borchart, M.; Hasegawa, M.; Kochanski, J.; Orhurhu, V.; Viswanath, O. An update of current cannabis-based pharmaceuticals in pain medicine. Pain Ther. 2019, 8, 41–51. [Google Scholar] [CrossRef]
- Dziadulewicz, E.K.; Bevan, S.J.; Brain, C.T.; Coote, P.R.; Culshaw, A.J.; Davis, A.J.; Edwards, L.J.; Fisher, A.J.; Fox, A.J.; Gentry, C.; et al. Naphthalen-1-yl-(4-pentyloxynaphthalen-1-yl) methanone: A potent, orally bioavailable human CB1/CB2 dual agonist with antihyperalgesic properties and restricted central nervous system penetration. J. Med. Chem. 2007, 50, 3851–3856. [Google Scholar] [CrossRef]
- Gardin, A.; Kucher, K.; Kiese, B.; Appel-Dingemanse, S. Cannabinoid receptor agonist 13, a novel cannabinoid agonist: First in human pharmacokinetics and safety. Drug Metab. Dispos. 2009, 37, 827–833. [Google Scholar] [CrossRef]
- Hassan, A.H.; Park, K.T.; Kim, H.J.; Lee, H.J.; Kwon, Y.H.; Hwang, J.Y.; Jang, C.-G.; Chung, J.H.; Park, K.D.; Lee, S.J.; et al. Fluorinated CRA13 analogues: Synthesis, in vitro evaluation, radiosynthesis, in silico and in vivo PET study. Bioorg. Chem. 2020, 99, 103834. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.H.; Cho, M.C.; Kim, H.I.; Yang, J.S.; Park, K.T.; Hwang, J.Y.; Jang, C.-G.; Park, K.D.; Lee, Y.S. Synthesis of oxidative metabolites of CRA13 and their analogs: Identification of CRA13 active metabolites and analogs thereof with selective CB2R affinity. Bioorg. Med. Chem. 2018, 26, 5069–5078. [Google Scholar] [CrossRef] [PubMed]
- Komsta, L.; Komsta, M.L. Package ‘Outliers’; Medical University of Lublin: Lublin, Poland, 2011. [Google Scholar]
- Zhang, S.; Golbraikh, A.; Oloff, S.; Kohn, H.; Tropsha, A. A novel automated lazy learning QSAR (ALL-QSAR) approach: Method development, applications, and virtual screening of chemical databases using validated ALL-QSAR models. J. Chem. Inf. Model. 2006, 46, 1984–1995. [Google Scholar] [CrossRef] [PubMed]
- Huffman, J.W.; Thompson, A.L.; Wiley, J.L.; Martin, B.R. Synthesis and pharmacology of 1-deoxy analogs of CP-47,497 and CP-55,940. Bioorg. Med. Chem. 2008, 16, 322–335. [Google Scholar] [CrossRef] [PubMed]
- Tai, S.; Fantegrossi, W.E. Synthetic cannabinoids: Pharmacology, behavioral effects, and abuse potential. Curr. Addict. Rep. 2014, 1, 129–136. [Google Scholar] [CrossRef]
- De Luca, M.A.; Bimpisidis, Z.; Melis, M.R.; Marti, M.J.; Caboni, P.; Valentini, V.; Margiani, G.; Pintori, N.; Polis, I.; Marsicano, G.; et al. Stimulation of in vivo dopamine transmission and intravenous self-administration in rats and mice by JWH-018, a Spice cannabinoid. Neuropharmacology 2015, 99, 705–714. [Google Scholar] [CrossRef]
- Lee, H.; Ahn, S.; Ann, J.; Ha, H.; Yoo, Y.D.; Kim, Y.H.; Hwang, J.-Y.; Hur, K.-H.; Jang, C.-G.; Pearce, L.V.; et al. Discovery of dual-acting opioid ligand and TRPV1 antagonists as novel therapeutic agents for pain. Eur. J. Med. Chem. 2019, 182, 111634. [Google Scholar] [CrossRef]
- SYBYL Molecular Modeling Software, Sybyl-X 2.1.1 ed.; Certara Inc.: Prinston, NJ, USA, 2013.
- Guha, R. Chemical informatics functionality in R. J. Stat. Softw. 2007, 18, 1–16. [Google Scholar] [CrossRef]
- Mevik, B.-H.; Wehrens, R. Introduction to the Pls Package; Help Section of The “Pls” Package of R Studio Software; R Foundation for Statistical Computing: Vienna, Austria, 2015; pp. 1–23. [Google Scholar]
- Melagraki, G.; Afantitis, A.; Sarimveis, H.; Igglessi-Markopoulou, O.; Koutentis, P.A.; Kollias, G. In silico exploration for identifying structure–activity relationship of MEK inhibition and oral bioavailability for isothiazole derivatives. Chem. Biol. Drug Des. 2010, 76, 397–406. [Google Scholar] [CrossRef]
| Model | R2 | Adjusted R2 (R2adj) | Predicted R2(Rpred2) | Training Set 1 RMSE | Test Se tRMSE | Q2 |
|---|---|---|---|---|---|---|
| MLR model 31 | 0.812 | 0.765 | 0.133 | 0.387 | 0.732 | 0.698 |
| PLSR | 0.864 | - | 0.777 | 0.330 | 0.371 | 0.573 |
| Compound Name | Observed pKi | PLSR | In Vivo Rewarding Responses | |||
|---|---|---|---|---|---|---|
| Predicted pKi | 1 Residual | 2 APD | ||||
| Training set | AM-694 | 6.553 | 6.474 | 0.079 | ||
| CRA-13 | 6.319 | 6.816 | −0.497 | |||
| CP47,497-C6 | 4.921 | 5.174 | −0.253 | |||
| CP47,497 | 6.066 | 6.075 | −0.009 | |||
| CP47,497-C8 | 6.921 | 6.308 | 0.613 | |||
| CRA13-F | 7.097 | 6.687 | 0.41 | |||
| CRA13-OH | 5.268 | 5.160 | 0.108 | |||
| RCS-4 | 4.921 | 5.26 | −0.339 | |||
| JWH-073 | 6.638 | 6.688 | −0.05 | 3 CPP [12] | ||
| JWH-081 | 7.208 | 6.92 | 0.288 | CPP [12] | ||
| JWH-210 | 7.658 | 8.007 | −0.349 | CPP [12] | ||
| Test set | CP47,497-C9 | 6.319 | 6.773 | −0.454 | 1.903 | |
| JWH-018 | 7.638 | 7.253 | 0.385 | 2.887 | 4 SA [17] | |
| THC | 6.678 | 6.917 | −0.239 | 3.917 | CPP [12] | |
Sample Availability: Samples of the compounds are not available from the authors. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, W.; Park, S.-J.; Hwang, J.-Y.; Hur, K.-H.; Lee, Y.S.; Kim, J.; Zhao, X.; Park, A.; Min, K.H.; Jang, C.-G.; et al. QSAR Model for Predicting the Cannabinoid Receptor 1 Binding Affinity and Dependence Potential of Synthetic Cannabinoids. Molecules 2020, 25, 6057. https://doi.org/10.3390/molecules25246057
Lee W, Park S-J, Hwang J-Y, Hur K-H, Lee YS, Kim J, Zhao X, Park A, Min KH, Jang C-G, et al. QSAR Model for Predicting the Cannabinoid Receptor 1 Binding Affinity and Dependence Potential of Synthetic Cannabinoids. Molecules. 2020; 25(24):6057. https://doi.org/10.3390/molecules25246057
Chicago/Turabian StyleLee, Wonyoung, So-Jung Park, Ji-Young Hwang, Kwang-Hyun Hur, Yong Sup Lee, Jongmin Kim, Xiaodi Zhao, Aekyung Park, Kyung Hoon Min, Choon-Gon Jang, and et al. 2020. "QSAR Model for Predicting the Cannabinoid Receptor 1 Binding Affinity and Dependence Potential of Synthetic Cannabinoids" Molecules 25, no. 24: 6057. https://doi.org/10.3390/molecules25246057
APA StyleLee, W., Park, S.-J., Hwang, J.-Y., Hur, K.-H., Lee, Y. S., Kim, J., Zhao, X., Park, A., Min, K. H., Jang, C.-G., & Park, H.-J. (2020). QSAR Model for Predicting the Cannabinoid Receptor 1 Binding Affinity and Dependence Potential of Synthetic Cannabinoids. Molecules, 25(24), 6057. https://doi.org/10.3390/molecules25246057







