Application 2D Descriptors and Artificial Neural Networks for Beta-Glucosidase Inhibitors Screening
Abstract
1. Introduction
2. Results
2.1. Descriptors Selection
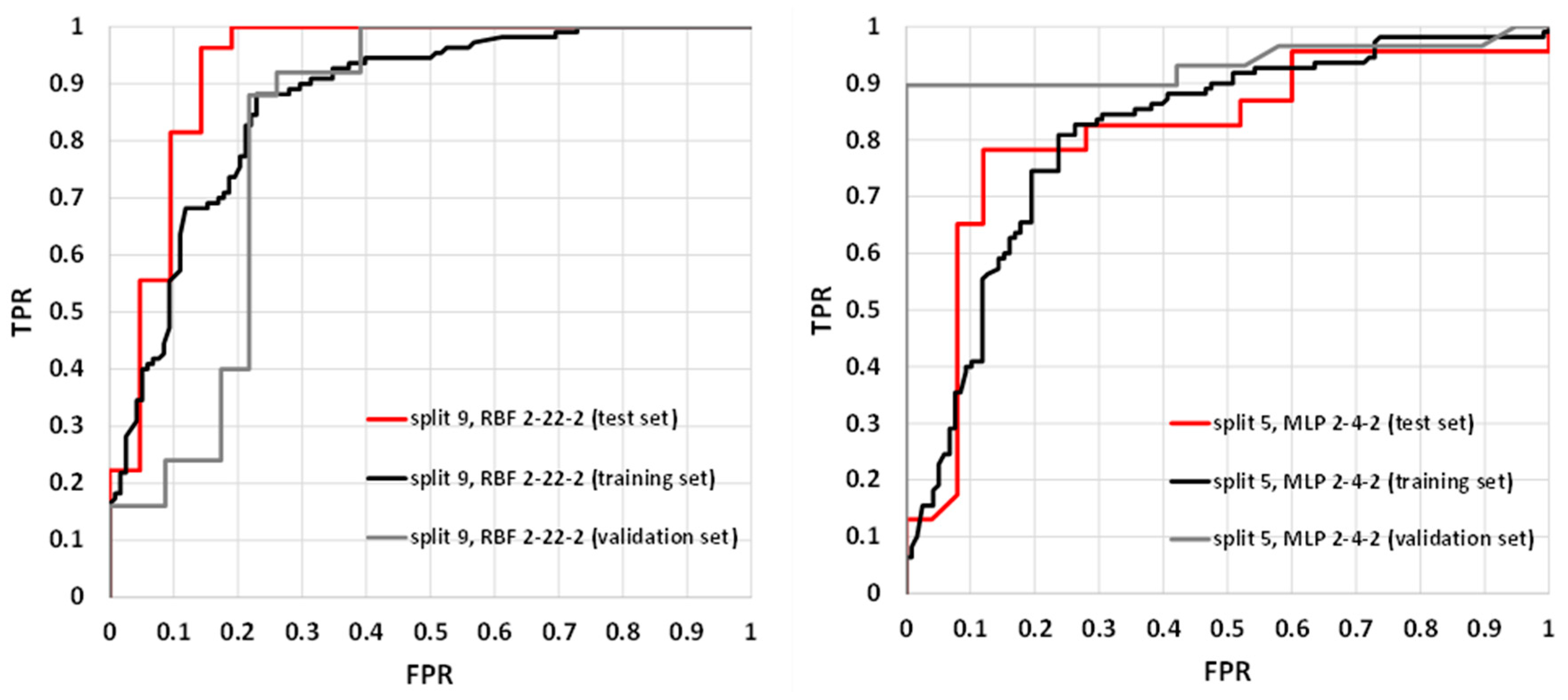
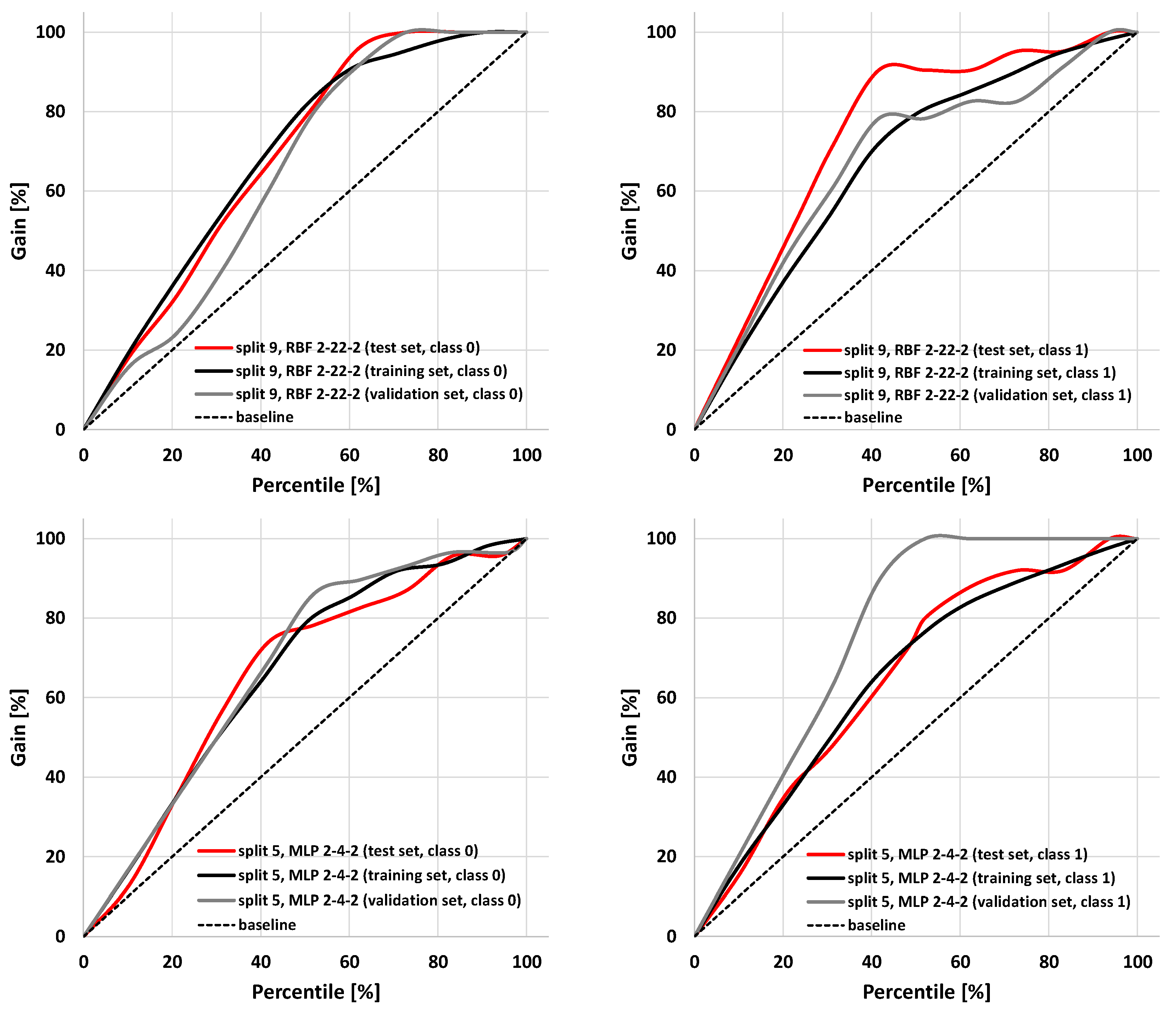
2.2. The SANN Models
2.3. Application of SANNs
3. Methods
3.1. Dataset Selection and Pretreatment
3.2. Descriptors Calculation
3.3. The Artificial Neutral Networks Models
3.4. Classification Quality Evaluation
4. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- De Melo, B.E.; Da Silveira, G.A.; Carvalho, I. α- and β-Glucosidase inhibitors: Chemical structure and biological activity. Tetrahedron 2006, 62, 10277–10302. [Google Scholar] [CrossRef]
- Campo, V.L.; Aragão-Leoneti, V.; Carvalho, I. Glycosidases and diabetes: Metabolic changes, mode of action and therapeutic perspectives. In Carbohydrate Chemistry; Royal Society of Chemistry: London, UK, 2013; Volume 39, pp. 181–203. [Google Scholar]
- Bieberich, E. Synthesis, Processing, and Function of N-glycans in N-glycoproteins. In Glycobiology of the Nervous System. Advances in Neurobiology; Yu, R., Schengrund, C.L., Eds.; Springer: New York, NY, USA, 2014; Volume 9, pp. 47–70. [Google Scholar]
- Heightman, T.D.; Vasella, A.T. Recent Insights into Inhibition, Structure, and Mechanism of Con-figuration-Retaining Glycosidases. Angew. Chem. Int. Ed. 1999, 38, 750–770. [Google Scholar] [CrossRef]
- Krasikov, V.V.; Karelov, D.V.; Firsov, L.M. α-Glucosidases. Biochemistry 2001, 66, 267–281. [Google Scholar]
- Lillelund, V.H.; Jensen, H.H.; Liang, X.; Bols, M. Recent Developments of Transition-State Analogue Glycosidase Inhibitors of Non-Natural Product Origin. Chem. Rev. 2002, 102, 515–554. [Google Scholar] [CrossRef] [PubMed]
- Legler, G. Glycoside Hydrolases: Mechanistic Information from Studies with Reversible and Irre-versible Inhibitors. Adv. Carbohydr. Chem. Biochem. 1990, 48, 319–384. [Google Scholar] [PubMed]
- Chiba, S. Molecular Mechanism in α-Glucosidase and Glucoamylase. Biosci. Biotechnol. Biochem. 1997, 61, 1233–1239. [Google Scholar] [CrossRef] [PubMed]
- Piszkiewicz, D.; Bruice, T.C. Glycoside Hydrolysis. II. Intramolecular Carboxyl and Acetamido Group Catalysis in β-Glycoside Hydrolysis. J. Am. Chem. Soc. 1968, 90, 2156–2163. [Google Scholar] [CrossRef]
- Bauer, M.W.; Bylina, E.J.; Swanson, R.V.; Kelly, R.M. Comparison of a β-Glucosidase and a β-Mannosidase from the Hyperthermophilic ArchaeonPyrococcus furiosus. J. Biol. Chem. 1996, 271, 23749–23755. [Google Scholar] [CrossRef]
- Mahapatra, S.; Vickram, A.S.; Sridharan, T.B.; Parameswari, R.; Pathy, M.R. Screening, production, optimization and characterization of β-glucosidase using microbes from shellfish waste. 3 Biotech 2016, 6, 213. [Google Scholar] [CrossRef]
- Zhang, S.; Xie, J.; Zhao, L.; Pei, J.; Su, E.; Xiao, W.; Wang, Z. Cloning, overexpression and character-ization of a thermostable β-xylosidase from Thermotoga petrophila and cooperated transformation of ginsenoside extract to ginsenoside 20(S)-Rg3 with a β-glucosidase. Bioorg. Chem. 2019, 85, 159–167. [Google Scholar] [CrossRef]
- Tiwari, P.; Misra, B.N.; Sangwan, N.S. β-Glucosidases from the FungusTrichoderma: An Efficient Cellulase Machinery in Biotechnological Applications. BioMed Res. Int. 2013, 2013, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, A.; Lübeck, M.; Lubeck, P.S.; Ahring, B.K. Fungal Beta-Glucosidases: A Bottleneck in Industrial Use of Lignocellulosic Materials. Biomolecules 2013, 3, 612–631. [Google Scholar] [CrossRef]
- Del Cueto, J.; Møller, B.L.; Dicenta, F.; Sánchez-Pérez, R. β-Glucosidase activity in almond seeds. Plant Physiol. Biochem. 2018, 126, 163–172. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.-K.; Chang, L.-F.; Shu, H.-H.; Chir, J. Characterization of an Isozyme of β-Glucosidase from Sweet Almond. J. Chin. Chem. Soc. 1997, 44, 81–87. [Google Scholar] [CrossRef]
- Cicek, M.; Esen, A. Structure and Expression of a Dhurrinase (β-Glucosidase) from Sorghum. Plant Physiol. 1998, 116, 1469–1478. [Google Scholar] [CrossRef]
- Pankoke, H.; Buschmann, T.; Müller, C. Role of plant β-glucosidases in the dual defense system of iridoid glycosides and their hydrolyzing enzymes in Plantago lanceolata and Plantago major. Phytochemistry 2013, 94, 99–107. [Google Scholar] [CrossRef]
- Barrett, T.; Suresh, C.G.; Tolley, S.P.; Dodson, E.J.; Hughes, M.A. The crystal structure of a cyanogenic β-glucosidase from white clover, a family 1 glycosyl hydrolase. Structure 1995, 3, 951–960. [Google Scholar] [CrossRef]
- Ioku, K.; Pongpiriyadacha, Y.; Konishi, Y.; Takei, Y.; Nakatani, N.; Terao, J. β-Glucosidase Activity in the Rat Small Intestine toward Quercetin Monoglucosides. Biosci. Biotechnol. Biochem. 1998, 62, 1428–1431. [Google Scholar] [CrossRef]
- Raychaudhuri, C.; Desai, I.D. Lysosomal β-glucosidase and β-xylosidase of rat intestine. Int. J. Biochem. 1972, 3, 684–690. [Google Scholar] [CrossRef]
- Gopalan, V.; Vander Jagt, D.J.; Libell, D.P.; Glew, R.H. Transglucosylation as a probe of the mecha-nism of action of mammalian cytosolic β-glucosidase. J. Biol. Chem. 1992, 267, 9629–9638. [Google Scholar]
- Philip, J.S.; Gilbert, H.J.; Smithard, R.R. Growth, viscosity and beta-glucanase activity of intestinal fluid in broiler chickens fed on barley-based diets with or without exogenous beta-glucanase. Br. Poult. Sci. 1995, 36, 599–603. [Google Scholar] [CrossRef] [PubMed]
- Lelieveld, L.T.; Mirzaian, M.; Kuo, C.L.; Artola, M.; Ferraz, M.J.; Peter, R.E.A.; Akiyama, H.; Greimel, P.; Van den Berg, R.J.B.H.N.; Overkleeft, H.S.; et al. Role of β-glucosidase 2 in aberrant glycosphin-golipid metabolism: Model of glucocerebrosidase deficiency in zebrafish. J. Lipid Res. 2019, 60, 1851–1867. [Google Scholar] [CrossRef] [PubMed]
- Yeoman, C.J.; Han, Y.; Dodd, D.; Schroeder, C.M.; Mackie, R.I.; Cann, I.K.O. Thermostable enzymes as biocatalysts in the biofuel industry. Adv. Appl. Microbiol. 2010, 70, 1–55. [Google Scholar] [PubMed]
- Asati, V.; Sharma, P.K. Purification and characterization of an isoflavones conjugate hydrolyzing β-glucosidase (ICHG) from Cyamopsis tetragonoloba (guar). Biochem. Biophys. Rep. 2019, 20, 100669. [Google Scholar] [CrossRef] [PubMed]
- Amiri, B.; Hosseini, N.S.; Taktaz, F.; Amini, K.; Rahmani, M.; Amiri, M.; Sadrjavadi, K.; Jangholi, A.; Esmaeili, S. Inhibitory effects of selected antibiotics on the activities of α-amylase and α-glucosidase: In-vitro, in-vivo and theoretical studies. Eur. J. Pharm. Sci. 2019, 138, 105040. [Google Scholar] [CrossRef]
- Martínez-Bailén, M.; Jiménez-Ortega, E.; Carmona, A.T.; Robina, I.; Sanz-Aparicio, J.; Talens-Perales, D.; Polaina, J.; Matassini, C.; Cardona, F.; Moreno-Vargas, A.J. Structural basis of the inhibition of GH1 β-glucosidases by multivalent pyrrolidine iminosugars. Bioorg. Chem. 2019, 89, 103026. [Google Scholar] [CrossRef]
- Durantel, D.; Alotte, C.; Zoulim, F. Glucosidase inhibitors as antiviral agents for hepatitis B and C. Curr. Opin. Investig. 2007, 8, 125–129. [Google Scholar]
- Pandey, S.; Sree, A.; Dash, S.S.; Sethi, D.P.; Chowdhury, L. Diversity of marine bacteria producing beta-glucosidase inhibitors. Microb. Cell Fact. 2013, 12, 35. [Google Scholar] [CrossRef]
- Puls, W.; Keup, U.; Krause, H.P.; Thomas, G.; Hoffmeister, F. Glucosidase inhibition—A new approach to the treatment of diabetes, obesity, and hyperlipoproteinaemia. Naturwissenschaften 1977, 64, 536–537. [Google Scholar] [CrossRef]
- Brogard, J.M.; Willemin, B.; Blicklé, J.F.; Lamalle, A.M.; Stahl, A. Inhibiteurs des alpha-glucosidases: Une nouvelle approche thérapeutique du diabète et des hypoglycémies fonctionnelles. Rev. Med. Intern. 1989, 10, 365–374. [Google Scholar] [CrossRef]
- Lankatillake, C.; Huynh, T.; Dias, D.A. Understanding glycaemic control and current approaches for screening antidiabetic natural products from evidence-based medicinal plants. Plant Methods 2019, 15, 1–35. [Google Scholar] [CrossRef]
- Teng, H.; Chen, L.; Fang, T.; Yuan, B.; Lin, Q. Rb2 inhibits α-glucosidase and regulates glucose me-tabolism by activating AMPK pathways in HepG2 cells. J. Funct. Foods 2017, 28, 306–313. [Google Scholar] [CrossRef]
- Kato, A.; Kato, N.; Kano, E.; Adachi, I.; Ikeda, K.; Yu, L.; Okamoto, T.; Banba, Y.; Ouchi, H.; Takahata, H.; et al. Biological properties of D- and L-1-deoxyazasugars. J. Med. Chem. 2005, 48, 2036–2044. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.-Q.; Ishii, S.; Asano, N.; Suzuki, Y. Accelerated transport and maturation of lysosomal α-galactosidase A in Fabry lymphoblasts by an enzyme inhibitor. Nat. Med. 1999, 5, 112–115. [Google Scholar] [CrossRef] [PubMed]
- Sawkar, A.R.; Cheng, W.C.; Beutler, E.; Wong, C.H.; Balch, W.E.; Kelly, J.W. Chemical chaperones increase the cellular activity of N370S β-glucosidase: A therapeutic strategy for Gaucher disease. Proc. Natl. Acad. Sci. USA 2002, 99, 15428–15433. [Google Scholar] [CrossRef] [PubMed]
- Gaulton, A.; Bellis, L.J.; Bento, A.P.; Chambers, J.; Davies, M.; Hersey, A.; Light, Y.; McGlinchey, S.; Michalovich, D.; Al-Lazikani, B.; et al. ChEMBL: A large-scale bioactivity database for drug discovery. Nucleic Acids Res. 2012, 40, D1100–D1107. [Google Scholar] [CrossRef]
- Bender, A. Databases: Compound bioactivities go public. Nat. Chem. Biol. 2010, 6, 309. [Google Scholar] [CrossRef]
- Kim, S.; Thiessen, P.A.; Bolton, E.E.; Chen, J.; Fu, G.; Gindulyte, A.; Han, L.; He, J.; He, S.; Shoemaker, B.A.; et al. PubChem Substance and Compound databases. Nucleic Acids Res. 2016, 44, D1202–D1213. [Google Scholar] [CrossRef]
- Toropov, A.A.; Toropova, A.P.; Raitano, G.; Benfenati, E. CORAL: Building up QSAR models for the chromosome aberration test. Saudi J. Biol. Sci. 2019, 26, 1101–1106. [Google Scholar] [CrossRef]
- Ahmadi, S.; Ghanbari, H.; Lotfi, S.; Azimi, N. Predictive QSAR modeling for the antioxidant activity of natural compounds derivatives based on Monte Carlo method. Mol. Divers. 2020, 1–11. [Google Scholar] [CrossRef]
- Przybyłek, M.; Jeliński, T.; Słabuszewska, J.; Ziółkowska, D.; Mroczyńska, K.; Cysewski, P. Application of Multivariate Adaptive Regression Splines (MARSplines) Methodology for Screening of Di-carboxylic Acid Cocrystal Using 1D and 2D Molecular Descriptors. Cryst. Growth Des. 2019, 19, 3876–3887. [Google Scholar] [CrossRef]
- Sundar, K.; Rosy, J.C.; Balamurali, S.; Mary, J.A.; Shenbagara, R. Generation of 2D-QSAR Model for Angiogenin Inhibitors: A Ligand-Based Approach for Cancer Drug Design. Trends Bioinform. 2016, 9, 1–13. [Google Scholar] [CrossRef][Green Version]
- Toropov, A.A.; Toropova, A.P.; Veselinović, A.M.; Leszczynska, D.; Leszczynski, J. SARS-CoV Mpro inhibitory activity of aromatic disulfide compounds: QSAR model. J. Biomol. Struct. Dyn. 2020. [Google Scholar] [CrossRef]
- Tran, T.-S.; Le, M.-T.; Tran, T.-D.; Tran, T.-H.; Thai, K.-M. Design of Curcumin and Flavonoid Derivatives with Acetylcholinesterase and Beta-Secretase Inhibitory Activities Using in Silico Approaches. Molecules 2020, 25, 3644. [Google Scholar] [CrossRef] [PubMed]
- Przybyłek, M.; Cysewski, P. Distinguishing Cocrystals from Simple Eutectic Mixtures: Phenolic Acids as Potential Pharmaceutical Coformers. Cryst. Growth Des. 2018, 18, 3524–3534. [Google Scholar] [CrossRef]
- Dieguez-Santana, K.; Pham-The, H.; Rivera-Borroto, O.M.; Puris, A.; Le-Thi-Thu, H.; Casanola-Martin, G.M. A Two QSAR Way for Antidiabetic Agents Targeting Using α-Amylase and α-Glucosidase In-hibitors: Model Parameters Settings in Artificial Intelligence Techniques. Lett. Drug Des. Discov. 2017, 14. [Google Scholar] [CrossRef]
- Taxak, N.; Bharatam, P.V. 2D QSAR study for gemfibrozil glucuronide as the mechanism-based in-hibitor of CYP2C8. Indian J. Pharm. Sci. 2013, 75, 680–687. [Google Scholar]
- Jafari, K.; Fatemi, M.H.; Toropova, A.P.; Toropov, A.A. Correlation Intensity Index (CII) as a criterion of predictive potential: Applying to model thermal conductivity of metal oxide-based ethylene glycol nanofluids. Chem. Phys. Lett. 2020, 754, 137614. [Google Scholar] [CrossRef]
- Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fin-gerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef]
- Lei, T.; Li, Y.; Song, Y.; Li, D.; Sun, H.; Hou, T.-J. ADMET evaluation in drug discovery: 15. Accurate prediction of rat oral acute toxicity using relevance vector machine and consensus modeling. J. Cheminform. 2016, 8, 1–19. [Google Scholar] [CrossRef]
- Goodarzi, M.; Dejaegher, B.; Heyden, Y. Vander Feature selection methods in QSAR studies. J. AOAC Int. 2012, 95, 636–651. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Dai, Z.; Cao, D.; Luo, F.; Chen, Y.; Yuan, Z. Chi-MIC-share: A new feature selection algorithm for quantitative structure–activity relationship models. RSC Adv. 2020, 10, 19852–19860. [Google Scholar] [CrossRef]
- Alsenan, S.A.; Al-Turaiki, I.M.; Hafez, A.M. Feature extraction methods in quantitative struc-ture-activity relationship modeling: A comparative study. IEEE Access 2020, 8, 78737–78752. [Google Scholar] [CrossRef]
- Newby, D.; Freitas, A.A.; Ghafourian, T. Pre-processing Feature Selection for Improved C&RT Models for Oral Absorption. J. Chem. Inf. Model. 2013, 53, 2730–2742. [Google Scholar] [CrossRef] [PubMed]
- Antanasijević, J.; Antanasijević, D.; Pocajt, V.; Trišović, N.; Fodor-Csorba, K. A QSPR study on the liquid crystallinity of five-ring bent-core molecules using decision trees, MARS and artificial neural networks. RSC Adv. 2016, 6, 18452–18464. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics. In Molecular Descriptors for Chemoinformatics; Wiley-VCH: Weinheim, Germany, 2009; Volume 2, ISBN 978-3-527-62876-6. [Google Scholar]
- Burden, F.R. Molecular identification number for substructure searches. J. Chem. Inf. Model. 1989, 29, 225–227. [Google Scholar] [CrossRef]
- Burden, F.R. A Chemically Intuitive Molecular Index Based on the Eigenvalues of a Modified Adjacency Matrix. Quant. Struct. Relatsh. 1997, 16, 309–314. [Google Scholar] [CrossRef]
- Broto, P.; Moreau, G.; Vandycke, C. Molecular structures: Perception, autocorrelation descriptor and sar studies: System of atomic contributions for the calculation of the n-octanol/water partition coef-ficients. Eur. J. Med. Chem. 1984, 19, 71–78. [Google Scholar]
- Broto, P.; Moreau, G.; Vandycke, C. Molecular structures: Perception, autocorrelation descriptor and sar studies: Autocorrelation descriptor. Eur. J. Med. Chem. 1984, 19, 66–70. [Google Scholar]
- Moreau, G.; Broto, P. Autocorrelation of molecular structures. Application to SAR studies. Nouv. J. Chim. 1980, 4, 757–764. [Google Scholar]
- Moreau, J.L.; Broto, P. The autocorrelation of a topologial structure: A new molecular descriptor. Nouv. J. Chim. 1980, 4, 359–360. [Google Scholar]
- Huuskonen, J.J.; Livingstone, D.J.; Tetko, I.V. Neural network modeling for estimation of partition coefficient based on atom-type electrotopological state indices. J. Chem. Inf. Comput. Sci. 2000, 40, 947–955. [Google Scholar] [CrossRef] [PubMed]
- Huuskonen, J.J.; Villa, A.E.P.; Tetko, I.V. Prediction of partition coefficient based on atom-type electrotopological state indices. J. Pharm. Sci. 1999, 88, 229–233. [Google Scholar] [CrossRef] [PubMed]
- Kier, L.B.; Hall, L.H. Molecular Structure Description: The Electrotopological State; Academic Press: London, UK, 1999; ISBN 978-0-12-406555-0. [Google Scholar]
- Kier, L.B.; Hall, L.H. An Electrotopological-State Index for Atoms in Molecules. Pharm. Res. 1990, 7, 801–807. [Google Scholar] [CrossRef] [PubMed]
- Kier, L.B.; Hall, L.H.; Frazer, J.W. An index of electrotopological state for atoms in molecules. J. Math. Chem. 1991, 7, 229–241. [Google Scholar] [CrossRef]
- Votano, J.R.; Parham, M.; Hall, L.H.; Kier, L.B.; Oloff, S.; Tropsha, A.; Xie, Q.; Tong, W. Three new consensus QSAR models for the prediction of Ames genotoxicity. Mutagenesis 2004, 19, 365–377. [Google Scholar] [CrossRef]
- Fjodorova, N.; Vračko, M.; Novič, M.; Roncaglioni, A.; Benfenati, E. New public QSAR model for carcinogenicity. Chem. Cent. J. 2010, 4, S3. [Google Scholar] [CrossRef]
- Parmeggiani, C.; Catarzi, S.; Matassini, C.; D’Adamio, G.; Morrone, A.; Goti, A.; Paoli, P.; Cardona, F. Human Acid β-Glucosidase Inhibition by Carbohydrate Derived Iminosugars: Towards New Pharmacological Chaperones for Gaucher Disease. ChemBioChem 2015, 16, 2054–2064. [Google Scholar] [CrossRef]
- Yamashita, T.; Yasuda, K.; Kizu, H.; Kameda, Y.; Watson, A.A.; Nash, R.J.; Fleet, G.W.J.; Asano, N. New polyhydroxylated pyrrolidine, piperidine, and pyrrolizidine alkaloids from Scilla sibirica. J. Nat. Prod. 2002, 65, 1875–1881. [Google Scholar] [CrossRef]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lyso-zyme. BBA Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef] [PubMed]
- Paul, S.; Arlehamn, C.S.L.; Schulten, V.; Westernberg, L.; Sidney, J.; Peters, B.; Sette, A. Experimental validation of the RATE tool for inferring HLA restrictions of T cell epitopes. BMC Immunol. 2017, 18, 20. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Klingspohn, W.; Mathea, M.; Ter Laak, A.; Heinrich, N.; Baumann, K. Efficiency of different measures for defining the applicability domain of classification models. J. Cheminform. 2017, 9, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Fang, J.; Guo, P.; Wang, Q.; Hong, H.; Moslehi, J.; Cheng, F. In Silico Pharmacoepidemiologic Evaluation of Drug-Induced Cardiovascular Complications Using Combined Classifiers. J. Chem. Inf. Model. 2018, 58, 943–956. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.; Goadrich, M. The relationship between precision-recall and ROC curves. ACM Int. Conf. Proc. Ser. 2006, 148, 233–240. [Google Scholar]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algo-rithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Brown, J. Classifiers and their Metrics Quantified. Mol. Inform. 2018, 37, 1700127. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 1–13. [Google Scholar] [CrossRef]
- Halimu, C.; Kasem, A.; Newaz, S.H.S. Empirical comparison of area under ROC curve (AUC) and Mathew correlation coefficient (MCC) for evaluating machine learning algorithms on imbalanced datasets for binary classification. ACM Int. Conf. Proc. Ser. 2019, 1–6. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jiménez-valverde, A.; Real, R. AUC: A misleading measure of the performance of pre-dictive distribution models. Glob. Ecol. Biogeogr. 2008, 17, 145–151. [Google Scholar] [CrossRef]
- Muschelli, J. ROC and AUC with a Binary Predictor: A Potentially Misleading Metric. J. Classif. 2020, 37, 696–708. [Google Scholar] [CrossRef] [PubMed]
- Kovalishyn, V.; Aires-de-Sousa, J.; Ventura, C.; Leitão, E.R.; Martins, F. QSAR modeling of an-titubercular activity of diverse organic compounds. Chemom. Intell. Lab. Syst. 2011, 107, 69–74. [Google Scholar] [CrossRef]
- Tropsha, A.; Gramatica, P.; Gombar, V.K. The Importance of Being Earnest: Validation is the Absolute Essential for Successful Application and Interpretation of QSPR Models. QSAR Comb. Sci. 2003, 22, 69–77. [Google Scholar] [CrossRef]
- Puzyn, T.; Mostrag-Szlichtyng, A.; Gajewicz-Skretna, A.; Skrzyński, M.; Worth, A. Investigating the influence of data splitting on the predictive ability of QSAR/QSPR models. Struct. Chem. 2011, 22, 795–804. [Google Scholar] [CrossRef]
- Pilón-Jiménez, B.A.; Saldívar-González, F.I.; Díaz-Eufracio, B.I.; Medina-Franco, J.L. BIOFACQUIM: A Mexican Compound Database of Natural Products. Biomolecules 2019, 9, 31. [Google Scholar] [CrossRef]
- Nikitina, A.; Orlov, A.; Kozlovskaya, L.; Palyulin, V.; Osolodkin, D.I. Enhanced taxonomy annotation of antiviral activity data from ChEMBL. Database 2019, 2019, 1–18. [Google Scholar] [CrossRef]
- Haudecoeur, R.; Peuchmaur, M.; Ahmed-Belkacem, A.; Pawlotsky, J.M.; Boumendjel, A. Structure-activity relationships in the development of allosteric hepatitis C virus RNA-dependent RNA polymerase inhibitors: Ten years of research. Med. Res. Rev. 2013, 33, 934–984. [Google Scholar] [CrossRef]
- Bankar, A.; Siriwardena, T.P.; Rizoska, B.; Rydergård, C.; Kylefjord, H.; Rraklli, V.; Eneroth, A.; Pinho, P.; Norin, S.; Bylund, J.; et al. 5-Fluorotroxacitabine Displays Potent Anti-Leukemic Effects and Circumvents Resistance to Ara-C. Blood 2018, 132, 3939. [Google Scholar] [CrossRef]
- Szilágyi, K.; Hajdú, I.; Flachner, B.; Lőrincz, Z.; Balczer, J.; Gál, P.; Závodszky, P.; Pirli, C.; Balogh, B.; Mándity, I.M.; et al. Design and Selection of Novel C1s Inhibitors by In Silico and In Vitro Approaches. Molecules 2019, 24, 3641. [Google Scholar] [CrossRef]
- Zhong, M.; Munzer, J.S.; Basak, A.; Benjannet, S.; Mowla, S.J.; Decroly, E.; Chrétien, M.; Seidah, N.G. The Prosegments of Furin and PC7 as Potent Inhibitors of Proprotein Convertases. J. Biol. Chem. 1999, 274, 33913–33920. [Google Scholar] [CrossRef]
- Poumale, H.M.P.; Hamm, R.; Zang, Y.; Shiono, Y.; Kuete, V. Coumarins and Related Compounds from the Medicinal Plants of Africa. In Medicinal Plant Research in Africa: Pharmacology and Chemistry; Newnes: Oxford, UK, 2013; pp. 261–300. [Google Scholar]
- Statsoft. Statistica; Version 12; Statsoft: Tulsa, OK, USA, 2012. [Google Scholar]
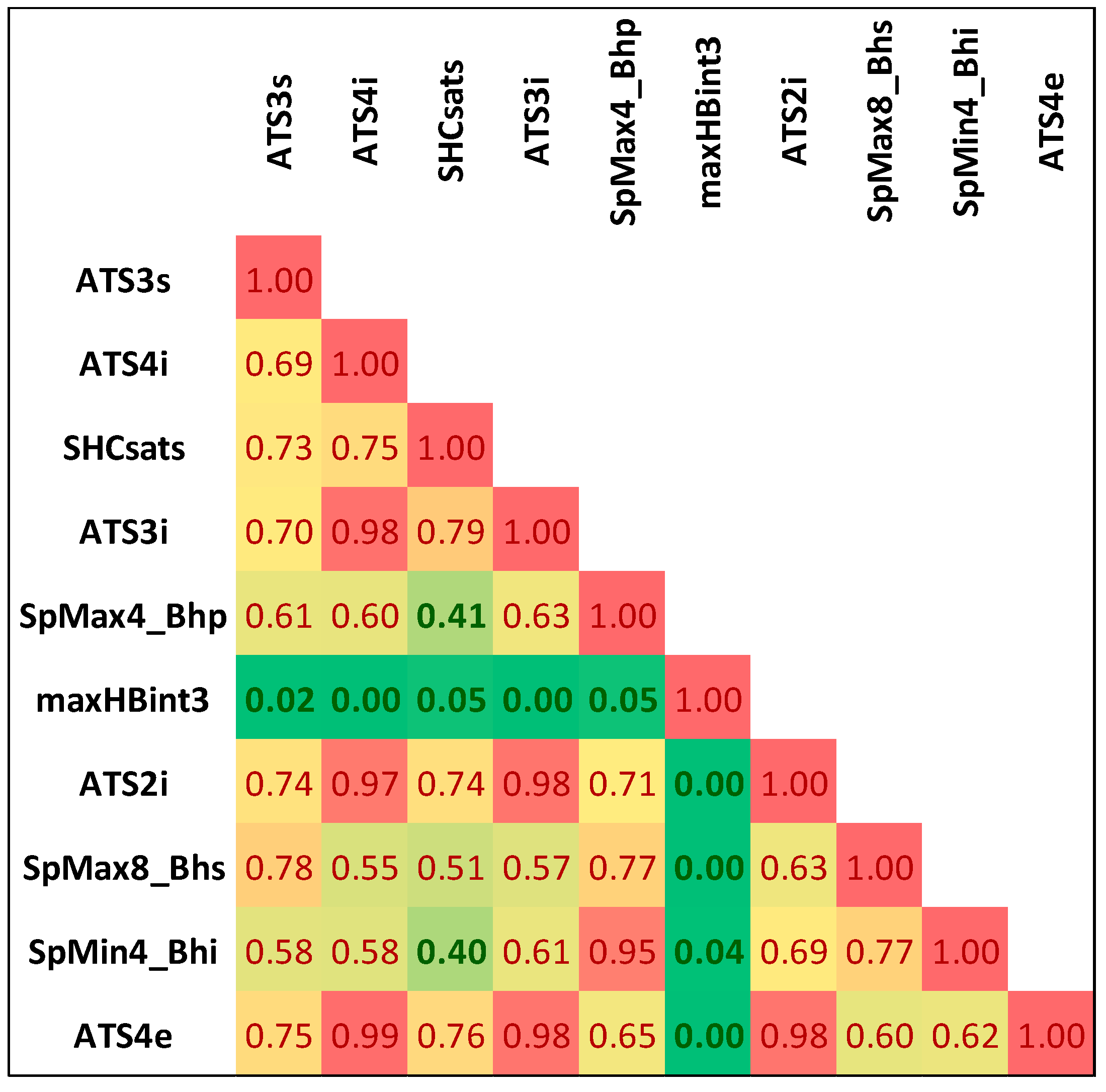
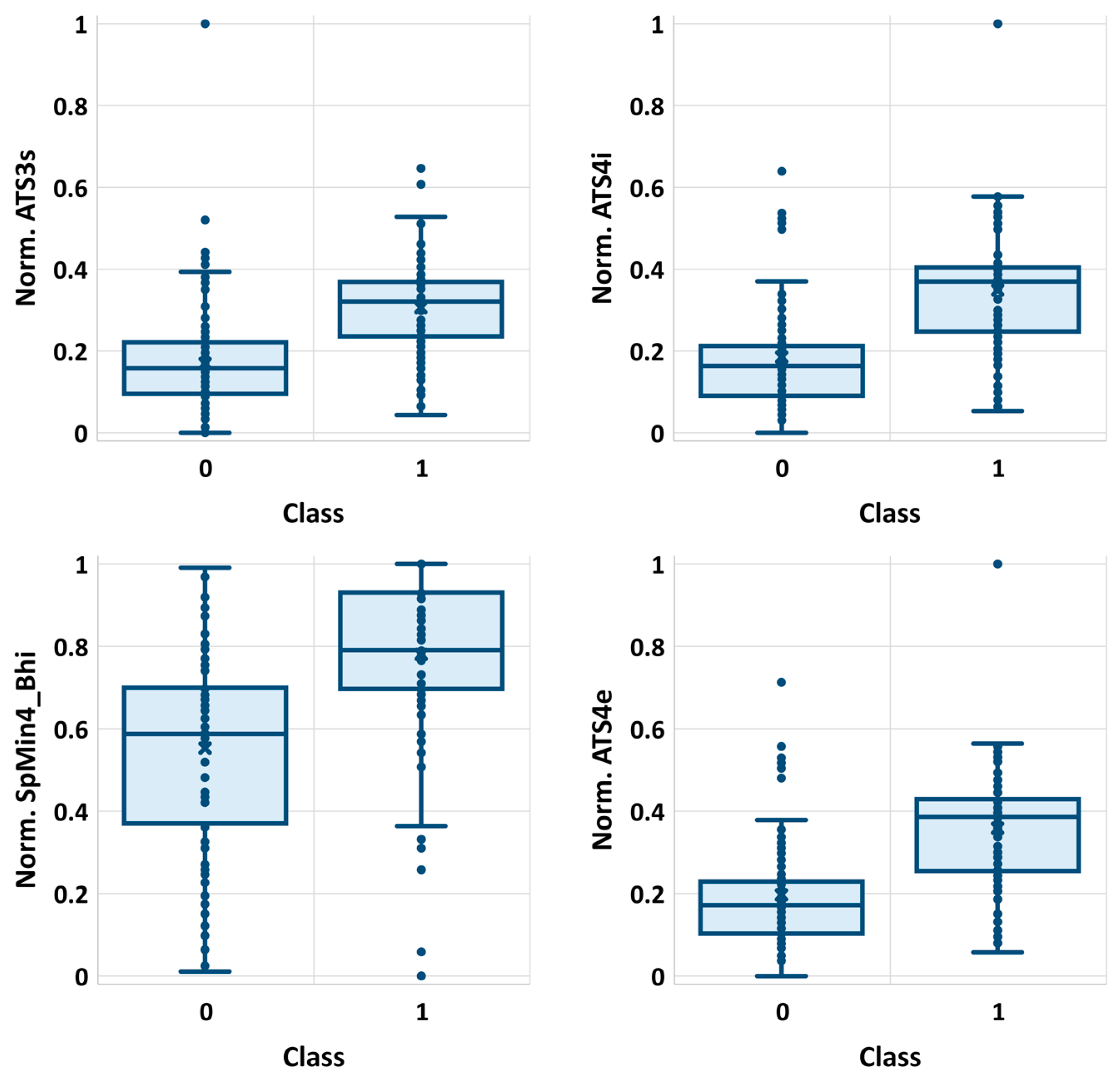
| Rank | Descriptor | χ2 | p-Value | ||
|---|---|---|---|---|---|
| χ2 Test | Mann-Whitney U | Kolmogorov-Smirnov | |||
| 1 | ATS3s | 124.6913 | 0.00 | 0.00 | <0.001 |
| 2 | ATS4i | 124.4754 | 0.00 | 0.00 | <0.001 |
| 3 | SHCsats | 122.8091 | 0.00 | 0.00 | <0.001 |
| 4 | ATS3i | 122.4608 | 0.00 | 0.00 | <0.001 |
| 5 | SpMax4_Bhp | 121.9436 | 0.00 | 0.00 | <0.001 |
| 6 | maxHBint3 | 121.1082 | 0.00 | 0.00 | <0.001 |
| 7 | ATS2i | 120.4616 | 0.00 | 0.00 | <0.001 |
| 8 | SpMax8_Bhs | 120.3141 | 0.00 | 0.00 | <0.001 |
| 9 | SpMin4_Bhi | 119.4392 | 0.00 | 0.00 | <0.001 |
| 10 | ATS4e | 118.9435 | 0.00 | 0.00 | <0.001 |
| No | Descriptor Pairs | %TN | %TP | %All | MCC | AUCROC |
|---|---|---|---|---|---|---|
| 1 | maxHBint3, SpMax8_Bhs | 89.0(6.7) | 81.4(5.7) | 85.3(4.3) | 0.748(0.063) | 0.860(0.059) |
| 2 | maxHBint3, SpMax4_Bhp | 89.3(8.8) | 77.3(9.0) | 83.4(5.3) | 0.722(0.070) | 0.854(0.05) |
| 3 | maxHBint3, SpMin4_Bhi | 81.5(8.1) | 84.0(10.0) | 82.4(4.5) | 0.715(0.063) | 0.868(0.055) |
| 4 | maxHBint3,SHCsats | 86.9(8.0) | 78.6(7.2) | 82.8(4.7) | 0.715(0.057) | 0.847(0.056) |
| 5 | SHCsats, SpMax4_Bhp | 83.0(8.6) | 81.5(8.4) | 82.2(5.2) | 0.711(0.069) | 0.853(0.057) |
| 6 | maxHBint3,ATS4i | 86.1(9.1) | 78.1(12.1) | 82.4(6.7) | 0.710(0.093) | 0.839(0.089) |
| 7 | maxHBint3,ATS3i | 86.2(9.0) | 78.5(7.4) | 82.4(4.5) | 0.710(0.062) | 0.848(0.052) |
| 8 | SHCsats, SpMin4_Bhi | 79.9(9.8) | 85.0(7.4) | 82.0(4.6) | 0.710(0.059) | 0.847(0.076) |
| 9 | maxHBint3,ATS3s | 83.9(9.6) | 78.2(9.1) | 80.9(5.7) | 0.696(0.076) | 0.818(0.071) |
| 10 | maxHBint3,ATS4e | 85.3(8.2) | 76.6(7.9) | 80.7(5.2) | 0.693(0.060) | 0.816(0.078) |
| 11 | maxHBint3,ATS2i | 83.6(6.7) | 71.7(9.9) | 77.6(5.4) | 0.654(0.061) | 0.794(0.088) |
| Data Split | SANN | Learning Algorithm | Error Function | Activation Function | MCC | |||
|---|---|---|---|---|---|---|---|---|
| Hidden Layer | Output Layer | Tr | V | Ts | ||||
| 1 | RBF 2-24-2 | RBFT | Entropy | Gauss | Softmax | 0.698 | 0.748 | 0.745 |
| 1 | RBF 2-22-2 | RBFT | Entropy | Gauss | Softmax | 0.733 | 0.748 | 0.745 |
| 2 | RBF 2-27-2 | RBFT | Entropy | Gauss | Softmax | 0.739 | 0.813 | 0.813 |
| 3 | MLP 2-4-2 | BFGS 22 | Entropy | Tanh | Softmax | 0.693 | 0.722 | 0.798 |
| 4 | RBF 2-24-2 | RBFT | Entropy | Gauss | Softmax | 0.734 | 0.660 | 0.742 |
| 5 | MLP 2-4-2 | BFGS 7 | Entropy | Exponential | Softmax | 0.603 | 0.745 | 0.720 |
| 5 | RBF 2-22-2 | RBFT | Entropy | Gauss | Softmax | 0.633 | 0.742 | 0.722 |
| 6 | MLP 2-5-2 | BFGS 33 | Entropy | Exponential | Softmax | 0.678 | 0.847 | 0.781 |
| 7 | MLP 2-4-2 | BFGS 42 | Entropy | Tanh | Softmax | 0.698 | 0.589 | 0.778 |
| 8 | RBF 2-27-2 | RBFT | Sum of squares | Gauss | Linear | 0.705 | 0.809 | 0.811 |
| 9 | RBF 2-22-2 | RBFT | Sum of squares | Gauss | Linear | 0.728 | 0.747 | 0.918 |
| 9 | RBF 2-28-2 | RBFT | Entropy | Gauss | Softmax | 0.667 | 0.750 | 0.918 |
| 10 | RBF 2-30-2 | RBFT | Entropy | Gauss | Softmax | 0.700 | 0.720 | 0.769 |
| Data Split | Dataset | MaxHBint3 | p-Value | SpMax8_Bhs | p-Value | ||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | U 1 | KS 2 | Min | Max | U 1 | KS 2 | ||
| 1 | training and validation | 0.0000 | 6.8353 | 0.92 | >0.1 | 1.2027 | 4.7812 | 0.87 | >0.1 |
| test set | 0.0000 | 6.5696 | 0.7059 | 4.7447 | |||||
| 2 | training and validation | 0.0000 | 6.5696 | 0.62 | >0.1 | 0.7059 | 4.7812 | 0.73 | >0.1 |
| test set | 0.0000 | 6.8353 | 1.2907 | 4.0981 | |||||
| 3 | training and validation | 0.0000 | 6.8353 | 0.10 | >0.1 | 0.7059 | 4.6921 | 0.17 | <0.1 |
| test set | 0.0000 | 5.0901 | 1.2907 | 4.7812 | |||||
| 4 | training and validation | 0.0000 | 6.5696 | 0.95 | >0.1 | 0.7059 | 4.7812 | 0.31 | >0.1 |
| test set | 0.0000 | 6.8353 | 1.2907 | 4.6316 | |||||
| 5 | training and validation | 0.0000 | 6.8353 | 0.97 | >0.1 | 1.2027 | 4.7812 | 0.43 | >0.1 |
| test set | 0.0000 | 5.5066 | 0.7059 | 4.0927 | |||||
| 6 | training and validation | 0.0000 | 6.5696 | 0.27 | >0.1 | 0.7059 | 4.7812 | 0.23 | >0.1 |
| test set | 0.0000 | 6.8353 | 1.4435 | 4.6613 | |||||
| 7 | training and validation | 0.0000 | 6.8353 | 0.89 | >0.1 | 1.2027 | 4.7812 | 0.54 | >0.1 |
| test set | 0.0000 | 5.5717 | 0.7059 | 4.6921 | |||||
| 8 | training and validation | 0.0000 | 6.8353 | 0.63 | >0.1 | 0.7059 | 4.7812 | 0.59 | >0.1 |
| test set | 0.0000 | 5.2672 | 1.6043 | 4.0981 | |||||
| 9 | training and validation | 0.0000 | 6.8353 | 0.69 | >0.1 | 0.7059 | 4.7812 | 0.26 | >0.1 |
| test set | 0.0000 | 5.1510 | 1.6609 | 4.2558 | |||||
| 10 | training and validation | 0.0000 | 6.8353 | 0.11 | >0.1 | 0.7059 | 4.6921 | 0.31 | >0.1 |
| test set | 0.0000 | 5.5574 | 1.2027 | 4.7812 | |||||
Sample Availability: Samples of the compounds are not available from the authors. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Przybyłek, M. Application 2D Descriptors and Artificial Neural Networks for Beta-Glucosidase Inhibitors Screening. Molecules 2020, 25, 5942. https://doi.org/10.3390/molecules25245942
Przybyłek M. Application 2D Descriptors and Artificial Neural Networks for Beta-Glucosidase Inhibitors Screening. Molecules. 2020; 25(24):5942. https://doi.org/10.3390/molecules25245942
Chicago/Turabian StylePrzybyłek, Maciej. 2020. "Application 2D Descriptors and Artificial Neural Networks for Beta-Glucosidase Inhibitors Screening" Molecules 25, no. 24: 5942. https://doi.org/10.3390/molecules25245942
APA StylePrzybyłek, M. (2020). Application 2D Descriptors and Artificial Neural Networks for Beta-Glucosidase Inhibitors Screening. Molecules, 25(24), 5942. https://doi.org/10.3390/molecules25245942






