Stacking Effects on Anthraquinone/DNA Charge-Transfer Electronically Excited States
Abstract
1. Introduction
2. Results and Discussion
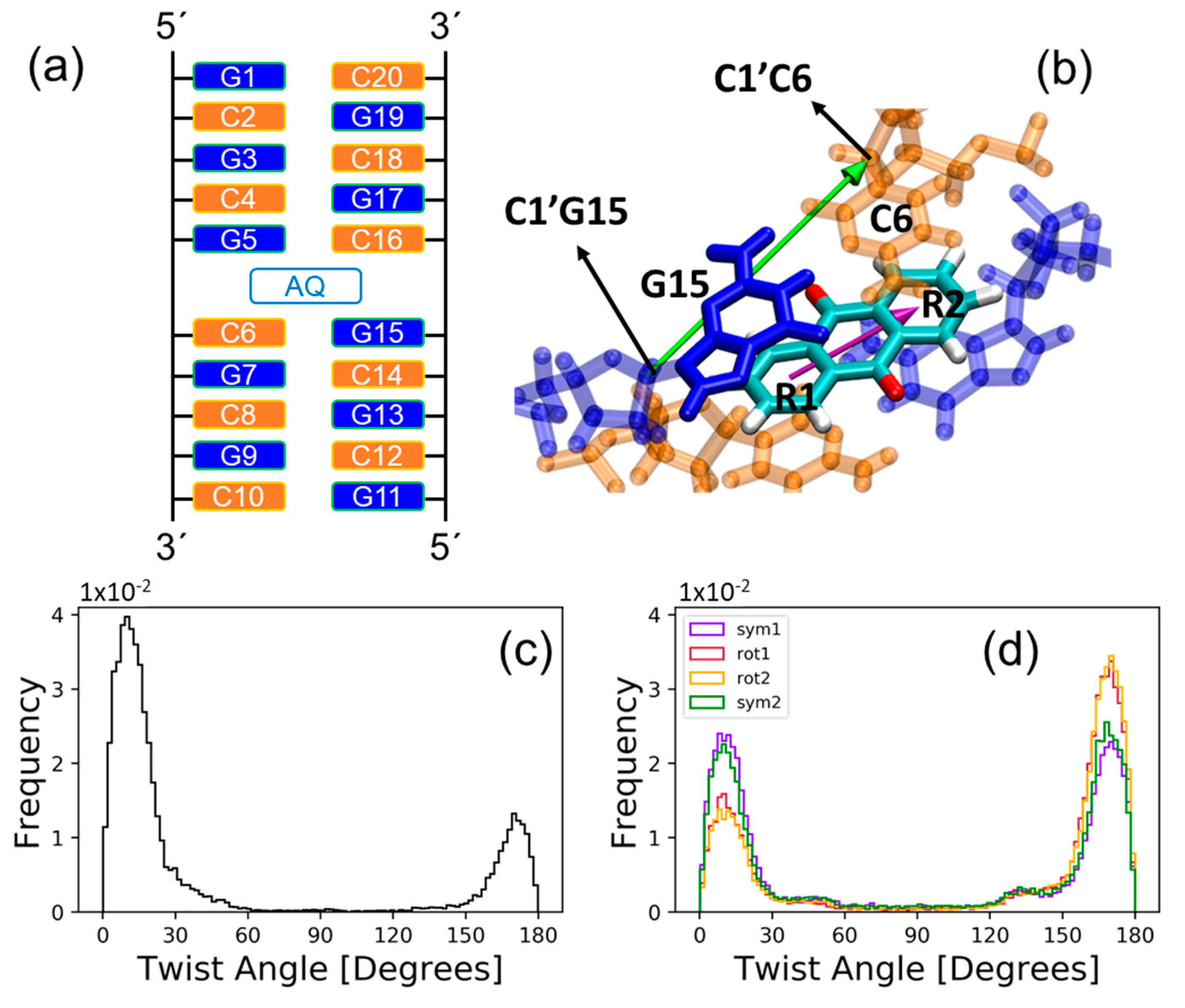
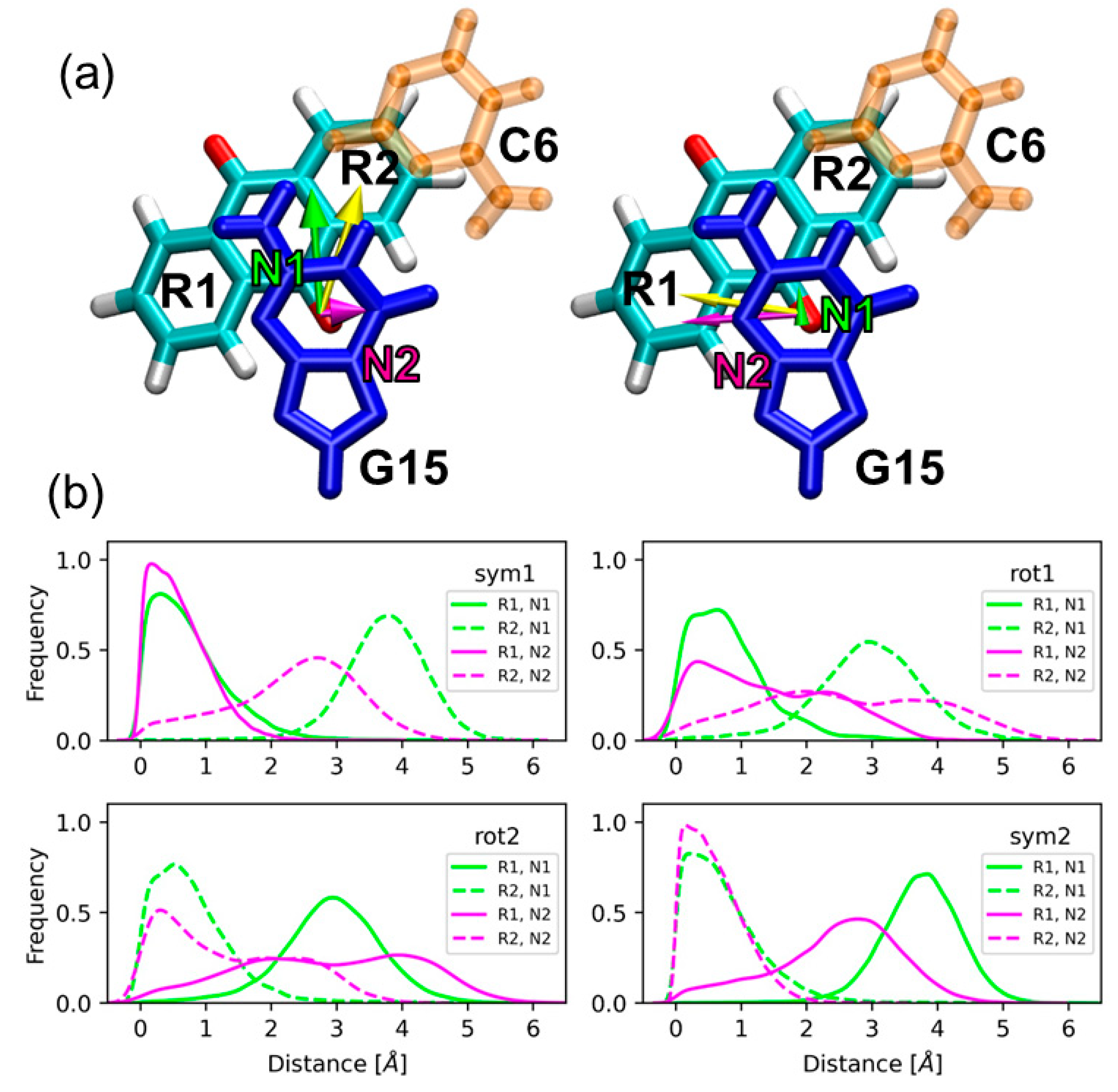
2.1. Sampling the Stacking Binding Pocket
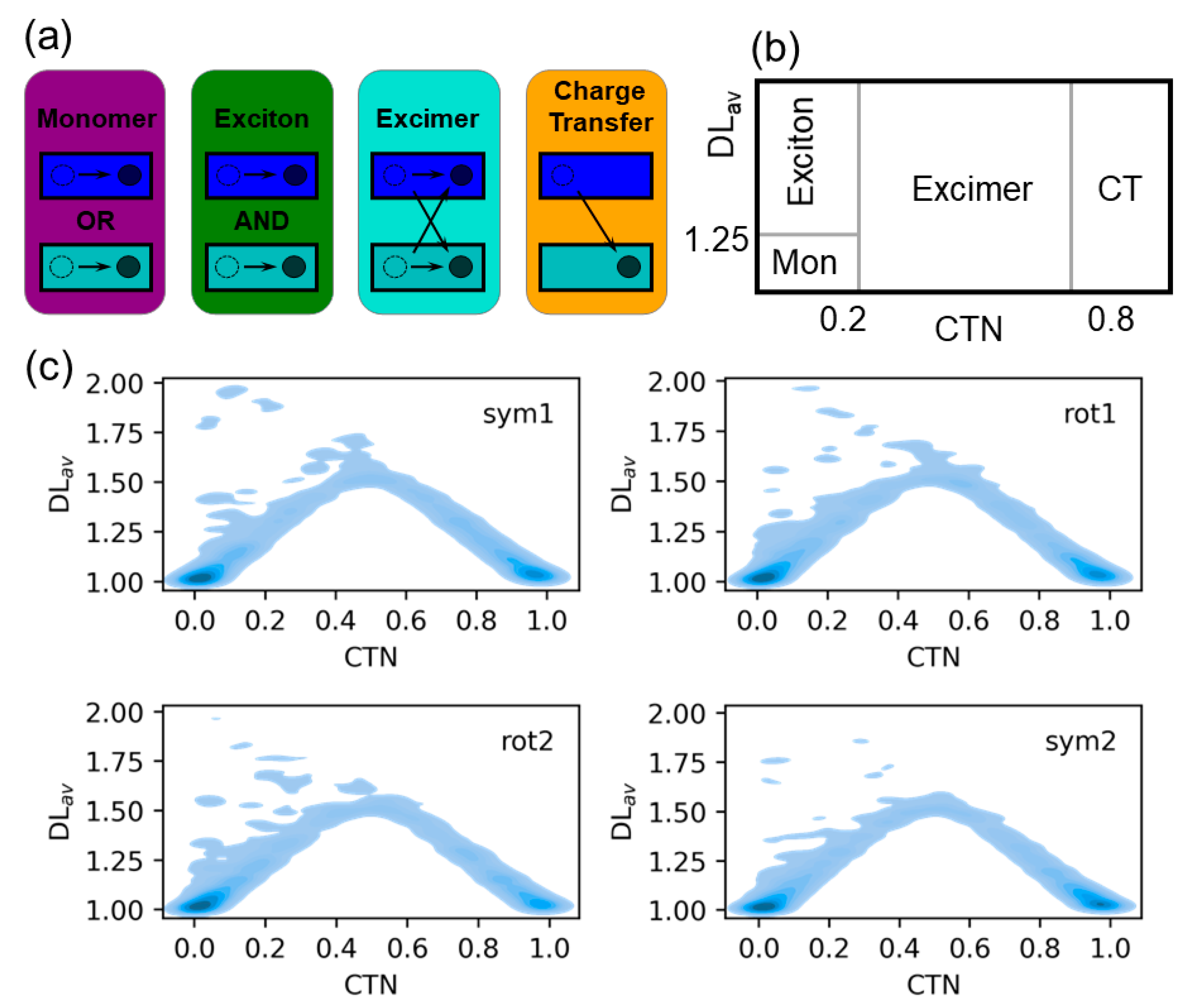
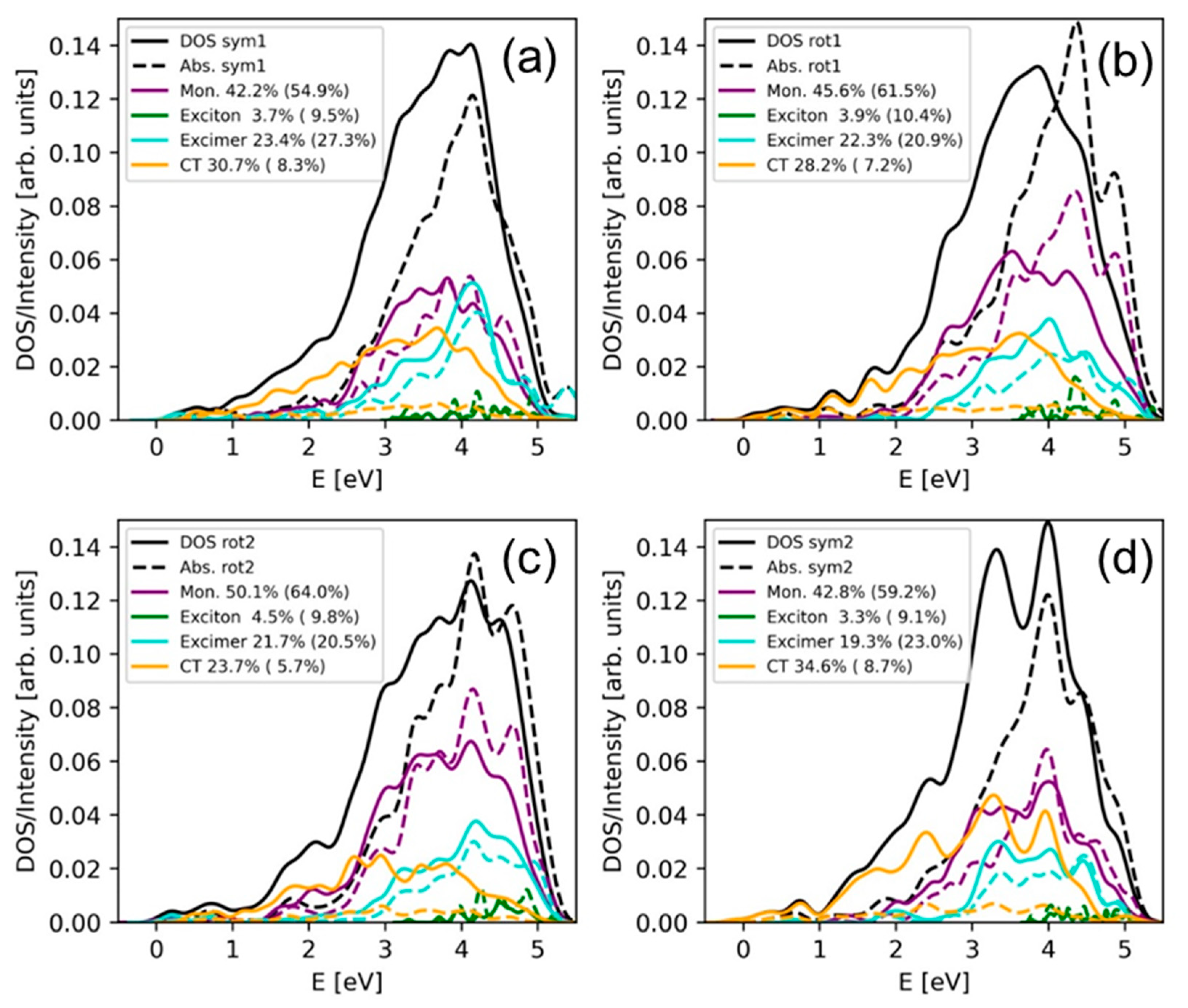
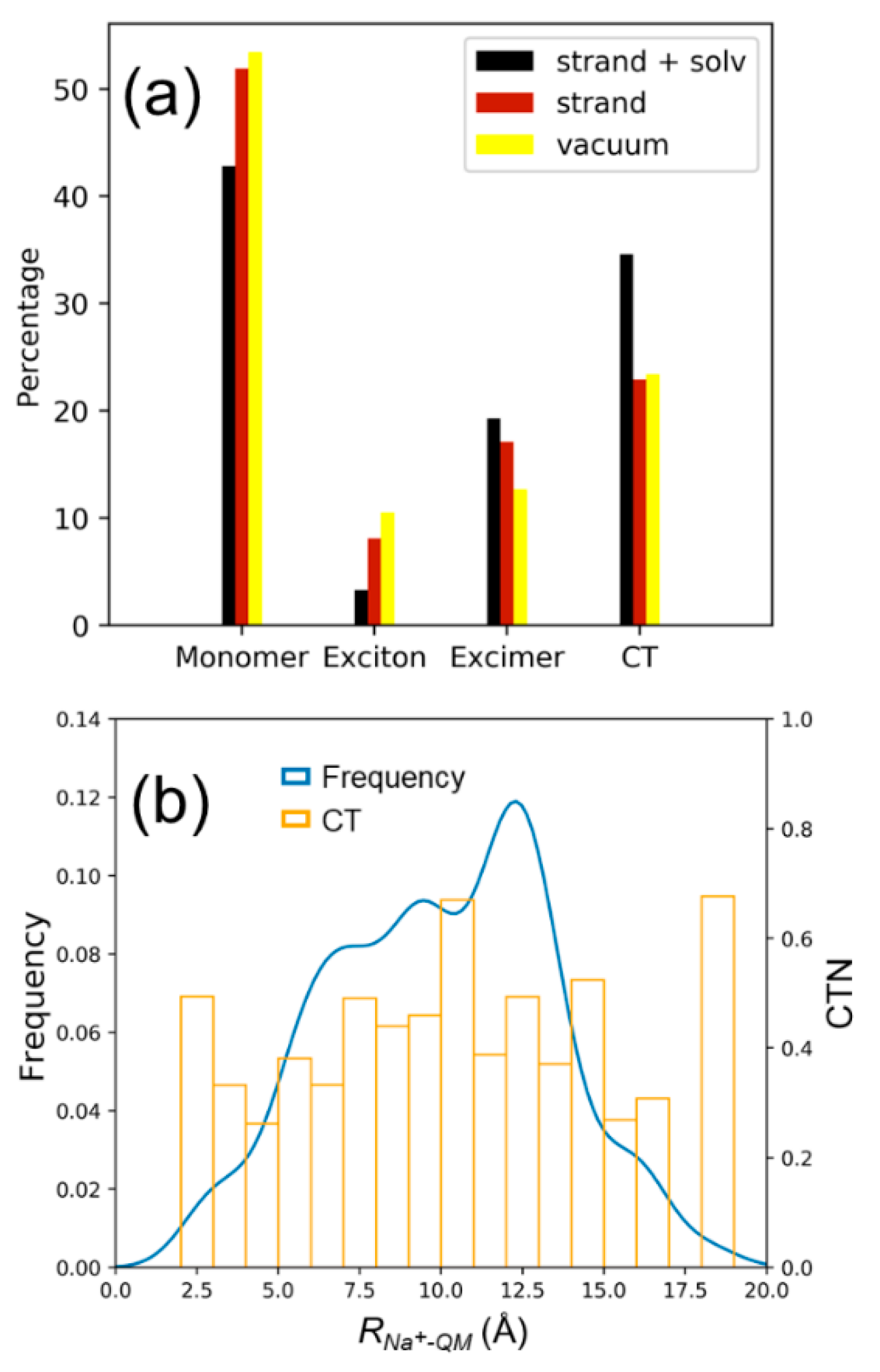
2.2. Electronically Excited States: Delocalization and Charge Transfer
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- O’Connor, A.E.; Gallagher, W.M.; Byrne, A.T. Porphyrin and Nonporphyrin Photosensitizers in Oncology: Preclinical and Clinical Advances in Photodynamic Therapy. Photochem. Photobiol. 2009, 85, 1053–1074. [Google Scholar] [CrossRef] [PubMed]
- Sharman, W.M.; Allen, C.M.; Van Lier, J.E. Photodynamic therapeutics: Basic principles and clinical applications. Drug Discov. Today 1999, 4, 507–517. [Google Scholar] [CrossRef]
- Phillips, D. Toward targeted photodynamic therapy. Pure Appl. Chem. 2011, 83, 733–748. [Google Scholar] [CrossRef]
- Wilson, B.; Patterson, M.S. The physics, biophysics and technology of photodynamic therapy. Phys. Med. Biol. 2008, 53, R61–R109. [Google Scholar] [CrossRef] [PubMed]
- Allison, R.R.; Moghissi, K. Oncologic photodynamic therapy: Clinical strategies that modulate mechanisms of action. Photodiagnosis Photodyn. Ther. 2013, 10, 331–341. [Google Scholar] [CrossRef] [PubMed]
- Kochevar, E.I.; Lynch, M.C.; Zhuang, S.; Lambert, C.R. Singlet Oxygen, but not Oxidizing Radicals, Induces Apoptosis in HL-60 Cells. Photochem. Photobiol. 2000, 72, 548–553. [Google Scholar]
- Dolmans, D.E.J.G.J.; Fukumura, D.; Jain, R.K. Photodynamic therapy for cancer. Nat. Rev. Cancer 2003, 3, 380–387. [Google Scholar] [CrossRef]
- Wyld, L.; Reed, M.W.R.; Brown, N.J. Differential cell death response to photodynamic therapy is dependent on dose and cell type. Br. J. Cancer 2001, 84, 1384–1386. [Google Scholar] [CrossRef]
- Castano, A.P.; Demidova, T.N.; Hamblin, M.R. Mechanisms in photodynamic therapy: Part one—Photosensitizers, photochemistry and cellular localization. Photodiagnosis Photodyn. Ther. 2004, 1, 279–293. [Google Scholar] [CrossRef]
- Muz, B.; De La Puente, P.; Azab, F.; Azab, A.K. The role of hypoxia in cancer progression, angiogenesis, metastasis, and resistance to therapy. Hypoxia 2015, 3, 83–92. [Google Scholar] [CrossRef]
- Monro, S.; Colón, K.L.; Yin, H.; Roque, I.J.; Konda, P.; Gujar, S.; Thummel, R.P.; Lilge, L.; Cameron, C.G.; McFarland, S.A. Transition Metal Complexes and Photodynamic Therapy from a Tumor-Centered Approach: Challenges, Opportunities, and Highlights from the Development of TLD1433. Chem. Rev. 2019, 119, 797–828. [Google Scholar] [CrossRef] [PubMed]
- Roque, J.; Barrett, P.C.; Cole, H.D.; Lifshits, L.M.; Shi, G.; Monro, S.; Von Dohlen, D.; Kim, S.; Russo, N.; Deep, G.; et al. Breaking the barrier: An osmium photosensitizer with unprecedented hypoxic phototoxicity for real world photodynamic therapy. Chem. Sci. 2020, 11, 9784–9806. [Google Scholar] [CrossRef]
- Nguyen, V.-N.; Qi, S.; Kim, S.; Kwon, N.; Kim, G.; Yim, Y.; Park, S.; Yoon, J. An Emerging Molecular Design Approach to Heavy-Atom-Free Photosensitizers for Enhanced Photodynamic Therapy under Hypoxia. J. Am. Chem. Soc. 2019, 141, 16243–16248. [Google Scholar] [CrossRef] [PubMed]
- Francés-Monerris, A.; Tuñón, I.; Monari, A. Hypoxia-Selective Dissociation Mechanism of a Nitroimidazole Nucleoside in a DNA Environment. J. Phys. Chem. Lett. 2019, 10, 6750–6754. [Google Scholar] [CrossRef]
- Kim, J.; Cho, H.R.; Jeon, H.; Kim, D.; Song, C.; Lee, N.; Choi, S.; Hyeon, T. Continuous O2-Evolving MnFe2O4 Nanoparticle-Anchored Mesoporous Silica Nanoparticles for Efficient Photodynamic Therapy in Hypoxic Cancer. J. Am. Chem. Soc. 2017, 139, 10992–10995. [Google Scholar] [CrossRef]
- Cheng, Y.; Jiang, C.; Qiu, X.; Wang, K.; Huan, W.; Yuan, A.; Yuan, A.; Hu, Y. Perfluorocarbon nanoparticles enhance reactive oxygen levels and tumour growth inhibition in photodynamic therapy. Nat. Commun. 2015, 6, 8785. [Google Scholar] [CrossRef]
- Morgan, J.; Oseroff, A.R. Mitochondria-based photodynamic anti-cancer therapy. Adv. Drug Deliv. Rev. 2001, 49, 71–86. [Google Scholar] [CrossRef]
- Runnels, J.M.; Chen, N.; Ortel, B.; Kato, D.; Hasan, T. BPD-MA-mediated photosensitization in vitro and in vivo: Cellular adhesion and β1 integrin expression in ovarian cancer cells. Br. J. Cancer 1999, 80, 946–953. [Google Scholar] [CrossRef]
- Singh, K.K.; Russell, J.; Sigala, B.; Zhang, Y.; Williams, J.; Keshav, K.F. Mitochondrial DNA determines the cellular response to cancer therapeutic agents. Oncogene 1999, 18, 6641–6646. [Google Scholar] [CrossRef]
- Chen, Q.-Y.; Li, D.-H.; Yang, H.-H.; Zhu, Q.-Z.; Xu, J.-G.; Zhao, Y. Interaction of a novel red-region fluorescent probe, Nile Blue, with DNA and its application to nucleic acids assay. Analyst 1999, 124, 901–906. [Google Scholar] [CrossRef]
- Gattuso, H.; Besancenot, V.; Grandemange, S.; Marazzi, M.; Pastore, M. From non-covalent binding to irreversible DNA lesions: Nile blue and nile red as photosensitizing agents. Sci. Rep. 2016, 6, 28480. [Google Scholar] [CrossRef] [PubMed]
- Hirakawa, K.; Ota, K.; Hirayama, J.; Oikawa, S.; Kawanishi, S. Nile Blue Can Photosensitize DNA Damage through Electron Transfer. Chem. Res. Toxicol. 2014, 27, 649–655. [Google Scholar] [CrossRef]
- Nogueira, J.J.; Oppel, M.; González, L. Enhancing Intersystem Crossing in Phenotiazinium Dyes by Intercalation into DNA. Angew. Chem. Int. Ed. 2015, 54, 4375–4378. [Google Scholar] [CrossRef] [PubMed]
- Ihmels, H.; Otto, D. Intercalation of Organic Dye Molecules into Double-Stranded DNA—General Principles and Recent Developments. In Supermolecular Dye Chemistry; Würthner, F., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 161–204. [Google Scholar]
- Strekowski, L.; Wilson, B. Noncovalent interactions with DNA: An overview. Mutat. Res. Mol. Mech. Mutagen. 2007, 623, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, D.; Pal, S.K. Dynamics in the DNA Recognition by DAPI: Exploration of the Various Binding Modes. J. Phys. Chem. B 2008, 112, 1016–1021. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.K.; Eriksson, S.; Kubista, M.; Nordén, B. Interaction of 4′,6-diamidino-2-phenylindole (DAPI) with poly[d(G-C)2] and poly[d(G-m5C)2]: Evidence for major groove binding of a DNA probe. J. Am. Chem. Soc. 1993, 115, 3441–3447. [Google Scholar] [CrossRef]
- Larsen, T.A.; Goodsell, D.S.; Cascio, D.; Grzeskowiak, K.; Dickerson, R.E. The Structure of DAPI Bound to DNA. J. Biomol. Struct. Dyn. 1989, 7, 477–491. [Google Scholar] [CrossRef]
- Wilson, W.D.; Tanious, F.A.; Barton, H.J.; Jones, R.L.; Strekowski, L.; Boykin, D.W. Binding of 4′,6-diamidino-2-phenylindole (DAPI) to GC and mixed sequences in DNA: Intercalation of a classical groove-binding molecule. J. Am. Chem. Soc. 1989, 111, 5008–5010. [Google Scholar] [CrossRef]
- Gatto, B.; Zagotto, G.; Sissi, C.; Cera, C.; Uriarte, E.; Palù, G.; Capranico, G.; Palumbo, M. Peptidyl Anthraquinones as Potential Antineoplastic Drugs: Synthesis, DNA Binding, Redox Cycling, and Biological Activity. J. Med. Chem. 1996, 39, 3114–3122. [Google Scholar] [CrossRef]
- Larsson, A.; Carlsson, C.; Jönsson, M.; Albinsson, B. Characterization of the Binding of the Fluorescent Dyes YO and YOYO to DNA by Polarized Light Spectroscopy. J. Am. Chem. Soc. 1994, 116, 8459–8465. [Google Scholar] [CrossRef]
- Ormond, A.B.; Freeman, H.S. Dye Sensitizers for Photodynamic Therapy. Materials 2013, 6, 817–840. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Su, X.; Liang, Y.; Zhang, J.; Shi, C.; Lu, Y.; Gu, L.; Fu, L. Emodin azide methyl anthraquinone derivative triggers mitochondrial-dependent cell apoptosis involving in caspase-8-mediated Bid cleavage. Mol. Cancer Ther. 2008, 7, 1688–1697. [Google Scholar] [CrossRef] [PubMed]
- Comini, L.; Fernandez, I.; Vittar, N.R.; Montoya, S.N.; Cabrera, J.L.; Rivarola, V.A. Photodynamic activity of anthraquinones isolated from Heterophyllaea pustulata Hook f. (Rubiaceae) on MCF-7c3 breast cancer cells. Phytomedicine 2011, 18, 1093–1095. [Google Scholar] [CrossRef] [PubMed]
- Vittar, N.B.R.; Comini, L.; Fernadez, I.M.; Agostini, E.; Montoya, S.C.N.; Cabrera, J.L.; Rivarola, V.A. Photochemotherapy using natural anthraquinones: Rubiadin and Soranjidiol sensitize human cancer cell to die by apoptosis. Photodiagnosis Photodyn. Ther. 2014, 11, 182–192. [Google Scholar] [CrossRef] [PubMed]
- Breslin, D.T.; Yu, C.; Ly, D.; Schuster, G.B. Structural Modification Changes the DNA Binding Mode of Cation-Substituted Anthraquinone Photonucleases: Association by Intercalation or Minor Groove Binding Determines the DNA Cleavage Efficiency†. Biochemistry 1997, 36, 10463–10473. [Google Scholar] [CrossRef]
- Minotti, G.; Menna, P.; Salvatorelli, E.; Cairo, G.; Gianni, L. Anthracyclines: Molecular Advances and Pharmacologic Developments in Antitumor Activity and Cardiotoxicity. Pharmacol. Rev. 2004, 56, 185–229. [Google Scholar] [CrossRef]
- Chaires, J.B.; Satyanarayana, S.; Suh, D.; Fokt, I.; Przewloka, A.T.; Priebe, W. Parsing the Free Energy of Anthracycline Antibiotic Binding to DNA. Biochemistry 1996, 35, 2047–2053. [Google Scholar] [CrossRef]
- Monneret, C. Recent developments in the field of antitumour anthracyclines. Eur. J. Med. Chem. 2001, 36, 483–493. [Google Scholar] [CrossRef]
- Dumont, E.; Pastore, M. Understanding DNA under oxidative stress and sensitization: The role of molecular modeling. Front. Chem. 2015, 3, 43. [Google Scholar] [CrossRef]
- Beckford, S.J.; Dixon, D.W. Molecular Dynamics of Anthraquinone DNA Intercalators with Polyethylene Glycol Side Chains. J. Biomol. Struct. Dyn. 2012, 29, 1065–1080. [Google Scholar] [CrossRef]
- Dumont, E.; Monari, A. Benzophenone and DNA: Evidence for a Double Insertion Mode and Its Spectral Signature. J. Phys. Chem. Lett. 2013, 4, 4119–4124. [Google Scholar] [CrossRef]
- Nogueira, J.J.; González, L. Molecular Dynamics Simulations of Binding Modes between Methylene Blue and DNA with Alternating GC and AT Sequences. Biochemistry 2014, 53, 2391–2412. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, M.; Mukherjee, A.; Bouvier, B.; Zakrzewska, K.; Hynes, J.T.; Lavery, R. Multistep Drug Intercalation: Molecular Dynamics and Free Energy Studies of the Binding of Daunomycin to DNA. J. Am. Chem. Soc. 2012, 134, 8588–8596. [Google Scholar] [CrossRef] [PubMed]
- Huix-Rotllant, M.; Dumont, E.; Ferré, N.; Pastore, M. Photophysics of Acetophenone Interacting with DNA: Why the Road to Photosensitization is Open. Photochem. Photobiol. 2014, 91, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Dumont, E.; Pastore, M. Interaction of Palmatine with DNA: An Environmentally Controlled Phototherapy Drug. J. Phys. Chem. B 2014, 119, 410–419. [Google Scholar] [CrossRef]
- Nogueira, J.J.; Roßbach, S.; Ochsenfeld, C.; González, L.; Rossbach, S. Effect of DNA Environment on Electronically Excited States of Methylene Blue Evaluated by a Three-Layered QM/QM/MM ONIOM Scheme. J. Chem. Theory Comput. 2018, 14, 4298–4308. [Google Scholar] [CrossRef]
- Terenzi, A.; Gattuso, H.; Spinello, A.; Keppler, B.K.; Chipot, C.; Dehez, F.; Barone, G.; Pastore, M. Targeting G-quadruplexes with Organic Dyes: Chelerythrine-DNA Binding Elucidated by Combining Molecular Modeling and Optical Spectroscopy. Antioxidants 2019, 8, 472. [Google Scholar] [CrossRef]
- Mukherjee, A.; Lavery, R.; Bagchi, B.; Hynes, J.T. On the Molecular Mechanism of Drug Intercalation into DNA: A Simulation Study of the Intercalation Pathway, Free Energy, and DNA Structural Changes. J. Am. Chem. Soc. 2008, 130, 9747–9755. [Google Scholar] [CrossRef]
- Seidel, C.A.M.; Schulz, A.; Sauer, M.H.M. Nucleobase-Specific Quenching of Fluorescent Dyes. 1. Nucleobase One-Electron Redox Potentials and Their Correlation with Static and Dynamic Quenching Efficiencies. J. Phys. Chem. 1996, 100, 5541–5553. [Google Scholar] [CrossRef]
- Ly, D.; Kan, Y.; Armitage, B.A.; Schuster, G.B. Cleavage of DNA by Irradiation of Substituted Anthraquinones: Intercalation Promotes Electron Transfer and Efficient Reaction at GG Steps. J. Am. Chem. Soc. 1996, 118, 8747–8748. [Google Scholar] [CrossRef]
- Schuster, G.B. Long-Range Charge Transfer in DNA: Transient Structural Distortions Control the Distance Dependence. Acc. Chem. Res. 2000, 33, 253–260. [Google Scholar] [CrossRef] [PubMed]
- Plasser, F. TheoDORE: A toolbox for a detailed and automated analysis of electronic excited state computations. J. Chem. Phys. 2020, 152, 084108. [Google Scholar] [CrossRef] [PubMed]
- Kreft, D.; Wang, Y.; Rattay, M.; Toensing, K.; Anselmetti, D. Binding mechanism of anti-cancer chemotherapeutic drug mitoxantrone to DNA characterized by magnetic tweezers. J. Nanobiotechnol. 2018, 16, 56. [Google Scholar] [CrossRef]
- Tanious, F.A.; Jenkins, T.C.; Neidle, S.; Wilson, W.D. Substituent position dictates the intercalative DNA-binding mode for anthracene-9,10-dione antitumor drugs. Biochemistry 1992, 31, 11632–11640. [Google Scholar] [CrossRef] [PubMed]
- Nordén, B.; Tjerneld, F. Structure of methylene blue-DNA complexes studied by linear and circular dichroism spectroscopy. Biopolym. Orig. Res. Biomol. 1982, 21, 1713–1734. [Google Scholar] [CrossRef] [PubMed]
- Gattuso, H.; Dumont, E.; Chipot, C.; Pastore, M.; Dehez, F. Thermodynamics of DNA: Sensitizer recognition. Characterizing binding motifs with all-atom simulations. Phys. Chem. Chem. Phys. 2016, 18, 33180–33186. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, J.J.; González, L. Computational Photophysics in the Presence of an Environment. Annu. Rev. Phys. Chem. 2018, 69, 473–497. [Google Scholar] [CrossRef]
- Dumont, E.; Wibowo, M.; Roca-Sanjuán, D.; Garavelli, M.; Assfeld, X.; Pastore, M. Resolving the Benzophenone DNA-Photosensitization Mechanism at QM/MM Level. J. Phys. Chem. Lett. 2015, 6, 576–580. [Google Scholar] [CrossRef]
- Plasser, F.; Lischka, H. Analysis of Excitonic and Charge Transfer Interactions from Quantum Chemical Calculations. J. Chem. Theory Comput. 2012, 8, 2777–2789. [Google Scholar] [CrossRef]
- Plasser, F.; Aquino, A.J.A.; Hase, W.L.; Lischka, H. UV Absorption Spectrum of Alternating DNA Duplexes. Analysis of Excitonic and Charge Transfer Interactions. J. Phys. Chem. A 2012, 116, 11151–11160. [Google Scholar] [CrossRef]
- Plasser, F.; Wormit, M.; Dreuw, A. New tools for the systematic analysis and visualization of electronic excitations. I. Formalism. J. Chem. Phys. 2014, 141, 024106. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, J.J.; Plasser, F.; González, L. Electronic delocalization, charge transfer and hypochromism in the UV absorption spectrum of polyadenine unravelled by multiscale computations and quantitative wavefunction analysis. Chem. Sci. 2017, 8, 5682–5691. [Google Scholar] [CrossRef] [PubMed]
- Ibele, L.M.; Sánchez-Murcia, P.A.; Mai, S.; Nogueira, J.J.; González, L. Excimer Intermediates en Route to Long-Lived Charge-Transfer States in Single-Stranded Adenine DNA as Revealed by Nonadiabatic Dynamics. J. Phys. Chem. Lett. 2020, 11, 7483–7488. [Google Scholar] [CrossRef] [PubMed]
- Huix-Rotllant, M.; Brazard, J.; Improta, R.; Burghardt, I.; Markovitsi, D. Stabilization of Mixed Frenkel-Charge Transfer Excitons Extended Across Both Strands of Guanine–Cytosine DNA Duplexes. J. Phys. Chem. Lett. 2015, 6, 2247–2251. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Gilson, M.K.; et al. AMBER 18; University of California: San Francisco, CA, USA, 2018. [Google Scholar]
- Zgarbová, M.; Šponer, J.; Otyepka, M.; Cheatham, T.E.; Galindo-Murillo, R.; Jurečka, P. Refinement of the Sugar–Phosphate Backbone Torsion Beta for AMBER Force Fields Improves the Description of Z- and B-DNA. J. Chem. Theory Comput. 2015, 11, 5723–5736. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Li, P.; Song, L.F.; Merz, J.K.M. Systematic Parameterization of Monovalent Ions Employing the Nonbonded Model. J. Chem. Theory Comput. 2015, 11, 1645–1657. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian: Wallingford, CT, USA, 2016. [Google Scholar]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Laurent, A.D.; Jacquemin, D. TD-DFT benchmarks: A review. Int. J. Quantum Chem. 2013, 113, 2019–2039. [Google Scholar] [CrossRef]
- Kupfer, S.; Guthmuller, J.; González, L. An Assessment of RASSCF and TDDFT Energies and Gradients on an Organic Donor–Acceptor Dye Assisted by Resonance Raman Spectroscopy. J. Chem. Theory Comput. 2012, 9, 543–554. [Google Scholar] [CrossRef]
Sample Availability: Not available. |

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cárdenas, G.; Nogueira, J.J. Stacking Effects on Anthraquinone/DNA Charge-Transfer Electronically Excited States. Molecules 2020, 25, 5927. https://doi.org/10.3390/molecules25245927
Cárdenas G, Nogueira JJ. Stacking Effects on Anthraquinone/DNA Charge-Transfer Electronically Excited States. Molecules. 2020; 25(24):5927. https://doi.org/10.3390/molecules25245927
Chicago/Turabian StyleCárdenas, Gustavo, and Juan J. Nogueira. 2020. "Stacking Effects on Anthraquinone/DNA Charge-Transfer Electronically Excited States" Molecules 25, no. 24: 5927. https://doi.org/10.3390/molecules25245927
APA StyleCárdenas, G., & Nogueira, J. J. (2020). Stacking Effects on Anthraquinone/DNA Charge-Transfer Electronically Excited States. Molecules, 25(24), 5927. https://doi.org/10.3390/molecules25245927






