Exploring Free Energy Profiles of Enantioselective Organocatalytic Aldol Reactions under Full Solvent Influence
Abstract
1. Introduction
2. Results and Discussion
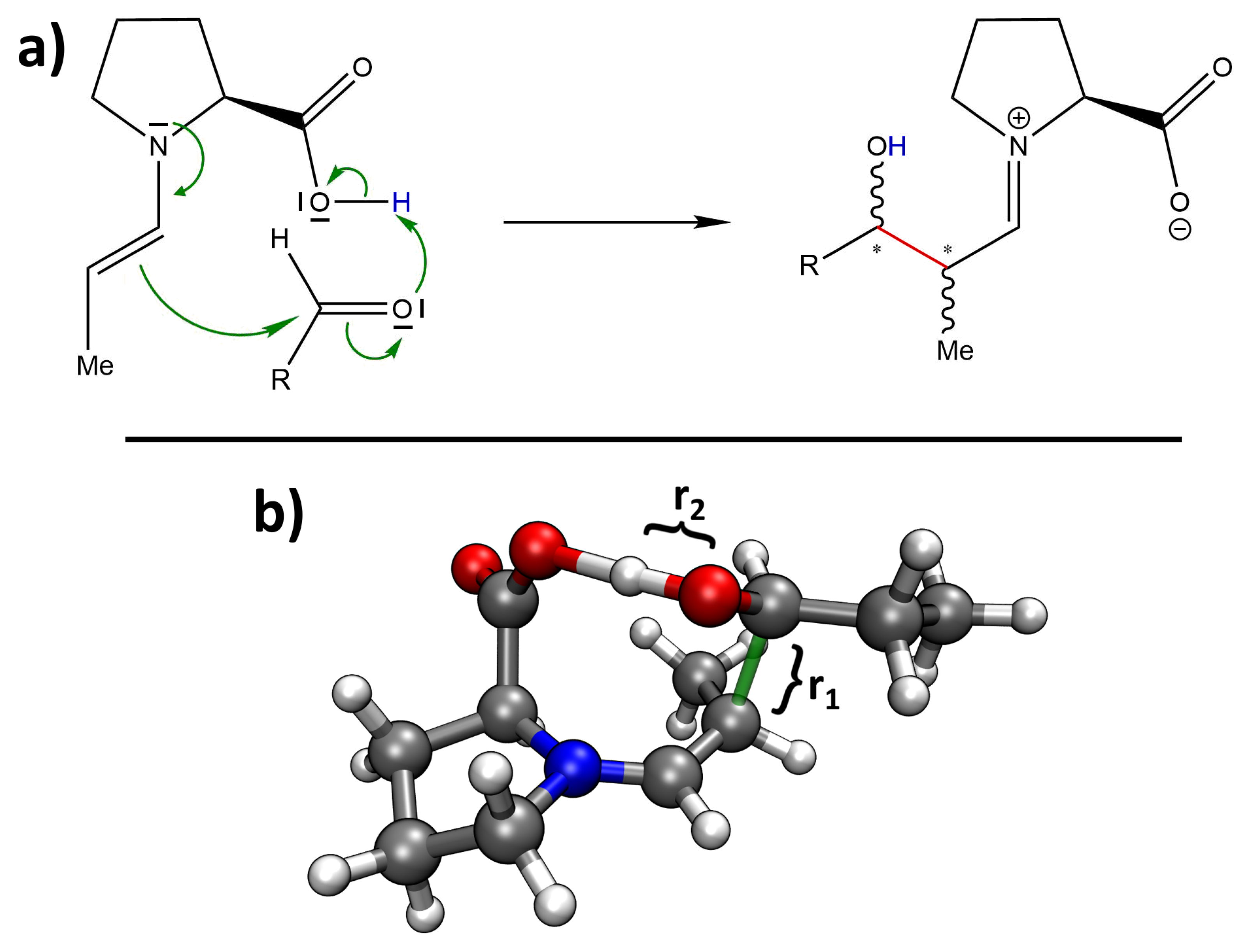
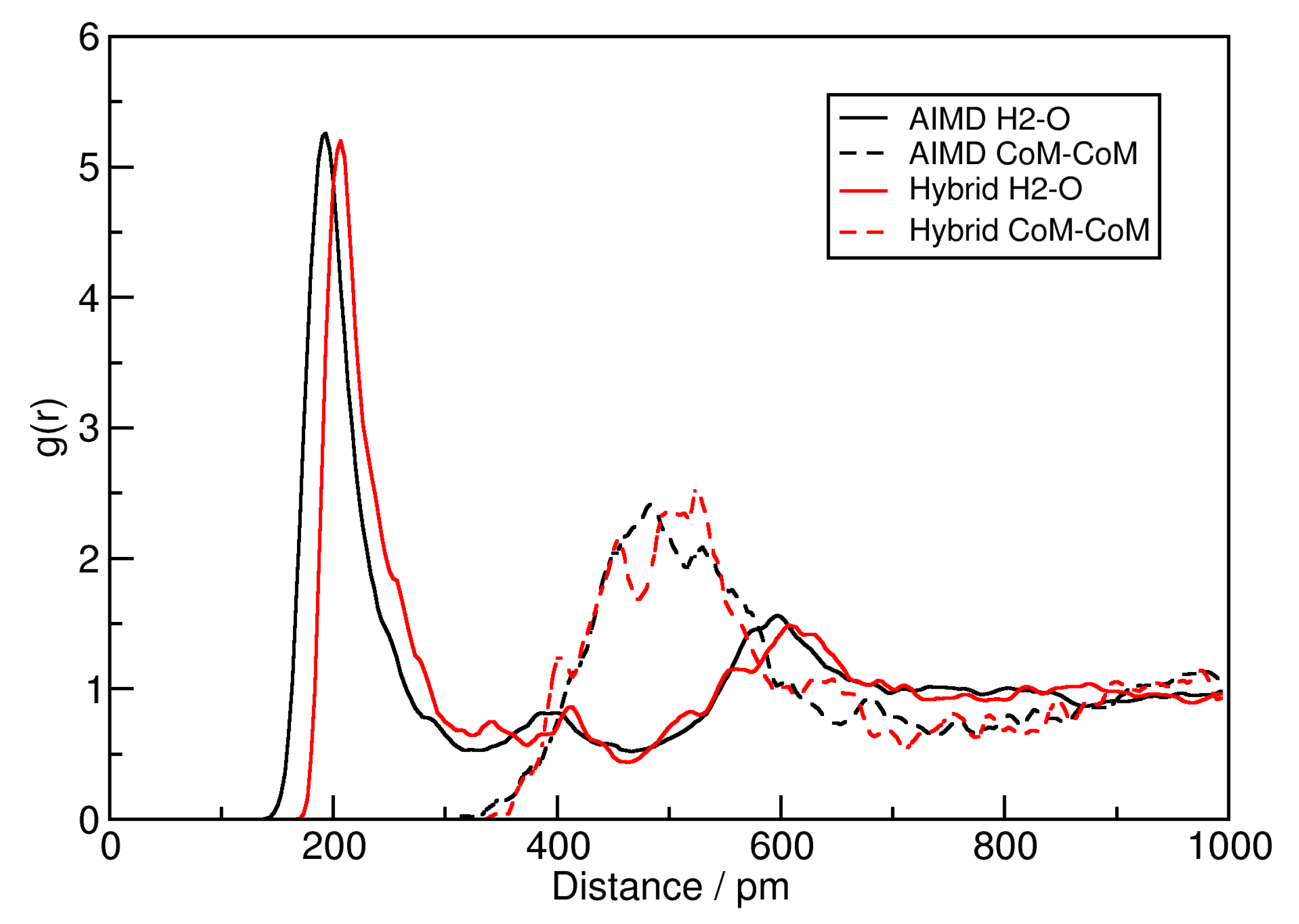
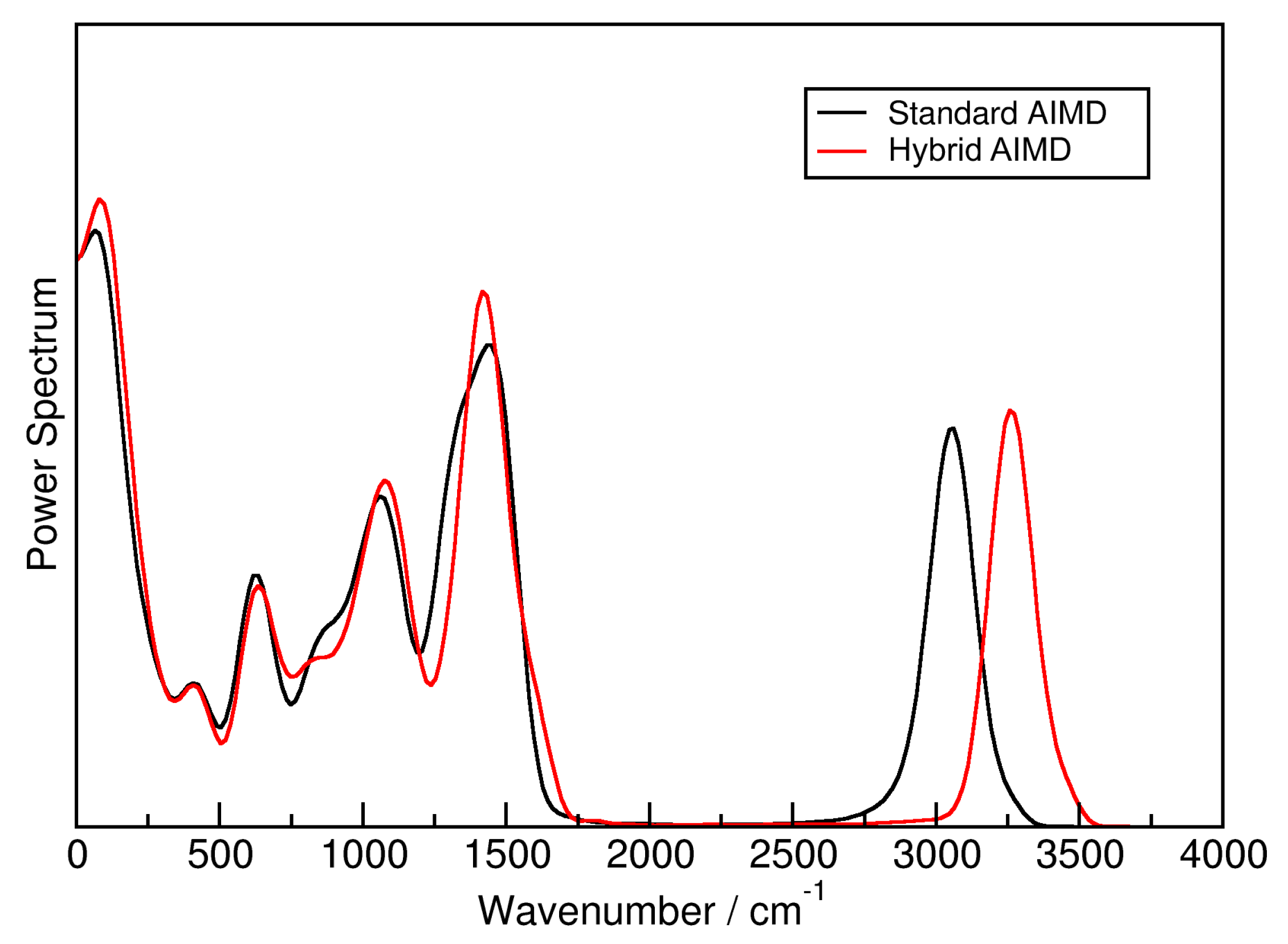
2.1. Hybrid Simulation Approach
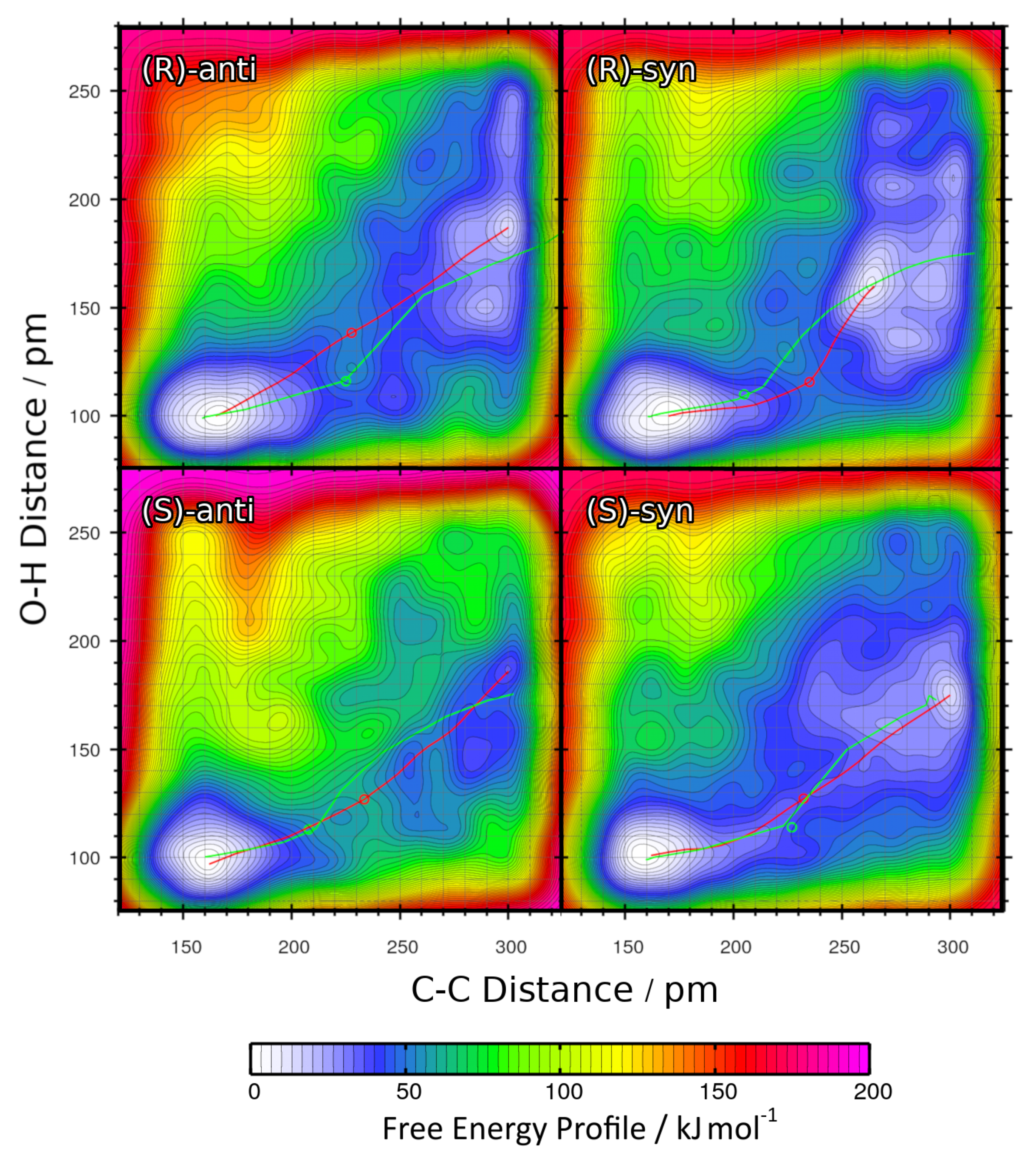
2.2. Static Nudged Elastic Band Calculations
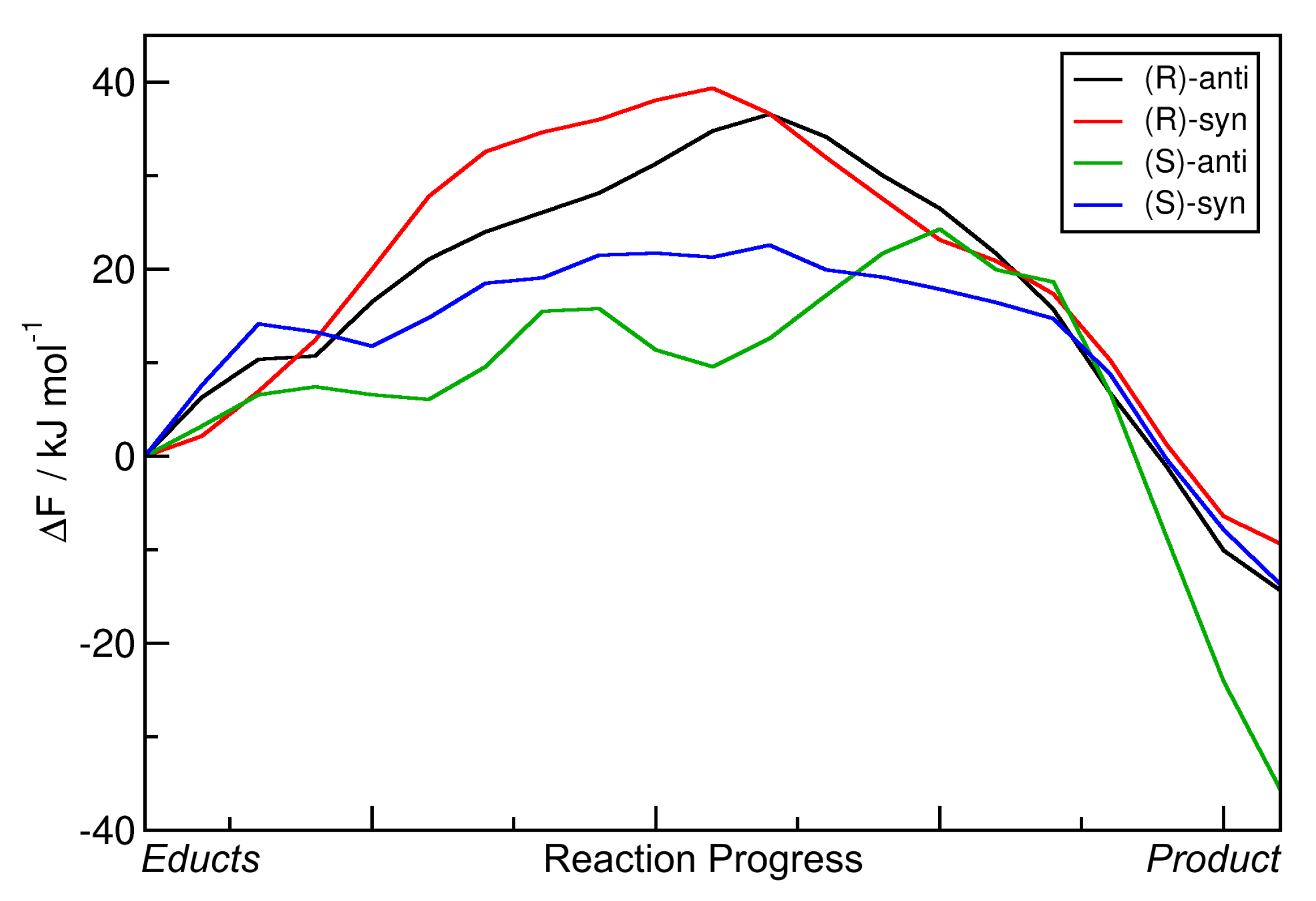
2.3. Metadynamics Simulations in Vacuum
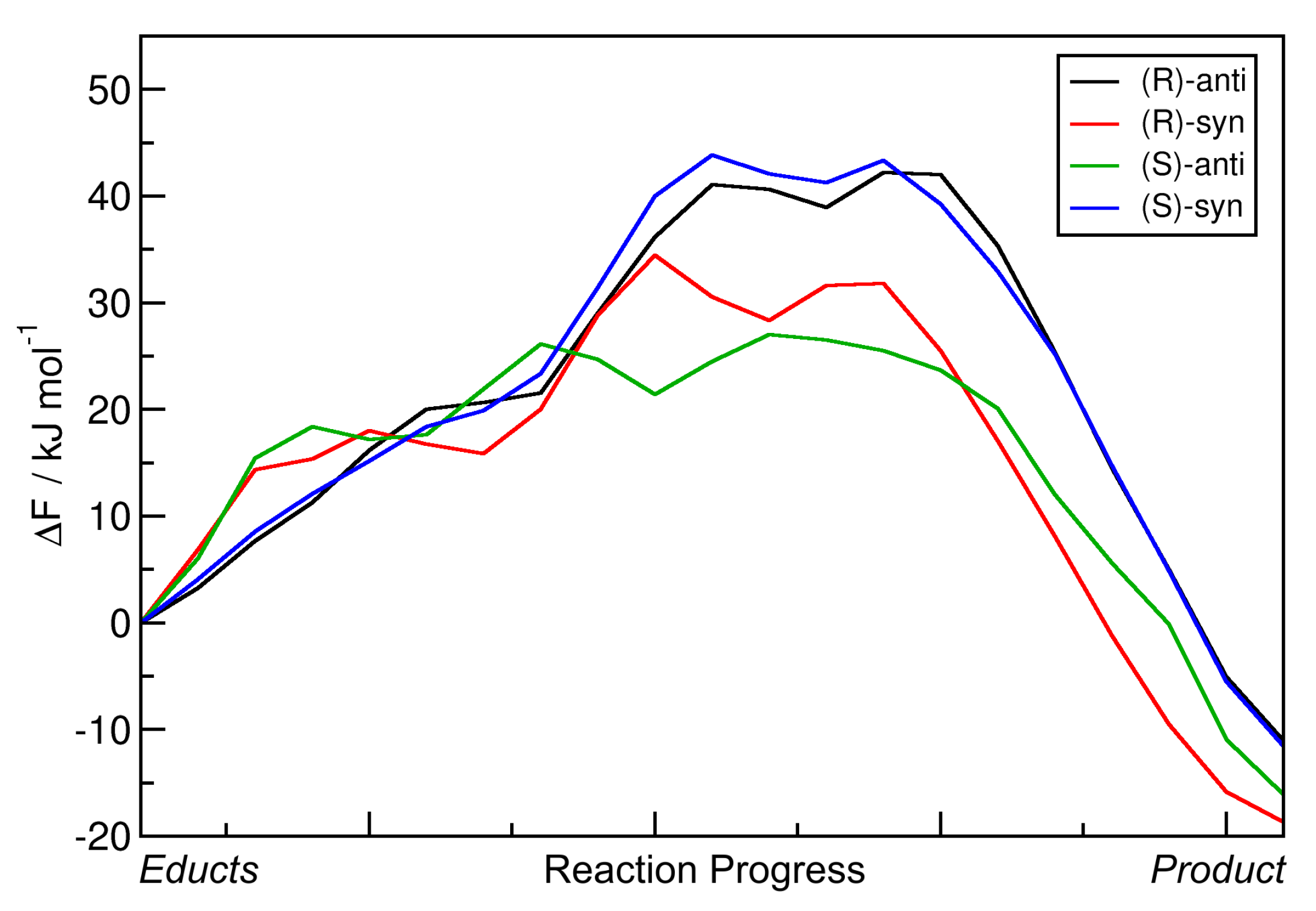
2.4. Metadynamics Simulations in DMF
2.5. Influence of Substituent
3. Methods
3.1. Static Calculations and Nudged Elastic Band
3.2. Force Field Pre-Equilibration
3.3. Ab Initio Molecular Dynamics Simulations
3.4. Hybrid Simulation Approach
3.5. Metadynamics Simulations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AIMD | ab initio molecular dynamics |
| BOMD | Born–Oppenheimer molecular dynamics |
| DFT | Density functional theory |
| DMF | Dimethylformamide |
| %ee | Enantiomeric excess |
| EMIm | 1-Ethyl-3-methylimidazolium cation |
| Et | Ethyl group |
| HyAIMD | The hybrid AIMD approach presented here |
| iPr | Isopropyl group |
| LJ | Lennard-Jones |
| MD | Molecular dynamics |
| NEB | Nudged elastic band |
| OAc | Acetate anion |
| RDF | Radial distribution function |
| RESP | Restraint electrostatic potential |
| SCF | Self-consistent field |
| TS | Transition state |
References
- Stinson, S.C. Chiral Drugs. Chem. Eng. News 2000, 78, 55–78. [Google Scholar] [CrossRef]
- Anastas, P.T.; Kirchhoff, M.M. Origins, Current Status, and Future Challenges of Green Chemistry. Acc. Chem. Res. 2002, 35, 686–694. [Google Scholar] [CrossRef] [PubMed]
- Anastas, P. Green Chemical Syntheses and Processes; American Chemical Society: Washington, DC, USA, 2000. [Google Scholar]
- Clark, J.H.; Luque, R.; Matharu, A.S. Green Chemistry, Biofuels, and Biorefinery. Annu. Rev. Chem. Biomol. Eng. 2012, 3, 183–207. [Google Scholar] [CrossRef] [PubMed]
- Cernansky, R. Chemistry: Green Refill. Nature 2015, 519, 379–380. [Google Scholar] [CrossRef]
- Sanderson, K. Chemistry: It’s Not Easy Being Green. Nature 2011, 469, 18–20. [Google Scholar] [CrossRef]
- Poliakoff, M.; Licence, P. Green Chemistry. Nature 2007, 450, 810–812. [Google Scholar] [CrossRef]
- Clark, J.H. Green Chemistry: Challenges and Opportunities. Green Chem. 1999, 1, 1–8. [Google Scholar] [CrossRef]
- Wasserscheid, P. Ionic Liquids in Synthesis; Wiley VCH Verlag GmbH: Weinheim, Germany, 2007. [Google Scholar]
- List, B. Introduction: Organocatalysis. Chem. Rev. 2007, 107, 5413–5415. [Google Scholar] [CrossRef]
- Dalko, P.I.; Moisan, L. In the Golden Age of Organocatalysis. Angew. Chem. Int. Ed. 2004, 43, 5138–5175. [Google Scholar] [CrossRef]
- Enders, D.; Grondal, C.; Hüttl, M. Asymmetric Organocatalytic Domino Reactions. Angew. Chem. Int. Ed. 2007, 46, 1570–1581. [Google Scholar] [CrossRef]
- Malberg, F.; Brehm, M.; Hollóczki, O.; Pensado, A.S.; Kirchner, B. Understanding the Evaporation of Ionic Liquids using the Example of 1-Ethyl-3-Methylimidazolium Ethylsulfate. Phys. Chem. Chem. Phys. 2013, 15, 18424–18436. [Google Scholar] [CrossRef] [PubMed]
- Hajos, Z.G.; Parrish, D.R. Asymmetric Synthesis of Bicyclic Intermediates of Natural Product Chemistry. J. Org. Chem. 1974, 39, 1615–1621. [Google Scholar] [CrossRef]
- Wieland, P.; Miescher, K. Über Die Herstellung Mehrkerniger Ketone. Helv. Chim. Acta 1950, 33, 2215–2228. [Google Scholar] [CrossRef]
- Woodward, R.B.; Logusch, E.; Nambiar, K.P.; Sakan, K.; Ward, D.E.; Au-Yeung, B.W.; Balaram, P.; Browne, L.J.; Card, P.J.; Chen, C.H. Asymmetric Total Synthesis of Erythromycin. 1. Synthesis of an Erythronolide a Secoacid Derivative via Asymmetric Induction. J. Am. Chem. Soc. 1981, 103, 3210–3213. [Google Scholar] [CrossRef]
- Woodward, R.B.; Au-Yeung, B.W.; Balaram, P.; Browne, L.J.; Ward, D.E.; Au-Yeung, B.W.; Balaram, P.; Browne, L.J.; Card, P.J.; Chen, C.H. Asymmetric Total Synthesis of Erythromycin. 2. Synthesis of an Erythronolide a Lactone System. J. Am. Chem. Soc. 1981, 103, 3213–3215. [Google Scholar] [CrossRef]
- Woodward, R.B.; Logusch, E.; Nambiar, K.P.; Sakan, K.; Ward, D.E.; Au-Yeung, B.W.; Balaram, P.; Browne, L.J.; Card, P.J.; Chen, C.H. Asymmetric Total Synthesis of Erythromycin. 3. Total Synthesis of Erythromycin. J. Am. Chem. Soc. 1981, 103, 3215–3217. [Google Scholar] [CrossRef]
- Borodin, A.V. von Richter, aus St. Petersburg am 17. October 1869. Ber. Dtsch. Chem. Ges. 1869, 2, 552–553. [Google Scholar]
- Wurtz, C.A. Ueber einen Aldehyd-Alkohol. J. Prakt. Chem. 1872, 5, 457–464. [Google Scholar] [CrossRef]
- Wulff, W.D.; Anderson, B.A.; Toole, A.J.; Xu, Y.C. Stereoselective Aldol Addition Reactions of Fischer Carbene Complexes via Electronic Tuning of the Metal Center for Enolate Reactivity. Inorg. Chim. Acta 1994, 220, 215–231. [Google Scholar] [CrossRef]
- Berdoulay, A.; English, R.V.; Nadelstein, B. Effect of Topical 0.02% Tacrolimus Aqueous Suspension on Tear Production in Dogs with Keratoconjunctivitis Sicca. Vet. Ophthalmol. 2005, 8, 225–232. [Google Scholar] [CrossRef]
- Gunasekera, S.P.; Gunasekera, M.; Longley, R.E.; Schulte, G.K. Discodermolide: A New Bioactive Polyhydroxylated Lactone from the Marine Sponge Discodermia Dissoluta. J. Org. Chem. 1990, 55, 4912–4915. [Google Scholar] [CrossRef]
- Khan, N.; Rawlings, B.; Caffrey, P. A Labile Point in Mutant Amphotericin Polyketide Synthases. Biotechnol. Lett. 2011, 33, 1121–1126. [Google Scholar] [CrossRef]
- Schetter, B.; Mahrwald, R. Modern Aldol Methods for the Total Synthesis of Polyketides. Angew. Chem. Int. Ed. 2006, 45, 7506–7525. [Google Scholar] [CrossRef] [PubMed]
- Erol, S.; Dogan, I. Stereochemical assignments of aldol products of 2-arylimino-3-aryl-thiazolidine-4-ones by 1H NMR. Magn. Reson. Chem. 2012, 50, 402–405. [Google Scholar] [CrossRef] [PubMed]
- Giernoth, R.; Bröhl, A.; Brehm, M.; Lingscheid, Y. Interactions in Ionic Liquids probed by in situ NMR Spectroscopy. J. Mol. Liq. 2014, 192, 55–58. [Google Scholar] [CrossRef]
- Thopate, Y.; Singh, R.; Sinha, A.K.; Kumar, V.; Siddiqi, M.I. NMR and DFT Insight into the Synergistic Role of Bovine Serum Albumin–Ionic Liquid for Multicomponent Cascade Aldol/Knoevenagel–thia-Michael/Michael Reactions in One Pot. ChemCatChem 2016, 8, 3050–3056. [Google Scholar] [CrossRef]
- Gaunt, M.J.; Johansson, C.C.; McNally, A.; Vo, N.T. Enantioselective Organocatalysis. Drug Discov. Today 2007, 12, 8–27. [Google Scholar] [CrossRef]
- Eder, U.; Sauer, G.; Wiechert, R. New Type of Asymmetric Cyclization to Optically Active Steroid CD Partial Structures. Angew. Chem. Int. Ed. 1971, 10, 496–497. [Google Scholar] [CrossRef]
- Hajos, Z.G.; Parrish, D.R. Synthesis and Conversion of 2-Methyl-2-(3-Oxobutyl)-1,3-Cyclopentanedione to the Isomeric Racemic Ketols of the [3.2.1]Bicyclooctane and of the Perhydroindane Series. J. Org. Chem. 1974, 39, 1612–1615. [Google Scholar] [CrossRef]
- Dalko, P.I.; Moisan, L. Enantioselective Organocatalysis. Angew. Chem. Int. Ed. 2001, 40, 3726–3748. [Google Scholar] [CrossRef]
- Northrup, A.B.; MacMillan, D.W.C. The First Direct and Enantioselective Cross-Aldol Reaction of Aldehydes. J. Am. Chem. Soc. 2002, 124, 6798–6799. [Google Scholar] [CrossRef]
- List, B. Proline-Catalyzed Asymmetric Reactions. Tetrahedron 2002, 58, 5573–5590. [Google Scholar] [CrossRef]
- Adda, A.; Hadjadj-Aoul, R.; Lebsir, F.; Krallafa, A.M. Ab initio Static and Metadynamics Investigations of the Wittig Reaction. Theor. Chem. Acc. 2018, 137. [Google Scholar] [CrossRef]
- Rufino, V.C.; Pliego, J.R. Is the Iminium Ion Mechanism Viable in the Piperidine-Catalyzed 1,4-Conjugate Addition Reaction of Nitroalkanes to α,β-Unsaturated Ketones? Comput. Theor. Chem. 2019, 1164, 112541. [Google Scholar] [CrossRef]
- Zhang, Q.X.; Li, Y.; Wang, J.; Yang, C.; Liu, C.J.; Li, X.; Cheng, J.P. B(C6F5)3 /Chiral Phosphoric Acid Catalyzed Ketimine–ene Reaction of 2-Aryl-3 H -indol-3-ones and α-Methylstyrenes. Angew. Chem. Int. Ed. 2020, 59, 4550–4556. [Google Scholar] [CrossRef] [PubMed]
- Tummanapelli, A.K.; Vasudevan, S. Dissociation Constants of Weak Acids from ab initio Molecular Dynamics Using Metadynamics: Influence of the Inductive Effect and Hydrogen Bonding on pKa Values. J. Phys. Chem. B 2014, 118, 13651–13657. [Google Scholar] [CrossRef] [PubMed]
- Pliego, J.R. Design of an Organocatalyst for Ion–Molecule SN2 Reactions: A New Solvent Effect on the Reaction Rate Predicted by ab initio Calculations. J. Mol. Catal. A Chem. 2005, 239, 228–234. [Google Scholar] [CrossRef]
- Pliego, J.R., Jr. Regioselective Organocatalysis: A Theoretical Prediction of the Selective Rate Acceleration of the SN2 Reaction between an Acetate Ion and Primary Alkyl Chlorides in DMSO Solution. Org. Biomol. Chem. 2006, 4, 1667. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, J.; Yang, X.; Chen, M.; Xue, Y. Effects of Solvents on the DACBO-Catalyzed Vinylogous Henry Reaction of Isatin with 3,5-Dimethyl-4-nitroisoxazole “on-water” and in Solution from QM/MM MC Simulations. RSC Adv. 2019, 9, 4932–4941. [Google Scholar] [CrossRef]
- Dalessandro, E.V.; Collin, H.P.; Valle, M.S.; Pliego, J.R. Mechanism and Free Energy Profile of Base-Catalyzed Knoevenagel Condensation Reaction. RSC Adv. 2016, 6, 57803–57810. [Google Scholar] [CrossRef]
- Dalessandro, E.V.; Collin, H.P.; Guimarães, L.G.L.; Valle, M.S.; Pliego, J.R. Mechanism of the Piperidine-Catalyzed Knoevenagel Condensation Reaction in Methanol: The Role of Iminium and Enolate Ions. J. Phys. Chem. B 2017, 121, 5300–5307. [Google Scholar] [CrossRef] [PubMed]
- Kalek, M.; Himo, F. Combining Meyer–Schuster Rearrangement with Aldol and Mannich Reactions: Theoretical Study of the Intermediate Interception Strategy. J. Am. Chem. Soc. 2012, 134, 19159–19169. [Google Scholar] [CrossRef] [PubMed]
- Zeindlhofer, V.; Hudson, P.; Pálvölgyi, Á.M.; Welsch, M.; Almarashi, M.; Woodcock, H.L.; Brooks, B.; Bica-Schröder, K.; Schröder, C. Enantiomerization of Axially Chiral Biphenyls: Polarizable MD Simulations in Water and Butylmethylether. Int. J. Mol. Sci. 2020, 21, 6222. [Google Scholar] [CrossRef] [PubMed]
- Ribas-Arino, J.; Carvajal, M.A.; Chaumont, A.; Masia, M. Unraveling the Role of Water in the Stereoselective Step of Aqueous Proline-Catalyzed Aldol Reactions. Chem. Eur. J 2012, 18, 15868–15874. [Google Scholar] [CrossRef]
- Hubin, P.O.; Jacquemin, D.; Leherte, L.; Vercauteren, D.P. Accessing the Free Energy Profile of a Ring Closure in a Proline-Catalyzed Reaction Using a Reactive Force Field. Theor. Chem. Acc. 2015, 135. [Google Scholar] [CrossRef]
- Cukrowski, I.; Dhimba, G.; Riley, D.L. A Reaction Energy Profile and Fragment Attributed Molecular System Energy Change (FAMSEC)-Based Protocol Designed to Uncover Reaction Mechanisms: A Case Study of the Proline-Catalysed Aldol Reaction. Phys. Chem. Chem. Phys. 2019, 21, 16694–16705. [Google Scholar] [CrossRef] [PubMed]
- Pusch, S.; Tröster, A.; Lefrancois, D.; Farahani, P.; Dreuw, A.; Bach, T.; Opatz, T. Mechanism and cis/trans Selectivity of Vinylogous Nazarov-type [6π] Photocyclizations. J. Org. Chem. 2018, 83, 964–972. [Google Scholar] [CrossRef]
- Leverenz, M.; Merten, C.; Dreuw, A.; Bach, T. Lewis Acid Catalyzed Enantioselective Photochemical Rearrangements on the Singlet Potential Energy Surface. J. Am. Chem. Soc. 2019, 141, 20053–20057. [Google Scholar] [CrossRef]
- Yang, X.; Hoffmann, M.; Rominger, F.; Kirschbaum, T.; Dreuw, A.; Mastalerz, M. Functionalized Contorted Polycyclic Aromatic Hydrocarbons by a One-Step Cyclopentannulation and Regioselective Triflyloxylation. Angew. Chem. Int. Ed. 2019, 58, 10650–10654. [Google Scholar] [CrossRef]
- Stark, A.; Brehm, M.; Brüssel, M.; Lehmann, S.B.C.; Pensado, A.S.; Schöppke, M.; Kirchner, B. A Theoretical and Experimental Chemist’s Joint View on Hydrogen Bonding in Ionic Liquids and Their Binary Mixtures. Top. Curr. Chem. 2014, 351, 149–187. [Google Scholar] [CrossRef]
- Scarbath-Evers, L.K.; Jähnigen, S.; Elgabarty, H.; Song, C.; Narikawa, R.; Matysik, J.; Sebastiani, D. Structural heterogeneity in a parent ground-state structure of AnPixJg2 revealed by theory and spectroscopy. Phys. Chem. Chem. Phys. 2017, 19, 13882–13894. [Google Scholar] [CrossRef] [PubMed]
- Pylaeva, S.; Böker, A.; Elgabarty, H.; Paul, W.; Sebastiani, D. The Conformational Ensemble of Polyglutamine-14 Chains: Specific Influences of Solubility Tail and Chromophores. ChemPhysChem 2018, 19, 2931–2937. [Google Scholar] [CrossRef] [PubMed]
- Laio, A.; Parrinello, M. Escaping Free-Energy Minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Cordero, B.; Gómez, V.; Platero-Prats, A.E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent Radii Revisited. Dalton Trans. 2008, 21, 2832–2838. [Google Scholar] [CrossRef] [PubMed]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; Vandevondele, J. CP2k: Atomistic Simulations of Condensed Matter Systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An Electronic Structure and Molecular Dynamics Software Package—Quickstep: Efficient and Accurate Electronic Structure Calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef]
- Brehm, M.; Weber, H.; Pensado, A.S.; Stark, A.; Kirchner, B. Proton transfer and polarity changes in ionic liquid-water mixtures: A perspective on hydrogen bonds from ab initio molecular dynamics at the example of 1-ethyl-3-methylimidazolium acetate-water mixtures-Part 1. Phys. Chem. Chem. Phys. 2012, 14, 5030–5044. [Google Scholar] [CrossRef]
- Brehm, M.; Weber, H.; Pensado, A.S.; Stark, A.; Kirchner, B. Liquid Structure and Cluster Formation in Ionic Liquid/Water Mixtures—An Extensive ab initio Molecular Dynamics Study on 1-Ethyl-3-Methylimidazolium Acetate/Water Mixtures—Part 2. Z. Phys. Chem. 2013, 227, 177–204. [Google Scholar] [CrossRef]
- Brehm, M.; Sebastiani, D. Simulating Structure and Dynamics in Small Droplets of 1-Ethyl-3-Methylimidazolium Acetate. J. Chem. Phys. 2018, 148, 193802. [Google Scholar] [CrossRef]
- Ranaghan, K.E.; Morris, W.G.; Masgrau, L.; Senthilkumar, K.; Johannissen, L.O.; Scrutton, N.S.; Harvey, J.N.; Manby, F.R.; Mulholland, A.J. Ab Initio QM/MM Modeling of the Rate-Limiting Proton Transfer Step in the Deamination of Tryptamine by Aromatic Amine Dehydrogenase. J. Phys. Chem. B 2017, 121, 9785–9798. [Google Scholar] [CrossRef]
- Vázquez-Montelongo, E.A.; Vázquez-Cervantes, J.E.; Cisneros, G.A. Polarizable ab initio QM/MM Study of the Reaction Mechanism of N-tert-Butyloxycarbonylation of Aniline in [EMIm][BF4]. Molecules 2018, 23. [Google Scholar] [CrossRef] [PubMed]
- Ambrosio, F.; Pasquarello, A. Reactivity and energy level of a localized hole in liquid water. Phys. Chem. Chem. Phys. 2018, 20, 30281–30289. [Google Scholar] [CrossRef] [PubMed]
- Dopilka, A.; Peng, X.; Chan, C.K. Ab Initio Investigation of Li and Na Migration in Guest-Free, Type I Clathrates. J. Phys. Chem. C 2019, 123, 22812–22822. [Google Scholar] [CrossRef]
- Krylow, S.; Garcia, M.E. Ab initio study of temperature- and laser-induced phase transitions in TiO2. Phys. Rev. B 2019, 100, 224101. [Google Scholar] [CrossRef]
- Buchwald, J.; Hennes, M. Adsorption and diffusion of Au, Pt, and Co adatoms on SrTiO3(001) surfaces: A density functional theory study. Surf. Sci. 2020, 701, 121683. [Google Scholar] [CrossRef]
- Grace, (c) 1996–2008 Grace Development Team. Available online: http://plasma-gate.weizmann.ac.il/Grace (accessed on 10 October 2020).
- Williams, T.; Kelley, C. Gnuplot 4.6: An Interactive Plotting Program. 2013. Available online: http://gnuplot.sourceforge.net/ (accessed on 10 October 2020).
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Gr. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Stone, J. An Efficient Library for Parallel Ray Tracing and Animation. Master’s Thesis, Computer Science Department, University of Missouri-Rolla, Rolla, MO, USA, 1998. [Google Scholar]
- Brehm, M.; Kirchner, B. TRAVIS—A free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories. J. Chem. Inf. Model. 2011, 51, 2007–2023. [Google Scholar] [CrossRef]
- Brehm, M.; Thomas, M.; Gehrke, S.; Kirchner, B. TRAVIS—A free analyzer for trajectories from molecular simulation. J. Chem. Phys. 2020, 152, 164105. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, S. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A Well-Behaved Electrostatic Potential Based Method using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Golze, D.; Hutter, J.; Iannuzzi, M. Wetting of Water on Hexagonal Boron Nitride@Rh(111): A QM/MM Model Based on Atomic Charges Derived for Nano-Structured Substrates. Phys. Chem. Chem. Phys. 2015, 17, 14307–14316. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Vandevondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and Accurate Density Functional Calculations Using a Mixed Gaussian and Plane Waves Approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Vandevondele, J.; Hutter, J. An Efficient Orbital Transformation Method for Electronic Structure Calculations. J. Chem. Phys. 2003, 118, 4365–4369. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. B 1964, 136, 864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L. Self-Consistent Equations Including Exchange and Correlation Effect. Phys. Rev. 1965, 140, 1133. [Google Scholar] [CrossRef]
- Becke, A. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R. Development of the Colle-Salvetti Correlation Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Smith, D.G.A.; Burns, L.A.; Patkowski, K.; Sherrill, C.D. Revised Damping Parameters for the D3 Dispersion Correction to Density Functional Theory. J. Phys. Chem. Lett. 2016, 7, 2197–2203. [Google Scholar] [CrossRef]
- Vandevondele, J.; Hutter, J. Gaussian Basis Sets for Accurate Calculations on Molecular Systems in Gas and Condensed Phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef]
- Goedecker, S.; Teter, M.; Hutter, J. Separable Dual-Space Gaussian Pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic Separable Dual-Space Gaussian Pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef]
- Nose, S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Nose, S. A Molecular Dynamics Method for Simulations in the Canonical Ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Martyna, G.; Klein, M.; Tuckerman, M. Nosé–Hoover Chains: The Canonical Ensemble via Continuous Dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
- Iannuzzi, M.; Laio, A.; Parrinello, M. Efficient Exploration of Reactive Potential Energy Surfaces Using Car–Parrinello Molecular Dynamics. Phys. Rev. Lett. 2003, 90, 238302. [Google Scholar] [CrossRef]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef]
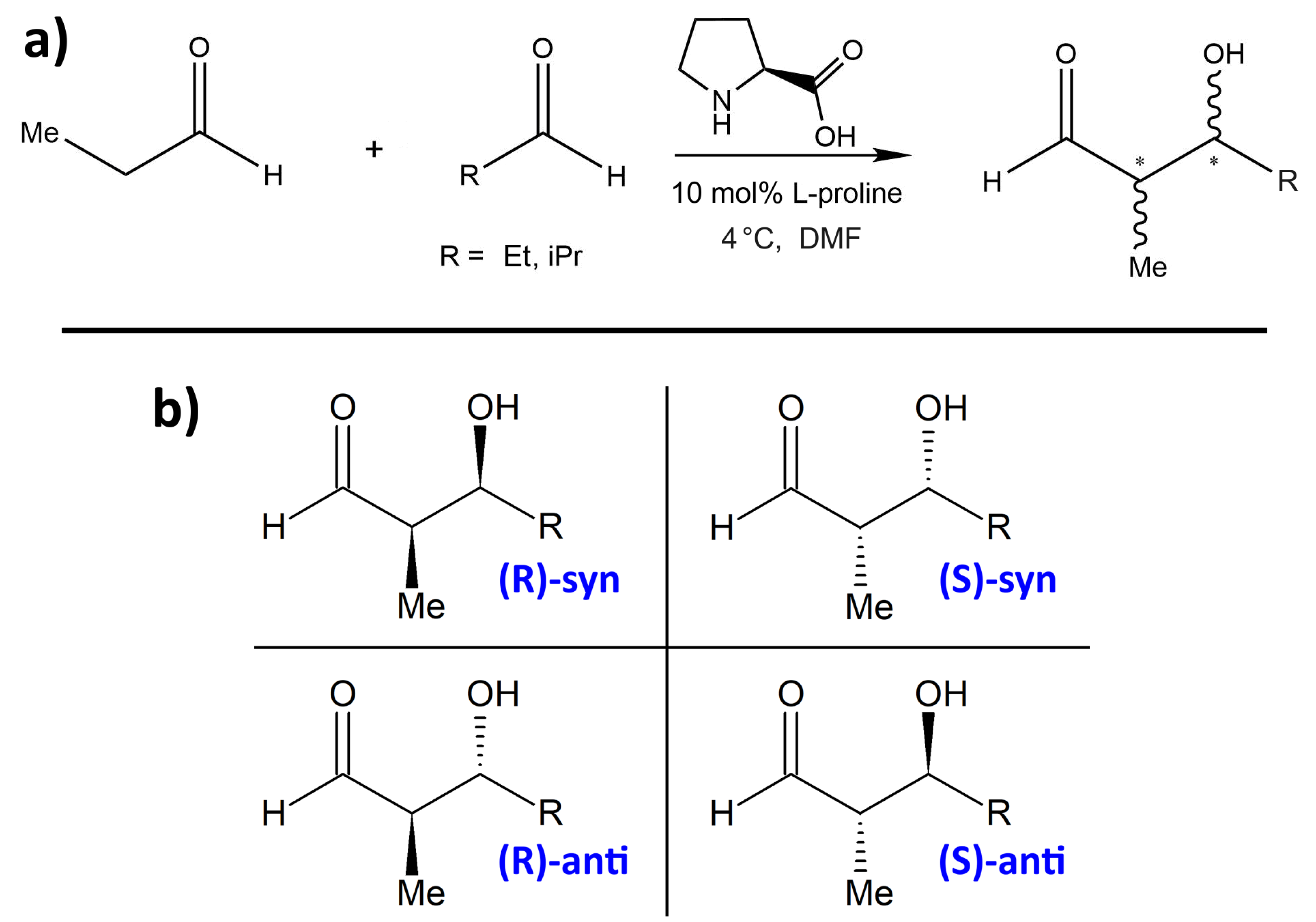
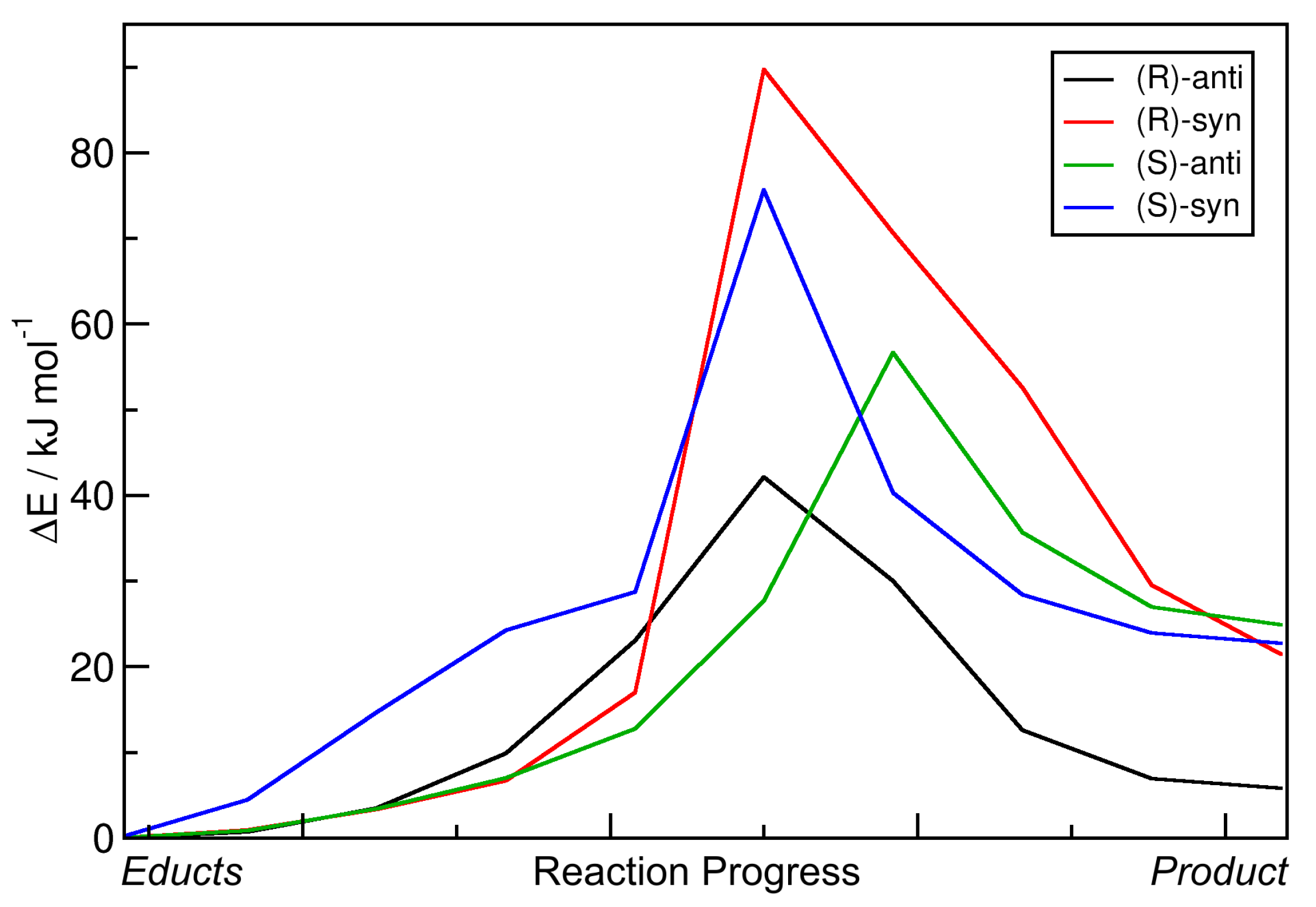
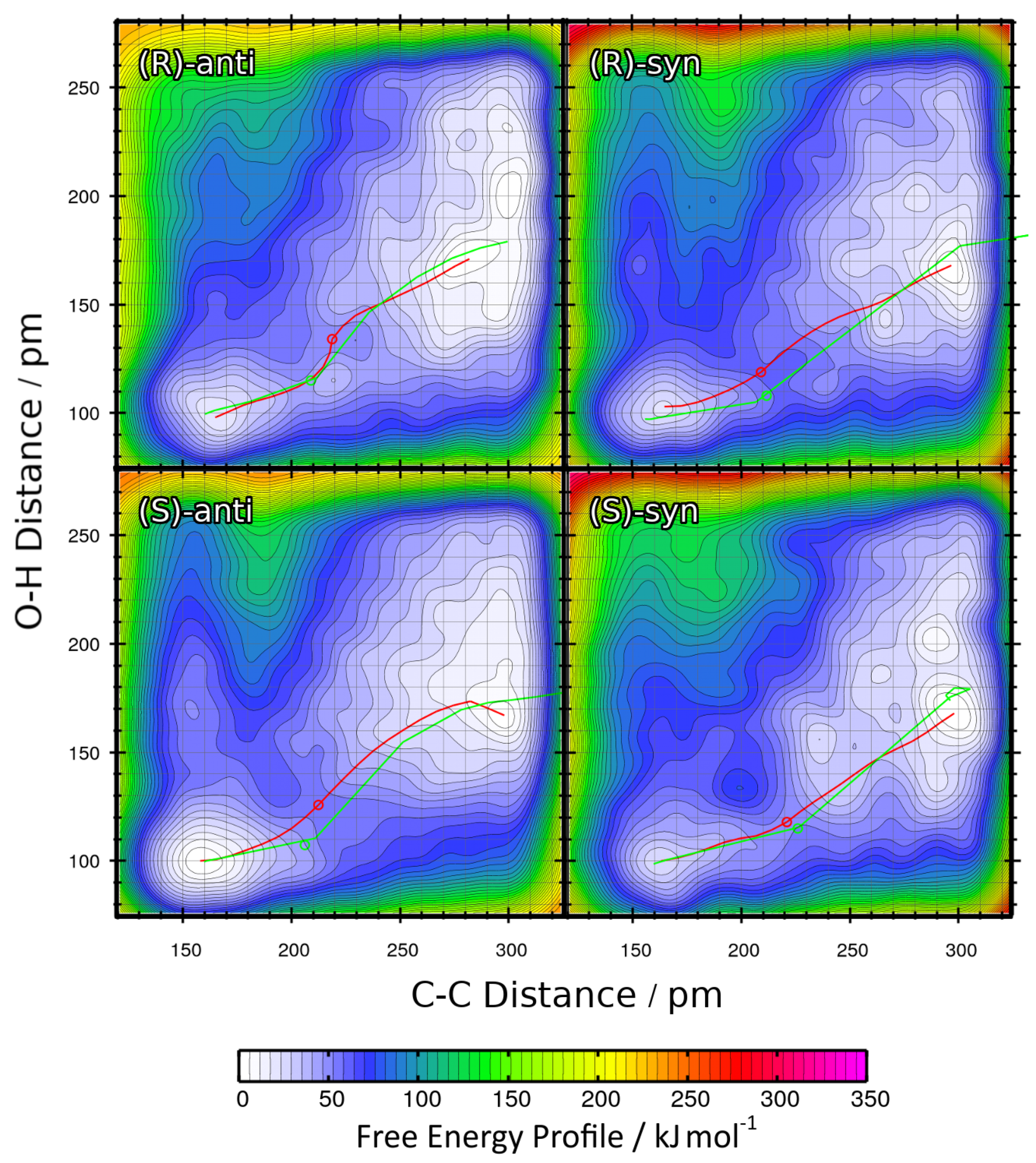
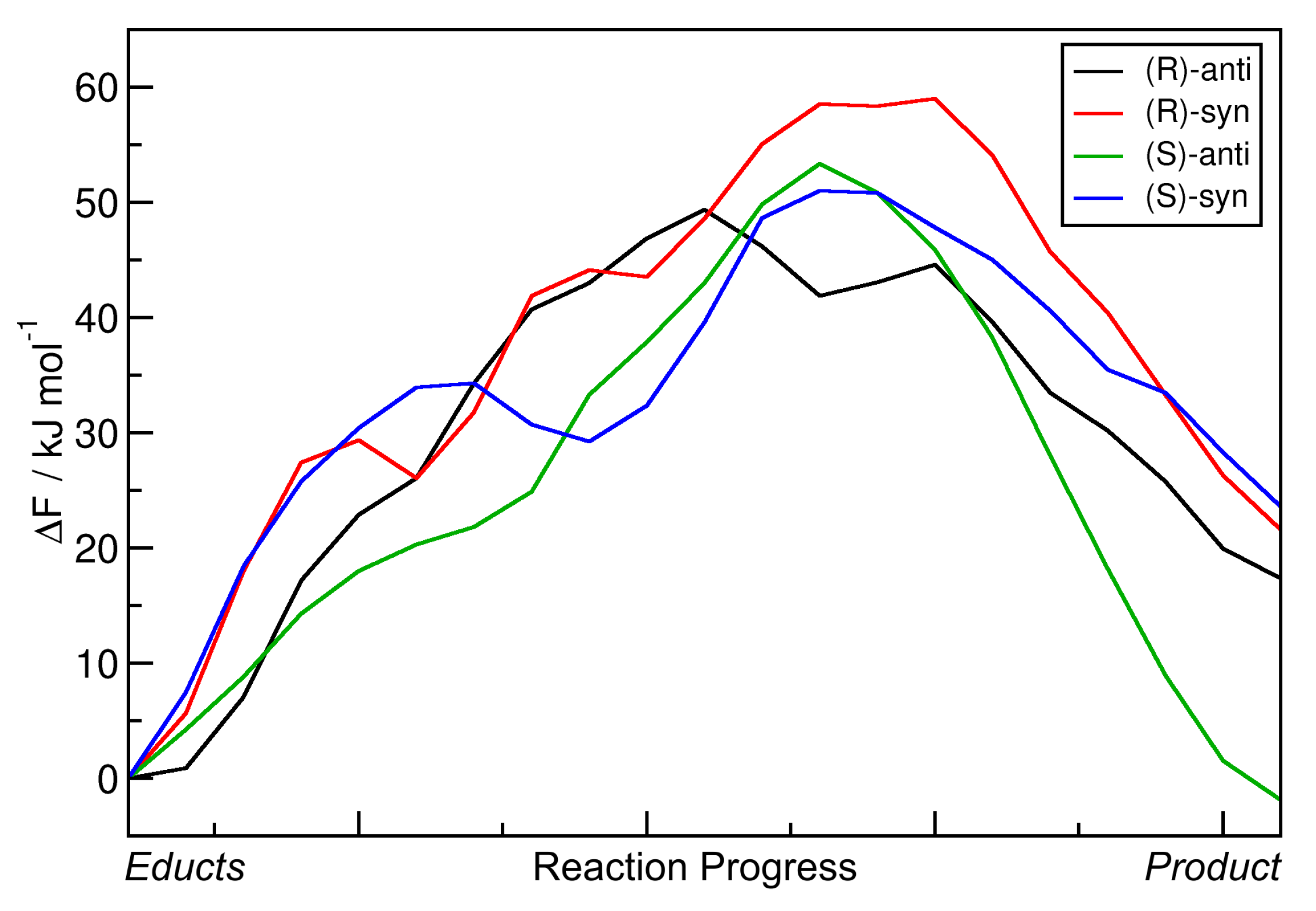
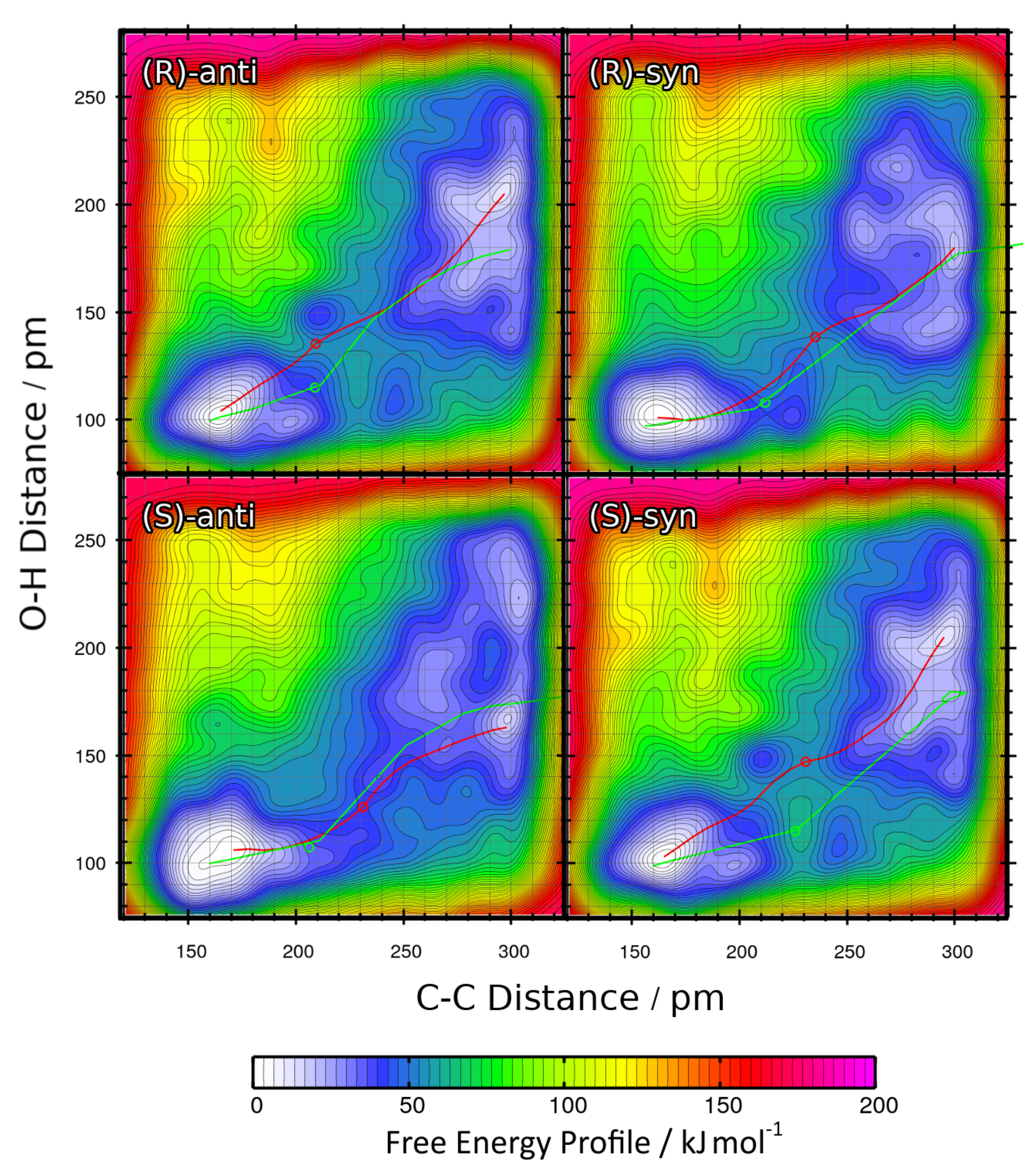
| R | %ee | syn:anti | Yield/% |
|---|---|---|---|
| Et | 99 | 1 : 4 | 80 |
| iPr | >99 | 1 : 24 | 82 |
| Product | E/J mol | G/kJ mol | E/kJ mol | G/kJ mol |
|---|---|---|---|---|
| (R)-anti | 5.86 | 23.77 | 40.79 | 44.78 |
| (R)-syn | 21.50 | 39.60 | 78.22 | 88.63 |
| (S)-anti | 24.89 | 43.23 | 51.63 | 62.91 |
| (S)-syn | 22.74 | 36.28 | 75.67 | 90.88 |
| Product | F/kJ mol | F/kJ mol |
|---|---|---|
| (R)-anti | 17.33 | 49.38 |
| (R)-syn | 21.56 | 59.01 |
| (S)-anti | −1.90 | 53.36 |
| (S)-syn | 23.59 | 50.99 |
| Product | F/kJ mol | F/kJ mol |
|---|---|---|
| (R)-anti | −11.06 | 42.24 |
| (R)-syn | −18.66 | 31.79 |
| (S)-anti | −17.71 | 25.40 |
| (S)-syn | −11.52 | 43.84 |
| Product | F/kJ mol | F/kJ mol |
|---|---|---|
| (R)-anti | −14.33 | 36.54 |
| (R)-syn | −9.35 | 39.35 |
| (S)-anti | −35.63 | 24.29 |
| (S)-syn | −13.70 | 22.59 |
Sample Availability: Samples of the compounds are not available from the authors. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weiß, M.; Brehm, M. Exploring Free Energy Profiles of Enantioselective Organocatalytic Aldol Reactions under Full Solvent Influence. Molecules 2020, 25, 5861. https://doi.org/10.3390/molecules25245861
Weiß M, Brehm M. Exploring Free Energy Profiles of Enantioselective Organocatalytic Aldol Reactions under Full Solvent Influence. Molecules. 2020; 25(24):5861. https://doi.org/10.3390/molecules25245861
Chicago/Turabian StyleWeiß, Moritz, and Martin Brehm. 2020. "Exploring Free Energy Profiles of Enantioselective Organocatalytic Aldol Reactions under Full Solvent Influence" Molecules 25, no. 24: 5861. https://doi.org/10.3390/molecules25245861
APA StyleWeiß, M., & Brehm, M. (2020). Exploring Free Energy Profiles of Enantioselective Organocatalytic Aldol Reactions under Full Solvent Influence. Molecules, 25(24), 5861. https://doi.org/10.3390/molecules25245861







