Vibrational Properties and DFT Calculations of Perovskite-Type Methylhydrazinium Manganese Hypophosphite
Abstract
1. Introduction
2. Experimental Section
2.1. Synthesis of Single Crystals
2.2. Materials and Methods
2.3. Computational Details
3. Results and Discussion
3.1. Structure
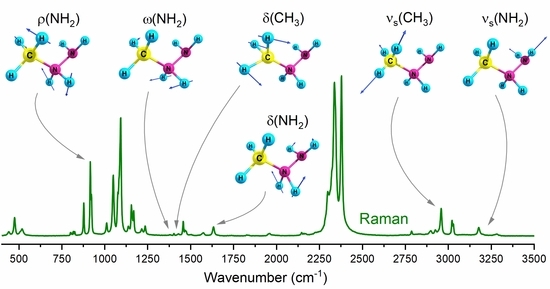
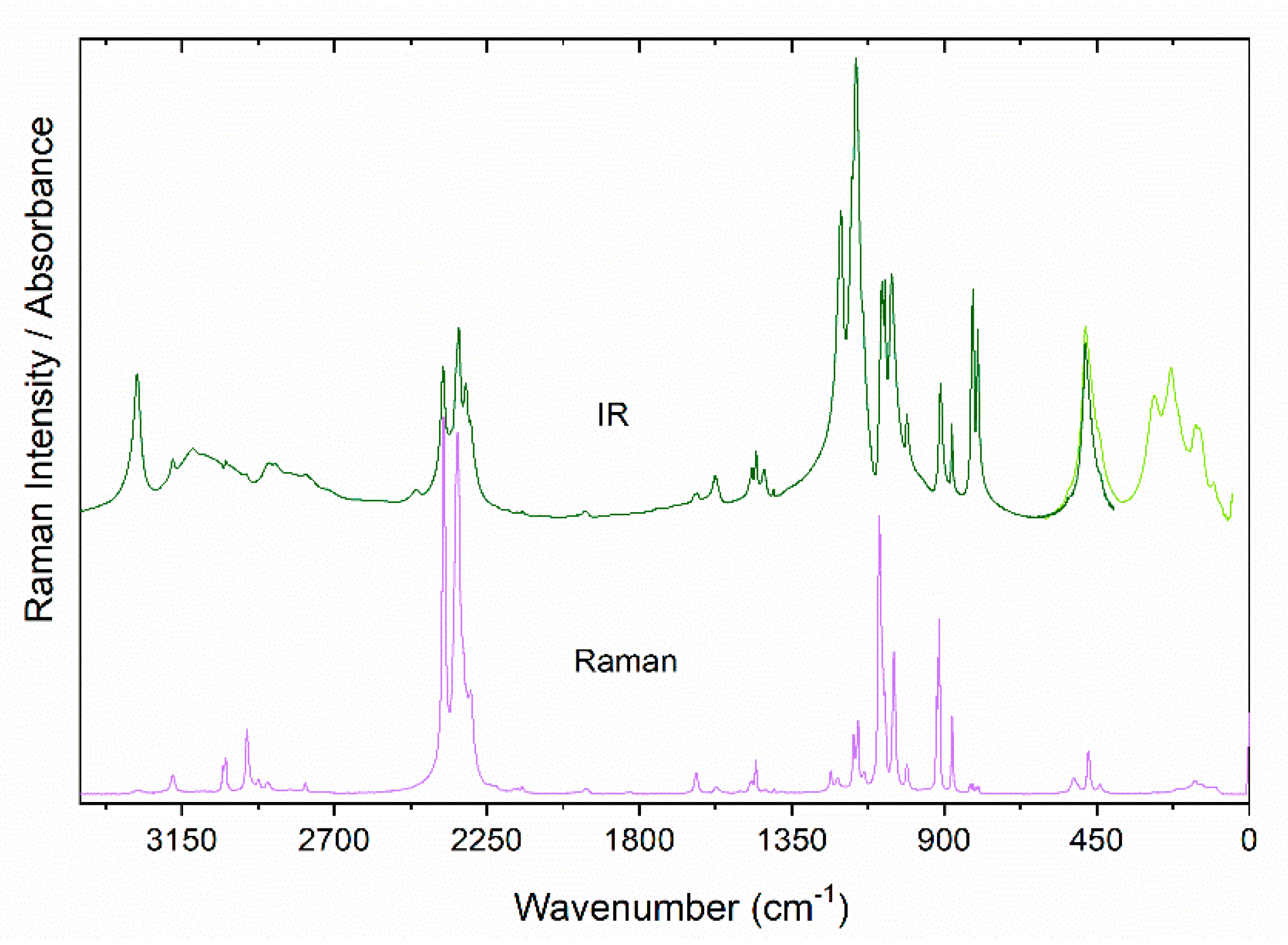
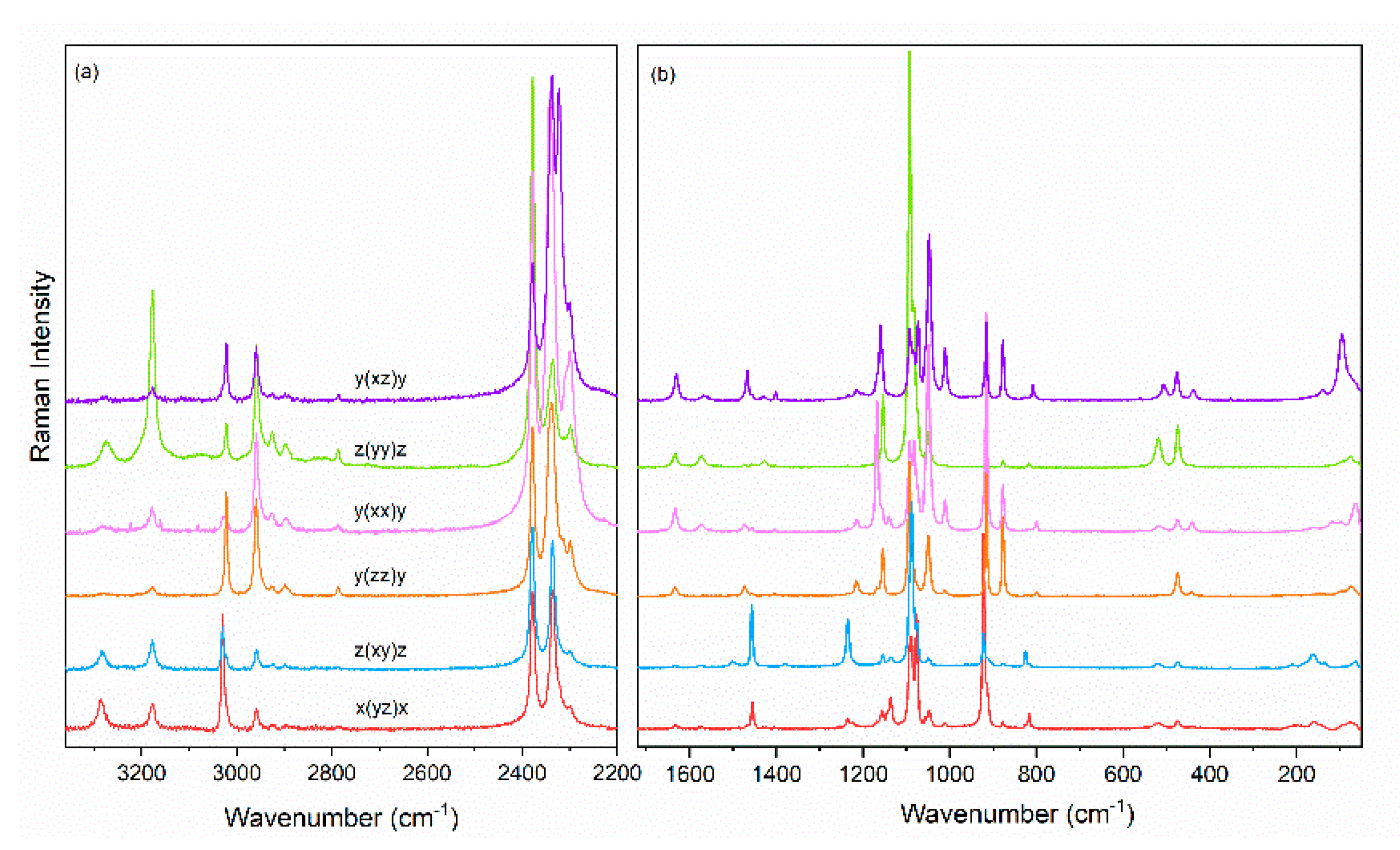
3.2. Vibrational Properties
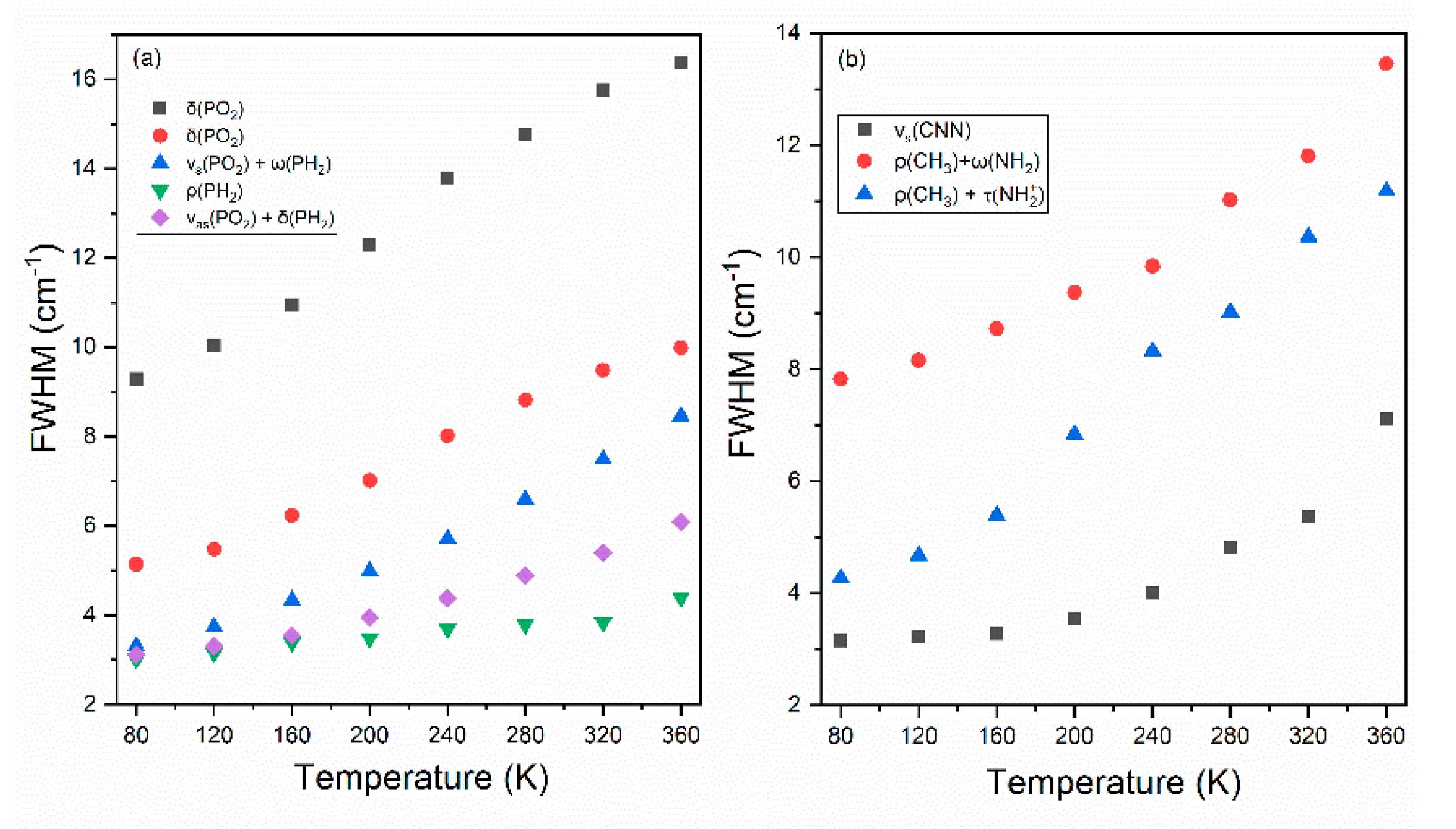
3.3. Temperature Dependence of Raman Modes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Wang, F.; Cao, Y.; Chen, C.; Chen, Q.; Wu, X.; Li, X.; Qin, T.; Huang, W. Materials Toward the Upscaling of Perovskite Solar Cells: Progress, Challenges, and Strategies. Adv. Funct. Mater. 2018, 28, 1803753. [Google Scholar] [CrossRef]
- Zhao, X.; Ng, J.D.A.; Friend, R.H.; Tan, Z.-K. Opportunities and Challenges in Perovskite Light-Emitting Devices. ACS Photonics 2018, 5, 3866–3875. [Google Scholar] [CrossRef]
- Mączka, M.; Ptak, M.; Gągor, A.; Stefańska, D.; Sieradzki, A. Layered Lead Iodide of [Methylhydrazinium]2PbI4 with a Reduced Band Gap: Thermochromic Luminescence and Switchable Dielectric Properties Triggered by Structural Phase Transitions. Chem. Mater. 2019, 31, 8563–8575. [Google Scholar] [CrossRef]
- Mączka, M.; Stefańska, D.; Zaręba, J.K.; Nyk, M.; Sieradzki, A. Temperature-dependent luminescence and second-harmonic generation of perovskite-type manganese and cadmium dicyanamide frameworks templated by tetrapropylammonium cations. J. Alloys Compd. 2020, 821, 153464. [Google Scholar] [CrossRef]
- Mączka, M.; Gągor, A.; Pikul, A.; Stefańska, D. Novel hypophosphite hybrid perovskites of [CH3NH2NH2][Mn(H2POO)3] and [CH3NH2NH2][Mn(H2POO)2.83(HCOO)0.17] exhibiting antiferromagnetic order and red photoluminescence. RSC Adv. 2020, 10, 19020–19026. [Google Scholar] [CrossRef]
- Jain, P.; Ramachandran, V.; Clark, R.J.; Zhou, H.D.; Toby, B.H.; Dalal, N.S.; Kroto, H.W.; Cheetham, A.K. Multiferroic behavior associated with an order-disorder hydrogen bonding transition in metal-organic frameworks (MOFs) with the perovskite ABX3 architecture. J. Am. Chem. Soc. 2009, 131, 13625–13627. [Google Scholar] [CrossRef]
- Tian, Y.; Stroppa, A.; Chai, Y.; Yan, L.; Wang, S.; Barone, P.; Picozzi, S.; Sun, Y. Cross coupling between electric and magnetic orders in a multiferroic metal-organic framework. Sci. Rep. 2015, 4, 6062. [Google Scholar] [CrossRef]
- Mączka, M.; Gągor, A.; Ptak, M.; Paraguassu, W.; Da Silva, T.A.; Sieradzki, A.; Pikul, A. Phase transitions and coexistence of magnetic and electric orders in the methylhydrazinium metal formate frameworks. Chem. Mater. 2017, 29, 2264–2275. [Google Scholar] [CrossRef]
- Bermúdez-Garcia, J.M.; Sánchez-Andújar, M.; Castro-García, S.; López-Beceiro, J.; Artiaga, R.; Señarís-Rodríguez, M.A. Giant barocaloric effect in the ferroic organic-inorganic hybrid [TPrA][Mn(dca)3] perovskite under easily accessible pressures. Nat. Commun. 2017, 8, 15715. [Google Scholar] [CrossRef]
- Mączka, M.; Gągor, A.; Ptak, M.; Stefańska, D.; Macalik, L.; Pikul, A.; Sieradzki, A. Structural, phonon, magnetic and optical properties of novel perovskite-like frameworks of TriBuMe[M(dca)3] (TriBuMe = tributylmethylammonium; dca=dicyanamide; M=Mn2+, Fe2+, Co2+, Ni2+). Dalton Trans. 2019, 48, 13006–13016. [Google Scholar] [CrossRef]
- Geng, F.-J.; Zhou, L.; Shi, P.-P.; Wang, X.-L.; Zheng, X.; Zhang, Y.; Fu, D.-W.; Ye, Q. Perovskite-type organic–inorganic hybrid NLO switches tuned by guest cations. J. Mater. Chem. C 2017, 5, 1529–1536. [Google Scholar] [CrossRef]
- Mączka, M.; Ptak, M.; Gągor, A.; Stefańska, D.; Zaręba, J.K.; Sieradzki, A. Methylhydrazinium Lead Bromide: Noncentrosymmetric Three-Dimensional Perovskite with Exceptionally Large Framework Distortion and Green Photoluminescence. Chem. Mater. 2020, 32, 1667–1673. [Google Scholar] [CrossRef]
- Mączka, M.; Gągor, A.; Zaręba, J.K.; Stefańska, D.; Drozd, M.; Balciunas, S.; Šimenas, M.; Banys, J.; Sieradzki, A. Three-Dimensional Perovskite Methylhydrazinium Lead Chloride with Two Polar Phases and Unusual Second-Harmonic Generation Bistability above Room Temperature. Chem. Mater. 2020, 32, 4072–4082. [Google Scholar] [CrossRef]
- Mączka, M.; Collings, I.E.; Furtado Leite, F.; Paraguassu, W. Raman and single-crystal X-ray diffraction evidence of pressure-induced phase transitions in a perovskite-like framework of [(C3H7)4N][Mn(N(CN)2)3]. Dalton Trans. 2019, 48, 9072–9078. [Google Scholar] [CrossRef]
- Mączka, M.; Ptak, M.; Gągor, A.; Sieradzki, A.; Peksa, P.; Usevicius, G.; Simenas, M.; Leite, F.F.; Paraguassu, W. Temperature- and pressure-dependent studies of a highly flexible and compressible perovskite-like cadmium dicyanamide framework templated with protonated tetrapropylamine. J. Mater. Chem. C 2019, 7, 2408–2420. [Google Scholar] [CrossRef]
- Wu, Y.; Shaker, S.; Brivio, F.; Murugavel, R.; Bristowe, P.D.; Cheetham, A.K. [Am]Mn(H2POO)3: A new family of hybrid perovskites based on the hypophosphite ligand. J. Am. Chem. Soc. 2017, 139, 16999–17002. [Google Scholar] [CrossRef]
- Gao, H.-Q.; Wei, W.-J.; Tan, Y.-H.; Tan, Y.-Z. Phase Transition and negative Thermal Expansion in Guanidinium Magnesium-Hypophosphite Hybrid Perovskite. Chem. Mater. 2020, 32, 6886–6891. [Google Scholar] [CrossRef]
- Wu, Y.; Halat, D.M.; Wei, F.; Binford, T.; Seymour, I.D.; Gaultois, M.W.; Shaker, S.; Wang, J.; Grey, C.P.; Cheetham, A.K. Mixed X-site formate–hypophosphite hybrid perovskites. Chem. A Eur. J. 2018, 24, 11309–11313. [Google Scholar] [CrossRef]
- Wu, Y.; Binford, T.; Hill, J.A.; Shaker, S.; Wang, J.; Cheetham, A.K. Hypophosphite hybrid perovskites: A platform for unconventional tilts and shifts. Chem. Commun. 2018, 54, 3751–3754. [Google Scholar] [CrossRef]
- Ptak, M.; Mączka, M. Phonon properties and mechanism of order-disorder phase transition in formamidinium manganese hypophosphite single crystal. Spectrochim. Acta A 2020, 230, 118010. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03, Revision A.1; Gaussian, Inc.: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Becke, D. Density-functional thermochemistry. IV. A new dynamical correlation functional and implications for exact-exchange mixing. J. Chem. Phys. 1996, 104, 1040–1046. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Zhurko, G.A.; Zhurko, D.A. Chemcraft Graphical Program of Visualization of Computed Results. Available online: http://chemcraftprog.com (accessed on 6 July 2020).
- Rostkowska, H.; Lapinski, L.; Nowak, M.J. Analysis of the normal modes of molecules with D3h symmetry Infrared spectra of monomeric s-triazine and cyanuric acid. Vib. Spectrosc. 2009, 49, 43–51. [Google Scholar] [CrossRef]
- Tabacik, V.; Abenoza, M. Quasi general harmonic force field and mode anharmonicity of the hypophosphite ion normal vibrations. J. Mol. Struct. 1975, 27, 369–381. [Google Scholar] [CrossRef]
- Tsuboi, M. Vibrational Spectra of Phosphite and hypophosphite anions, and the characteristic frequencies of PO3− and PO2− groups. J. Am. Chem. Soc. 1957, 79, 1351–1354. [Google Scholar] [CrossRef]
- Liu, R.; Moody, P.R.; Vanburen, A.S.; Clark, J.A.; Crauser, J.A.; Tate, D.R. On assignemnt of fundametal vibrational modes of hypophosphite anion and its deuterated analogue. Vib. Spectrosc. 1996, 10, 325–329. [Google Scholar] [CrossRef]
- Tanner, P.A.; Yu-Long, L.; Mak, T.C.W. Synthesis, crystal structures and vibrational spectra of zinc hypophosphites. Polyhedron 1997, 16, 495–505. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compound ([CH3NH2NH2][Mn(H2PO2)3] is available from the authors. |


| No. | νharm | νharm 1 | νanharm | PED |
|---|---|---|---|---|
| 1 | 3564 | 3421 | 3388 | νasNH2-99 |
| 2 | 3477 | 3338 | 3306 | νsNH2-100 |
| 3 | 3461 | 3323 | 3292 | νasNH2+-99 |
| 4 | 3425 | 3288 | 3289 | νsNH2+-98 |
| 5 | 3180 | 3053 | 3049 | νasCH3-100 |
| 6 | 3166 | 3039 | 3029 | νasCH3-100 |
| 7 | 3075 | 2952 | 3014 | νsCH3-100 |
| 8 | 1700 | 1666 | 1679 | δNH2-80 + δNH2+-20 |
| 9 | 1670 | 1637 | 1607 | δNH2+-80 + δNH2-20 |
| 10 | 1499 | 1469 | 1472 | δasCH3-91 |
| 11 | 1499 | 1469 | 1458 | δasCH3-62 + ρNH2-22 + τNH2+-14 |
| 12 | 1490 | 1460 | 1449 | τNH2+-38 + δasCH3-35 + ρNH2-26 |
| 13 | 1461 | 1432 | 1439 | δsCH3-97 |
| 14 | 1443 | 1415 | 1401 | ωNH2+-86 + δasCH3-15 |
| 15 | 1336 | 1309 | 1297 | τNH2+-41 + ρCH3-36 + ρNH2-22 |
| 16 | 1219 | 1194 | 1176 | ρCH3-50 + ωNH2-25 + νNH2+-NH2-13 + δNH2+-13 |
| 17 | 1117 | 1095 | 1091 | ρCH3-42 + ρNH2-25 + τNH2+-32 |
| 18 | 1065 | 1043 | 1031 | ωNH2-37 + ρCH3-30 + νNH2+-NH2-20 + νNH2+-CH3-12 |
| 19 | 953 | 934 | 907 | νNH2+-CH3-48 + ωNH2-27 + νNH2+-NH2-22 |
| 20 | 841 | 824 | 821 | ρNH2+-75 + ρCH3-22 |
| 21 | 836 | 819 | 811 | νNH2+-NH2-46 + νNH2+-CH3-37 + ωNH2-12 |
| 22 | 405 | 397 | 404 | δCNN-87 |
| 23 | 281 | 275 | 252 | τNH2-73 + τCH3-27 |
| 24 | 225 | 220 | 245 | τCH3-73 + τNH2-27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciupa-Litwa, A.; Ptak, M.; Kucharska, E.; Hanuza, J.; Mączka, M. Vibrational Properties and DFT Calculations of Perovskite-Type Methylhydrazinium Manganese Hypophosphite. Molecules 2020, 25, 5215. https://doi.org/10.3390/molecules25215215
Ciupa-Litwa A, Ptak M, Kucharska E, Hanuza J, Mączka M. Vibrational Properties and DFT Calculations of Perovskite-Type Methylhydrazinium Manganese Hypophosphite. Molecules. 2020; 25(21):5215. https://doi.org/10.3390/molecules25215215
Chicago/Turabian StyleCiupa-Litwa, Aneta, Maciej Ptak, Edyta Kucharska, Jerzy Hanuza, and Mirosław Mączka. 2020. "Vibrational Properties and DFT Calculations of Perovskite-Type Methylhydrazinium Manganese Hypophosphite" Molecules 25, no. 21: 5215. https://doi.org/10.3390/molecules25215215
APA StyleCiupa-Litwa, A., Ptak, M., Kucharska, E., Hanuza, J., & Mączka, M. (2020). Vibrational Properties and DFT Calculations of Perovskite-Type Methylhydrazinium Manganese Hypophosphite. Molecules, 25(21), 5215. https://doi.org/10.3390/molecules25215215