Mass Spectrometric Analysis of Antibody—Epitope Peptide Complex Dissociation: Theoretical Concept and Practical Procedure of Binding Strength Characterization
Abstract
1. Introduction
1.1. ESI Mass Spectrometric Analysis of Non-Covalent Complexes
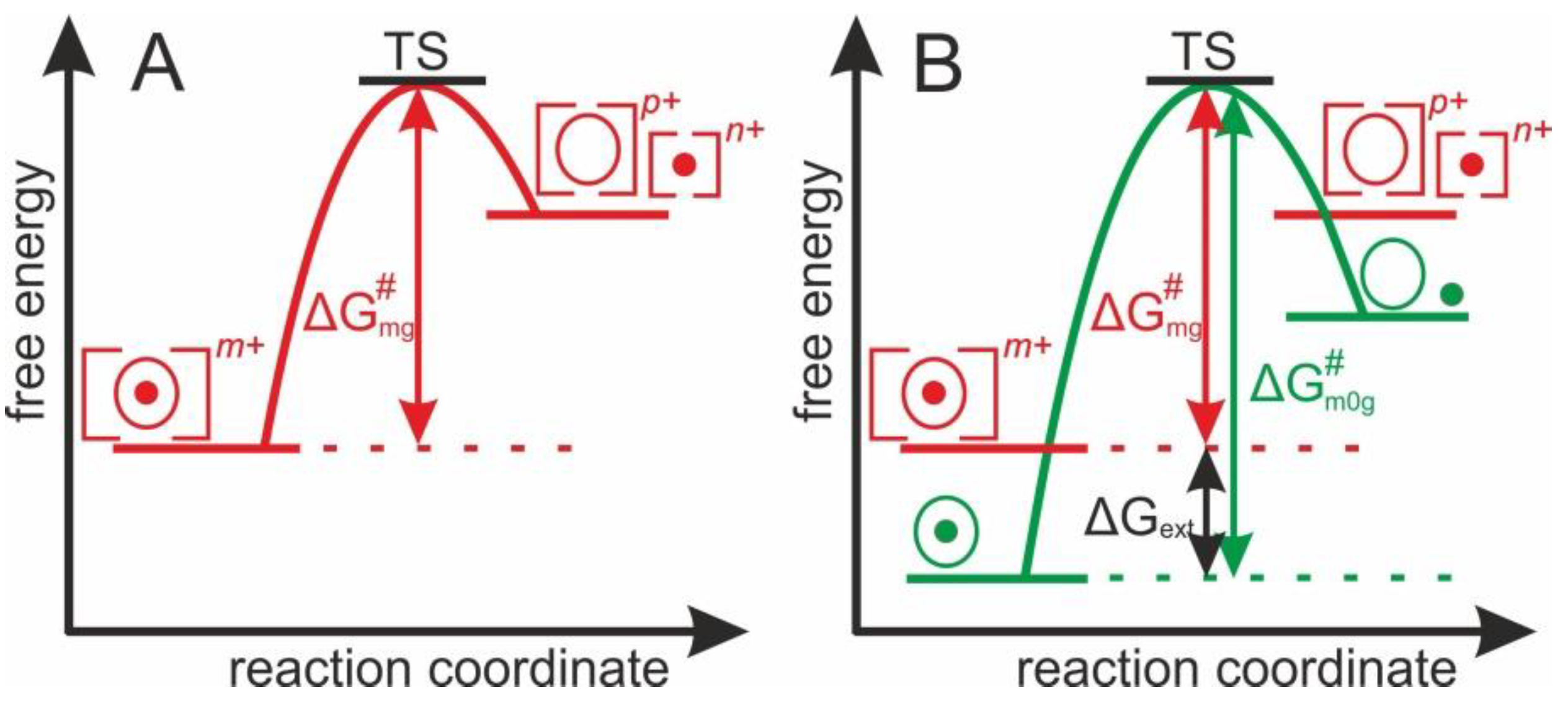
1.2. Theoretical Concept of Dissociation of Protein-Ligand Complex Ions in the Gas Phase
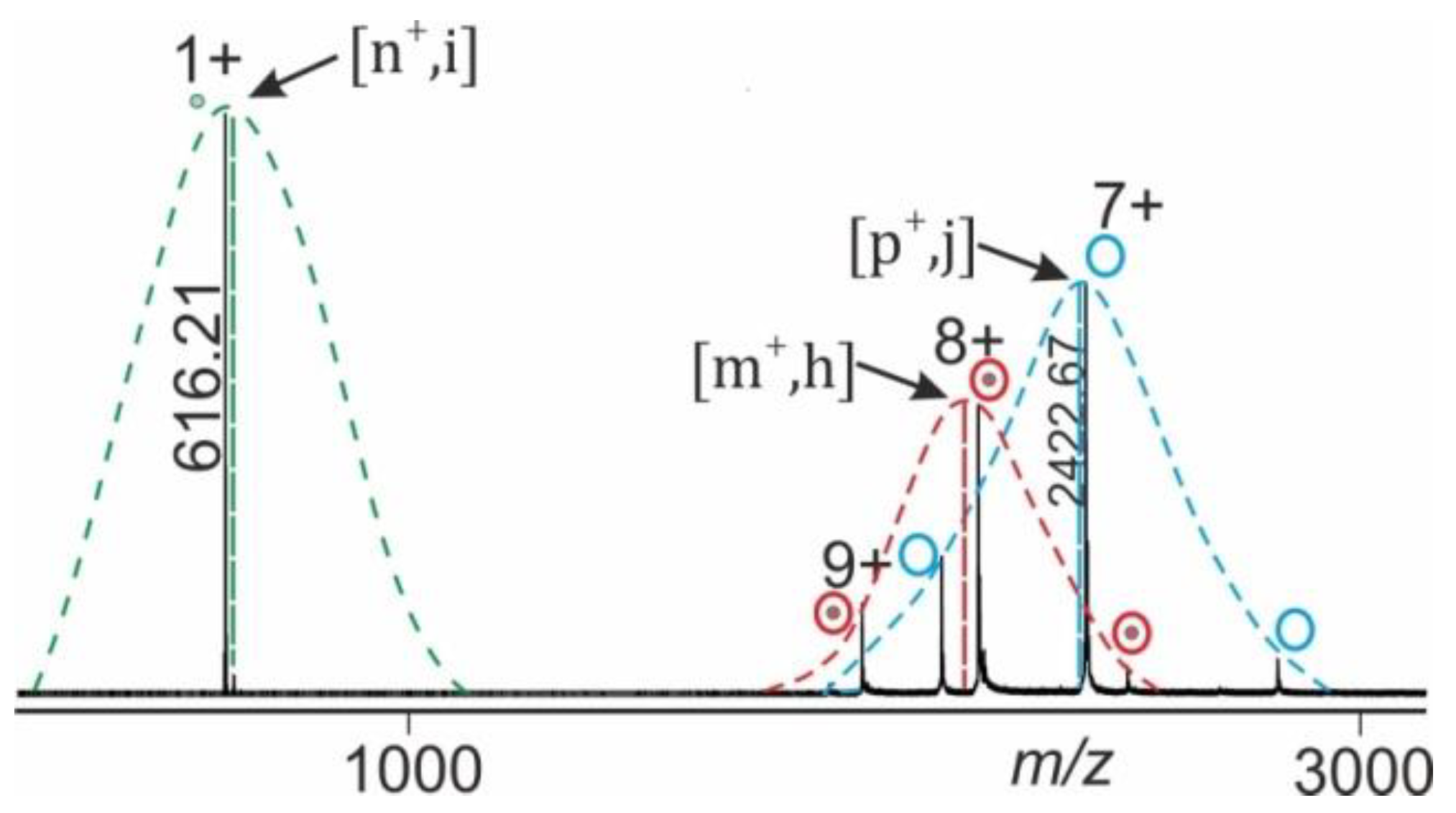
1.3. ESI Mass Spectral Information Extraction
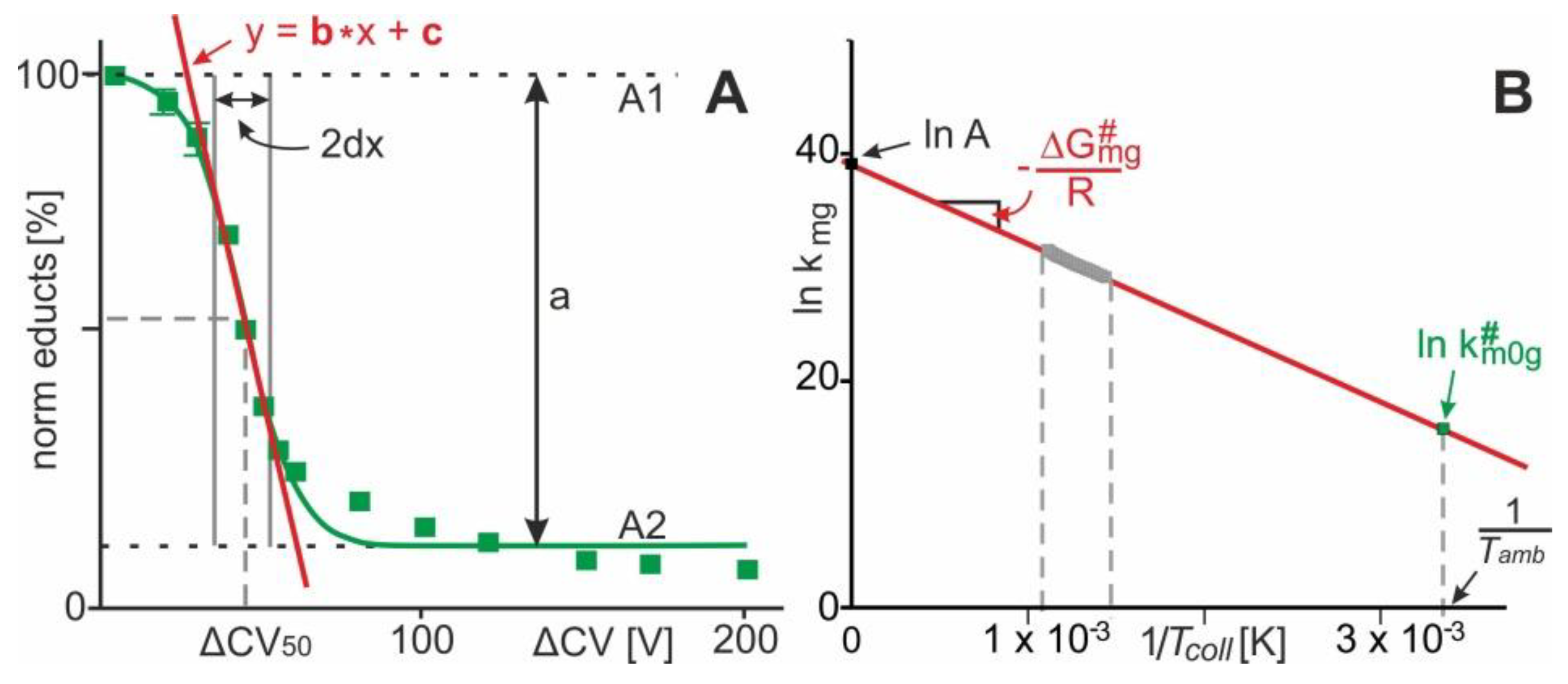
1.4. Data Analysis Procedure
2. Results
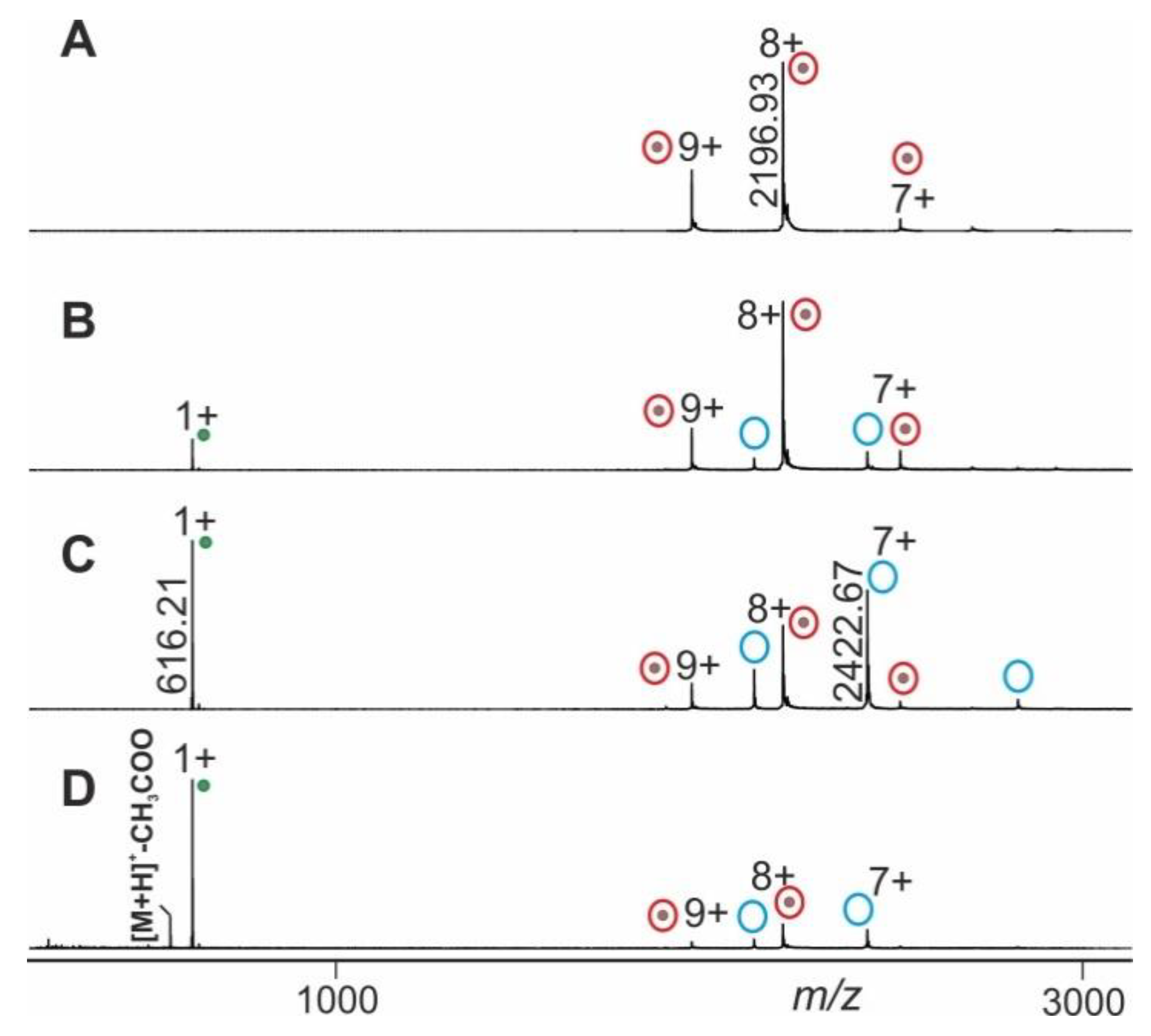
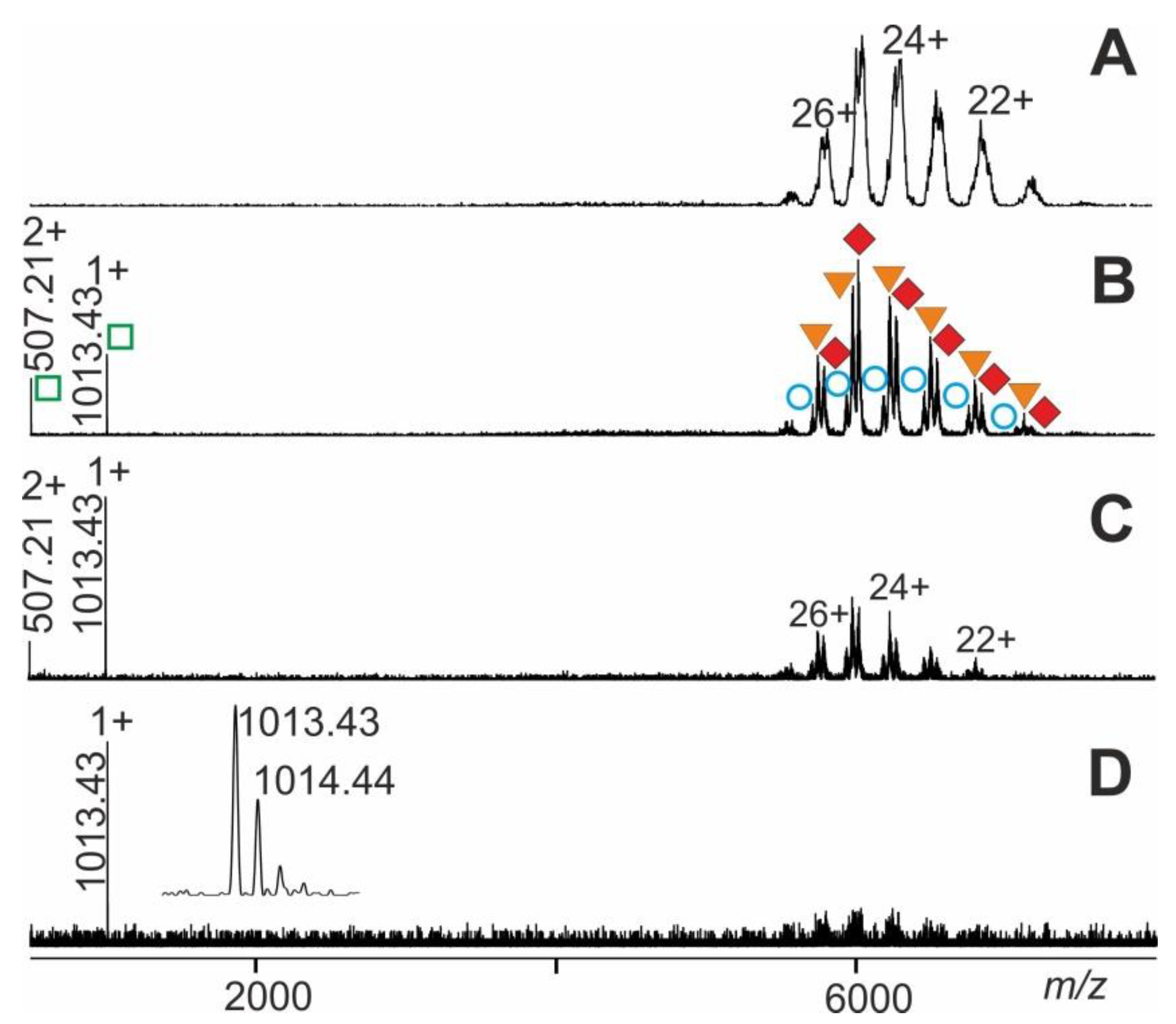
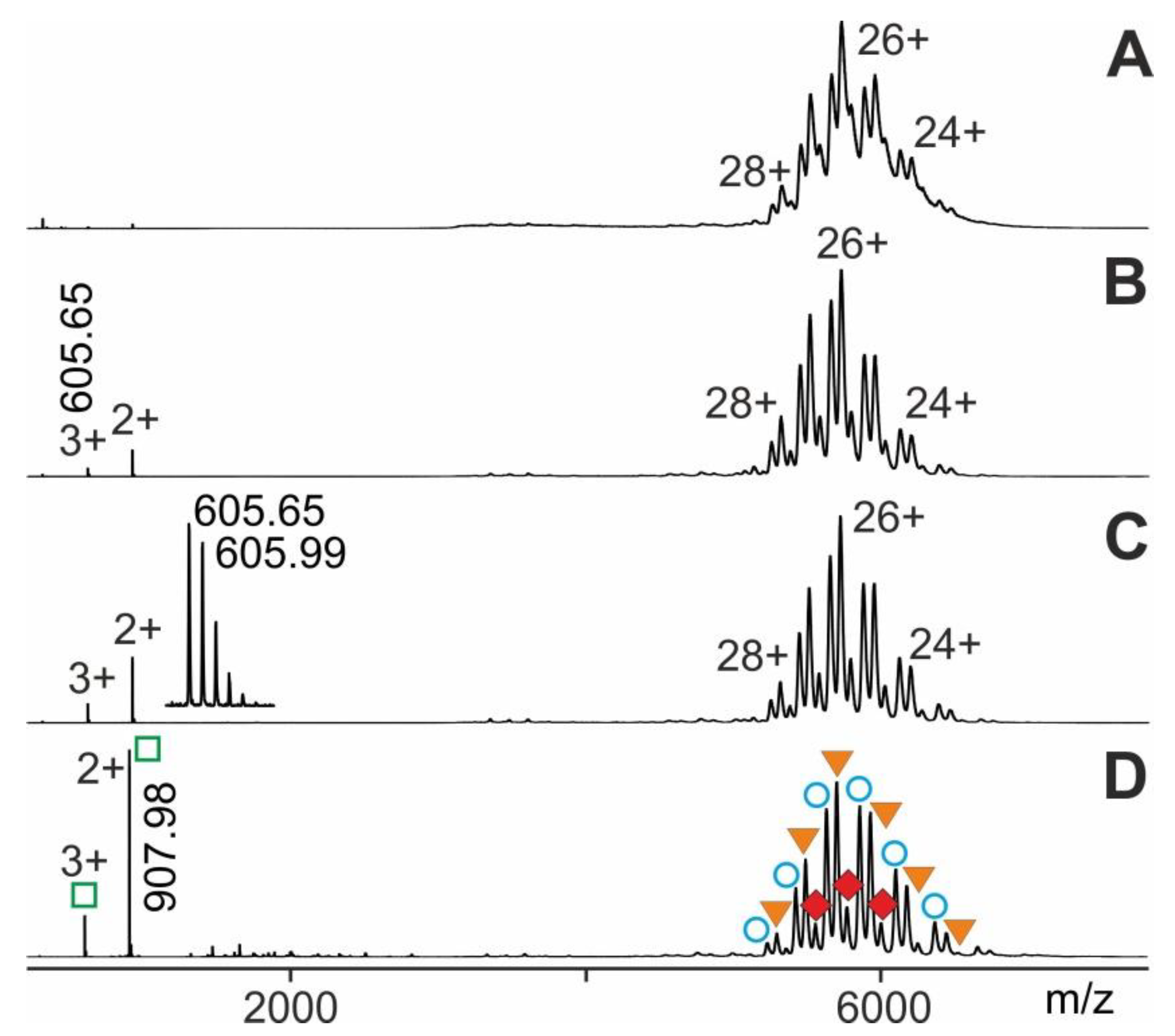
2.1. Procedure Development with Myoglobin and Application to RNAse S Dissociation
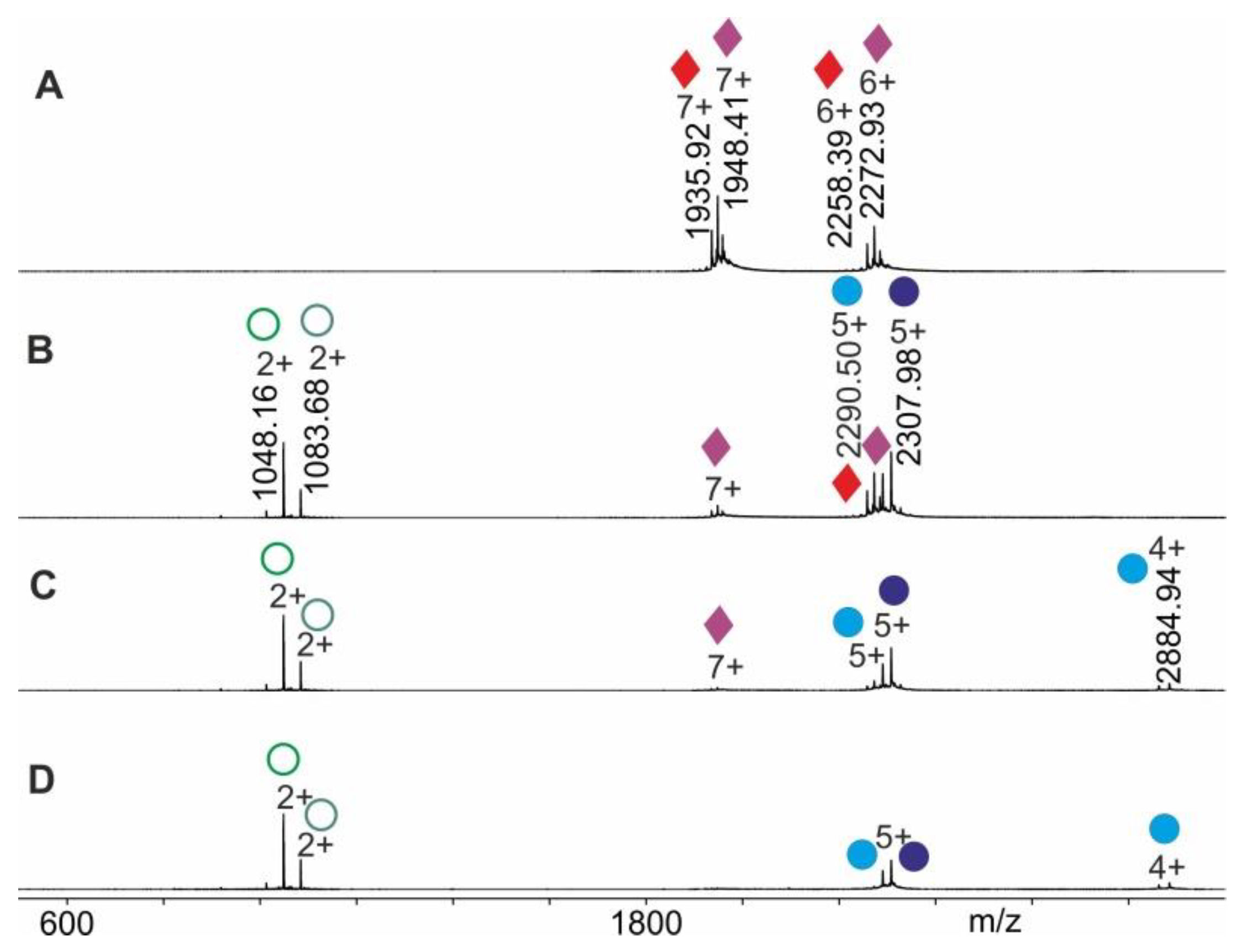
2.2. Application Examples with Epitope Peptide-Antibody Immune Complexes
3. Discussion
4. Materials and Methods
4.1. Preparation of Myoglobin-Containing Solution
4.2. Preparation of RNAse S-Containing Solution
4.3. Preparation of FLAG-Peptide-AntiFLAG Antibody Immune Complex-Containing Solution
4.4. Preparation of Troponin I-Peptide-AntiTn I Antibody Immune Complex-Containing Solution
4.5. Production of NanoESI Capillaries
4.6. Q-ToF 2 Instrument Settings and Data Aquisition
4.7. Synapt G2S Instrument Settings and Data Aquisition
4.8. Mass Spectral Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Opuni, K.F.M.; Al-Majdoub, M.; Yefremova, Y.; El-Kased, R.F.; Koy, C.; Glocker, M.O. Mass spectrometric epitope mapping. Mass Spectrom. Rev. 2016, 37, 229–241. [Google Scholar] [CrossRef]
- Sunner, J.; Magnera, T.F.; Kebarle, P. Ion–molecule equilibria measurements by high pressure mass spectrometry. Some recent advances in concepts and technique. Can. J. Chem. 1981, 59, 1787–1796. [Google Scholar] [CrossRef]
- Kebarle, P. Equilibrium studies of the solvated proton by high pressure mass spectrometry. Thermodynamic determinations and implications for the electrospray ionization process. J. Mass Spectrom. 1997, 32, 922–929. [Google Scholar] [CrossRef]
- Armentrout, P.B.; Rodgers, M.T. Thermochemistry of Non-Covalent Ion–Molecule Interactions. Mass Spectrom. 2013, 2, S0005. [Google Scholar] [CrossRef] [PubMed]
- Armentrout, P.B.; Heaton, A.L.; Ye, S.J. Thermodynamics and Mechanisms for Decomposition of Protonated Glycine and Its Protonated Dimer. J. Phys. Chem. A 2011, 115, 11144–11155. [Google Scholar] [CrossRef] [PubMed]
- Meot-Ner, M.; Dongre, A.R.; Somogyi, A.; Wysocki, V.H. Thermal decomposition kinetics of protonated peptides and peptide dimers, and comparison with surface-induced dissociation. Rapid Commun. Mass Spectrom. 1995, 9, 829–836. [Google Scholar] [CrossRef]
- Price, W.D.; Schnier, P.D.; Jockusch, R.A.; Strittmatter, A.E.F.; Williams, E.R. Unimolecular Reaction Kinetics in the High-Pressure Limit without Collisions. J. Am. Chem. Soc. 1996, 118, 10640–10644. [Google Scholar] [CrossRef]
- Li, C.; Ross, P.; Szulejko, A.J.E.; McMahon, T.B. High-Pressure Mass Spectrometric Investigations of the Potential Energy Surfaces of Gas-Phase SN2 Reactions. J. Am. Chem. Soc. 1996, 118, 9360–9367. [Google Scholar] [CrossRef]
- Pan, S.; Sun, X.J.; Lee, J.K. Stability of complementary and mismatched DNA duplexes: Comparison and contrast in gas versus solution phases. Int. J. Mass Spectrom. 2006, 253, 238–248. [Google Scholar] [CrossRef]
- Jørgensen, T.J.D.; Delforge, D.; Remacle, J.; Bojesen, G.; Roepstorff, P. Collision-induced dissociation of noncovalent complexes between vancomycin antibiotics and peptide ligand stereoisomers: Evidence for molecular recognition in the gas phase. Int. J. Mass Spectrom. 1999, 188, 63–85. [Google Scholar] [CrossRef]
- Kitov, P.I.; Kitova, E.N.; Han, L.; Li, Z.X.; Jung, J.; Rodrigues, E.; Hunter, C.D.; Cairo, C.W.; Macauley, M.S.; Klassen, J.S. A quantitative, high-throughput method identifies protein–glycan interactions via mass spectrometry. Commun. Biol. 2019, 2, 268. [Google Scholar] [CrossRef]
- Yefremova, Y.; Opuni, K.F.M.; Danquah, B.D.; Thiesen, H.-J.; Glocker, M.O. Intact Transition Epitope Mapping (ITEM). J. Am. Soc. Mass Spectrom. 2017, 28, 1612–1622. [Google Scholar] [CrossRef]
- Danquah, B.D.; Rower, C.; Opuni, K.F.M.; El-Kased, R.; Frommholz, D.; Illges, H.; Koy, C.; Glocker, M.O. Intact Transition Epitope Mapping—Targeted High-Energy Rupture of Extracted Epitopes (ITEM-THREE). Mol. Cell. Proteom. 2019, 18, 1543–1555. [Google Scholar] [CrossRef] [PubMed]
- Yefremova, Y.; Melder, F.T.I.; Danquah, B.D.; Opuni, K.F.M.; Koy, C.; Ehrens, A.; Frommholz, D.; Illges, H.; Koelbel, K.; Sobott, F.; et al. Apparent activation energies of protein–protein complex dissociation in the gas–phase determined by electrospray mass spectrometry. Anal. Bioanal. Chem. 2017, 409, 6549–6558. [Google Scholar] [CrossRef] [PubMed]
- Donor, M.T.; Mroz, A.M.; Prell, J.S. Experimental and theoretical investigation of overall energy deposition in surface-induced unfolding of protein ions. Chem. Sci. 2019, 10, 4097–4106. [Google Scholar] [CrossRef]
- Danquah, B.D.; Yefremova, Y.; Opuni, K.F.; Röwer, C.; Koy, C.; Glocker, M.O. Intact Transition Epitope Mapping—Thermodynamic Weak-force Order (ITEM—TWO). J. Proteom. 2019, 212, 103572. [Google Scholar] [CrossRef] [PubMed]
- Przybylski, M.; Glocker, M.O. Electrospray Mass Spectrometry of Biomacromolecular Complexes with Noncovalent Interactions—New Analytical Perspectives for Supramolecular Chemistry and Molecular Recognition Processes. Angew. Chem. Int. Ed. 1996, 35, 806–826. [Google Scholar] [CrossRef]
- Loo, J.A. Studying noncovalent protein complexes by electrospray ionization mass spectrometry. Mass Spectrom. Rev. 1997, 16, 1–23. [Google Scholar] [CrossRef]
- Donor, M.T.; Shepherd, S.O.; Prell, J.S. Rapid Determination of Activation Energies for Gas-Phase Protein Unfolding and Dissociation in a Q-IM-ToF Mass Spectrometer. J. Am. Soc. Mass Spectrom. 2020, 31, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Wells, J.M.; McLuckey, S.A. Collision-Induced Dissociation (CID) of Peptides and Proteins. Biol. Mass Spectrom. 2005, 402, 148–185. [Google Scholar] [CrossRef]
- Douglas, D.J. Applications of collision dynamics in quadrupole mass spectrometry. J. Am. Soc. Mass Spectrom. 1998, 9, 101–113. [Google Scholar] [CrossRef]
- Chang, R. Physical Chemistry for the Biosciences; University Science Books: Mill Valley, CA, USA, 2005. [Google Scholar]
- Hargrove, M.S.; Barrick, D.; Olson, J.S. The Association Rate Constant for Heme Binding to Globin Is Independent of Protein Structure. Biochemistry 1996, 35, 11293–11299. [Google Scholar] [CrossRef] [PubMed]
- Culbertson, D.S.; Olson, J.S. Role of Heme in the Unfolding and Assembly of Myoglobin. Biochemistry 2010, 49, 6052–6063. [Google Scholar] [CrossRef] [PubMed]
- Enyenihi, A.A.; Yang, H.; Ytterberg, A.J.; Lyutvinskiy, Y.; Zubarev, R.A. Heme Binding in Gas-Phase Holo-Myoglobin Cations: Distal Becomes Proximal? J. Am. Soc. Mass Spectrom. 2011, 22, 1763–1770. [Google Scholar] [CrossRef]
- Hunter, C.L.; Mauk, A.G.; Douglas, D.J. Dissociation of Heme from Myoglobin and Cytochromeb5: Comparison of Behavior in Solution and the Gas Phase. Biochemistry 1997, 36, 1018–1025. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, A.; Karas, M. The influence of electrostatic interactions on the detection of heme-globin complexes in ESI-MS. J. Am. Soc. Mass Spectrom. 2001, 12, 1092–1098. [Google Scholar] [CrossRef]
- Ito, W.; Kurosawa, Y. Development of an artificial antibody system with multiple valency using an Fv fragment fused to a fragment of protein A. J. Biol. Chem. 1993, 268, 20668–20675. [Google Scholar]
- Ito, W.; Iba, Y.; Kurosawa, Y. Effects of substitutions of closely related amino acids at the contact surface in an antigen-antibody complex on thermodynamic parameters. J. Biol. Chem. 1993, 268, 16639–16647. [Google Scholar]
- Hoaglund, C.S.; Valentine, S.J.; Sporleder, C.R.; Reilly, J.P.; Clemmer, D.E. Three-Dimensional Ion Mobility/TOFMS Analysis of Electrosprayed Biomolecules. Anal. Chem. 1998, 70, 2236–2242. [Google Scholar] [CrossRef]
- Konijnenberg, A.; Butterer, A.; Sobott, F. Native ion mobility-mass spectrometry and related methods in structural biology. Biochim. Biophys. Acta (BBA) Proteins Proteom. 2013, 1834, 1239–1256. [Google Scholar] [CrossRef]
- Seo, J.; Hoffmann, W.; Warnke, S.; Bowers, M.T.; Pagel, K.; Von Helden, G. Retention of Native Protein Structures in the Absence of Solvent: A Coupled Ion Mobility and Spectroscopic Study. Angew. Chem. Int. Ed. 2016, 55, 14173–14176. [Google Scholar] [CrossRef]
- Hopper, J.T.S.; Oldham, N.J. Collision induced unfolding of protein ions in the gas phase studied by ion mobility-mass spectrometry: The effect of ligand binding on conformational stability. J. Am. Soc. Mass Spectrom. 2009, 20, 1851–1858. [Google Scholar] [CrossRef]
- Zhong, Y.; Hyung, S.-J.; Ruotolo, B.T. Ion mobility–mass spectrometry for structural proteomics. Expert Rev. Proteom. 2012, 9, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Breuker, K.; McLafferty, F.W. Stepwise evolution of protein native structure with electrospray into the gas phase, 10–12 to 102 s. Proc. Natl. Acad. Sci. USA 2008, 105, 18145–18152. [Google Scholar] [CrossRef] [PubMed]
- Heck, A.J.R. Native mass spectrometry: A bridge between interactomics and structural biology. Nat. Methods 2008, 5, 927–933. [Google Scholar] [CrossRef] [PubMed]
- Perez-Riverol, Y.; Csordas, A.; Bai, J.; Bernal-Llinares, M.; Hewapathirana, S.; Kundu, D.J.; Inuganti, A.; Griss, J.; Mayer, G.; Eisenacher, M.; et al. The PRIDE database and related tools and resources in 2019: Improving support for quantification data. Nucleic Acids Res. 2018, 47, D442–D450. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the peptide compounds are available from the authors on request. |
| Complex (a) | Mean Charge ± std. dev. (b) | ∆CV50 (V) | dx (V) | (1/s) | (Ø) (b) | (kJ/mol) |
|---|---|---|---|---|---|---|
| myoglobin | 8.1 ± 0.01 | 44.0 | 8.5 | 5.1 × 10 9 | 3.60 × 10−12 | 65.3 |
| RNAse S | 6.4 ± 0.20 | 12.5 | 4.6 | 7.3 × 10 10 | 4.03 × 10−12 | 65.0 |
| FLAG | 24.6 ± 0.30 | 89.0 | 19.8 | 7.9 × 10 10 | 4.04 × 10−12 | 65.0 |
| troponin I | 25.9 ± 0.14 | 26.4 | 15.9 | 2.2 × 10 12 | 4.58 × 10−12 | 64.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danquah, B.D.; Opuni, K.F.M.; Roewer, C.; Koy, C.; Glocker, M.O. Mass Spectrometric Analysis of Antibody—Epitope Peptide Complex Dissociation: Theoretical Concept and Practical Procedure of Binding Strength Characterization. Molecules 2020, 25, 4776. https://doi.org/10.3390/molecules25204776
Danquah BD, Opuni KFM, Roewer C, Koy C, Glocker MO. Mass Spectrometric Analysis of Antibody—Epitope Peptide Complex Dissociation: Theoretical Concept and Practical Procedure of Binding Strength Characterization. Molecules. 2020; 25(20):4776. https://doi.org/10.3390/molecules25204776
Chicago/Turabian StyleDanquah, Bright D., Kwabena F. M. Opuni, Claudia Roewer, Cornelia Koy, and Michael O. Glocker. 2020. "Mass Spectrometric Analysis of Antibody—Epitope Peptide Complex Dissociation: Theoretical Concept and Practical Procedure of Binding Strength Characterization" Molecules 25, no. 20: 4776. https://doi.org/10.3390/molecules25204776
APA StyleDanquah, B. D., Opuni, K. F. M., Roewer, C., Koy, C., & Glocker, M. O. (2020). Mass Spectrometric Analysis of Antibody—Epitope Peptide Complex Dissociation: Theoretical Concept and Practical Procedure of Binding Strength Characterization. Molecules, 25(20), 4776. https://doi.org/10.3390/molecules25204776







