Numerical Simulations as Means for Tailoring Electrically Conductive Hydrogels towards Cartilage Tissue Engineering by Electrical Stimulation
Abstract
1. Introduction
2. Results and Discussion
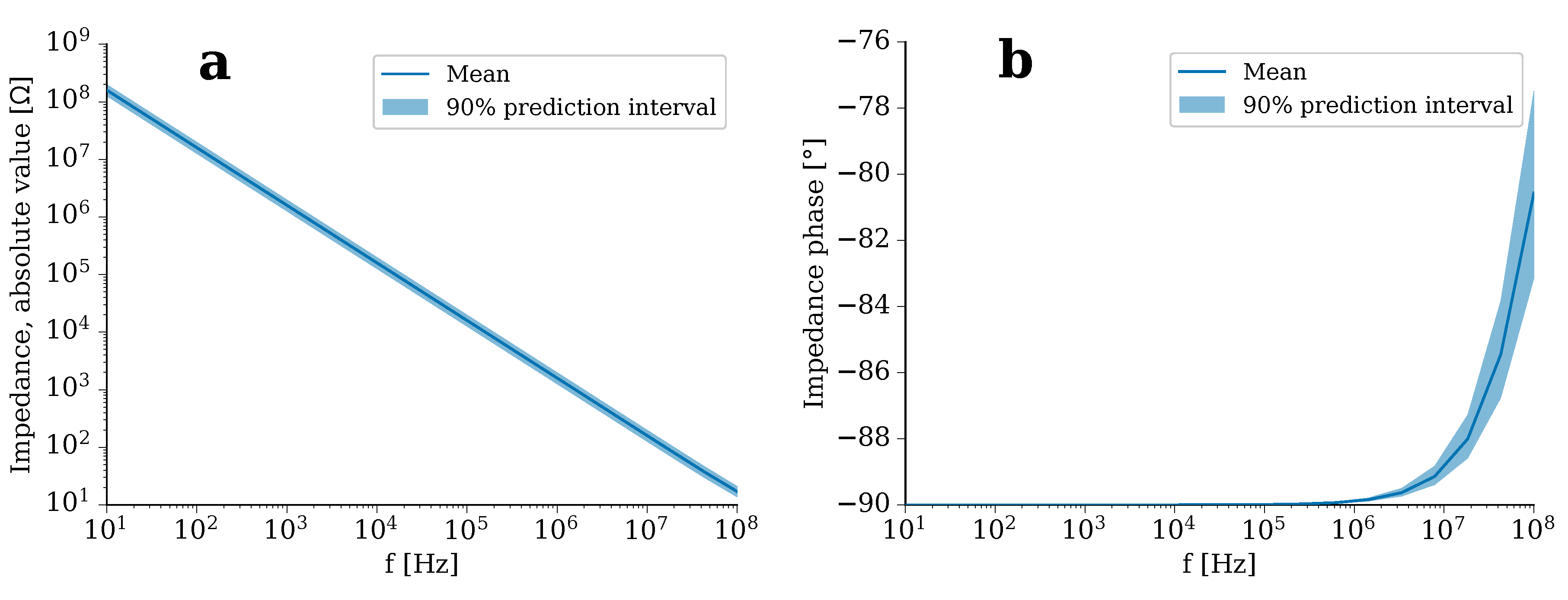
2.1. Validation of the Modelling Approach
2.2. A Numerical Model for Cell-Laden Electrically Conductive Hydrogels
- .
- .
- .
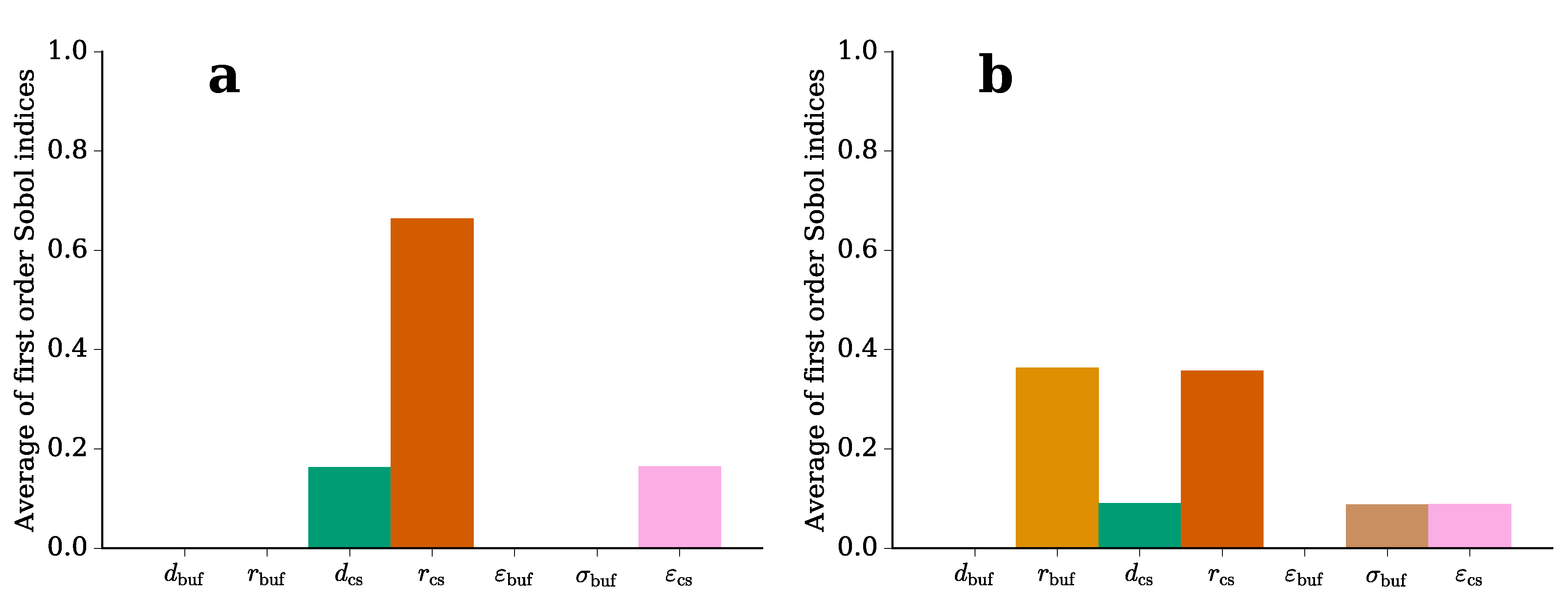
2.3. Theoretical Considerations Regarding Cellular Organisation
3. Materials and Methods
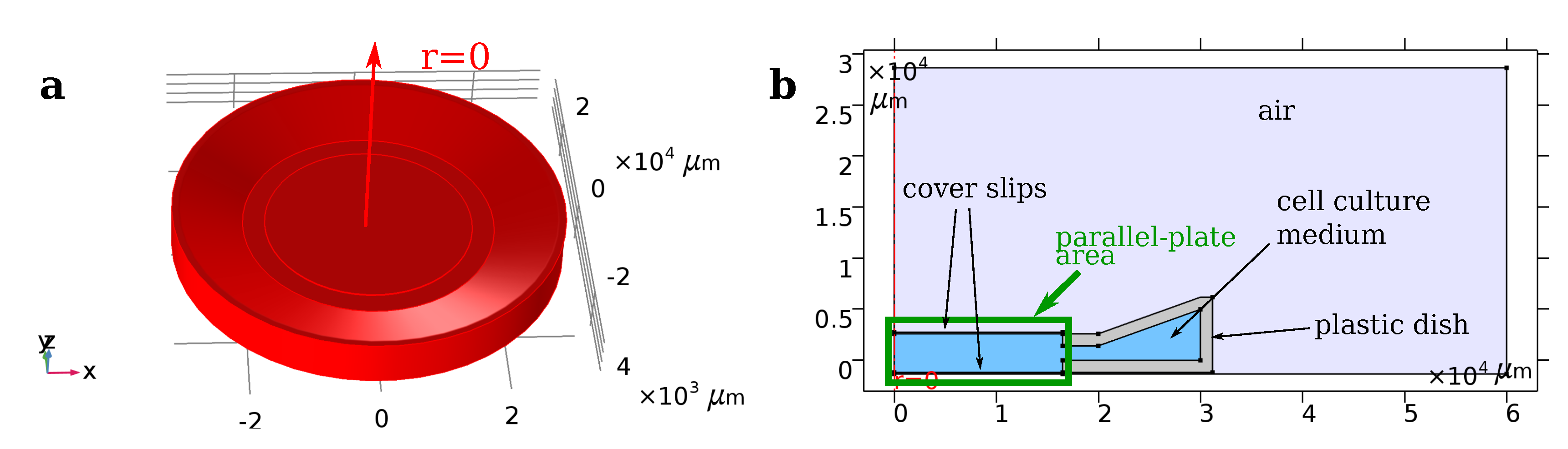
3.1. Geometric Modelling and Equivalent Circuits
3.2. Finite Element Analysis and Uncertainty Quantification
4. Conclusions
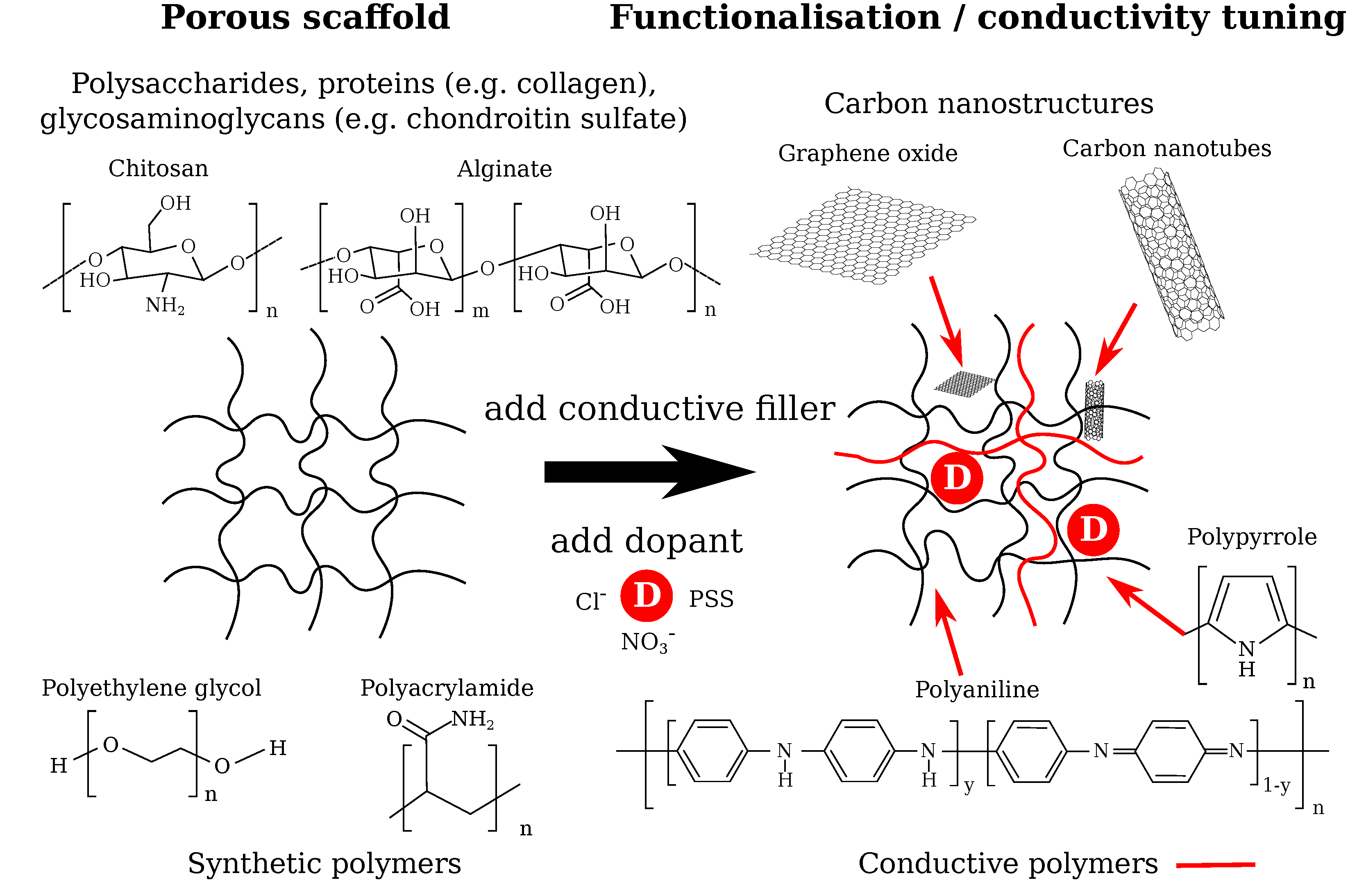
- Development of chemically and electrically stable low-conductivity hydrogels (<) to increase the electrical field strength acting on the chondrocytes and thus increased change in their TMP. Here, low-impedance insulation of the electrodes from the cell culture medium becomes highly relevant to ensure an electrically efficient solution. Possible hydrogel materials could be, for example, solely ionically conductive hydrogels [7] or a suitable hydrogel functionalised with, for example, polypyrrole [25] or reduced graphene oxide [24].
- Usage of high-conductivity hydrogels (>) together with non-uniform, strong electric fields much greater than to exploit the attraction of chondrocytes by low-field regions. This could be used to influence cellular ingrowth inside hydrogels and increase efficiency of initial cell seeding. Such high conductivities might only be reached by the use of, for example, highly conductive carbon nanotubes [20], reduced graphene oxide [21,24], or well-percolating doped conductive polymer networks made from, among others, polypyrrole or polyaniline [15,19].
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| UQ | Uncertainty Quantification |
| FEA | Finite Element Analysis |
| ECM | Extracellular Matrix |
| TMP | Transmembrane Potential |
| CM | Clausius-Mossotti |
| MC | Monte Carlo |
| PC | Polynomial Chaos |
| TE | Tissue Engineering |
| CTE | Cartilage Tissue Engineering |
| ES | Electrical Stimulation |
| GO | Graphene Oxide |
Appendix A
References
- Makris, E.A.; Gomoll, A.H.; Malizos, K.N.; Hu, J.C.; Athanasiou, K.A. Repair and tissue engineering techniques for articular cartilage. Nat. Rev. Rheumatol. 2016, 11, 21–34. [Google Scholar] [CrossRef] [PubMed]
- Medvedeva, E.V.; Grebenik, E.A.; Gornostaeva, S.N.; Telpuhov, V.I.; Lychagin, A.V.; Timashev, P.S.; Chagin, A.S. Repair of damaged articular cartilage: Current approaches and future directions. Int. J. Mol. Sci. 2018, 19, 2366. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Jin, X.; Cong, Y.; Liu, Y.; Fu, J. Degradable natural polymer hydrogels for articular cartilage tissue engineering. J. Chem. Technol. Biotechnol. 2013, 88, 327–339. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y.S.; Yue, K.; Khademhosseini, A. Cell-laden hydrogels for osteochondral and cartilage tissue engineering. Acta Biomater. 2017, 57, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Ning, C.; Zhou, Z.; Tan, G.; Zhu, Y.; Mao, C. Electroactive polymers for tissue regeneration: Developments and perspectives. Prog. Polym. Sci. 2018, 81, 144–162. [Google Scholar] [CrossRef]
- Drury, J.L.; Mooney, D.J. Hydrogels for tissue engineering: Scaffold design variables and applications. Biomaterials 2003, 24, 4337–4351. [Google Scholar] [CrossRef]
- Distler, T.; Boccaccini, A.R. 3D printing of electrically conductive hydrogels for tissue engineering and biosensors—A review. Acta Biomater. 2020, 101, 1–13. [Google Scholar] [CrossRef]
- Caron, M.M.; Emans, P.J.; Coolsen, M.M.; Voss, L.; Surtel, D.A.; Cremers, A.; van Rhijn, L.W.; Welting, T.J. Redifferentiation of dedifferentiated human articular chondrocytes: Comparison of 2D and 3D cultures. Osteoarthr. Cartil. 2012, 20, 1170–1178. [Google Scholar] [CrossRef]
- Krueger, S.; Achilles, S.; Zimmermann, J.; Tischer, T.; Bader, R.; Jonitz-Heincke, A. Re-Differentiation Capacity of Human Chondrocytes in Vitro Following Electrical Stimulation with Capacitively Coupled Fields. J. Clin. Med. 2019, 8, 1771. [Google Scholar] [CrossRef] [PubMed]
- Vaca-González, J.J.; Guevara, J.M.; Moncayo, M.A.; Castro-Abril, H.; Hata, Y.; Garzón-Alvarado, D.A. Biophysical Stimuli: A Review of Electrical and Mechanical Stimulation in Hyaline Cartilage. Cartilage 2019, 10, 157–172. [Google Scholar] [CrossRef] [PubMed]
- Vaca-González, J.J.; Clara-Trujillo, S.; Guillot-Ferriols, M.; Ródenas-Rochina, J.; Sanchis, M.J.; Ribelles, J.L.G.; Garzón-Alvarado, D.A.; Ferrer, G.G. Effect of electrical stimulation on chondrogenic differentiation of mesenchymal stem cells cultured in hyaluronic acid—Gelatin injectable hydrogels. Bioelectrochemistry 2020, 134. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wang, Z.; Zhang, G.; Clark, C.C.; Brighton, C.T. Up-regulation of chondrocyte matrix genes and products by electric fields. Clin. Orthop. Relat. Res. 2004. [Google Scholar] [CrossRef] [PubMed]
- Brighton, C.T.; Wang, W.; Clark, C.C. The effect of electrical fields on gene and protein expression in human osteoarthritic cartilage explants. J. Bone Jt. Surg. Am. 2008, 90, 833–848. [Google Scholar] [CrossRef]
- Jahr, H.; Matta, C.; Mobasheri, A. Physicochemical and Biomechanical Stimuli in Cell-Based Articular Cartilage Repair. Curr. Rheumatol. Rep. 2015, 17. [Google Scholar] [CrossRef]
- Kaur, G.; Adhikari, R.; Cass, P.; Bown, M.; Gunatillake, P. Electrically conductive polymers and composites for biomedical applications. RSC Adv. 2015, 5, 37553–37567. [Google Scholar] [CrossRef]
- Mawad, D.; Lauto, A.; Wallace, G.G. Conductive Polymer Hydrogels. In Polymeric Hydrogels as Smart Biomaterials; Kalia, S., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 19–44. [Google Scholar] [CrossRef]
- Mawad, D.; Artzy-Schnirman, A.; Tonkin, J.; Ramos, J.; Inal, S.; Mahat, M.; Darwish, N.; Zwi-Dantsis, L.; Malliaras, G.; Gooding, J.; Lauto, A.; Stevens, M. Electroconductive Hydrogel Based on Functional Poly(Ethylenedioxy Thiophene). Chem. Mater. 2016, 28, 6080–6088. [Google Scholar] [CrossRef]
- Armiento, A.R.; Stoddart, M.J.; Alini, M.; Eglin, D. Biomaterials for articular cartilage tissue engineering: Learning from biology. Acta Biomater. 2018, 65, 1–20. [Google Scholar] [CrossRef]
- Balint, R.; Cassidy, N.J.; Cartmell, S.H. Conductive polymers: Towards a smart biomaterial for tissue engineering. Acta Biomater. 2014, 10, 2341–2353. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, D.; Bosi, S.; Melchionna, M.; Da Ros, T.; Marchesan, S. The Glitter of Carbon Nanostructures in Hybrid/Composite Hydrogels for Medicinal Use. Curr. Top. Med. Chem. 2016, 16, 1976–1989. [Google Scholar] [CrossRef]
- Han, L.; Lu, X.; Wang, M.; Gan, D.; Deng, W.; Wang, K.; Fang, L.; Liu, K.; Chan, C.W.; Tang, Y.; Weng, L.T.; Yuan, H. A Mussel-Inspired Conductive, Self-Adhesive, and Self-Healable Tough Hydrogel as Cell Stimulators and Implantable Bioelectronics. Small 2017, 13, 1–9. [Google Scholar] [CrossRef]
- Lee, H.P.; Gu, L.; Mooney, D.J.; Levenston, M.E.; Chaudhuri, O. Mechanical confinement regulates cartilage matrix formation by chondrocytes. Nat. Mater. 2017, 16, 1243–1251. [Google Scholar] [CrossRef] [PubMed]
- Dadsetan, M.; Pumberger, M.; Casper, M.E.; Shogren, K.; Giuliani, M.; Ruesink, T.; Hefferan, T.E.; Currier, B.L.; Yaszemski, M.J. The effects of fixed electrical charge on chondrocyte behavior. Acta Biomater. 2011, 7, 2080–2090. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.F.; Qu, Y.; Chu, B.; Zhang, X.; Qian, Z. Biodegradable CSMA/PECA/graphene porous hybrid scaffold for cartilage tissue engineering. Sci. Rep. 2015, 5, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Kashi, M.; Baghbani, F.; Moztarzadeh, F.; Mobasheri, H.; Kowsari, E. Green synthesis of degradable conductive thermosensitive oligopyrrole/chitosan hydrogel intended for cartilage tissue engineering. Int. J. Biol. Macromol. 2018, 107, 1567–1575. [Google Scholar] [CrossRef]
- Daly, A.C.; Freeman, F.E.; Gonzalez-Fernandez, T.; Critchley, S.E.; Nulty, J.; Kelly, D.J. 3D Bioprinting for Cartilage and Osteochondral Tissue Engineering. Adv. Healthc. Mater. 2017, 6, 1–20. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Chu, P.K.; Gelinsky, M. 3D printing of hydrogels: Rational design strategies and emerging biomedical applications. Mater. Sci. Eng. R Rep. 2020, 140, 100543. [Google Scholar] [CrossRef]
- Nuernberger, S.; Cyran, N.; Albrecht, C.; Redl, H.; Vécsei, V.; Marlovits, S. The influence of scaffold architecture on chondrocyte distribution and behavior in matrix-associated chondrocyte transplantation grafts. Biomaterials 2011, 32, 1032–1040. [Google Scholar] [CrossRef]
- Lu, Z.; Doulabi, B.Z.; Huang, C.; Bank, R.A.; Helder, M.N. Collagen type II enhances chondrogenesis in adipose tissue-derived stem cells by affecting cell shape. Tissue Eng. Part A 2010, 16, 81–90. [Google Scholar] [CrossRef]
- Sarker, B.; Li, W.; Zheng, K.; Detsch, R.; Boccaccini, A.R. Designing Porous Bone Tissue Engineering Scaffolds with Enhanced Mechanical Properties from Composite Hydrogels Composed of Modified Alginate, Gelatin, and Bioactive Glass. ACS Biomater. Sci. Eng. 2016, 2, 2240–2254. [Google Scholar] [CrossRef]
- Annabi, N.; Nichol, J.W.; Zhong, X.; Ji, C.; Koshy, S.; Khademhosseini, A.; Dehghani, F. Controlling the porosity and microarchitecture of hydrogels for tissue engineering. Tissue Eng. Part B Rev. 2010, 16, 371–383. [Google Scholar] [CrossRef]
- Taghian, T.; Narmoneva, D.A.; Kogan, A.B. Modulation of cell function by electric field: A high-resolution analysis. J. R. Soc. Interface 2015, 12, 20150153. [Google Scholar] [CrossRef] [PubMed]
- Binette, J.S.; Garon, M.; Savard, P.; McKee, M.D.; Buschmann, M.D. Tetrapolar measurement of electrical conductivity and thickness of articular cartilage. J. Biomech. Eng. 2004, 126, 475–484. [Google Scholar] [CrossRef] [PubMed]
- Brighton, C.T.; Unger, A.S.; Stambough, J.L. In vitro growth of bovine articular cartilage chondrocytes in various capacitively coupled electrical fields. J. Orthop. Res. 1984, 2, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Brighton, C.T.; Jensen, L.; Pollack, S.R.; Tolin, B.S.; Clark, C.C. Proliferative and synthetic response of bovine growth plate chondrocytes to various capacitively coupled electrical fields. J. Orthop. Res. 1989, 7, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Brighton, C.T.; Wang, W.; Clark, C.C. Up-regulation of matrix in bovine articular cartilage explants by electric fields. Biochem. Biophys. Res. Commun. 2006, 342, 556–561. [Google Scholar] [CrossRef]
- Xu, J.; Wang, W.; Clark, C.C.; Brighton, C.T. Signal transduction in electrically stimulated articular chondrocytes involves translocation of extracellular calcium through voltage-gated channels. Osteoarthr. Cartil. 2009, 17, 397–405. [Google Scholar] [CrossRef]
- Brighton, C.T.; Wang, W.; Clark, C.C.; Praestgaard, A. A Spectrophotometric Analysis of Human Osteoarthritic Cartilage Explants Subjected to Specific Capacitively Coupled Electric Fields. Open J. Biophys. 2013, 3, 158–164. [Google Scholar] [CrossRef]
- Vaca-González, J.J.; Guevara, J.M.; Vega, J.F.; Garzón-Alvarado, D.A. An In Vitro Chondrocyte Electrical Stimulation Framework: A Methodology to Calculate Electric Fields and Modulate Proliferation, Cell Death and Glycosaminoglycan Synthesis. Cell. Mol. Bioeng. 2016, 9, 116–126. [Google Scholar] [CrossRef]
- Thrivikraman, G.; Boda, S.K.; Basu, B. Unraveling the mechanistic effects of electric field stimulation towards directing stem cell fate and function: A tissue engineering perspective. Biomaterials 2018, 150, 60–86. [Google Scholar] [CrossRef]
- Schopf, A.; Boehler, C.; Asplund, M. Analytical methods to determine electrochemical factors in electrotaxis setups and their implications for experimental design. Bioelectrochemistry 2016, 109, 41–48. [Google Scholar] [CrossRef][Green Version]
- Brighton, C.T.; Okereke, E.; Pollack, S.R.; Clark, C.C. In Vitro Bone-Cell Response to a Capacitively Coupled Electrical Field. Clin. Orthop. Relat. Res. 1992, 285, 255–262. [Google Scholar] [CrossRef]
- Fear, E.C.; Stuchly, M.A. Biological cells with gap junctions in low-frequency electric fields. IEEE Trans. Biomed. Eng. 1998, 45, 856–866. [Google Scholar] [CrossRef] [PubMed]
- Pall, M.L. Electromagnetic fields act via activation of voltage-gated calcium channels to produce beneficial or adverse effects. J. Cell. Mol. Med. 2013, 17, 958–965. [Google Scholar] [CrossRef] [PubMed]
- Grant, F.A. Use of complex conductivity in the representation of dielectric phenomena. J. Appl. Phys. 1958, 29, 76–80. [Google Scholar] [CrossRef]
- Budde, K.; Zimmermann, J.; Neuhaus, E.; Schroder, M.; Uhrmacher, A.M.; van Rienen, U. Requirements for Documenting Electrical Cell Stimulation Experiments for Replicability and Numerical Modeling. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 1082–1088. [Google Scholar] [CrossRef]
- Glen, G.; Isaacs, K. Estimating Sobol sensitivity indices using correlations. Environ. Model. Softw. 2012, 37, 157–166. [Google Scholar] [CrossRef]
- Feinberg, J.; Langtangen, H.P. Chaospy: An open source tool for designing methods of uncertainty quantification. J. Comput. Sci. 2015, 11, 46–57. [Google Scholar] [CrossRef]
- Abasi, S.; Aggas, J.R.; Venkatesh, N.; Vallavanatt, I.G.; Guiseppi-Elie, A. Design, fabrication and testing of an electrical cell stimulation and recording apparatus (ECSARA) for cells in electroculture. Biosens. Bioelectron. 2020, 147, 111793. [Google Scholar] [CrossRef]
- Kubáň, P.; Hauser, P.C. Contactless conductivity detection for analytical techniques— Developments from 2014 to 2016. Electrophoresis 2017, 38, 95–114. [Google Scholar] [CrossRef]
- Ruland, A.; Jalili, R.; Mozer, A.J.; Wallace, G.G. Quantitative characterisation of conductive fibers by capacitive coupling. Analyst 2018, 143, 215–223. [Google Scholar] [CrossRef]
- Timoshkin, I.V.; MacGregor, S.J.; Fouracre, R.A.; Crichton, B.H.; Anderson, J.G. Transient electrical field across cellular membranes: Pulsed electric field treatment of microbial cells. J. Phys. D Appl. Phys. 2006, 39, 596–603. [Google Scholar] [CrossRef]
- Escobar, J.F.; Vaca-González, J.J.; Garzón-Alvarado, D.A. Effect of magnetic and electric fields on plasma membrane of single cells: A computational approach. Eng. Rep. 2020, e12125, 1–14. [Google Scholar] [CrossRef]
- Van Tam, J.K.; Uto, K.; Ebara, M.; Pagliari, S.; Forte, G.; Aoyagi, T. Mesenchymal stem cell adhesion but not plasticity is affected by high substrate stiffness. Sci. Technol. Adv. Mater. 2012, 13, 064205. [Google Scholar] [CrossRef]
- Grogan, S.P.; Miyaki, S.; Asahara, H.; D’Lima, D.D.; Lotz, M.K. Mesenchymal progenitor cell markers in human articular cartilage: Normal distribution and changes in osteoarthritis. Arthritis Res. Ther. 2009, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Feldman, Y.; Ermolina, I.; Hayashi, Y. Time domain dielectric spectroscopy study of biological systems. IEEE Trans. Dielectr. Electr. Insul. 2003, 10, 728–753. [Google Scholar] [CrossRef]
- Mistani, P.; Guittet, A.; Poignard, C.; Gibou, F. A parallel Voronoi-based approach for mesoscale simulations of cell aggregate electropermeabilization. J. Comput. Phys. 2019, 380, 48–64. [Google Scholar] [CrossRef]
- Albrecht, D.R.; Underhill, G.H.; Wassermann, T.B.; Sah, R.L.; Bhatia, S.N. Probing the role of multicellular organization in three-dimensional microenvironments. Nat. Methods 2006, 3, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Weizel, A.; Zimmermann, J.; Riess, A.; Kruger, S.; Bader, R.; van Rienen, U.; Seitz, H. Numerical simulation of the electric field distribution in an electrical stimulation device for scaffolds settled with cartilaginous cells. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 6481–6484. [Google Scholar] [CrossRef]
- Sukhorukov, V.L.; Mussauer, H.; Zimmermann, U. The effect of electrical deformation forces on the electropermeabilization of erythrocyte membranes in low- and high- conductivity media. J. Membr. Biol. 1998, 163, 235–245. [Google Scholar] [CrossRef] [PubMed]
- MacQueen, L.A.; Buschmann, M.D.; Wertheimer, M.R. Mechanical properties of mammalian cells in suspension measured by electro-deformation. J. Micromech. Microeng. 2010, 20. [Google Scholar] [CrossRef]
- Chen, J.; Abdelgawad, M.; Yu, L.; Shakiba, N.; Chien, W.Y.; Lu, Z.; Geddie, W.R.; Jewett, M.A.; Sun, Y. Electrodeformation for single cell mechanical characterization. J. Micromech. Microeng. 2011, 21. [Google Scholar] [CrossRef]
- Guido, I.; Jaeger, M.S.; Duschl, C. Dielectrophoretic stretching of cells allows for characterization of their mechanical properties. Eur. Biophys. J. 2011, 40, 281–288. [Google Scholar] [CrossRef]
- Ermolina, I.; Polevaya, Y.; Feldman, Y. Analysis of dielectric spectra of eukaryotic cells by computer modeling. Eur. Biophys. J. 2000, 29, 141–145. [Google Scholar] [CrossRef] [PubMed]
- Cho, M.R.; Thatte, H.S.; Silvia, M.T.; Golan, D.E. Transmembrane calcium influx induced by ac electric fields. FASEB J. 1999, 13, 677–683. [Google Scholar] [CrossRef] [PubMed]
- Shamoon, D.; Lasquellec, S.; Brosseau, C. Perspective: Towards understanding the multiscale description of cells and tissues by electromechanobiology. J. Appl. Phys. 2018, 123, 240902. [Google Scholar] [CrossRef]
- Li, S.; Tallia, F.; Mohammed, A.A.; Stevens, M.M.; Jones, J.R. Scaffold channel size influences stem cell differentiation pathway in 3-D printed silica hybrid scaffolds for cartilage regeneration. Biomater. Sci. 2020, 8, 4458–4466. [Google Scholar] [CrossRef]
- Cho, M.R.; Thatte, H.S.; Lee, R.C.; Golan, D.E. Induced redistribution of cell surface receptors by alternating current electric fields. FASEB J. 1994, 8, 771–776. [Google Scholar] [CrossRef]
- Lin, B.J.; Tsao, S.H.; Chen, A.; Hu, S.K.; Chao, L.; Chao, P.H.G. Lipid rafts sense and direct electric field-induced migration. Proc. Natl. Acad. Sci. USA 2017, 114, 8568–8573. [Google Scholar] [CrossRef]
- Bennetts, C.J.; Sibole, S.; Erdemir, A. Automated generation of tissue-specific three-dimensional finite element meshes containing ellipsoidal cellular inclusions. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1293–1304. [Google Scholar] [CrossRef] [PubMed]
- Ni, Y.; Mulier, S.; Miao, Y.; Michel, L.; Marchal, G. A review of the general aspects of radiofrequency ablation. Abdom. Imaging 2005, 30, 381–400. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Thermal ablation of biological tissues in disease treatment: A review of computational models and future directions. Electromagn. Biol. Med. 2020, 39, 49–88. [Google Scholar] [CrossRef]
- MacDonald, R.A.; Voge, C.M.; Kariolis, M.; Stegemann, J.P. Carbon nanotubes increase the electrical conductivity of fibroblast-seeded collagen hydrogels. Acta Biomater. 2008, 4, 1583–1592. [Google Scholar] [CrossRef]
- Vaitkuviene, A.; Kaseta, V.; Voronovic, J.; Ramanauskaite, G.; Biziuleviciene, G.; Ramanaviciene, A.; Ramanavicius, A. Evaluation of cytotoxicity of polypyrrole nanoparticles synthesized by oxidative polymerization. J. Hazard. Mater. 2013, 250–251, 167–174. [Google Scholar] [CrossRef] [PubMed]
- Ibarra, L.E.; Tarres, L.; Bongiovanni, S.; Barbero, C.A.; Kogan, M.J.; Rivarola, V.A.; Bertuzzi, M.L.; Yslas, E.I. Assessment of polyaniline nanoparticles toxicity and teratogenicity in aquatic environment using Rhinella arenarum model. Ecotoxicol. Environ. Saf. 2015, 114, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Farooqi, A.R.; Zimmermann, J.; Bader, R.; van Rienen, U. Numerical Simulation of Electroactive Hydrogels for Cartilage–Tissue Engineering. Materials 2019, 12, 2913. [Google Scholar] [CrossRef] [PubMed]
- Sieber, S.; Michaelis, M.; Gühring, H.; Lindemann, S.; Gigout, A. Importance of osmolarity and oxygen tension for cartilage tissue engineering. BioRes. Open Access 2020, 9, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Keysight Technologies. Impedance Measurement Handbook: A Guide to Measurement Technology and Techniques, 6th ed.; Keysight Technologies: Santa Rosa, CA, USA, 2016. [Google Scholar]
- Van Rienen, U.; Flehr, J.; Schreiber, U.; Schulze, S.; Gimsa, U.; Baumann, W.; Weiss, D.G.; Gimsa, J.; Benecke, R.; Pau, H.W. Electro-quasistatic simulations in bio-systems engineering and medical engineering. Adv. Radio Sci. 2005, 3, 39–49. [Google Scholar] [CrossRef]
- Zimmermann, J.; Altenkirch, R.; van Rienen, U. Effect of electrical stimulation on biological cells by capacitive coupling—An efficient numerical study considering model uncertainties. Generic Color. J. 2020. [Google Scholar] [CrossRef]
- Lemieux, C. Monte Carlo and Quasi-Monte Carlo Sampling; Springer Series in Statistics; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar] [CrossRef]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Tennøe, S.; Halnes, G.; Einevoll, G.T. Uncertainpy: A Python Toolbox for Uncertainty Quantification and Sensitivity Analysis in Computational Neuroscience. Front. Neuroinform. 2018, 12, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Eck, V.G.; Donders, W.P.; Sturdy, J.; Feinberg, J.; Delhaas, T.; Hellevik, L.R.; Huberts, W. A guide to uncertainty quantification and sensitivity analysis for cardiovascular applications. Int. J. Numer. Methods Biomed. Eng. 2016, 32, e02755. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.; Gabriel, C.; Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef]
- Cooper, W.G. A Modified Plastic Petri Dish for Cell and Tissue Cultures. Exp. Biol. Med. 1961, 106, 801–803. [Google Scholar] [CrossRef]
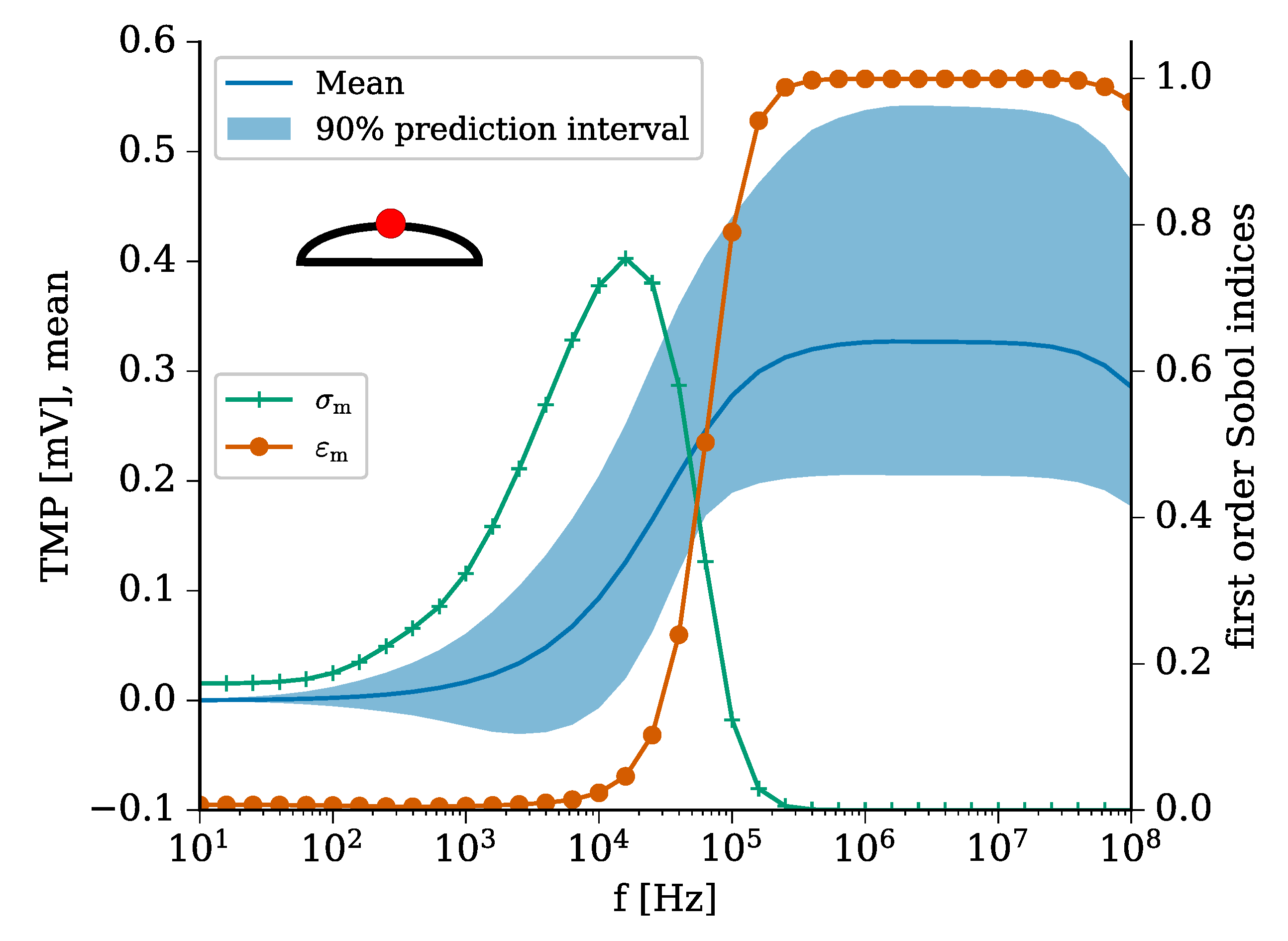
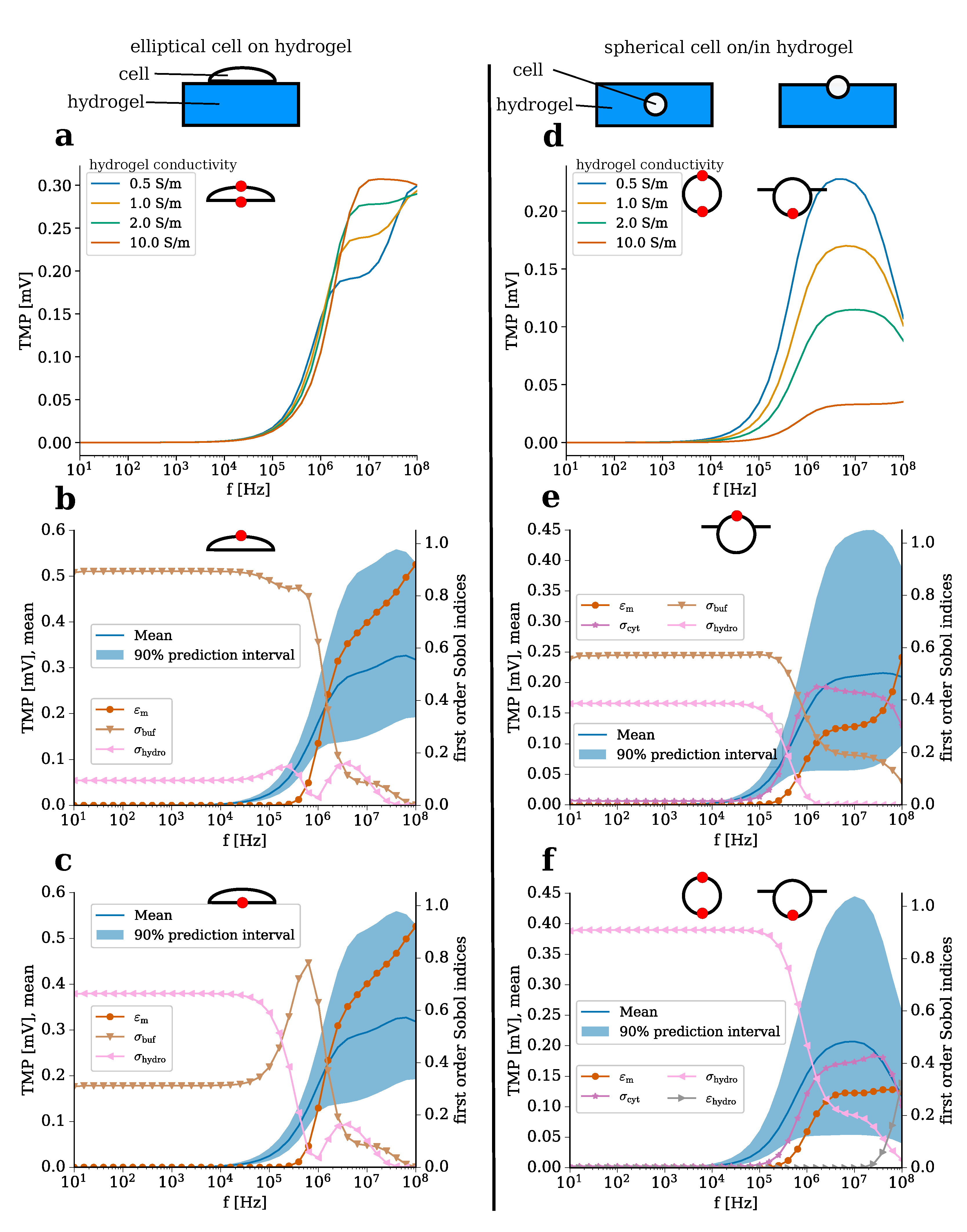
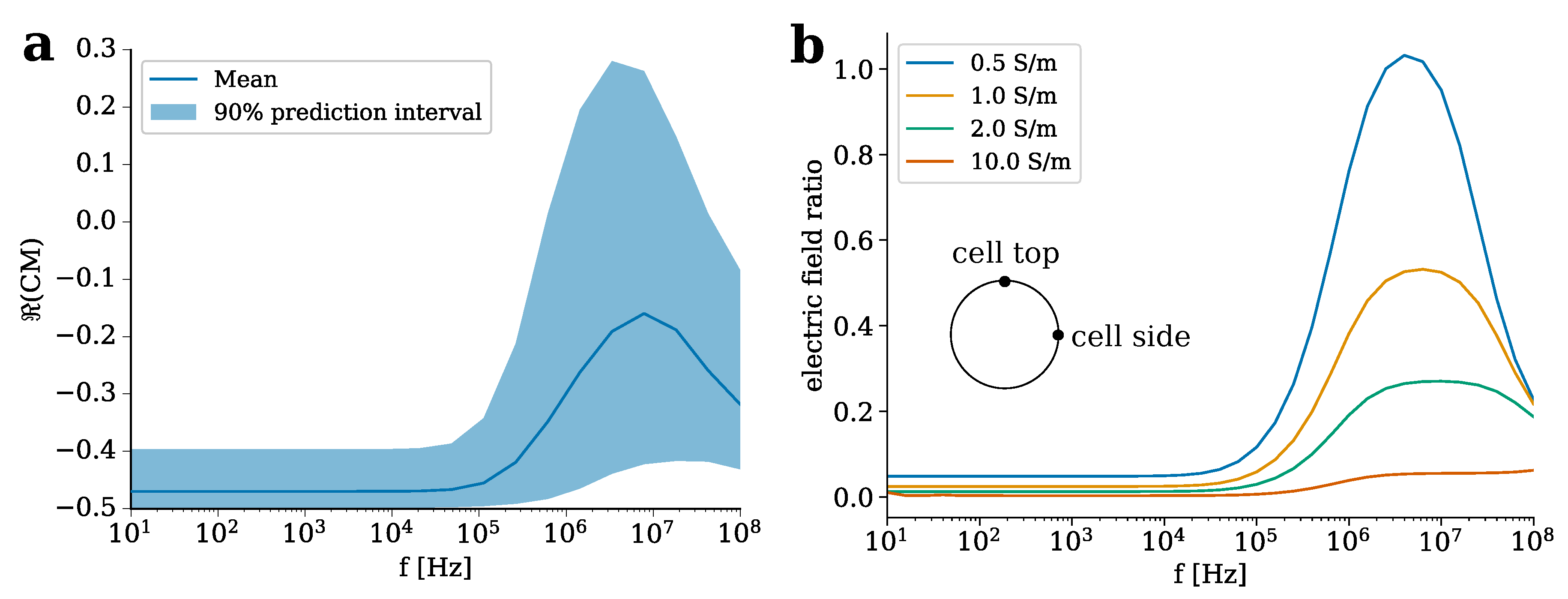
| Domain (Subscript) | Conductivity [S m] | Permittivity |
|---|---|---|
| Hydrogel (hydro) | ||
| Buffer medium (buf) | (benchmark) or 80 | |
| Membrane (m) | ||
| Cytoplasm (cyt) | 60 |
| Domain | Subscript | Electrical Conductivity [S m] | Rel. Permittivity |
|---|---|---|---|
| Insulator/Lid | ins | 0 | |
| Cover slip | cs | 0 | 4 |
| Culture medium | buf | 80 | |
| Cytoplasm | cyt | 60 | |
| Cell membrane | m | 0 |
| Domain (Subscript) | Conductivity [S m] | Permittivity |
|---|---|---|
| Membrane (m) | ||
| Cytoplasm (cyt) | ||
| Nuclear envelope (ne) | ||
| Nucleoplasm (np) |
| Parameter | Symbol | Probability Distribution |
|---|---|---|
| Cell radius | ||
| Membrane thickness | nm | |
| scale | ||
| Nuclear envelope thickness | nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimmermann, J.; Distler, T.; Boccaccini, A.R.; van Rienen, U. Numerical Simulations as Means for Tailoring Electrically Conductive Hydrogels towards Cartilage Tissue Engineering by Electrical Stimulation. Molecules 2020, 25, 4750. https://doi.org/10.3390/molecules25204750
Zimmermann J, Distler T, Boccaccini AR, van Rienen U. Numerical Simulations as Means for Tailoring Electrically Conductive Hydrogels towards Cartilage Tissue Engineering by Electrical Stimulation. Molecules. 2020; 25(20):4750. https://doi.org/10.3390/molecules25204750
Chicago/Turabian StyleZimmermann, Julius, Thomas Distler, Aldo R. Boccaccini, and Ursula van Rienen. 2020. "Numerical Simulations as Means for Tailoring Electrically Conductive Hydrogels towards Cartilage Tissue Engineering by Electrical Stimulation" Molecules 25, no. 20: 4750. https://doi.org/10.3390/molecules25204750
APA StyleZimmermann, J., Distler, T., Boccaccini, A. R., & van Rienen, U. (2020). Numerical Simulations as Means for Tailoring Electrically Conductive Hydrogels towards Cartilage Tissue Engineering by Electrical Stimulation. Molecules, 25(20), 4750. https://doi.org/10.3390/molecules25204750









