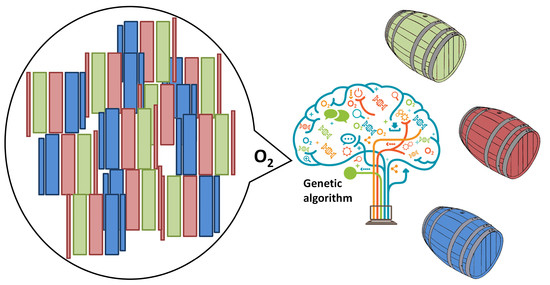
Artificial Intelligence Methods for Constructing Wine Barrels with a Controlled Oxygen Transmission Rate
Abstract
1. Introduction
2. Materials and Methods
2.1. Oak Wood Samples
2.2. Barrel Construction Process
3. Calculation
3.1. Head and Body OTR Calculation
3.2. Genetic Algorithms
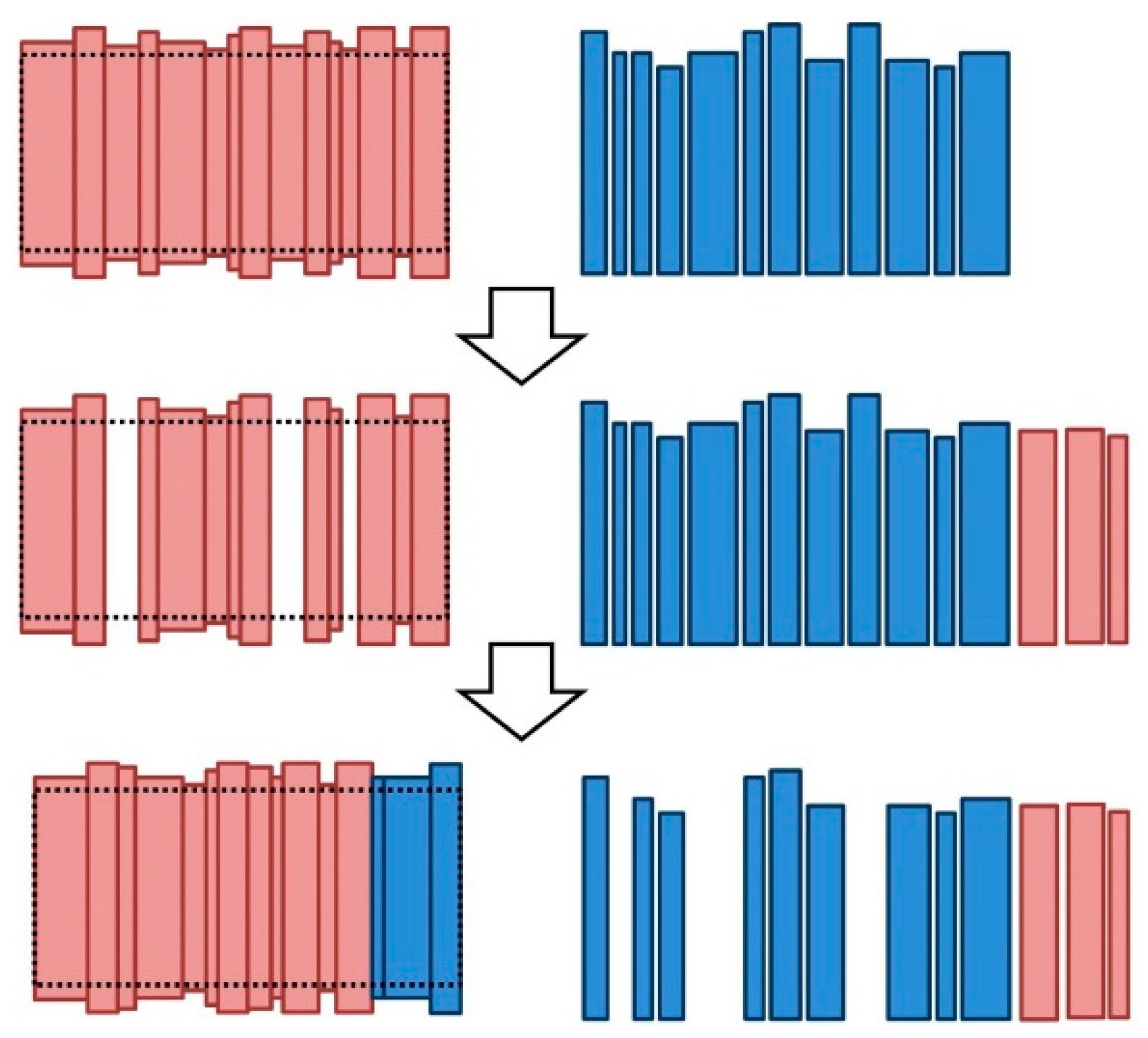
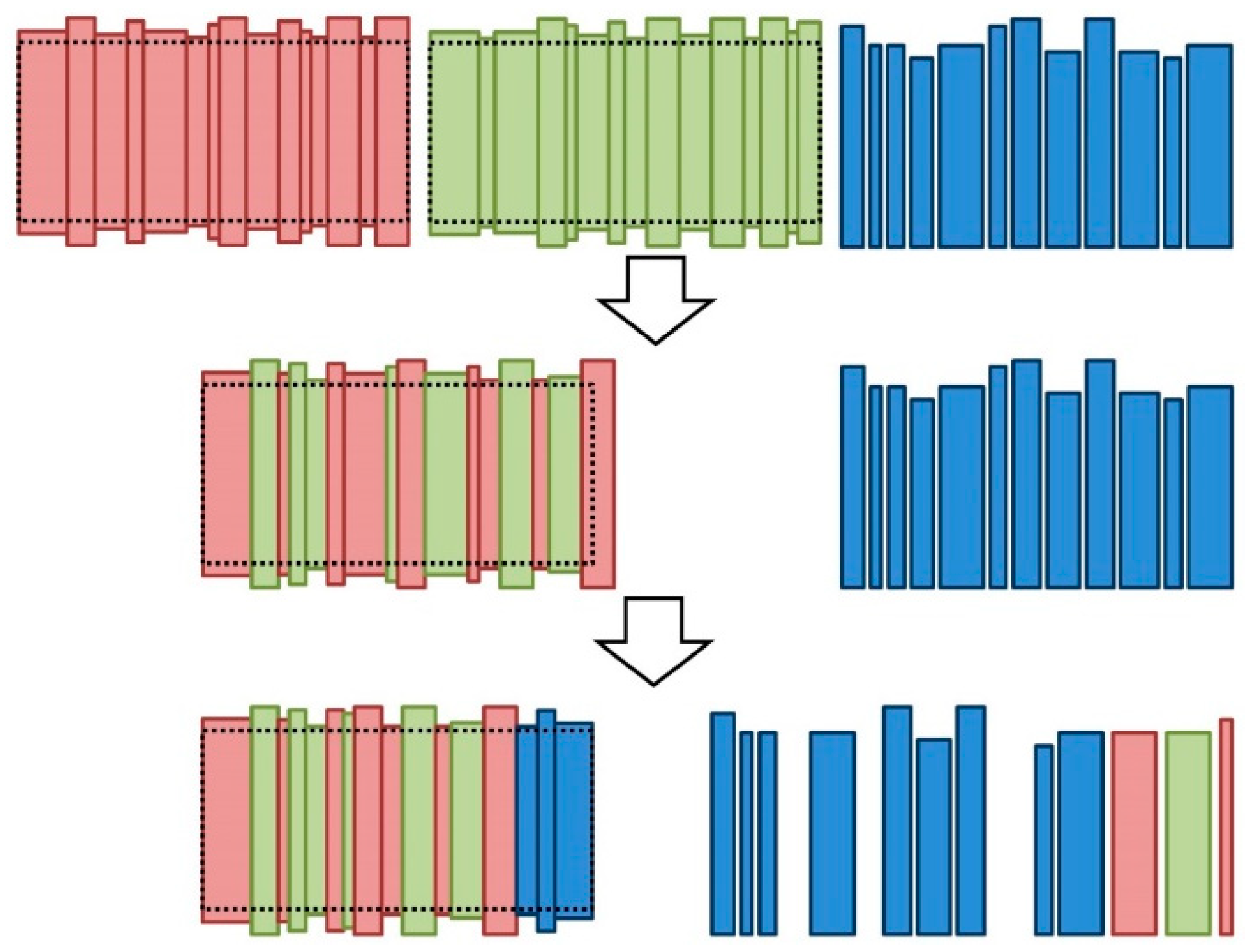
3.2.1. Barrel Head Construction
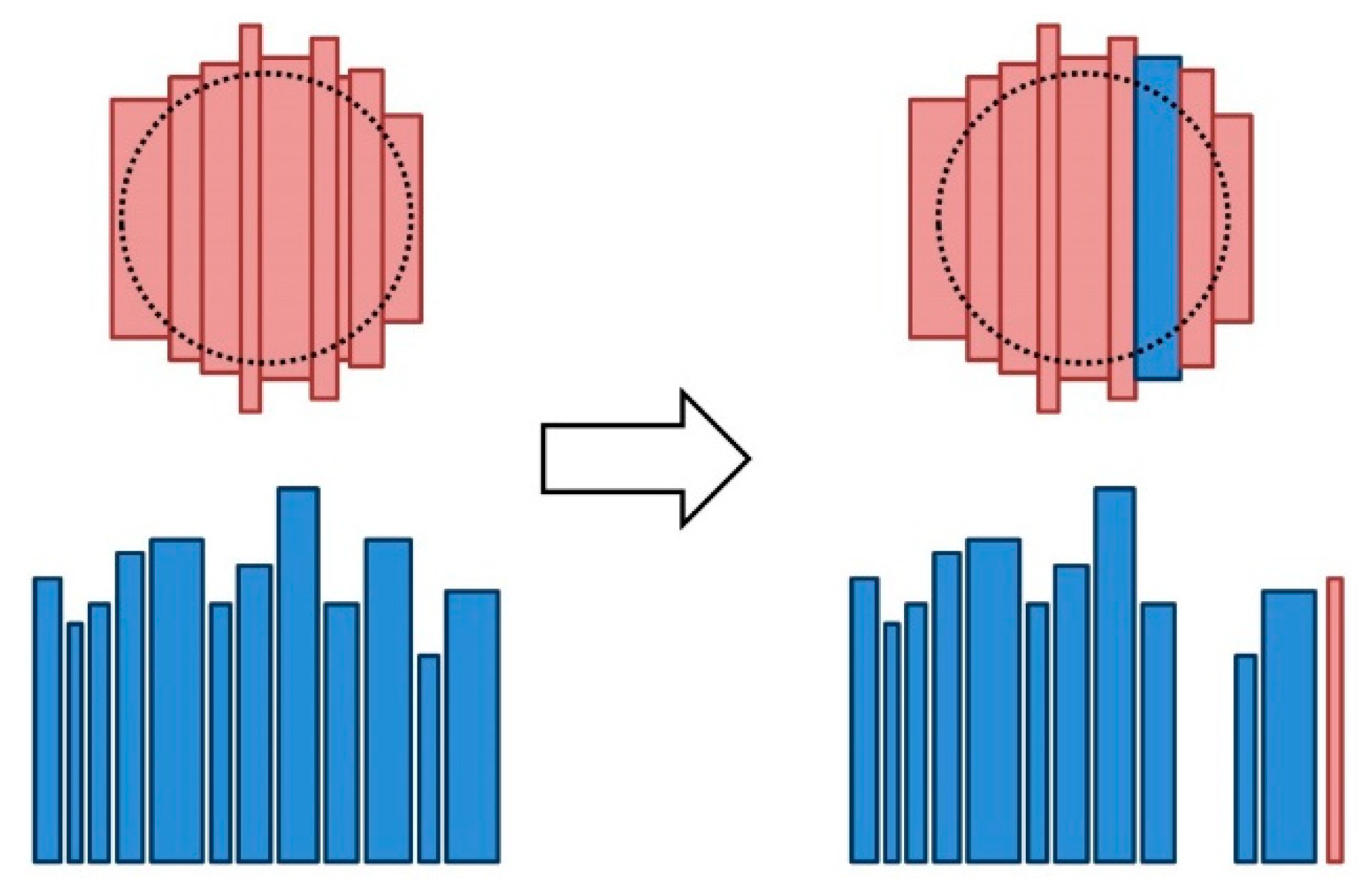
Barrel Head Mutation
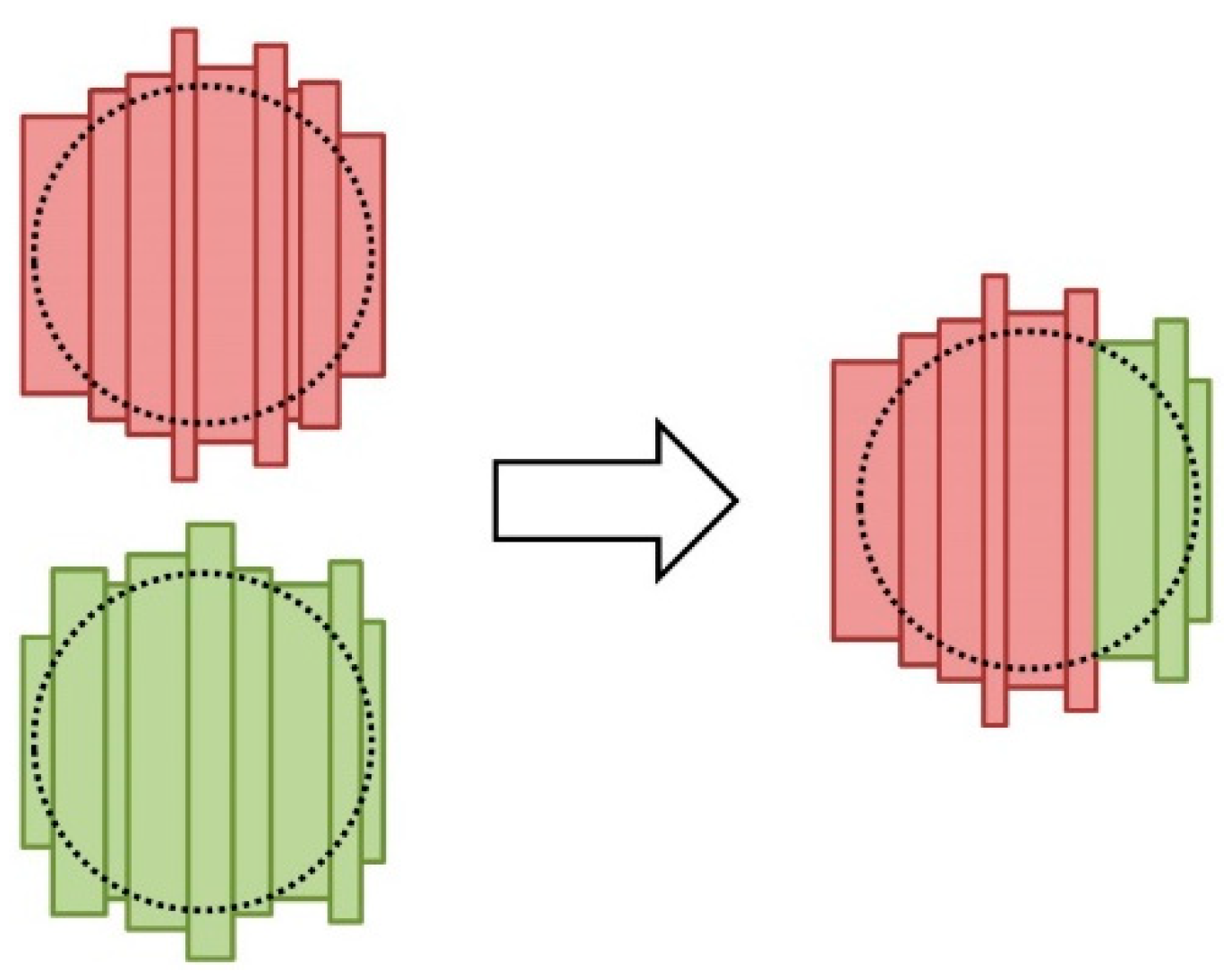
Barrel Head External Crossing
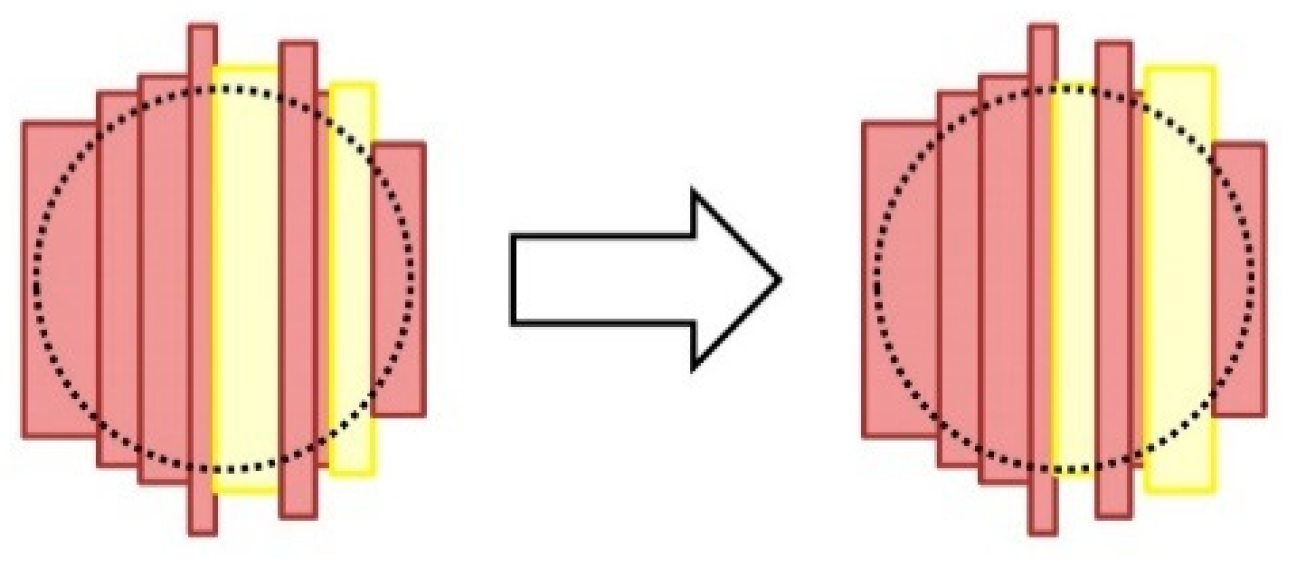
Barrel Head Internal Crossing
3.2.2. Barrel Body Construction
Barrel Body Mutation
Barrel Body External Crossing
3.2.3. GA-Based Method Implementation
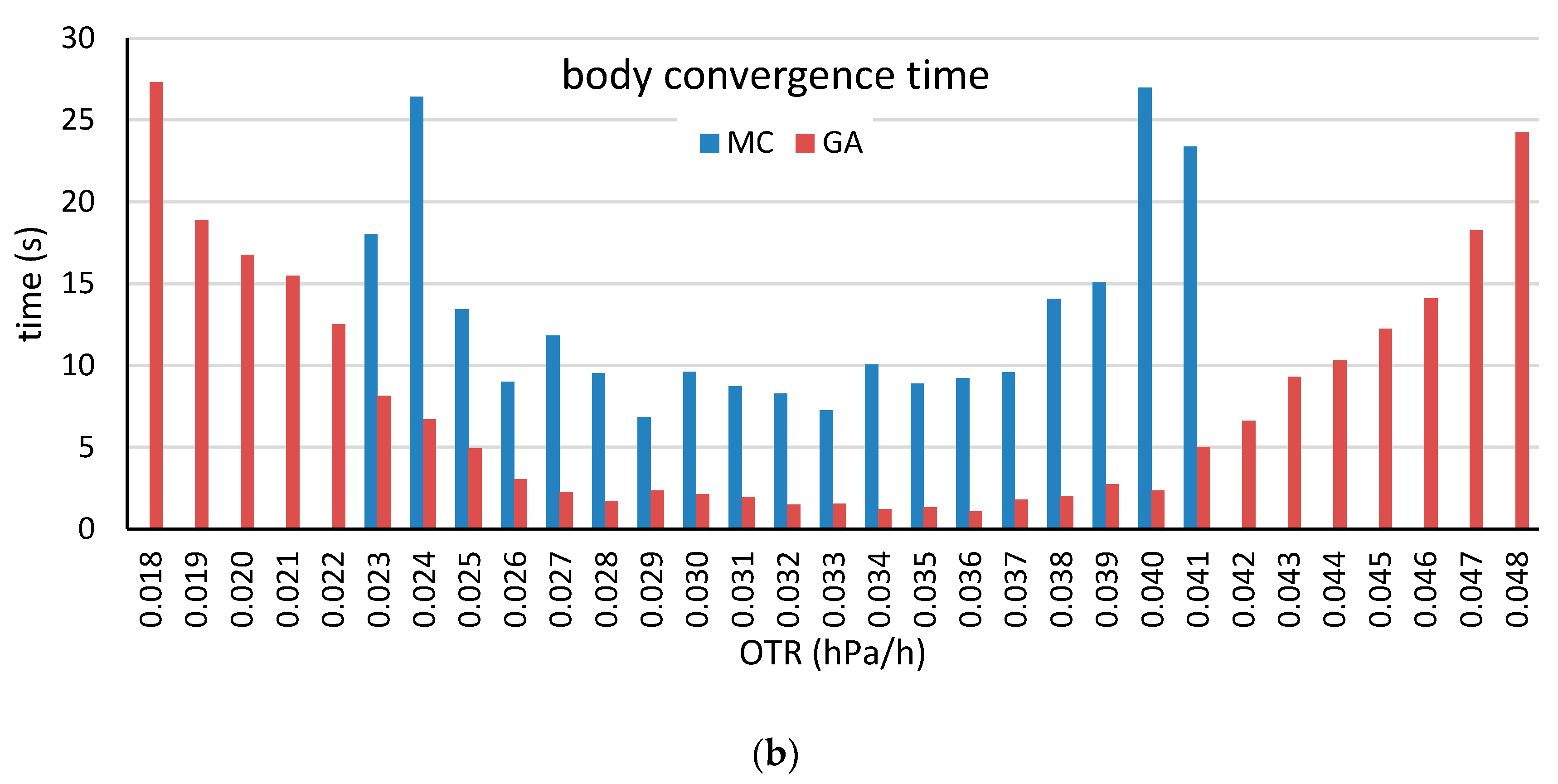
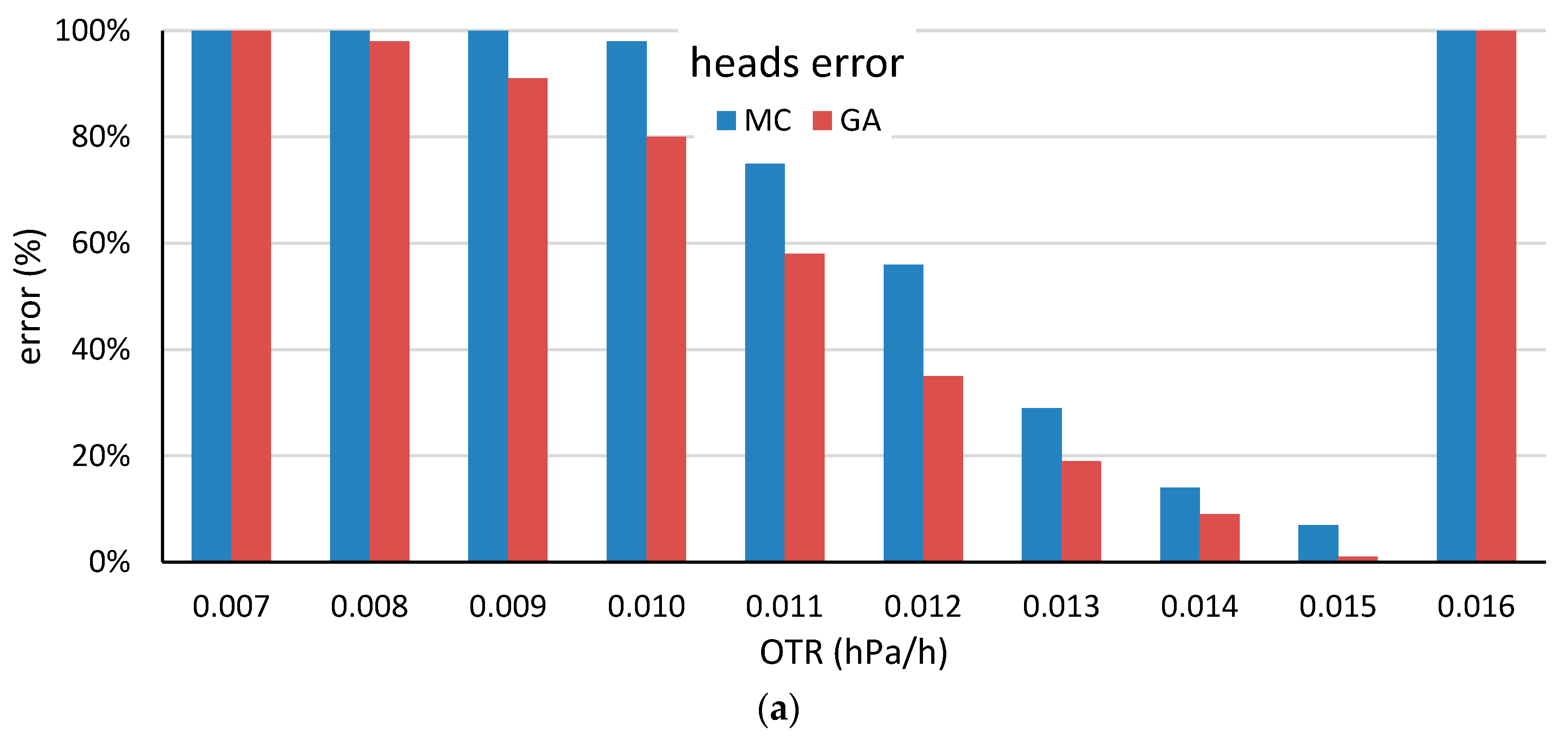
3.3. GA-Based Method Comparison
4. Results and Discussion
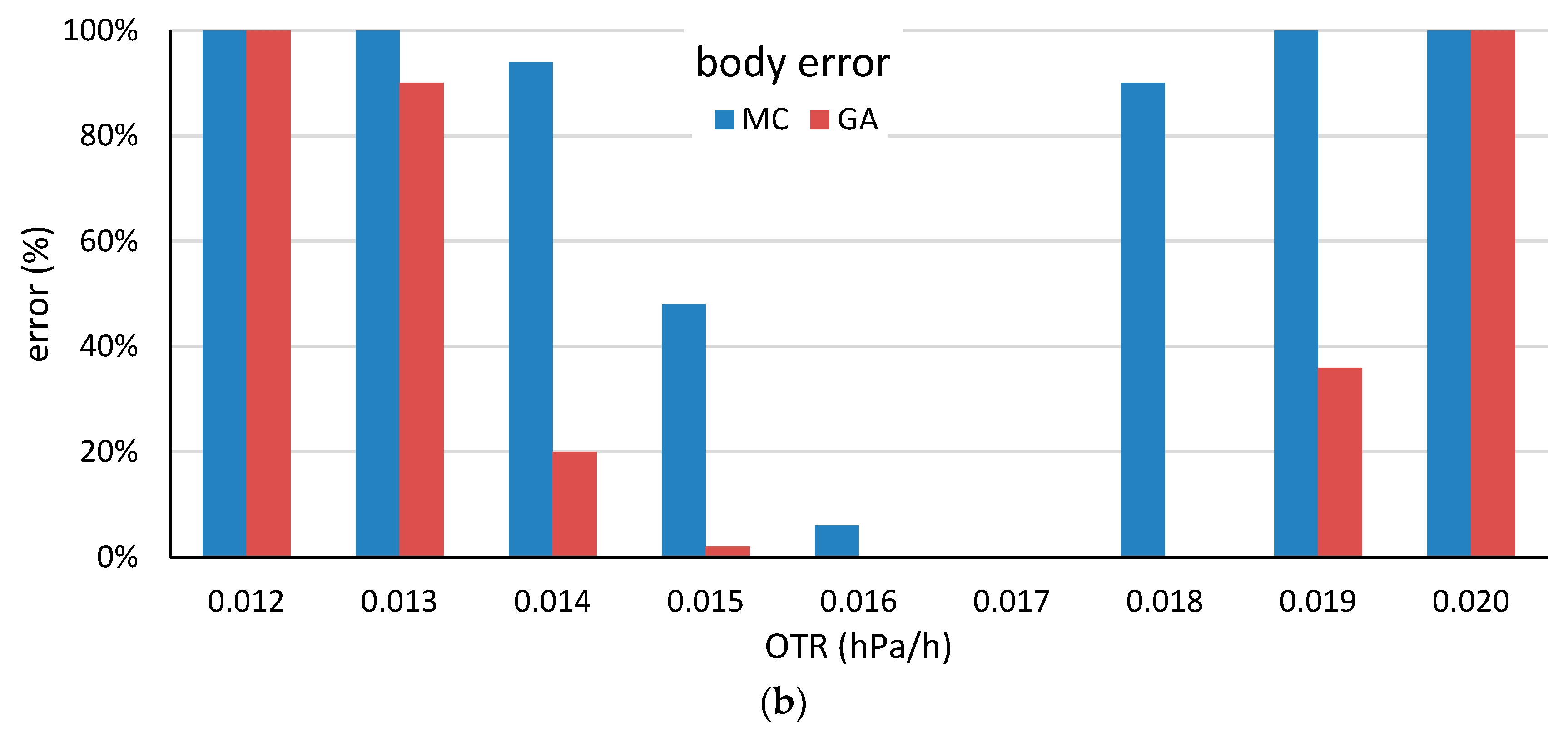
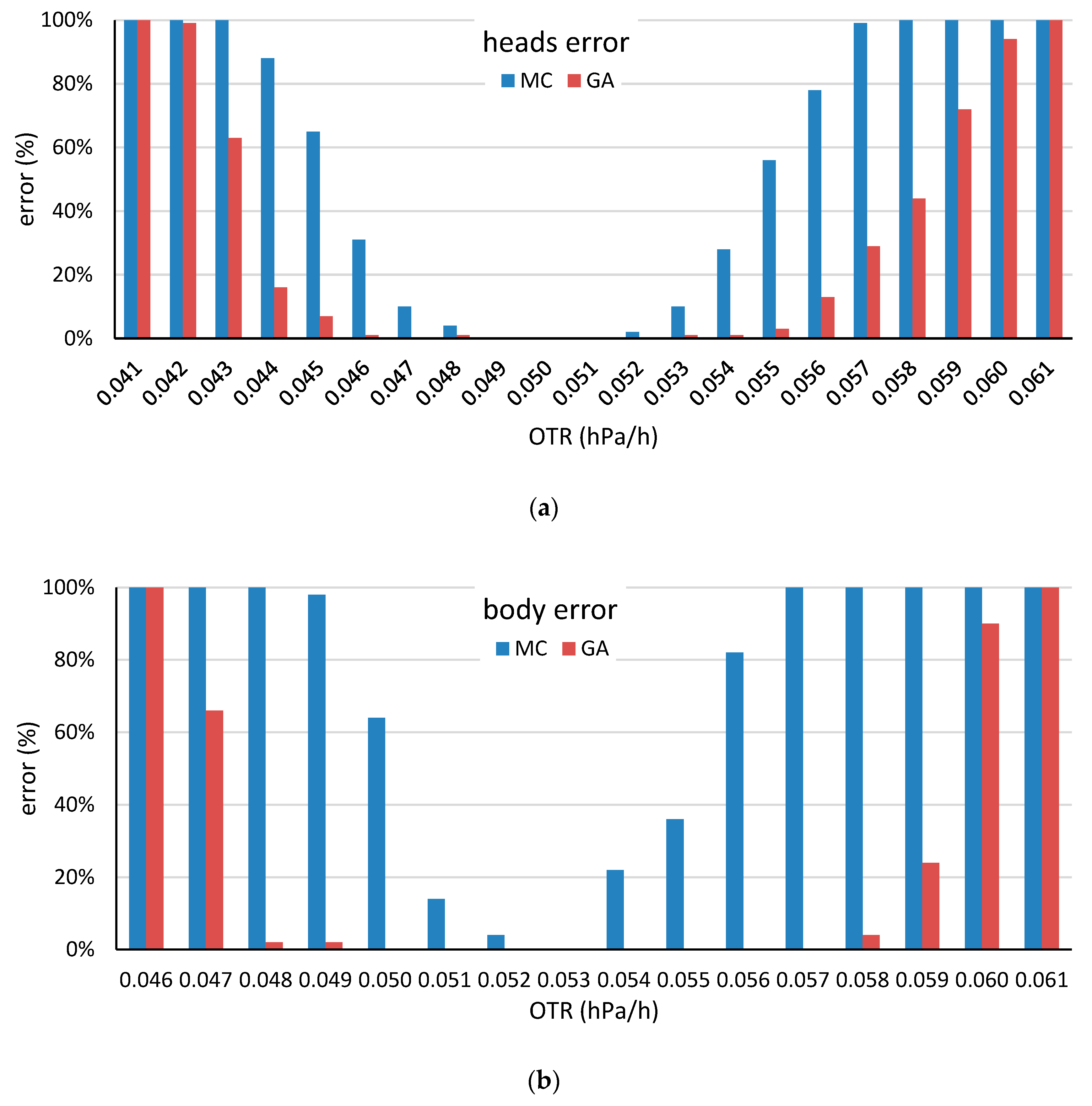
4.1. Barrel Homogenization
4.2. Low-OTR and High-OTR Barrel Production
4.3. Real Cooperage Simulation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Twede, D. The cask age: The technology and history of wooden barrels. Packag. Technol. Sci. An Int. J. 2005, 18, 253–264. [Google Scholar] [CrossRef]
- Bassanezi, R.C. Ensino-Aprendizagem Com Modelagem Matemática: Uma Nova Estratégia; Editora Contexto: São Paulo, Brazil, 2002. [Google Scholar]
- Rosa, M.; Orey, D.C. Ethnomodeling as a Research Theoretical Framework on Ethnomathematics and Mathematical Modeling. J. Urban Math. Educ. 2013, 6, 62–80. [Google Scholar]
- Prat-García, S.; Nevares, I.; Martínez-Martínez, V.; del Alamo-Sanza, M. Customized oxygenation barrels as a new strategy for controlled wine aging. Food Res. Int. 2020, 131, 108982. [Google Scholar] [CrossRef]
- Hansmann, C.; Gindl, W.; Wimmer, R. Permeability of wood—A review. Wood Res. 2002, 47, 1–16. [Google Scholar]
- Jinman, W.; Chengyue, D.; Yixing, L. Wood permeability. J. Northeast. For. Univ. 1991, 2, 91–97. [Google Scholar]
- Bao, F.; Lu, J.; Avramidis, S. On the Permeability of Main Wood Species in China. Holzforschung 1999, 53, 350–354. [Google Scholar] [CrossRef]
- Comstock, G.L. Longitudinal Permeability of Wood to Gases and Nonswelling Liquids. For. Prod. J. 1967, 17, 41–46. [Google Scholar]
- Comstock, G.L. Directional permeability of softwoods. Wood Fiber. 1970, 1, 283–289. [Google Scholar]
- Choong, E.T.; Tesoro, F.O.; Manwiller, F. Permeability ot twenty-two small diameter hardwoods growing on southern pine sites. Wood Fiber. 1974, 6, 91–101. [Google Scholar]
- Kininmonth, J.A. Permeability and Fine Structure of Certain Hardwoods and Effects on Drying: II. Differences in Fine Structure of Nothofagus fusca Sapwood and Heartwood. Holzforschung 1972, 26, 32–38. [Google Scholar] [CrossRef]
- Sorz, J.; Hietz, P. Gas diffusion through wood: Implications for oxygen supply. Trees—Struct. Funct. 2006, 20, 34–41. [Google Scholar] [CrossRef]
- Nevares, I.; Crespo, R.; González, C.; del Alamo-Sanza, M. Imaging of oxygen permeation in the oak wood of wine barrels using optical sensors and a colour camera. Aust. J. Grape Wine Res. 2014, 20, 353–360. [Google Scholar] [CrossRef]
- Nevares Domínguez, I.; del Alamo-Sanza, M. Oxygène et barriques: Actualisation des connaissances Quantité et voies de pénétration de l’oxygène dans la barrique. Revue des Oenologues et des Techniques Vitivinicoles et Oenologiques: Magazine Trimestriel D’information Professionnelle 2014, 41, 41–44. [Google Scholar]
- Nevares, I.; Del Alamo-Sanza, M. Oak stave oxygen permeation: A new tool to make barrels with different wine oxygenation potentials. J. Agric. Food Chem. 2015, 63, 1268–1275. [Google Scholar] [CrossRef]
- Nevares, I.; Mayr, T.; Baro, J.A.; Ehgartner, J.; Crespo, R.; Del Alamo-Sanza, M. Ratiometric Oxygen Imaging to Predict Oxygen Diffusivity in Oak Wood During Red Wine Barrel Aging. Food Bioprocess Technol. 2016, 9, 1049–1059. [Google Scholar] [CrossRef]
- Del Alamo-Sanza, M.; Nevares, I.; Mayr, T.; Baro, J.A.; Martínez-Martínez, V.; Ehgartner, J. Analysis of the role of wood anatomy on oxygen diffusivity in barrel staves using luminescent imaging. Sens. Actuators B Chem. 2016, 237, 1035–1043. [Google Scholar] [CrossRef]
- Nevares, I.; Del Alamo-Sanza, M.; Martínez-Martínez, V.; Menéndez-Miguélez, M.; Van den Bulcke, J.; Van Acker, J. Influence of Quercus petraea Liebl. wood structure on the permeation of oxygen through wine barrel staves. Wood Res. Technol. Holzforsch. 2019, 73, 859–870. [Google Scholar] [CrossRef]
- Martínez-Martínez, V.; Del Alamo-Sanza, M.; Nevares, I. Application of image analysis and artificial neural networks to the prediction in-line of OTR in oak wood planks for cooperage. Mater. Des. 2019, 181, 107979. [Google Scholar] [CrossRef]
- Anantharaman, T.; Campbell, M.S.; Hsu, F.H. Singular extensions. Adding selectivity to brute-force searching. Artif. Intell. 1990, 43, 99–109. [Google Scholar] [CrossRef]
- Liu, J.S. Monte Carlo Strategies in Scientific Computing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Dorigo, M.; Di Caro, G. Ant colony optimization: A new meta-heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington DC, USA, 6–9 July 1999. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Kennedy, J.R. A new optimizer using particles swarm theory. In MHS’95, Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; IEEE: Piscataway, NJ, USA; pp. 39–43.
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology. Control, and Artificial Intelligence; MIT Press: London, UK, 1992. [Google Scholar]
- Melville, N.; Gurbaxani, V.; Kraemer, K. The productivity impact of information technology across competitive regimes: The role of industry concentration and dynamism. Decis. Support Syst. 2007, 43, 229–242. [Google Scholar] [CrossRef]
- Shaw, M.J.; Menon, U. Knowledge-based manufacturing quality management: A qualitative reasoning approach. Decis. Support Syst. 1990, 6, 59–81. [Google Scholar] [CrossRef]
- Guyer, D.; Yang, X. Use of genetic artificial neural networks and spectral imaging for defect detection on cherries. Comput. Electron. Agric. 2000, 29, 179–194. [Google Scholar] [CrossRef]
- Hopper, E.; Turton, B.C.H. Genetic algorithm for a 2D industrial packing problem. Comput. Ind. Eng. 1999, 37, 375–378. [Google Scholar] [CrossRef]
- Bennell, J.A.; Soon Lee, L.; Potts, C.N. A genetic algorithm for two-dimensional bin packing with due dates. Int. J. Prod. Econ. 2013, 145, 547–560. [Google Scholar] [CrossRef]
- Wang, C.H.; Hsu, L.C. Using genetic algorithms grey theory to forecast high technology industrial output. Appl. Math. Comput. 2008, 195, 256–263. [Google Scholar] [CrossRef]
- Hsu, L.C. Forecasting the output of integrated circuit industry using genetic algorithm based multivariable grey optimization models. Expert Syst. Appl. 2009, 36, 7898–7903. [Google Scholar] [CrossRef]
- Wang, L.; Wang, P.; Liang, S.; Zhu, Y.; Khan, J.; Fang, S. Monitoring maize growth on the North China Plain using a hybrid genetic algorithm-based back-propagation neural network model. Comput. Electron. Agric. 2020, 170, 105238. [Google Scholar] [CrossRef]
- Lee, Y.S.; Tong, L.I. Forecasting energy consumption using a grey model improved by incorporating genetic programming. Energy Convers. Manag. 2011, 52, 147–152. [Google Scholar] [CrossRef]
- Buratti, S.; Ballabio, D.; Benedetti, S.; Cosio, M.S. Prediction of Italian red wine sensorial descriptors from electronic nose, electronic tongue and spectrophotometric measurements by means of Genetic Algorithm regression models. Food Chem. 2007, 100, 211–218. [Google Scholar] [CrossRef]
- Beltrán, N.H.; Duarte-Mermoud, M.A.; Salah, S.A.; Bustos, M.A.; Peña-Neira, A.I.; Loyola, E.A.; Jalocha, J.W. Feature selection algorithms using Chilean wine chromatograms as examples. J. Food Eng. 2005, 67, 483–490. [Google Scholar] [CrossRef]
- Cao, F.; Wu, D.; He, Y. Soluble solids content and pH prediction and varieties discrimination of grapes based on visible-near infrared spectroscopy. Comput. Electron. Agric. 2010, 71, S15–S18. [Google Scholar] [CrossRef]
- Corcoran, P.; Anglesea, J.; Elshaw, M. The application of genetic algorithms to sensor parameter selection for multisensor array configuration. Sens. Actuators A Phys. 1999, 76, 57–66. [Google Scholar] [CrossRef]
- Kuo, R.J.; Lin, L.M. Application of a hybrid of genetic algorithm and particle swarm optimization algorithm for order clustering. Decis. Support Syst. 2010, 49, 451–462. [Google Scholar] [CrossRef]
- Qiu, Y.; Lacampagne, S.; Mirabel, M.; Mietton-Peuchot, M.; Ghidoss, R. Oxygen desorption and oxygen transfer through oak staves and oak stave gaps: An innovative permeameter. OENO One 2018, 52, 1–14. [Google Scholar] [CrossRef]
- Vivas, N.; Glories, Y. Modélisation et calcul du bilan des apports d’oxygène au cours de l’élevage des vins rouges. II. Les apports liés au passage d’oxygène au travers de la barrique. Progrès Agricole et Viticole 1997, 114, 315–316. [Google Scholar]





| Procedure | Head | Body |
|---|---|---|
| Generating a new solution | 40.0% | 40.0% |
| Reapplying a solution from the previous generation | 12.0% | 13.4% |
| Applying the mutation operator | 21.0% | 23.3% |
| Applying the internal crossing operator | 6.0% | 0.0% |
| Applying the external crossing operator | 21.0% | 23.3% |
| Method Staves | Time (s) | Mean | Coefficient of Variation | ||||
|---|---|---|---|---|---|---|---|
| Current | MC | GA | Current | MC | GA | ||
| 25 | 1 | 0.029107 | 0.029219 | 0.029252 | 15.53% | 1.4264% | 0.8387% |
| 50 | 1 | 0.028177 | 0.029283 | 0.029282 | 14.83% | 0.0948% | 0.0618% |
| 150 | 1 | 0.029049 | 0.029279 | 0.029280 | 15.86% | 0.0443% | 0.0131% |
| 25 | 5 | 0.028636 | 0.029268 | 0.029270 | 15.72% | 0.4678% | 0.3351% |
| 50 | 5 | 0.028052 | 0.029279 | 0.029280 | 15.64% | 0.0275% | 0.0030% |
| 150 | 5 | 0.028852 | 0.029280 | 0.029280 | 16.79% | 0.0079% | 0.0020% |
| Method Staves | Time (s) | Mean | Coefficient of Variation | ||||
|---|---|---|---|---|---|---|---|
| Current | MC | GA | Current | MC | GA | ||
| 50 | 1 | 0.032259 | 0.032711 | 0.032789 | 7.749% | 1.7901% | 1.0290% |
| 100 | 1 | 0.032094 | 0.032744 | 0.032734 | 6.716% | 0.8282% | 0.1383% |
| 300 | 1 | 0.032538 | 0.032737 | 0.032746 | 7.752% | 0.4966% | 0.1090% |
| 50 | 5 | 0.032762 | 0.032776 | 0.032751 | 8.053% | 0.4985% | 0.0218% |
| 100 | 5 | 0.032650 | 0.032743 | 0.032749 | 7.289% | 0.1223% | 0.0263% |
| 300 | 5 | 0.032412 | 0.032757 | 0.032750 | 6.751% | 0.1030% | 0.0166% |
| Barrel Element | Stave Type | Target OTR | Mean | Coefficient of Variation | ||||
|---|---|---|---|---|---|---|---|---|
| Current | MC | GA | Current | MC | GA | |||
| Heads | L-OTR | 0.0148985 | 0.014750 | 0.014917 | 0.014915 | 5.585% | 0.6261% | 0.4849% |
| Body | L-OTR | 0.0165681 | 0.016483 | 0.016583 | 0.016566 | 3.155% | 0.2608% | 0.0650% |
| Heads | H-OTR | 0.0501335 | 0.050293 | 0.050133 | 0.050133 | 4.178% | 0.0298% | 0.0284% |
| Body | H-OTR | 0.0528710 | 0.052992 | 0.052873 | 0.052869 | 1.804% | 0.1110% | 0.0387% |
| L-OTR | H-OTR | |||
|---|---|---|---|---|
| MC | GA | MC | GA | |
| mean | 0.01615057 | 0.01614661 | 0.05216888 | 0.05219895 |
| standard deviation | 2.6795 × 10−5 | 1.6284 × 10−5 | 1.0365 × 10−4 | 9.1959 × 10−5 |
| coefficient of variation | 0.16591% | 0.10085% | 0.19868% | 0.17617% |
| minimum | 0.01607707 | 0.01608685 | 0.05182518 | 0.05179106 |
| maximum | 0.01626386 | 0.01622588 | 0.05243214 | 0.05244636 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Martínez, V.; Nevares, I.; del Alamo-Sanza, M. Artificial Intelligence Methods for Constructing Wine Barrels with a Controlled Oxygen Transmission Rate. Molecules 2020, 25, 3312. https://doi.org/10.3390/molecules25143312
Martínez-Martínez V, Nevares I, del Alamo-Sanza M. Artificial Intelligence Methods for Constructing Wine Barrels with a Controlled Oxygen Transmission Rate. Molecules. 2020; 25(14):3312. https://doi.org/10.3390/molecules25143312
Chicago/Turabian StyleMartínez-Martínez, Víctor, Ignacio Nevares, and Maria del Alamo-Sanza. 2020. "Artificial Intelligence Methods for Constructing Wine Barrels with a Controlled Oxygen Transmission Rate" Molecules 25, no. 14: 3312. https://doi.org/10.3390/molecules25143312
APA StyleMartínez-Martínez, V., Nevares, I., & del Alamo-Sanza, M. (2020). Artificial Intelligence Methods for Constructing Wine Barrels with a Controlled Oxygen Transmission Rate. Molecules, 25(14), 3312. https://doi.org/10.3390/molecules25143312