Magnetic Elements for Neuromorphic Computing
Abstract
1. Introduction
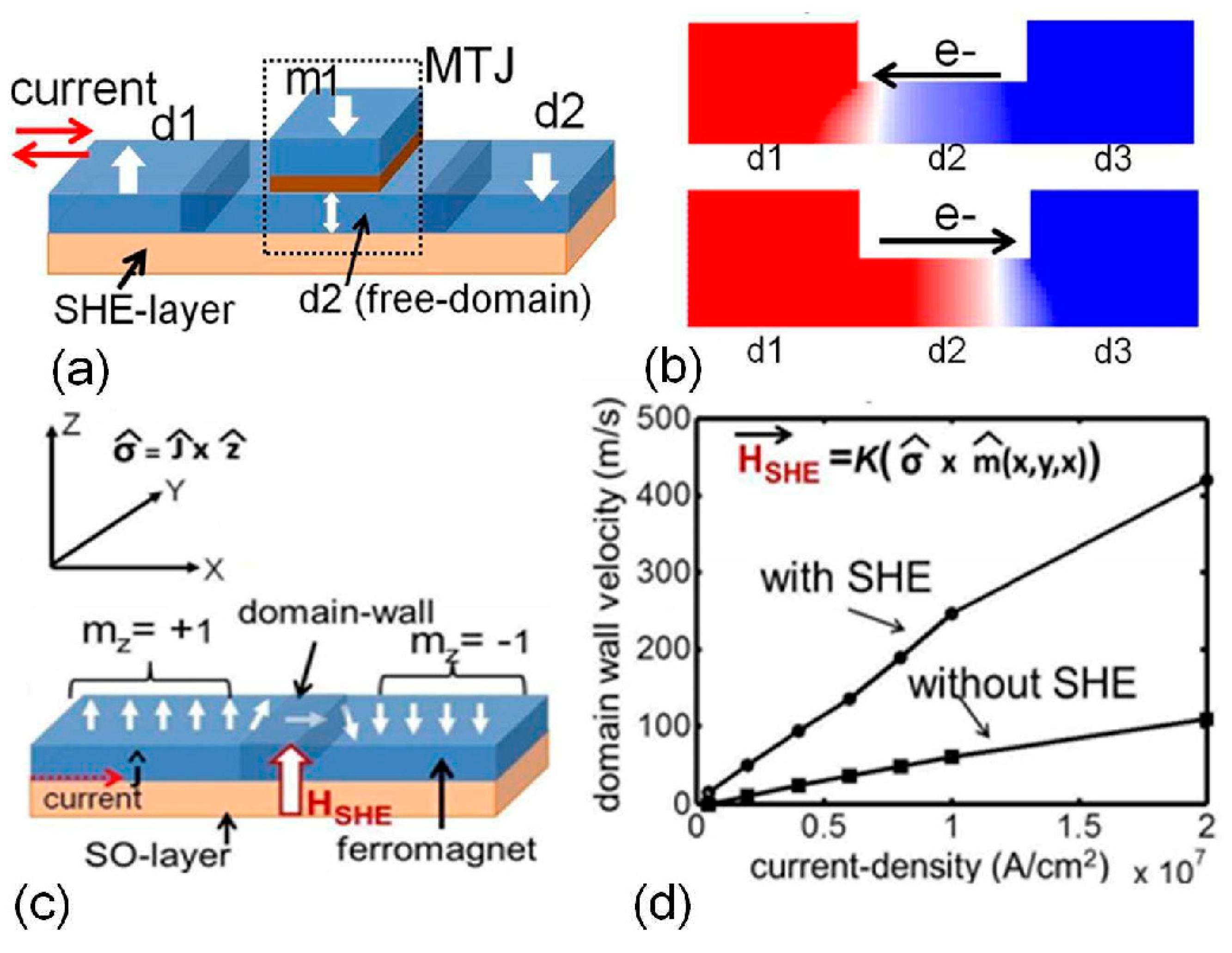
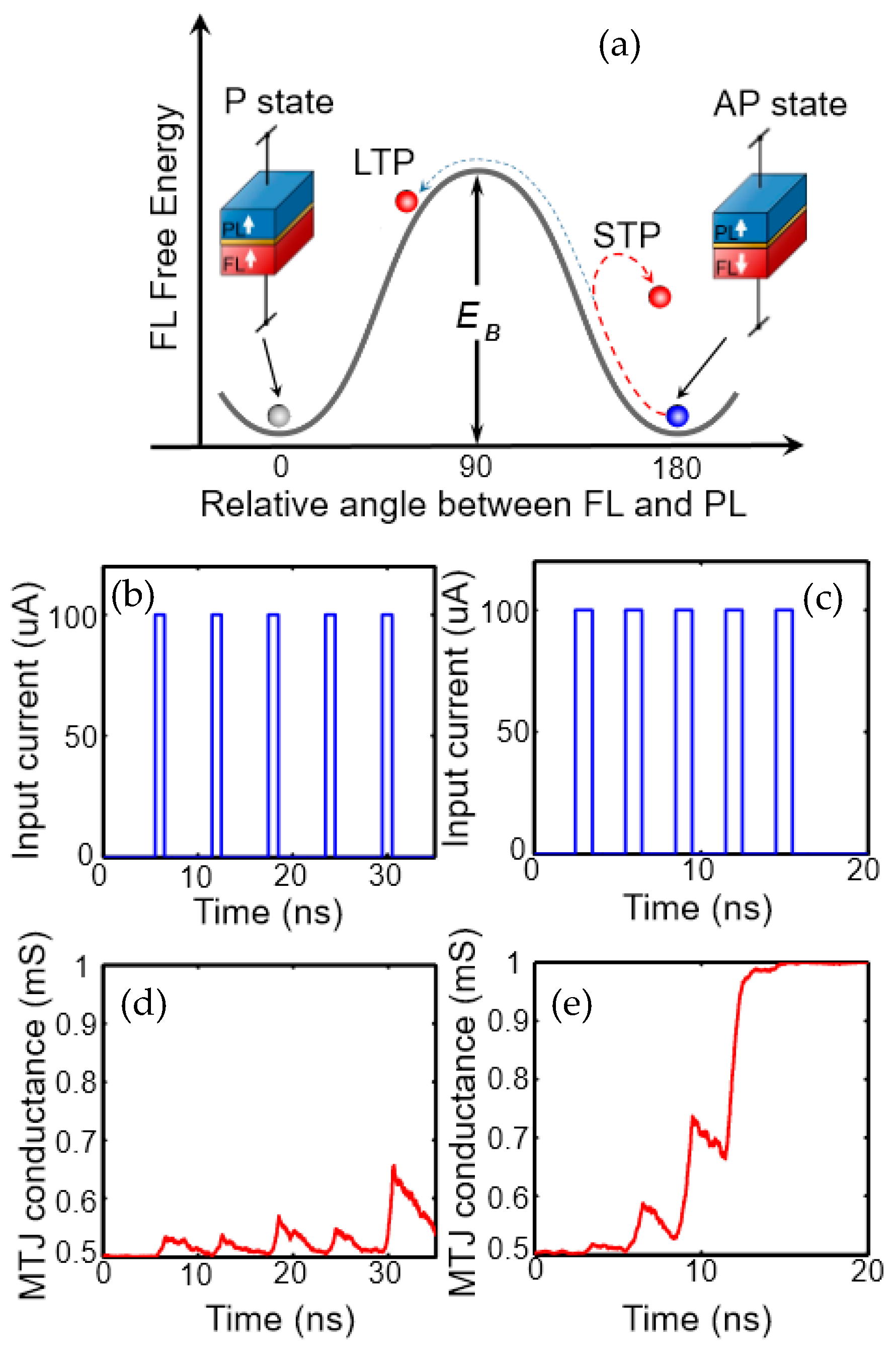
2. Magnetic Tunnel Junctions–Domain Wall Propagation and Different Switching Mechanisms
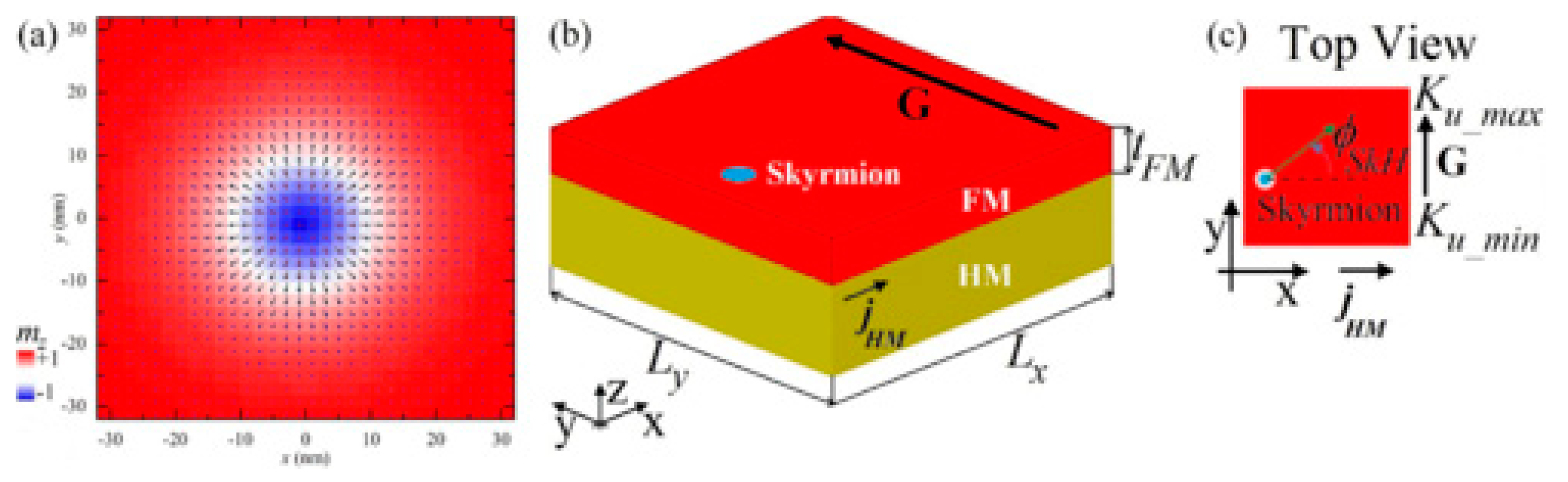
3. Skyrmions
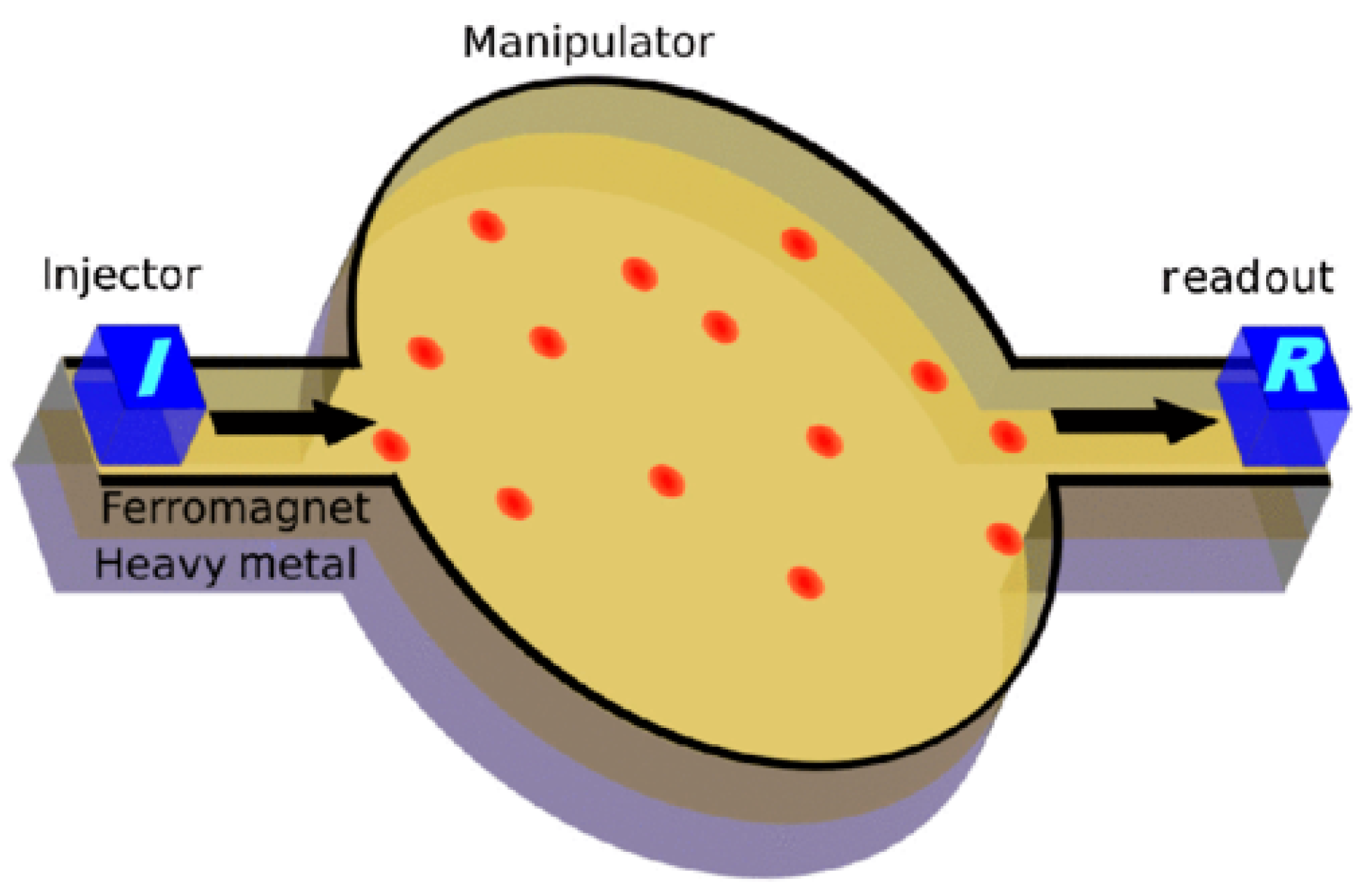
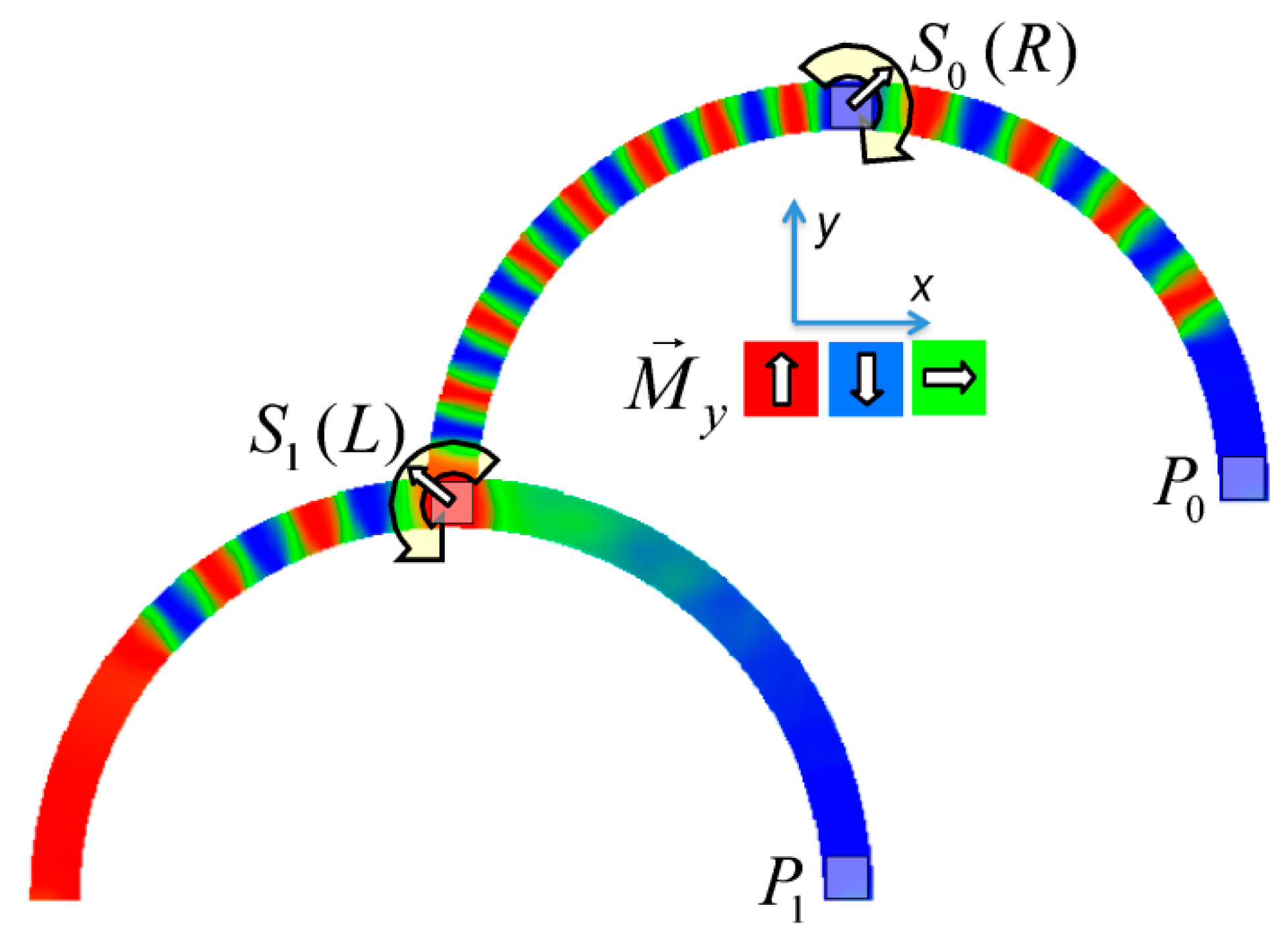
4. Magnetic Nanowires and Other Magnetic Nanostructures
5. Memristors and Other Nonmagnetic Neuromorphic Computing Elements
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Neumann, J. First Draft of a Report on the EDVAC. In The Origins of Digital Computers; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1982; pp. 383–392. [Google Scholar]
- Emma, P.G. Understanding some simple processor-performance limits. IBM J. Res. Dev. 1997, 41, 215–232. [Google Scholar] [CrossRef]
- Backus, J. Can programming be liberated from the von Neumann style? A functional style and its algebra of programs. Commun. ACM 1978, 21, 613–641. [Google Scholar] [CrossRef]
- Schemmel, J.; Briiderle, D.; Griibl, A.; Hock, M.; Meier, K.; Millner, S. A wafer-scale neuromorphic hardware system for large-scale neural modeling. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 1947–1950. [Google Scholar]
- Schuman, C.; Potok, T.; Patton, R.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A Survey of Neuromorphic Computing and Neural Networks in Hardware, 2017. Available online: https://www.mdpi.com/1420-3049/21/9/1255/htm (accessed on 18 May 2020).
- Burr, J.B. Digital neural network implementations. Neural Netw. Concepts Appl. Implement. 1991, 3, 237–285. [Google Scholar]
- Theil, S. Why the Human Brain Project Went Wrong–and How to Fix it. Scientific American 2015. Available online: https://www.scientificamerican.com/article/why-the-human-brain-project-went-wrong-and-how-to-fix-it (accessed on 4 April 2020).
- Modha, D.S. Introducing a Brain-Inspired Computer–TrueNorth’s Neurons to Revolutionize System Architecture. IBM Research: Brain-inspired Chip. 2018. Available online: http://www.research.ibm.com/articles/brain-chip.shtml (accessed on 4 April 2020).
- Murray, A.; Smith, A. Asynchronous VLSI neural networks using pulse-stream arithmetic. IEEE J. Solid-State Circuits 1988, 23, 688–697. [Google Scholar] [CrossRef]
- Bibyk, S.; Ismail, M.; Borgstrom, T.; Adkins, K.; Kaul, R.; Khachab, N.; Dupuie, S. Current-mode neural network building blocks for analog MOS VLSI. IEEE Int. Symp. Circuits Syst. 2002, 4, 3283–3285. [Google Scholar] [CrossRef]
- Ryu, K.-S.; Thomas, L.; Yang, S.-H.; Parkin, S. Chiral spin torque at magnetic domain walls. Nat. Nanotechnol. 2013, 8, 527–533. [Google Scholar] [CrossRef]
- Bhowmik, D.; Nowakowski, M.E.; You, L.; Lee, O.J.; Keating, D.; Wong, M.; Bokor, J.; Salahuddin, S. Deterministic domain wall mition orthogonal to current flow due to spin orbit torque. Sci. Rep. 2015, 5, 11823. [Google Scholar] [CrossRef]
- Sengupta, A.; Shim, Y.; Roy, K. Proposal for an All-Spin Artificial Neural Network: Emulating Neural and Synaptic Functionalities Through Domain Wall Motion in Ferromagnets. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 1152–1160. [Google Scholar] [CrossRef]
- Sharad, M.; Fan, D.; Roy, K. Spin-neurons: A possible path to energy-efficient neuromorphic computers. J. Appl. Phys. 2013, 114, 234906. [Google Scholar] [CrossRef]
- Emori, S.; Bauer, U.; Ahn, S.-M.; Martínez, E.; Beach, G.S.D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 2013, 12, 611–616. [Google Scholar] [CrossRef]
- Ryu, K.-S.; Yang, S.-H.; Thomas, L.; Parkin, S.S.P. Chiral spin torque arising from proximity-induced magnetization. Nat. Commun. 2014, 5, 3910. [Google Scholar] [CrossRef]
- Emori, S.; Martínez, E.; Lee, K.-J.; Bauer, U.; Ahn, S.-M.; Agrawal, P.; Bono, D.C.; Beach, G.S.D. Spin Hall torque magnetometry of Dzyaloshinskii domain walls. Phys. Rev. B 2014, 90, 184427. [Google Scholar] [CrossRef]
- Hirohata, A.; Sukegawa, H.; Yanagihara, H.; Žutić, I.; Seki, T.; Mizukami, S.; Swaminathan, R. Roadmap for Emerging Materials for Spintronic Device Applications. IEEE Trans. Magn. 2015, 51, 1–11. [Google Scholar] [CrossRef]
- Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Maass, W. On the computational complexity of networks of spiking neurons. Adv. Neural Inf. Process. Syst. 1995, 7, 183–190. [Google Scholar]
- Maass, W. Lower bounds for the computational power of networks of spiking neutrons. Neural Comput. 1996, 8, 1–40. [Google Scholar] [CrossRef]
- Sengupta, A.; Roy, K. Encoding neural and synaptic functionalities in electron spin: A pathway to efficient neuromorphic computing. Appl. Phys. Rev. 2017, 4, 041105. [Google Scholar] [CrossRef]
- Sengupta, A.; Roy, K. A Vision for All-Spin Neural Networks: A Device to System Perspective. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 2267–2277. [Google Scholar] [CrossRef]
- Sengupta, A.; Han, B.; Roy, K. Toward a spintronic deep learning spiking neural processor. In Proceedings of the 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, 17–19 October 2016; pp. 544–547. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Bhowmik, D.; Saxena, U.; Dankar, A.; Verma, A.; Kaushik, D.; Chatterjee, S.; Singh, U. On-chip learning for domain wall synapse based Fully Connected Neural Network. J. Magn. Magn. Mater. 2019, 489, 165434. [Google Scholar] [CrossRef]
- Brigner, W.H.; Hu, X.; Hassan, N.; Bennett, C.H.; Incorvia, J.A.C.; Garcia-Sanchez, F.; Friedman, J.S. Graded-Anisotropy-Induced Magnetic Domain Wall Drift for an Artificial Spintronic Leaky Integrate-and-Fire Neuron. IEEE J. Explor. Solid-state Comput. Devices Circuits 2019, 5, 19–24. [Google Scholar] [CrossRef]
- Phuoc, N.N.; Hung, L.T.; Ong, C. FeCoHfN thin films fabricated by co-sputtering with high resonance frequency. J. Alloy. Compd. 2011, 509, 4010–4013. [Google Scholar] [CrossRef]
- Li, S.; Huang, Z.; Duh, J.-G.; Yamaguchi, M. Ultrahigh-frequency ferromagnetic properties of FeCoHf films deposited by gradient sputtering. Appl. Phys. Lett. 2008, 92, 92501. [Google Scholar] [CrossRef]
- Agrawal, A.; Roy, K. Mimicking Leaky-Integrate-Fire Spiking Neuron Using Automotion of Domain Walls for Energy-Efficient Brain-Inspired Computing. IEEE Trans. Magn. 2018, 55, 1–7. [Google Scholar] [CrossRef]
- Zhang, D.; Hou, Y.; Zeng, L.; Zhao, W. Hardware Acceleration Implementation of Sparse Coding Algorithm With Spintronic Devices. IEEE Trans. Nanotechnol. 2019, 18, 518–531. [Google Scholar] [CrossRef]
- Hassan, N.; Hu, X.; Jiang-Wei, L.; Brigner, W.H.; Akinola, O.G.; Garcia-Sanchez, F.; Pasquale, M.; Bennett, C.H.; Incorvia, J.A.C.; Friedman, J.S. Magnetic domain wall neuron with lateral inhibition. J. Appl. Phys. 2018, 124, 152127. [Google Scholar] [CrossRef]
- Skyrme, T. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Boni, P. Skyrmion Lattice in a Chiral Magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef]
- Jonietz, F.; Mühlbauer, S.; Pfleiderer, C.; Neubauer, A.; Münzer, W.; Bauer, A.; Adams, T.; Georgii, R.; Böni, P.; Duine, R.A.; et al. Spin Transfer Torques in MnSi at Ultra-low Current Densities. Science 2010, 330, 1648–1651. [Google Scholar] [CrossRef]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152–156. [Google Scholar] [CrossRef]
- Zhang, X.; Ezawa, M.; Xiao, D.; Zhao, G.P.; Liu, Y.; Zhou, Y. All-magnetic control of skyrmions in nanowires by a spin wave. Nanotechnology 2015, 26, 225701. [Google Scholar] [CrossRef] [PubMed]
- Uzdin, V.; Potkina, M.; Lobanov, I.; Bessarab, P.; Jónsson, H. Energy surface and lifetime of magnetic skyrmions. J. Magn. Magn. Mater. 2018, 459, 236–240. [Google Scholar] [CrossRef]
- Zhang, S.L.; Wang, W.; Burn, D.M.; Peng, H.; Berger, H.; Bauer, A.; Pfleiderer, C.; Van Der Laan, G.; Hesjedal, T. Manipulation of skyrmion motion by magnetic field gradients. Nat. Commun. 2018, 9, 2115. [Google Scholar] [CrossRef] [PubMed]
- Tomasello, R.; Komineas, S.; Siracusano, G.; Carpentieri, M.; Finocchio, G. Chiral skyrmions in an anisotropy gradient. Phys. Rev. B 2018, 98, 024421. [Google Scholar] [CrossRef]
- Psaroudaki, C.; Loss, D. Skyrmions Driven by Intrinsic Magnons. Phys. Rev. Lett. 2018, 120, 237203. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Huang, Y.; Wang, C.; Zhang, X.; Liu, Y.; Zhou, Y.; Kang, W.; Koli, S.C.; Lei, N. Strain-controlled skyrmion creation and propagation in ferroelectric/ferromagnetic hybrid wires. J. Magn. Magn. Mater. 2018, 455, 19–24. [Google Scholar] [CrossRef]
- Saxena, U.; Kaushik, D.; Bansal, M.; Sahu, U.; Bhowmik, D. Low-Energy Implementation of Feed-Forward Neural Network With Back-Propagation Algorithm Using a Spin-Orbit Torque Driven Skyrmionic Device. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Chen, X.; Kang, W.; Zhu, D.; Zhang, X.; Lei, N.; Zhang, Y.; Zhou, Y.; Zhao, W.; Wang, K. A compact skyrmionic leaky–integrate–fire spiking neuron device. Nanoscale 2018, 10, 6139–6146. [Google Scholar] [CrossRef]
- Chen, M.-C.; Sengupta, A.; Roy, K. Magnetic Skyrmion as a Spintronic Deep Learning Spiking Neuron Processor. IEEE Trans. Magn. 2018, 54, 1–7. [Google Scholar] [CrossRef]
- Pinna, D.; Araujo, F.A.; Kim, J.-V.; Cros, V.; Querlioz, D.; Bessiere, P.; Droulez, J.; Grollier, J. Skyrmion Gas Manipulation for Probabilistic Computing. Phys. Rev. Appl. 2018, 9, 064018. [Google Scholar] [CrossRef]
- Prychynenko, D.; Sitte, M.; Litzius, K.; Krueger, B.; Burianoff, G.; Kläui, M.; Sinova, J.; Everschor-Sitte, K. Magnetic Skyrmion as a Nonlinear Resistive Element: A Potential Building Block for Reservoir Computing. Phys. Rev. Appl. 2018, 9, 14034. [Google Scholar] [CrossRef]
- Huang, Y.; Kang, W.; Zhang, X.; Zhou, Y.; Zhao, W. Magnetic skyrmion-based synaptic devices. Nanotechnology 2017, 28, 08LT02. [Google Scholar] [CrossRef]
- Li, S.; Kang, W.; Huang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Magnetic skyrmion-based artificial neuron device. Nanotechnology 2017, 28, 31LT01. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Jin, T.; Al Risi, S.; Sbiaa, R.; Lew, W.S.; Piramanayagam, S.N. Domain Wall Motion Control for Racetrack Memory Applications. IEEE Trans. Magn. 2018, 55, 1–8. [Google Scholar] [CrossRef]
- Tanaka, Y.; Hirai, T.; Koyama, T.; Chiba, D. Electric-field-induced magnetic domain writing in a Co wire. Appl. Phys. Express 2018, 11, 053005. [Google Scholar] [CrossRef]
- Dutta, S.; Siddiqui, S.A.; Currivan-Incorvia, J.A.; Ross, C.A.; Baldo, M.A. The Spatial Resolution Limit for an Individual Domain Wall in Magnetic Nanowires. Nano Lett. 2017, 17, 5869–5874. [Google Scholar] [CrossRef] [PubMed]
- Blachowicz, T.; Ehrmann, A. Magnetization reversal in bent nanofibers of different cross sections. J. Appl. Phys. 2018, 124, 152112. [Google Scholar] [CrossRef]
- Blachowicz, T.; Kosmalska, D.; Döpke, C.; Leiste, H.; Hahn, L.; Ehrmann, A. Varying steps in hysteresis loops of Co square nano-frames. J. Magn. Magn. Mater. 2019, 491, 165619. [Google Scholar] [CrossRef]
- Kern, P.; Döpke, C.; Blachowicz, T.; Steblinski, P.; Ehrmann, A. Magnetization reversal in ferromagnetic Fibonacci nano-spirals. J. Magn. Magn. Mater. 2019, 484, 37–41. [Google Scholar] [CrossRef]
- Kunz, A. Field induced domain wall collisions in thin magnetic nanowires. Appl. Phys. Lett. 2009, 94, 132502. [Google Scholar] [CrossRef]
- Moreno, R.; Carvalho-Santos, V.L.; Espejo, A.P.; Laroze, D.; Chubykalo-Fesenko, O.; Altbir, D. Oscillatory behavior of the domain wall dynamics in a curved cylindrical magnetic nanowire. Phys. Rev. B 2017, 96, 184401. [Google Scholar] [CrossRef]
- Kim, S.-K.; Park, H.-K.; Yang, J.; Kim, J.; Yoo, M.-W. Spin-wave duplexer studied by finite-element micromagnetic simulation. Sci. Rep. 2018, 8, 16511. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Brächer, T.; Mohseni, M.; Hillebrands, B.; Vasyuchka, V.I.; Chumak, A.V.; Pirro, P. Nanoscale spin-wave wake-up receiver. Appl. Phys. Lett. 2019, 115, 092401. [Google Scholar] [CrossRef]
- Garg, C.; Pushp, A.; Yang, S.-H.; Phung, T.; Hughes, B.P.; Rettner, C.; Parkin, S.S.P. Highly Asymmetric Chiral Domain-Wall Velocities in Y-Shaped Junctions. Nano Lett. 2018, 18, 1826–1830. [Google Scholar] [CrossRef]
- Scholz, W.; Fidler, J.; Schrefl, T.; Suess, D.; Dittrich, R.; Forster, H.; Tsiantos, V. Scalable parallel micromagnetic solvers for magnetic nanostructures. Comput. Mater. Sci. 2003, 28, 366–383. [Google Scholar] [CrossRef]
- Chua, L.O. Memristor–the missing circuit element. IEEE Trans. Circuit Theor. 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Wang, Q.; Shang, D.-S.; Wu, Z.; Chen, L.; Li, X. “Positive” and “negative” electric-pulse-induced reversible resistance switching effect in Pr0.7Ca0.3MnO3 films. Appl. Phys. A 2006, 86, 357–360. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Gutmann, E. Maintaining Moore’s Law with New Memristor Circuits. Ars Technica 2008. Available online: https://arstechnica.com/uncategorized/2008/05/maintaining-moores-law-with-new-memristor-circuits (accessed on 4 April 2020).
- Zayer, F.; Dghais, W.; Belgacem, H.; Fakhreddine, Z. Modeling framework and comparison of memristive devices and associated STDP learning windows for neuromorphic applications. J. Phys. D Appl. Phys. 2019, 52, 393002. [Google Scholar] [CrossRef]
- Dang, B.; Wu, Q.; Sun, J.; Zhao, M.; Wang, S.; Song, F.; Yang, M.; Ma, X.; Wang, H.; Hao, Y. Physically Transient Memristor Synapse Based on Embedding Magnesium Nanolayer in Oxide for Security Neuromorphic Electronics. IEEE Electron Device Lett. 2019, 40, 1265–1268. [Google Scholar] [CrossRef]
- Pan, X.; Shuai, Y.; Wu, C.; Zhang, L.; Guo, H.; Cheng, H.; Peng, Y.; Qiao, S.; Luo, W.; Wang, T.; et al. Ar+ ions irradiation induced memristive behavior and neuromorphic computing in monolithic LiNbO3 thin films. Appl. Surf. Sci. 2019, 484, 751–758. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Xu, M.; Yang, Y.; Ma, M.; Li, H.; Pei, J.; Shi, L. Self-Doping Memristors with Equivalently Synaptic Ion Dynamics for Neuromorphic Computing. ACS Appl. Mater. Interfaces 2019, 11, 24230–24240. [Google Scholar] [CrossRef] [PubMed]
- Nagata, Z.; Shimizu, T.; Isaka, T.; Tohei, T.; Ikarashi, N.; Sakai, A. Author Correction: Gate Tuning of Synaptic Functions Based on Oxygen Vacancy Distribution Control in Four-Terminal TiO2-x Memristive Devices. Sci. Rep. 2019, 9, 15166. [Google Scholar] [CrossRef] [PubMed]
- An, H.; Ehsan, M.A.; Zhou, Z.; Shen, F.; Yi, Y. Monolithic 3D neuromorphic computing system with hybrid CMOS and memristor-based synapses and neurons. Integration 2019, 65, 273–281. [Google Scholar] [CrossRef]
- Bao, L.; Kang, J.; Fang, Y.; Yu, Z.; Wang, Z.; Yang, Y.; Cai, Y.; Huang, R. Artificial Shape Perception Retina Network Based on Tunable Memristive Neurons. Sci. Rep. 2018, 8, 13727. [Google Scholar] [CrossRef]
- Irmanova, A.; James, A.P. Neuron inspired data encoding memristive multi-level memory cell. Analog. Integr. Circuits Signal Process. 2018, 95, 429–434. [Google Scholar] [CrossRef]
- Chakraborty, I.; Saha, G.; Roy, K. Photonic In-Memory Computing Primitive for Spiking Neural Networks Using Phase-Change Materials. Phys. Rev. Appl. 2019, 11, 014063. [Google Scholar] [CrossRef]
- Nandakumar, S.R.; Le Gallo, M.; Boybat, I.; Rajendran, B.; Sebastian, A.; Eleftheriou, E. A phase-change memory model for neuromorphic computing. J. Appl. Phys. 2018, 124, 152135. [Google Scholar] [CrossRef]
- Ambrogio, S.; Ciocchini, N.; Laudato, M.; Milo, V.; Pirovano, A.; Fantini, P.; Ielmini, D. Unsupervised Learning by Spike Timing Dependent Plasticity in Phase Change Memory (PCM) Synapses. Front. Mol. Neurosci. 2016, 10, 384012. [Google Scholar] [CrossRef]
- Sun, Y.; Qian, L.; Xie, D.; Lin, Y.; Sun, M.; Li, W.; Ding, L.; Ren, T.; Palacios, T. Photoelectric Synaptic Plasticity Realized by 2D Perovskite. Adv. Funct. Mater. 2019, 29. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Abbas, S.; Kim, J. All-Oxide-Based Highly Transparent Photonic Synapse for Neuromorphic Computing. ACS Appl. Mater. Interfaces 2018, 10, 34370–34376. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J.; Wade, E.; Hurtado, A. Electrically Controlled Neuron-Like Spiking Regimes in Vertical-Cavity Surface-Emitting Lasers at Ultrafast Rates. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–7. [Google Scholar] [CrossRef]
- Chakraborty, I.; Saha, G.; Sengupta, A.; Roy, K. Toward Fast Neural Computing using All-Photonic Phase Change Spiking Neurons. Sci. Rep. 2018, 8, 12980. [Google Scholar] [CrossRef] [PubMed]
- Grollier, J.; Querlioz, D.; Camsari, K.Y.; Everschor-Sitte, K.; Fukami, S.; Stiles, M.D. Neuromorphic spintronics. Nat. Electron. 2020, 1–11. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, W.; Klein, J.-O.; Kang, W.; Querlioz, D.; Zhang, Y.; Ravelosona, D.; Chappert, C. Spintronics for low-power computing. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 24–28 March 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Ostwal, V.; Zand, R.; Demara, R.F.; Appenzeller, J. A Novel Compound Synapse Using Probabilistic Spin–Orbit-Torque Switching for MTJ-Based Deep Neural Networks. IEEE J. Explor. Solid-state Comput. Devices Circuits 2019, 5, 182–187. [Google Scholar] [CrossRef]
- Song, K.M.; Jeong, J.-S.; Pan, B.; Zhang, X.; Xia, J.; Cha, S.; Park, T.-E.; Kim, K.; Finizio, S.; Raabe, J.; et al. Skyrmion-based artificial synapses for neuromorphic computing. Nat. Electron. 2020, 3, 148–155. [Google Scholar] [CrossRef]
- Qi, J.; Huang, J.; Paul, D.; Ren, J.; Chu, S.; Liu, J. Current self-complianced and self-rectifying resistive switching in Ag-electroded single Na-doped ZnO nanowires. Nanoscale 2013, 5, 2651. [Google Scholar] [CrossRef]
- Nafea, S.F.; Dessouki, A.A.; El-Rabaie, S.; Elnaghi, B.E.; Ismail, Y.; Mostafa, H. An accurate model of domain-wall-based spintronic memristor. Integration 2019, 65, 149–162. [Google Scholar] [CrossRef]
- Rajendran, B.; Alibart, F. Neuromorphic Computing Based on Emerging Memory Technologies. IEEE J. Emerg. Sel. Top. Circuits Syst. 2016, 6, 198–211. [Google Scholar] [CrossRef]
- Tomasello, R.; Ricci, M.; Burrascano, P.; Puliafito, V.; Carpentieri, M.; Finocchio, G. Electrical detection of single magnetic skyrmion at room temperature. AIP Adv. 2017, 7, 056022. [Google Scholar] [CrossRef]
- Schuller, I.K.; Stevens, R.; Pino, R.; Pechan, M. Neuromorphic Computing–from Materials Research to Systems Architecture Roundtable; USDOE Office of Science (SC): Gaithersburg, MD, USA, 2015. [Google Scholar]
- Siddiqui, S.A.; Dutta, S.; Tang, A.; Liu, L.; Ross, C.A.; Baldo, M.A. Magnetic Domain Wall Based Synaptic and Activation Function Generator for Neuromorphic Accelerators. Nano Lett. 2019, 20, 1033–1040. [Google Scholar] [CrossRef] [PubMed]
- Caretta, L.; Mann, M.; Büttner, F.; Ueda, K.; Pfau, B.; Günther, C.M.; Hessing, P.; Churikova, A.; Klose, C.; Schneider, M.; et al. Fast current-driven domain walls and small skyrmions in a compensated ferrimagnet. Nat. Nanotechnol. 2018, 13, 1154–1160. [Google Scholar] [CrossRef] [PubMed]
- Upadhyay, N.K.; Jiang, H.; Wang, Z.; Asapu, S.; Xia, Q.; Yang, J.J. Emerging Memory Devices for Neuromorphic Computing. Adv. Mater. Technol. 2019, 4, 1800589. [Google Scholar] [CrossRef]
- Blachowicz, T.; Döpke, C.; Ehrmann, A. Micromagnetic Simulations of Chaotic Ferromagnetic Nanofiber Networks. Nanomaterials 2020, 10, 738. [Google Scholar] [CrossRef]
- Kumar, D.; Sengupta, P.; Sbiaa, R.; Piramanayagam, S.N. Spin transfer torque induced domain wall oscillations in ferromagnetic nanowire with a nanoscale Dzyaloshinskii–Moriya interaction region. J. Magn. Magn. Mater. 2020, 507, 166807. [Google Scholar] [CrossRef]
- Munch, C.; Bishnoi, R.; Tahoori, M.B. Tolerating Retention Failures in Neuromorphic Fabric based on Emerging Resistive Memories. In Proceedings of the 2020 25th Asia and South Pacific Design Automation Conference (ASP-DAC), Beijing, China, 13–16 January 2020; pp. 393–400. [Google Scholar]
- Burr, G.W.; Shelby, R.M.; Sebastian, A.; Kim, S.; Kim, S.; Sidler, S.; Virwani, K.; Ishii, M.; Narayanan, P.; Fumarola, A.; et al. Neuromorphic computing using non-volatile memory. Adv. Phys. X 2016, 2, 89–124. [Google Scholar] [CrossRef]
- Dong, Q.; Yang, K.; Fick, L.; Fick, D.; Blaauw, D.; Sylvester, D. Low-Power and Compact Analog-to-Digital Converter Using Spintronic Racetrack Memory Devices. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 25, 1–12. [Google Scholar] [CrossRef]

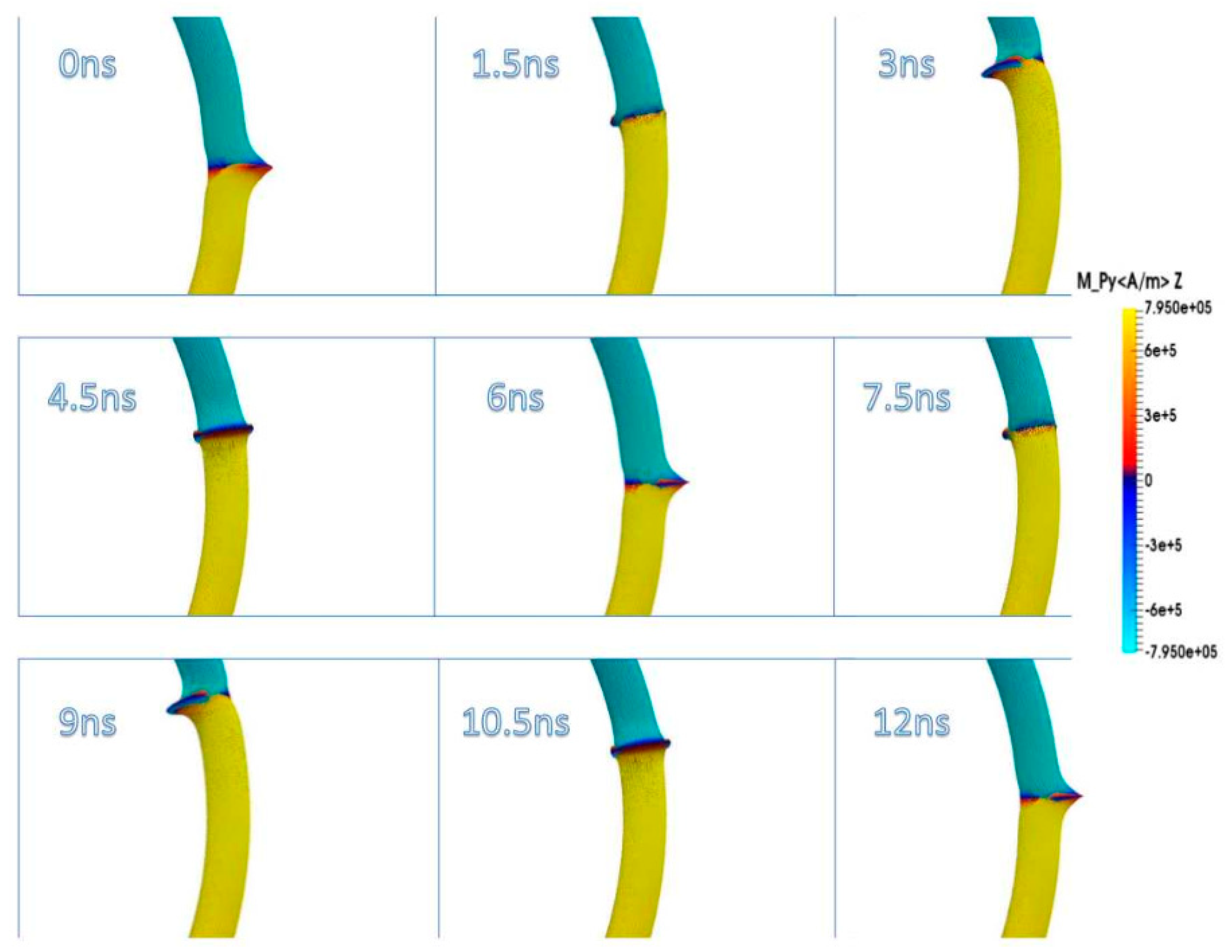
| t (ns) | LL | RL | LR | RR |
|---|---|---|---|---|
| 10 | 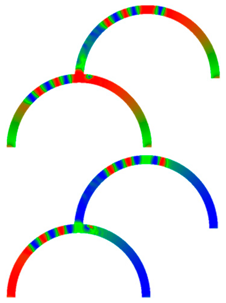 | 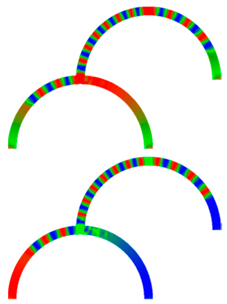 |  | 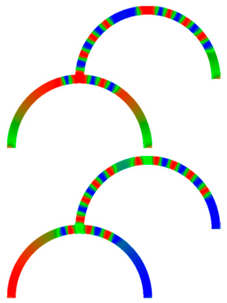 |
| Mx | ||||
| My | ||||
| 40 | 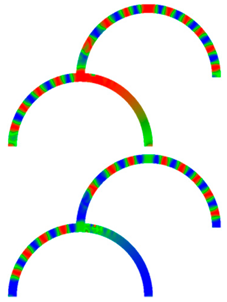 | 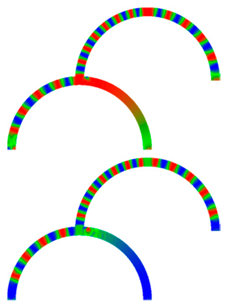 | 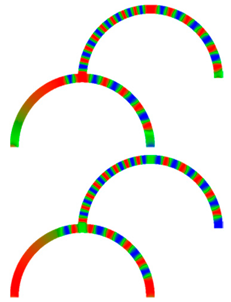 |  |
| Mx | ||||
| My |
| Properties | MTJ–Domain Wall Based | MTJ–Spiking Neurons | Skyrmions | Nanowires | Memristors |
|---|---|---|---|---|---|
| Endurance | High [83] | High [84] | High [85] | High [86] | High [87] |
| Programming accuracy | High [88] | Low, algorithmic scaling is necessary [88] | Can be high [89] | High [86] | Can be sufficiently controlled [90] |
| Power consumption | Low [13,83,91] | Very low (~100 nW) possible [83] | Low [92] | Low [83] | Low [93] |
| Speed | High (few ns) [13,83] | High (~100 ns) [88] | High [92] | Low (e.g., <100 kHz) [93] | High (~10 ns) [90] |
| Area consumption | Relatively high [13] | High due to high synaptic density [88] | Low [92] | Low, depends on technique [94,95] | Low [87] |
| Retention | <10 years [91] or more with sophisticated concepts [96] | ~10 years with a sophisticated concept [96] | High [85] | ~10 years [86] | Enabling short- and long-term memory [97] |
| Scalability | Possible [13] | Possible, but challenging [88] | Improvable based on recent findings [85] | Possible [98] | Good [87,92] |
| CMOS process integration | Possible [91] | Not yet possible [88] | Not possible/planned [45] | Not possible/planned [98] | Possible [93] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blachowicz, T.; Ehrmann, A. Magnetic Elements for Neuromorphic Computing. Molecules 2020, 25, 2550. https://doi.org/10.3390/molecules25112550
Blachowicz T, Ehrmann A. Magnetic Elements for Neuromorphic Computing. Molecules. 2020; 25(11):2550. https://doi.org/10.3390/molecules25112550
Chicago/Turabian StyleBlachowicz, Tomasz, and Andrea Ehrmann. 2020. "Magnetic Elements for Neuromorphic Computing" Molecules 25, no. 11: 2550. https://doi.org/10.3390/molecules25112550
APA StyleBlachowicz, T., & Ehrmann, A. (2020). Magnetic Elements for Neuromorphic Computing. Molecules, 25(11), 2550. https://doi.org/10.3390/molecules25112550







