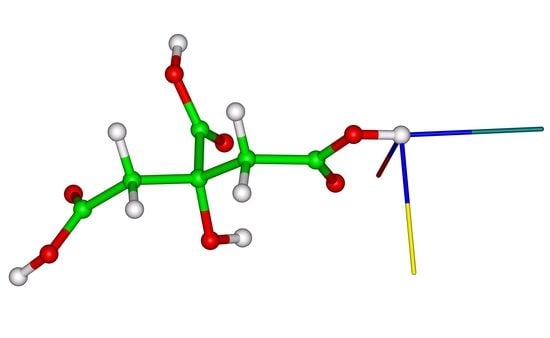
Exploring Accuracy Limits of Predictions of the 1H NMR Chemical Shielding Anisotropy in the Solid State
Abstract
1. Introduction
2. Results
2.1. Comparison of the DFT and SC SSNMR Data
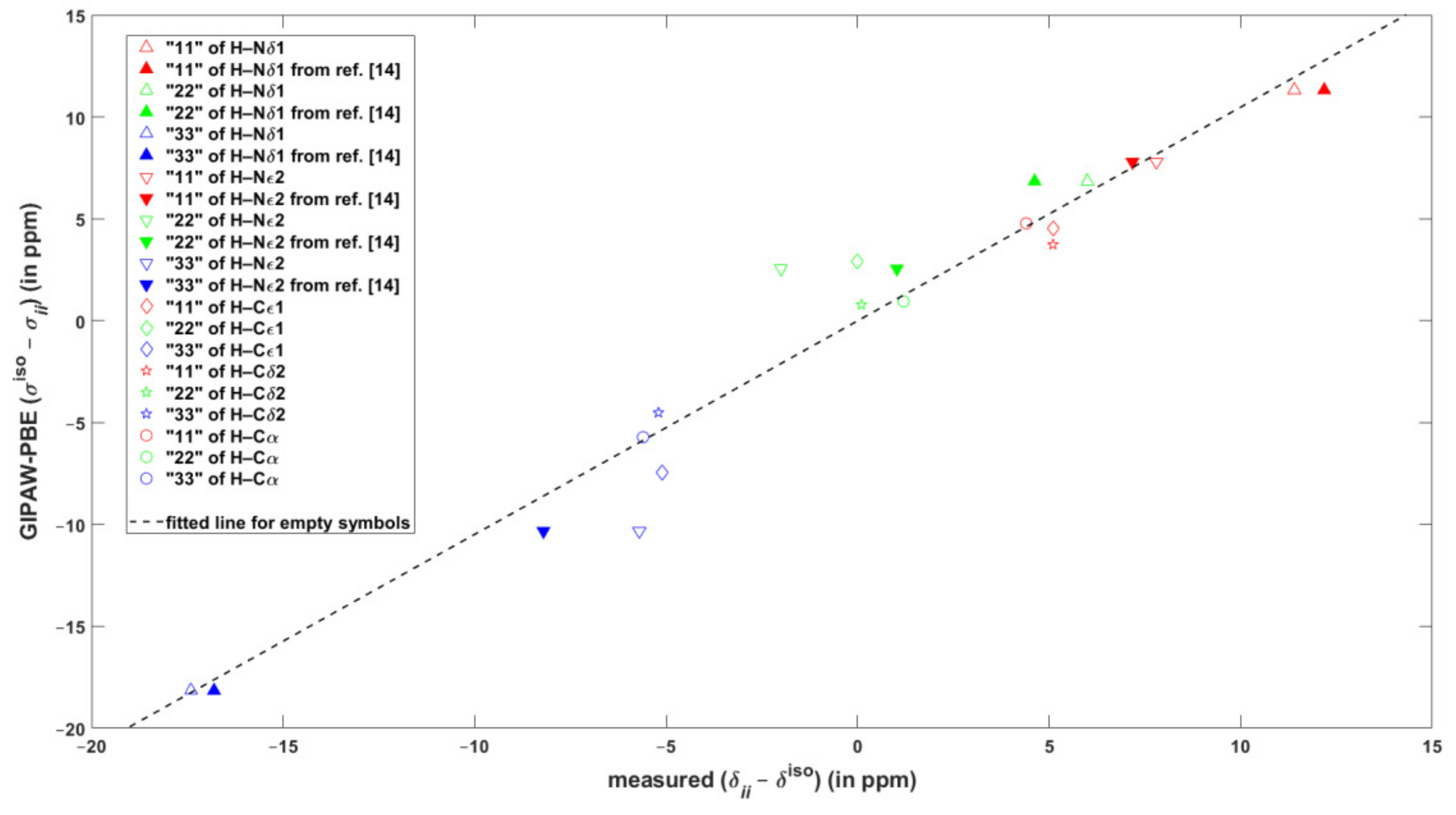
2.2. The {13C, 15N, 1H} Results for Biprotonated l-Histidine
2.3. The 1H CSA in Citric Acid
3. Discussion
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Vasa, S.K.; Rovó, P.; Linser, R. Protons as versatile reporters in solid-state NMR spectroscopy. Acc. Chem. Res. 2019, 51, 1386–1395. [Google Scholar] [CrossRef] [PubMed]
- Duncan, T.M. Compilation of Chemical Shift Anisotropies; Faragut Press: Chicago, IL, USA, 1990. [Google Scholar]
- Hou, G.; Gupta, R.; Polenova, T.; Vega, A.J. A magic-angle spinning NMR method for the site-specific measurement of proton chemical-shift anisotropy in biological and organic solids. Isr. J. Chem. 2014, 54, 171–183. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Hou, G.; Bao, X. Measurement of proton chemical shift anisotropy in solid-state NMR spectroscopy. Solid State Nucl. Magn. Reson. 2018, 93, 16–28. [Google Scholar] [CrossRef] [PubMed]
- Damron, J.T.; Kersten, K.M.; Pandey, M.K.; Nishiyama, Y.; Matzger, A. Role of anomalous water constraints in the efficacy of pharmaceuticals probed by 1H solid-state NMR. ChemistrySelect 2017, 2, 6797–6800. [Google Scholar] [CrossRef]
- Pandey, M.K.; Damron, J.T.; Ramamoorthy, A.; Nishiyama, Y. Proton-detected 3D 1H anisotropic/14N/1H isotropic chemical shifts correlation NMR under fast magic angle spinning on solid samples without isotopic enrichment. Solid State Nucl. Magn. Reson. 2019, 97, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Brouwer, D.H.; Ripmeester, J.A. Symmetry-based recoupling of proton chemical shift anisotropies in ultrahigh-field solid-state NMR. J. Magn. Reson. 2007, 185, 173–178. [Google Scholar] [CrossRef] [PubMed]
- Pickard, C.J.; Mauri, F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B 2001, 63, 245101. [Google Scholar] [CrossRef]
- Yates, J.R.; Pickard, J.; Mauri, F. Calculation of NMR chemical shifts for extended systems using ultrasoft pseudopotentials. Phys. Rev. B 2007, 76, 024401. [Google Scholar] [CrossRef]
- Grosescu, R.; Achlama, A.M.; Haeberlen, U.; Spiess, H.W. Multiple pulse study of the proton shielding in single crystals of maleic acid. Chem. Phys. 1974, 5, 119–128. [Google Scholar] [CrossRef]
- Sagnowski, S.F.; Aravamudhan, S.; Haeberlen, U. Wide-line and high-resolution proton magnetic resonance in single crystals of malonic acid. J. Magn. Reson. 1977, 28, 271–288. [Google Scholar] [CrossRef]
- Li, S.; Hong, M. Protonation, tautomerization, and rotameric structure of histidine: A comprehensive study by magic-angle-spinning solid-state NMR. J. Am. Chem. Soc. 2011, 133, 1534–1544. [Google Scholar] [CrossRef]
- Harbison, G.; Herzfeld, J.; Griffin, R.G. Nitrogen-15 chemical shift tensors in l-histidine hydrochloride monohydrate. J. Am. Chem. Soc. 1981, 103, 4752–4754. [Google Scholar] [CrossRef]
- Pandey, M.K.; Nishiyama, Y. Determination of NH proton chemical shift anisotropy with 14N-1H heteronuclear decoupling using ultrafast magic angle spinning solid-state NMR. J. Magn. Reson. 2015, 261, 133–140. [Google Scholar] [CrossRef] [PubMed]
- Pandey, M.K.; Nishiyama, Y. Determination of relative orientation between 1H CSA tensors from a 3D solid-state NMR experiment mediated through 1H/1H RFDR mixing under ultrafast MAS. Solid State Nucl. Magn. Reson. 2015, 70, 15–20. [Google Scholar] [CrossRef]
- Beran, G.J.O. Modeling polymorphic molecular crystals with electronic structure theory. Chem. Rev. 2016, 116, 5567–5613. [Google Scholar] [CrossRef] [PubMed]
- Widdifield, C.M.; Lill, S.O.N.; Broo, A.; Lindkvist, A.; Pettersen, A.; Ankarberg, A.S.; Aldred, P.; Schantz, S.; Emsley, L. Does Z′ equal 1 or 2? Enhanced powder NMR crystallography verification of a disordered room temperature crystal structure of a p38 inhibitor for chronic obstructive pulmonary disease. Chem. Phys. Phys. Chem. 2017, 19, 16650–16661. [Google Scholar] [CrossRef]
- Wang, L.; Uribe-Romo, F.J.; Mueller, L.J.; Harper, J.K. Predicting anisotropic thermal displacements for hydrogens from solid-state NMR: A study on hydrogen bonding in polymorphs of palmitic acid. Chem. Phys. Phys. Chem. 2018, 20, 8475–8487. [Google Scholar] [CrossRef]
- Czernek, J.; Urbanova, M.; Brus, J. NMR crystallography of the polymorphs of metergoline. Crystals 2018, 8, 378. [Google Scholar] [CrossRef]
- Cui, J.; Olmsted, D.L.; Mehta, A.K.; Asta, M.; Hayes, S.E. NMR crystallography: evaluation of hydrogen positions in hydromagnesite by 13C{1H} REDOR solid-state NMR and density functional theory calculation of chemical shielding tensors. Angew. Chem. Int. Ed. 2019, 58, 4210–4216. [Google Scholar] [CrossRef]
- Soss, S.E.; Flynn, P.F.; Iuliucci, R.J.; Young, R.P.; Mueller, L.J.; Hartman, J.D.; Beran, G.J.O.; Harper, J.K. Measuring and modeling highly accurate 15 N chemical shift tensors in a peptide. ChemPhysChem 2017, 18, 2225–2232. [Google Scholar] [CrossRef]
- Dawson, D.M.; Moran, R.F.; Sneddon, S.; Ashbrook, S.E. Is the 31P Chemical shift anisotropy of aluminophosphates a useful parameter for NMR crystallography? Magn. Reson. Chem. 2018, 57, 176–190. [Google Scholar] [CrossRef] [PubMed]
- Beran, G.J.O.; Hartman, J.D.; Heit, Y.N. Predicting molecular crystal properties from first principles: Finite-temperature thermochemistry to NMR crystallography. Acc. Chem. Res. 2016, 49, 2501–2508. [Google Scholar] [CrossRef]
- Paruzzo, F.M.; Hofstetter, A.; Musil, F.; De, S.; Ceriotti, M.; Emsley, L. Chemical shifts in molecular solids by machine learning. Nat. Commun. 2018, 9, 4501. [Google Scholar] [CrossRef]
- Brus, J.; Czernek, J.; Kobera, L.; Urbanová, M.; Abbrent, S.; Hušák, M. Predicting the crystal structure of decitabine by powder NMR crystallography: Influence of long-range molecular packing symmetry on NMR parameters. Cryst. Growth Des. 2016, 16, 7102–7111. [Google Scholar] [CrossRef]
- Brus, J.; Czernek, J.; Hrubý, M.; Švec, P.; Kobera, L.; Abbrent, S.; Urbanová, M. Efficient strategy for determining the atomic-resolution structure of micro- and nanocrystalline solids within polymeric microbeads: Domain-edited NMR crystallography. Macromolecules 2018, 51, 5364–5374. [Google Scholar] [CrossRef]
- Czernek, J. On the solid-state NMR spectra of naproxen. Chem. Phys. Lett. 2015, 619, 230–235. [Google Scholar] [CrossRef]
- Bonhomme, C.; Gervais, C.; Babonneau, F.; Coelho, C.; Pourpoint, F.; Azais, T.; Ashbrook, S.E.; Griffin, J.M.; Yates, J.R.; Mauri, F.; et al. First-principles calculation of NMR parameters using the gauge including projector augmented wave method: A chemist’s point of view. Chem. Rev. 2012, 112, 5733–5779. [Google Scholar] [CrossRef]
- James, M.N.G.; Williams, G.J.B. A refinement of the crystal structure of maleic acid. Acta Cryst. B 1974, 30, 1249–1257. [Google Scholar] [CrossRef]
- Goedkoop, J.A.; MacGillavry, C.H. The crystal structure of malonic acid. Acta Cryst. 1957, 10, 125–127. [Google Scholar] [CrossRef]
- Fuess, H.; Hohlwein, D.; Mason, S.A. Neutron diffraction study of l-histidine hydrochloride monohydrate. Acta Cryst. B 1977, 33, 654–659. [Google Scholar] [CrossRef]
- The Cambridge Structural Database Code CITRAC11. Available online: https://www.ccdc.cam.ac.uk/ (accessed on 2 May 2019).
- Miah, H.K.; Bennett, D.A.; Iuga, D.; Titman, J.J. Measuring proton shift tensors with ultrafast MAS NMR. J. Magn. Reson. 2013, 235, 1–5. [Google Scholar] [CrossRef]
- Hou, G.; Byeon, I.L.; Ahn, J.; Gronenborn, A.M.; Polenova, T. Recoupling of chemical shift anisotropy by R-symmetry sequencesin magic angle spinning NMR spectroscopy. J. Chem. Phys. 2012, 137, 134201. [Google Scholar] [CrossRef] [PubMed]
- Pandey, M.K.; Malon, M.; Ramamoorthy, A.; Nishiyama, Y. Composite-180° pulse-based symmetry sequences to recouple proton chemical shift anisotropy tensors under ultrafast MAS solid-state NMR spectroscopy. J. Magn. Reson. 2015, 250, 45–54. [Google Scholar] [CrossRef]
- Monserrat, B.; Needs, R.J.; Pickard, C.J. Temperature effects in first-principles solid state calculations of the chemical shielding tensor made simple. J. Chem. Phys. 2014, 141, 134113. [Google Scholar] [CrossRef]
- Dračínský, M.; Bouř, P.; Hodkinson, P. Temperature dependence of NMR parameters calculated from path integral molecular dynamics simulations. J. Chem. Theory Comput. 2016, 12, 968–973. [Google Scholar] [CrossRef][Green Version]
- Carignani, E.; Borsacchi, S.; Concistre, M.; Johannessen, O.G.; Geppi, M. Direct observation of the effects of small-amplitude motions on 13C nuclear shielding tensors by means of low-temperature 2D MAS NMR spectroscopy. Chem. Phys. Lett. 2018, 706, 107–112. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Mat. 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Norskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Feller, D.; Feyereisen, M.W. Ab initio study of hydrogen bonding in the phenol–water system. J. Comput. Chem. 1993, 14, 1027–1035. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J. On the predictions of the 11B solid state NMR parameters. Chem. Phys. Lett. 2016, 655–656, 66–70. [Google Scholar] [CrossRef]


| Parameter | Isotropic | Eigenvalues |
|---|---|---|
| slope | –1.255 | –1.211 |
| (–1.194) | (–1.159) | |
| standard error of slope | 0.034 | 0.026 |
| (0.030) | (0.024) | |
| intercept/(ppm) | 28.78 | 28.47 |
| (28.88) | (28.64) | |
| standard error of intercept/(ppm) | 0.28 | 0.28 |
| (0.25) | (0.26) | |
| standard deviation/(ppm) | 0.39 | 1.03 |
| (0.34) | (0.96) | |
| average absolute deviation/(ppm) | 0.30 | 0.81 |
| (0.30) | (0.77) | |
| maximum absolute deviation/(ppm) | 0.73 | 2.43 |
| (0.55) | (2.26) | |
| adjusted R2 | 0.9949 | 0.9895 |
| (0.9956) | (0.9899) | |
| number of data points | 8 | 24 |
| (8) | (24) |
| Parameter | 1H isotropic | 13C isotropic | 15N eigenvalues |
|---|---|---|---|
| slope | –1.108 | –1.019 | –1.047 |
| (–1.121) | (–1.016) | (–1.057) | |
| standard error of slope | 0.019 | 0.010 | 0.028 |
| (0.020) | (0.010) | (0.032) | |
| intercept/ (ppm) | 31.43 | 171.72 | 206.5 |
| (31.80) | (171.71) | (204.8) | |
| standard error of intercept/(ppm) | 0.19 | 1.23 | 5.2 |
| (0.19) | (1.22) | (5.9) | |
| standard deviation/(ppm) | 0.21 | 1.15 | 5.6 |
| (0.21) | (1.15) | (6.4) | |
| average absolute deviation/(ppm) | 0.16 | 0.76 | 4.6 |
| (0.19) | (0.73) | (5.3) | |
| maximum absolute deviation/(ppm) | 0.30 | 2.15 | 7.8 |
| (0.26) | (2.16) | (9.6) | |
| adjusted R2 | 0.9982 | 0.9995 | 0.9964 |
| (0.9982) | (0.9995) | (0.9954) | |
| number of data points | 7 | 6 | 6 |
| (7) | (6) | (6) |
| Parameter | GIPAW-PBE | GIPAW-revPBE |
|---|---|---|
| slope | 1.049 | 1.053 |
| standard error of slope | 0.079 | 0.080 |
| intercept/(ppm) | –0.007 | –0.007 |
| standard error of intercept/(ppm) | 0.550 | 0.554 |
| standard deviation/(ppm) | 2.05 | 2.07 |
| average absolute deviation/(ppm) | 4.65 | 4.63 |
| maximum absolute deviation/(ppm) | 1.36 | 1.38 |
| adjusted R2 | 0.9258 | 0.9249 |
| Parameter | GIPAW-PBE | GIPAW-revPBE | GIAO-B3LYP |
|---|---|---|---|
| slope | –1.151 | –1.095 | –1.183 |
| standard error of slope | 0.052 | 0.048 | 0.075 |
| intercept/(ppm) | 30.23 | 30.56 | 31.31 |
| standard error of intercept/(ppm) | 0.75 | 0.69 | 1.07 |
| standard deviation/(ppm) | 1.77 | 1.63 | 2.54 |
| average absolute deviation/(ppm) | 1.34 | 1.22 | 1.92 |
| maximum absolute deviation/(ppm) | 3.15 | 2.97 | 5.20 |
| adjusted R2 | 0.9779 | 0.9793 | 0.9580 |
| Direction | |||
|---|---|---|---|
| 47° | 118° | 74° | |
| of H5 | 56° | 125° | 77° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czernek, J.; Brus, J. Exploring Accuracy Limits of Predictions of the 1H NMR Chemical Shielding Anisotropy in the Solid State. Molecules 2019, 24, 1731. https://doi.org/10.3390/molecules24091731
Czernek J, Brus J. Exploring Accuracy Limits of Predictions of the 1H NMR Chemical Shielding Anisotropy in the Solid State. Molecules. 2019; 24(9):1731. https://doi.org/10.3390/molecules24091731
Chicago/Turabian StyleCzernek, Jiří, and Jiří Brus. 2019. "Exploring Accuracy Limits of Predictions of the 1H NMR Chemical Shielding Anisotropy in the Solid State" Molecules 24, no. 9: 1731. https://doi.org/10.3390/molecules24091731
APA StyleCzernek, J., & Brus, J. (2019). Exploring Accuracy Limits of Predictions of the 1H NMR Chemical Shielding Anisotropy in the Solid State. Molecules, 24(9), 1731. https://doi.org/10.3390/molecules24091731