Metal-Ligand Recognition Index Determination by NMR Proton Relaxation Study

Abstract

In this study, we developed and validated a new proposed parameter quantifying the interaction strength between natural and/or synthetic molecules with paramagnetic metal ions. The Metal ion Recognition Index, Miri, is a quantitative parameter to describe the proton environment and to define their involvement in the inner and/or outer sphere of the paramagnetic metal ion. The method is based on the analysis of NMR proton spin-lattice relaxation rates of a specific ligand in both the diamagnetic and paramagnetic conditions. The proposed procedure is also useful to calculate the ligand proton spin-lattice relaxation rate in the paramagnetic bound conditions, which is typically very difficult to determine experimentally. Miri was used to compare the ligand proton involvement toward different paramagnetic species, in particular the Copper(II)-Piroxicam system. Copper(II)-Piroxicam complex is one of the most active anti-inflammatory and anti-arthritic species. Miri provides an opportunity to improve our knowledge of metal-ligand complexes that play a fundamental role in bioinorganic interactions.

1. Introduction

Theoretical and experimental studies on metal-ligand interactions are an important field of research [1,2,3,4,5]. Metal-ligand complexes are very important for their applications in medicine, biology, chemistry, agriculture, etc. [6,7,8,9,10,11,12,13]. The formation of complexes between bioactive substances and metal ions, can produce different outcomes: (i) increase the pharmacological effects [14,15], (ii) reduce possible toxic side effects [16,17], (iii) modulate biological activities of both ligands and metal ions [18,19], (iv) contribute to the delivery of the bioactive substances towards their biological targets [20,21]. In the latter case, the metal complexing represents one of the possible methods to couple synergic pharmacological contributions and more efficient delivery systems (e.g., the formation of molecular clusters [22], the encapsulation of the metal complex into lipid or liposomal formulations [23,24,25], and the inclusion of complexes in carrier based hydrogels [26].

Natural and synthetic anti-inflammatory molecules have been widely investigated to find more effective compounds being able to interact with specific receptor sites of the biochemical pathway involved in the activation and maintenance of the inflammatory processes [27,28,29,30]. Metal complexes of the most active anti-inflammatory molecules are good candidates to become potent inhibitors of inflammation processes. The presence of a paramagnetic center in solution was used in the past [31,32,33,34,35,36,37], and more recently to investigate the structural and dynamical properties of metal-biopolymer complexes of peptides and proteins [38,39,40,41,42,43,44,45,46,47].

In the present study, a new method to determine the strength of the interaction between a ligand and a paramagnetic metal ion in solution, was developed and validated. The method is based on the analysis of the paramagnetic contributions to the ligand NMR proton spin-lattice relaxation rates. The experimental results obtained in both diamagnetic and paramagnetic systems were used with developing a new parameter, the “Metal Ion Recognition Index”, Miri. This new parameter provides a number of important uses: (a) as a quantitative parameter associated to a specific mathematical and chemical meaning, (b) to discriminate the proton environment around the paramagnetic metal ion and (c) to compare the paramagnetic contributions for different metal-ligand systems. Miri can be determined for any stoichiometry of the metal-ligand complex, it is formally related to the thermodynamic equilibrium constant (K_eq). The method offers the possibility to calculate a parameter that is very rarely reported, i.e., the proton spin-lattice relaxation rates in the pure paramagnetic environment (R_1m).

The method was validated using Copper(II)-Piroxicam, Cu(II)-Pix, being one of the most active anti-inflammatory and anti-arthritic species [48,49,50,51]. The crystal structure of the Cu(II)-Piroxicam complex is known [49].

2. Results and Discussion

2.1. Theory

Both the proton relaxation rate and line shape analysis suggested that, in a diamagnetic system, Piroxicam underwent fast motion conditions, i.e., ω₀τ_c << 1, where ω₀ is the proton Larmor frequency and τ_c is the correlation time modulating the re-orientational motions. In the presence of the paramagnetic Cu(II) ions, the ligand may exist in either the bound (m) or in the free (f) environments. In the presence of fast chemical exchange between the bound and the free environments, a paramagnetic contribution to the ligand proton relaxation rates can be detected as:

$$R_{1p}=R_{1\exp }-R_{1f}$$

(1)

where R_1p is the paramagnetic contribution to the relaxation rate, R_1exp the experimental relaxation rate in the paramagnetic system, and R_1f the relaxation rate in the diamagnetic system.

Considering the following equilibrium:

$$Cu(II)+L\to Cu(II)-L$$

if fast chemical exchange conditions apply, R_1exp is defined as:

$$R_{1\exp }={\chi }_m{R}_{1m}+{\chi }_f{R}_{1f}$$

(2)

where, R_1m is the proton relaxation rate of the paramagnetic complex, and χ_m and χ_f are the molar fractions of the metal complex and the free ligand, respectively. Assuming that χ_f is close to 1 (as the Ligand concentration is usually much higher than the paramagnetic ion concentration):

$$R_{1\exp }={\chi }_m{R}_{1m}+R_{1f}$$

(3)

and

$$R_{1\exp }-R_{1f}={\chi }_m{R}_{1m}$$

(4)

or

$$R_{1p}={\chi }_m{R}_{1m}$$

(5)

χ_m can be defined as:

$${\chi }_m=\frac{[Cu(II)-L]}{[Cu(II)]+[L]}$$

(6)

where, [Cu(II)–L], is the concentration of the complex, [L] is the concentration of the free ligand, and [Cu(II)] is the concentration of the free metal ion. Considering, as previously pointed out, that the ligand concentration is much higher than the metal ion concentration, [L] >> [Cu(II)], then:

$${\chi }_m\cong \frac{[Cu(II)-L]}{[L]}$$

(7)

The thermodynamic equilibrium constant for the Cu(II)-L interaction (at equilibrium) can be defined as:

$$K_{eq}=\frac{[Cu(II)-L]}{[Cu(II)]+[L]}=\frac{[Cu(II)-L]}{([Cu{(II)}_0]-[Cu(II)-L])[L]}$$

(8)

being the [Cu(II)] concentration equal to: [Cu(II)₀] − [Cu(II)-L]. Then:

$$[Cu(II)-L]=\frac{K_{eq}[Cu{(II)}_0][L]}{1+K_{eq}[L]}$$

(9)

Introducing this equation in Equation (7), then:

$${\chi }_m=\frac{K_{eq}[Cu{(II)}_0][L]}{(1+K_{eq}[L])[L]}$$

(10)

or

$${\chi }_m=\frac{K_{eq}[Cu{(II)}_0]}{1+K_{eq}[L]}$$

(11)

Substituting χ_m, in Equation (5), then:

$$R_{1p}=\frac{K_{eq}[Cu{(II)}_0]}{1+K_{eq}[L]}{R}_{1m}$$

(12)

Assuming the term:

$$\frac{K_{eq}}{1+K_{eq}[L]}{R}_{1m}=Miri$$

(13)

Miri is then defined as “Metal Ion Recognition Index”. Miri is a constant at constant temperature and constant ligand concentration. From Equation (12):

$$R_{1p}=Miri[Cu{(II)}_0]$$

(14)

Equation (14) is the equation of a straight line passing through the origin. Plotting the calculated R_1p values, as a function of [Cu(II)₀], the value of Miri can be calculated from the slope of the linear regression line. Miri measures the strength of the paramagnetic interaction, between the metal ion and a specific proton of the ligand molecule. It also helps define the proton environment around the paramagnetic ion.

In case of the presence of more ligand molecules in the metal coordination site, the equilibrium is defined as:

$$nL+Cu(II)\to [Cu(II)-{(L)}_n]$$

Following a similar logic:

$$R_{1p}=\frac{K_{eq}{[L]}^{n-1}[Cu{(II)}_0]}{1+K_{eq}{[L]}^n}{R}_{1m}$$

(15)

which is an equation of a straight line passing through the origin, when R_1p vs. [Cu(II)₀] is reported (maintaining both the temperature and ligand concentration [L], constants).

Similarly to Equation (14), Equation (15) can be reduced to:

$$R_{1p}=Miri[Cu{(II)}_0]$$

(16)

where Miri in this case is:

$$Miri=\frac{K_{eq}{[L]}^{n-1}}{1+K_{eq}{[L]}^n}{R}_{1m}$$

(17)

Equations (12) and (15) are powerful, in fact Equation (12) can be transformed to:

$$\frac{1}{R_{1p}}=\frac{1+K_{eq}[L]}{[Cu{(II)}_0]K_{eq}{R}_{1m}}$$

(18)

or

$$\frac{1}{R_{1p}}=\frac{1}{[Cu{(II)}_0]K_{eq}{R}_{1m}}+\frac{[L]}{[Cu{(II)}_0]R_{1m}}$$

(19)

In this case, there is a linear dependence between 1/R_1p and [L], as the paramagnetic ion concentration [Cu(II)₀], is maintained constant. The slope of the straight line between them leads to the determination of R_1m, while the intercept allows for the estimation of the thermodynamic equilibrium constant. In the case of the formation of the metal-ligand complex with a higher stoichiometry, like Cu(II)–(L)_n, Equation (15), can be transformed as:

$$\frac{1}{R_{1p}}=\frac{1+K_{eq}{[L]}^n}{K_{eq}{R}_{1m}{[L]}^{n-1}[Cu{(II)}_0]}=\frac{1}{K_{eq}{R}_{1m}{[L]}^{n-1}[Cu{(II)}_0]}+\frac{K_{eq}{[L]}^n}{K_{eq}{R}_{1m}{[L]}^{n-1}[Cu{(II)}_0]}$$

(20)

The linearity of 1/R_1p versus [L] is lost and both R_1m and K_eq cannot be calculated directly from geometrical analysis.

2.2. The case of Cu(II)-Piroxicam Complex

The proton spin-lattice relaxation rates of Piroxicam (Figure 1) in both the diamagnetic and paramagnetic systems are reported in

Table 1. Non-selective proton relaxation rate R_1f (s⁻¹) of Piroxicam solution (0.1 mol L⁻¹) versus Cu(II) concentration. Maximum experimental error, ≤5%.

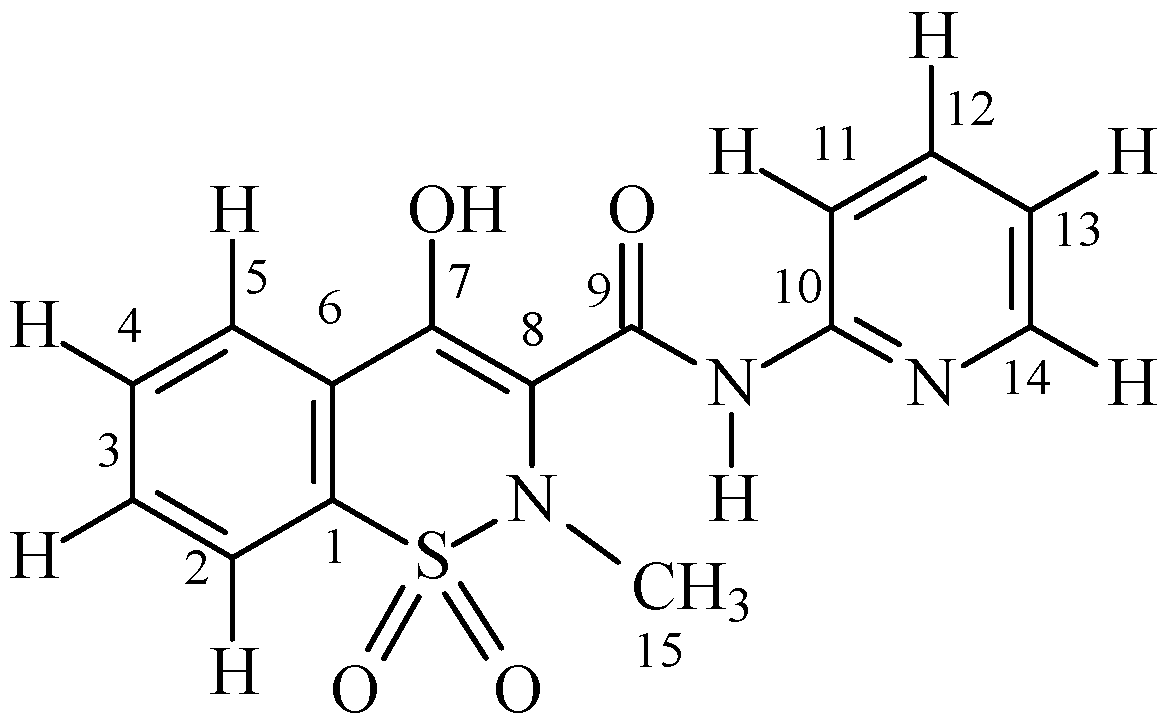
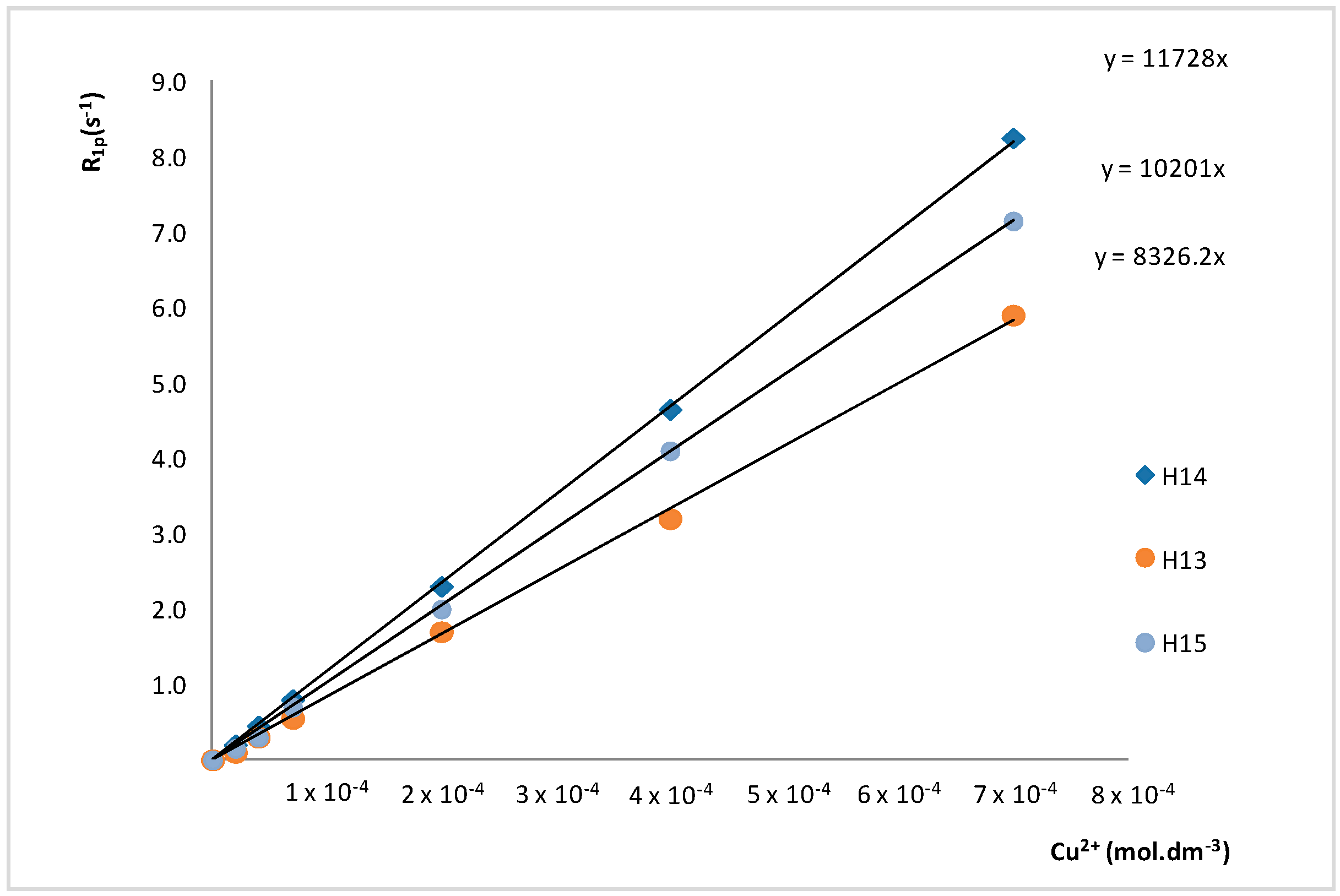
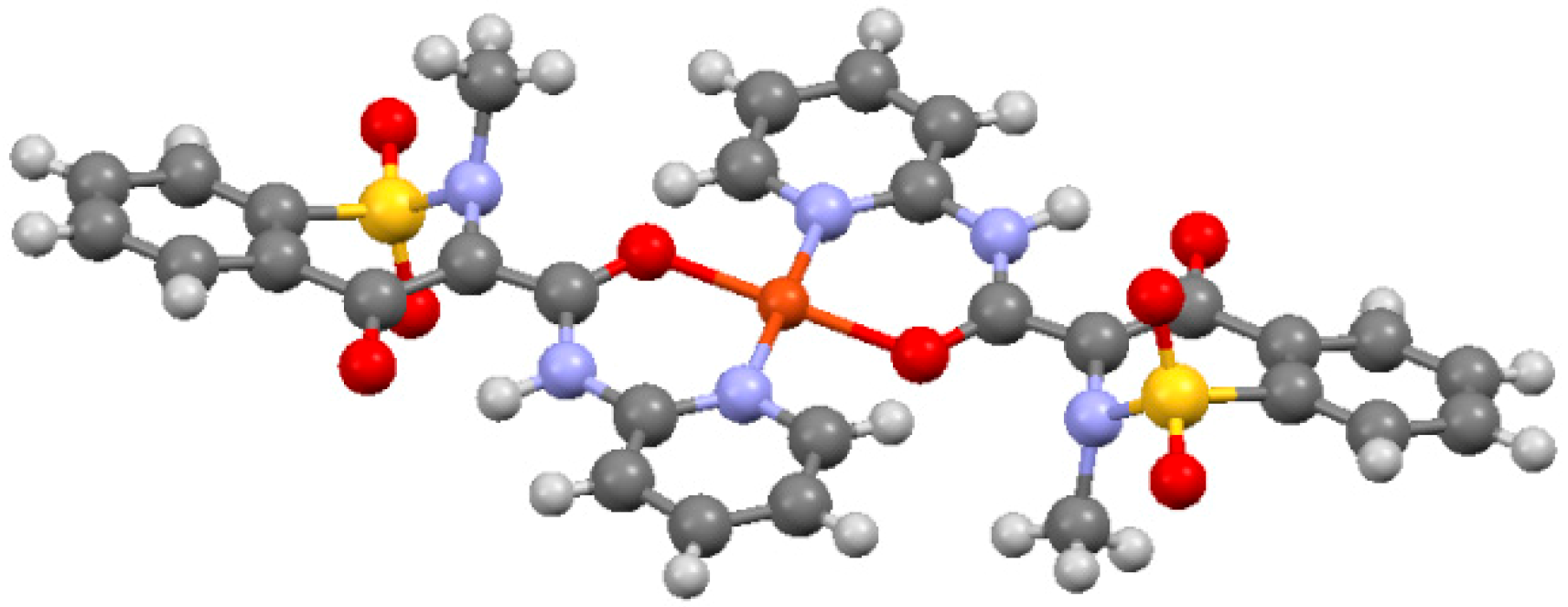
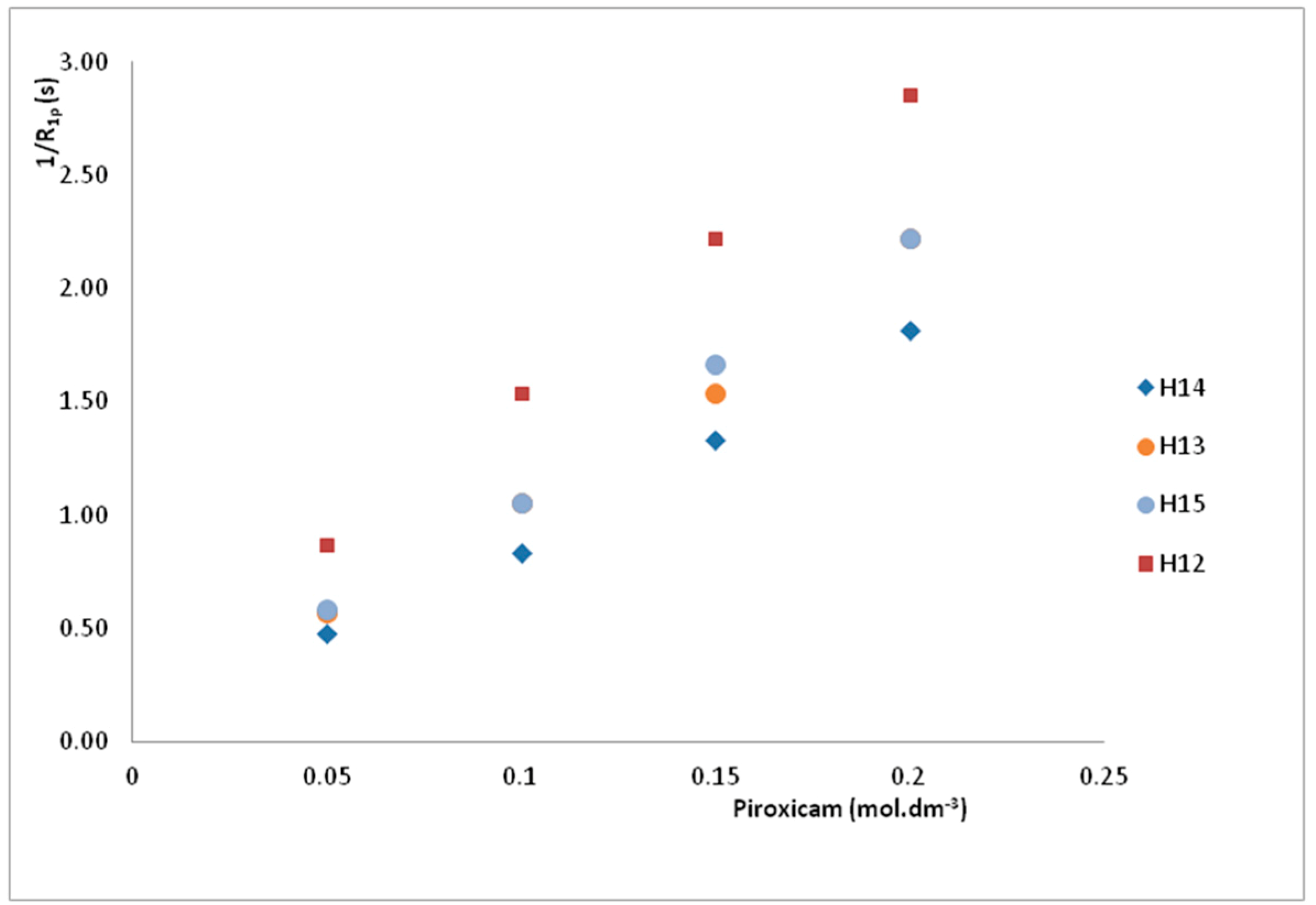
Proton	δ (ppm)	[Cu] (mol L−1)
		0	2 × 10−5	4 × 10−5	7 × 10−5	2 × 10−4	4 × 10−4	7 × 10−4
H14	8.42	0.40	0.60	0.85	1.20	2.70	5.05	8.65
H2/H5	8.06	0.40	0.45	0.50	0.60	0.80	1.25	1.85
H12	7.99	0.45	0.55	0.65	0.80	1.55	2.65	4.45
H11/H3	7.89	0.50	0.55	0.56	0.70	0.95	1.40	2.27
H4	7.86	0.55	0.60	0.65	0.85	0.95	1.25	1.85
H13	7.28	0.45	0.55	0.75	1.00	2.15	3.65	6.35
H15	2.87	1.10	1.25	1.40	1.80	3.10	5.20	8.25

. The paramagnetic system refers to the proton spin-lattice relaxation rate measured as a function of the copper(II) concentration, in the range of 2 × 10⁻⁵ to 7 × 10⁻⁴ mol L⁻¹. The paramagnetic contribution to proton spin-lattice relaxation, (R_1p = R_1exp − R_1f; Equation (1)), of Piroxicam proton nuclei are reported in

Table 2. Paramagnetic proton relaxation rate contribution R_1p (s⁻¹) of Piroxicam solution (0.1 mol L⁻¹) versus Cu(II) concentration. Maximum experimental error, ≤5%.

Proton	δ (ppm)	[Cu] (mol L−1)
		2 × 10−5	4 × 10−5	7 × 10−5	2 × 10−4	4 × 10−4	7 × 10−4
H14	8.42	0.20	0.45	0.80	2.30	4.65	8.25
H2/H5	8.06	0.05	0.10	0.20	0.40	0.85	1.45
H12	7.99	0.10	0.20	0.35	1.10	2.20	4.00
H11/H3	7.89	0.05	0.10	0.20	0.45	0.90	1.60
H4	7.86	0.05	0.10	0.30	0.40	0.70	1.30
H13	7.28	0.10	0.30	0.55	1.70	3.20	5.90
H15	2.87	0.15	0.30	0.70	2.00	4.10	7.15

.

The “Metal ion Recognition Index” Miri, for the different molecular moieties of Piroxicam was calculated from the linear regression analysis (Figure 2), which resulted in Miri values by 11,728, 8326, and 10,201 s⁻¹ mol⁻¹ L for the H14, H13 and the methyl H15 protons, respectively. These results confirm the validity of Equations (14) and (16) and allow for the quantification of the specific strength of the Cu(II)-Piroxicam complex.

We also explored the applicability of equations (19) and (20) to the Cu(II)-Piroxicam system. On the basis of previous studies on the Cu(II)-Piroxicam complex in solution [50,52,53] and on Cu(II)-Piroxicam crystal structure (Figure 3, [49]), we assumed the prevalence of the Cu(II)(Pix)₂ complex in solution.

As the Piroxicam concentration is a much higher than that of the Copper ion, we consider a predominance of the Cu(II)(Pix)₂ complex in the present experimental conditions. On the basis of these considerations, Equation (19) cannot be applied and Equation (20), is then modified to:

$$\frac{1}{R_{1p}}=\frac{1}{K_{eq}{R}_{1m}[Pix][Cu{(II)}_0]}+\frac{[Pix]}{R_{1m}[Cu{(II)}_0]}$$

(21)

Equation (21) presents two terms, the first term can be neglected if the equilibrium constant of the complex, K_eq, is higher than 1 × 10². However, a higher value of K_eq for the complex was previously reported [52,53].

If we neglect the first term, Equation (21) is a linear equation where 1/R_1p varies with Piroxicam concentration.

Table 3. Paramagnetic proton relaxation rate R_1p (s⁻¹) of Piroxicam solutions at several concentrations in the presence of Cu(II) (1 × 10⁻⁴ mol L⁻¹). Maximum experimental error, ≤5%.

Proton	δ (ppm)	[Cu] (mol L−1)
		0.25	0.20	0.15	0.10	5 × 10−5
H14	8.42	0.46	0.55	0.75	1.20	2.10
H2/H5	8.06	0.12	0.15	0.20	0.35	0.45
H12	7.99	0.30	0.35	0.45	0.65	1.15
H11/H3	7.89	0.10	0.12	0.17	0.25	0.45
H4	7.86	0.12	0.15	0.20	0.30	0.60
H13	7.28	0.37	0.45	0.65	0.95	1.75
H15	2.87	0.38	0.45	0.60	0.95	1.70

reports the paramagnetic contributions to proton spin-lattice relaxation, (R_1p = R_1exp − R_1f; Equation (1)) of Piroxicam proton nuclei as a function of Piroxicam concentration (in the range of 0.25 to 5 × 10⁻² mol L⁻¹), in the presence of Cu(II), 1 × 10⁻⁴ mol L⁻¹ concentration.

These data can be used to determine R_1m, the proton spin-lattice relaxation rate in the pure paramagnetic site. As expected from Equation (21), it is a linear dependence of 1/R_1p on Piroxicam concentration (Figure 4).

The values of R_1m, calculated from the slopes of the fitted lines for the H12, H13, H14, and H15 (

Table 4. Calculated R_1m values from linear regression analysis of the data reported in Figure 2, for H14, H12, H13, and H15 protons of Piroxicam.

Proton	δ (ppm)	R1m (s−1)
H14	8.42	1129 ± 55
H12	7.99	730 ± 36
H13	7.28	943 ± 46
H15	2.87	917 ± 44

) indicated that each proton experience a specific paramagnetic environment as a consequence of the different metal ion proton distances [54].

The calculated spin-lattice relaxation rates in the pure paramagnetic site (R_1m), were then used to study the dynamical properties of the metal-ligand complex. The relaxation rate at the paramagnetic site was defined as [55,56,57]:

$$\frac{1}{T_{1,M}}=\frac{2}{15}\frac{{\gamma }_I^2{g}^{2}S(S+1){\beta }^2}{r^6}\left(\frac{3{\tau }_c}{1+{\omega }_I^2{\tau }_c^2}+\frac{7{\tau }_c}{1+{\omega }_S^2{\tau }_c^2}\right)+\frac{2}{3}S(S+1){\left(\frac{A}{\hslash }\right)}^2\left(\frac{{\tau }_e}{1+{\omega }_S^2{\tau }_e^2}\right)$$

(22)

where the dipolar term originates from the electron-nucleus dipolar contribution, while the scalar one from the modulation of the scalar interaction between the electron spin S and the nuclear one I. In Equation (22), ω_I and ω_S are the Larmor frequencies of nucleus and electron, respectively (where ω_I >> ω_S), g is the Lande g factor, β is the Bohr magneton, r is the distance between the nucleus and the paramagnetic species, and (A/ħ) is the electron-nuclear hyperfine coupling constant. Values τ_c and τ_s are correlation times that modulate dipolar and scalar interactions, and are defined as:

$${\tau }_c^{-1}={\tau }_r^{-1}+{\tau }_s^{-1}+{\tau }_m^{-1}$$

(23)

and

$${\tau }_e^{-1}={\tau }_s^{-1}+{\tau }_m^{-1}$$

(24)

where τ_r is the rotational correlation time, τ_s the electron spin relaxation time, and τ_m the life time of the nucleus in the bound site.

In the case of paramagnetic systems containing Cu(II) ions in solution, Equation (22) is dominated essentially by the dipolar contribution [58,59,60]. This allows for the determination of the correlation time value τ_c, in fact from the crystalline structure of the [Cu(II)(Pix)₂] complex [50], each Cu(II)…proton nuclei distance can be calculated. In this specific case, the distances between the paramagnetic ion Cu(II) and the nuclei H2 and H3 are 4.14, 4.58 Å, respectively. Introducing the metal-ligand distances and the R_1m values in Equation (22), the correlation time (τ_c) modulating the dipolar contribution was calculated. In the present case, this value was determined ranging 3 × 10⁻¹⁰–5 × 10⁻¹⁰ s. These data are compatible to the value of the rotational correlation time of the complex. This important result confirms that for Cu(II) complexes in solution, the dipolar correlation time is dominated by the molecular tumbling rotation τ_r.

3. Materials and Methods

3.1. Materials

Piroxicam (4-hydroxy-2-methyl-1,1-dioxo-N-pyridinyl-2H-1,2-benzothiazine-3-carboxamide) and copper perchlorate hexahydrate Cu(ClO₄)₂·6H₂O, were purchased from Sigma-Aldrich (Milan, Italy) and used without any further purification. The deuterated solvent, DMSO-d₆, was 99.96 atom %D and was also from Sigma-Aldrich.

3.2. NMR Measurements

The solutions for the NMR experiments were obtained by dissolving the appropriate amounts of Piroxicam (0.1 mol L⁻¹) and Cu(ClO₄)₂·6H₂O in DMSO-d₆. Paramagnetic purity of the Piroxicam solution was tested by analyzing the NMR proton spin-lattice relaxation rates of both the solvent and water signals.

¹H-NMR spectra were obtained on a Bruker DRX 600 spectrometer, operating at 600.13 MHz. The proton spin–lattice relaxation rates (R₁) were measured using the inversion-recovery (180–τ–90–t)_n sequence, where t is the recovery delay after the inversion-recovery perturbation. The R₁ values were calculated by computer fitting of the relaxation curves. The maximum experimental error in the relaxation rate measurements was ≤5%. All the spectra were processed using the Bruker Software TOPSPIN3.5. The temperature was held constant at 298 ± 1 K for all experiments; and the maximum experimental error on chemical shifts was ≤2%.

4. Conclusions

A new approach was developed to study the interaction processes between paramagnetic species and biological and/or synthetic ligands. A new parameter, the metal ion recognition index, Miri, was determined by plotting proton spin-lattice relaxation versus the concentration of the paramagnetic ion. The main advantage of this approach, with respect to the measurement of the experimental paramagnetic contribution to nuclear relaxation, is the possibility to define a new parameter, Miri. It is formally related to two important chemical parameters, the formation constant of the complex and the relaxation rate of the nuclear species in the pure paramagnetic site, R_1m. The developed method provides a new way to their calculation. In the case of 1:1 complexes, both parameters can be calculated. For complexes with more ligands at the metal site, it is only possible to calculate the relaxation rate in the pure paramagnetic site. In the present investigation, combining this information with structural data, obtained from diffraction study of the crystal structure, the rotational correlation time of the complex was also calculated.

The Miri is also an easy-to-calculate index giving the opportunity to compare the interaction behavior between a selected metal and different ligands or different metals and a selected ligand.