Wavelength Selection for NIR Spectroscopy Based on the Binary Dragonfly Algorithm
Abstract
:1. Introduction
2. Dragonfly Algorithm
2.1. Continuous Dragonfly Algorithm
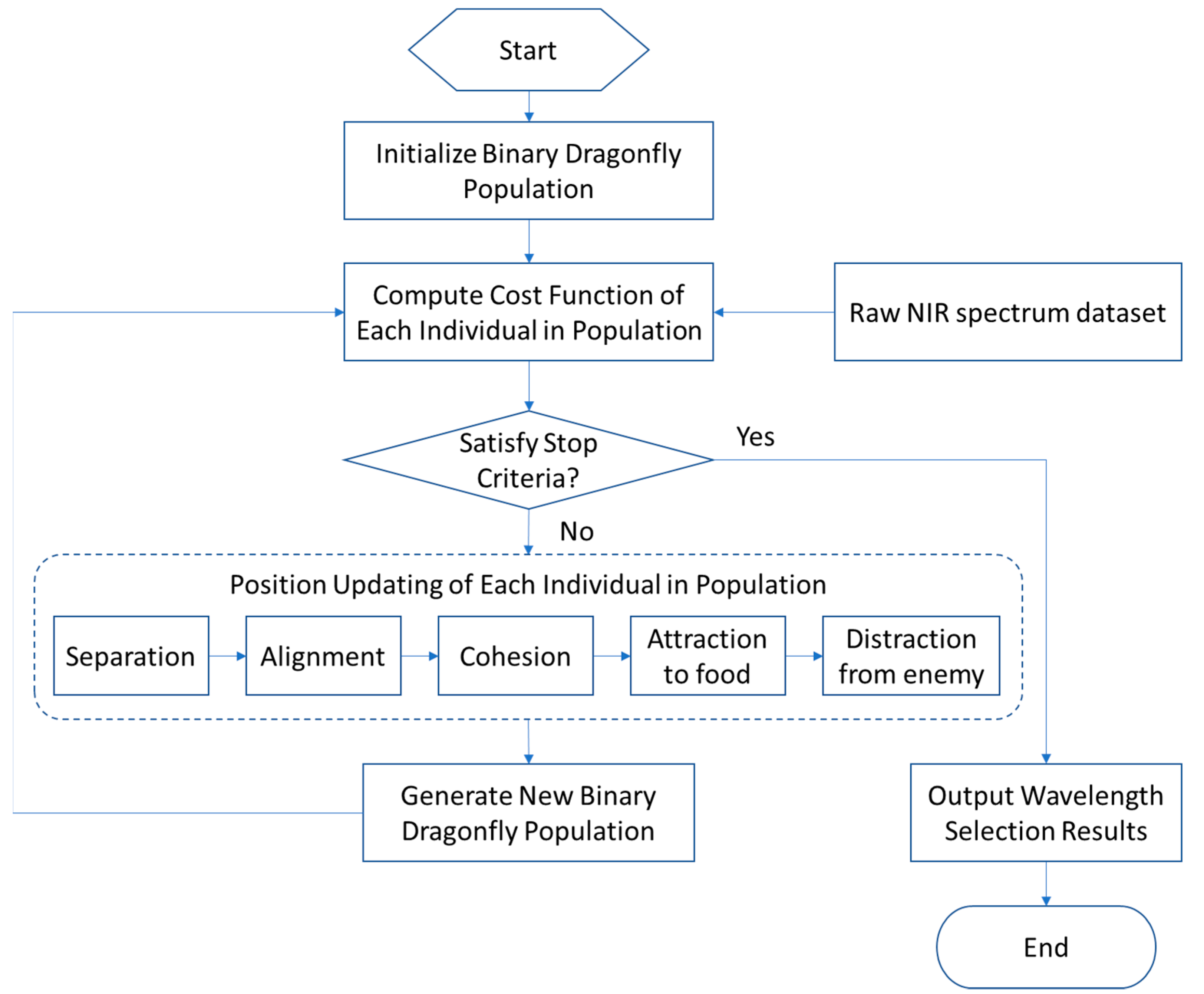
2.2. Binary Dragonfly Algorithm (BDA)
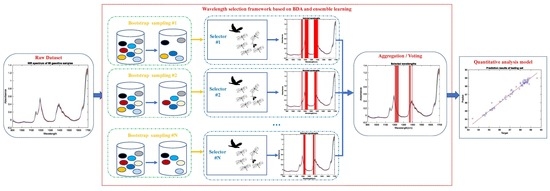
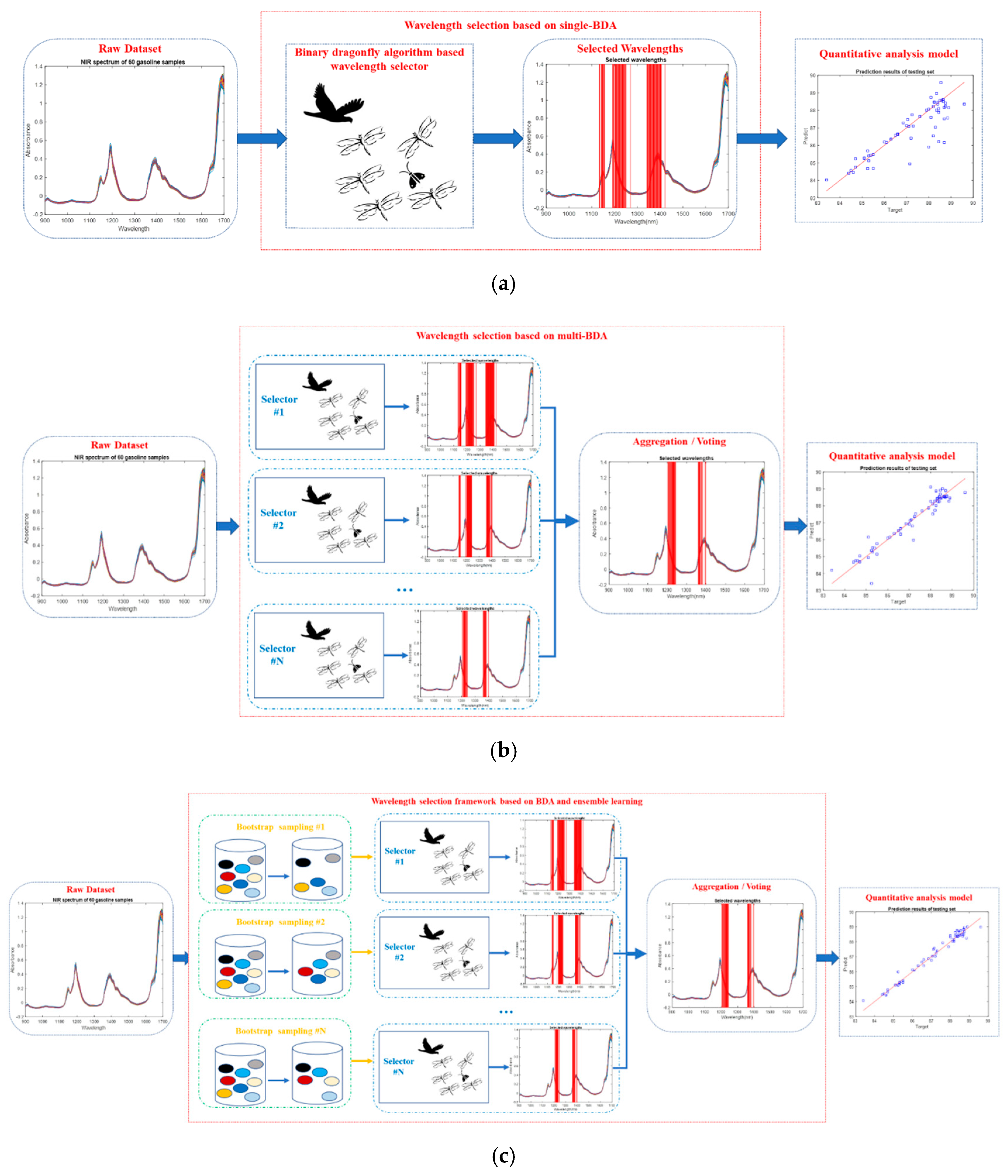
3. Wavelength Selection Framework Based on BDA and Ensemble Learning
4. Experimental Results and Discussion
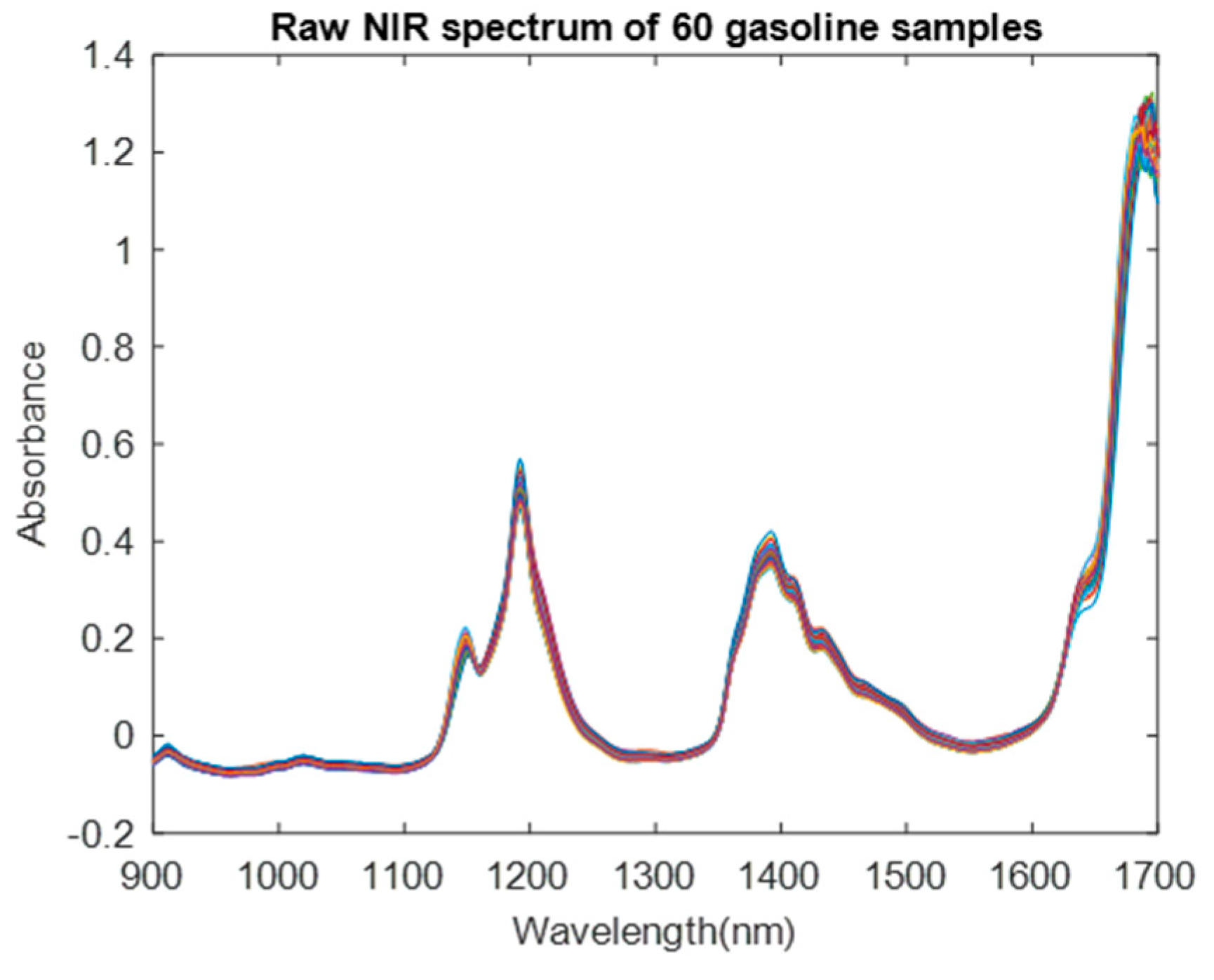
4.1. Dataset Description
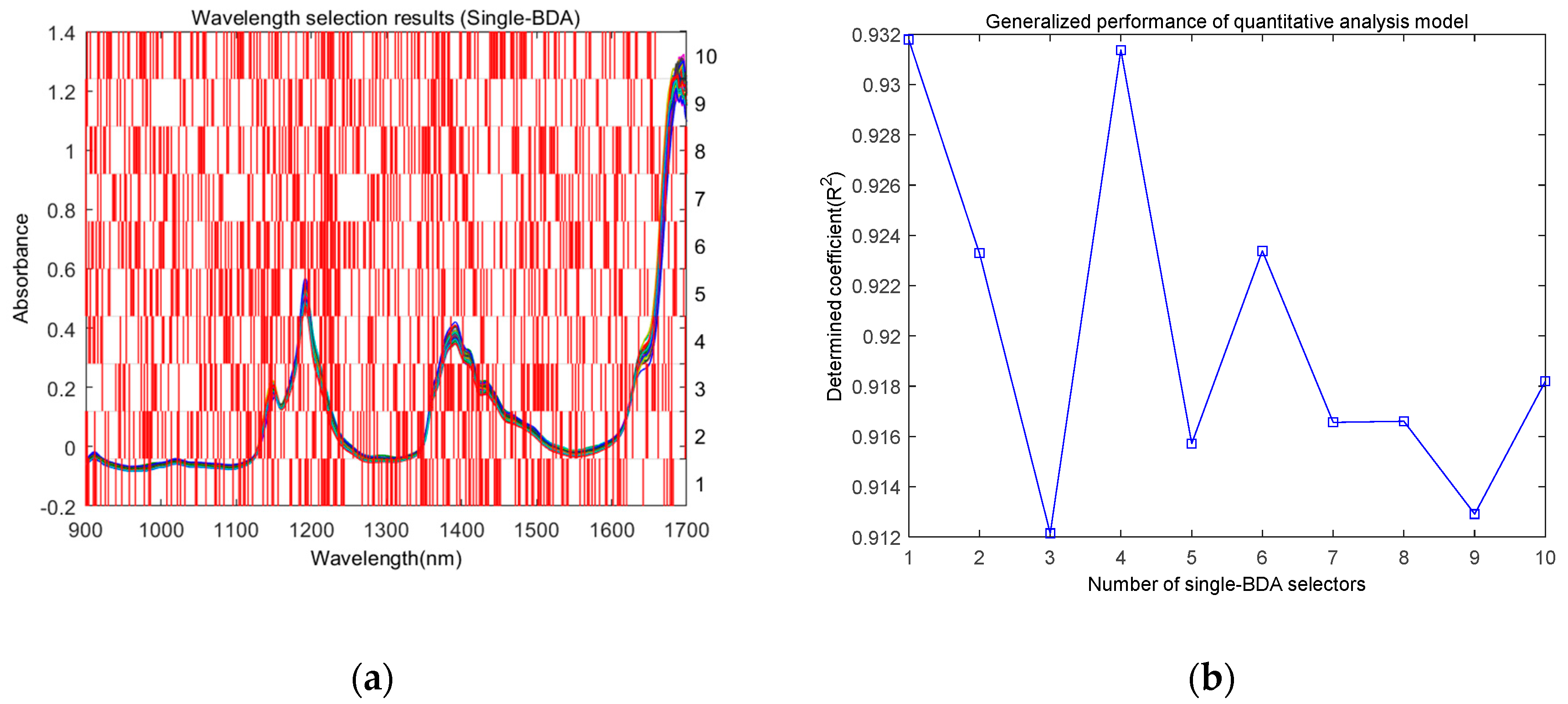
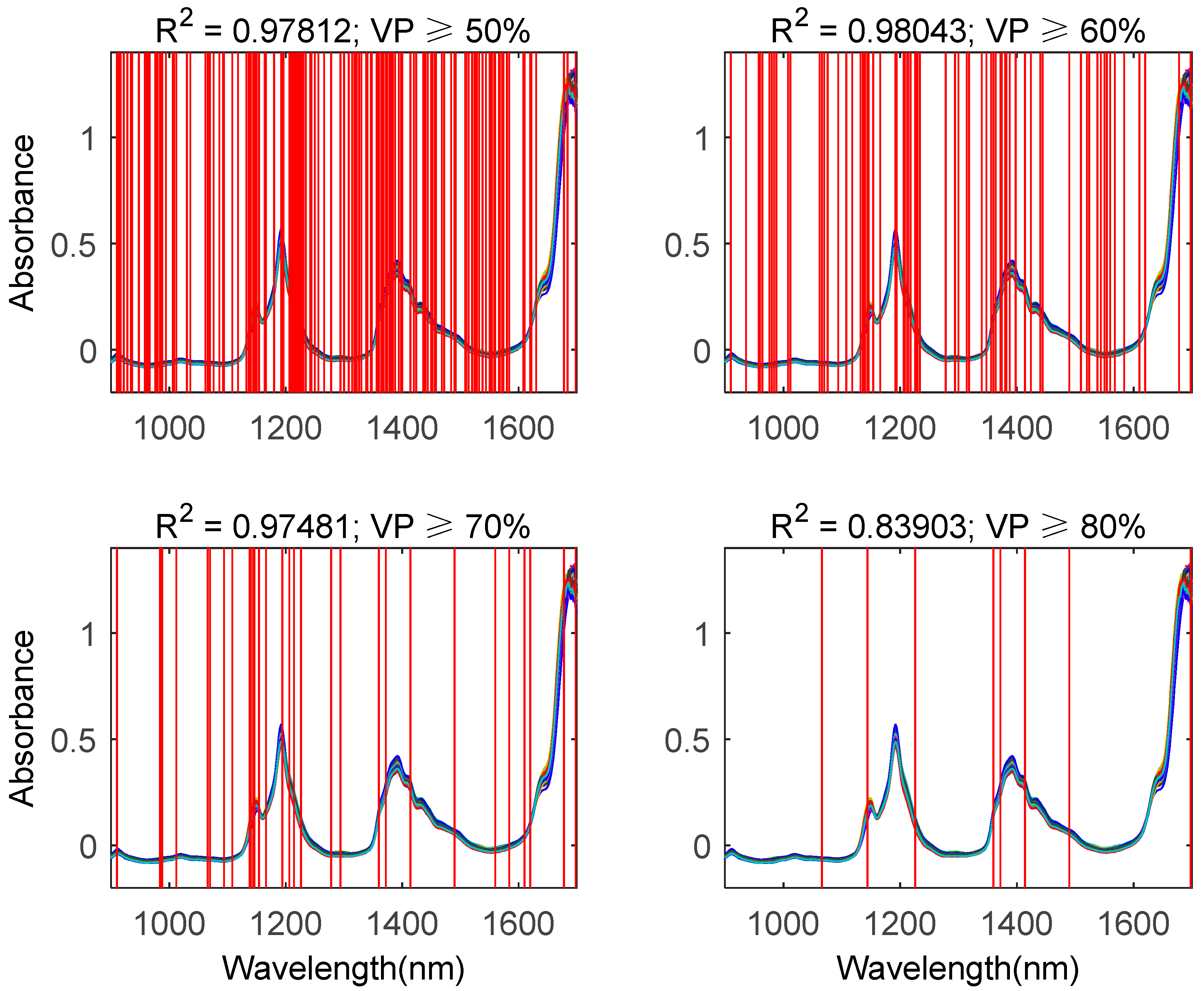
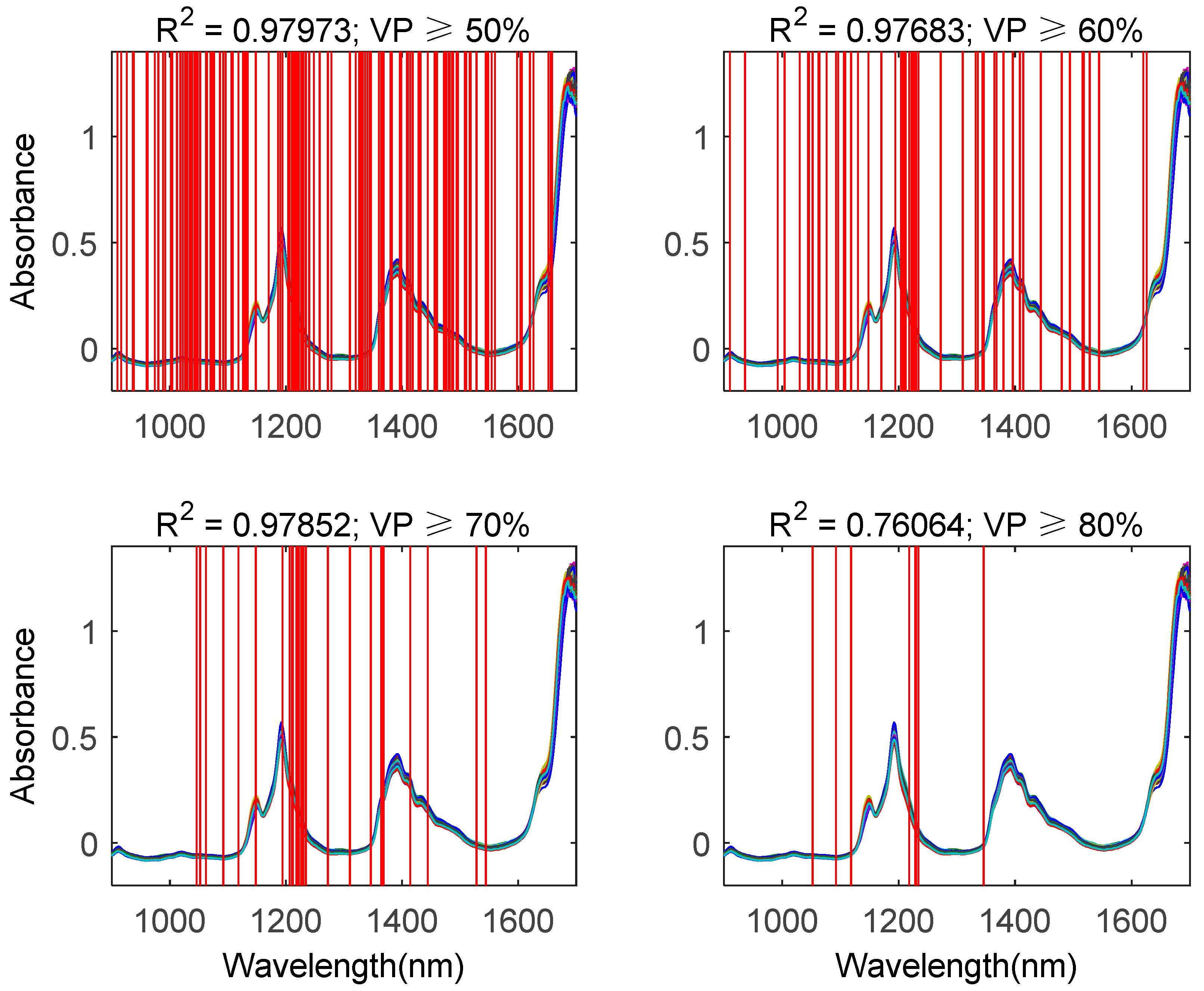
4.2. Experimental Results
4.3. Discussion
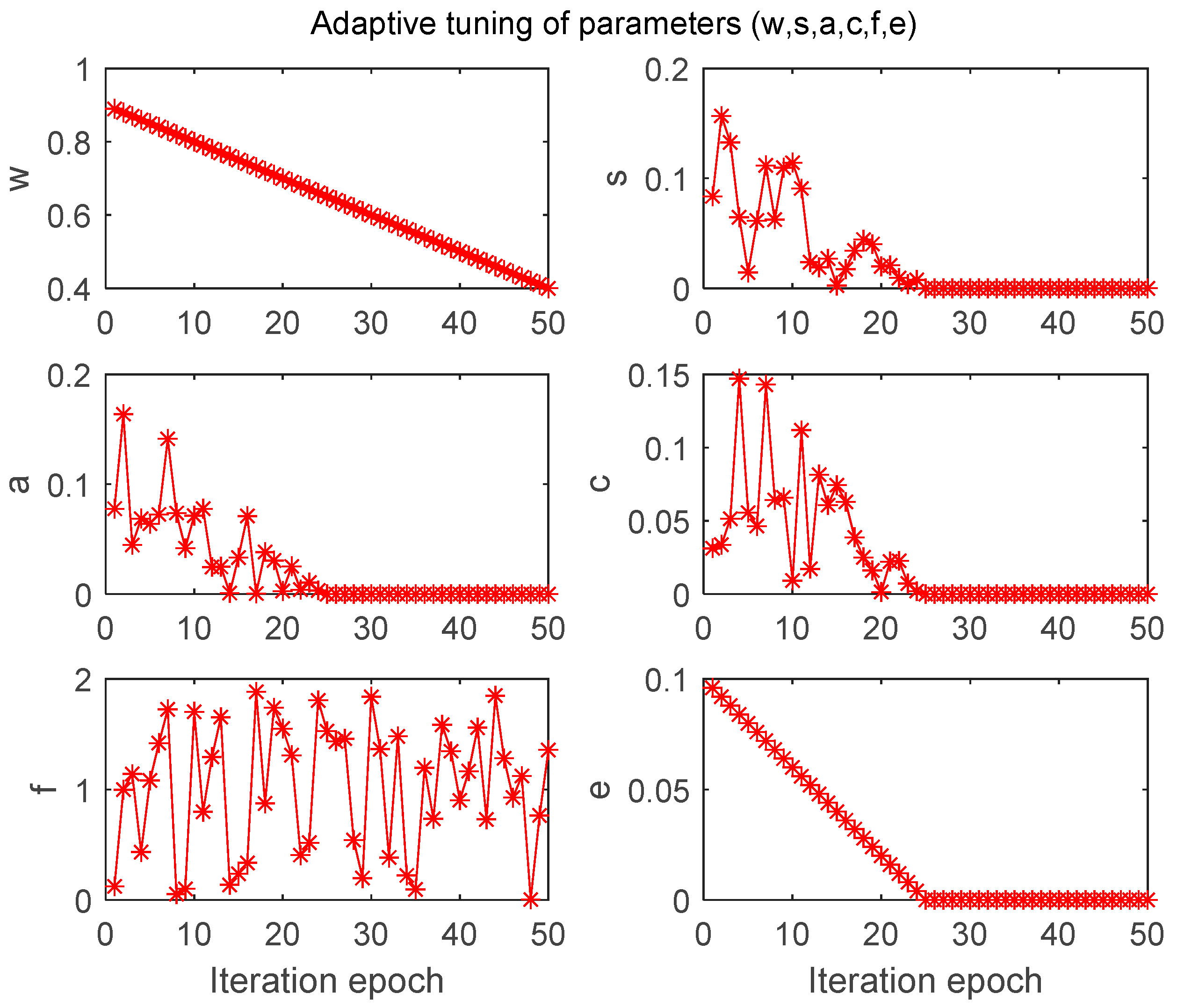
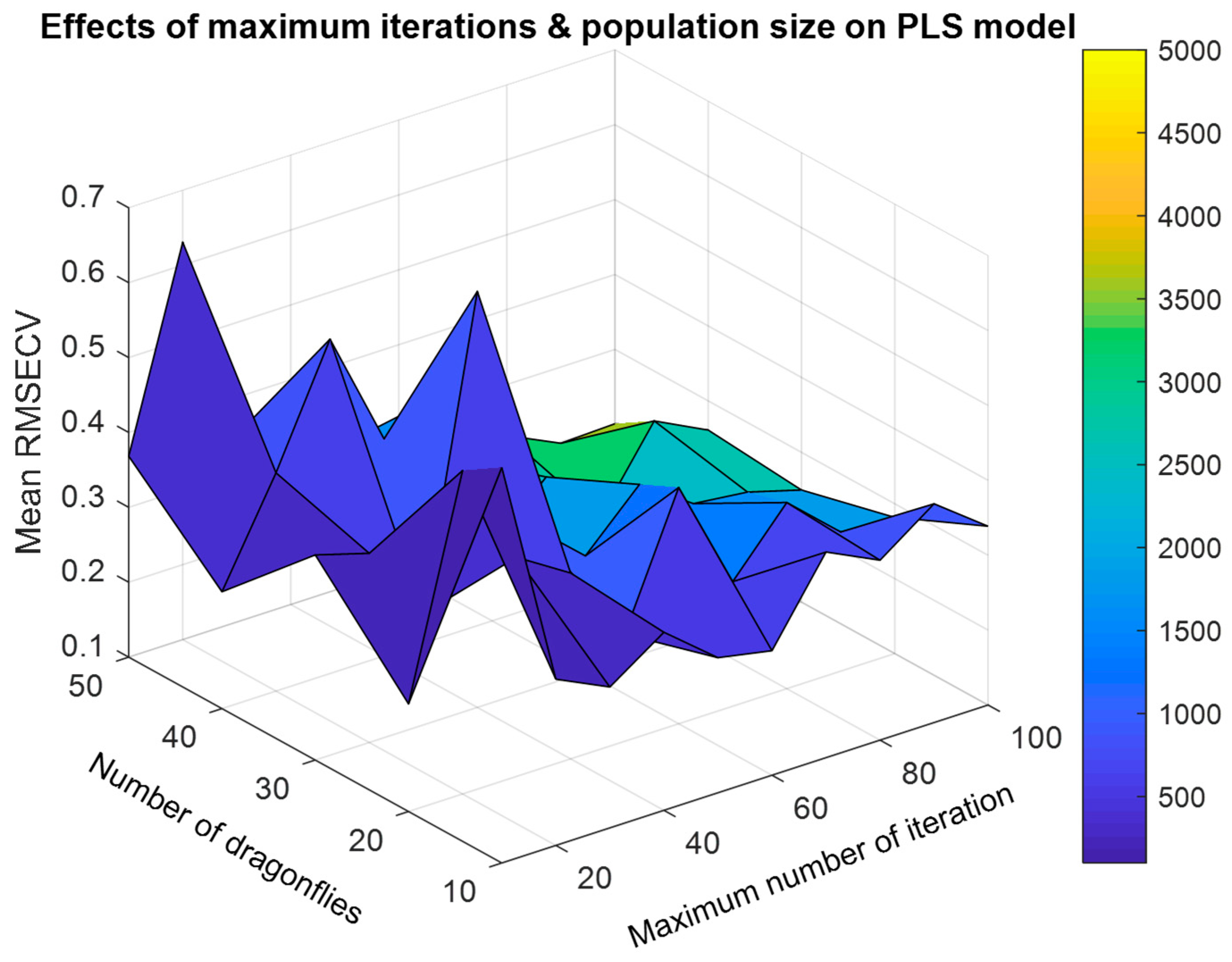
4.3.1. Influence of the Values of the BDA Parameters on the Generalized Performance of the Model
4.3.2. Comparison Between Proposed Methods and Traditional Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zou, X.; Zhao, J.; Povey, M.J.; Holmes, M.; Mao, H. Variables selection methods in near-infrared spectroscopy. Anal. Chim. Acta 2010, 667, 14–32. [Google Scholar] [CrossRef] [PubMed]
- Norgaard, L.; Saudland, A.; Wagner, J.; Nielsen, J.P.; Munck, L.; Engelsen, S.B. Interval partial least-squares regression (iPLS): A comparative chemometric study with an example from near-infrared spectroscopy. Appl. Spectrosc. 2000, 54, 413–419. [Google Scholar] [CrossRef]
- Centner, V.; Massart, D.L.; de Noord, O.E.; de Jong, S.; Vandeginste, B.M.; Sterna, C. Elimination of uninformative variables for multivariate calibration. Anal. Chem. 1996, 68, 3851–3858. [Google Scholar] [CrossRef] [PubMed]
- Moros, J.; Kuligowski, J.; Quintás, G.; Garrigues, S.; de la Guardia, M. New cut-off criterion for uninformative variable elimination in multivariate calibration of near-infrared spectra for the determination of heroin in illicit street drugs. Anal. Chim. Acta 2008, 6, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Chen, Y.; Wang, Z.; Li, K. A novel ensemble L1 regularization based variable selection framework with an application in near infrared spectroscopy. Chemom. Intell. Lab. Syst. 2017, 163, 7–15. [Google Scholar]
- Givianrad, M.H.; Saber-Tehrani, M.; Zarin, S. Genetic algorithm-based wavelength selection in multicomponent spectrophotometric determinations by partial least square regression: Application to a sulfamethoxazole and trimethoprim mixture in bovine milk. J. Serb. Chem. Soc. 2013, 78, 555–564. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z. Feature Selection of Infrared Spectrum Based on Improved Bat Algorithm. Available online: http://journal02.magtech.org.cn/Jwk_irla/CN/Y2014/V43/I8/2715 (accessed on 15 December 2018).
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Eleyan, D.; Jaber, I. Binary dragonfly algorithm for feature selection. In Proceedings of the 2017 International Conference on New Trends in Computing Sciences (ICTCS), Amman, Jordan, 11–13 October 2017. [Google Scholar]
- Saremi, S.; Mirjalili, S.; Lewis, A. How important is a transfer function in discrete heuristic algorithms. Neural Comput. Appl. 2015, 26, 625–640. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. S-shaped versus V-shaped transfer functions for binary particle swarm optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Yuanyuan, C.; Zhibin, W. Quantitative analysis modeling of infrared spectroscopy based on ensemble convolutional neural networks. Chemom. Intell. Lab. Syst. 2018, 181, 1–10. [Google Scholar] [CrossRef]
- Kalivas, J.H. Two data sets of near infrared spectra. Chemom. Intell. Lab. Syst. 1997, 37, 255–259. [Google Scholar] [CrossRef]
- Le, B.T.; Xiao, D.; Mao, Y.; He, D. Coal analysis based on visible-infrared spectroscopy and a deep neural network. Infrared Phys. Technol. 2018, 93, 34–40. [Google Scholar] [CrossRef]
- Wang, C.; Wu, X.-H.; Li, L.Q.; Wang, Y.-S.; Li, Z.-W. University, Convolutional Neural Network Application in Prediction of Soil Moisture Content. Available online: http://www.gpxygpfx.com/article/2018/1000-0593-38-1-36.html (accessed on 15 December 2018).
- Acquarelli, J.; Laarhoven, T.V.; Gerretzen, J.; Tran, T.N.; Buydens, L.M.C.; Marchiori, E. Convolutional neural networks for vibrational spectroscopic data analysis. Anal. Chim. Acta 2017, 954, 22–31. [Google Scholar] [CrossRef] [PubMed]
- Afara, I.O.; Sarin, J.K.; Ojanen, S.; Finnilä, M.; Herzog, W.; Saarakkala, S.; Töyräs, J. Deep Learning Classification of Cartilage Integrity Using Near Infrared Spectroscopy. In Proceedings of the Biomedical Optics Congress 2018, Hollywood, FL, USA, 3–6 April 2018. [Google Scholar]
- Malek, S.; Melgani, F.; Bazi, Y. One-dimensional convolutional neural networks for spectroscopic signal regression. J. Chemom. 2018, 32, e2977. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, W.; Hou, Y.; Qiu, C.; Yang, S.; Li, C.; Nie, L. Sparse Representation Classification of Tobacco Leaves Using Near-Infrared Spectroscopy and a Deep Learning Algorithm. Anal. Lett. 2018, 51, 1029–1038. [Google Scholar] [CrossRef]
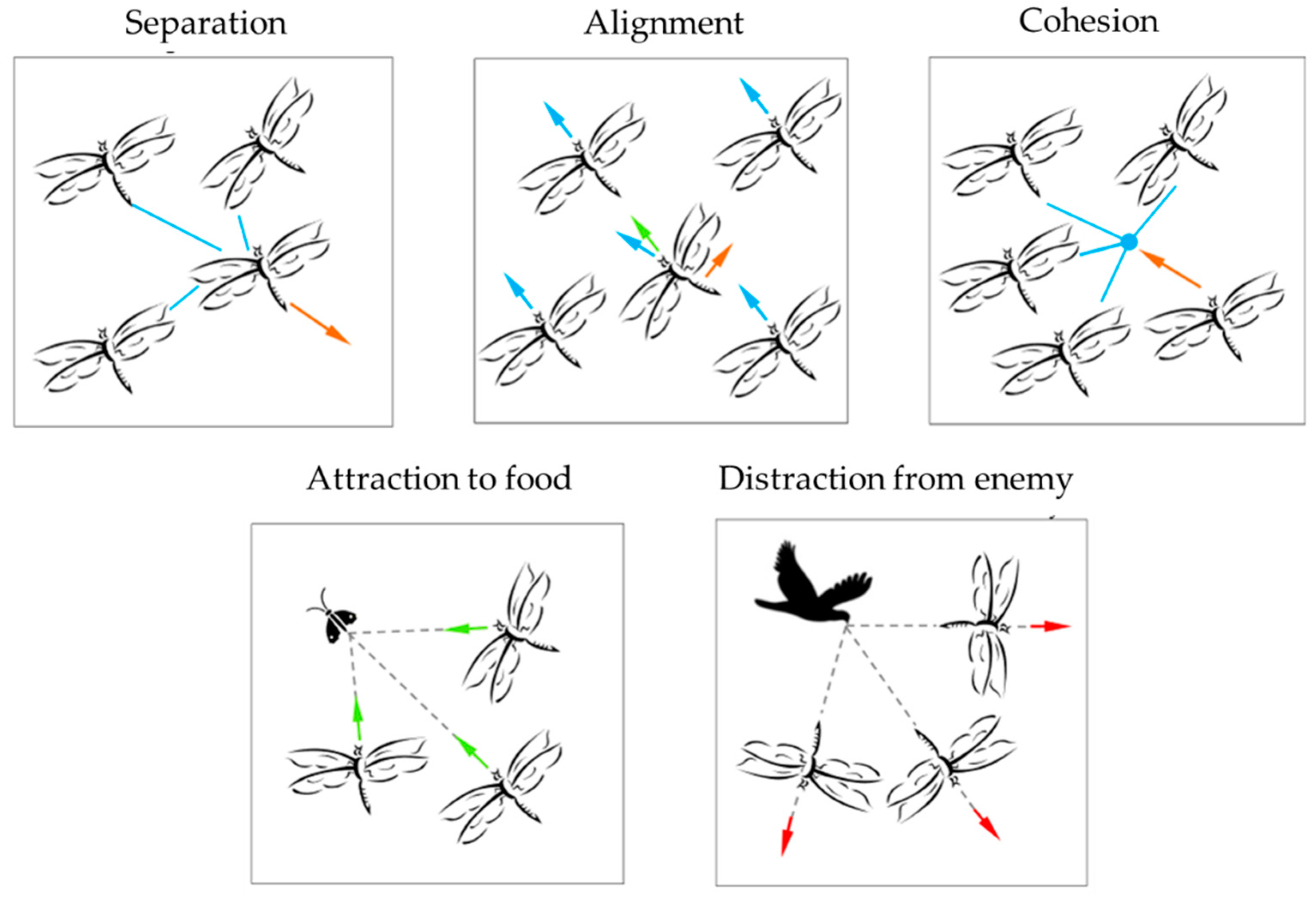
| Position Updating Strategies | Equations | Description |
|---|---|---|
| Separation | : position of the current individual : position of the j-th neighboring individual : number of the neighboring individuals : velocity of the j-th neighboring individual : position of the food source : position of the enemy (, , , , : separation, alignment, cohesion, food, and enemy factors : inertia weight : current iteration | |
| Alignment | ||
| Cohesion | ||
| Attraction to food | ||
| Distraction from enemy | ||
| Position updating | ||
| Position updating with Lévy flight | Lévy | : dimension of the position vectors , : random numbers in [0, 1] : constant |
| Parameters | Values |
|---|---|
| Maximum number of iterations | 50 |
| Number of dragonflies | 10 |
| Number of wavelengths | 401 |
| Separation, alignment, cohesion, food, and enemy factors | adaptive tuning |
| Number of principal components | 2 |
| Number of folds of cross validation | 5 |
| Parameters | Mean RMSECV of 10 Times Repeated PLS Models with Selected Wavelengths | ||
|---|---|---|---|
| Adaptive Tuning | Fixed (Maximum) | Fixed (Minimum) | |
| w (0.4–0.9) | 0.3801 | 0.5196 | 0.2583 |
| s (0–0.2) | 0.5500 | 0.3700 | |
| a (0–0.2) | 0.4833 | 0.4186 | |
| c (0–0.2) | 0.4955 | 0.4071 | |
| f (0–2) | 0.4871 | 0.5224 | |
| e (0–0.1) | 0.3796 | 0.4570 | |
| Methods | Population Size | Maximum of Iteration | RMSECV of 10 Times Repeated PLS Models with Selected Wavelengths | |
|---|---|---|---|---|
| Mean | Std | |||
| Genetic algorithm | 20 | 50 | 0.4016 | 0.0624 |
| Binary bat algorithm | 0.3672 | 0.0482 | ||
| Single-BDA | 0.3801 | 0.0549 | ||
| Multi-BDA | 0.3265 | 0.0215 | ||
| Ensemble learning based BDA | 0.3294 | 0.0168 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, Z. Wavelength Selection for NIR Spectroscopy Based on the Binary Dragonfly Algorithm. Molecules 2019, 24, 421. https://doi.org/10.3390/molecules24030421
Chen Y, Wang Z. Wavelength Selection for NIR Spectroscopy Based on the Binary Dragonfly Algorithm. Molecules. 2019; 24(3):421. https://doi.org/10.3390/molecules24030421
Chicago/Turabian StyleChen, Yuanyuan, and Zhibin Wang. 2019. "Wavelength Selection for NIR Spectroscopy Based on the Binary Dragonfly Algorithm" Molecules 24, no. 3: 421. https://doi.org/10.3390/molecules24030421
APA StyleChen, Y., & Wang, Z. (2019). Wavelength Selection for NIR Spectroscopy Based on the Binary Dragonfly Algorithm. Molecules, 24(3), 421. https://doi.org/10.3390/molecules24030421