Path Integral Calculation of the Hydrogen/Deuterium Kinetic Isotope Effect in Monoamine Oxidase A-Catalyzed Decomposition of Benzylamine
Abstract
:1. Introduction
2. Computational Details
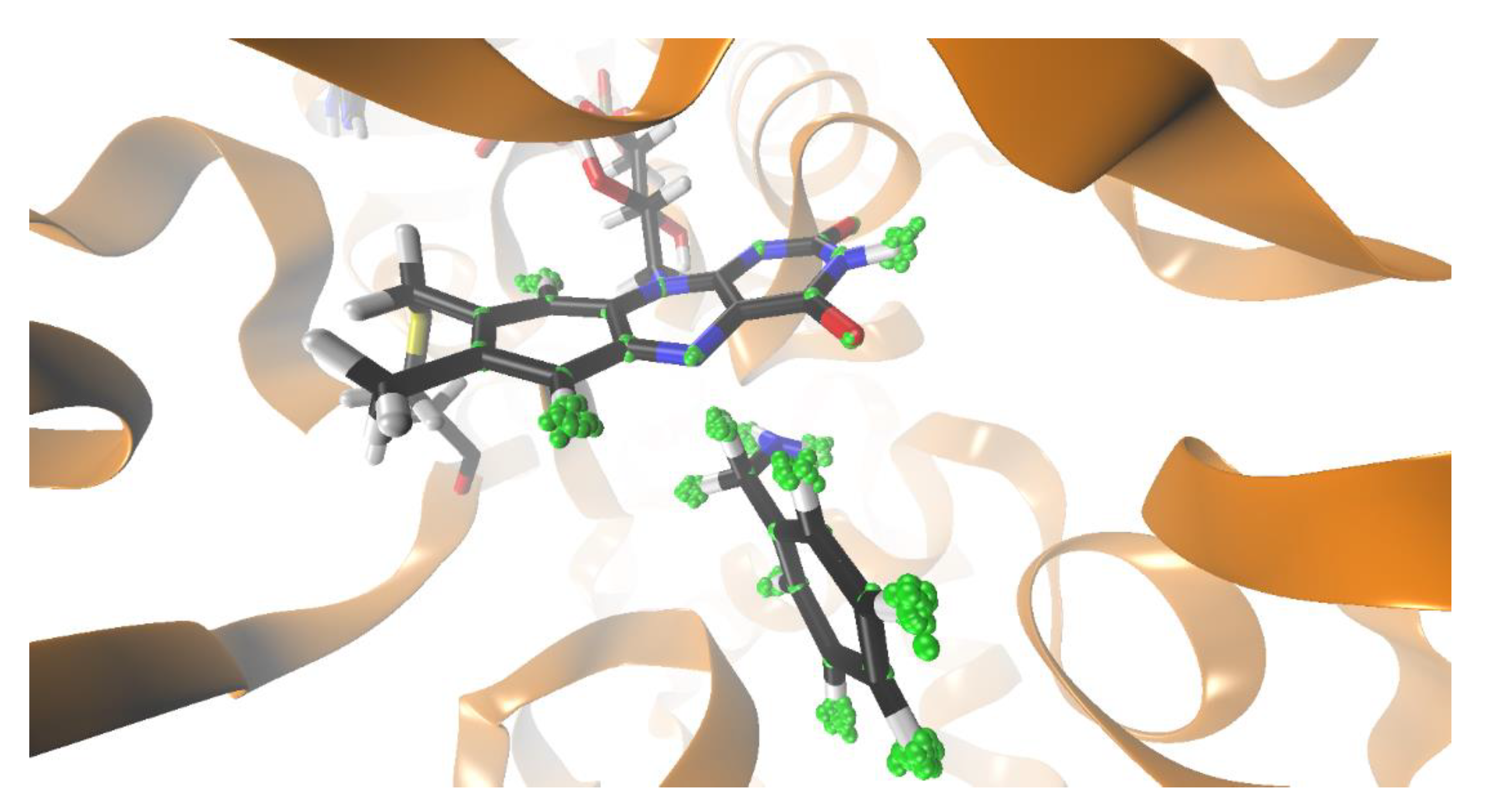
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Di Giovanni, G.; Di Matteo, V.; Esposito, E. Serotonin-Dopamine Interaction: Experimental Evidence and Therapeutic Relevance; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Ramsay, R.R. Monoamine Oxidases: The Biochemistry of the Proteins As Targets in Medicinal Chemistry and Drug Discovery. Curr. Top. Med. Chem. 2012, 12, 2189–2209. [Google Scholar] [CrossRef] [PubMed]
- Vianello, R.; Repič, M.; Mavri, J. How are biogenic amines metabolized by monoamine oxidases? Eur. J. Org. Chem. 2012, 36, 7057–7065. [Google Scholar] [CrossRef]
- Youdim, M.B.; Edmondson, D.; Tipton, K.F. The therapeutic potential of monoamine oxidase inhibitors. Nat. Rev. Neurosci. 2006, 7, 295–309. [Google Scholar] [CrossRef] [PubMed]
- De Deurwaerdere, P.; Binda, C.; Corne, R.; Leone, C.; Valeri, A.; Valoti, M.; Ramsay, R.R.; Fall, Y.; Marco-Contelles, J. Comparative Analysis of the Neurochemical Profile and MAO Inhibition Properties of N-(Furan-2-ylmethyl)-N-methylprop-2-yn-1-amine. ACS Chem. Neurosci. 2017, 8, 1026–1035. [Google Scholar] [CrossRef]
- Shih, J.C.; Chen, K.; Ridd, M.J. Monoamine oxidase: From genes to behavior. Annu. Rev. Neurosci. 1999, 22, 197–217. [Google Scholar] [CrossRef]
- Finberg, J.P. Update on the pharmacology of selective inhibitors of MAO-A and MAO-B: Focus on modulation of CNS monoamine neurotransmitter release. Pharmacol. Ther. 2014, 143, 133–152. [Google Scholar] [CrossRef]
- Binda, C.; Hubalek, F.; Li, M.; Edmondson, D.E.; Mattevi, A. Crystal structure of human monoamine oxidase B, a drug target enzyme monotopically inserted into the mitochondrial outer membrane. FEBS Lett. 2004, 564, 225–228. [Google Scholar] [CrossRef]
- Son, S.Y.; Ma, A.; Kondou, Y.; Yoshimura, M.; Yamashita, E.; Tsukihara, T. Structure of human monoamine oxidase A at 2.2-angstrom resolution: The control of opening the entry for substrates/inhibitors. Proc. Natl. Acad. Sci. USA 2008, 105, 5739–5744. [Google Scholar] [CrossRef]
- Borštnar, R.; Repič, M.; Kržan, M.; Mavri, J.; Vianello, R. Irreversible Inhibition of Monoamine Oxidase B by the Antiparkinsonian Medicines Rasagiline and Selegiline: A Computational Study. Eur. J. Org. Chem. 2011, 2011, 6419–6433. [Google Scholar] [CrossRef]
- Pavlin, M.; Mavri, J.; Repič, M.; Vianello, R. Quantum-chemical approach to determining the high potency of clorgyline as an irreversible acetylenic monoamine oxidase inhibitor. J. Neural Transm. 2013, 120, 875–882. [Google Scholar] [CrossRef]
- Silverman, R.B.; Lu, X.; Zhou, J.J.P.; Swihart, A. Monoamine Oxidase B-Catalyzed Oxidation of Cinnamylamine 2,3-Oxide. Further Evidence against a Nucleophilic Mechanism. J. Am. Chem. Soc. 1994, 116, 11590–11591. [Google Scholar] [CrossRef]
- MacMillar, S.; Edmondson, D.E.; Matsson, O. Nitrogen Kinetic Isotope Effects for the Monoamine Oxidase B-Catalyzed Oxidation of Benzylamine and (1,1-H-2(2))Benzylamine: Nitrogen Rehybridization and CH Bond Cleavage Are Not Concerted. J. Am. Chem. Soc. 2011, 133, 12319–12321. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Levitt, M. Theoretical Studies of Enzymic Reactions–Dielectric, Electrostatic and Steric Stabilization of Carbonium-Ion in Reaction of Lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Warshel, A. Multiscale modeling of biological functions: From enzymes to molecular machines (Nobel Lecture). Angew. Chem. 2014, 53, 10020–10031. [Google Scholar] [CrossRef] [PubMed]
- Kamerlin, S.C.; Warshel, A. Multiscale modeling of biological functions. PCCP 2011, 13, 10401–10411. [Google Scholar] [CrossRef] [PubMed]
- Kamerlin, S.C.L.; Warshel, A. The empirical valence bond model: Theory and applications. WIREs Comput. Mol. Sci. 2011, 1, 30–45. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. 2009, 48, 1198–1229. [Google Scholar] [CrossRef]
- van der Kamp, M.W.; Mulholland, A.J. Combined Quantum Mechanics/Molecular Mechanics (QM/MM) Methods in Computational Enzymology. Biochemistry 2013, 52, 2708–2728. [Google Scholar] [CrossRef]
- Aqvist, J.; Warshel, A. Simulation of Enzyme-Reactions Using Valence-Bond Force-Fields and Other Hybrid Quantum-Classical Approaches. Chem. Rev. 1993, 93, 2523–2544. [Google Scholar] [CrossRef]
- Warshel, A.; Weiss, R.M. An Empirical Valence Bond Approach for Comparing Reactions in Solutions and in Enzymes. J. Am. Chem. Soc. 1980, 102, 6218–6226. [Google Scholar] [CrossRef]
- Miller, J.R.; Edmondson, D.E. Structure-activity relationships in the oxidation of para-substituted benzylamine analogues by recombinant human liver monoamine oxidase A. Biochemistry 1999, 38, 13670–13683. [Google Scholar] [CrossRef] [PubMed]
- Gadda, G. Oxygen Activation in Flavoprotein Oxidases: The Importance of Being Positive. Biochemistry 2012, 51, 2662–2669. [Google Scholar] [CrossRef] [PubMed]
- Edmondson, D.E. Hydrogen peroxide produced by mitochondrial monoamine oxidase catalysis: Biological implications. Curr. Pharm. Des. 2014, 20, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Pavlin, M.; Repič, M.; Vianello, R.; Mavri, J. The Chemistry of Neurodegeneration: Kinetic Data and Their Implications. Mol. Neurobiol. 2016, 53, 3400–3415. [Google Scholar] [CrossRef]
- Bauer, P.; Barrozo, A.; Purg, M.; Amrein, B.A.; Esguerra, M.; Wilson, P.B.; Major, D.T.; Åqvist, J.; Kamerlin, S.C.L. Q6: A comprehensive toolkit for empirical valence bond and related free energy calculations. SoftwareX 2018, 7, 388–395. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; TiradoRives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509. [Google Scholar] [CrossRef]
- Hwang, J.K.; Warshel, A. A Quantized Classical Path Approach for Calculations of Quantum-Mechanical Rate Constants. J. Phys. Chem. 1993, 97, 10053–10058. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Non-Physical Sampling Distributions in Monte-Carlo Free-Energy Estimation—Umbrella Sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Kollman, P. Free-Energy Calculations—Applications to Chemical and Biochemical Phenomena. Chem. Rev. 1993, 93, 2395–2417. [Google Scholar] [CrossRef]
- Warshel, A.; King, G. Polarization Constraints in Molecular-Dynamics Simulation of Aqueous-Solutions—The Surface Constraint All Atom Solvent (SCAAS) Model. Chem. Phys. Lett. 1985, 121, 124–129. [Google Scholar] [CrossRef]
- Abad, E.; Zenn, R.K.; Kastner, J. Reaction Mechanism of Monoamine Oxidase from QM/MM Calculations. J. Phys. Chem. B 2013, 117, 14238–14246. [Google Scholar] [CrossRef] [PubMed]
- Zenn, R.K.; Abad, E.; Kastner, J. Influence of the environment on the oxidative deamination of p-substituted benzylamines in monoamine oxidase. J. Phys. Chem. B 2015, 119, 3678–3686. [Google Scholar] [CrossRef] [PubMed]
- Olsson, M.H.; Siegbahn, P.E.; Warshel, A. Simulations of the large kinetic isotope effect and the temperature dependence of the hydrogen atom transfer in lipoxygenase. J. Am. Chem. Soc. 2004, 126, 2820–2828. [Google Scholar] [CrossRef]
- Katsnelson, A. Heavy drugs draw heavy interest from pharma backers. Nat. Med. 2013, 19, 656. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds are not available from the authors. |
| FEP Lengths | Applied Restraint | ΔG#(H) | ΔG#(D) | H/D KIE | |
|---|---|---|---|---|---|
| [ps] Per Replica | Distance [Å] | Force Constant [(kcal (mol−1 × Å−2)] | [kcal/mol] | [kcal/mol] | |
| 510 | 0–2.5 | 1 | 17.17 | 18.26 | 6.34 ± 1.55 |
| 510 | 0–2.5 | 5 | 17.23 | 18.32 | 6.34 ± 1.42 |
| 510 | 0–3.0 | 1 | 17.23 | 18.29 | 6.03 ± 1.44 |
| 510 | 0–3.0 | 5 | 17.22 | 18.29 | 6.03 ± 1.55 |
| 510 | 0–3.0 | 10 | 17.18 | 18.28 | 6.45 ± 1.37 |
| 2550 | 0–3.0 | 5 | 17.27 | 18.27 | 5.93 ± 1.68 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brela, M.Z.; Prah, A.; Boczar, M.; Stare, J.; Mavri, J. Path Integral Calculation of the Hydrogen/Deuterium Kinetic Isotope Effect in Monoamine Oxidase A-Catalyzed Decomposition of Benzylamine. Molecules 2019, 24, 4359. https://doi.org/10.3390/molecules24234359
Brela MZ, Prah A, Boczar M, Stare J, Mavri J. Path Integral Calculation of the Hydrogen/Deuterium Kinetic Isotope Effect in Monoamine Oxidase A-Catalyzed Decomposition of Benzylamine. Molecules. 2019; 24(23):4359. https://doi.org/10.3390/molecules24234359
Chicago/Turabian StyleBrela, Mateusz Z., Alja Prah, Marek Boczar, Jernej Stare, and Janez Mavri. 2019. "Path Integral Calculation of the Hydrogen/Deuterium Kinetic Isotope Effect in Monoamine Oxidase A-Catalyzed Decomposition of Benzylamine" Molecules 24, no. 23: 4359. https://doi.org/10.3390/molecules24234359
APA StyleBrela, M. Z., Prah, A., Boczar, M., Stare, J., & Mavri, J. (2019). Path Integral Calculation of the Hydrogen/Deuterium Kinetic Isotope Effect in Monoamine Oxidase A-Catalyzed Decomposition of Benzylamine. Molecules, 24(23), 4359. https://doi.org/10.3390/molecules24234359






