Superadiabatic Forces via the Acceleration Gradient in Quantum Many-Body Dynamics
Abstract
1. Introduction
2. Theoretical Background
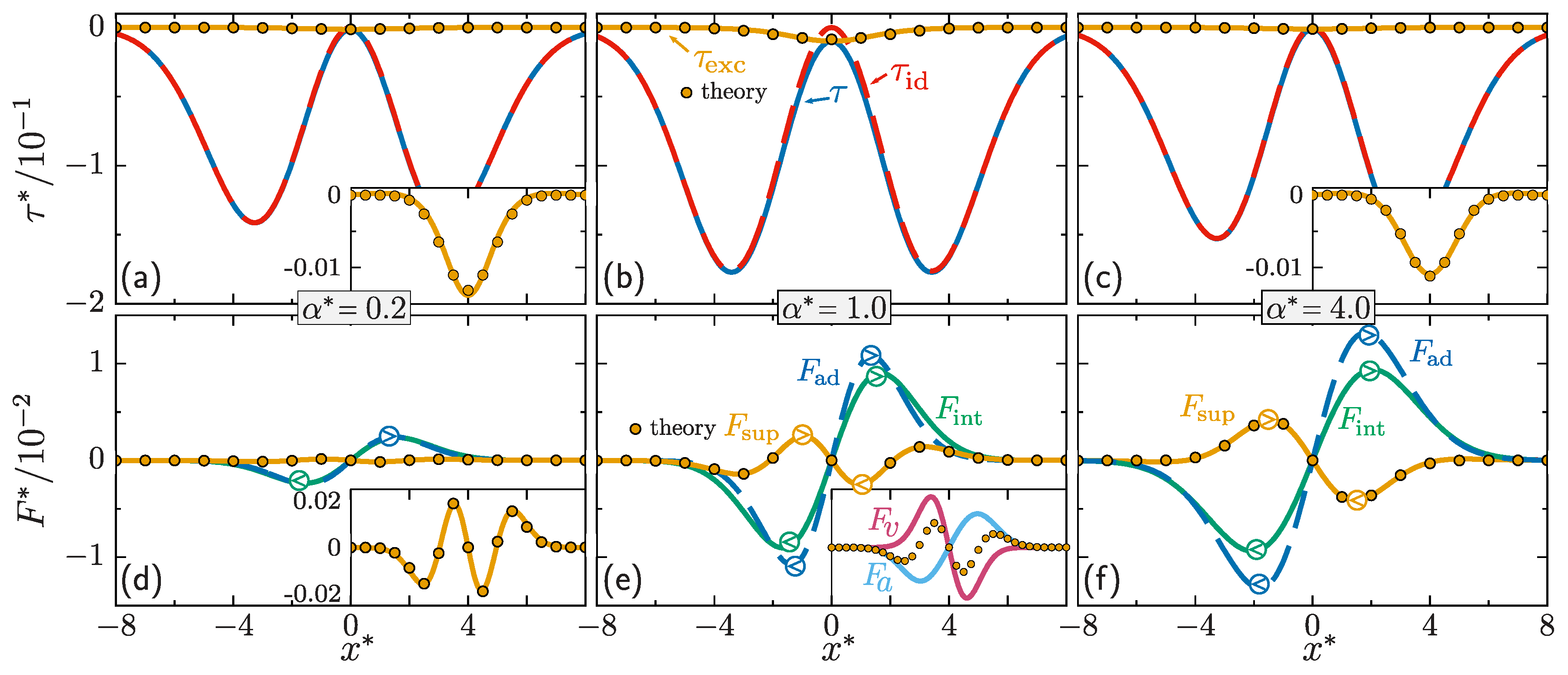
3. Hooke’s Atom
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Burke, K. Perspective on density functional theory. J. Chem. Phys. 2012, 136, 150901. [Google Scholar] [CrossRef] [PubMed]
- Vignale, G.; Rasolt, M. Density-functional theory in strong magnetic fields. Phys. Rev. Lett. 1987, 59, 2360. [Google Scholar] [CrossRef] [PubMed]
- Vignale, G.; Rasolt, M. Current- and spin-density-functional theory for inhomogeneous electronic systems in strong magnetic fields. Phys. Rev. B 1988, 37, 10685. [Google Scholar] [CrossRef] [PubMed]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997. [Google Scholar] [CrossRef]
- Marques, M.A.L.; Maitra, N.T.; Nogueira, F.M.S.; Gross, E.K.U.; Rubio, A. (Eds.) Fundamentals of Time-Dependent Density Functional Theory; Springer: Berlin, Germany, 2012. [Google Scholar]
- Ullrich, C.A.; Yang, Z.-H. A Brief Compendium of Time-Dependent Density Functional Theory. Braz. J. Phys. 2014, 44, 154. [Google Scholar] [CrossRef]
- Maitra, N.T. Perspective: Fundamental aspects of time-dependent density functional theory. J. Chem. Phys. 2016, 144, 220901. [Google Scholar] [CrossRef] [PubMed]
- Vignale, G.; Kohn, W. Current-dependent exchange–correlation potential for dynamical linear response theory. Phys. Rev. Lett. 1996, 77, 2037. [Google Scholar] [CrossRef] [PubMed]
- Vignale, G.; Ullrich, C.A.; Conti, S. Time-dependent density functional theory beyond the adiabatic local density approximation. Phys. Rev. Lett. 1997, 79, 4878. [Google Scholar] [CrossRef]
- Gosh, S.K.; Dhara, A.K. Density-functional theory of many-electron systems subjected to time-dependent electric and magnetic fields. Phys. Rev. A 1988, 38, 1149. [Google Scholar] [CrossRef]
- Vignale, G. Mapping from current densities to vector potentials in time-dependent current density functional theory. Phys. Rev. B 2004, 70, 201102(R). [Google Scholar] [CrossRef]
- Van Leeuwen, R. Key concepts in time-dependent density-functional theory. Int. J. Mod. Phys. B 2001, 15, 1969. [Google Scholar] [CrossRef]
- Thiele, M.; Gross, E.K.U.; Kümmel, S. Adiabatic approximation in nonperturbative time-dependent density-functional theory. Phys. Rev. Lett. 2008, 100, 153004. [Google Scholar] [CrossRef] [PubMed]
- Thiele, M.; Kümmel, S. Hydrodynamic perspective on memory in time-dependent density-functional theory. Phys. Rev. E 2009, 79, 052503. [Google Scholar] [CrossRef]
- Tokatly, I.V. Quantum many-body dynamics in a Lagrangian frame: I. Equations of motion and conservation laws. Phys. Rev. B 2005, 71, 165104. [Google Scholar] [CrossRef]
- Tokatly, I.V. Quantum many-body dynamics in a Lagrangian frame: II. Geometric formulation of time-dependent density functional theory. Phys. Rev. B 2005, 71, 165105. [Google Scholar] [CrossRef]
- Tokatly, I.V. Time-dependent current density functional theory via time-dependent deformation functional theory: A constrained search formulation in the time domain. Phys. Chem. Chem. Phys. 2009, 11, 4621. [Google Scholar] [CrossRef] [PubMed]
- Diaw, A.; Murillo, M.S. A viscous quantum hydrodynamics model based on dynamic density functional theory. Sci. Rep. 2017, 7, 15352. [Google Scholar] [CrossRef] [PubMed]
- Bousquet, D.; Hughes, K.H.; Micha, D.A.; Burghardt, I. Extended hydrodynamic approach to quantum-classical nonequilibrium evolution. I. Theory. J. Chem. Phys. 2011, 134, 064116. [Google Scholar] [CrossRef]
- Wijewardane, H.O.; Ullrich, C.A. Time-Dependent Kohn-Sham Theory with Memory. Phys. Rev. Lett. 2005, 95, 086401. [Google Scholar] [CrossRef]
- Ullrich, C.A. Time-dependent density-functional theory beyond the adiabatic approximation: Insights from a two-electron model system. J. Chem. Phys. 2006, 125, 234108. [Google Scholar] [CrossRef] [PubMed]
- Hessler, P.; Maitra, N.T.; Burke, K. Correlation in time-dependent density-functional theory. J. Chem. Phys. 2002, 117, 72. [Google Scholar] [CrossRef]
- Ullrich, C.A.; Tokatly, I.V. Nonadiabatic electron dynamics in time-dependent density-functional theory. Phys. Rev. B 2006, 73, 235102. [Google Scholar] [CrossRef]
- Evans, R. The nature of the liquid-vapour interface and other topics in the statistical mechanics of non-uniform, classical fluids. Adv. Phys. 1979, 28, 143. [Google Scholar] [CrossRef]
- Archer, A.J.; Evans, R. Dynamical density functional theory and its application to spinodal decomposition. J. Chem. Phys. 2004, 121, 4246. [Google Scholar] [CrossRef] [PubMed]
- Marconi, U.M.B.; Tarazona, P. Dynamic density functional theory of fluids. J. Chem. Phys. 1999, 110, 8032. [Google Scholar] [CrossRef]
- Schmidt, M.; Brader, J.M. Power functional theory for Brownian dynamics. J. Chem. Phys. 2013, 138, 214101. [Google Scholar] [CrossRef]
- Fortini, A.; de las Heras, D.; Brader, J.M.; Schmidt, M. Superadiabatic forces in Brownian many-body dynamics. Phys. Rev. Lett. 2014, 113, 167801. [Google Scholar] [CrossRef]
- Bernreuther, E.; Schmidt, M. Superadiabatic forces in the dynamics of the one-dimensional Gaussian core model. Phys. Rev. E 2016, 94, 022105. [Google Scholar] [CrossRef]
- De las Heras, D.; Schmidt, M. Velocity Gradient Power Functional for Brownian Dynamics. Phys. Rev. Lett. 2018, 120, 028001. [Google Scholar] [CrossRef]
- Stuhlmüller, N.C.X.; Eckert, T.; de las Heras, D.; Schmidt, M. Structural nonequilibrium forces in driven colloidal systems. Phys. Rev. Lett. 2018, 121, 098002. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M. Power functional theory for Newtonian many-body dynamics. J. Chem. Phys. 2018, 148, 044502. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M. Quantum power functional theory for many-body dynamics. J. Chem. Phys. 2015, 143, 174108. [Google Scholar] [CrossRef] [PubMed]
- Elliott, P.; Fuks, J.I.; Rubio, A.; Maitra, N.T. Universal dynamical steps in the exact time-dependent exchange–correlation potential. Phys. Rev. Lett. 2012, 109, 266404. [Google Scholar] [CrossRef]
- Maitra, N.T.; Burke, K. Demonstration of initial-state dependence in time-dependent density-functional theory. Phys. Rev. A 2001, 63, 042501. [Google Scholar] [CrossRef]
- Wijewardane, H.O.; Ullrich, C.A. Real-time electron dynamics with exact-exchange time-dependent density-functional theory. Phys. Rev. Lett. 2008, 100, 056404. [Google Scholar] [CrossRef]
- Ullrich, C.A.; Gossmann, U.J.; Gross, E.K.U. Time-dependent optimized effective potential. Phys. Rev. Lett. 1995, 74, 872. [Google Scholar] [CrossRef] [PubMed]
- Van Leeuwen, R. The Sham-Schlüter equation in time-dependent density-functional theory. Phys. Rev. Lett. 1996, 76, 3610. [Google Scholar] [CrossRef]
- Van Leeuwen, R. Causality and symmetry in time-dependent density-functional theory. Phys. Rev. Lett. 1998, 80, 1280. [Google Scholar] [CrossRef]
- Fuks, J.I.; Luo, K.; Sandoval, E.D.; Maitra, N.T. Time-Resolved Spectroscopy in Time-Dependent Density Functional Theory: An Exact Condition. Phys. Rev. Lett. 2015, 114, 183002. [Google Scholar] [CrossRef]
- Luo, K.; Fuks, J.I.; Sandoval, E.D.; Elliott, P.; Maitra, N.T. Kinetic and interaction components of the exact time-dependent correlation potential. J. Chem. Phys. 2014, 140, 18A515. [Google Scholar] [CrossRef] [PubMed]
- Fuks, J.I.; Elliott, P.; Rubio, A.; Maitra, N.T. Dynamics of charge-transfer processes with time-dependent density functional theory. J. Phys. Chem. Lett. 2013, 4, 735. [Google Scholar] [CrossRef] [PubMed]
- Hodgson, M.J.P.; Ramsden, J.D.; Chapman, J.B.J.; Lillystone, P.; Godby, R.W. Exact time-dependent density-functional potentials for strongly correlated tunneling electrons. Phys. Rev. B 2013, 88, 241102. [Google Scholar] [CrossRef]
- Ruggenthaler, M.; Bauer, D. Rabi oscillations and few-level approximations in time-dependent density functional theory. Phys. Rev. Lett. 2009, 102, 233001. [Google Scholar] [CrossRef]
- Madelung, E. Eine anschauliche Deutung der Gleichung von Schrödinger. Naturwissenschaften 1926, 14, 1004. [Google Scholar] [CrossRef]
- Madelung, E. Quantentheorie in hydrodynamischer Form. Z. Phys. A Hadron. Nucl. 1927, 40, 322. [Google Scholar] [CrossRef]
- Askar, A.; Cakmak, A.S. Explicit integration method for the time-dependent Schrödinger equation for collision problems. J. Chem. Phys. 1978, 68, 2794. [Google Scholar] [CrossRef]
- Visscher, P.B. A fast explicit algorithm for the time-dependent Schrödinger equation. Comp. Phys. 1991, 5, 596. [Google Scholar] [CrossRef]
- De las Heras, D.; Renner, J.; Schmidt, M. Custom flow in overdamped Brownian dynamics. Phys. Rev. E 2019, 99, 023306. [Google Scholar] [CrossRef]
- Hansen, J.-P.; McDonald, I.R. Theory of Simple Liquids, 4th ed.; Academic Press: Oxford, UK, 2013. [Google Scholar]
Sample Availability: Not available. |

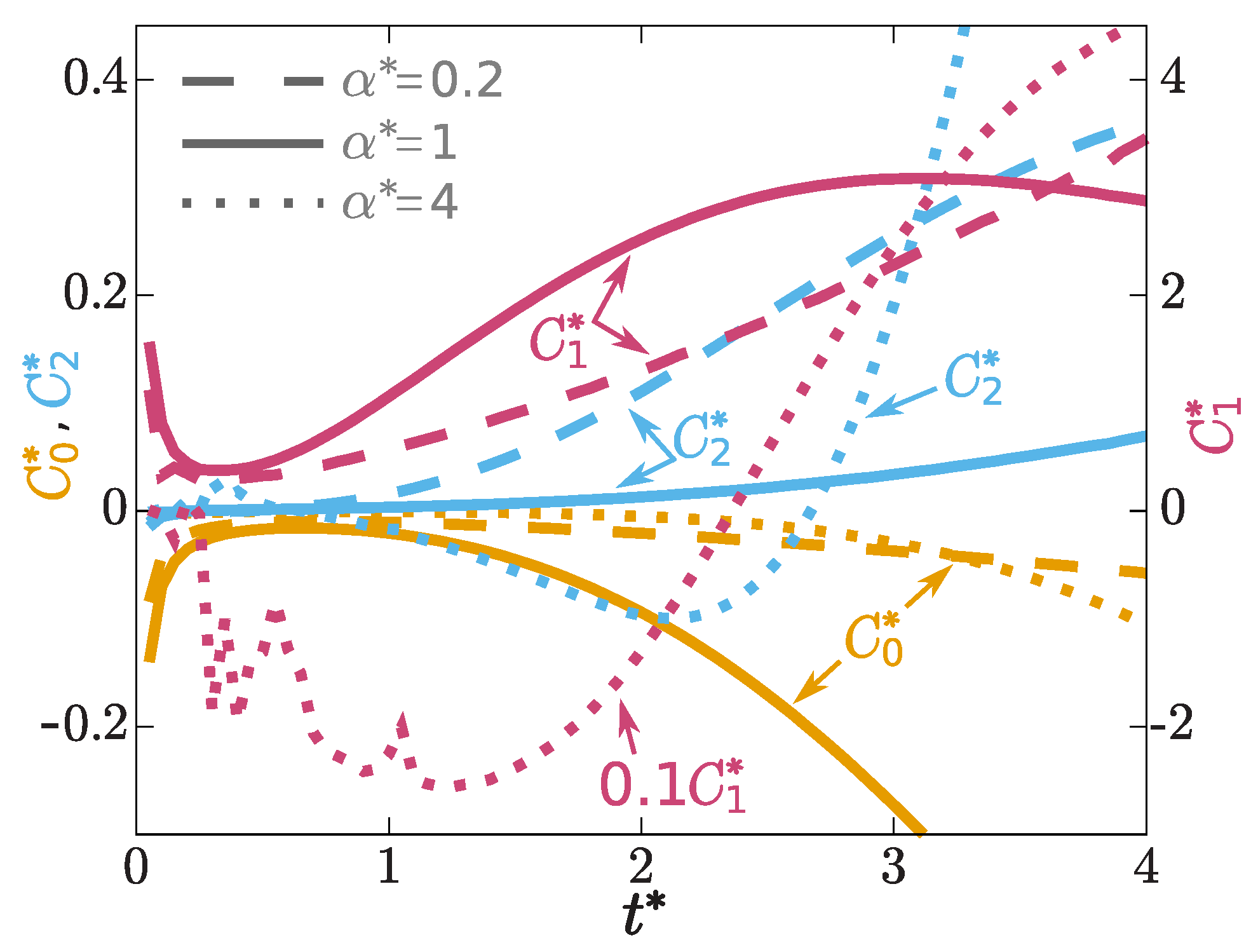
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brütting, M.; Trepl, T.; de las Heras, D.; Schmidt, M. Superadiabatic Forces via the Acceleration Gradient in Quantum Many-Body Dynamics. Molecules 2019, 24, 3660. https://doi.org/10.3390/molecules24203660
Brütting M, Trepl T, de las Heras D, Schmidt M. Superadiabatic Forces via the Acceleration Gradient in Quantum Many-Body Dynamics. Molecules. 2019; 24(20):3660. https://doi.org/10.3390/molecules24203660
Chicago/Turabian StyleBrütting, Moritz, Thomas Trepl, Daniel de las Heras, and Matthias Schmidt. 2019. "Superadiabatic Forces via the Acceleration Gradient in Quantum Many-Body Dynamics" Molecules 24, no. 20: 3660. https://doi.org/10.3390/molecules24203660
APA StyleBrütting, M., Trepl, T., de las Heras, D., & Schmidt, M. (2019). Superadiabatic Forces via the Acceleration Gradient in Quantum Many-Body Dynamics. Molecules, 24(20), 3660. https://doi.org/10.3390/molecules24203660





