Electrical Behavior of a Catalyst Composed of Laminar Manganese Oxide Supported on γ-Al2O3
Abstract
:1. Introduction
2. Results and Discussion
2.1. Chemical Composition
2.2. Structural Analysis
2.3. Morphological Analysis and Adsorption Isotherms—N2 Desorption at 77 K
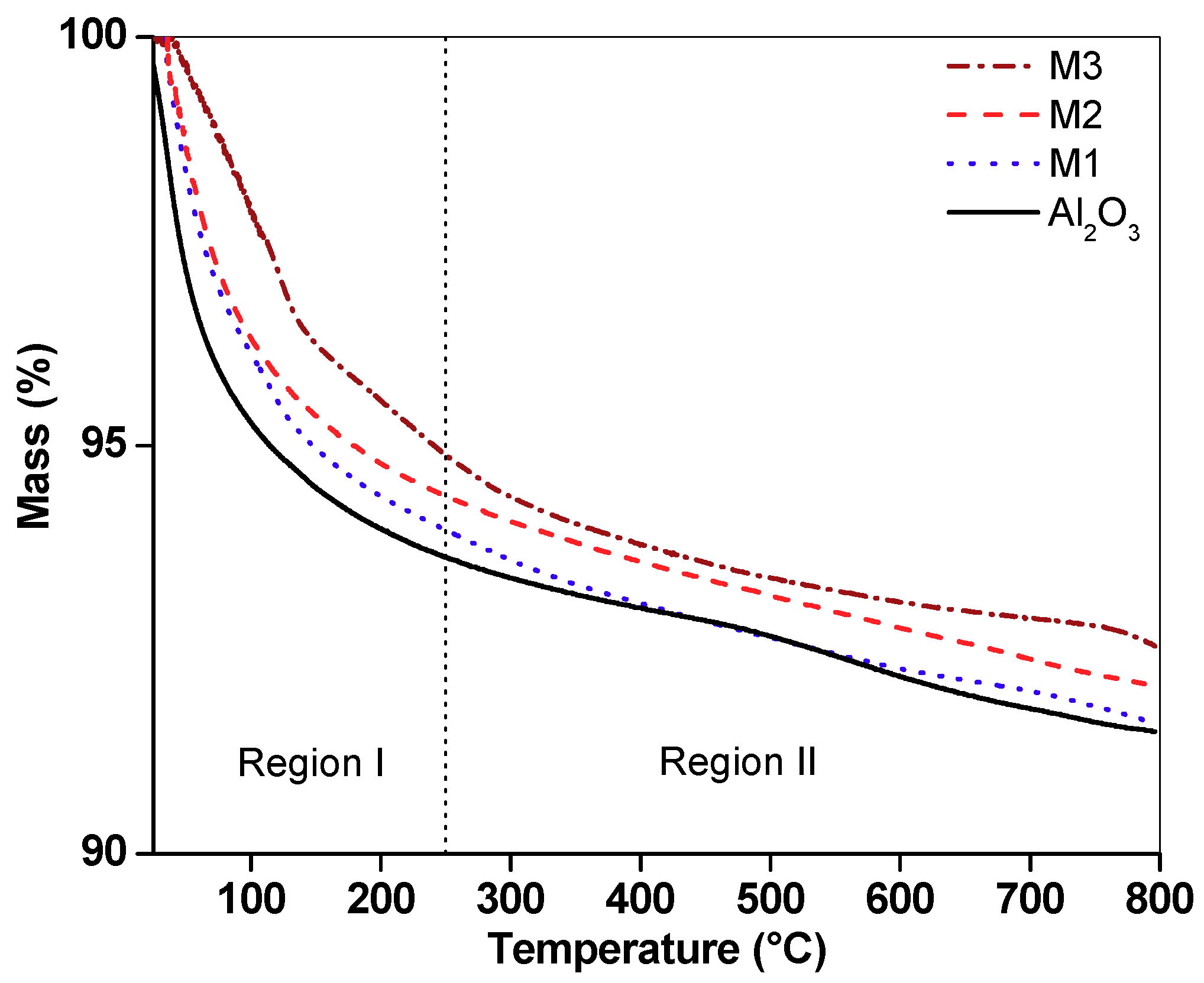
2.4. Thermogravimetric Analysis
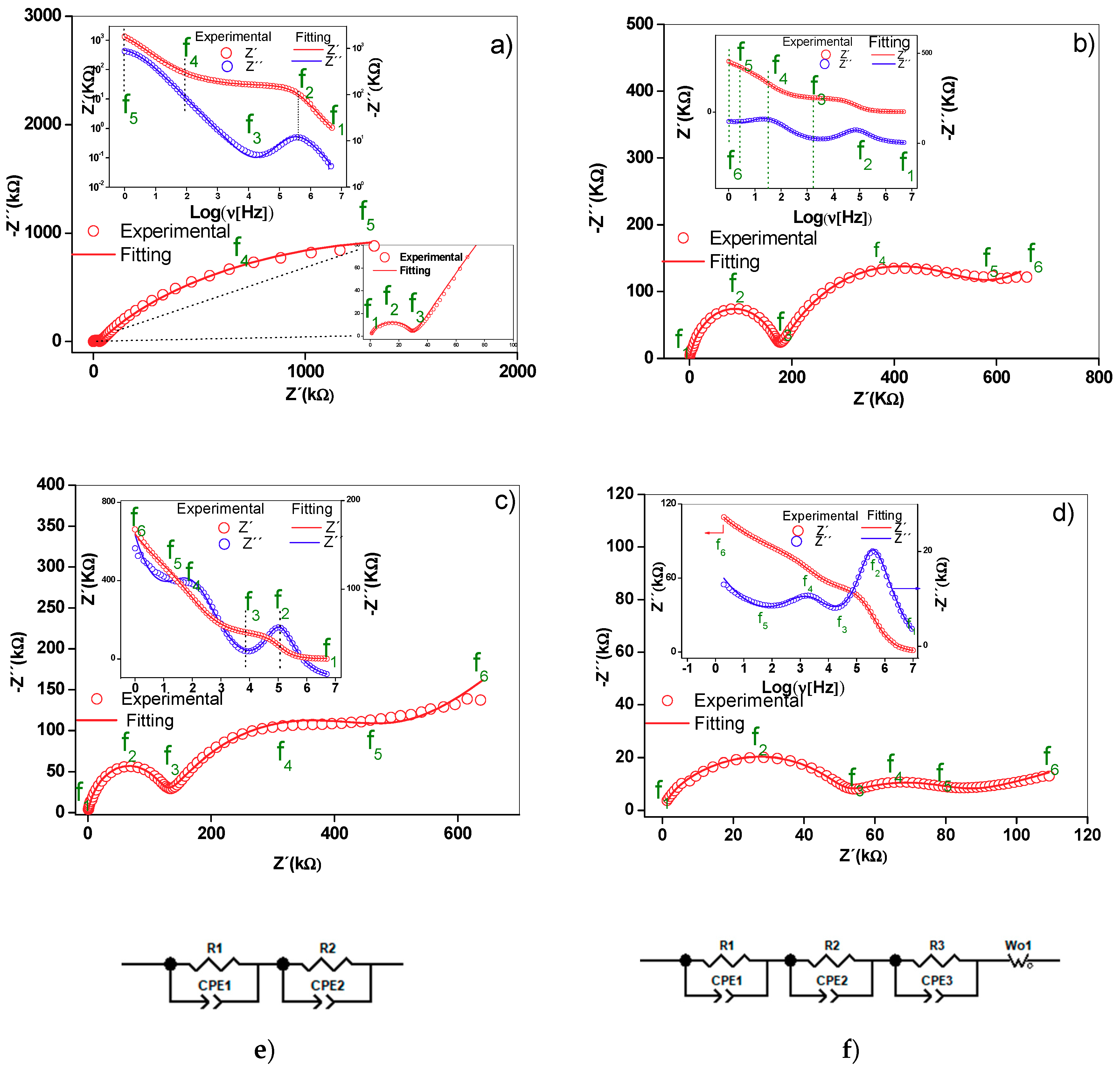
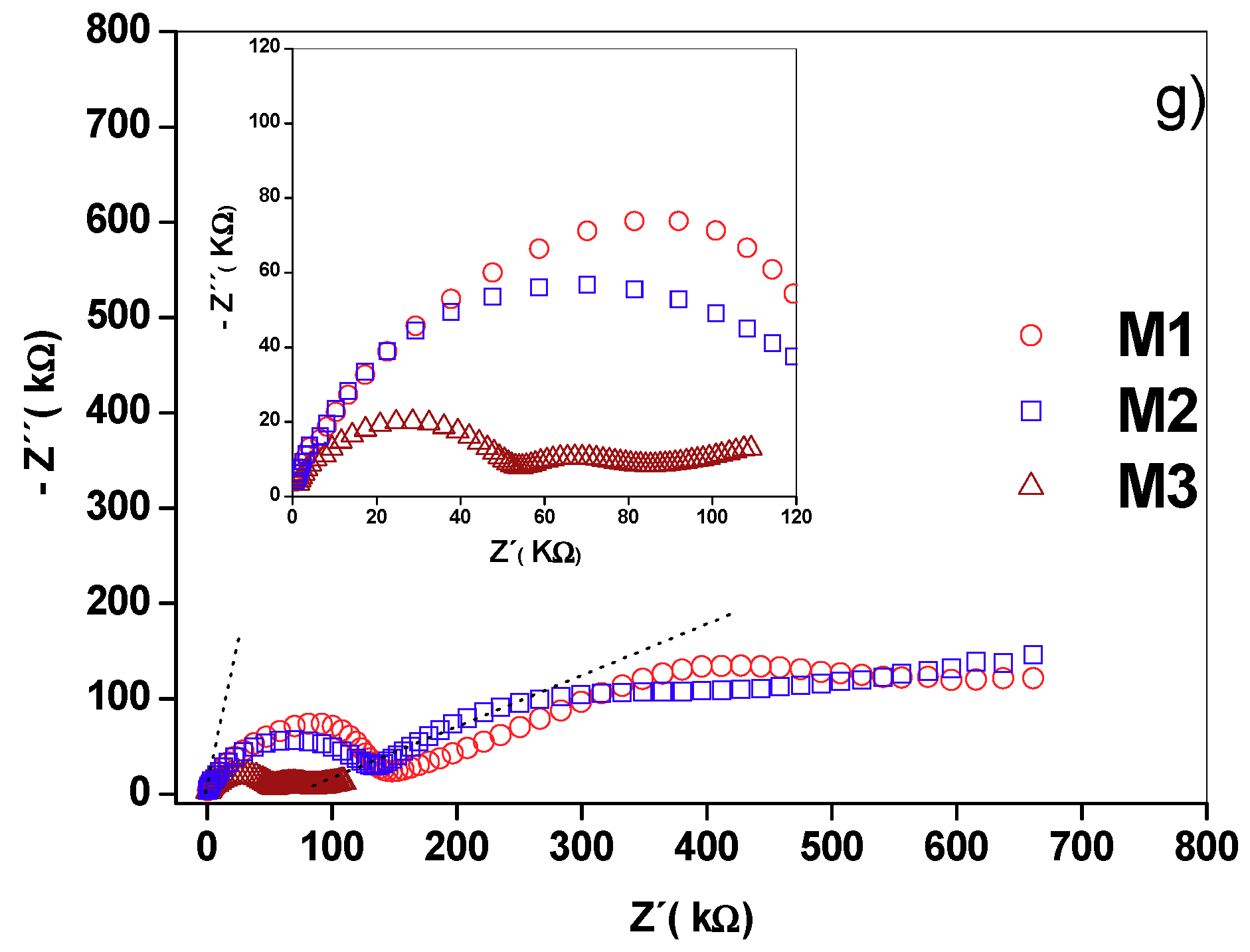
2.5. Nyquist Diagrams and Equivalent Circuits
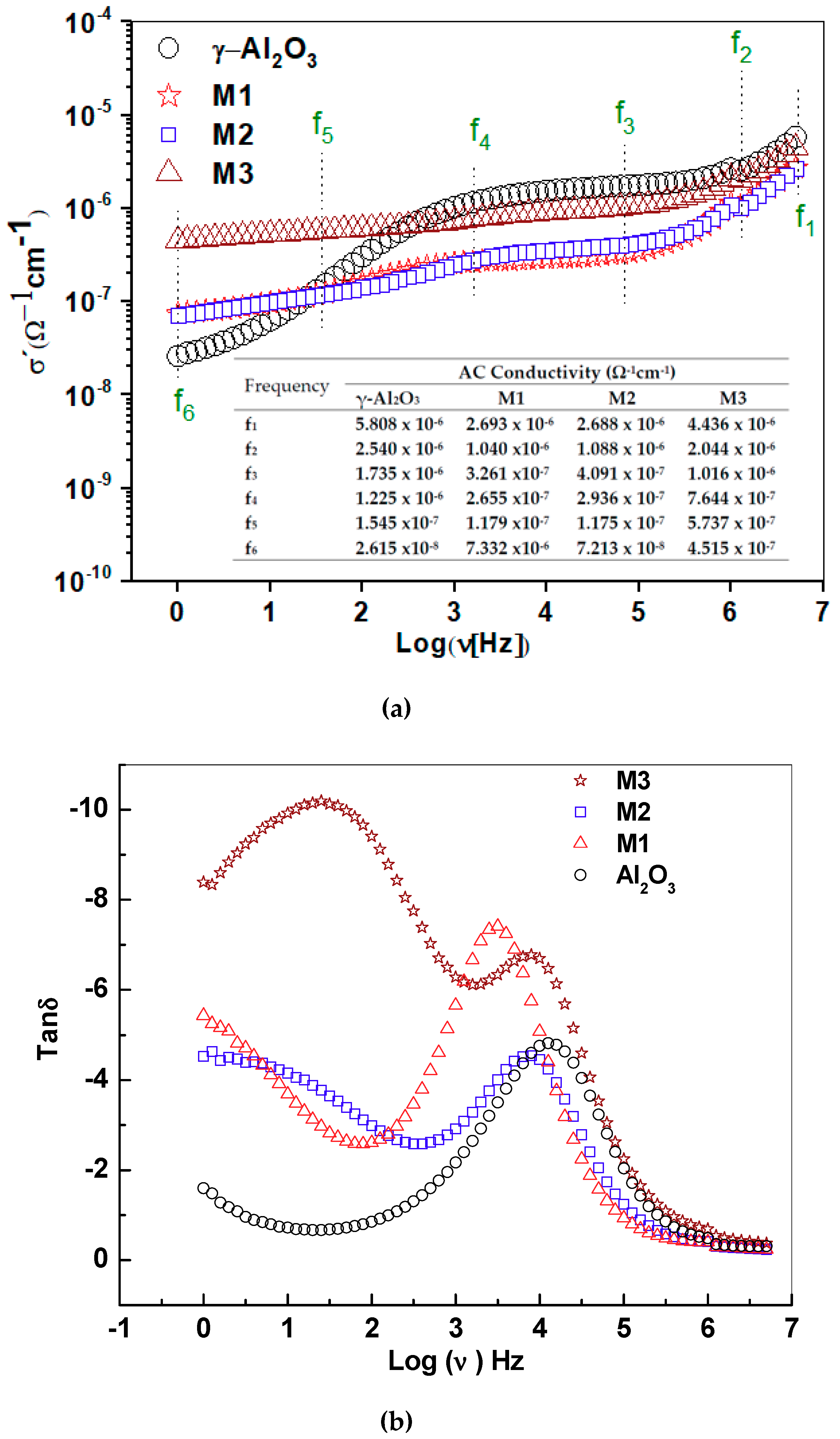
2.6. AC Conductivity and Loss Diagram Tan δ
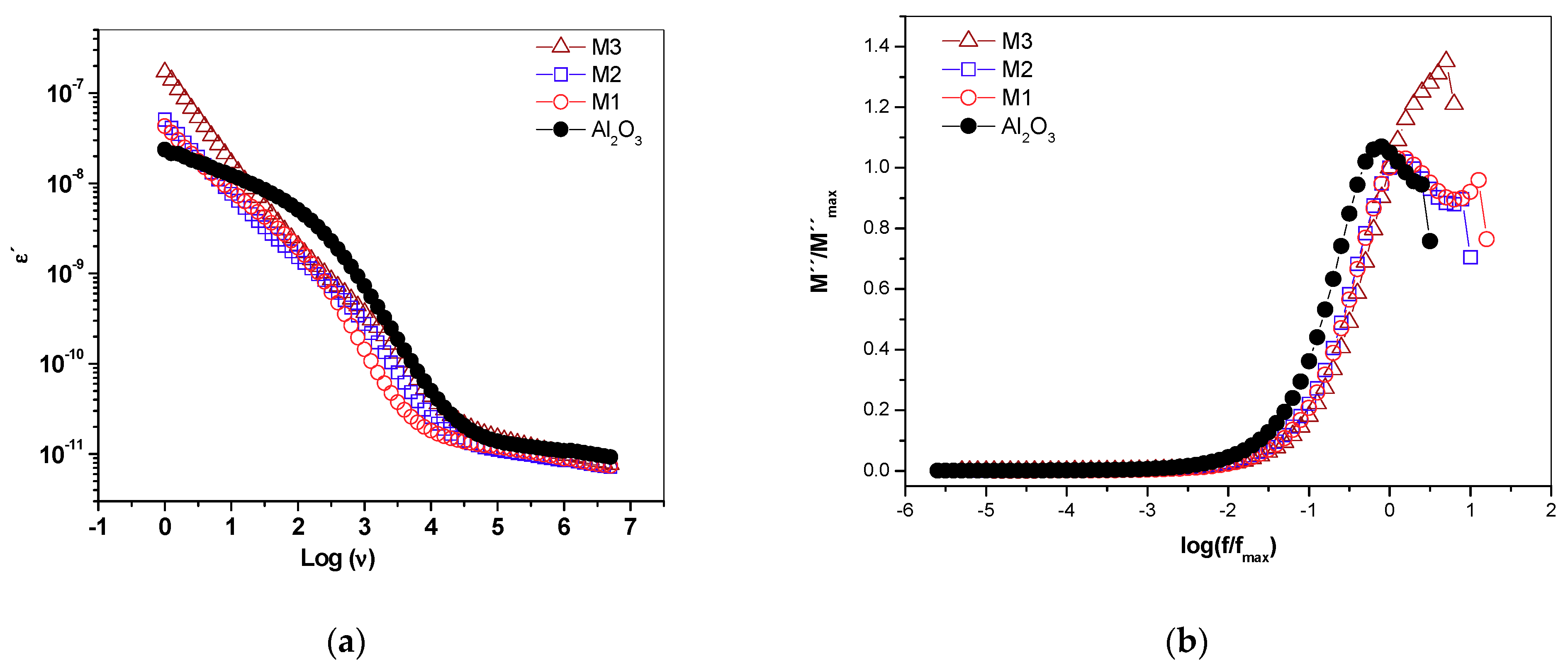
2.7. Real Permittivity and Dielectric Module
3. Materials and Methods
3.1. Synthesis
3.2. Characterization
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Lee, D.W.; Yoo, B.R. Advanced metal oxide (supported) catalysts: Synthesis and applications. J. Ind. Eng. Chem. 2014, 20, 3947–3959. [Google Scholar] [CrossRef]
- Cortés Corberán, V.; Rives, V.; Stathopoulos, V. Chapter 7—Recent Applications of Nanometal Oxide Catalysts in Oxidation Reactions. In Advanced Nanomaterials for Catalysis and Energy; Sadykov, V.A., Ed.; Elsevier: Amsterdam, Netherlands, 2019; pp. 227–293. [Google Scholar]
- Mobini, S.; Meshkani, F.; Rezaei, M. Supported Mn catalysts and the role of different supports in the catalytic oxidation of carbon monoxide. Chem. Eng. Sci. 2019, 197, 37–51. [Google Scholar] [CrossRef]
- Bing, W.; Wei, M. Recent advances for solid basic catalysts: Structure design and catalytic performance. J. Solid State Chem. 2019, 269, 184–194. [Google Scholar] [CrossRef]
- Hita, I.; Deuss, P.J.; Bonura, G.; Frusteri, F.; Heeres, H.J. Biobased chemicals from the catalytic depolymerization of Kraft lignin using supported noble metal-based catalysts. Fuel Process. Technol. 2018, 179, 143–153. [Google Scholar] [CrossRef]
- Losch, P.; Huang, W.; Goodman, E.D.; Wrasman, C.J.; Holm, A.; Riscoe, A.R.; Schwalbe, J.A.; Cargnello, M. Colloidal nanocrystals for heterogeneous catalysis. Nano. Today 2019, 24, 15–47. [Google Scholar] [CrossRef]
- Keyvanloo, K.; Hecker, W.C.; Woodfield, B.F.; Bartholomew, C.H. Highly active and stable supported iron Fischer–Tropsch catalysts: Effects of support properties and SiO2 stabilizer on catalyst performance. J. Catal. 2014, 319, 220–231. [Google Scholar] [CrossRef]
- Becerra, M.E.; Arias, N.P.; Giraldo, O.H.; López-Suárez, F.E.; Illán-Gómez, M.J.; Bueno-López, A. Alumina-Supported Manganese Catalysts for Soot Combustion Prepared by Thermal Decomposition of KMnO4. Catalysts 2012, 2, 352–367. [Google Scholar] [CrossRef]
- Aghbolaghy, M.; Soltan, J.; Sutarto, R. The role of surface carboxylates in catalytic ozonation of acetone on alumina-supported manganese oxide. Chem. Eng. Res. Des. 2017, 128, 73–84. [Google Scholar] [CrossRef]
- Tatibouët, J.M.; Valange, S.; Touati, H. Near-ambient temperature ozone decomposition kinetics on manganese oxide-based catalysts. Appl. Cataly. A 2019, 569, 126–133. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Nakhostin Panahi, P. Modeling and optimization of NH3-SCR performance of MnOx/γ-alumina nanocatalysts by response surface methodology. J. Taiwan Inst. Chem. Eng. 2016, 69, 68–77. [Google Scholar] [CrossRef]
- Becerra, M.E.; Arias, N.P.; Giraldo, O.H.; López Suárez, F.E.; Illán Gómez, M.J.; Bueno López, A. Soot combustion manganese catalysts prepared by thermal decomposition of KMnO4. Appl. Cataly. B 2011, 102, 260–266. [Google Scholar] [CrossRef]
- Giraldo, O.; Arias, N.P.; Becerra, M.E. Electrical properties of TiO2-pillared bidimensional manganese oxides. Appl. Clay Sci. 2017, 141, 157–170. [Google Scholar] [CrossRef]
- Arias, N.P.; Becerra, M.E.; Giraldo, O. Caracterización eléctrica de un óxido de manganeso laminar tipo birnesita. Rev. Mex. Fis. 2015, 61, 380–387. [Google Scholar]
- Arias, N.P.; Dávila, M.T.; Giraldo, O. Electrical behavior of an octahedral layered OL-1-type manganese oxide material. Ionics 2013, 19, 201–214. [Google Scholar] [CrossRef]
- Gomaa, M.M.; Gobara, H.M. Electrical properties of Ni/silica gel and Pt/γ-alumina catalysts in relation to metal content in the frequency domain. Mater. Chem. Phys. 2009, 113, 790–796. [Google Scholar] [CrossRef]
- Gobara, H.M.; Gomaa, M.M., II. Electrical Properties of Ni/Silica Gel and Pt/γ-Alumina Catalysts in Relation to Catalytic Activity. Pet. Sci. Technol. 2009, 27, 1572–1591. [Google Scholar] [CrossRef]
- Chaplin, R.; Chapman, P.R.; Griffith, R.H. Electrical Properties of Chromium Oxide-Alumina Catalysts. Nature 1953, 172, 77–78. [Google Scholar] [CrossRef]
- ICDD. Data Collection of the Joint Committee on Powder Diffraction Standard, pdf number:00-046-1215 (CD).
- Sing, K.S.W.; Everett, D.H.; Haul, R.A.W.; Moscou, L.; Pierotti, R.A.; Rouquerol, J.; Siemieniewska, T. Reporting Physisorption Data for Gas/Solid Systems. In Handbook of Heterogeneous Catalysis; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008; p. 791. [Google Scholar]
- Gregori, G.; Merkle, R.; Maier, J. Ion conduction and redistribution at grain boundaries in oxide systems. Prog. Mater. Sci. 2017, 89, 252–305. [Google Scholar] [CrossRef]
- Rozita, Y.; Brydson, R.; Scott, A.J. An investigation of commercial gamma-Al2O3 nanoparticles. J. Phys. Conf. Ser. 2010, 241, 012096. [Google Scholar] [CrossRef]
- Samain, L.; Jaworski, A.; Edén, M.; Ladd, D.M.; Seo, D.K.; Javier Garcia-Garcia, F.; Häussermann, U. Structural analysis of highly porous γ-Al2O3. J. Solid State Chem. 2014, 217, 1–8. [Google Scholar] [CrossRef]
- Stoica, M.; Caldararu, M.; Ionescu, N.I.; Auroux, A. Protonic conductivity of Pt/Al2O3 in hydrogen- and water-containing atmospheres. Appl. Surf. Sci. 2000, 153, 218–222. [Google Scholar] [CrossRef]
- Agmon, N. The Grotthuss mechanism. Chem. Phys. Lett. 1995, 244, 456–462. [Google Scholar] [CrossRef]
- Caldararu, M.; Postole, G.; Hornoiu, C.; Bratan, V.; Dragan, M.; Ionescu, N.I. Electrical conductivity of γ-Al2O3 at atmospheric pressure under dehydrating/hydrating conditions. Appl. Surf. Sci. 2001, 181, 255–264. [Google Scholar] [CrossRef]
- Sarkar, S.; Das, P.K. Role of interface on electrical conductivity of carbon nanotube/alumina nanocomposite. Ceram. Int. 2014, 40, 2723–2729. [Google Scholar] [CrossRef]
- Jonscher, A.K. Dielectric relaxation in solids. J. Phys. D: Appl. Phys. 1999, 32, R57–R70. [Google Scholar] [CrossRef]
- Penn, S.J.; Alford, N.M.; Templeton, A.; Wang, X.; Xu, M.; Reece, M.; Schrapel, K. Effect of Porosity and Grain Size on the Microwave Dielectric Properties of Sintered Alumina. J. Am. Ceram. Soc. 1997, 80, 1885–1888. [Google Scholar] [CrossRef]
- Ryabov, Y.E.; Puzenko, A.; Feldman, Y. Nonmonotonic relaxation kinetics of confined systems. Phys. Rev. B: Condens. Matter 2004, 69, 014204. [Google Scholar] [CrossRef]
- Sing, K.S.W. 7—Assessment of Surface Area by Gas Adsorption. In Adsorption by Powders and Porous Solids, 2nd ed.; Rouquerol, F., Rouquerol, J., Sing, K.S.W., Llewellyn, P., Maurin, G., Eds.; Academic Press: Oxford, UK, 2014; pp. 237–268. [Google Scholar]
Sample Availability: Samples of the materials M1, M2, and M3 are available from the authors. |


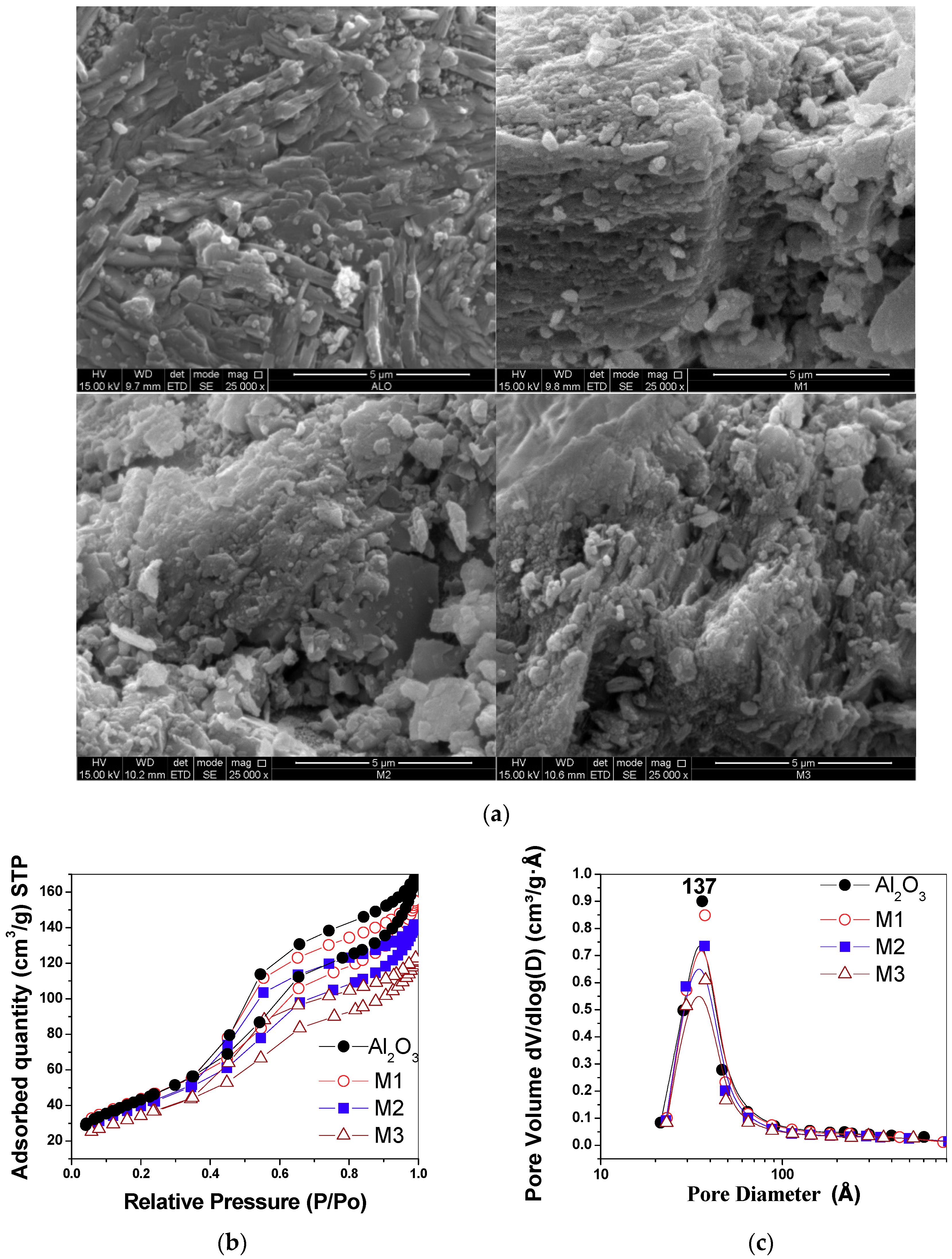

| Material | K (%) | Mn (%) | Estimated Crystal Size (nm)* | Specific Surface Area (m2/g) | Pore Volume (cm3/g) |
|---|---|---|---|---|---|
| Al2O3 | ND | ND | ND | 163 ± 1.1 | 0.2557 |
| M1 | 0.73 | 2.77 | 3 | 159 ± 1.1 | 0.2501 |
| M2 | 1.80 | 5.80 | 4 | 145 ± 1.0 | 0.2286 |
| M3 | 3.59 | 12.95 | 11 | 125 ± 1.2 | 0.1981 |
| Element | Alumina | Error (%) | M1 | Error (%) | M2 | Error (%) | M3 | Error (%) |
|---|---|---|---|---|---|---|---|---|
| R2 (Ω) | 2.999 × 104 | 8 | 1.197 × 103 | 8 | 9.010 × 102 | 8 | 3.891 × 103 | 8 |
| CPE1-T (F) | 1.099 × 10−10 | 5 | 3.831 × 10−12 | 6 | 1.518 × 10−12 | 8 | 2.092 × 10−11 | 8 |
| CPE1-P | 0.86 | 3 | 1.18 | 3 | 1.28 | 3 | 1.03 | 3 |
| R3(Ω) | 3.067 × 106 | 9 | 3.623 × 105 | 8 | 3.289 × 105 | 5 | 2.852 × 104 | 6 |
| CPE2-T (F) | 1.156 × 10−7 | 3 | 6.927 × 10−8 | 7 | 6.090 × 10−8 | 9 | 1.494 × 10−7 | 6 |
| CPE2-P | 0.69 | 5 | 0.70 | 3 | 0.61 | 5 | 0.63 | 4 |
| R4 (Ω) | NA | NA | 1.657 × 105 | 6 | 1.153 × 105 | 8 | 4.335 × 104 | 4 |
| CPE3-T (F) | NA | NA | 4.218 × 10−11 | 2 | 3.002 × 10−11 | 7 | 8.136 × 10−11 | 6 |
| CPE3-P | NA | NA | 0.91 | 3 | 0.93 | 3 | 0.89 | 3 |
| Wo1-R (Ω) | NA | NA | 8.323 × 102 | 8 | 4.800 × 10−1 | 8 | 1.017 × 103 | 8 |
| Wo1-T (s) | NA | NA | 4.764 × 10−7 | 7 | 3.811 × 10−16 | 6 | 8.401 × 10−17 | 8 |
| Wo1-P | NA | NA | 0.21 | 2 | 0.19 | 2 | 0.02 | 3 |
| Material | Relaxation Time (s) | |
|---|---|---|
| τ2 | τ4 | |
| Alumina | 4.01 × 10−7 | 6.34 × 10−2 |
| M1 | 2.01 × 10−6 | 5.05 × 10−5 |
| M2 | 1.60 × 10−6 | 1.60 × 10−5 |
| M3 | 7.96 × 10−8 | 6.34 × 10−4 |
| Frequency | Alumina | M1 | M2 | M3 |
|---|---|---|---|---|
| f1 | 5 MHz | 5 MHz | 5 MHz | 5 MHz |
| f2 | 397.16 kHz | 79.24 kHz | 99.76 kHz | 2.00 MHz |
| f3 | 19.90 kHz | 1.99 kHz | 7.92 kHz | 50.12 kHz |
| f4 | 2.51 Hz | 31.54 Hz | 99.74 Hz | 251.12 Hz |
| f5 | 1.00 Hz | 2.51 Hz | 19.90 Hz | 15.84 Hz |
| f6 | N.D | 1.00 Hz | 1.00 Hz | 1.00 Hz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arias, N.P.; Becerra, M.E.; Giraldo, O. Electrical Behavior of a Catalyst Composed of Laminar Manganese Oxide Supported on γ-Al2O3. Molecules 2019, 24, 2984. https://doi.org/10.3390/molecules24162984
Arias NP, Becerra ME, Giraldo O. Electrical Behavior of a Catalyst Composed of Laminar Manganese Oxide Supported on γ-Al2O3. Molecules. 2019; 24(16):2984. https://doi.org/10.3390/molecules24162984
Chicago/Turabian StyleArias, Nayda P., María E. Becerra, and Oscar Giraldo. 2019. "Electrical Behavior of a Catalyst Composed of Laminar Manganese Oxide Supported on γ-Al2O3" Molecules 24, no. 16: 2984. https://doi.org/10.3390/molecules24162984
APA StyleArias, N. P., Becerra, M. E., & Giraldo, O. (2019). Electrical Behavior of a Catalyst Composed of Laminar Manganese Oxide Supported on γ-Al2O3. Molecules, 24(16), 2984. https://doi.org/10.3390/molecules24162984






