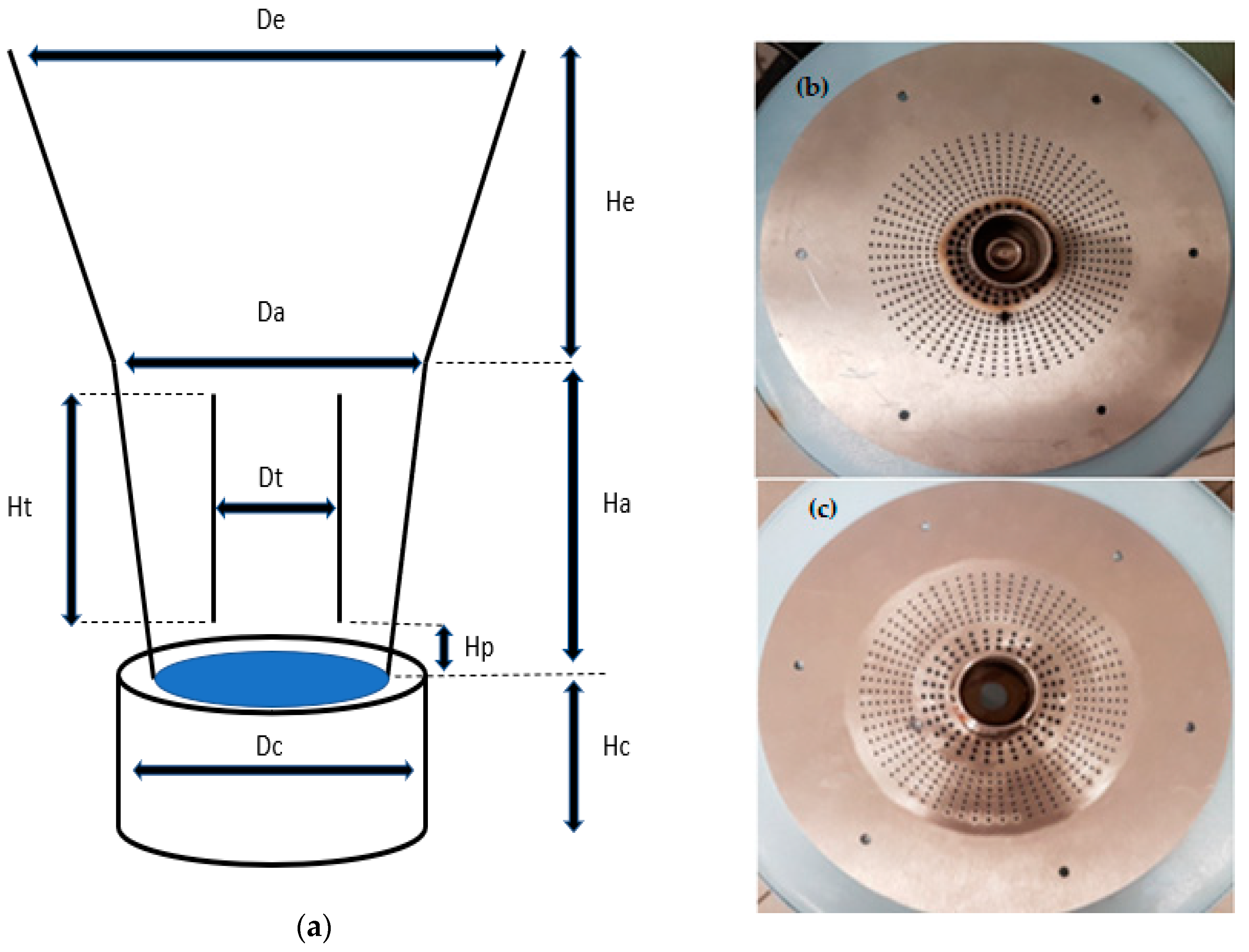
3.1. General Particle Movement
For aerogel particles, different regimes of fluidization in a Wurster fluidized bed were observed which depended on the superficial air velocity. As an example, the movement of the particles in the Wurster fluidized bed with 150 mL batch volume, 2 cm partition gap and wide tube (Run #9) is shown in
Figure 3.
At the beginning of each run (
Table 2), particles were placed uniformly on the perforated plate (
Figure 3a). Compressed air was then supplied to the bed at a particular flow rate. Particles started to vibrate when a certain flow rate was reached which is indicative of a transition from a fixed bed to a fluidized bed (
Figure 3b). At the onset of fluidization, the weight of particles equals drag force exerted by the ascending gas. At that point porosity of bed increases and particles exhibit ‘liquidlike’ behavior. Corresponding air velocity at that point is minimum fluidization velocity, (
umf) [
20]. After reaching the
umf, air flow rate was slightly increased, and particles moved towards to the Wurster tube by the pressure difference between annular zone and tube zone due to the Venturi effect. At that step, air velocity was not sufficient for particle elevation inside the Wurster tube so that particles fluidized at bubbling phase (
Figure 3c). By further increasing the air flow rate, turbulent flow of the particles was achieved. In this step, particles reached the upper edge of the tube in dilute and disperse phase and then fell into the annular zone (
Figure 3d). Particles started following the U-shaped trajectory and fully circulated inside the bed when a particular air velocity was reached (
Figure 3e).
3.2. Effects of Design and Process Parameters on Particle Fluidization Behavior
The conditions for the various runs which were conducted are given in
Table 2. At the beginning of each run the
umf was measured at the vibration point of the particles. All measurements were repeated three times and the
umf was found nearly identical for each run. The average of the 40 runs is 0.19 ± 0.01 m/s. Thus, one can say that that the
umf does not depend on the design parameters of the bed or operating parameters such as batch volume. It just depends on the physical properties of the particle.
umf can also be calculated using an expression which is obtained by rearranging Ergun Equation [
21] and is given by:
Parameters of Ergun Equation are given in
Table 3. Void fraction under minimum fluidization (
) was calculated with Wen & Yu correlation [
22]. Density and viscosity of air were taken from literature [
23]. Particle sphericity was assumed as 1 for spherical aerogel particles.
umf was calculated as 0.18 m/s using Equation (2). Thus, Ergun Equation (2) gave a good estimate of measured
umf of aerogel particles.
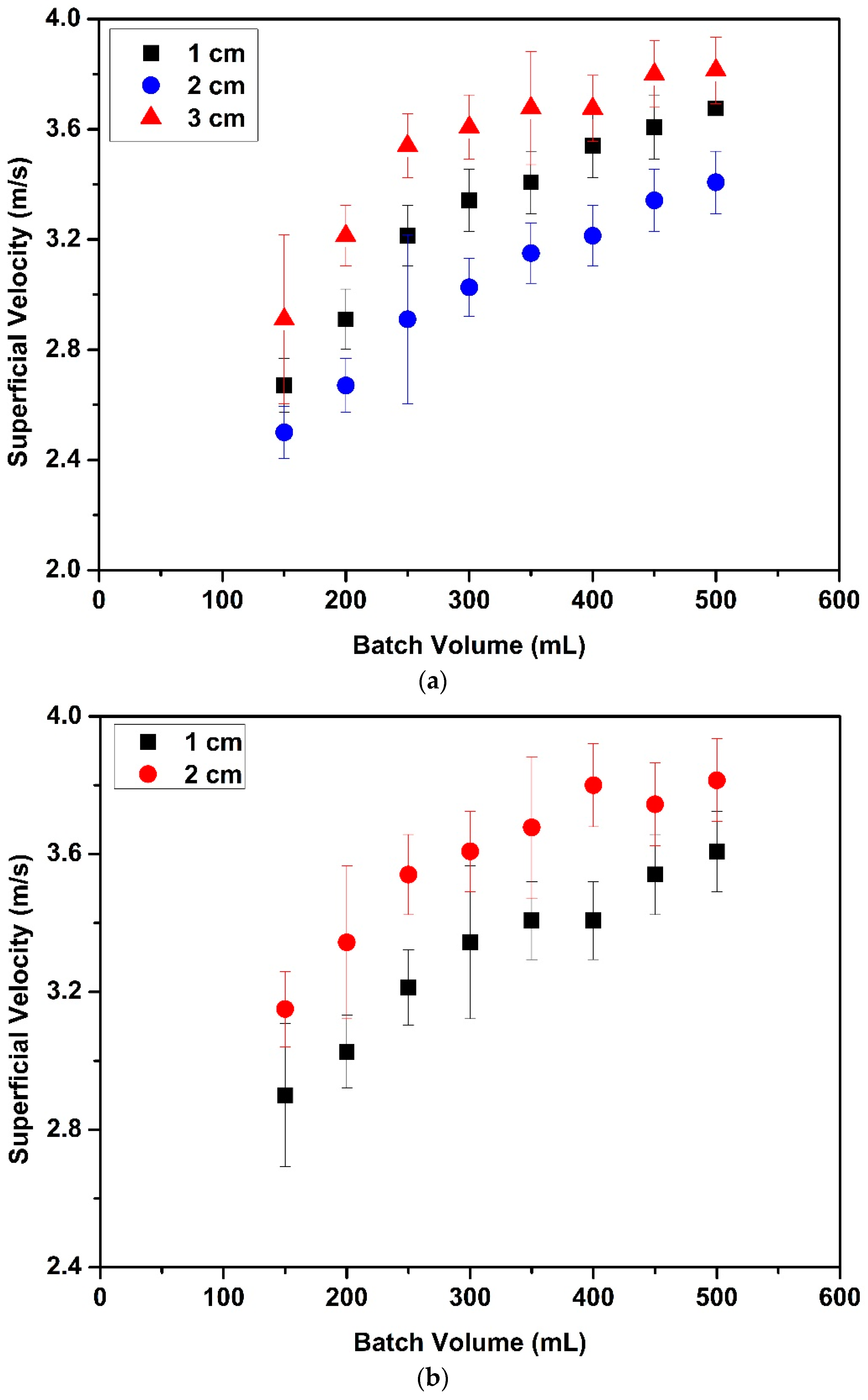
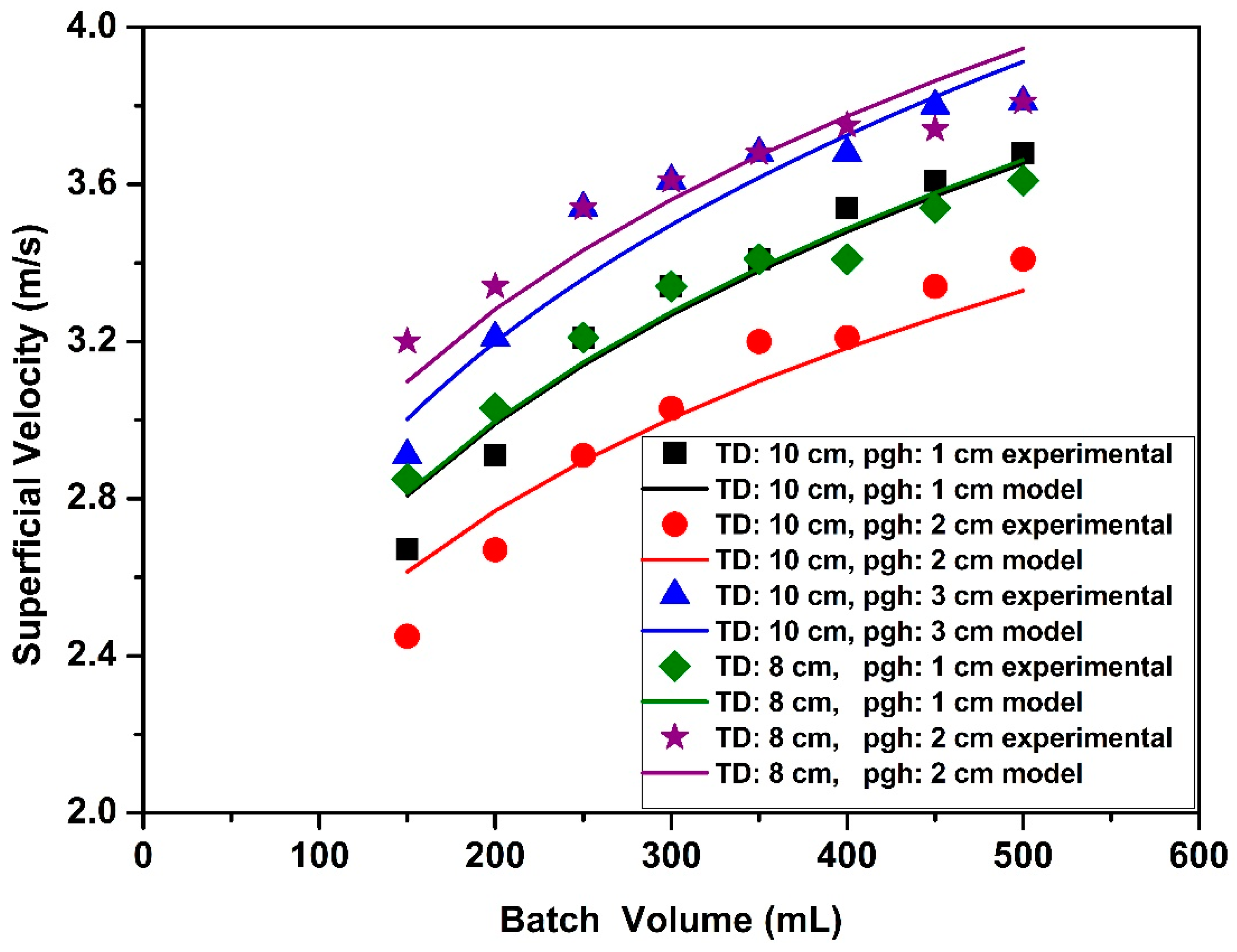
Superficial velocities were also measured at onset of circulatory motion. Effects of partition gap height, tube diameter and batch volume on the superficial velocities are given in
Figure 4.
Figure 4a,b illustrate that the superficial velocities for the narrow tube were higher than for the wide tube. For instance, the superficial velocity for 150 mL batch volume with 2 cm partition gap height (Run #33) with the narrow tube was 1.3 times higher than in the wide tube with same partition gap height (Run #9). This can be attributed to the fact that a higher suction pressure was needed to move particles from the annular zone to the tube zone for the narrow tube since the particles traverse a larger distance in the annual zone for the narrow tube. Thus, the superficial velocity is higher to provide the required suction pressure for fluidization. It was also found that variations of the process (batch volume) and the design (partition gap height and tube length) parameters resulted in more significant changes in the fluidization behavior of aerogel particles for the narrow Wurster tube than the wide Wurster tube.
Figure 4a,b also show the effect of batch volume on superficial velocity. Superficial velocity linearly increased when the batch volume increased from 150 mL to 250 mL. Increasing superficial velocity with increasing batch volume was expected since a higher flow rate of air is required to carry more particles to a certain height. There was a change in the rate of increase when the batch volume was increased to 250 mL from 500 mL. This change can be attributed to the hydrostatic pressure effect which increases the mass flow rate of particles from the annular zone to the tube zone. This additional force results in a lower superficial velocity than expected. A similar phenomenon was also observed by Chan et al. for fluidization of sugar pellets in Wurster fluidized bed [
24].
Experiments with batch volumes larger than 500 mL were also carried out. It was observed that some of the particles were fluidized in the annular zone which can be attributed to the Venturi effect which is mainly responsible for particle movement from the annular zone to the tube zone [
25]. Air enters the bed through the holes of perforated plate. At that point, air velocity has only a vertical component. Venturi effect is observed when the air passes through the partition gap. The Wurster tube causes a pressure difference between the annular zone and the tube zone leading to a suction pressure at the bottom of the partition gap. Thus, air velocity obtains a horizontal component which decreases the magnitude of the vertical component of the air velocity at constant air flow rate. Particles move from annular zone to the tube zone because of the horizontal component of the air velocity [
11]. Inside the Wurster tube, vertical component of the air velocity should be sufficiently higher than the horizontal component for particle elevation. However, high batch volumes above 500 mL lead to a decrease in the pressure difference between the annular zone and the Wurster tube zone resulting in a decrease of the vertical component of the velocity. Thus, one could see random particle fluidization in these runs. Some of the particles recirculated inside the tube and some of the particles accumulated at the bottom edge of the Wurster tube. Some of the particles were stationary inside the Wurster tube zone. Moreover, some of the particles were observed to stick to each other and agglomerated in various zones in the bed. This is because the particles became electrostatically charged due to collisions with other particles and the wall of the bed because of high velocities.
Such a high superficial velocity also crushed some of the aerogel particles at higher batch volumes.
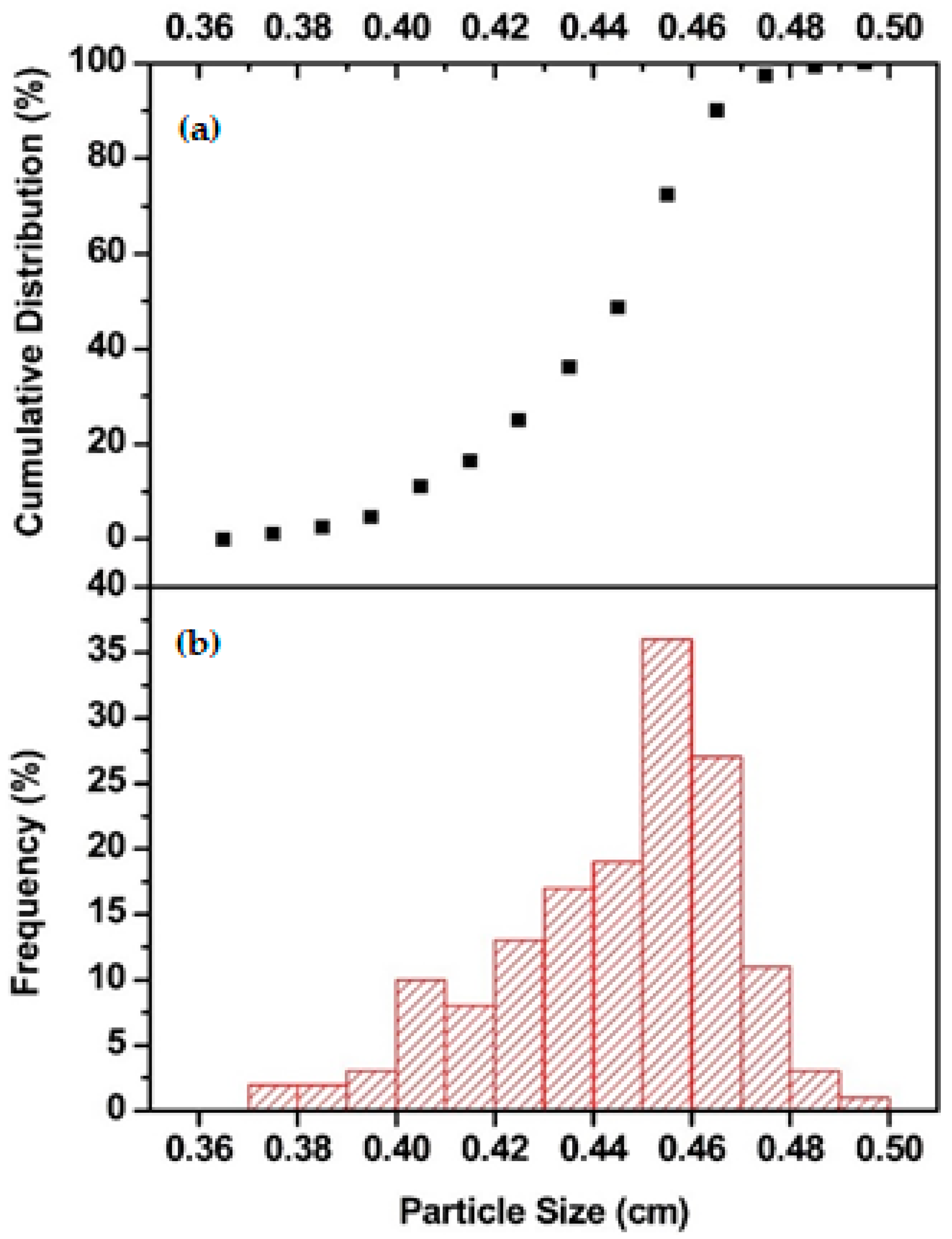
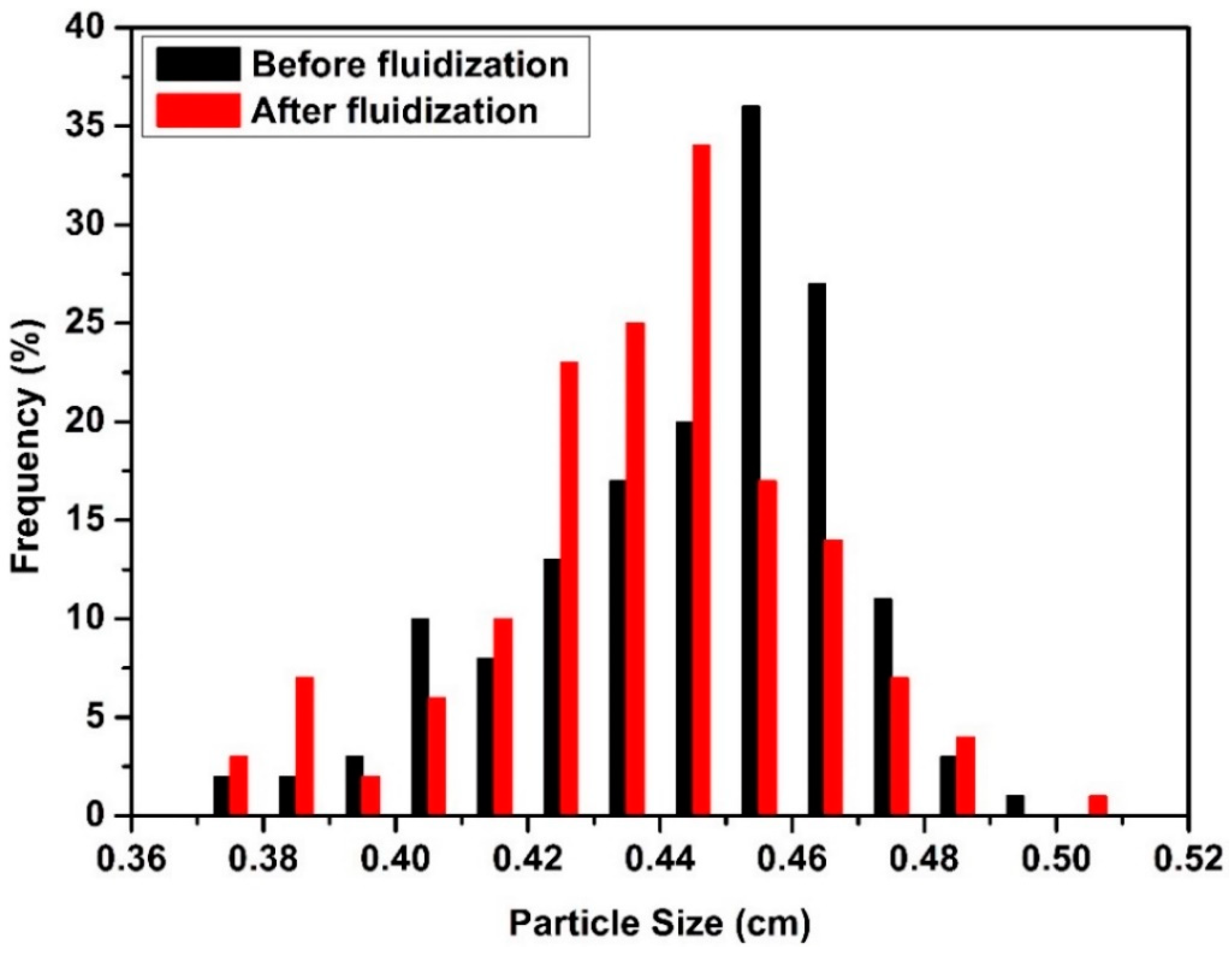
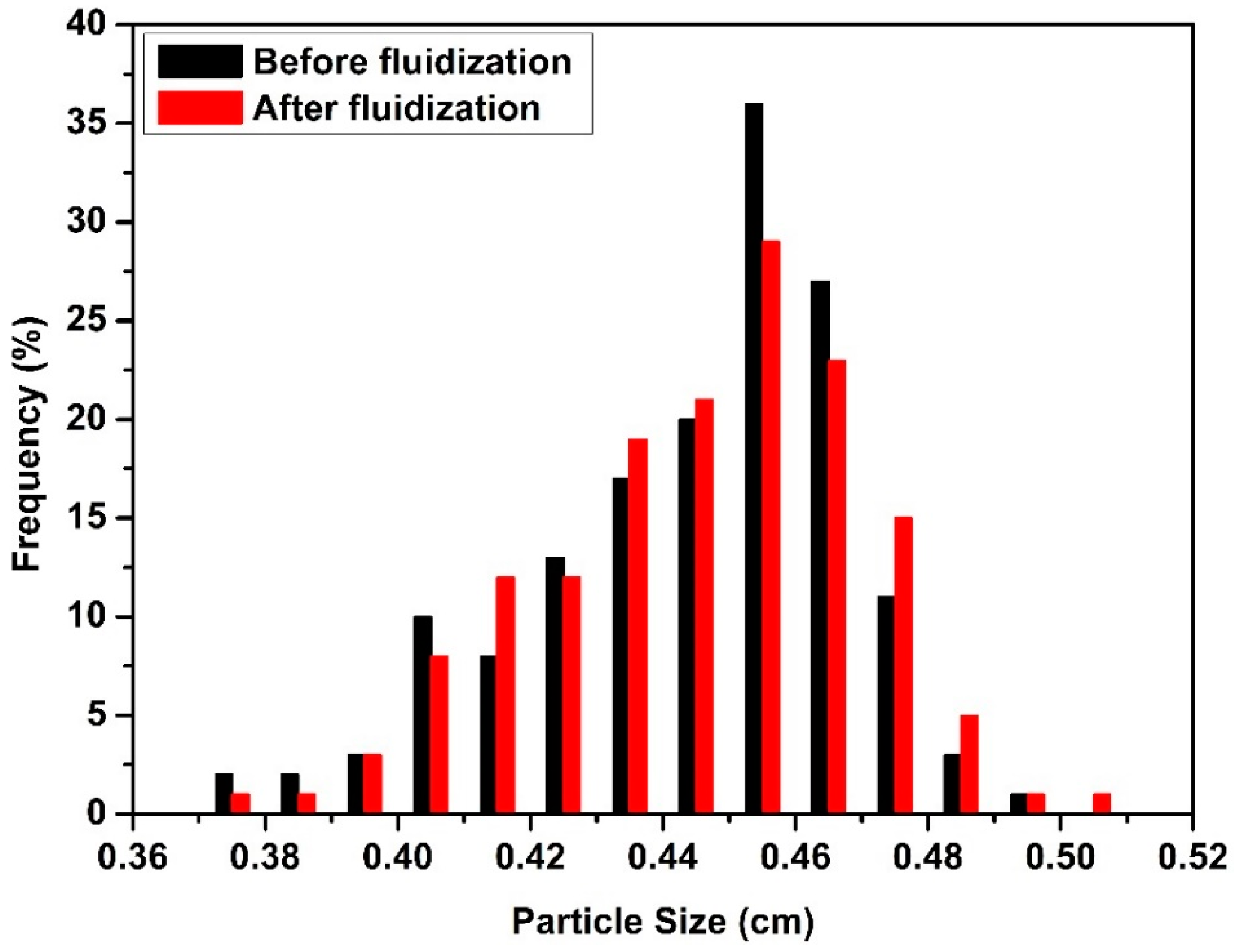
Figure 5 shows that PSD of 500 mL batch volume before and after Run #16. One can see that the size of particles decreased after the fluidization and PSD shifted to the left. Crushed particles destroyed regular particle fluidization due to their different fluidization pathway. Crushed particles stuck to bed and tube walls which resulted in an increase in the number of agglomerates. There was no significant change in PSD with batch volumes lower than 500 mL.
Figure 6 illustrates PSD of 250 mL batch volume before and after Run #11. Thus, a batch of volume of 500 mL can be expected to be the upper limit for operation for the tube with the 10 cm diameter. The same behavior was observed at a much smaller batch volume (250 mL compared to 500 mL) for the narrow tube due to lower ratio of tube diameter/perforated plate diameter which resulted in higher velocity for smaller batch volumes.
The effects of changing the partition gap height were also investigated. When partition gap height was increased from 1 cm to 2 cm with the narrow tube (
Figure 4b), it was found that superficial velocities increased. Since pressure difference between the annular zone and the Wurster tube zone decreases with increasing partition gap height, the vertical component of the velocity inside the tube decreases [
26]. Further increasing partition gap height from 2 cm to 3 cm induced a transition from regular fluidization to bubbling phase which resulted in over fluidization in the annular zone. Therefore, superficial velocities were not measured for 3 cm gap height.
It is interesting to note that superficial velocities did not increase with increase of partition gap height from 1 cm to 2 cm for the wide tube (
Figure 4a). This phenomenon may be explained by the following factors. With 1 cm partition gap, particles accumulated at the lower edge of the tube, stacked there and formed clusters before moving into the tube due to higher ratio of particle size/partition gap height. After a certain time, these clusters disrupted circulatory motion of the particles. Therefore, superficial velocity at onset of circulatory motion increased with 1 cm partition gap height for both dissociating clusters into individual particles and achieving circulatory motion. Increasing the partition gap height from 1 cm to 2 cm provides a larger opening to the particles at above the partition gap. Particles followed circulatory motion at lower superficial velocities with 2 cm partition gap height than with 1 cm partition gap height since larger partition gap height prevented the formation of agglomerates. Subsequently, increasing partition gap height from 2 cm to 3 cm, significantly increased superficial velocities. Some of the aerogel particles were crushed and agglomerated at these higher velocities and disrupted the circulatory motion. Consequently, partition gap height should not exceed 2 cm for both tubes.
Finally, we developed three correlations to predict the superficial velocity at onset of circulatory motion as a function of batch volume and tube diameter. It was not possible to represent superficial velocities with one equation since velocity for the 10 cm tube first increased and then decreased with partition gap height. Therefore, we separately developed three correlations for each partition gap height. The correlation for 1 cm and 2 cm partition gap heights is given by:
where
u is the superficial velocity at onset of circulatory motion,
TD is the tube diameter and
BV is the batch volume.
The constants
α,
β and
γ in the correlation were determined for 1 cm and 2 cm partition gap heights, separately. A nonlinear regression solver in PYTHON was used to find the constants by fitting the model results to experimental data. For 3 cm partition gap height, the correlation was developed as a function of batch volume and is given by:
The constants
α,
β and
γ,
and
in the correlations and calculated
values are given in
Table 4.
Figure 7 shows the comparison of experimental data and model results. There is a good agreement between the model results and experimental data.
3.3. Fluidization Regimes of Alginate Aerogel Particles in the Classical and Modified Geldart Classification
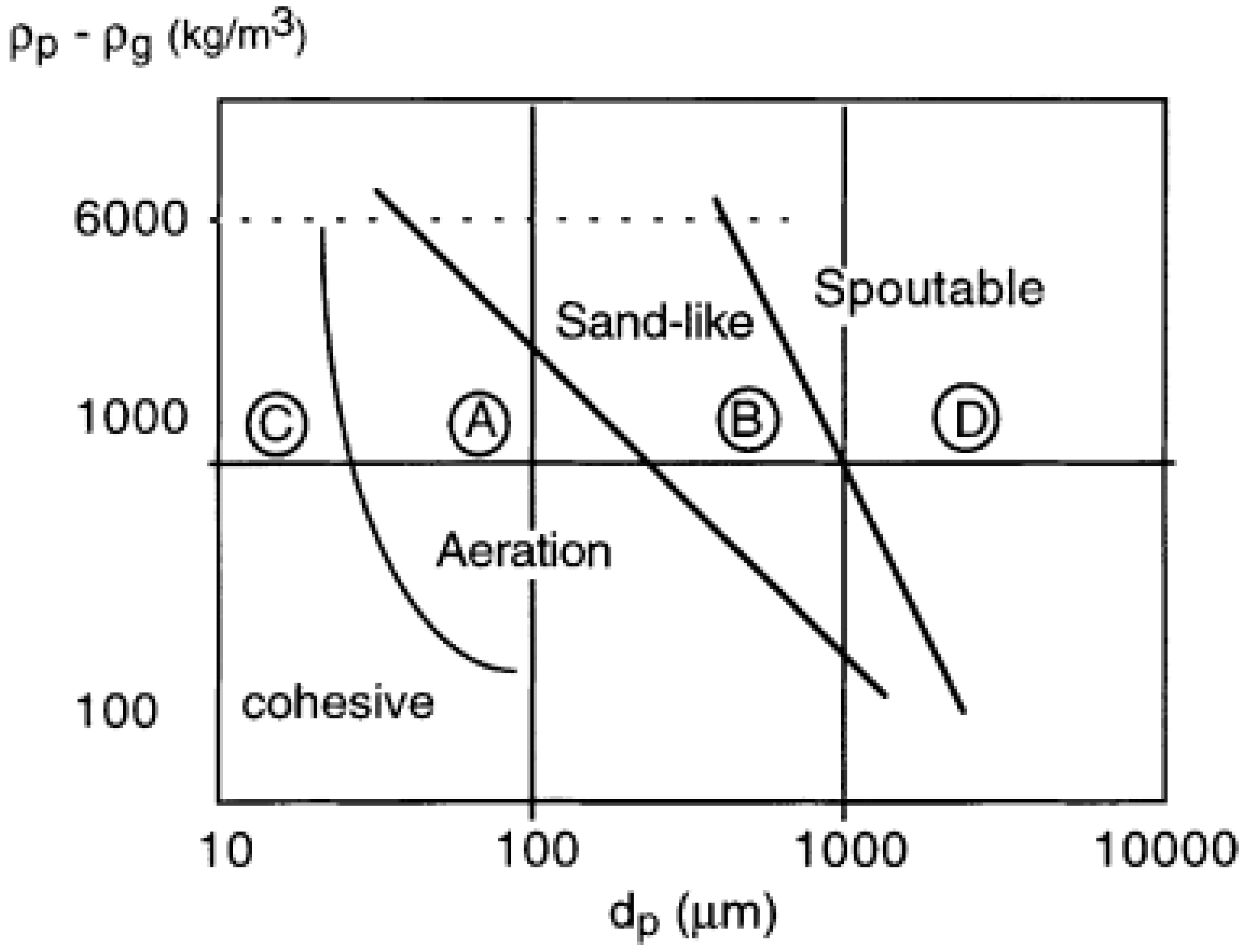
In the literature, particle fluidization behavior in fluidized beds generally falls into one of the four regions as classified by Geldart [
27]. These regions (A, B, C, D) are shown in
Figure 8 and depend on particle size and density difference between the solids and the fluid at ambient temperature and the pressure [
28]. In Geldart A region, particles fluidize well. Most particles investigated in fluidization studies belong to this region. In Geldart B region, bubbling fluidization regime is observed and the fluidization behavior of these particles is highly affected by the gas bubbles [
29]. In Geldart C region, agglomeration and bubbling fluidization is observed and it is often difficult to fluidize the particles [
29,
30]. In Geldart D region, high fluidization velocities are needed due to large particle sizes and high densities [
29]. The aerogels used in this study have very low density (
-
43.8 kg/m
3) and large particle size (
4400 µm). Therefore, they fall outside these regions. At low superficial velocities, aerogel particles may fall into region B due to bubble formation. At moderate superficial velocities and small batch volumes, aerogel particles fluidized well and may fall into region A. At higher superficial velocities and batch volumes, agglomerates were observed as in region C.
Thus, classical Geldart classification is not quite suitable to describe the fluidization behavior of alginate aerogel particles. Superficial velocity also affects the particle fluidization behavior as discussed above.
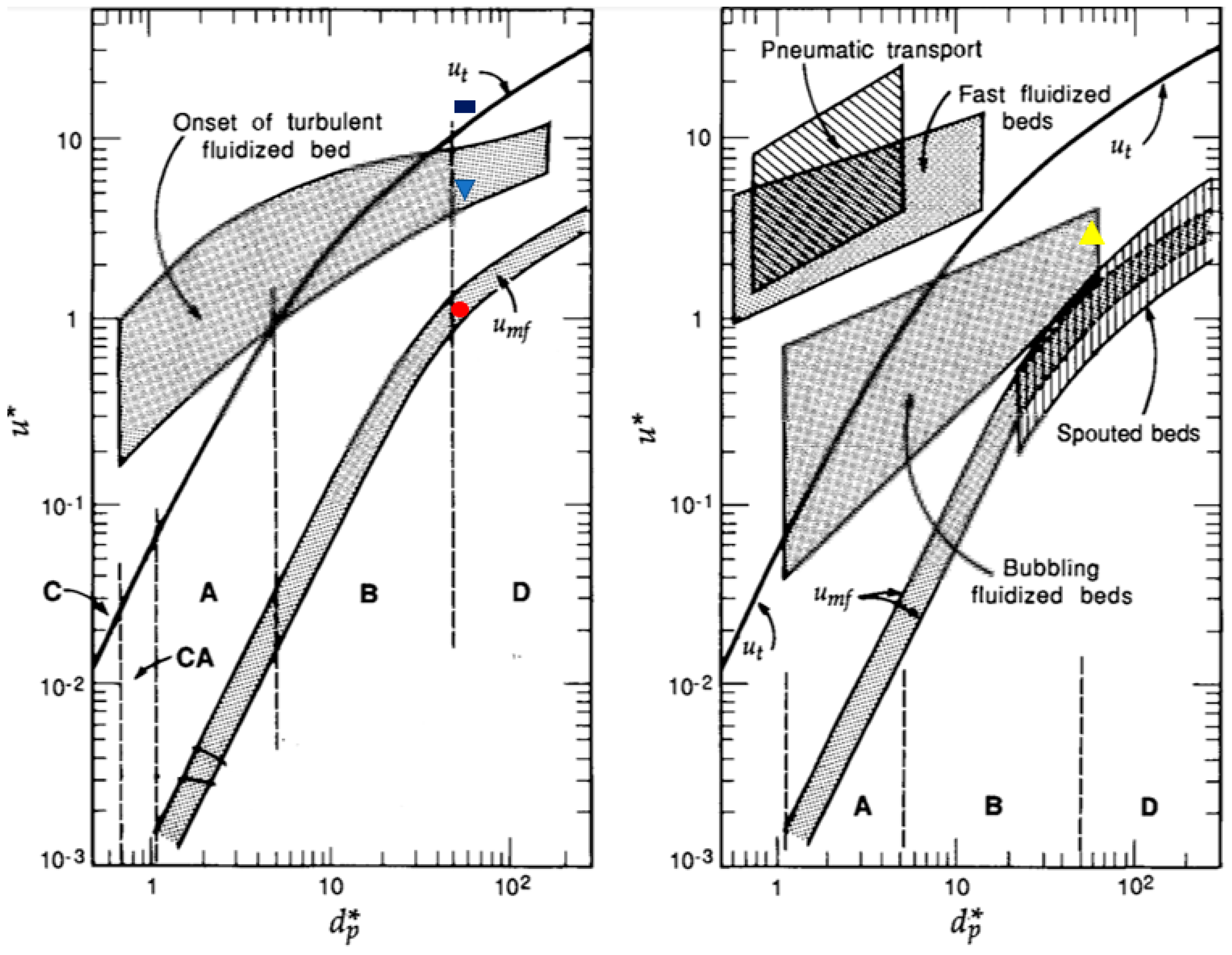
Figure 9 shows two diagrams which combine most of the information about different fluidization regimes based on air velocity and particle diameter [
31]. These diagrams also include modified boundaries of Geldart classification.
In
Figure 9, the minimum fluidization regime occurs only for Geldart A, B and D particles. Bubbling regime occurs for Geldart A and B particles for a wide range of particle size and air velocity whereas Geldart D particles can be bubbled in a very narrow region of particles size. Onset of the turbulent fluidized bed regime is above the terminal velocity for Geldart C and A particles whereas it is below the terminal velocity for Geldart D particles. Besides the minimum, bubbling and turbulent fluidization regimes discussed above, three other regimes are given in
Figure 9 which are pneumatic transport, fast fluidized and spouted bed. These three regimes were not observed for the aerogel particles with a diameter of 4.40 mm in our Wurster fluidized bed.
The x and y-axes of
Figure 9 are dimensionless diameter,
dp*, and dimensionless velocity,
u* which can be calculated by Equations (5) and (6) given by:
where
is the particle diameter,
is the particle density,
is the gas density,
is the gas viscosity, and
is the superficial velocity. Superficial velocities were also measured at the onset of fluidization, bubbling, turbulent flow regimes and circulatory motion for Run #9 to see if these diagrams also captured the fluidization behavior of aerogel particles.
dp* and
u* were calculated using superficial velocity and particle diameter for Run #9. The velocities, dimensionless velocities, diameter and dimensionless particle diameter are given in
Table 5.
The four points in
Table 5 are also plotted in
Figure 9 as red solid circle, blue triangle, yellow triangle and black rectangle. One can see that the dimensionless particle diameter is in Region D for the aerogel used in this study. The red circle representing the data obtained for the onset of fluidization for Run #9 falls right inside the area representing minimum fluidization region in
Figure 9. The yellow triangle representing the data obtained at the onset of bubbling regime also falls inside the area covering bubbling region in
Figure 9. The blue triangle representing the data obtained for the onset of turbulent flow regime in Run #9 also falls in the area representing the onset of turbulent flow region. These indicate that
Figure 9 also captures the fluidization behavior of aerogel particles investigated in this study. There is no region for circulatory motion in
Figure 9. The black rectangle representing the data obtained for the onset of circulatory motion just falls above the line for terminal velocity.
3.4. Particle Residence Time in the Wurster Tube
Particle residence time in the Wurster tube is another significant parameter. In this study, an aerogel particle which had a diameter of 4.40 mm and a density of 0.045 g/cm
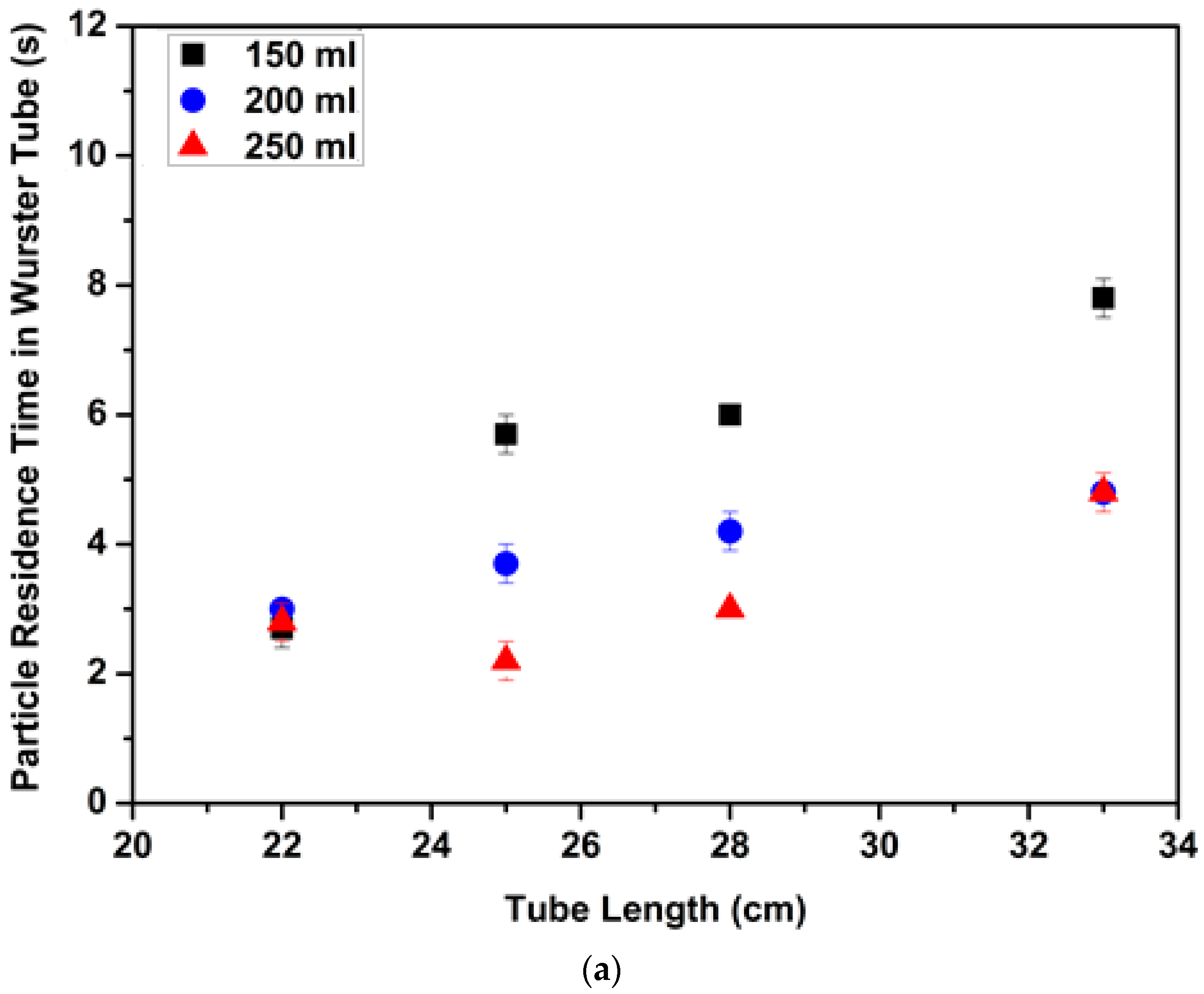
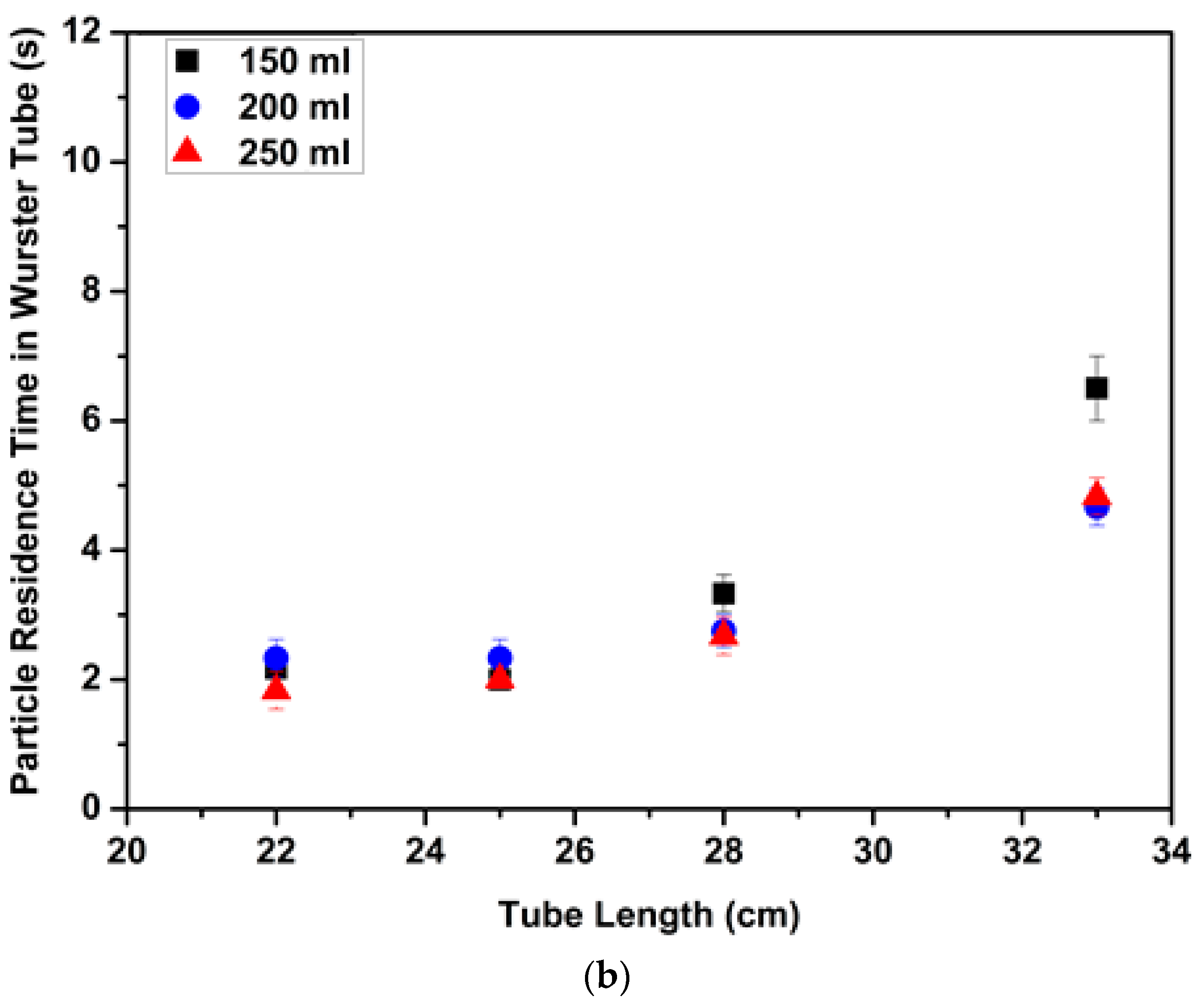
3 was selected and dyed with green coloring. At the beginning of each run, the same green particle was placed near the bed wall. Each run was operated at a constant velocity (3.7 m/s) which was higher than superficial velocities at onset of circulatory motion of each run. The particle movement in the bed was monitored with a camera (Samsung ISOCELL S5K2L1) during the run which lasted 15 s. Particle residence time in the tube was measured by timing the entrance and exit of the green colored particle to and from the narrow Wurster tube with lengths of 22 cm, 25 cm, 28 cm and 33 cm. Exclusively, batch volumes from 150 mL to 250 mL were investigated with 1 cm and 2 cm partition gap heights since fluidization behavior of the aerogel particles for the narrow tube which was 33 cm long started to change for batch volumes above 250 mL. After each run PSD was measured and there was no significant change in PSD. Effects of tube length, batch volume and partition gap height on particle residence time in the Wurster tube are shown in
Figure 10.
Figure 10a,b show the effect of batch volume on mean values of particle residence time in the tube. Increasing batch volume resulted in a decrease in particle residence time. On one hand, as explained in
Section 3.2. the horizontal component of the air velocity increased with increasing batch volume leading to a decrease in the vertical component of the air velocity in the tube. On the other hand, number of particles in the tube zone, which is one of the driving forces for particle elevation inside the Wurster tube, increased with increasing horizontal component of the air velocity resulting in shorter particle residence time in the tube.
Figure 10a,b also illustrate the effect of tube length on the particle residence time. The most pronounced effect of increasing the tube length is the increase in particle residence time due to a longer path inside the tube. Moreover, increasing tube length had different effects when batch volume was varied. The highest change in particle residence time with increasing tube length was observed for 150 mL batch volume. For example, a 50% increase in tube length resulted in a 200% increase in residence time (
Figure 10a). Particle residence time with 250 mL batch volume slightly increased when tube length increased from 22 cm to 33 cm due to the higher number of particles in the annular zone (
Figure 10a,b).
Figure 10a,b also show how particle residence time changes with partition gap height. Particle residence time decreased when partition gap height increased from 1 cm to 2 cm due to increasing horizontal component of the air velocity as explained
Section 3.2. Increasing horizontal component of the air velocity with increasing partition gap height resulted in a higher number of particles at the tube zone which contributed to particle elevation inside the tube. Li et al. investigated the effect of partition gap height on the cycle time of microcrystalline cellulose (MCC) pellets [
13]. Cycle time increased when partition gap height increased from 1 cm to 1.5 cm. Subsequently, increasing partition gap height from 1.5 cm to 2 cm resulted in decreasing cycle time. However, we did not observe an increase in residence time with increasing partition gap height from 1 cm to 1.5 cm or from 2 cm to 2.5 cm most likely due to the different fluidization properties of aerogel and MCC particles.
Particle residence time with 150 mL batch volume significantly changed with partition gap height for tubes with lengths of 25 cm, 28 cm and 33 cm (
Figure 10a,b). Residence times decreased 2–3 s on average when the partition gap height increased from 1 cm to 2 cm for 150 mL batch volume. There was no significant change in the particle residence times with partition gap height for batch volumes of 200 mL and 250 mL (except 33 cm). Thus, one can say that design parameters control the particle residence time for the smallest batch volume used in the experiments.
Residence time of the particles with diameters of 4.60 mm and 4.20 mm were also investigated for 22 cm length and batch volumes of 150 mL and 250 mL with 1 cm partition gap height. These particles were dyed with green coloring. Same measurement method used for the particle with the diameter of 4.40 mm was used to measure residence time of the small and large particles. It was found that the residence time of the large and the small particles in the narrow Wurster tube were almost the same (
Table 6). We expected that large particles will move up more slowly than small ones due to their higher weight. This surprisingly similar residence time of small and large particles was also recorded by Li et al. for large and small MCC particles in the Wurster tube [
13]. This was attributed to the collisions between small and large particles. Velocity of small particles decreases whereas velocity of the large particles increases due to collisions. This gives similar residence time for all particles.