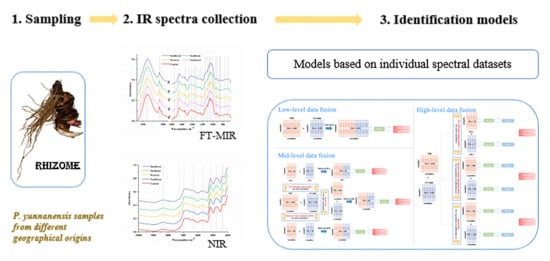
Data Fusion of Fourier Transform Mid-Infrared (MIR) and Near-Infrared (NIR) Spectroscopies to Identify Geographical Origin of Wild Paris polyphylla var. yunnanensis
Abstract
:1. Introduction
2. Results and Discussion
2.1. Macroscopic Chemistry Components in IR Spectra
2.2. Single Block Models
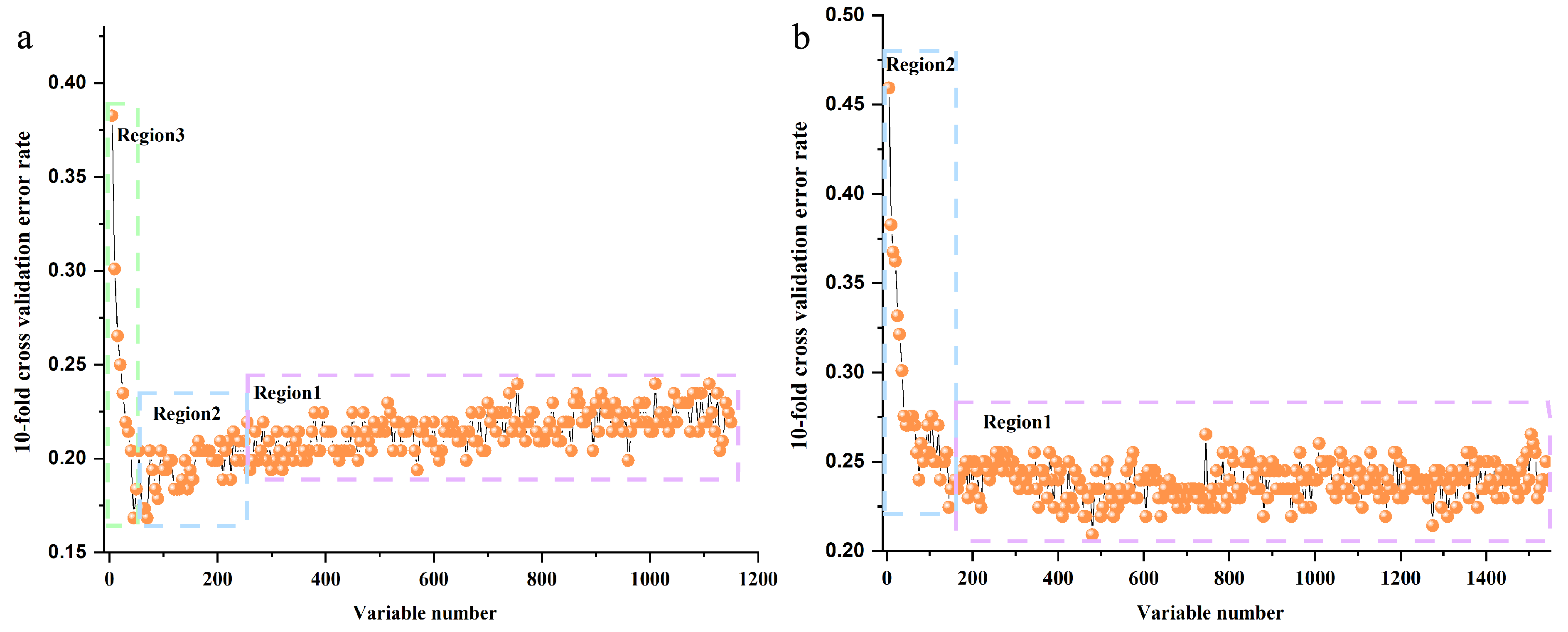
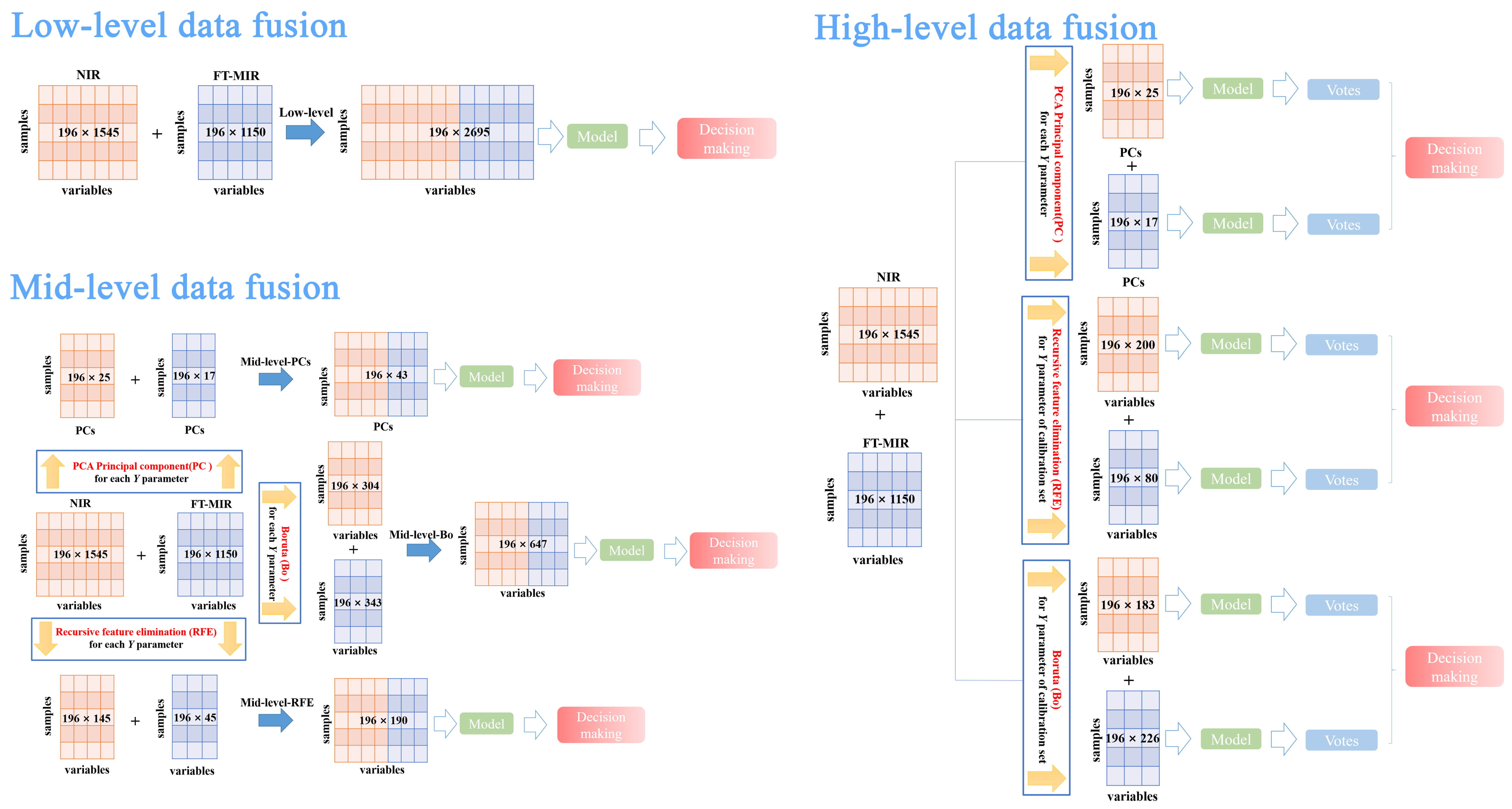
2.3. Important Variable Datasets Selected for Mid-Level Data Fusion
2.4. Important Variables Datasets Selected for High-Level Data Fusion
2.5. Low-Level Data Fusion Models
2.6. Mid-Level Data Fusion Models
2.7. High-Level Data Fusion Models
3. Materials and Methods
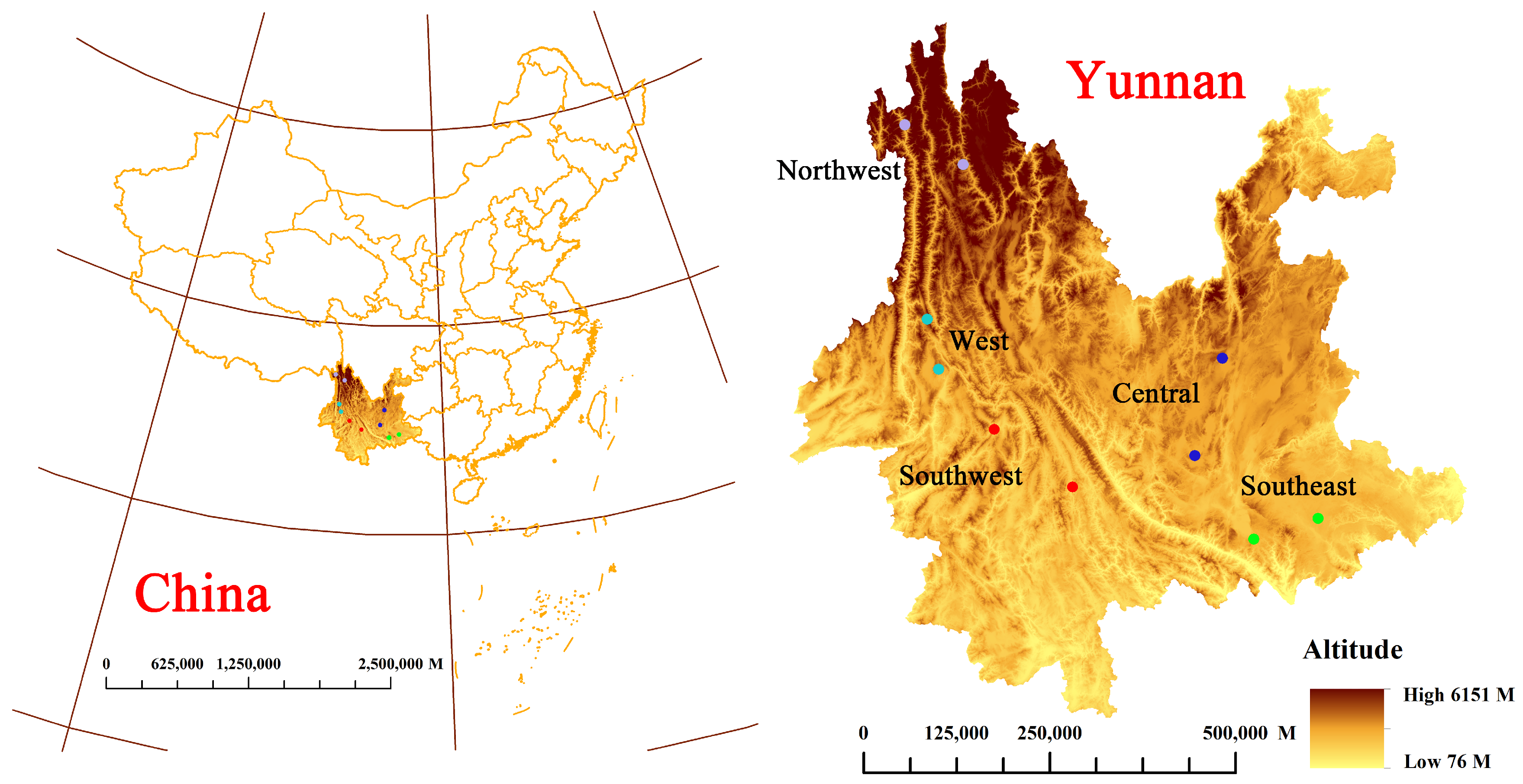
3.1. Samples Preparation
3.2. Fourier Transform Mid-Infrared Spectroscopy (FT-MIR)
3.3. Near-Infrared Spectroscopy (NIR)
3.4. Spectral Data Analysis and Software
3.5. Data Fusion Strategy
- Mid-level-PCs consisted of principal components, which were selected by PCA of FT-MIR and NIR spectral datasets, respectively. PCs were selected based on values of eigenvalue greater than 1. Hence, the mid-level-PCs data matrix was obtained with 196 rows and 42 columns, namely 196 samples and 42 PCs variables (= 25 NIR PCs variables + 17 PCs FT-MIR variables).
- Mid-level-RFE, which consisted of merging together the important variables of FT-MIR and NIR spectral datasets, was selected by the recursive feature elimination algorithm based on the RF model. The mid-level-REF dataset size was equal to 196 rows and 190 columns (= 145 NIR REF variables + 45 FT-MIR REF variables).
- Mid-level-Bo, which consisted of merging together the important (confirmed and tentative) variables of FT-MIR and NIR spectral datasets, was selected by the Boruta algorithm based on the RF model. The mid-level-Bo data matrix consisted of 196 rows and 647 columns (= 153 NIR Bo confirmed variables + 151 NIR Bo tentative variables + 207 FT-MIR Bo confirmed variables + 136 FT-MIR Bo tentative variables).
- NIR-PCs data matrix obtained 196 rows and 25 columns (25 NIR PCs variables) and the FT-MIR-PCs data matrix obtained 196 rows and 17 columns (17 FT-MIR PCs variables).
- NIR-RFE data matrix obtained 196 rows and 200 columns (200 NIR RFE variables) and the FT-MIR-RFE data matrix obtained 196 rows and 80 columns (80 FT-MIR RFE variables).
- NIR-Bo data matrix obtained 196 rows and 183 columns (83 NIR Bo confirmed variables + 108 NIR Bo tentative variables) and the FT-MIR-Bo data matrix obtained 196 rows and 226 columns (117 FT-MIR Bo confirmed variables + 109 FT-MIR Bo tentative variables).
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jing, S.; Wang, Y.; Li, X.; Man, S.; Gao, W. Chemical constituents and antitumor activity from Paris polyphylla Smith var. yunnanensis. Nat. Prod. Res. 2017, 31, 660–666. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.P.; Huang, Y.Y.; Zhan, Z.L.; Liu, D.H.; Peng, H.S.; Nan, T.G.; Zhang, Y.; Hao, Q.X.; Tang, J.F.; Zhu, S.D.; et al. Structural characterization and discrimination of the Paris polyphylla var. yunnanensis and Paris vietnamensis based on metabolite profiling analysis. J. Pharm. Biomed. 2017, 142, 252–261. [Google Scholar]
- Wu, X.; Wang, L.; Wang, G.C.; Wang, H.; Dai, Y.; Yang, X.X.; Ye, W.C.; Li, Y.L. Triterpenoid saponins from rhizomes of Paris polyphylla var. yunnanensis. Carbohydr. Res. 2013, 368, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.; Lauren, D.R.; Cooney, J.M.; Jensen, D.J.; Wurms, K.V.; Upritchard, J.E.; Cannon, R.D.; Wang, M.Z.; Li, M.Z. Antifungal saponins from Paris polyphylla Smith. Planta Med. 2008, 74, 1397–1402. [Google Scholar] [CrossRef]
- Li, P.; Fu, J.H.; Wang, J.K.; Ren, J.G.; Liu, J.X. Extract of Paris polyphylla Smith protects cardiomyocytes from anoxia-reoxia injury through inhibition of calcium overload. Chin. J. Integr. Med. 2011, 17, 283–289. [Google Scholar] [CrossRef]
- Hwang, S.J.; Lin, H.C.; Chang, C.F.; Lee, F.Y.; Lu, C.W.; Hsia, H.C.; Wang, S.S.; Lee, S.D.; Tsai, Y.T.; Lo, K.J. A randomized controlled trial comparing octreotide and vasopressin in the control of acute esophageal variceal bleeding. J. Hepatol. 1992, 16, 320. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, W.; Li, X.; Wei, J.; Jing, S.; Xiao, P. Chemotaxonomic study of the genus Paris based on steroidal saponins. Biochem. Syst. Ecol. 2013, 48, 163–173. [Google Scholar] [CrossRef]
- Cunningham, A.B.; Brinckmann, J.A.; Bi, Y.F.; Pei, S.J.; Schippmann, U.; Luo, P. Paris in the spring: A review of the trade, conservation and opportunities in the shift from wild harvest to cultivation of Paris polyphylla (Trilliaceae). J. Ethnopharmacol. 2018, 222, 208–216. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Yuan, T.; Shen, T.; Li, W.; Yang, S.; Hou, Y.; Wang, Y.; Jin, H. Discrimination of wild Paris based on near-infrared spectroscopy and high-performance liquid chromatography combined with multivariate analysis. PLoS ONE 2014, 9, e89100. [Google Scholar] [CrossRef]
- Yang, Y.G.; Jin, H.; Zhang, J.; Zhang, J.Y.; Wang, Y.Z. Quantitative evaluation and discrimination of wild Paris polyphylla var. yunnanensis (Franch.) Hand.-Mazz from three regions of Yunnan Province using UHPLC-UV-MS and UV spectroscopy couple with partial least squares discriminant analysis. J. Nat. Med. 2017, 71, 148–157. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Liu, E.H.; Li, P. Chemotaxonomic studies of nine Paris species from China based on ultra-high performance liquid chromatography tandem mass spectrometry and Fourier transform infrared spectroscopy. J. Pharm. Biomed. 2017, 140, 20–30. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, J.; Zhao, Y.L.; Huang, H.Y.; Wang, Y.Z. Comprehensive Quality Assessment Based Specific Chemical Profiles for Geographic and Tissue Variation in Gentiana rigescens Using HPLC and FTIR Method Combined with Principal Component Analysis. Front. Chem. 2017, 5, 125. [Google Scholar] [CrossRef] [PubMed]
- Ballabio, D.; Robotti, E.; Grisoni, F.; Quasso, F.; Bobba, M.; Vercelli, S.; Gosetti, F.; Calabrese, G.; Sangiorgi, E.; Orlandi, M.; et al. Chemical profiling and multivariate data fusion methods for the identification of the botanical origin of honey. Food Chem. 2018, 266, 79–89. [Google Scholar] [CrossRef] [PubMed]
- Gad, H.A.; Bouzabata, A. Application of chemometrics in quality control of Turmeric (Curcuma longa) based on Ultra-violet, Fourier transform-infrared and 1H NMR spectroscopy. Food Chem. 2017, 237, 857–864. [Google Scholar] [CrossRef] [PubMed]
- Qi, L.; Liu, H.; Li, J.; Li, T.; Wang, Y. Feature Fusion of ICP-AES, UV-Vis and FT-MIR for Origin Traceability of Boletus edulis Mushrooms in Combination with Chemometrics. Sensors 2018, 18, 241. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.H.; Zhang, Z.M.; Zhao, X.B.; Zhang, S.F.; Lu, H.M. The rapid determination of total polyphenols content and antioxidant activity in Dendrobium officinale using near-infrared spectroscopy. Anal. Methods 2016, 8, 4584–4589. [Google Scholar] [CrossRef]
- Pei, Y.F.; Wu, L.H.; Zhang, Q.Z.; Wang, Y.Z. Geographical traceability of cultivated Paris polyphylla var. yunnanensis using ATR-FTMIR spectroscopy with three mathematical algorithms. Anal. Methods 2019, 11, 113–122. [Google Scholar] [CrossRef]
- Wu, X.M.; Zhang, Q.Z.; Wang, Y.Z. Traceability the provenience of cultivated Paris polyphylla Smith var. yunnanensis using ATR-FTIR spectroscopy combined with chemometrics. Spectrochim. Acta A 2019, 212, 132–145. [Google Scholar] [CrossRef]
- Pei, Y.F.; Zhang, Q.Z.; Zuo, Z.T.; Wang, Y.Z. Comparison and Identification for Rhizomes and Leaves of Paris yunnanensis Based on Fourier Transform Mid-Infrared Spectroscopy Combined with Chemometrics. Molecules 2018, 23, 3343. [Google Scholar] [CrossRef]
- Yang, Y.G.; Zhang, J.; Jin, H.; Zhang, J.Y.; Wang, Y.Z. Quantitative Analysis in Combination with Fingerprint Technology and Chemometric Analysis Applied for Evaluating Six Species of Wild Paris Using UHPLC-UV-MS. J. Anal. Methods Chem. 2016, 1–9. [Google Scholar] [CrossRef]
- Yang, L.F.; Ma, F.; Zhou, Q.; Sun, S.Q. Analysis and identification of wild and cultivated Paridis Rhizoma by infrared spectroscopy. J. Mol. Struct. 2018, 1165, 37–41. [Google Scholar] [CrossRef]
- Biancolillo, A.; Bucci, R.; Magrì, A.L.; Magrì, A.D.; Marini, F. Data-fusion for multiplatform characterization of an italian craft beer aimed at its authentication. Anal. Chim. Acta 2014, 820, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, J.Y.; Wang, Y.Z. FT-MIR and NIR spectral data fusion: A synergetic strategy for the geographical traceability of Panax notoginseng. Anal. Bioanal. Chem. 2018, 410, 91–103. [Google Scholar] [CrossRef]
- Wu, X.M.; Zhang, Q.Z.; Wang, Y.Z. Traceability of wild Paris polyphylla Smith var. yunnanensis based on data fusion strategy of FT-MIR and UV-Vis combined with SVM and random forest. Spectrochim. Acta A 2018, 205, 479–488. [Google Scholar] [CrossRef] [PubMed]
- Horn, B.; Esslinger, S.; Pfister, M.; Fauhl-Hassek, C.; Riedl, J. Non-targeted detection of paprika adulteration using mid-infrared spectroscopy and one-class classification-Is it data preprocessing that makes the performance? Food Chem. 2018, 257, 112–119. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.B.; Guo, B.L.; Yan, R.; Sun, S.Q.; Zhou, Q. Rapid and automatic chemical identification of the medicinal flower buds of Lonicera plants by the benchtop and hand-held Fourier transform infrared spectroscopy. Spectrochim. Acta A 2017, 182, 81–86. [Google Scholar] [CrossRef]
- Xu, C.H.; Chen, J.B.; Zhou, Q.; Sun, S.Q. Classification and identification of TCM by macro-interpretation based on FT-IR combined with 2DCOS-IR. Biomed. Spectrosc. Imaging 2015, 4, 139–158. [Google Scholar]
- Türker-Kaya, S.; Huck, C. A Review of Mid-Infrared and Near-Infrared Imaging: Principles, Concepts and Applications in Plant Tissue Analysis. Molecules 2017, 22, 168. [Google Scholar] [CrossRef]
- Socrates, G. Infrared and Raman Characteristic Group Frequencies, 3rd ed.; John Wiley & Sons, Ltd.: Chichester, UK; New York, NY, USA, 2001. [Google Scholar]
- Fu, H.Y.; Huang, D.C.; Yang, T.M.; She, Y.B.; Zhang, H. Rapid recognition of Chinese herbal pieces of Areca catechu by different concocted processes using Fourier transform mid-infrared and near-infrared spectroscopy combined with partial least-squares discriminant analysis. Chin. Chem. Lett. 2013, 24, 639–642. [Google Scholar] [CrossRef]
- Wang, Y.; Zuo, Z.T.; Shen, T.; Huang, H.Y.; Wang, Y.Z. Authentication of Dendrobium Species Using Near-Infrared and Ultraviolet-Visible Spectroscopy with Chemometrics and Data Fusion. Anal. Lett. 2018, 51, 2792–2821. [Google Scholar] [CrossRef]
- Ma, N.; Liu, X.W.; Kong, X.J.; Li, S.H.; Jiao, Z.H.; Qin, Z.; Yang, Y.J.; Li, J.Y. Aspirin eugenol ester regulates cecal contents metabolomic profile and microbiota in an animal model of hyperlipidemia. BMC Vet. Res. 2018, 14, 405. [Google Scholar] [CrossRef]
- Rodrigues, D.; Pinto, J.; Araújo, A.M.; Monteiro-Reis, S.; Jerónimo, C.; Henrique, R.; de Lourdes Bastos, M.; de Pinho, P.G.; Carvalho, M. Volatile metabolomic signature of bladder cancer cell lines based on gas chromatography-mass spectrometry. Metabolomics 2018, 14, 62. [Google Scholar] [CrossRef]
- Chen, D.; Shao, X.G.; Hu, B.; Su, Q.D. A Background and noise elimination method for quantitative calibration of near-infrared spectra. Anal. Chim. Acta 2004, 511, 37–45. [Google Scholar] [CrossRef]
- Li, X.L.; Xu, K.L.; Li, H.; Yao, S.; Li, Y.F.; Liang, B. Qualitative analysis of chiral alanine by UV-visible-shortwave near-infrared diffuse reflectance spectroscopy combined with chemometrics. RSC Adv. 2016, 6, 8395–8450. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.W.; Pu, H.; Cheng, J.H. Quality analysis, classification, and authentication of liquid foods by near-infrared spectroscopy: A review of recent research developments. Crit. Rev. Food Sci. Nutr. 2017, 57, 1524–1538. [Google Scholar] [CrossRef]
- Saptoro, A.; Tadé, M.O.; Vuthaluru, H. A Modified Kennard-Stone Algorithm for Optimal Division of Data for Developing Artificial Neural Network Models. Chem. Prod. Proc. Mode. 2012, 7. [Google Scholar] [CrossRef]
- Rajer-Kanduč, K.; Zupan, J.; Majcen, N. Separation of data on the training and test set for modelling: A case study for modelling of five colour properties of a white pigment. Chemom. Intel. Lab. 2003, 65, 221–229. [Google Scholar] [CrossRef]
- Xie, L.J.; Ye, X.Q.; Liu, D.H.; Ying, Y.B. Quantification of glucose, fructose and sucrose in bayberry juice by NIR and PLS. Food Chem. 2009, 114, 1135–1140. [Google Scholar] [CrossRef]
- Ståle, L.; Wold, S. Partial least squares analysis with cross-validation for the two-class problem: A Monte Carlo study. J. Chemometr. 1987, 1, 185–196. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
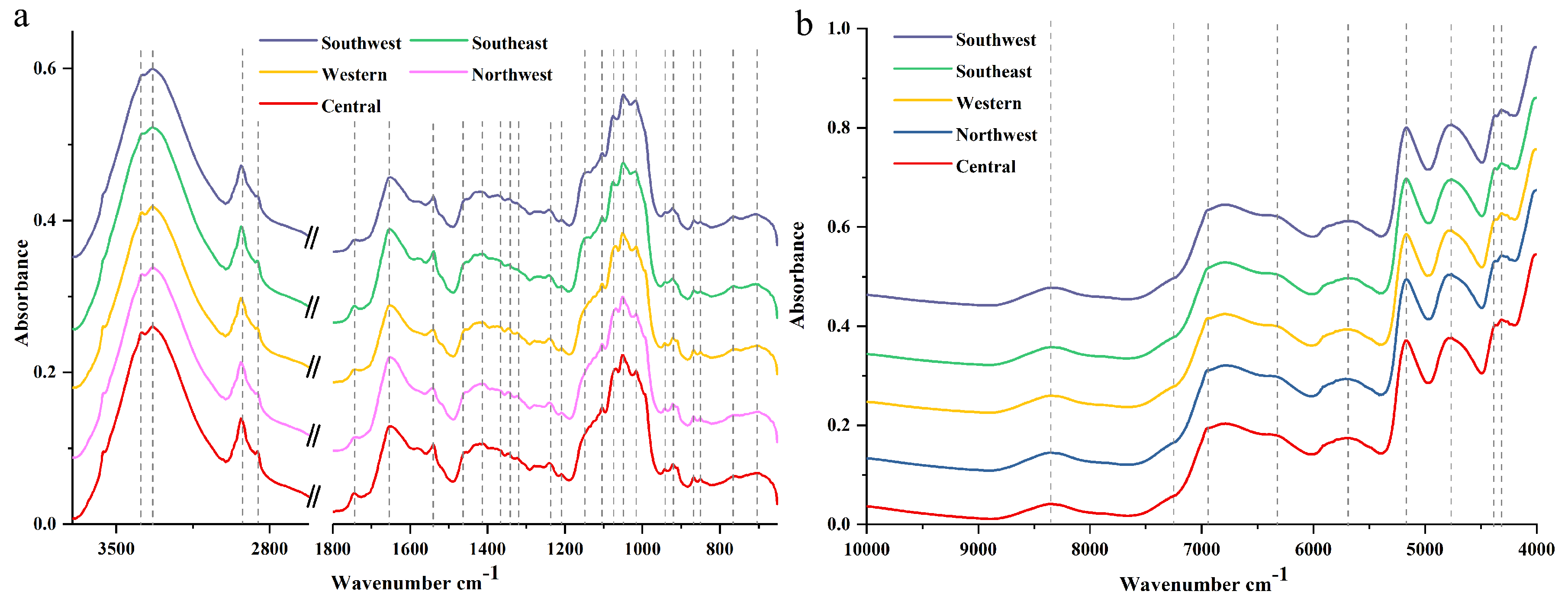


| Spectral Type | Wavenumber (cm−1) | Base Group and Vibration Mode | Contribution |
|---|---|---|---|
| NIR | 8347 | C–H, N–H and O–H stretching vibration mode | CH2, saccharides, and glycosides |
| 7256 | C–H stretching and deformation vibration mode | CH2 | |
| 6950 | C–H, N–H and O–H stretching vibration mode | CH2, saccharides, and glycosides | |
| 6324 | C–H, N–H and O–H stretching vibration mode | CH2, saccharides, and glycosides | |
| 5686 | C–H, N–H and O–H stretching vibration mode | CH2, saccharides, and glycosides | |
| 5169 | C–H, N–H and O–H and hydrogen bond stretching vibration mode | CH2, saccharides, glycosides, and water molecule | |
| FT-MIR | 3382 | O–H asymmetric and hydrogen bond stretching vibration mode | Saccharides, glycosides, and water molecule |
| 3334 | O–H asymmetric and hydrogen bond stretching vibration mode | Saccharides, glycosides, and water molecule | |
| 2930 | C–H asymmetric stretching vibration mode | CH2 and CH3 | |
| 1743 | C═O stretching vibration mode | Free carboxyl groups of pectins or/and fatty acids | |
| 1653 | asymmetric stretching vibrations of carboxyl groups participating in the hydrogen bonds and hydrogen bond scissoring vibration mode | Flavonoids, saccharides, steroid saponin, and water molecules | |
| 1610 | COO symmetric normal vibrations mode | The carboxyl group present in pectin | |
| 1456 | CH3 asymmetric deformation and CH2 scissoring vibration | CH2 and CH3 | |
| 1414 | C–H symmetric bending vibration mode and OH–O in-plane bending mode | CH2 | |
| 1370 | C–H symmetric deformation vibration mode | CH3 | |
| 1242 | C–O stretching vibration mode | Saccharides and oils | |
| 1150 | C–C and C–O stretching and C–OH bending vibration mode | Saccharides and glycosides | |
| 1078 | C–C and C–O stretching and C–OH bending vibration mode | Saccharides and glycosides | |
| 1020 | C–C and C–O stretching and C–OH bending vibration mode | Saccharides and glycosides | |
| 922 | Sugar skeleton vibration mode | Saccharides |
| Model | Calibration Set | Validation Set | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class1 | Class2 | Class3 | Class4 | Class5 | Accuracy | Class1 | Class2 | Class3 | Class4 | Class5 | Accuracy | ||
| FT-MIR | PLS-DA | 0.961 | 1.000 | 0.995 | 0.981 | 0.990 | 97.66% | 1.000 | 0.991 | 0.913 | 1.000 | 0.991 | 97.06% |
| RF | 0.772 | 0.888 | 0.801 | 0.829 | 0.790 | 71.88% | 0.886 | 0.964 | 0.973 | 1.000 | 0.946 | 92.65% | |
| NIR | PLS-DA | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 100% | 0.870 | 0.964 | 0.940 | 0.936 | 0.964 | 89.71% |
| RF | 0.803 | 0.854 | 0.775 | 0.837 | 0.834 | 72.66% | 0.813 | 0.917 | 0.491 | 0.923 | 0.955 | 76.47% | |
| FT-MIR (RFE) | PLS-DA | 0.911 | 0.990 | 0.881 | 0.961 | 0.975 | 91.41% | 0.794 | 1.000 | 0.694 | 0.955 | 0.923 | 82.35% |
| RF | 0.947 | 0.951 | 0.853 | 0.876 | 0.942 | 86.72% | 0.845 | 0.917 | 0.964 | 0.964 | 0.936 | 88.24% | |
| FT-MIR (Bo) | PLS-DA | 0.951 | 0.961 | 0.995 | 0.961 | 0.985 | 95.31% | 0.886 | 0.991 | 0.905 | 0.964 | 0.962 | 91.18% |
| RF | 0.890 | 0.942 | 0.829 | 0.881 | 0.922 | 83.59% | 0.886 | 0.964 | 0.973 | 1.000 | 0.946 | 92.65% | |
| FT-MIR (PCs) | PLS-DA | 0.906 | 0.911 | 0.868 | 0.927 | 0.863 | 83.59% | 0.926 | 0.991 | 0.843 | 0.926 | 0.972 | 89.71% |
| RF | 0.780 | 0.922 | 0.730 | 0.764 | 0.772 | 68.75% | 0.964 | 1.000 | 0.991 | 0.917 | 0.991 | 95.59% | |
| NIR (RFE) | PLS-DA | 0.807 | 0.922 | 0.926 | 0.902 | 0.966 | 85.16% | 0.779 | 0.845 | 0.675 | 0.891 | 0.953 | 75% |
| RF | 0.733 | 0.888 | 0.791 | 0.888 | 0.942 | 77.34% | 0.813 | 0.964 | 0.567 | 0.889 | 0.955 | 77.94% | |
| NIR (Bo) | PLS-DA | 0.807 | 0.922 | 0.858 | 0.906 | 0.947 | 82.81% | 0.779 | 0.837 | 0.551 | 0.962 | 0.962 | 75% |
| RF | 0.729 | 0.878 | 0.764 | 0.893 | 0.922 | 75.78% | 0.772 | 0.878 | 0.486 | 0.870 | 0.955 | 72.06% | |
| NIR (PCs) | PLS-DA | 0.860 | 0.937 | 0.974 | 0.915 | 0.990 | 89.84% | 0.927 | 0.926 | 0.991 | 0.878 | 0.955 | 90% |
| RF | 0.745 | 0.922 | 0.881 | 0.881 | 0.951 | 81.25% | 0.955 | 0.964 | 1.000 | 1.000 | 0.991 | 97.06% | |
| Model | Calibration Set | Validation Set | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class1 | Class2 | Class3 | Class4 | Class5 | Accuracy | Class1 | Class2 | Class3 | Class4 | Class5 | Accuracy | ||
| Low-level | PLS-DA | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 100% | 0.926 | 1.000 | 0.949 | 1.000 | 0.981 | 95.59% |
| RF | 0.872 | 0.885 | 0.858 | 0.897 | 0.932 | 82.81% | 0.886 | 1.000 | 0.905 | 0.972 | 0.991 | 92.65% | |
| Low-level (VIP) | PLS-DA | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 100% | 0.926 | 1.000 | 0.991 | 1.000 | 0.991 | 97.06% |
| RF | 0.927 | 0.927 | 0.849 | 0.922 | 0.947 | 86.72% | 0.926 | 1.000 | 0.991 | 1.000 | 0.991 | 97.06% | |
| Mid-level (RFE) | PLS-DA | 0.946 | 0.712 | 0.764 | 0.864 | 0.878 | 75% | 0.705 | 0.794 | 0.000 | 0.727 | 0.798 | 55.88% |
| RF | 0.966 | 0.888 | 0.868 | 0.894 | 0.881 | 84.38% | 0.764 | 0.861 | 0.491 | 0.900 | 0.854 | 69.12% | |
| Mid-level (Bo) | PLS-DA | 0.961 | 1.000 | 1.000 | 0.995 | 0.995 | 98.44% | 0.926 | 1.000 | 0.991 | 0.991 | 1.000 | 97.06% |
| RF | 0.947 | 0.942 | 0.885 | 0.922 | 0.951 | 89.06% | 0.926 | 1.000 | 0.949 | 0.991 | 0.991 | 95.59% | |
| Mid-level (PCs) | PLS-DA | 0.951 | 0.961 | 0.974 | 0.995 | 0.995 | 96.09% | 1.000 | 1.000 | 0.957 | 0.991 | 1.000 | 98.53% |
| RF | 0.927 | 0.951 | 0.922 | 0.922 | 0.981 | 90.63% | 0.886 | 1.000 | 0.991 | 0.981 | 0.955 | 94.12% | |
| High-level (RFE) | PLS-DA | 0.951 | 0.981 | 0.953 | 1.000 | 0.990 | 96.09% | 0.870 | 1.000 | 0.802 | 0.991 | 0.981 | 89.71% |
| RF | 0.976 | 0.976 | 0.904 | 0.922 | 0.995 | 91.21% | 0.926 | 1.000 | 0.991 | 1.000 | 0.991 | 97.06% | |
| High-level (Bo) | PLS-DA | 0.976 | 0.981 | 0.979 | 1.000 | 0.990 | 97.66% | 0.926 | 0.991 | 0.850 | 1.000 | 0.981 | 92.65% |
| RF | 0.966 | 0.976 | 0.904 | 0.902 | 0.951 | 90.63% | 0.917 | 0.964 | 0.850 | 0.972 | 1.000 | 91.18% | |
| High-level (PCs) | PLS-DA | 0.981 | 1.000 | 0.990 | 0.981 | 1.000 | 98.44% | 0.964 | 1.000 | 1.000 | 0.991 | 1.000 | 98.53% |
| RF | 0.881 | 0.971 | 0.872 | 0.911 | 0.961 | 87.5% | 0.966 | 1.000 | 1.000 | 0.991 | 1.000 | 100% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, Y.-F.; Zuo, Z.-T.; Zhang, Q.-Z.; Wang, Y.-Z. Data Fusion of Fourier Transform Mid-Infrared (MIR) and Near-Infrared (NIR) Spectroscopies to Identify Geographical Origin of Wild Paris polyphylla var. yunnanensis. Molecules 2019, 24, 2559. https://doi.org/10.3390/molecules24142559
Pei Y-F, Zuo Z-T, Zhang Q-Z, Wang Y-Z. Data Fusion of Fourier Transform Mid-Infrared (MIR) and Near-Infrared (NIR) Spectroscopies to Identify Geographical Origin of Wild Paris polyphylla var. yunnanensis. Molecules. 2019; 24(14):2559. https://doi.org/10.3390/molecules24142559
Chicago/Turabian StylePei, Yi-Fei, Zhi-Tian Zuo, Qing-Zhi Zhang, and Yuan-Zhong Wang. 2019. "Data Fusion of Fourier Transform Mid-Infrared (MIR) and Near-Infrared (NIR) Spectroscopies to Identify Geographical Origin of Wild Paris polyphylla var. yunnanensis" Molecules 24, no. 14: 2559. https://doi.org/10.3390/molecules24142559
APA StylePei, Y.-F., Zuo, Z.-T., Zhang, Q.-Z., & Wang, Y.-Z. (2019). Data Fusion of Fourier Transform Mid-Infrared (MIR) and Near-Infrared (NIR) Spectroscopies to Identify Geographical Origin of Wild Paris polyphylla var. yunnanensis. Molecules, 24(14), 2559. https://doi.org/10.3390/molecules24142559