2.1. Extraction Kinetics and Model Analysis
M3G extraction from fresh pre-fermentative Merlot grape pomace was examined using a 2
3 full factorial design under forced convective conditions with solutions differing in temperature, and sugar and ethanol concentrations to simulate fermentative extraction. Although forced convective conditions are usually only present during fermentative maceration during mechanical mixing operations (with the exception of the mixing effect caused by CO
2 evolution and temperature stratification), constant mixing was employed for this experiment so that the liquid phase could be considered a homogenous mixture without an anthocyanin concentration gradient. This allowed for the mass transfer properties of internal and external diffusion to be evaluated independently from one another and to provide an accurate evaluation of the extractive behaviour within the grape solids under the chosen experimental conditions. For all factor combinations, mean values of solid and liquid phase extraction and accumulation of M3G throughout maceration together with the model solution using the method described in
Section 3.2 and
Section 3.3 are presented in
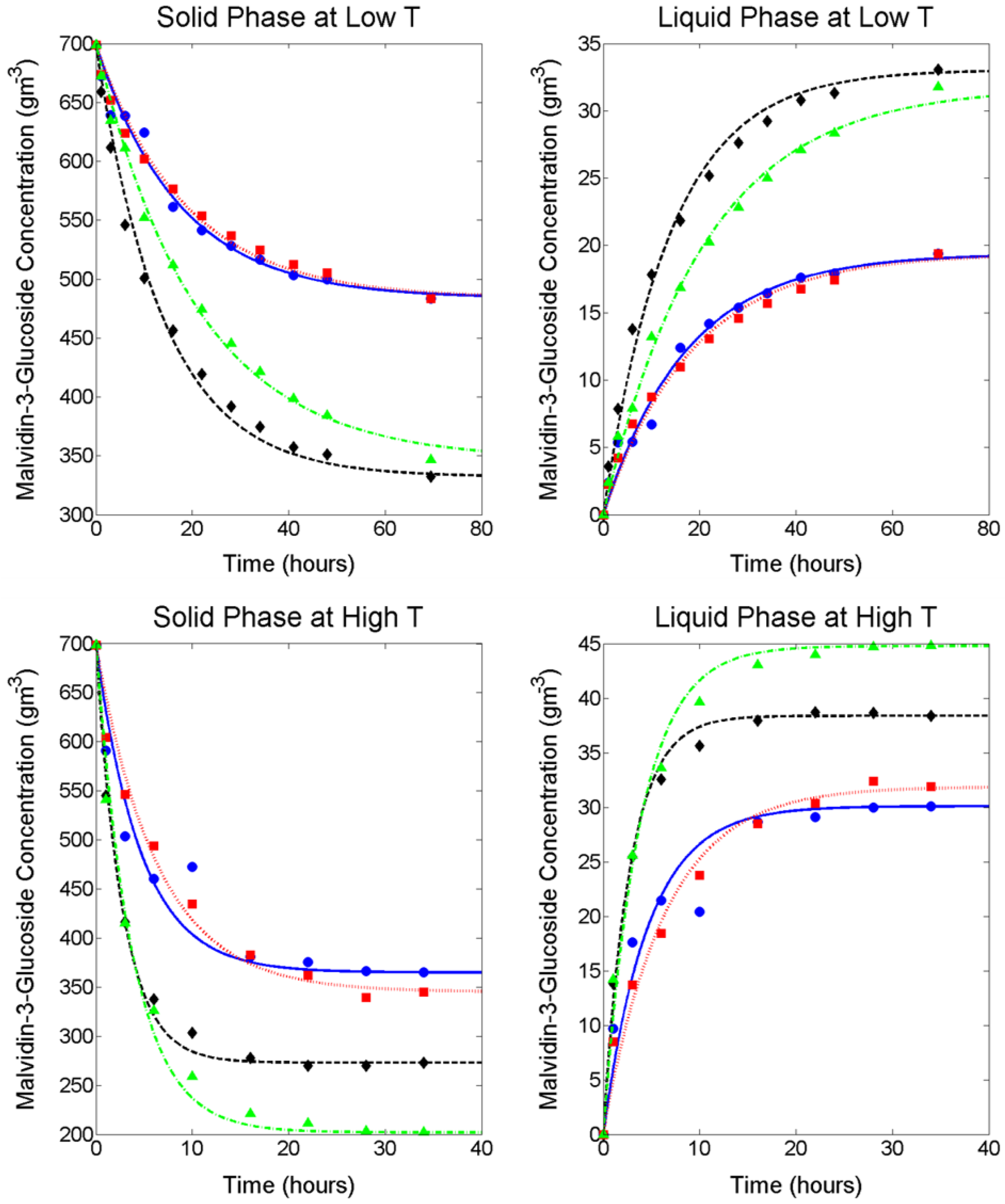
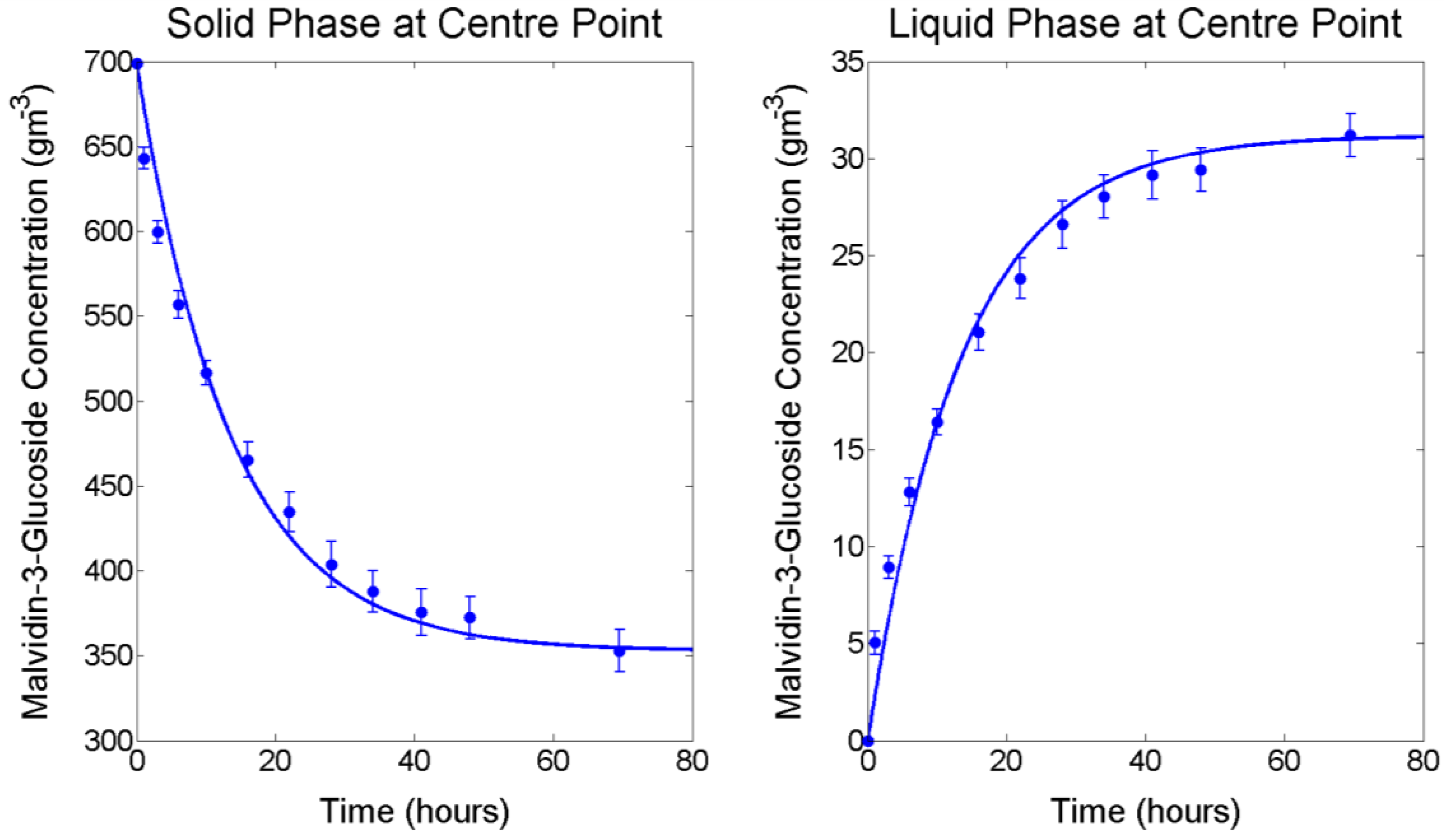
Figure 1 and the mid-point is presented in
Figure 2. For low- and mid-temperature levels (4.4 °C and 12.2 °C respectively), the concentration of M3G in the liquid phase increased throughout the extraction period, whereas at the high temperature level (23.1 °C) the concentration began to decrease after reaching a maximum. Because this work is concerned with modelling the extraction of M3G and the majority of anthocyanin extraction takes place within the first days of liquid contacting, experimental data up to and including the maximum concentration in the liquid phase was used for modelling the extraction process according to Fick’s second law.
A summary of the internal and external diffusion and mass transfer coefficients, as well as several relevant mass transfer properties calculated are presented for each experimental condition in
Table 1, together with
and
RMSE values were >0.92 and small
RMSE values were observed in all cases. Inclusion of a replicated centre point within the full factorial design provided an estimate of standard error (ranging from 0.29 to 0.62 g m
−3) and repeatability (coefficient of variation (CV) of 0.12 for the initial 1 h extraction sample, followed by CV values ranging from 0.036 to 0.067) throughout the extraction process. Regression residuals are consistent with this standard error range, indicating the model developed and presented in
Section 3.2 and
Section 3.3 can be used to effectively predict M3G extraction rates from fresh grape solids at conditions simulating various stages of the fermentation process.
Complete ANOVA tables for
,
and
are provided in
Tables S1–S3 respectively. As evidenced from the factorial analysis (presented in
Table 2) and
Figure 1, the inclusion of ethanol in the liquid phase had a positive influence on both the rate of extraction (
) as well as the final concentration of M3G (
) at all temperature conditions (
< 0.05), although glucose was not found to significantly affect internal diffusion (
) and mass transfer (
). This may be due to ethanol improving the solvent properties of the penetrating liquid allowing easier dissolution of anthocyanins. The main effect of glucose on
is significant (
< 0.01), however the factor effect is approximately 70% smaller than that of either temperature or ethanol. Therefore, at low temperature conditions, it appears that the inclusion of glucose in the liquid phase had only a minor influence on the final concentration of M3G when compared to the pure water extracts and 14% ethanol extracts, respectively. In contrast, at high temperature conditions, the inclusion of both glucose and ethanol resulted in an increase in final concentration of M3G in the liquid phase when compared to the extract containing only 14% ethanol, with factorial analysis confirming temperature, glucose and ethanol effects on
were all significant (
< 0.05). This result indicates a previously unobserved phenomenon whereby at higher temperatures, glucose in the presence of ethanol appeared to aid the extraction rate and maximum extractability of M3G. Although interesting, the scenario of high sugar and high ethanol concentrations is unlikely to be observed in a typical red winemaking operation and was necessary only to fulfil the requirements of the experimental design. In agreement with other studies [
12,
13], increasing the temperature of the system had a large positive impact on both the rate and the final extraction yield of anthocyanins.
This result could be explained by the increased solubility and diffusivity of M3G at higher temperatures as well as an increased rate of swelling and softening of the solid material [
12].
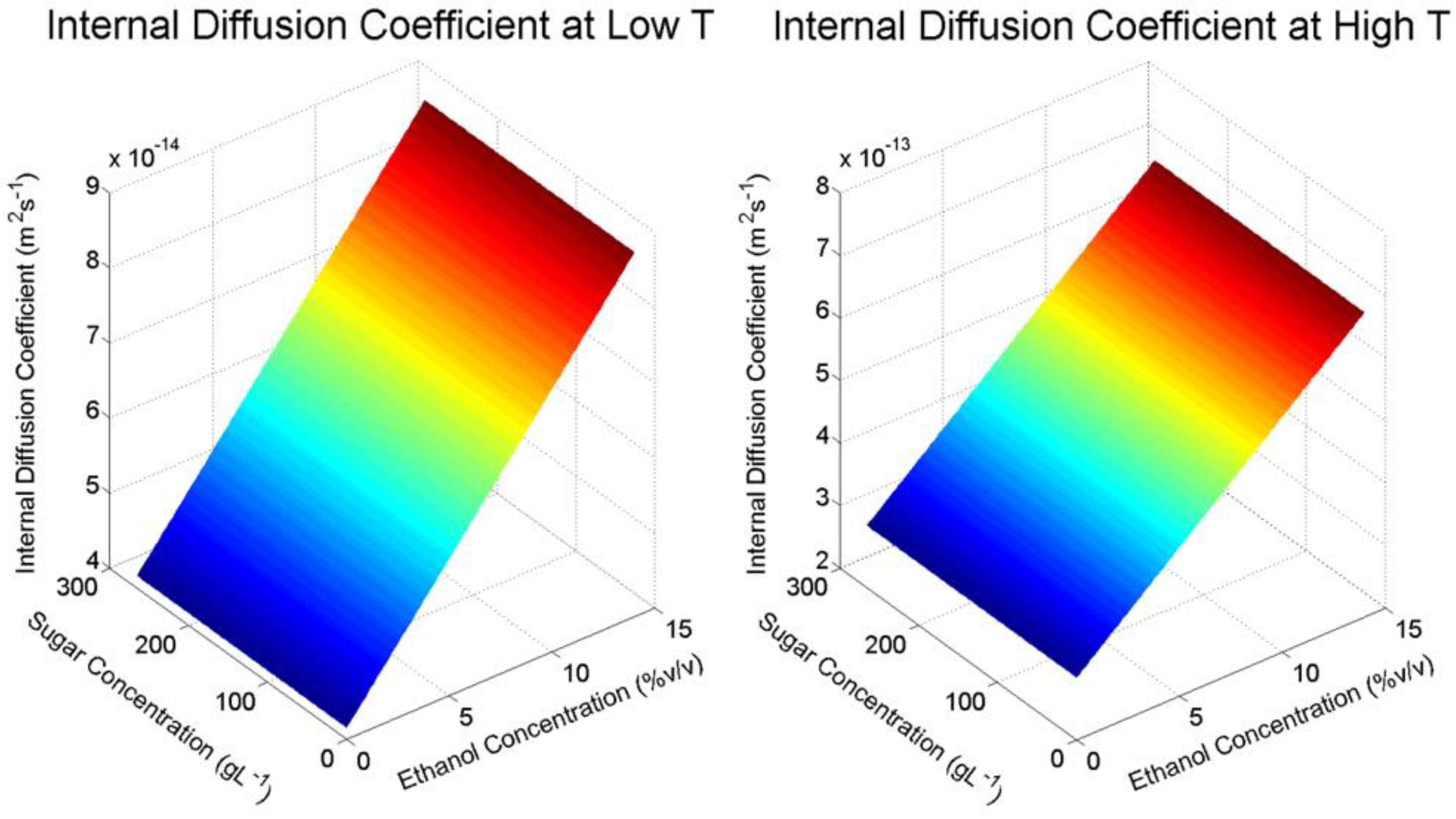
As shown in
Table 1, internal solid diffusion rates obtained from the model solution are approximately one to two orders of magnitude smaller than their respective external diffusion rates in the liquid phase. This is expected, as internal diffusion encompasses liquid penetration, solute dissolution and the subsequent diffusion through the solid matrix, which is a tortuous diffusion path [
10]. Furthermore, the internal mass transfer coefficients are six to seven times smaller in order of magnitude than the respective external mass transfer coefficients, giving a good indication that the extraction of M3G in this system is heavily dependent on diffusion within the solid. In general, diffusion within the solid is typically the rate-controlling step during solid-liquid extraction of phenolic compounds [
13,
14]. The extent of control can be numerically indicated as the mass analogue of the Biot number (full nomenclature and equation notation can be found in
Appendix A,
Appendix B,
Appendix C and
Appendix D):
A Biot number exceeding 10 indicates that internal diffusion within the solid is the controlling step of the extraction process. In the present study, values of > 104 were determined for all factor combinations, confirming that the internal diffusion within the solid was indeed the rate limiting step of the extraction process. Such high Biot numbers are due to the constant mixing and relatively high liquid velocity, whereas in a traditional red wine fermentation scenario this is unlikely to be the case. Mixing operations during fermentation are typically performed intermittently throughout the extraction process, and for the majority of the time, any mixing in the liquid phase would be the result of evolved CO2 displacing the liquid. Because of this, the internal mass transfer rates solved for each set of conditions in this study represent the maximum extraction rates possible for a real red wine fermentation and provide insight into the minimum time required to achieve the maximum potential M3G concentration.
Nonetheless, understanding the Biot number and how it can be manipulated under different conditions could be used in the targeted development of mixing technology to optimise the mass transfer coefficient in the liquid phase. This could be accomplished by controlling the fluid velocity in a way that does not compromise the quality of the wine through increased oxidation nor interfere with downstream processing through the potentially increased destruction of grape solids (primarily skins) resulting from vigorous extraction procedures and mixing operations. Schmidt and Velten [
15] found the average velocity of the liquid phase at the most active stages of wine fermentation to be approximately 0.21–0.60 m s
−1. At the lower end of these velocities and where the effects of mixing due to fermentation are minimal, extraction could be such that internal diffusion is no longer the rate-determining step in the extraction of M3G (and other phenolic compounds). As such, an interesting area for further study would be to examine the effects of free convective conditions at various stages of red wine fermentation in order to calculate external mass transfer coefficients and gain further insight into the importance of mixing operations, their induced liquid velocities, the timing of mixing, and the length of time required to adequately facilitate the extraction process. Such insight would be of additional value due to the compressible nature of grape solids, whereby the upward force of evolving carbon dioxide during fermentative maceration results in a separation of the solids with the bulk of the liquid. This could be considered to be causing an additional liquid phase mass transfer step, as the solute at the solid-liquid interface must first diffuse into the interstitial liquid within the skin cap before making its way into the liquid bulk via liquid phase diffusion through the cap or by forced convection caused by mixing operations.
In agreement with other studies that model the extraction of anthocyanins from various biological materials [
7,
9,
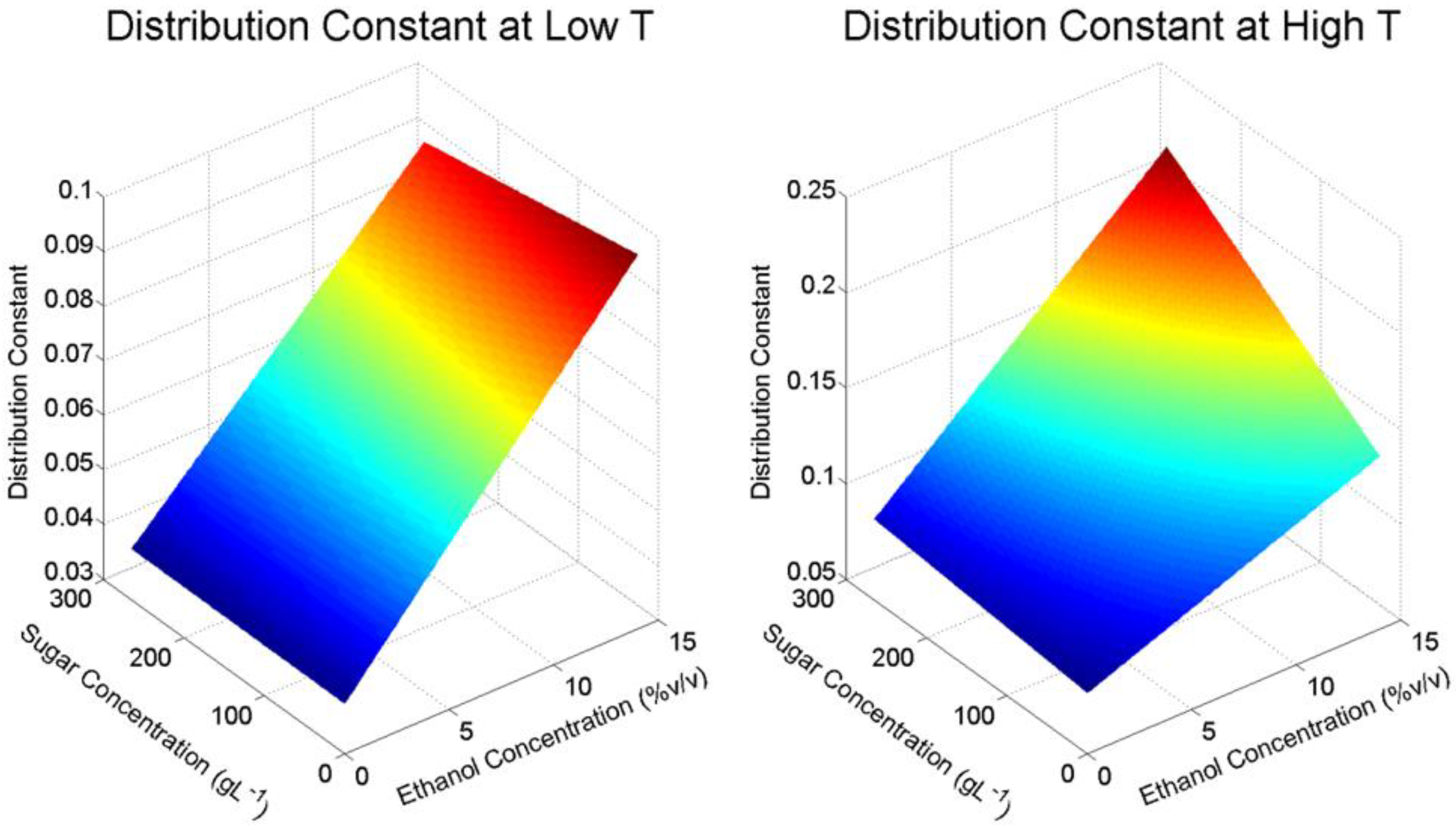
13], the internal diffusion and mass transfer coefficients were found to be higher at higher temperatures, and the inclusion of ethanol in the liquid phase at wine-relevant concentrations was also found to promote the rate of internal diffusion. For each set of solvent conditions, the distribution constant
at high temperature is found to be approximately double that found at the respective low temperature (shown in
Table 1). Because the distribution constant is a linear function of the solid-liquid ratio (as shown in Equation (8)), the values found at each condition could be used to either help maximise the concentration of M3G or optimise it towards a specific desired concentration in red wine ferments that will maximise the perceived quality of the finished product. Notably, the lower distribution constant values found in this study at low ethanol concentrations (
Table 1) provide evidence that maceration techniques prior to fermentation (particularly when conducted at colder temperatures) may have little impact on the final concentration of anthocyanins after the skins are removed from the wine, and that extended maceration upon the completion of fermentation, where a higher concentration of ethanol is in the liquid phase, is more likely to increase the final anthocyanin concentration. This finding also helps to explain experimental results from other studies such as that by Koyama et al. [
16], who found that undertaking a cold soaking operation prior to the fermentation of red wine resulted in a slower initial extraction rate of anthocyanins and proanthocyanidins but has no significant effect on the maximum concentrations of these phenolic compounds at the end of a 10-day maceration period.